正弦定理余弦定理综合练习试题
正弦定理余弦定理综合应用试题单招

正弦定理余弦定理综合应用试题单招应用一《海上小岛的距离测量难题》嘿,咱今儿来讲讲正弦定理和余弦定理在实际生活中那些有趣的应用哈。
就说有这么个事儿,我有个朋友老林,他特喜欢户外运动,尤其是喜欢划船出海啥的,探索那些鲜为人知的小岛。
有一回呀,老林和他的几个小伙伴一块儿出海了。
他们划着那小船,一路乘风破浪,瞧见了两座离岸边有一段距离的小岛。
老林这人好奇心就上来了,他就琢磨着,这两座小岛之间到底相距多远呢?这时候,正弦定理和余弦定理就派上用场了。
他们先在岸边找了个合适的观测点,这个点选得可费了一番工夫啊。
得找个视野开阔,不受遮挡,又能清楚看到两个小岛的地儿。
他们在这个观测点分别测量出了到两个小岛的角度,就跟用自己的眼睛当一个超级精准的量角器似的。
比如说,观测点看到其中一个小岛的角度是30度,看到另一个小岛的角度是45度,然后又量出了观测点到其中一个小岛的距离,假设是100米吧。
这有了角度,有了距离,就正好可以用正弦定理和余弦定理来计算两座小岛之间的距离啦。
正弦定理就好比是一把神奇的钥匙,把那些看似杂乱无章的角度和距离关系给梳理得明明白白的。
通过计算,最后得出了两座小岛之间的具体距离,老林和他的小伙伴们那叫一个兴奋啊,就感觉自己像是破解了一个神秘的宝藏密码似的。
老林后来跟我说,这次出海探索,因为有了正弦定理和余弦定理的帮忙,让这次旅程更有意思了。
不然啊,面对那两座小岛,光好奇它们之间的距离却算不出来,那多扫兴呐。
看来这正弦定理和余弦定理在咱实际生活中还真是能帮大忙,即便在这茫茫大海上,它们也能让人解开那些关于距离的小谜团呢。
应用二《装修房子的角度计算趣事》再来说说另外一件事儿哈。
我有个亲戚打算装修房子,这一装修啊,问题就来了。
他想在客厅装一个特别造型的天花板,就是那种有斜角设计的,看起来更时尚、更有层次感。
装修师傅来了之后,就得开始计算各种角度和长度啦。
这里面啊,正弦定理和余弦定理又闪亮登场了。
比如说,师傅得先测量客厅的长和宽,这一量,嘿,客厅长是5米,宽是4米。
专题3.2 正弦定理、余弦定理(解析版)

专题3.2 正弦定理、余弦定理一、单选题1、(2020届山东实验中学高三上期中)在ABC △中,若 3,120AB BC C ==∠=,则AC =( ) A .1 B .2C .3D .4【答案】A【解析】余弦定理2222?cos AB BC AC BC AC C =+-将各值代入 得2340AC AC +-=解得1AC =或4AC =-(舍去)选A. 2、(2020年全国3卷)7.在△ABC 中,cos C =23,AC =4,BC =3,则cos B =( ) A.19B.13C.12D.23【答案】A 【解析】在ABC 中,2cos 3C =,4AC =,3BC = 根据余弦定理:2222cos AB AC BC AC BC C =+-⋅⋅2224322433AB =+-⨯⨯⨯可得29AB = ,即3AB =由22299161cos 22339AB BC AC B AB BC +-+-===⋅⨯⨯故1cos 9B =. 故选:A.3、(2020届山东省济宁市高三上期末)在ABC ∆中,1,3,AB AC == 1AB AC =-,则ABC ∆的面积为( )A .12B .1CD .2【答案】C【解析】11,3,cos 1cos 3AB AC AB AC AB AC A A ====-∴=-故sin A =,1sin 2S AB AC A =⋅=故选:C4、(2020届河北省衡水中学高三下学期一调)在ABC ∆中,222sin a b c C ++=,则ABC ∆的形状是 ( ) A .锐角三角形 B .直角三角形C .钝角三角形D .等边三角形【答案】D【解析】由余弦定理可知2222cos a b c ab C +-=,222sin a b c C ++=两式相加,得到()22cos 2cos 3a b ab C C ab C π⎛⎫+=+=-⎪⎝⎭所以222cos 1322a b ab C ab ab π+⎛⎫-== ⎪⎝⎭≥,当且仅当a b =时,等号成立, 而[]cos 1,13C π⎛⎫-∈- ⎪⎝⎭所以cos 13C π⎛⎫-= ⎪⎝⎭,因为()0,C π∈,所以2,333C πππ⎛⎫-∈- ⎪⎝⎭所以03C π-=,即3C π=,又a b =,所以ABC ∆是等边三角形,故选D 项.5、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,△ABC 的面积为S ,且2S =(a +b )2﹣c 2,则tan C =( ) A .34B .43C .43-D .34-【答案】C【解析】△ABC 中,∵S △ABC 12ab sinC =⋅,由余弦定理:c 2=a 2+b 2﹣2ab cos C , 且 2S =(a +b )2﹣c 2,∴ab sin C =(a +b )2﹣(a 2+b 2﹣2ab cos C ), 整理得sin C ﹣2cos C =2,∴(sin C ﹣2cos C )2=4. ∴()2222sinC cosC sin C cos C-=+4,化简可得 3tan 2C +4tan C =0.∵C ∈(0,180°),∴tan C 43=-,故选:C .6、(2020届山东师范大学附中高三月考)泉城广场上矗立着的“泉标”,成为泉城济南的标志和象征.为了测量“泉标”高度,某同学在“泉标”的正西方向的点A 处测得“泉标”顶端的仰角为45︒,沿点A 向北偏东30︒前进100 m 到达点B ,在点B 处测得“泉标”顶端的仰角为30︒,则“泉标”的高度为( ) A .50 m B .100 mC .120 mD .150 m【答案】A【解析】如图,CD 为“泉标”高度,设高为h 米,由题意,CD ⊥平面ABD ,100AB =米,60BAD ︒∠=,,4530CAD CBD ︒∠=∠=.在CBD 中,BD 3h =,在CAD 中,AD h =,在ABD △中,3,BD h AD h ==,,100AB =,60BAD ︒∠=,由余弦定理可得223100002100cos 60(50)(100)0h h h h h ︒=+-⨯∴-+=, 解得50h =或100h =- (舍去), 故选:A.7、(2020届浙江省宁波市余姚中学高考模拟)在ABC ∆中,“tan tan 1B C >”是“ABC ∆为钝角三角形”的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既不充分也不必要条件【答案】D【解析】由题意可得,在ABC ∆中,因为tan tan 1A B >, 所以sin sin 1cos cos A BA B>,因为0,0A B ππ<<<<,所以sin sin 0A B >,cos cos 0A B >,结合三角形内角的条件,故A,B 同为锐角,因为sin sin cos cos A B A B >, 所以cos cos sin sin 0A B A B -<,即cos()0A B +<,所以2A B ππ<+<,因此02C <<π,所以ABC ∆是锐角三角形,不是钝角三角形,所以充分性不满足,反之,若ABC ∆是钝角三角形,也推不出“tan tan 1B C >,故必要性不成立, 所以为既不充分也不必要条件,故选D.8、(2020届山东省潍坊市高三上学期统考)已知△ABC 的内角,,A B C 的对边分别为,,a b c ,若2cos cos cos b B a C c A =+,2b =,则△ABC 面积的最大值是A .1BC .2D .4【答案】B【解析】由题意知60B =︒,由余弦定理,262x ππ-=,故22424ac a c ac =+-≥-,有4ac ≤,故1sin 2ABC S ac B ∆=≤ 故选:B9、已知ABC ∆中, sin 2sin cos 0A B C +=,则tan A 的最大值是( )A B C D 【答案】A【解析】∵2020sinA sinBcosC sin B C sinBcosC +=∴++=,(),∴3000sinBcosC cosBsinC cosC cosB +=≠≠,,.化为3tanB tanC =-.可得:B 为锐角,C 为钝角.∴tanA tan B C =-+()=-tan tan1tan tan B C B C +- =22tan 13tan BB + =213tan tan B B+ ≤=,当且仅当tanB=3时取等号.∴tanA 故选A二、多选题10、(2019春•市中区校级月考)在ABC ∆中,根据下列条件解三角形,其中有两解的是( )A .10b =,45A =︒,70C =︒B .45b =,48c =,60B =︒C .14a =,16b =,45A =︒D .7a =,5b =,80A =︒【答案】.BC【解析】:选项B 满足sin60c b c ︒<<,选项C 满足sin45b a b ︒<<,所以B ,C 有两解, 对于选项A ,可求18065B A C =︒--=︒,三角形有一解, 对于选项D ,由sin sin b AB a=,且b a <,可得B 为锐角,只有一解,三角形只有一解. 故选:BC .11、在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,下列结论正确的是( ) A .2222cos a b c bc A =+- B .sin sin a B b A = C .cos cos a b C c B =+ D .cos cos sin a B b A C +=【答案】ABC【解析】:由在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,知: 在A 中,由余弦定理得:2222cos a b c bc A =+-,故A 正确; 在B 中,由正弦定理得:sin sin a bA B=, sin sin a B b A ∴=,故B 正确;在C 中,cos cos a b C c B =+,∴由余弦定理得:22222222a b c a c b a b c ab ac+-+-=⨯+⨯, 整理,得2222a a =,故C 正确;在D 中,由余弦定理得222222cos cos sin 22a c b b c a a B b A a b c C ac bc+-+-+=⨯+⨯=≠,故D 错误. 故选:ABC .12.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若sin sin sin (34A B Ck k ==为非零实数),则下列结论正确的是( )A .当5k =时,ABC ∆是直角三角形B .当3k =时,ABC ∆是锐角三角形 C .当2k =时,ABC ∆是钝角三角形D .当1k =时,ABC ∆是钝角三角形【答案】ABC .【解析】:对于A ,当5k =时,sin sin sin 534A B C==,根据正弦定理不妨设5a m =,3b m =,4c m =,显然ABC ∆是直角三角形; 对于B ,当3k =时,sin sin sin 334A B C==,根据正弦定理不妨设3a m =,3b m =,4c m =, 显然ABC ∆是等腰三角形,2222222991620a b c m m m m +-=+-=>, 说明C ∠为锐角,故ABC ∆是锐角三角形; 对于C ,当2k =时,sin sin sin 234A B C==,根据正弦定理不妨设2a m =,3b m =,4c m =, 可得2222222491630a b c m m m m +-=+-=-<,说明C ∠为钝角,故ABC ∆是钝角三角形; 对于D ,当1k =时,sin sin sin 134A B C==,根据正弦定理不妨设a m =,3b m =,4c m =, 此时a b c +=,不等构成三角形,故命题错误. 故选:ABC .13.下列命题中,正确的是( ) A .在ABC ∆中,A B >,sin sin A B ∴> B .在锐角ABC ∆中,不等式sin cos A B >恒成立C .在ABC ∆中,若cos cos a A b B =,则ABC ∆必是等腰直角三角形D .在ABC ∆中,若060B =,2b ac =,则ABC ∆必是等边三角形 【答案】ABD【解析】:对于A ,由A B >,可得:a b >,利用正弦定理可得:sin sin A B >,正确;对于B ,在锐角ABC ∆中,A ,(0,)2B π∈,2A B π+>,∴022A B ππ>>->,sin sin()cos 2A B B π∴>-=,因此不等式sin cos A B >恒成立,正确对于C ,在ABC ∆中,由cos cos a A b B =,利用正弦定理可得:sin cos sin cos A A B B =, sin2sin2A B ∴=,A ,(0,)B π∈,22A B ∴=或222A B π=-, A B ∴=或2A B π+=,ABC ∴∆是等腰三角形或直角三角形,因此是假命题,C 错误.对于D ,由于060B =,2b ac =,由余弦定理可得:222b ac a c ac ==+-,可得2()0a c -=,解得a c =,可得60A C B ===︒,故正确. 故选:ABD .14、(2020届山东省潍坊市高三上学期统考)在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若1tan A ,1tan B ,1tan C依次成等差数列,则下列结论中不一定成立.....的是( ) A .a ,b ,c 依次成等差数列B C .2a ,2b ,2c 依次成等差数列 D .3a ,3b ,3c 依次成等差数列 【答案】ABD【解析】ABC 中,内角,,A B C 所对的边分别为,,a b c ,若1tan A ,1tan B ,1tan C依次成等差数列, 则:211tan tan tan B A C=+, 利用sin tan cos ααα=,整理得:2cos cos cos sin sin sin B C AB C A=+,利用正弦和余弦定理得:2222222222222a c b a b c b c a abc abc abc+-+-+-⋅=+, 整理得:2222b a c =+,即:222,,a b c 依次成等差数列.此时对等差数列222,,a b c 的每一项取相同的运算得到数列a ,b ,c 3a ,3b ,3c ,这些数列一般都不可能是等差数列,除非a b c ==,但题目没有说ABC 是等边三角形, 故选:ABD.三、填空题15、(2020届江苏省七市第二次调研考试)在ABC ∆中,已知2B A =,AC =,则A 的值是______. 【答案】6π【解析】3AC =,b ∴=,即sin B A ,2B A =,sin 2A A ∴=,则2sin cos A A A =,sin 0A ≠,cos A ∴=,()0,A π∈,则6A π=.故答案为:6π 16、(2020届江苏省南通市海门中学高三上学期10月检测)在ABC ∆中,若60A =︒,2AC =,BC =则sin B 的值为______.【答案】7; 【解析】因为60A =︒,2AC =,BC =由正弦定理可得sin sin a b A B =2sin B =,解得sin B =故答案为:717、(2020届江苏省南通市海门中学高三上学期10月检测)在ABC ∆中,若4C π,且1tan 1sin 2tan AA B=+,则BCAC的值为______.【答案】2; 【解析】因为sin 1tan sin cos cos 111sin sin 2tan cos sin cos AA A BA B A B A B B=+=+=+ cos sin sin cos cos sin A B A B A B +=()sin sin cos sin cos sin A B CA B A B +==1sin 2sin cos cos sin CA A A B∴=,又4Cπsin142sin cos cos sin A A A Bπ∴=sin sin 2A B ∴=由正弦定理得2a b =即BC AC =18、(2019年高考全国Ⅱ卷理数)ABC △的内角,,A B C 的对边分别为,,a b c .若π6,2,3b ac B ===,则ABC △的面积为_________.【答案】【解析】由余弦定理得2222cos b a c ac B =+-,所以2221(2)2262c c c c +-⨯⨯⨯=,即212c =,解得c c ==-,所以2a c ==11sin 22ABC S ac B ==⨯=△ 19、(2019年高考浙江卷)在ABC △中,90ABC ∠=︒,4AB =,3BC =,点D 在线段AC 上,若45BDC ∠=︒,则BD =___________,cos ABD ∠=___________.【答案】5,10【解析】如图,在ABD △中,由正弦定理有:sin sin AB BD ADB BAC =∠∠,而3π4,4AB ADB =∠=,5AC ,34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==,所以5BD =ππcos cos()cos cos sin sin 44ABD BDC BAC BAC BAC ∠=∠-∠=∠+∠=.20、(2020届江苏省南通市如皋市高三下学期二模)在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,若CD 是边AB 上的中线,且CD CA =,则cos cos b Aa B+的最小值为__________.【解析】过点C 作CH AB ⊥,设222BD HD HA t ===,由三角函数定义得cos 2=33cos 333tb A b b a b t a B a a b a b a++=+≥= 当且仅当3a b 时取等号.所以cos cos b A a B +的最小值为321、(2020年全国1卷)如图,在三棱锥P –ABC 的平面展开图中,AC =1,AB AD ==AB ⊥AC ,AB⊥AD ,∠CAE =30°,则cos ∠FCB =______________.【答案】14-【解析】AB AC ⊥,AB =1AC =,由勾股定理得2BC ==,同理得BD =BF BD ∴==在ACE △中,1AC =,AE AD ==,30CAE ∠=,由余弦定理得2222cos3013211CE AC AE AC AE =+-⋅=+-⨯=, 1CF CE ∴==,在BCF 中,2BC =,BF =1CF =, 由余弦定理得2221461cos 22124CF BC BF FCB CF BC +-+-∠===-⋅⨯⨯. 故答案为:14-.四、解答题22、(2020届山东省临沂市高三上期末)在①3cos 5A =,cos C =②sin sin sin c C A b B =+,60B =,③2c =,1cos 8A =三个条件中任选一个补充在下面问题中,并加以解答.:已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若3a =,______,求ABC 的面积S . 【解析】选①∵3cos 5A =,cos C =,∴4sin 5A =,sin C =, ∴()sin sin sin cos cos sin B A C A C A C =+=+4355=+=,由正弦定理得3sin 254sin 5a B b A ===,∴1199sin 32240S ab C ==⨯=.选②∵sin sin sin c C A b B =+,∴由正弦定理得22c a b =+.∵3a =,∴223b c =-.又∵60B =, ∴222192332b c c c =+-⨯⨯⨯=-,∴4c =,∴1sin 2S ac B == 选③∵ 2c =,1cos 8A =, ∴ 由余弦定理得222123822b b +-=⨯,即2502b b --=,解得52b =或2b =-(舍去).sin A ∴==∴ABC 的面积115sin 2222816S bc A ==⨯⨯⨯=.故答案为:选①为9940;选②为16. 23、(2020届江苏省南通市如皋市高三下学期二模)在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,已知πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭. (1)求角B 的大小;(2)若2a =,3c =,求()cos A B -的值.【解析】(1)因为πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭,根据正弦定理sin sin a b A B=, 得πsin sin sin cos 6B A A B ⎛⎫=- ⎪⎝⎭, 因为()0,πA ∈,所以sin 0A >, 所以πsin cos 6B B ⎛⎫=- ⎪⎝⎭,即ππsin cos cos sin sin 66B B B =+,整理得sin B B =,所以tan B =又()0,πB ∈,故π3B =. (2)在ABC 中,2a =,3c =,π3B =, 由余弦定理得2222cos b a c ac B =+-⋅,得222π23232cos 3b =+-⨯⨯⨯,故b =由正弦定理sin sin a b A B =得2πsin sin 3A =,解得sin 7A =. 因为a b <,故AB <,π0,3A ⎛⎫∈ ⎪⎝⎭,所以cos A ===.所以()ππcos cos cos sin sin cos sin 33A B A B A B -=+=+=. 24、(2020届山东省枣庄市高三上学期统考)ABC ∆的内角A ,B ,C 的对边分别为,,a b c ,已知()2cos cos 0a c B b A ++=.(I )求B ;(II )若3,b ABC =∆的周长为3ABC +∆的面积.【答案】(Ⅰ)23B π= (Ⅰ) 4ABC S =△ 【解析】(Ⅰ)()2cos cos 0a c B b A ++=,()sin 2sin cos sin cos 0A C B B A ∴++=,()sin cos sin cos 2sin cos 0A B B A C B ++=,()sin 2cos sin 0A B B C ++=,()sin sin A B C +=.1cos 2B ∴=-, 20,3B B ππ<<∴=. (Ⅰ)由余弦定理得221922a c ac ⎛⎫=+-⨯-⎪⎝⎭, ()2229,9a c ac a c ac ++=∴+-=,33,a b c b a c ++=+=∴+=3ac ∴=,11sin 322ABC S ac B ∴==⨯=. 25、(2020届山东省潍坊市高三上期中)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c .已知10a b +=,5c =,sin 2sin 0B B +=.(1)求a ,b 的值:(2)求sin C 的值.【解析】(1)由sin 2sin 0B B +=,得2sin cos sin 0B B B +=,因为在ABC ∆中,sin 0B ≠,得1cos 2B =-, 由余弦定理2222cos b a c ac B =+-,得22215252b a a ⎛⎫=+-⨯⨯⨯- ⎪⎝⎭, 因为10b a =-,所以2221(10)5252a a a ⎛⎫-=+-⨯⨯⨯-⎪⎝⎭, 解得3a =,所以7b =.(2)由1cos 2B =-,得sin B =由正弦定理得5sin sin 7214c C B b ==⨯=26、(2020年江苏卷).在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ===︒.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值. 【解析】(1)由余弦定理得2222cos 922352b ac ac B =+-=+-⨯=,所以b =由正弦定理得sin sin sin sin c b c B C C B b =⇒==. (2)由于4cos 5ADC ∠=-,,2ADC ππ⎛⎫∠∈ ⎪⎝⎭,所以3sin 5ADC ∠==. 由于,2ADC ππ⎛⎫∠∈ ⎪⎝⎭,所以0,2C π⎛⎫∈ ⎪⎝⎭,所以cos C == 所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅34555525⎛⎫=⨯+-⨯= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭,所以cos DAC ∠== 所以sin 2tan cos 11DAC DAC DAC ∠∠==∠. 27、(2020年全国2卷).ABC 中,sin 2A -sin 2B -sin 2C =sin B sin C.(1)求A ;(2)若BC =3,求ABC 周长的最大值.【解析】(1)由正弦定理可得:222BC AC AB AC AB --=⋅, .2221cos 22AC AB BC A AC AB +-∴==-⋅, ()0,A π∈,23A π∴= (2)由余弦定理得:222222cos 9BC AC AB AC AB A AC AB AC AB =+-⋅=++⋅=, 即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭(当且仅当AC AB =时取等号), ()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭,解得:AC AB +≤(当且仅当AC AB =时取等号), ABC ∴周长3L AC AB BC =++≤+ABC ∴周长的最大值为3+ 28、(2020届江苏南通市高三基地学校第一次大联考数学试题)在ABC 中,角,,A B C 所对边分别为,,a b c .已知sin sin 2B C a B b +=. (1)求角A 的值; (2)若1cos()64B π+=,求cos C 的值. 【解析】(1)在ABC 中,因为sin sin 2B C a B b +=, 所以sin sin cos 22A A a B b b π-==. 结合正弦定理得,sin sin sin cos 2A A B B =,即2sin cos sin sin cos 222A A A B B =. 因为,(0,)A B π∈,所以sin 0,cos 02A B >>, 所以1sin 22A =. 可得,263A A ππ==; (2)在ABC 中,因为3A π=,则250,,,3666B B ππππ⎛⎫⎛⎫∈+∈ ⎪ ⎪⎝⎭⎝⎭,sin()06B π+>. 又因为1cos()64B π+=,则sin()64B π+==. .所以cos cos()C A B π=--cos()A B =-+cos()3B π=-+ cos ()66B ππ⎡⎤=-++⎢⎥⎣⎦ cos()cos sin()sin 6666B B ππππ=-+++1124248-=-⨯+⨯= 29、(2020年天津卷).在ABC 中,角,,A B C 所对的边分别为,,a b c.已知5,a b c ===. (Ⅰ)求角C 的大小;(Ⅰ)求sin A 的值;(Ⅰ)求sin 24A π⎛⎫+ ⎪⎝⎭的值. 【解析】(Ⅰ)在ABC中,由5,a b c ===222cos 22a b c C ab +-===, 又因为(0,)C π∈,所以4C π;(Ⅰ)在ABC 中,由4C π,a c ==可得sin sin a C A c === (Ⅰ)由a c <知角A为锐角,由sin A =,可得cos A == 进而2125sin 22sin cos ,cos22cos 11313A A A A A ===-=,所以125sin(2)sin 2cos cos2sin 444132132A A A πππ+=+=⨯+⨯=26.。
正弦定理和余弦定理专题试题及答案

正弦定理和余弦定理专题试题及答案1.在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形2.在△ABC 中,已知b =40,c =20,C =60°,则此三角形的解的情况是( ) A .有一解 B .有两解 C .无解 D .有解但解的个数不确定3.已知△ABC 中,内角A ,B ,C 的对边分别为ɑ,b ,c ,若ɑ2=b 2+c 2-bc ,bc =4,则△ABC 的面积为( ) A.12 B .1 C.3 D .24.在△ABC 中,内角A ,B ,C 的对边分别为ɑ,b ,c ,且bsin A =3ɑcos B .则B =( ) A.π6 B.π4 C.π3 D.π25.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.若3a =2b ,则2sin 2B -sin 2Asin 2A的值为( )A .-19B .13C .1D .726.在△ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,且满足c sin A =3a cos C ,则sin A +sin B 的最大值是( )A .1B . 2C . 3D .37.在△ABC 中,若A=,B=,BC=3,则AC=( )A. B. C.2D.48.在△ABC 中,若a 2+b 2<c 2,则△ABC 的形状是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定9.已知△ABC 的内角A,B,C 的对边分别为a,b,c,且=,则B= ( ) A.B. C. D.10.在△ABC 中,角A,B,C 所对的边长分别为a,b,c.若C=120°,c=a,则 ( )A.a>bB.a<bC.a=bD.a 与b 的大小关系不能确定11.在△ABC 中,已知AB →·AC →=tan A ,当A =π6时,△ABC =的面积为________.12.若△ABC 的内角满足sin A +2sin B =2sin C ,则cos C 的最小值是________.13.△ABC 中,点D 是BC 上的点,AD 平分∠BAC,BD=2DC. (1)求.(2)若∠BAC=60°,求B.14.在△ABC 中,角A,B,C 的对边分别为a,b,c,且bcosC=3acosB-ccosB. (1)求cosB 的值. (2)若·=2,且b=2,求a 和c 的值.15.如图,在△ABC 中,点P 在BC 边上,∠PAC =60°,PC =2,AP +AC =4.(1)求∠ACP ;(2)若△APB 的面积是332,求sin ∠BAP .16.在△ABC 中,角A ,B ,C 的对边分别是ɑ,b ,c ,且b 2=ɑc =ɑ2-c 2+bc. (1)求bsin Bc的值; (2)试判断△ABC 的形状,并说明理由.正弦定理和余弦定理专题试题及答案1.在△ABC 中,若sin 2A +sin 2B <sin 2C ,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形答案:C2.在△ABC 中,已知b =40,c =20,C =60°,则此三角形的解的情况是( ) A .有一解 B .有两解 C .无解 D .有解但解的个数不确定 解析:由正弦定理得b sin B =csin C,∴sin B =bsin Cc=40×3220=3>1.∴角B 不存在,即满足条件的三角形不存在. 答案:C3.已知△ABC 中,内角A ,B ,C 的对边分别为ɑ,b ,c ,若ɑ2=b 2+c 2-bc ,bc =4,则△ABC 的面积为( ) A.12B .1 C. 3 D .2 解析:∵ɑ2=b 2+c 2-bc ,∴cos A =12,∴A =π3,又bc =4,∴△ABC 的面积为12bcsin A =3,故选C.答案:C4.在△ABC 中,内角A ,B ,C 的对边分别为ɑ,b ,c ,且bsin A =3ɑcos B .则B =( ) A.π6 B.π4 C.π3 D.π2解析:根据题意结合正弦定理, 得sin Bsin A =3sin Acos B. 因为sin A ≠0,所以sin B =3cos B , 即sin B cos B =tan B =3,所以B =π3. 答案:C5.在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.若3a =2b ,则2sin 2B -sin 2A sin 2A的值为( )A .-19B .13C .1D .72解析:由正弦定理可得2sin 2B -sin 2A sin 2A =2⎝ ⎛⎭⎪⎫sinB sin A 2-1=2⎝ ⎛⎭⎪⎫b a 2-1,因为3a =2b ,所以b a =32,所以2sin 2B -sin 2A sin 2A =2×⎝ ⎛⎭⎪⎫322-1=72。
正余弦定理练习题(含答案)[1]
![正余弦定理练习题(含答案)[1]](https://img.taocdn.com/s3/m/51c33bba1eb91a37f0115c52.png)
在“ABC 中,0, b, c 分別是角4 8. C 所对的边,若^ = 105% 8=45% 则c=(A. 1C. 2在茲 ABC 中,已知 a=3y[2. cosC=j, Sg=4品 则 b= ____________. 在茲ABC 中,b=4{i, C=30。
,c=2,则此三角形有 ________组解. 如图所示,货轮在海上以40 km/h 的速度沿着方位角(指从正北方向顺时针转到目标方 向线的水平转角)为140。
的方向航行,为了确定船位,船在B 点观测灯塔A 的方位角为110% 航行半小时后船到达C 点,观测灯塔人的方位角是65。
・则货轮到达C 点时,与灯塔A 的距离是多少18. ii :A ABC 中,0、b 、c 分別为角 A 、8. C 的对边•若 a=2晶 sin|cos|=^r sin Bsin C=cos^.求 A 、 6 及 b 、c.19. (2009年高考四川卷)^A ABC 中,久B 为锐角•角久B 、C 所对应的边分別为6 b 、c,且cos 2A= sin ⑴求 A+B 的值:(2)若 o —/?=匹一1,求 a, b, c 的值.20. 'ABC 中,0b=65/5,sin fi=sinC △ ABC 的面枳为 15 羽,求边 b 的长.在AAfiC 中,Z&=45°, ZB=60°, a=2.2. 3. 已知 0=8, S=60°, C=75°, B ・ 45/3 C. 角A 、B 、C 的对边分別为a 、 B ・ 135" 正弦定理练习题则b 等于()D. 2& 则b 等于()4& b. G &=60。
,0=4羽,b=4品则角 5为( D.以上答案都不对 4. 在△ ABC 中, A. 4迈在△ ABC 中, A. 45°或 135° B ・ 135" C・ 45° 在 A ABC 中,o: b : c=i: 5 : 6.贝 IJsiM: sinB : sinC 等于( ) A. 1:5:6 B. 6:5:1 C. 6:1:5解析J 选 A.由正弦定理知 siM : 5in8 : sinC=o : b : c=l : 5 : 6.D-不确泄5. 6. 8.9.10. 在^ ABC 中,若签?=夕,则^ ABC 是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰三角形或直角三角形 己知A ABC 中,AB=E AC=1, Z 8 = 30% 则A ABC 的面积为()或或誓'ABC 的内角A 、B 、C 的对边分别为a 、b. c •若c=迈,b=E S=120\则o 等于( B ・ 2 c"在4 ABC 中,角久B 、C 所对的边分別为6 b 、G 若0=1, c=Ql C 岭 则A=_ 已知 a=響,fa=4,4 = 30% 则 sin8= _____________________________________ .li:A ABC 中,11. 12. 在茲ABC 中, 在4 ABC 中, 已知ZA=30°, Z S = 120\ 6=12,贝I] o+c=o=2facosC,贝ijA^fiC 的形状为 ________ • 13.14- 在△AB C 中,人= 60°, O = 6A /3, 6=12, S“8c=18 羽,则;;活三篇行花a — 2b + cc —已知"阮中,ZA :ZB :Z C=l: 2:3. a-1,则 sM_2sinB+sinC15. 16. 17.2.3. 4. 5. 6- 1. 8. 9. 10. 11. 12. 13. 14- IS 16. 17. 余弦定理练习题在“ABC 中,如果BC=6, AB=4, cosB=p 那么AC 等于( A. 6 B. 2& C ・ 3yf6 在A ABC 中,0=2, C=30\ 则 c 等于( D. 2 在AAfiC 中,Q2=b2+s+羽be.则ZA 等于( ) A. 60° B ・ 45° C ・ 120° 在4 ABC 中,厶A 、Z 8、ZC 的对边分别为6 b 、c, T 、5n 2n riv tfV 以6 以3 在A ABC 中,0、b 、c 分别是A 、B 、C 的对边,则a cosB+bcosA 等于( A. o B. b C ・c D.以上均不对D. 150" 若(a^+c^—b2)tanB=dlac,则Z B 的值为( 如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为() A-锐角三角形 B.直角三角形 C.钝角三角形 D ・由增加的长度决;4^ 已知锐角三角形A3C 中,I 為1=4, I 為1=1., A- 2 B. -2 C. 4在4 ABC 中,b=y[3, c=3, 0=30。
正弦定理余弦定理练习题及答案

正弦定理、余弦定理练习题年级__________ 班级_________ 学号_________ 姓名__________ 分数____ 一、选择题(共20题,题分合计100分)已知在△ABC中,sin A:sin B:sin C=3:2:4,那么cos C的值为 1.A.-B.C.-D.λλ则满足此==中,在△ABCa,b,°=45A,2.条件的三角形的个数是D.无数个A.0B. 1 C.2,则三角形为a cos Bb在△ABC中,cos A=3. D.C.锐角三角形等边三角形等腰三角形. A.直角三角形 B22,则最大角为x2x+1(>1)x已知三角形的三边长分别为+1,+xx和-14.° C.60 D.75°120B A.150° .°在△ABC中,=1,5.,=2.+((·)+)则=5+2边等于||A.5-2.B.C.D.,b°BABC在△中,已知=30,=50=150c,6.那么这个三角形是等腰三角形或直角等边三角形 B. 直角三角形 C.D. 等腰三角形A.三角形2222C+c,则此三角形为sin B=2bc cos B cos C在△ABC中,若b sin7.等腰直角三角形 C.D.等边三角形A. 直角三角形B.等腰三角形正弦定理适应的范围是8. D.任意△钝角△ A.Rt△B.锐角△ C.==45°,则c°a已知△ABC中,=10,B=60,C9.B. 10 A.10+ C. )-1(.(+1 )D.10A sin<a<b,则此三角形有ABC在△中,b10.无解 C. 两解 D.不确定.A.一解B5和3,它们夹角的余弦是方程5x-7x-6=0的根,则三角形的另一11.边2三角形的两边分别为长为C.16D.4 A.52B. 2222ABC=b等于+c中,a+bc,则A在△12.° C.120 D.3045 A.60°B.°在△ABC中,,则△ABC是13. D.任意三角形.直角三角形 C.钝角三角形B A.锐角三角形ABC=45,=30,aABC在△中,=2A°C°,则△的面积等于S14.ABC△.A.B.2 +1C.(D.+1)CA sin Ba已知三角形ABC的三边、b、c成等比数列,它们的对角分别是A、、C,则sin15.等于2222B C.1+cos B B.1-cos B A.cosD.1+sin B是在△ABC中,sin A>sin BA>B的16.既不充分也不必要不充分条件 C.D.充要条件 A.充分不必要条件 B.必要条件=在△ABC中,b Cos Aa cos B,则三角形为17.等边三角形等腰三角形 D. A.直角三角形 B. 锐角三角形 C.222ABC为△ABC中,sin A=sin B+sin,则△C18.等腰三角形D. 等边三角形C. 等腰直角三角形B. 直角三角形A.△ABC中,A=60°,b=1,这个三角形的面积为19.,则△ABC外接圆的直径为A.B.C.D.为k则,中,ABC在△20.为△(R B.R C.4D.R A.2R)ABC外接圆半径)分共18题,题分合计75二、填空题(. ,则此三角形的最小边长为b=45°,AABC在△中,=60C°,=2 1.. = 中,ABC在△2.在△ABC中,a∶b∶c=(+1)∶3.∶2,则△ABC的最小角的度数为.在△ABC中,已知sin A∶sin B∶sin C=6∶5∶4,则sec A= . 4.△ABC中,,则三角形为 5._________.在△ABC中,角A、B均为锐角且cos A>sin B,则△ABC是___________. 6.在△ABC中,若此三角形有一解,则a、b、A满足的条件为____________________.7.已知在△ABC中,a=10,b=5,A=45°,则8.B= .已知△ABC中,a=181,b=209,A=121°14′,此三角形解.9.在△ABC中,a=1,b=1,C=120°则c= .10.222222,则△ABC为b+c 中,若在△ABCab>a+c,则△ABC为;若;若=11.222222222,则△ABC为a <+b.cbba<+c且<a+且c在△ABC中,sin A=2cos B sin C,则三角形为_____________.12.在△ABC中,BC=3,AB=2,且,13.. A=则°BC,B==3,=30,在△ABC中,14.. A=.= °,B=45°,则a= ,b Aa在△ABC中,+b=12,=6015..的范围为2,3,若x为三边组成一个锐角三角形,则x16.. cb在△ABC中,化简cos C+cos B= 17.钝角三角形的边长是三个连续自然数,则三边长为.18.)244分共三、解答题(24题,题分合计.B 和b、a°,求=30C°,=45A,=10c中,ABC 已知在△1.已知△ABC的三边长a=3,b=4,c=,求三2.角形的最大内角.已知在△ABC中,∠A=45°,a=2,c=,3.解此三角形.在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求4.AB的长..,求此三角形三边之比B=2C+A,C=2A最小,且C最大,A中,ABC在△5.ABCRABC的为△中,.证明:在△(其中6.外接圆的半径)在△ABC中,最大角A为最小角C的2倍,且三边a、b、c为三个连续整数,求a、b、7.c的值.如下图所示,半圆O的直径MN=2,OA=2,B为半圆上任意一点,以AB为一边作正三角8.形ABC,问B在什么位置时,四边形OACB面积最大?最大面积是多少?在△ABC中,若sin A∶sin B∶sin C=m∶n∶l,且a+b+c=S,求a.9.根据所给条件,判断△ABC 的形状10.Bcos b=A cos a)1(.(2)2-3x-2=0的一个根,求△是方程2xABC周长的最小值.,而ABC△中,a+b=10cos C11.、、、、C的对边,设a+c=2b,A是分,ABC在△中abc别角BA-12..的值B sin求,=C.已知△ABC中,a=1,b=,A=30°,求B、C13..c和,、=2中,在△ABCca试求=2,B=3,tan A tan14..及此三角形的面积b已知S=10,一个角为60°,这个角的15.ABC△∶.2,求三角形内切圆的半径5两边之比为.的形状ABC,试判断△中,ABC已知△16.已知△ABC的面积为1,tan B=,求△ABC17.的各边长.求值:18.ABC,解此三角形.的面积已知△19.在△ABC中,20.=2,c=ba=,、、,求+1ABCS及.△.22+2=0是关于)xx已知(a的二次方+bc21.程,其中a、b、c是△ABC的三边,(1)若∠A为钝角,试判断方程根的情况.(2)若方程有两相等实根,求∠A的度数.2222.的形状ABC,判断△)B+A)sin(b-a)=(B-A sin()b+a中,(ABC在△22.在△ABC中,a>23.、b以及此,试求a=6A,且有,bC=tan·tan B.三角形的面积、、、、cba所对的边分别为CBA的三内角ABC是整数,钝角△k已知:24.1)若方程组有实数解,求k的值.((k值,若且有关系式)中的)对于(21、、.的度数CBA 试求,.正弦定理、余弦定理答案一、选择题(共20题,合计100分)A A CB 5CD A D B B B C C C B C C A C A20.7817910:116121813141915.123416.二、填空题(共18题,合计75分)2(-1) 21. 45 ° 8 等腰三角形5.4.3.钝角三角形:6.a=b sin A或b<a60°或120°无10.8.7.9钝角三角形直角三角形锐角三角形11.等120 角三腰形°或14.13.12.2 15. 36-12.x<<16.、、 2 a3417.18.)题,合计24(三、解答题共244分=a1.°B=105=b°∠C=1202.°=15B°或∠=75B∠3.b=+1,∠C=60°,∠B=75°或-=15°,∠C1b=,∠=120B° AB的长为4.4∶5∶6此三角形三边之比为:5.a=6,b=5,c=47.θS最大时,当=,8.OACB四边形+2最大值为9.ABC 1)△是等腰三角形或直角三角形(10为等边三角形)△ABC(2 ABC周长的最小值为△BCBc=1=90=120°=60,°;°,=2,=30°;13.212121.. 14.15.等边三角形16.17.18. A=60°,B=45°,C=75°,S=20.△°(2)60 没有实数根(1) 21.等腰三角形或直角三角形22.23.(1)k=1,2,324.(2)C=45°,B=15°。
正弦定理与余弦定理练习题

正弦定理与余弦定理7斥 6.已知心ABC 中,BC =6, AC =8,cosC =— ,^U 心ABC 的形状是( )96A.锐角三角形 B •直角三角形 C.等腰三角形D •钝角三角形7.在|MBC 中,内角代B,C 的对边分别为a,b,c ,且B = 2C ,|2bcosC — 2ccosB = a ,则角A 的大小为(A.JIB.JIC.31D.123462 2 2 ______________________________________________&在△ ABC 中,若sin A + sin B v sin 。
,则厶ABC 的形状是()B. 直角三角形C. 等腰三角形D. 等腰或直角三角形11. 在△ ABC 中,cos 2 =—二,则△ ABC 为()三角形.2A. 正 B .直角 C .等腰直角 D .等腰12. 在△ ABC 中,A=60° , a=4 I:, b=< :•:,则 B 等于() A. B=45° 或 135° B. B=135 C. B=45° D.以上答案都不对13.在也ABC ,内角A, B,C 所对的边长分别为a,b, c. a sin BcosC +cs in Bcos A =丄匕,且a 〉b ,则Z B —(-------- 2A. 30°B.30° 或150°C.60°D . 60° 或 120°2. 已知锐角厶 ABC 的面积为 3品,BC=4, CA=3 则角C 的大小为( )A.75°B .60°C .45°D .30°3.已知右ABC 中,a,b, c 分别是角A, B,C 所对的边,若(2a + c )cosB + bcosC = 0,则角B 的大小为( A.JI62 ■:4. 在 ABC 中, a 、b 、 c 分别是角A 、B 、 — a = 3ac ,则三 B =() A. 300B.60°C.1200D.15005. A. 在厶ABC 中, 105°B, C 的对边分别是 B . 60° C . 15° D . 105° 或角A , a , b ,c .已知 a=5g :l |, c=10, A=30°,贝U B 等于( 15° A. 9. A.锐角三角形在AABC 中, 1 ,那么cosC = .不能确定)B.410 .在 ABC 中,等腰直角三角形a =2bcosC ,则此三角形一定是A. 1 已知△ ABC 中,a=4, b=4j3, A=30$ 贝U B 等于( )C 的对边•若sin A:sin B :sin C =3:2:4 B .直角三角形 C .钝角三角形D (18. 在AABC 中,内角|A , | B , C 所对的边分别是 (1) 求tanC 的值;(2) 若 MBC 的面积为3,求b 的值.19. 在△ ABC 的内角A, B , C 对应的边分别是 a , b , (1) 求 B;(2) 若b=2,A ABC 的周长为2 ;+2,求厶ABC 的面积.ABC A,B,C a, b,c a 二bcosC csinBBb = 2 ABC21•在△ ABC 中,a , b , c 分别是角A , B , C 的对边,已知3 b 2 - c ^^3a 2 2bc (1) 求 si nA ;3 <2 (2)若 a , △ ABC 的面积 S = -------- ,且 b>c ,求 b , c . 2222.已知△ ABC 的内角A , B , C 的对边分别为a , b , c ,且满足sin(2A 十B)=2+2cos( A + B). sin A(I)求b的值;a(n)若 a =1, c = 7,求△ ABC 的面积.23•在 ABC 中,角A,B,C 所对的边分别为a,b,c ,已知a ^2 , c ^5 , cosB = 3.5(1) 求b 的值;评卷人 得分、解答题(题型注释)n A. 6n:B.㊁C.5614. 设△ ABC 的内角A, B, C 所对的边分别为 a, b, c, A.锐角三角形 B. 直角三角形 C. 钝角三角形 若 bcosC+ccosB = as inA ,贝忆 ABC 的形状为( D. 不确定 15 .已知在也ABC 中, A .直角三角形2Acos 2 2cB .等腰三角形或直角三角形—-,则也ABC 的形状是( D .等腰直角三角16.已知AABC 内角 A..15 6B.17.在△ ABC 中,角 A.A, B,C 的对边分别是、15 4C.B 、C 的对边分别为C. 2C.正三角形 1a, b, c ,若 cos B = —,b = 2,sin C = 2sin A ,则△ ABC 的面积..15 2b 、c ,已知 D. 1D.A = 、‘15,b = 1,贝U c =()a ,b ,c .已知JIA=— ,221 2,b —a =— c42(2)求sinC的值.二、填空题24•已知在AABC中,£C=1§|, 10,川工石0。
正弦定理余弦定理综合应用解三角形经典例题(学生)

1, b
2 , cosC
1
.
4
(Ⅰ)求 ABC 的周长;(Ⅱ)求 cos A C 的值 .
【解题思路】本小题主要考查三角函数的基本公式和余弦定理,同时考查基本运算能力
【注】常利用到的三角公式两角和与差的正弦、余弦、正切公式及倍角公式:
sin
sin cos cos sin 令
sin 2 2sin cos
【解题思路】判定三角形形状时,一般考虑两个方向进行变形:
(1)一个方向是边,走代数变形之路,通常是正、余
弦定理结合使用; ( 2)另一个方向是角,走三角变形之路 .通常是运用正弦定理
【解析】
.
【思考】判断三角形形状时一般从角入手,利用三角形内角和定理,实施关于三角形内角的一些变形公式
.
【例 9】 . 在△ ABC中,在
tan 2
2 tan 1 tan2
【例 4】( 2010 重庆文数) 设 ABC 的内角 A、 B、 C 的对边长分别为 a 、 b 、 c , 且 3 b 2 +3 c2 -3 a2 =4 2 b c .
2sin( A )sin( B C )
( Ⅰ ) 求 sinA 的值; ( Ⅱ ) 求
4
【例 6】( 2009 全国卷Ⅰ理)在 ABC 中,内角 A、 B、 C 的对边长分别为 a 、 b 、 c ,已知 a 2 c2 2b ,且 sin A cosC 3cos Asin C , 求 b
【解题思路】对已知条件 (1) a 2 c 2 2b 左侧是二次的右侧是一次的 , 可以考虑余弦定理;而对已知条件 (2) sin AcosC 3cos A sin C , 化角化边都可以。
(边角转化的重要工具 )
余弦定理练习题(含答案)
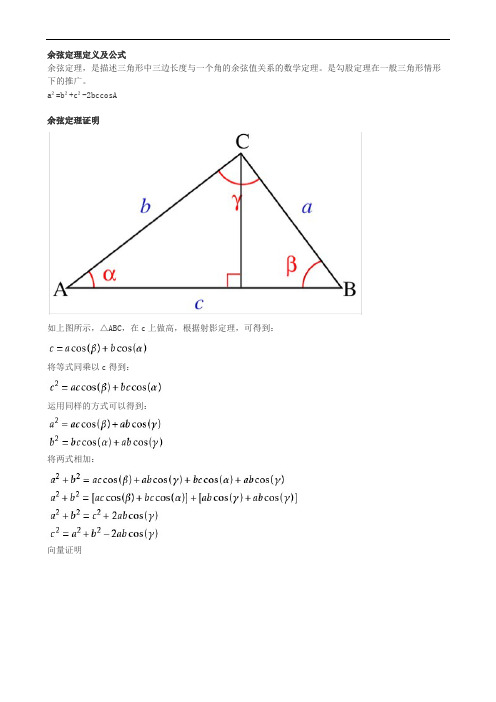
余弦定理定义及公式余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理。
是勾股定理在一般三角形情形下的推广。
a²=b²+c²-2bccosA余弦定理证明如上图所示,△ABC,在c上做高,根据射影定理,可得到:将等式同乘以c得到:运用同样的方式可以得到:将两式相加:向量证明正弦定理和余弦定理正弦定理 a/sinA=b/sinB=c/sinC=2R(1)已知三角形的两角与一边,解三角形(2)已知三角形的两边和其中一边所对的角,解三角形(3)运用a :b :c=sinA :sinB :sinC 解决角之间的转换关系直角三角形的一个锐角的对边与斜边的比叫做这个角的正弦。
余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值余弦定理练习题1.在△ABC 中,如果BC =6,AB =4,cos B =,那么AC 等于( )13A .6 B .2 C .3 D .46662.在△ABC 中,a =2,b =-1,C =30°,则c 等于( )3A. B. C. D .23253.在△ABC 中,a 2=b 2+c 2+bc ,则∠A 等于( )3A .60° B .45° C .120° D .150°4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =ac ,则∠B 的值为( )3A. B. C.或 D.或π6π3π65π6π32π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定7.已知锐角三角形ABC 中,||=4,||=1,△ABC 的面积为,则·的值为( )AB → AC → 3AB → AC → A .2 B .-2 C .4 D .-48.在△ABC 中,b =,c =3,B =30°,则a 为( )3A. B .2 C.或2 D .233339.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.10.△ABC 中,sin A ∶sin B ∶sin C =(-1)∶(+1)∶,求最大角的度数.331011.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =5,则边c 的值为3________.12.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.13.在△ABC 中,a =3,cos C =,S △ABC =4,则b =________.213314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则·的值为________.AB → BC → 15.已知△ABC 的三边长分别是a 、b 、c ,且面积S =,则角C =________.a 2+b 2-c 2416.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________.17.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-2x +2=0的两根,且2cos(A +B )=1,求AB 的3长.18.已知△ABC 的周长为+1,且sin A +sin B =sin C .(1)求边AB 的长;(2)若△ABC 的面积为sin 2216C ,求角C 的度数.19.在△ABC 中,BC =,AC =3,sin C =2sin A .(1)求AB 的值;(2)求sin(2A -)的值.5π420.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.余弦定理答案1.在△ABC 中,如果BC =6,AB =4,cos B =,那么AC 等于( )13A .6 B .26C .3D .466解析:选A.由余弦定理,得AC =AB 2+BC 2-2AB ·BC cos B ==6.42+62-2×4×6×132.在△ABC 中,a =2,b =-1,C =30°,则c 等于( )3A. B.32C. D .25解析:选B.由余弦定理,得c 2=a 2+b 2-2ab cos C=22+(-1)2-2×2×(-1)cos30°33=2,∴c =.23.在△ABC 中,a 2=b 2+c 2+bc ,则∠A 等于( )3A .60° B .45°C .120°D .150°解析:选D.cos ∠A ===-,b 2+c 2-a 22bc -3bc2bc 32∵0°<∠A <180°,∴∠A =150°.4.在△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)tan B =ac ,则∠B 的值为( )3A. B.π6π3C.或D.或π65π6π32π3解析:选D.由(a 2+c 2-b 2)tan B =ac ,联想到余弦定理,代入得3cos B ==·=·.a 2+c 2-b 22ac 321tan B 32cos Bsin B 显然∠B ≠,∴sin B =.∴∠B =或.π232π32π35.在△ABC 中,a 、b 、c 分别是A 、B 、C 的对边,则a cos B +b cos A 等于( )A .aB .bC .cD .以上均不对解析:选C.a ·+b ·==c .a 2+c 2-b 22ac b 2+c 2-a 22bc 2c 22c 6.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .由增加的长度决定解析:选A.设三边长分别为a ,b ,c 且a 2+b 2=c 2.设增加的长度为m ,则c +m >a +m ,c +m >b +m ,又(a +m )2+(b +m )2=a 2+b 2+2(a +b )m +2m 2>c 2+2cm +m 2=(c +m )2,∴三角形各角均为锐角,即新三角形为锐角三角形.7.已知锐角三角形ABC 中,||=4,||=1,△ABC 的面积为,则·的值为()AB → AC → 3AB →AC → A .2 B .-2C .4D .-4解析:选A.S △ABC ==||·||·sin A312AB →AC →=×4×1×sin A ,12∴sin A =,又∵△ABC 为锐角三角形,32∴cos A =,12∴·=4×1×=2.AB →AC → 128.在△ABC 中,b =,c =3,B =30°,则a 为( )3A. B .233C.或2 D .233解析:选C.在△ABC 中,由余弦定理得b 2=a 2+c 2-2ac cos B ,即3=a 2+9-3a ,3∴a 2-3a +6=0,解得a =或2.3339.已知△ABC 的三个内角满足2B =A +C ,且AB =1,BC =4,则边BC 上的中线AD 的长为________.解析:∵2B =A +C ,A +B +C =π,∴B =.π3在△ABD 中,AD =AB 2+BD 2-2AB ·BD cos B==.1+4-2×1×2×123答案:310.△ABC 中,sin A ∶sin B ∶sin C =(-1)∶(+1)∶,求最大角的度数.3310解:∵sin A ∶sin B ∶sin C =(-1)∶(+1)∶,3310∴a ∶b ∶c =(-1)∶(+1)∶.3310设a =(-1)k ,b =(+1)k ,c =k (k >0),3310∴c 边最长,即角C 最大.由余弦定理,得cos C ==-,a 2+b 2-c 22ab 12又C ∈(0°,180°),∴C =120°.11.已知a 、b 、c 是△ABC 的三边,S 是△ABC 的面积,若a =4,b =5,S =5,则边c 的值为3________.解析:S =ab sin C ,sin C =,∴C =60°或120°.1232∴cos C =±,又∵c 2=a 2+b 2-2ab cos C ,12∴c 2=21或61,∴c =或.2161答案:或216112.在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos A ∶cos B ∶cos C =________.解析:由正弦定理a ∶b ∶c =sin A ∶sin B ∶sin C =2∶3∶4,设a =2k (k >0),则b =3k ,c =4k ,cos B ===,a 2+c 2-b 22ac 2k 2+ 4k 2- 3k 22×2k ×4k 1116同理可得:cos A =,cos C =-,7814∴cos A ∶cos B ∶cos C =14∶11∶(-4).答案:14∶11∶(-4)13.在△ABC 中,a =3,cos C =,S △ABC =4,则b =________.2133解析:∵cos C =,∴sin C =.13223又S △ABC =ab sin C =4,123即·b ·3·=4,1222233∴b =2.3答案:2314.已知△ABC 的三边长分别为AB =7,BC =5,AC =6,则·的值为________.AB → BC → 解析:在△ABC 中,cos B =AB 2+BC 2-AC 22AB ·BC=49+25-362×7×5=,1935∴·=||·||·cos(π-B )AB → BC → AB → BC → =7×5×(-)1935=-19.答案:-1915.已知△ABC 的三边长分别是a 、b 、c ,且面积S =,则角C =________.a 2+b 2-c 24解析:ab sin C =S ==·12a 2+b 2-c 24a 2+b 2-c 22ab ab 2=ab cos C ,∴sin C =cos C ,∴tan C =1,∴C =45°.12答案:45°16.(2011年广州调研)三角形的三边为连续的自然数,且最大角为钝角,则最小角的余弦值为________.解析:设三边长为k -1,k ,k +1(k ≥2,k ∈N ),则Error!⇒2<k <4,∴k =3,故三边长分别为2,3,4,∴最小角的余弦值为=.32+42-222×3×478答案:7817.在△ABC 中,BC =a ,AC =b ,a ,b 是方程x 2-2x +2=0的两根,且2cos(A +B )=1,求AB 的3长.解:∵A +B +C =π且2cos(A +B )=1,∴cos(π-C )=,即cos C =-.1212又∵a ,b 是方程x 2-2x +2=0的两根,3∴a +b =2,ab =2.3∴AB 2=AC 2+BC 2-2AC ·BC ·cos C=a 2+b 2-2ab (-)12=a 2+b 2+ab =(a +b )2-ab=(2)2-2=10,3∴AB =.1018.已知△ABC 的周长为+1,且sin A +sin B =sin C .22(1)求边AB 的长;(2)若△ABC 的面积为sin C ,求角C 的度数.16解:(1)由题意及正弦定理得AB +BC +AC =+1,BC +AC =AB ,22两式相减,得AB =1.(2)由△ABC 的面积BC ·AC ·sin C =sin C ,得BC ·AC =,121613由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC ==,AC +BC 2-2AC ·BC -AB 22AC ·BC 12所以C =60°.19.在△ABC 中,BC =,AC =3,sin C =2sin A .5(1)求AB 的值;(2)求sin(2A -)的值.π4解:(1)在△ABC 中,由正弦定理=,AB sin C BCsin A 得AB =BC =2BC =2.sin Csin A 5(2)在△ABC 中,根据余弦定理,得cos A ==,AB 2+AC 2-BC 22AB ·AC 255于是sin A ==.1-cos2A 55从而sin 2A =2sin A cos A =,45cos 2A =cos 2 A -sin 2 A =.35所以sin(2A -)=sin 2A cos -cos 2A sin =.π4π4π421020.在△ABC 中,已知(a +b +c )(a +b -c )=3ab ,且2cos A sin B =sin C ,确定△ABC 的形状.解:由正弦定理,得=.sin C sin B cb 由2cos A sin B =sin C ,有cos A ==.sin C 2sin B c2b 又根据余弦定理,得cos A =,所以=,b 2+c 2-a 22bc c 2b b 2+c 2-a 22bc 即c 2=b 2+c 2-a 2,所以a =b .又因为(a +b +c )(a +b -c )=3ab ,所以(a +b )2-c 2=3ab ,所以4b 2-c 2=3b 2,所以b =c ,所以a =b =c ,因此△ABC 为等边三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正弦定理、余弦定理习题课(2)
知识点:
1、正弦定理:在 圆的半径,则有
C 中, a 、 b 、 c 分别为角
、 、C 的对边, R 为
C 的外接
a
b c 2R .
sin
sin sin C
2、正弦定理的变形公式:① a
2Rsin
, b
2Rsin , c 2Rsin C ;
② sin
a , sin
b c
;
2R , sin C
2R
2R
③ a : b : c
sin :sin :sin C ;
④ a b c a b
c .
sin sin sin C sin
sin sin C
3、三角形面积公式: S
C
1
bcsin
1
ab sinC
1
acsin .
2
2
2
4、余弦定理:在
C 中,有 a 2
b 2
c 2 2bc cos , b 2
a 2
c 2
2ac cos ,
c 2
a 2
b 2 2ab cosC .
5、余弦定理的推论: cos
b 2
c 2 a 2 ,cos
a 2 c 2
b 2 ,cosC a 2 b 2
c 2 .
2bc 2ac
2ab 6、设 a 、b 、c 是
C 的角 、 、C 的对边,则:①若 a 2 b 2
c 2 ,则 C 90 ;
②若 a 2 b 2 c 2 ,则 C 90 ;③若 a 2 b 2 c 2 ,则 C 90 .
典型综合练习:
1、(09 广东 )已知△ ABC 中, A , B , C 的对边分别为 a,b,c.若 a c 6
2 ,
且 A = 75 ,则 b =
A .2
B . 4+2 3
C .4-23
D .6-2
、( 09 湖南)在锐角 ABC 中, BC AC
的值等于
,AC 的
2 1,B 2A 则
cos A
取值范围为 。
3、(09 北京)在 ABC 中,角 A, B,C 的对边分别为 a,b,c, B
,cos A
4 3 .
, b
w.w.w.k.s.5.u.c.o.
3
5
(Ⅰ)求 sin C 的值;
(Ⅱ)求 ABC 的面积 .
4、(08 辽宁)在 ABC 中,内角 A ,B,C 对边的边长分别是 a,b,c , 已知 c=2, C=
.
3
( Ⅰ ) 若 ABC 的面积等于 3 ,求 a,b ;
(
Ⅱ ) 若 sin C sin( B A) 2sin 2 A ,求 ABC 的面积 .
A2 5
5、(09 浙江)在 ABC 中,角 A 、B 、C 所对应的边分别为 a 、b 、c ,且知足cos =,
AB AC =3.
(Ⅰ)求ABC 的面积;
(Ⅱ)若 b+c=6, 求 a 的值。
6、(09 天津)在⊿ ABC 中, BC=5 ,AC=3, (I) 求 AB 的值: (II) 求 sin 2A 的值
4
2的答案 2、( 2, 3)
3 解:(Ⅰ)∵ A 、B 、 C 为△ ABC 的内角,且 B
3 ,cos A
4 ,
2
3 ,
5
∴ C
A,sin A
3
5
∴ sin C sin 2
A
3
cos A
1
sin A
3 4 3 .
3
2
2
10
(Ⅱ)由(Ⅰ)知 sin A
3
,sin C
3 4 3
,
5
10
又∵ B
, b 3 ,∴在△ ABC 中,由正弦定理,得
3
∴ a
b sin A 6
sin B
.
5
∴△ ABC 的面积 S
1
ab sin C 1 6
3 3
4 3
3693.
2 2 5
10 50
4 分析:(Ⅰ)由余弦定理及已知条件得, a 2 b 2 ab 4 ,
又由于 △ ABC 的面积等于 3,因此
1
ab sin C 3 ,得 ab 4 . ······4 分
2
联立方程组 2 b 2
ab ,
2 , b 2 . ··········· ···6 分 a
4 解得 a ab ,
4
(Ⅱ)由题意得 sin( B A) sin( B A) 4sin Acos A , 即 sin B cos A 2sin Acos A , ·· ························8 分 当 cos A 0时, A
2 , B
, a
4 3
, b 2 3 ,
6
3
3
当 cos A 0 时,得 sin B 2sin A ,由正弦定理得 b 2a ,
联立方程组 2 b 2
ab
,
2 3
, b 4 3 .
a
4 解得 a
b ,
3
3
2a
因此 △ ABC 的面积 S
1
ab sin C
2 3
. · ···············12 分
2
3
5 解 析 :( I ) 因 为 cos
A
2 5 , cos A 2cos 2
A 1 3 ,sin A 4
,又由
2 5 2 5
5
AB AC3
, 得 b c o s A
bc
5
,
1 bc sin A 2
S ABC
2
( II )对 于 bc 5 , 又 b c 6 , b 5, c
1 或 b
1,c
5,由余弦定理得
a 2
b 2
c 2 2 b c o s A 2,0 a 2 5
6 解:(Ⅰ)在△ ABC 中,依据正弦定理,
AB BC
sin C
sin A
于是 AB=
sin C
BC
2BC 2 5
sin A
(Ⅱ)在△ ABC 中,依据余弦定理,得 cosA=
AB
2
AC 2 BD 2 2 5
2AB AC
5
于是 sinA= 1 cos 2 A
5 5
2 2
进而 sin2A=2sinAcosA= 4
,cos2A=cos A-sin A= 3
5
5
因此 sin(2A-
)=sin2Acos -cos2Asin = 2
4
4
4 10。
