4-1-3巧求周长.题库学生版
巧求周长例题及练习
授课:XXX 巧 求 周 长 1.把3个边长为2厘米的正方形拼成一个大长方形,大长方形的周长是多少厘米?
2.把4个边长为3厘米的正方形拼成一个大正方形,大正方形的周长是多少厘米? 3.有一个长方形和一个正方形的桌布,它们周长相等。已知正方形桌布的边长是80厘米,长方形桌布的宽是50厘米,则长方形的宽是多少厘米? 授课:XXX
4.一个长方形,它的周长是40厘米,长是宽的3倍,则这个长方形的长是多少厘米?宽是多少厘米? 5.把一张长24厘米,宽16厘米的长方形剪开成两个完全相等的小长方形,求小长方形的周长? 6.如图,已知一块长方形的场地长为20米,宽为14米,周围有一条2米宽的道路环绕着,求大长方形的周长?
7.一块长方形的土地,长是65米,长是宽的3倍多5米,求这块长方形的周长是多少? 授课:XXX
8.下图是一块草坪示意图,求这块草坪的周长: 30 米 60米
9.已知,长方形的长是9,宽是6,求图中阴影部分周长
10.一个长方形被分成4个大小、形状完全一样的长方形,每个小长方形的周长都是75厘米,求这个正 授课:XXX
方形的周长。 授课:XXX
11.如图,长方形的长为120厘米,截去一个正方形后,剩下一个长方形,即阴影部分,求剩下的长方形的周长。
巧求周长练习 授课:XXX
1.试求左下图的周长(单位:厘米)。 2.上页右下图是由边长为1厘米的11个正方形堆成的“土”字图形。试求出其周长。
3.右图是某小学教学楼的平面示意图,设计者在图上只标明了三条线段的长度(单位:米)。请你算出它的周长。
4.下图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形。求这个图形的周长。 授课:XXX
5.如右图所示,一个正方形被分成了三个相同的长方形。如果其中一个长方形的周长是16米,那么这个正方形的周长是多少米?
(注:可编辑下载,若有不当之处,请指正,谢谢!)
小学数学竞赛:巧求周长.学生版解题技巧 培优 易错 难

一、基本概念①周长:封闭图形一周的长度就是这个图形的周长.②面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式:①长方形的周长2=⨯(长+宽),面积=长⨯宽.②正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法:(1)对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(2)转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.(3)寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.(4)在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段.四、几个重要的解题思想 (1)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.(2)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.知识点拨4-2-2.巧求周长(3)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(4)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(5)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.小结:本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲模块一、图形的周长和面积——割补法【例 1】求图中所有线段的总长(单位:厘米)【例 2】如图所示,点B是线段AD的中点,由A、B、C、D四个点所构成的所有线段的长度均为整数,若这些线段的长度之积为10500,则线段AB的长度是。
巧求周长_2
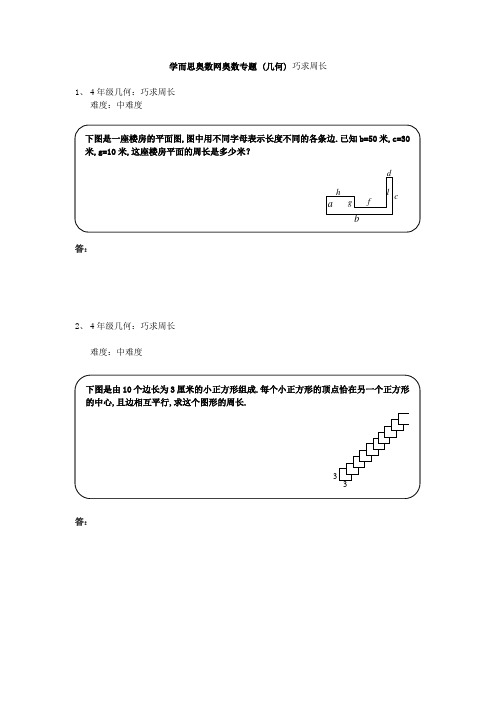
学而思奥数网奥数专题 (几何) 巧求周长1、 4年级几何:巧求周长难度:中难度答:2、 4年级几何:巧求周长难度:中难度答:下图是一座楼房的平面图,图中用不同字母表示长度不同的各条边.已知b=50米,c=30米,g=10米,这座楼房平面的周长是多少米?bacdhglf下图是由10个边长为3厘米的小正方形组成.每个小正方形的顶点恰在另一个正方形的中心,且边相互平行,求这个图形的周长.333、 4年级几何:巧求周长难度:中难度答:4、 4年级几何:巧求周长难度:中难度答:5、 4年级几何:巧求周长难度:中难度答:在4cm 7cm 的正方形网格(如图)中,所有正方形的周长的和是多少cm?如下图所示,长方形长4厘米,宽2厘米.现沿其对角线BD 对折得到一几何图形,试求图形阴影部分周长.ABC DEF如图,在长方形ABCD 中,EFGH 是正方形.如果AF=10厘米,HC=7厘米,那么长方形ABCD 的周长是多少厘米?ABCDEF GH学而思奥数网奥数专题(几何)巧求周长答案1、4年级巧求周长习题答案:解析:平移线段得到一个长是50米,宽是30米的长方形,还剩两段如图所示,所以周长是(50+30)⨯2+2⨯10=180(米)2、4年级巧求周长习题答案:解析:此题如仍用平移的方法,不仅移动的次数多且较为麻烦,不妨我们分水平方向和竖直方向两种分别讨论,水平方向上有(3+1.5⨯9)⨯2=33厘米,同理,竖直方向也为(3+1.5⨯9)⨯2=33厘米,周长可求.(3+1.5⨯9)⨯2⨯2=33⨯2=66(厘米)3、4年级巧求周长习题答案:解析:把图中△BDE以BD为轴再转回去,使之与△ADB完全重合,不难看出要求的阴影部分的周长正好等于长方形的周长.阴影部分周长由BE+ED+DC+BC而BE=AB、DE=AD.所以阴影部分周长为AD+AB+BC+DC=(4+2)⨯2=6⨯2=12厘米. 4、4年级巧求周长习题答案:解析:分类进行统计,得:边长为1cm的正方形周长的和是1⨯4⨯(4⨯7)=112(cm);边长为2cm的正方形周长的和是:2⨯4⨯(3⨯6)=144(cm);边长为3cm的正方形周长的和是:3⨯4⨯(2⨯5)=120(cm);边长为4cm的正方形周长的和是:4⨯4⨯(1⨯4)=64(cm);图中所有正方形周长的和是:112+144+120+64=440(cm).5、4年级巧求周长习题答案:解析:由题目已知条件可知:四边形EHCB,ADGF都是矩形.所以EB=HC=7(厘米).AD=FG=EF.由以上分析结果,AB+AD=AB+EF.因为AB=AF+FB,所以AB+AD=AF+FB+EF=AF+EF+FB=AF+EB=10+7=17 (厘米).所以长方形ABCD的周长=17⨯2=34(厘米).g c b。
第七讲 巧求周长习题课
授课老师:王睿 新三年级暑期选修课 习题课第七讲 巧求周长 必会点 1 基本图形求周长 1.三只猴子走得一样快,所走的路线如下图.( )号猴子先吃到桃子.
2.一个正方形的边长是3厘米,这个正方形的周长是__________厘米. 3.一个长方形的长是4厘米,宽是2厘米,求这个长方形的周长是__________厘米.
必会点 2 图形剪拼的周长变化 4.把一个边长为4 的正方形分成两个完全相同的长方形,则这两个长方形的周长的和是 ______ 厘米.
5.如图,两个长方形拼成了一个正方形. 如果正方形的周长比两个长方形的周长的和少18厘米,则正方形边长是__________厘米. 授课老师:王睿 新三年级暑期选修课 必会点 3 平移法 6. 如图所示,在一个长为8厘米、宽为6厘米的长方形纸片上剪去一个边长为3厘米的正方形. (1)如果剪去的正方形在右上角,那么剩下的图形周长是多少厘米?
(2)如果剪去的正方形在右边,那么剩下的图形周长是多少厘米? 练一练 (1) 如图,正方形树林每边长1000米,里面种有白杨树和榆树.小朋友从树林的西南角走入树林,向正东方前进.他每碰见一株白杨树就王正北走,每碰到一株榆树就往正东走,最后他走到了东北角上.问小明一共走了多少米的距离?
(2) 下边这个图形的周长等于_________厘米. 授课老师:王睿 新三年级暑期选修课 (3) 学校对喷水池进行重新改建,你能求出改建后喷水池的周长吗?(单位:米)
【拓展】小兔和小刺猬一起去小松鼠家看画展,展厅的平面图如图所示(单位:米),如果小兔和小刺猬沿着展厅游览一圈,一共要走多少米?
难题拓展部分 图形剪拼中的周长变化 例1. 如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和. 授课老师:王睿 新三年级暑期选修课 练一练 如图,正方形ABCD的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形.这9个小长方形的周长之和是 _____ 厘米.
3-1-4多人相遇和追及问题,题库学生版

1.能够将学过的简单相遇和追及问题进行综合运用 2. 根据题意能够画出多人相遇和追及的示意图3. 能将复杂的多人相遇问题转化多个简单相遇和追及环节进行解题。
二是多人相遇追及问题,即在同一直线上,3个或3个以上的对象之间的相遇追及问题。
所有行程问题都是围绕“=⨯ 路程速度”这一条基本关系式展开的,比如我们遇到的两大典型行程题相遇问题和追及问题的本质也是这三个量之间的关系转化.由此还可以得到如下两条关系式:=⨯ 路程和速度和相遇;=⨯ 路程差速度差追及;多人相遇与追及问题虽然较复杂,但只要抓住这两条公式,逐步表征题目中所涉及的数量,问题即可迎刃而解.板块一、多人从两端出发——相遇、追及【例 1】 (难度级别 ※※)有甲、乙、丙3人,甲每分钟走100米,乙每分钟走80米,丙每分钟走75米.现在甲从东村,乙、丙两人从西村同时出发相向而行,在途中甲与乙相遇6分钟后,甲又与丙相遇. 那么,东、西两村之间的距离是多少米?【巩固】 一条环形跑道长400米,甲骑自行车每分钟骑450米,乙跑步每分钟250米,两人同时从同地同向出发,经过多少分钟两人相遇?【例 2】 (难度级别 ※※)(2009年四中入学测试题)在公路上,汽车A 、B 、C 分别以80km /h ,70km /h ,50km /h 的速度匀速行驶,若汽车A 从甲站开往乙站的同时,汽车B 、C 从乙站开往甲站,并且在途中,汽车A 在与汽车B 相遇后的两小时又与汽车C 相遇,求甲、乙两站相距多少km ?知识精讲教学目标多人相遇和追及问题【巩固】(难度等级※※)甲、乙、丙三人每分分别行60米、50米和40米,甲从B地、乙和丙从A 地同时出发相向而行,途中甲遇到乙后15分又遇到丙.求A,B两地的距离.【巩固】(难度级别※※)甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走67.5米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米?【巩固】(难度级别※※)小王的步行速度是4.8千米/小时,小张的步行速度是5.4千米/小时,他们两人从甲地到乙地去.小李骑自行车的速度是10.8千米/小时,从乙地到甲地去.他们3人同时出发,在小张与小李相遇后5分钟,小王又与小李相遇.问:小李骑车从乙地到甲地需要多少时间?【巩固】(难度级别※※)甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走65米,丙每分钟走70米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过1分钟与甲相遇,求东西两镇间的路程有多少米?【巩固】(难度级别※※)甲、乙、丙三人行路,甲每分钟走50米,乙每分钟走60米,丙每分钟走70米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米?【巩固】(难度级别※※)甲、乙、丙三人行路,甲每分钟走80米,乙每分钟走90米,丙每分钟走100米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过5分钟与甲相遇,求东西两镇间的路程有多少米?【巩固】(难度级别※※※※※)小王的步行速度是5千米/小时,小张的步行速度是6千米/小时,他们两人从甲地到乙地去.小李骑自行车的速度是10千米/小时,从乙地到甲地去.他们3人同时出发,在小张与小李相遇后30分钟,小王又与小李相遇.问:小李骑车从乙地到甲地需要多少时间?【巩固】甲、乙、丙三人,他们的步行速度分别为每分钟480、540、720米,甲、乙、丙3人同时动身,甲、乙二人从A地出发,向B地行时,丙从B地出发向A地行进,丙首先在途中与乙相遇,3分钟后又与甲相遇,求甲、乙、丙3人行完全程各用多长时间?【巩固】甲乙丙三人沿环形林荫道行走,同时从同一地点出发,甲、乙按顺时针方向行走,丙按逆时针方向行走。
三年级奥数专题巧求周长习题及答案A

第五章 巧求周长(A)年级 班 姓名 得分一、填空米.“十〞“十〞间周长是 厘米.“凹〞形周长.单位:厘米“土山〞两个字,每个正方形边长是3厘米,这两个字周长分别是 、 厘米.50“5〞字,长方形长4厘米,宽2厘米,“5〞字周长是 厘米.米.7.求下列图周长.单位:厘米8.下列图是一个公园平面图,A 是公园大门.问:小明从A 门进公园,不重复地沿道路走公园一圈,他走了多少米9.下列图是某建立物设计图,如下图(单位:米)现依据须要在它四周绕电线一圈,试求需电线多少米23171 111 123 34 4 360米 240米 A 15 5 40 50410.用15个边长2厘米小正方形摆成如下列图形态,求图形周长是多少厘米二、解答题11.一个正方形被分成了5个相等长方形.每个长方形周长都是40厘米,求正方形周长是多少厘米如下图.ABCD 边长为4cm,每边被四等分.求图中全部正方形周长和.13.把边长分别是5厘米、4厘米、3厘米和2厘米4个正方形按从大到小依次排成一行(如图),排成图形周长是多少厘米BC14.将一张边长为12厘米正方形纸对折,再将对折后纸沿它竖直中线(右图虚纸)剪开,得到三个矩形纸片,其中两个较小矩形周长之和是多少厘米———————————————答案——————————————————————1.200米经过平移线段原图可转化为一边长为50米正方形,所以周长50⨯4=200(米).2. 24厘米从图中可看出,“十〞字周长是由12条相等线段组成,而题目又告知我们,“横竖都长6厘米〞,可知每3条相等线段长度和是6厘米,于是可求出“十〞字周长,当然,我们也可把“十〞中竖上、下两个横放置中间,同理横左右两个竖放置中间变成如下列图所示:这样,每条线段均长6厘米,也不难求出“十〞周长.解法一:6⨯(1⨯12÷3)=6⨯4=24(厘米)答:这个“十〞周长是24厘米.解法二:6⨯4=24(厘米)答:这个“十〞周长是24厘米.3. 18厘米我们可把它转化一下,变成下列图所示:这时,解法就同B 卷第2题一样了.解:[5+(3+1)]⨯2=[5+4]⨯2=9⨯2=18(厘米)4. 72厘米、72厘米分析:图中“土〞字周长等于24条3厘米长线段和;“山〞字周长也正好等于24条3厘米长线段和.所以,“土山〞这两个字周长分别等于24条3厘米长线段和.3⨯24=72(厘米)答:这两个字周长分别是72厘米.5. 28厘米我们可按下列图所示方向把ab 移到、移到,把cd 移到、把移到位置,则此图形变成一规则长方形,它长边为4+2+2=8厘米,宽边为4+2=6厘米,它周长可求.答:此图形周长为28厘米.解:(4+2+2+4+2)⨯2=14⨯2=28(厘米)6. 80米经过线段平移,原图形可变为长是23米,宽是17米长方形,所以周长为(23+17)⨯2=80(米). 1 3 5 a b c d7. 218厘米为分析表达便利,我们如下图编上字母,我们可把a 移至、b 移至、c 移至、d 移至,这样厘米,所以图中全部横线长是50⨯2=100厘米,图中全部竖线长为40+5+15⨯2+4+40-(5-4)=118(厘米)则整个图形周长可求.解:50⨯2+40+5+15⨯2+4+40-(5-4)=100+118=218(厘米)答:这个图形周长为218厘米.8. 我们把与分析题有关线段编号,如图:我们可把移到,移到位置,把移到,移到,把移到,把移到,则此图变成为一个规则长方形,它长是360米,宽是240米,周长可求:即(360+240)⨯2=1200(米).9. 40米我们如下图将有关线段标上字母,将a 、b 、c 、d 、e 、f 、g 、h 、i 、j 、k 、l 、m 分别移至相对应处,即、、、、、、、、、、、、位置,其中还有两段末挪动,再加上这两段和挪动后拼成长方形即为本图周长. 4 15 5 40 50 a b c d a b ′ ′ c ′ d ′ e 360米 240米 A b c d e f g解:(4+2+4+1+1+1+3)⨯2+(3+1)⨯ 2 =16⨯2+4⨯ 2=40(米)1` 答:需电线40米.10. 48厘米我们可从程度方向和竖直方向分析此题,在程度方向上,全部线段长度和为9⨯2⨯2=36厘米,在竖直方向上,全部线段长度为3⨯2⨯2=12厘米.因此,此图形周长可求.解:9⨯2⨯2=18⨯2=36(厘米)3⨯2⨯2=6⨯2=12(厘米)36+12=48(厘米)答:它周长为48厘米.11. 因为每个小长方形周长都是40厘米,所以每个小长方形一个长与一个宽和为:40÷2=20厘米.因为5个小长方形宽等于小长方形长(或大正方形边长)所以20厘米是6个小长形宽,而1个小长方形长应为20÷6⨯5,所以大正方形周长可求.方法一:解:40÷2÷6⨯5⨯4=20÷6⨯5⨯4≈66.7(厘米) ah g e fd c b i m l k j答:周长为66.7厘米.方法二:每个小长方形周长都是40厘米,这时我们再把正方形用横线平均分成5个相等长方形(如下列图).40÷12≈⨯5⨯4=66.6(厘米)答:正方形周长是66.6厘米.12. 解 分类进展统计,得:边长为1cm 正方形周长和是:1⨯4⨯(4⨯4)=64(cm);边长为2cm 正方形周长和是:2⨯4⨯(3⨯3)=72(cm);边长为3cm 正方形周长和是:3⨯4⨯(2⨯2)=48(cm);边长为4cm 正方形周长和是:4⨯4⨯(1⨯1)=16(cm);图中全部正方形周长和是:64+72+48+16=200(cm);13. 平移线段,可把原图形变为一个标准长方形如下列图所示:明显该长方形长是(5+4+3+2)=14(厘米),宽是5厘米,所以周长是(14+5)⨯2=38(厘米)14. 分析与解:依据题目条件可知两个较小长方形周长一样.54小矩形长=12(厘米)小矩形宽=12÷2÷2=3(厘米)小矩形周长=(12+3)⨯2=30(厘米)两个小矩形周长=30⨯2=60(厘米)答:其中两个较小矩形周长之和是60厘米.。
第四讲 巧求周长
第四讲巧求周长
例1:下图中每个转角均为直角,求它的周长。
(单位:厘米)
练习1:下图中每个转角均为直角,求它的周长。
(单位:厘米)
例2:如图,一个正方形被分成了5个大小一样的长方形,已知每一个长方形的周长是24厘米。
求这个正方形的周长。
练习1:如图,一个正方形被分成了5个大小一样的长方形,已知每一个长方形的周长是48厘米。
求正方形的周长。
例3:由四个同样的长方形和一个小正方形围成一个边长25厘米的大正方形(如下图)。
每个小长方形的周长是多少?
练习1:由四个同样的长方形和一个小正方形围成一个边长30厘米的大正方形(如下图)。
每个小长方形的周长是多少?
课后作业
1、下图是某花坛的平面图,每个转角为直角,求它的周长。
2、一个正方形被分成6个大小形状一样的长方形,每个长方形的周长是28厘米。
原正方形的周长是多少厘米?
3、由四个同样的长方形和一个小正方形围成一个边长24厘米的大正方形(如下图)。
每个小长方形的周长是多少?
4、如下图,每个转角都是直角,线段上标出的数表示这条线段的长,单位是厘米,那么此图形的周长是多少厘米?
5、如下图,由三个长为10cm,宽为5cm的长方形拼成的图形,这个图形的周长为多少厘米?
6、下图是一个楼梯的侧面图,已知每级台阶宽35厘米,高25厘米,这个楼梯侧面图的周长是多少米?
7、一张长方形纸片的周长是80厘米。
三张这样的纸片恰好可以拼成一张正方形纸片(如下图所示)。
拼成的正方形纸片的周长是多少厘米?。
小学奥数习题版三年级几何巧求周长学生版
知识要点不规则图形—平移【例1】下图是由6个边长都是2厘米的正方形拼成的,你能算出这个图形的周长是多少厘米吗?【例2】计算下面各图的周长。
(单位:厘米)巧求周长51015381053【例3】 求下列图形的周长.(单位:米)10040404040408040302013【例4】 计算下面各图的周长(单位:厘米)11432852049【例5】 (第七届小机灵杯复赛第8题)下面两张图中,周长比较大的是 。
(在横线上填写表示图名的字母)【例6】(第一届小机灵杯第7题)把边长分别是10厘米、9厘米、8厘米和7厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是()厘米。
【例7】下图是一座楼房的平面图,图中不同字母表示长度不同的各条边.已知50c=米,10b=米,30g=米,这座楼房平面的周长是米。
【例8】(第五届小机灵杯第10题)如图,线段10c=厘米,图形的周长为()a=厘米,8b=厘米,3厘米。
ac b【例9】(2008年第六届“走进美妙的数学花园”决赛)一个长为12厘米,宽为10厘米的长方形,挖去一个边长为4厘米的正方形补在另一边上(如图)。
所得图形的周长为_____厘米。
【例10】 下图是某校操场的平面图,已知线段120a =米,130b =米,70c =米,60d =米,250l =米.王老师每天早晨绕学校跑3圈,问每天跑多少米?ldc b aldc b a【例11】 如图所示,是由16个同样大小的正方形组成的,如果每个小正方形的周长是20厘米,那么这个图形的周长是多少?【例12】 如图所示,是由8个边长为3厘米的正方形组成的图形,你能求出这个图形的周长吗?【例13】 有一批长20厘米,宽16厘米的长方形按图所示方法:一层、二层、三层的摆下去,共要摆80层,求摆好后图形的周长?【例14】 下图是一座古城堡的外观图,图中每条最短的线段长均为2米,古城堡高12米,宽16米,求这个外观图的周长是多少米?1612【例15】 将19张边长为1分米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候,要求后摆的纸片必须有一个顶点与前一张纸片的中心重合(图中表示已经摆好的5张),地板上摆好后图形的周长是多少?【例16】 李明将5张扑克牌像下图那样摆放,已知扑克牌的长是86毫米,宽56毫米,那么这个摆成后的图形的周长是多少?等量代换【例17】8个同样的小长方形拼成一个大长方形,大长方形的周长是84厘米,小长方形的周长是多少厘米?【例18】由9个相等的小长方形拼成的大长方形,已知小长方形的宽是12厘米,求大长方形的周长是多少厘米?【例19】下图是由三个同样的长方形拼成的,求周长是多少?【例20】李明从A走到B再走到C再到D,走了38米,马力从B到C再到D再到A走了31米,问此长方形的水池ABCD的周长是多少米?CDB A规则图形的变化【例21】 用一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形.拼成的正方形的周长是多少分米?【例22】 一个正方形被分成了三个相同的长方形.如果其中一个长方形的周长是16米,那么这个正方形的周长是多少米?【例23】 有一个长方形纸片,长比宽多2厘米,周长是36厘米,用剪刀剪3下(如图),这6个长方形的周长之和是_____。
求周长的练习题
求周长的练习题求周长的练习题在数学中,求周长是一个常见的练习题。
无论是学生还是教师,都需要通过解决这些问题来加深对周长概念的理解。
本文将提供一些有趣的练习题,以帮助读者更好地掌握求周长的方法和技巧。
1. 矩形的周长假设有一个矩形,长为5cm,宽为3cm。
如何求出它的周长呢?很简单,我们只需要将长和宽分别乘以2,然后将两个结果相加即可。
所以,这个矩形的周长为(5+3)×2=16cm。
2. 正方形的周长正方形是一种特殊的矩形,它的四条边长度相等。
假设有一个正方形,边长为4cm。
我们如何求出它的周长呢?由于正方形的四条边长度相等,所以我们只需要将边长乘以4即可。
因此,这个正方形的周长为4×4=16cm。
3. 圆的周长圆是一个非常有趣的几何图形,它没有直线边界,而是由无数个点组成的。
圆的周长也被称为圆周长或圆周。
我们知道,圆的周长与直径有关。
直径是连接圆上任意两点,并通过圆心的线段。
圆周长的计算公式是:周长=π×直径。
假设有一个圆,直径为6cm,我们如何求出它的周长呢?根据公式,周长=π×6≈18.85c m。
4. 三角形的周长三角形是一种有三条边的多边形。
根据三角形的不同形状,求周长的方法也有所不同。
假设有一个等边三角形,边长为5cm。
由于等边三角形的三条边长度都相等,所以我们只需要将边长乘以3即可。
因此,这个等边三角形的周长为5×3=15cm。
而对于其他形状的三角形,我们需要将各边的长度相加才能得到周长。
5. 多边形的周长多边形是一个有多条边的封闭图形。
根据多边形的形状和边长,求周长的方法也有所不同。
假设有一个五边形,边长分别为3cm、4cm、5cm、6cm和7cm。
我们如何求出它的周长呢?只需要将五条边的长度相加即可。
所以,这个五边形的周长为3+4+5+6+7=25cm。
通过以上的练习题,我们可以看到,求周长并不难。
只需要根据不同的几何图形,选择合适的计算方法,就能轻松求得周长。
巧求周长与面积(学生)1.1
巧求周长与面积
1. 掌握巧求周长与面积的基本方法;
2. 理解并掌握割补、平移等数学思想方法。
知识装备:
周长与面积,公式需紧记;
周长用平移,面积用割补。
初级挑战1
一个长方形和一个正方形的周长相等,已知正方形的边长是8厘米,长方形的长为10
厘米,这个长方形的面积是多少?
思维导航:你能先求出长方形的宽是多少吗?
能力探索1
把一个大正方形平均分成4个小正方形后,每个小正方形的周长为12厘米,求这个大
正方形的面积。
初级挑战2 10
求右图的周长。(单位:厘米) 10 4 6
3
学习目标
精讲精练
思维导航:你能将图中的某些线段进行平移,变成规则的图形再计算吗?
能力探索2
求下图的周长。(单位:厘米)
4 8
3 8 3
4
3
中级挑战1
求下图的面积。
思维导航:你能添加辅助线将图形变成一个规则图形再计算吗?
10
5
30
18
20
8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1-3.巧求周长 学生版 page 1 of 9 基本概念 ①周长:封闭图形一周的长度就是这个图形的周长. ②面积:物体的表面或封闭图形的大小,叫做它们的面积. 基本公式: ①长方形的周长2(长宽),面积长宽. ②正方形的周长4边长,正方形的面积边长边长. 常用方法: 对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解. 转化是一种重要的数学思想方法,在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形.
寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.
在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段. 平移:在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意. 割补:割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明
原有图形结构 例题精讲 巧求周长 对称 旋转 平移 新的图形结构 在原有图形结构中解决问题较困难 在新的图形结构中解决问题较容易 4-1-3.巧求周长 学生版 page 2 of 9
确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变. 旋转:在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题. 对称:平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助. 代换:在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.
本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.
【例 1】 求图中所有线段的总长(单位:厘米) 21
3
4
EDCBA
【例 2】 如图所示,一个大长方形被三条线段分成了四个小长方形,各条线段长度见图(单位:厘米).求:图中所有长方形的周长之和.
21342
【例 3】 如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和.
【巩固】(“希望杯”第一试)如右图,正方形ABCD的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形。这9个小长方形的周长之和是多少厘米?
A
BCD 4-1-3.巧求周长 学生版 page 3 of 9
【例 4】 下图表示一块地,四周都用篱笆围起来,转弯处都是直角.已知西边篱笆长17米,南边篱笆长23
米.四周篱笆长多少米?
北
南西东17
23
【巩固】(希望杯培训题)右图的周长是 分米.
6分米7分米
【巩固】计算右边图形的周长(单位:厘米)。
1510
【巩固】下图是一个锯齿状的零件,每一个锯齿的两条线段都长2厘米,求这个零件的周长.
【例 5】 下图中标出的数表示每边长,单位是厘米.它的周长是多少厘米? 4-1-3.巧求周长 学生版 page 4 of 9
【巩固】右图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形.求这个图形的周长? 【例 6】 一个周长是20厘米的正方形,剪下一个周长是6厘米的正方形,剩下的图形的周长是 . (写出所有可能的结果)
【例 7】 求下图的周长. 【巩固】求右图的周长. 【巩固】下图的小正方形边长为1厘米.这个图形的外沿的周长是多少厘米? 【例 8】 如下图是某校的平面图,已知线段a=120米,b=130米,c=70米,d=60米,l=250米.杨老师 4-1-3.巧求周长 学生版 page 5 of 9
每天早晨绕学校跑3圈,问每天跑多少米? 【例 9】 (第七届”小机灵杯”数学竞赛初赛)下面两张图中,周长较大的是 .(在横线上填写表示图名的字母)
第题 141410BA
【巩固】如下图,正方形操场边长100米,一只蚂蚁沿甲地走了一圈,另一只蚂蚁沿乙地走了一圈,谁走的路长? 它们各走了多少米?
【巩固】求右图所示图形的周长(单位:分米) 501050
【例 10】 如图是一个机器零件的侧面图,图中每一条最短线段长5厘米,这个零件高30厘米,求这个零件侧面的周长是多少厘米? 4-1-3.巧求周长 学生版 page 6 of 9
【例 11】 下图是一面砖墙的平面图,每块砖长20厘米,高8厘米,像图中那样一层、二层…一共摆十层,求摆好后这十层砖墙的周长是多少?
【巩固】把长2厘米、宽1厘米的长方形砖块摆成如图的形状,求该图形的周长? 【例 12】 右图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?
【巩固】图中是由周长都是20厘米的小正方形组成的,它的周长是多少厘米? 【巩固】下图是由边长为1厘米的11个正方形堆成的“土”字图形.试求出其周长. 【巩固】如图,每个小方格是一个正方形,如果该图总面积是52个平方单位,试求这个图形的外沿周长是多少个长度单位? 4-1-3.巧求周长 学生版 page 7 of 9
【例 13】 图⑴、图⑵都是由完全相同的正方形拼成的,并且图⑴的周长是22厘米,那么图⑵的周长是多少厘米?
(2)(1) 【例 14】 边长是15厘米的3个正方形拼成一个长方形,这个长方形的周长是多少?
【巩固】用一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形.拼成的正方形的周长是多少分米?
48
【例 15】 两个大小相同的正方形拼成了一个长方形,长方形的周长比原来的两个正方形周长的和减少了6厘米,原来一个正方形的周长是多少厘米?
【例 16】 (2007年”希望杯”第一试)右图中的阴影部分BCGF是正方形,线段FH长18厘米,线段AC
长24厘米,则长方形ADHE的周长是 厘米.
HGFE
DACB
【巩固】如图,在长方形ABCD中,EFGH是正方形.已知10cmAF,7cmHC,求长方形ABCD的周长. 4-1-3.巧求周长 学生版 page 8 of 9
HGFEDC
BA
【例 17】 如右图所示,在一个正方形内画中、小两个正方形,使三个正方形具有公共顶点,这样大正方形被分割成了正方形区域甲,和L形区域乙和丙.甲的周长为4厘米,乙的边长是甲的周长的1.5倍,丙的周长是乙的周长的1.5倍,那么丙的周长为多少厘米?EF长多少厘米?
乙丙
甲J
IFE
HGDCBA 【例 18】 用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是244厘米,那么平行四边形和三角形各有多少个?
【巩固】用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是236厘米,那么平行四边形和三角形各有多少个?
【例 19】 有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45
平方厘米,求这个大长方形的周长.
【巩固】右图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽. 4-1-3.巧求周长 学生版 page 9 of 9
【例 20】 冯大叔给儿子做玩具用8个一样大的小长方形拼图,拼出了如图甲、乙的两种图案:图案甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是2cm的正方形小洞.求小长方形的长和宽?
【例 21】 用同样的长方形条砖,在一个盆的周围砌成一个正方形边框,如右图所示.已知外面大正方形的周长是264厘米,里面小正方形的面积是900平方厘米,每块长方形条砖的长是_________厘米,宽是______厘米.
【例 22】 (第二届希望杯复试)将若干个边长为1的正六边形(即单位六边形)拼接起来,得到一个拼接图形,如图:
周长=14周长=12周长=10周长=6
那么,要拼接成周长等于18的拼接图形,需要多少个单位六边形?画出对应的一种图形.
乙 甲
