平面应力状态
(仅供参考)平面应力状态分析-主应力主平面详细推导

平面应力状态分析--主应力主平面详细推导老和尚小方丈(storylee_dut@)大连理工大学+哈尔滨电机厂有限责任公司平面应力状态有一个主应力为0,全部应力分量假设位于一个平面,鉴于市场上材料力学教材关于平面应力状态分析公式推导不尽详细,在此进行详细推导,为广大力学人士提供参考,敬请批评指正。
任意斜截面上的应力公式为:ατασσσσσα2sin 2cos 22xy yx y x --++=(1)ατασστα2cos 2sin 2xy yx +-=(2)式中,α为斜截面外法线n 与x 轴正向的夹角。
对于主平面方位的确定,根据主平面定义可知,主平面上的切应力为0,由(2)式得:02cos 2sin 2000=+-=ατασσταxy yx (3)即yx xyσστα--=22tan 0(4)方程(4)有两个解,主平面方位角0α与 900+α,说明两个主平面互为垂直关系。
将公式(3)的解回代公式(1),可得另外两个主应力,代数值较大的记为max σ,较小的记为min σ,则22max 22xy y x y x τσσσσσ+⎪⎪⎭⎫ ⎝⎛-++=(5)22min22xyy x y x τσσσσσ+⎪⎪⎭⎫ ⎝⎛--+=(6)关于公式(3)的解诸多材力教材没有此部分推导,本文列如下:对于方程yx xyσστα--=22tan 0更改等效形式002cos 22sin ασσταyx xy--=(7)添加方程12cos 2sin 0202=+αα(8)联立(7)、(8)求得:2220222cos xy y x y x τσσσσα+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛-±=(9)222022sin xy y x xyτσστα+⎪⎪⎭⎫ ⎝⎛-=(10)注意(9)、(10)公式正负号的对应,再将(9)、(10)代入公式(3)推得主应力计算公式(5)、(6),至此,详细推导完成!。
材料力学8-3-平面应力状态分析-课件

02
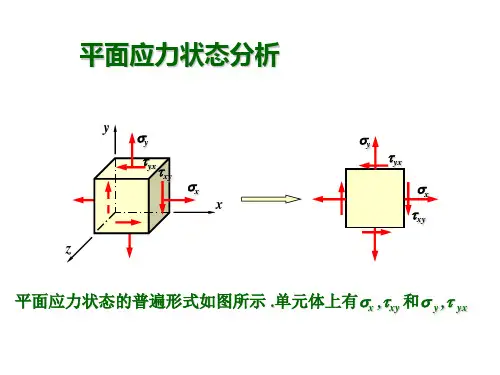
平面应力状态分析的基本概念
应力状态
1 2
定义
应力状态是指物体在某一点处的应力分布情况。
表示方法
通常采用主应力、应力张量和应力矩阵来表示。
3
分类
根据应力分量的变化规律,可分为平面应力状态、 空间应力状态和轴对称应力状态。
平面应力状态
定义
平面应力状态是指物体在某一平面内 的应力分布情况,其应力分量只有三 个,即σx、σy和τxy。
材料力学8-3-平面应力状 态分析-课件
• 引言 • 平面应力状态分析的基本概念 • 平面应力状态的分类与表示 • 平面应力状态的平衡方程与几何方程 • 平面应力状态分析的实例 • 总结与展望
01
引言
平面应力状态分析的定义
平面应力状态分析是材料力学中一个重要的概念,它主要研究物体在受力时,其内 部应力的分布情况。
特点
在平面应力状态下,物体内的剪切力分 量τxy与正应力分量σx、σy成比例关系, 即剪切力分量与正应力分量成正比。
应力分量与主应力
定义
主应力与材料性质的关系
应力分量是指物体在某一点处各个方 向的应力值,而主应力则是应力分量 中的最大和最小值。
主应力的大小反映了材料在该点所受 的应力和应变状态,与材料的弹性模 量、泊松比等性质有关。
应力集中系数
为了描述应力集中的程度,引入了应力集中系数,该系数反映了孔 边应力和平均应力的比值。
弯曲梁的平面应力状态分析
弯曲梁
当梁受到垂直于轴线的力矩作用时,梁发生 弯曲变形。
平面应力状态
在弯曲梁的横截面上,剪应力和正应力的分布情况 。
弯矩和剪力的关系
通过分析剪应力和正应力的分布和大小,可 以确定梁的弯矩和剪力之间的关系,从而进 行受力分析和设计。
工程力学(高教版)教案:8.2 平面应力状态

第二节 平面应力状态如图8-3(a)所示的单元体,因外法线与z 轴重合的平面上其剪应力、正应力均为零,说明该单元体至少有一个主应力的为零,因此该单元体处于平面应力状态。
为便于研究,取其中平面abcd 来代表单元体的受力情况(图8-3b )。
任意斜截面的表示方法及有关规定如下:(1)用x 轴与截面外法线n 间的夹角α表示该截面。
(2)α得正负号:由x 轴向n 旋转,逆时针转向为正,顺时针转向为负(图8-3b 的α角为正)。
(3)ασ得正负号:拉应力为正,压应力为负(图8-3的x σ、y σ、ασ均为正值)。
(4)ατ得正负号:ατ对截面内此任一点的力矩转向,顺时针转向为正,逆时针转向为负(图8-3的x τ、ατ均为正值,y τ为负值)。
图8-3一、任意斜截面上的应力计算任意斜截面上应力有两种方法:解析法和图解法。
(一)解析法因研究的构件是平衡的,因此从构件内一点取单元体,并从单元体上取一部分(图8-3c ),则该部分也处于平衡。
由平衡条件可以求得平面应力状态下单元体任一斜截面上的应力计算公式ατασσσσσα2sin 2cos 22x yx yx --++= (8-1)ατασστα2cos 2sin 2x yx +-=(8-2)应用上式 计算ασ、ατ时,各已知应力x σ、y σ、x τ和α均用其代数值。
例8-1 求图8-4所示各点应力状态下斜截面上的应力(各应力单位是Mpa ),并用图表示出来。
解 (1) 已知:x σ=30Mpa ,y σ=-40 Mpa ,x τ=60 Mpa ,α=30º,将各数值代入式(8-1)、(8-2)得斜截面上的应力46.3960sin 6060cos 240302403030-=-++-=σ Mpa 31.6060cos 6060sin 2403030=++= τ Mpa将 30σ、 30τ方向画在斜截面上,如图8-4(1-b)所示。
(2)已知:x σ=-80Mpa ,y σ=0 Mpa ,x τ=-40 Mpa ,α=120º,将各数值代入式(8-1)、(8-2)得斜截面上的应力64.54240sin 40240cos 280280120-=+-+-=σ Mpa 64.54240cos 40240sin 280120=--=τ Mpa将 120σ、 120τ方向画在斜截面上,如图8-4(2-b)所示。
材料学 平面应力状态分析
ayx
f
y
t
e
dA
dAcos α
a dAsinf
3.任意斜截面上的应力(The stress acting on any inclined plane)
设斜截面的面积为dA , a-e的面积为dAcos, a-f 的面积为 dAsin
对研究对象列 n和 t 方向的平衡方程得
化简以上两个平衡方程最后得
的方位.
m
m a
l
A
解: 把从A点处截取的单元体放大如图
A
1 3
因为 x < y ,所以 0= 27.5°与min对应
3
0
A
x
1
例题5 图示单元体,已知 x =-40MPa,y =60MPa,xy=-50MPa.试求e-f截面上的应力情
况及主应力和主单元体的方位.
解:(1)求 e-f 截面上的应力
不难看出 即两相互垂直面上的正应力之和保持一个常数
二、最大正应力及方位 (Maximum normal stress and it’s direction)
1.最大正应力的方位(The direction of maximum normal stress ) 令
0 和 0+90°确定两个互相垂直的平面,一个是最大正应力
y n
e
x
a
yx
x xy
f
e
x
x
xy
α
α n
α
α
ayx
f
y
e
x
a
y
yx x
xy
f
n
x
2.符号的确定(Sign convention)
e
《平面应力状态》课件

优化方法:采用 有限元分析方法, 对零部件进行应 力分析,找出应 力集中区域
优化结果:通过 优化设计,提高 了零部件的强度 和刚度,降低了 重量和成本,提 高了产品的市场 竞争力
感谢您的耐心观看
汇报人:PPT
纯剪切应力状态:物体在两个相互垂直的平面内受到剪切应力的作用, 应力在两个平面内是均匀分布的。
应力状态与变形关系
应力状态:物体内部受到的力与面 积的比值
应力与变形的关系:应力越大,变 形越大
添加标题
添加标题
添加标题
添加标题
变形:物体在外力作用下产生的形 状和尺寸变化
应力状态与变形的关系:应力状态 决定了物体的变形程度
预防措施:优化设计、选用 优质材料、改进制造工艺等
稳定性准则及判据
稳定性准则:平面应力状态下,结构在受到外力作用下保持稳定状态的条件 判据:根据应力状态、材料性质和几何形状等因素,判断结构是否满足稳定性准则 稳定性分析方法:包括能量法、变分法、有限元法等 稳定性判据的应用:在工程设计中,用于评估结构的稳定性,确保结构的安全性和可靠性
平面应力状态下的应变 分析
应变概念及测量方法
应变:物体在外力作用下产生的形变 应变类型:线应变、面应变、体应变 应变测量方法:光学测量法、机械测量法、电学测量法 应变分析:通过测量应变来研究物体的应力状态和变形规律
应变与应力关系
应变:物体在外力作用下产生的形变
应变与应力的量纲:应变的单位是长度,应力的 单位是力/面积
强度计算方法
应力状态: 平面应力状 态
强度指标: 最大主应力、 最小主应力、 剪应力
强度条件: 最大主应力、 最小主应力、 剪应力均小 于材料的许 用应力
强度计算公
材料力学-7-应力状态分析

7.1 应力状态的基本概念
y
y
1 1 4
z
4
Mz
x
x
l
S FP
2
3
Mx
z
3
a
第7章 应力状态分析
7.2 平面应力状态任意方向面上的应力 ——解析法
7.2 平面应力状态任意方向面上的应力 ——解析法
一、方向角与应力分量的正负号约定
x
正应力
x
x
拉为正
压为负
x
7.2 平面应力状态任意方向面上的应力 ——解析法
?
第7章 应力状态分析 7.1 应力状态的基本概念
7.2 平面应力状态任意方向面上的应力 ——解析法 7.3 主应力、主平面与面内最大切应力 ——解析法 7.4 应力圆及其应用——图解法
7.5 三向应力状态的特例分析
7.6 广义胡克定律
7.7 应变能密度
第7章 应力状态分析
tan 2q p=- 2 τ
xy
x y
主平面(principal plane):切应力q=0的方向面,用 qp表示。 主应力(principal stress):主平面上的正应力。 主方向(principal directions):主平面法线方向,用方 向角qp表示。
7.3 主应力、主平面与面内最大切应力 ——解析法
第7章 应力状态分析
第7章 应力状态分析
1
3
2
max
max
拉压、弯曲正应力 扭转、弯曲切应力
这些强度问题的共同特点是:
1、危险截面上的危险点只承受正应力 或切应力; 2、都是通过实验直接确定失效时的极限应力,并以此为依据建立强度 设计准则。 复杂受力:危险截面上危险点同时承受正 应力和切应力,或者危险点的其他面上同 时承受正应力或切应力。 → 强度条件
材料力学72平面应力状态应力分析主应力
一、公式推导:
a x
y
y
c
x
a
x
x
b
y
n
c
y
Fn 0 F 0
cos2 1 cos 2
2
sin 2 1 cos 2
2
x y
dA x dAcoscosx 2x dyAcosxs2inycoysd2Asin cxossin 2y dAsin sin 0
sin 2
max
x y sin 2
2
x cos 2
cos 2
450
450
max
450
max
450 0
铸铁圆试样扭转试验时,正是沿着最大拉 应力作用面(即450螺旋面)断开的。因此, 可以认为这种脆性破坏是由最大拉应力引起 的。
应力圆
一、应力圆的方程式
x y
300 600 x y 40MPa
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面,说明低碳钢 拉伸时发生屈服的主要原因。
低碳钢拉伸时,其上任意一点都是单向应力状态。
450
x y
2
x y cos 2
2
x sin 2
x
x
2
y
2
x y cos 2
2
x sin 2
x y sin 2
2
x cos 2
轴向拉伸压缩
x (1 cos 2)
1
x
y
2
x
2
y
2
2 x
2
切应力等于零的截面为主平面 主平面上的正应力称为主应力
2
第13章 平面应力状态分析
0
法线的面上的应力为(-40。0), x 大切应力截面上的应力。 45 连接两点,以中点为半径,20为半 解: 1、选取杆上任一点及其 径做圆,得到应力莫尔圆。 3MP 40 MP 3 40 a a 邻域,如图,上下两截面正应 / MPa 450 4、圆上点D切应力最大,可见,是 力为-40MPa,切应力为0。纵向 由x轴逆时针转动900得到的。所以截 20 截面上无应力作用。 D 0即得到最大切应力平面。 面转动 45 450 90 2、建立σ-τ右手直角 0 20 / MP 40 5 、由图中可以得到最大切应力截面 a 坐标系,如图,选取相同比例 上的应力为: 尺(如1mm=1MPa)。
a( x , xy )
p 可见,利用Cauchy应力定理,由
p
(n)
px
(n)
(n) T
y
应用实例
如图,试确定承受内压薄壁容器内壁任
意点的应力状态.
重要应用实例
m t
p
l
D
pDl
m
m(p D)
D
pp D 2 4
p
m
t
t (2 l )
t
重要应用实例
m
m(p D)
D
pp d 2 4
yx
x'
x
应力的面的概念。
微元平衡分析结果表明:即使同一点不 同方向面上的应力也是各不相同的,此即
应 力
指明 哪一个面上?
哪一点? 哪一点? 哪个方向面?
过一点不同方向面上应力的集合,称之为这
一点的应力状态(State of the Stresses of a
平面问题中一点的应力状态
问题:
平面问题中,
(a)已知一点的应力为 方向的正应力n为 (b)已知 那么
,那么任一 1 2 n 为 ; a , b x y ? 1 2
⑶ 它是在边界上物体保持连续性的条 件,或位移保持连续性的条件。
应力边界条件--设在 s 上给定了面力分 量
fx (s), f y (s).
通过三角形微分体的平衡条件,导出坐标面应力 与斜面应力的关系式,
p l σ m , p m σ l , x x y x y y x y
A
N
B
N
1 1 2 l ( ) N 2 1 4 2
2
s
N
1 显然,当 1l2 0 (l ) 时,τN为最大、最小值: 2 2
max 1 2 min 2
由 l
1 得, τmax、 τmin 的方向与σ1 2
( σ2 )成45°。
⑹ 所有边界均应满足,无面力的边界
(自由边) fx f也必须满足。 , y 0
坐标面
当边界面为坐标面时, 若x=a为正x 面,l = 1, m = 0, 则式(d)成为
() σ f ,() f . x x a x x y y x a
b a x
( e )
fx
xy
σ
x
σ
x
fx
n
B
py
xy
2
x
xy
y
σ2-(σx+σy)σ+(σxσy-τ2xy)=0
解释平面应力和平面应变状态
1. 脆性断裂:断裂前,材料未发生明显的宏观塑性变形的断裂,或指断裂应力低于材料屈服强度的断裂2. 包申格效应:是指金属材料经预先加载产生少量塑性变形(残余应力小于4%),而后再同向加载,规定残余伸长应力(屈服强度、弹性极限)增加,反向加载,规定残余伸长(屈服强度、弹性极限)应力降低的现象。
3. 应力状态软性系数:应力状态中最大切应力和最大正应力的比值4. 刚度:在弹性变形范围内,构件抵抗变形的能力。
5.热疲劳:由周期变化的热应力或热应变引起的材料破坏称为热疲劳。
6.蠕变:材料在长时间的恒温、恒载荷作用下缓慢地产生塑性变形的现象。
7.疲劳强度:在指定疲劳寿命下,材料能承受的上限循环应力。
8.断裂韧度:裂纹失稳扩展的临界状态所对应的应力场强度因子称为材料的断裂韧度9.技术磁化:铁磁材料在外加磁场的作用下所产生的磁化称为技术磁化。
10.允带:电子可以具有的能级所组成的能带称为允带。
1. 韧性:是指材料在断裂前吸收塑性变形功和断裂功的能力。
4.松弛稳定性:材料抵抗应力松弛的能力称为松弛稳定性。
7.低温脆性:材料随着温度下降,脆性增加,当其低于某一温度时,材料由韧性状态变为脆性状态,这种现象为低温脆性。
8.解理断裂:材料在拉应力的作用下原于间结合破坏,沿一定的结晶学平面(即所谓“解理面”)劈开的断裂过程。
6. 破损安全:构件内部即使存在裂纹也不导致断裂的情况。
7.平面应力:只在一个平面内存在应力的现象。
10. △K th :疲劳裂纹扩展的门槛值,表征材料阻止疲劳裂纹开始扩展的能力1. 解释形变强化的概念,并阐述其工程意义。
答:材料进入塑性变形阶段后,随着变形量增大,形变应力不断提高的现象称为形变强化。
(2分)形变强化是金属材料最重要的性质之一,其工程意义在于:1)形变强化可使材料或零件具有抵抗偶然过载的能力,阻止塑性变形的继续发展,保证材料安全。
2)形变强化是工程上强化材料的重要手段,尤其对于不能进行热处理强化的材料,形变强化成为提高其强度的非常重要的手段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
就是研究一点处沿各个不同方位的 截面上的应力及其变化规律。
应力状态的研究方法
dx dy dz 0
dz
dy
dx
应力状态的分类
轴向拉伸
σ
弯曲变形
τ σ τ
扭 转
τ σ
τ σ
τ
σ
σ
σ τ
τσ
FN A
T Ip
MZ y Iz
Fs S IZb
* z
§8-1-2 应力状态的实例
F
N A
2.圆轴扭转时:
T
3.剪切弯曲的梁:
A B
T Ip
P
M ( x) y Iz
Q Sz Iz b
得出:
应力:不同横截面应力不同;同一横截面上
不同点处应力不同。 同一点不同截面方位,应力是不是变化? 如果变化,又以怎样的规律变化?
F A
N
K F
A
F
K
x
x
xz
xy yx
y
y
平面(二向) 应力状态
( Plane State of Stresses )
y
x
yx
xy
x
y
y
x
y
yx
xy
x
x
单向应力状态
( One Dimensional State of Stresses )
纯剪应力状态
( Shearing State of Stresses )
本章要点
(1)平面应力状态的解析法和图解法
(2)强度理论
重要概念
单元体、平面应力状态、平面应变状态、主应力、 主应变、广义虎克定律、第一强度理论、第二强度
理论、第三强度理论、第四强度理论。
目录
§8-1 应力状态的概念和实例 §8-2 平面应力状态下的应力状态分析 §8-3 三向应力状态 §8-4 变形与应变 §8-5 广义虎克定律与弹性变形比能
1 =75MPa, 2 =150MPa, 3 0
例2 求应力
’A= ’p Dt=P
pp P= 4
2 D
pD ’= 4t
§8-6 强度理论的概念及应用
轴向拉压
对称弯曲
扭 转
内力分量 轴力FN
内力分量 弯矩M,剪力Q 应力分布规律 正应力与中性轴距离成正比
My IZ
* FS S Z IZb
内力分量 扭矩T 应力分布规律
应力分布规律 正应力均匀分布
FN A
切应力与距圆心 距离成正比分布
切应力沿截面高度呈抛物线 强度条件 强度条件
T IP
强度条件
轴向拉压
对称弯曲
扭 转
变形公式
变形公式
变形公式
Mn GI P
轴向线应变 刚度条件 挠曲线曲率 刚度条件
f max f L L
单位长度扭转角 刚度条件
max
应变能
应变能
应变能
1. 直杆受轴向拉(压)时:
F
m m
S平面
l/2
l/2
FP
S平面
S平面
4
FP 52 FP l Mz 4
M 1 WZ
l/2
l/2
3
5
2 1
4
3
2
1 2
My IZ
2
1
2
QS Z IZb
3
QS max 3 IZb
l
S
F a
S平面
y
1 4
z
2 3
x
l
y
1
F
Fa FQy
Mx 1 Wp
1 4
情况。
研究方法: 取单元体的方法。
F
2、单元体: 围绕受力构件内任意点切取的微元体。
F
单 元 体 的 特 点
1.单元体各侧面上的应力分布是均匀的。 2.两个相互平行侧面上的应力情况是相同的。 3.代表该点三个相互垂直方向上的应力情况。
3、原始单元体: 各侧面上的应力情况为已知的单元体。
FP 5 4 3 2 1
根据单元体的局部平衡:
y
n
y
拉中有剪
y
y
n
x
x
y
剪中有拉 结论
不仅横截面上存在应力,斜截面上也存 在应力;不仅要研究横截面上的应力,而 且也要研究斜截面上的应力。
应力的三个重要概念 m m m 应力的点的概念; 应力的面的概念; 应力状态的概念.
FN
Mz
FQ
应力状态分类:
单向应力状态: 二向应力状态:
(平面应力状态)
只有一个主应力不等于零。 只有一个主应力等于零,其它两个 主应力不等于零。 三个主应力都不等于零。
三向应力状态:
三向(空间)应力状态
( Three-Dimensional State of Stresses )
z
z
zy yz
zx
横截面上正应力分析和切应力分析 的结果表明:同一面上不同点的应力各 不相同,此即应力的点的概念。
x
y
y
单元体平衡分析结果表明:即 使同一点不同方向面上的应力也是各 不相同的,此即应力的面的概念。
哪一个面上 哪一点?
应 力
指明
哪一点 哪个方向面?
过一点不同方向 面上应力的集合, 称之为这一点的应 力状态。
’A= ’p Dt=P
pD ’= 4t
”=?
2N=pDl N= ”tl
pD ”= 2t
’ ” ”
’
二向应力状态
三向压缩
例1
• 由A3钢制成的蒸汽锅炉,t=10mm, D=1m。p=3MPa。求三个主应力
pD ’= =75MPa 4t
pD ”= =150MPa 2t
F p cos 0 cos A
p
p cos cos2
p sin 0
2 sin 2
A
§8-1-1 应力状态的概念
State of the Stresses of a Given Point
1、应力状态:受力构件内任意点各截面方位上的应力
z
x
1
Mz Wz
Mz
x
3
Mx 3 Wp
2 3
Mx
Mz x Wz
3
4
3
Mx Wp
4、主单元体: 各侧面上只有正应力作用,而无
剪应力作用的单元体。 5、主平面:
6、主应力: 单元体上剪应力为零的面。 主平面上作用的正应力。
主应力按代数值大小排列:
1 2 3
