高二数学天天练(01)
高二数学天天练(56)

高二数学天天练(56) 姓名 课题:抛物线及标准方程(1)一、选择题:1.已知抛物线的焦点坐标是(2,0),则抛物线的标准方程是 [ ]A.y 2=4xB.y 2=-4xC.y 2=-8xD.y 2=8x2.已知抛物线的准线方程是x=-7,则抛物线的标准方程是 [ ]A.x 2=-28yB.y 2=-28yC.y 2=28xD.x 2=28x3.经过点P (4,-2)的抛物线标准方程为 [ ]A.y 2=x 或x 2=-8yB.y 2=x 或y 2=8xC.y 2=-8xD.x 2=-8y4.抛物线y 2=-4px (p >0)的焦点为F ,准线为L ,则p 表示 [ ]A.F 到L 的距离B.F 到y 轴的距离C.F 点横坐标D.F 到L 的距离的415.抛物线x 2=4ay 的准线方程是 [ ]A.x=-aB.x=aC.y=-aD.y=a6.抛物线6x-ay 2=0准线方程是x=-43,则a 为 [ ]A.2B.-2C.3D.-37.抛物线y=a 1x 2(a ≠0)的焦点坐标是 [ ] A.(0,4a )或(0,-4a ) B.(0,4a)C.(0,a 41)或(0,-a 41) D.(0,a 41)8.已知抛物线y 2=6x 定点A (2,3),F 为焦点,P 为抛物线上的动点,则|PF|+|PA|的最小值为 [ ]A.5B.4.5C.3.5D.不能确定二、填空题:9.抛物线y 2=2x 上的两点A 、B 到焦点的距离之和为5,则线段AB 中点到y 轴的距离为 .10.若点M 到点F (1,0)的距离比它到直线x=0的距离大1,则点M 的轨迹方程 为 .11.在抛物线y 2=8x 上与焦点F 的距离等于6的点的坐标为 .12.在抛物线y 2=8x 上一点到x 轴的距离为4,则该点到焦点F 的距离为 .三、解答题:13.点N 到点(4,0)的距离等于点N 到直线4x-3y-16=0的距离,求点N 的轨迹方程. 14. ①点M 与点F (0,-2)的距离比它到直线L :y-3=0的距离小于1,求M 点的轨迹方程. ②已知圆C 的方程为x 2+y 2-10=0,求与y 轴相切且与C 外切的动圆的圆心P 的轨迹 方程.。
高二数学天天练(26)

高二数学天天练(26) 姓名课题:两直线的位置关系(2)一、选择题:1.若直线1l 到直线2l 的角为1θ,2l 到1l 的角为2θ,则cos (1222θθ+)的值为( )不能确定2.直线1l 到直线2l 的角为α,tan α的值为 ( )A.正数B.负数C.实数或不存在D.实数3.已知直线1l :x-3y+7=0,2l :x+2y+4=0,下列说法正确的是 ( )A.1l 到2l 的角是34πB.1l 到2l 的角是4πC.2l 到1l 的角是34πD.1l 到2l 的夹角是34π4.两条直线x-y+6=0与x+y+6=0的夹角是 ( ) A.4π B. 34π C.0 D.2π5.直线2x+4y+9=0到直线3x+ay+24=0的角是34π。
则a 等于 ( )A.-9B.1C.-3D.-16.直线x=2和直线的夹角是 ( ) A.3π B.6π C. 2π D.23π7.若直线1l ,2l 的斜率分别是62x +x-1=0的两根,则1l 与2l 的夹角是 ( )A.15°B.30°C.45°D.60°8.直线3x+3y+8=0到直线xsin α+ycos α+1=0(4π<α<2π) 的角是 ( )A.α-4πB. 4π-α C.α-34π D.54π-α二、填空题:9.两条直线y=x (x ≥0)和y=-x (x ≤0)的夹角是 .10.若直线y=3x+6与直线y=kx+1的夹角为45°,则k 的值为 .11.的夹角等于30°,则其方程是 . 三、解答题: 12.直线l 在y 轴上的截距是1,并且l 到直线2x+3y+6=0的角为6π,求直线l 的方程. 13.如图,已知△ABC 的一条内角平分线CD 的方程是2x+y-1=0,两个顶点A (1,2),B (-1,-1),求第三个顶点C 的坐标.14.如图,在y 轴上给定两点A (0,a ),B (0,b )(a >b >0),试在x 轴的正半轴上(原ACB 取最大值. 15.已知正方形的中心为(1,4),一个顶点为A (0,2),求过A 的正方形的两边所在直线的方程.。
高二数学天天练(66)
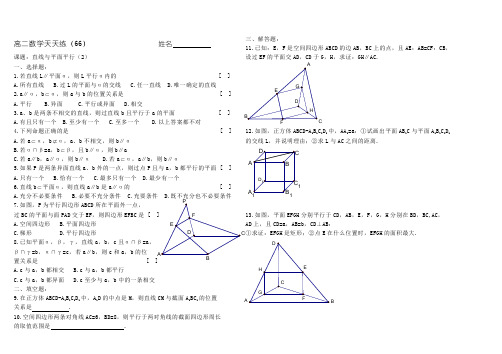
高二数学天天练(66)姓名课题:直线与平面平行(2)一、选择题:1.若直线L∥平面α,则L平行α内的 [ ]A.所有直线B.过L的平面与α的交线C.任一直线D.唯一确定的直线2.a∥α,b⊂α,则a与b的位置关系是 [ ]A.平行B.异面C.平行或异面D.相交3.a、b是两条不相交的直线,则过直线b且平行于a的平面 [ ]A.有且只有一个B.至少有一个C.至多一个D.以上答案都不对4.下列命题正确的是 [ ]A.若a⊂α,b⊄α,a、b不相交,则b∥αB.若α∩β=a,b⊂β,且b∥α,则b∥aC.若a∥b,a∥α,则b∥αD.若a⊂α,a∥b,则b∥α5.如果P是两条异面直线a、b外的一点,则过点P且与a,b都平行的平面 [ ]A.只有一个B.恰有一个C.最多只有一个D.最少有一个6.直线b⊂平面α,则直线a∥b是a∥α的 [ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.如图,P为平行四边形ABCD所在平面外一点,过BC的平面与面PAD交于EF,则四边形EFBC是A.空间四边形B.平面四边形C.梯形D.平行四边形8.已知平面α,β,γ,直线a,b,c且α∩β=a,β∩γ=b,α∩γ=c,若a∥b,则c和a,b的位置关系是 [ ] A.c与a,b都相交 B.c与a,b都平行C.c与a,b都异面D.c至少与a,b中的一条相交二、填空题:9.在正方体ABCD-A1B1C1D1中,A1D的中点是M,则直线CM与截面A1BC1的位置关系是 .10.空间四边形两条对角线AC=6,BD=8,则平行于两对角线的截面四边形周长的取值范围是 .三、解答题:11.已知:E,F是空间四边形ABCD的边AB,BC上的点,且AE:AB=CF:CB,设过EF的平面交AD,CD于G,H,求证:GH∥AC.12.如图,正方体ABCD-A1B1C1D1中,AA1=a:①试画出平面AB1C与平面A1B1C1D1 的交线L,并说明理由;②求L与AC之间的距离.13.如图,平面EFGH分别平行于CD,AB,E,F,G,H分别在BD,BC,AC,AD上,且CD=a,AB=b,CD⊥AB:①求证:EFGH是矩形;②点E在什么位置时,EFGH的面积最大.CBC1AA1A B。
高二数学天天练(45)

高二数学天天练(45) 姓名课题:椭圆的简单几何性质(1) 一、选择题:1.椭圆6x 2+y 2=6的长轴的端点坐标是 [ ]A.(-1,0),(1,0)B.(-6,0),(6,0)C.(-6,0),(6,0)D.(0,-6),(0,6) 2.已知点(3,2)在椭圆b 2x 2+a 2y 2=a 2b 2上,则 [ ] A.点(-3,-2)不在椭圆上 B.点(3,-2)不在椭圆上 C.点(-3,2)在椭圆上D.无法判断点(-3,-2),(3,-2),(-3,2)是否在椭圆上 3.椭圆3x 2+2y 2=1的焦点坐标是[ ] A.(0,-66),(0,66) B.(0,-1),(0,1) C.(-1,0),(1,0) D.(-66,0),(66,0)4.椭圆的短轴的一个端点到一个焦点的距离是5,焦点到椭圆中心的距离为3,则椭圆的标准方程是[ ]A.191622=+y x 或116922=+y x B. 192522=+y x C.1162522=+y x 或1251622=+y x D.椭圆的方程无法确定 5.椭圆的一焦点与两顶点为等边三角形的三个顶点,则长轴是短轴长的 [ ] A.3倍 B.2倍 C.2倍 D.32倍 6.椭圆的一个焦点与短轴两顶点组成一个等边三角形,则椭圆的离心率为 [ ] A.23 B.43 C. 22D. 217.椭圆12222=+by a x 和λ=+2222b y a x (λ>0)具有 [ ]A.相同的焦点B.相同的顶点C.相同的离心率D.相同的长、短轴8.已知椭圆1522=+m y x 的离心率 =510,则m 的值为 [ ] A.3 B.3或35 C.15 D. 15或3155 二填空题:9.对于椭圆x 2+ky 2=2(0<k<1),k 越接近 椭圆越扁,k 越接近 椭圆越接近圆.10.由椭圆短轴的一个端点看长轴的端点的视角为1200,则离心率为 . 11.若椭圆b 2x 2+a 2y 2=a 2b 2(a>b>0)的左焦点为F 1,右顶点A ,左顶点为B ,且离心率为215-,则∠ABF 1= . 12.中心在原点,焦点在x 轴,若长轴为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是 .三、解答题: 13.求符合下列条件的椭圆标准方程: ①焦距为8,离心率为0.8②焦点与长轴较接近的端点的距离为510-,焦点与短轴两端点的连线互 相垂直.14.已知椭圆的对称轴是坐标轴,O 为坐标原点,F 是一个焦点,A 是一个顶点,若椭圆的长轴是6,且cos ∠OFA=32,求椭圆方程.。
高二数学天天练(77)

高二数学天天练(77) 姓名课题:不等式性质一、选择题:1.不等式a>b 和b a 11>同时成立的充要条件是 [ ] A.a>b>0 B.a>0>b C.011<<a b D. b a 11>>02.若x<1,则下列关系式正确的是 [ ] A.x 1>1 B.x 3<1 C.x 2<1 D.|x|<13.a>b>c 且a+b+c=0则 [ ]A.ab>bcB.ac>bcC.ab>acD.a|b|>c|b|4.与a>b 等价的不等式是 [ ]A.|a|>|b|B.a 2>b 2C.a b>1 D.b a 22>5.a<c 是a 2<c 2成立的 [ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.a>b>0,x>0则x a xb ++的范围是 [ ] A. x a x b ++<1 B. x a x b ++>1 C.a b < x a x b ++<1 D. x a xb ++<a b7.设a ,b ,c ∈R ,下面各不等式正确的是 [ ]A.a 2+b 2≥2|ab|B.a+b ≥2abC.a 3+b 3+c 3≥3abcD.33abc cb a ≥++8.若x 、y ∈R ,且x+y=5,则3x +3y 的最小值是 [ ] A.10 B.63 C.46 D.1839.已知a >1,那么a+11-a 的最小值是 [ ] A.12-a a B.5+1 C.3 D.210.若x >y >1,a=21(lgx+lgy ),b=y x lg lg ,c=lg 2yx +,则 [ ]A.c <b <aB.b <a <cC.b <c <aD.a <b <c二、填空题: 11.已知x >y >0,且xy=1,则y x y x -+22的最小值是 . 12.实数x 、y 满足x 2+y 2=3,那么2+x y 的最大值是 . 三、解答题: 13.某小区要建一座中心对称的八边形的休闲小区,它的立体造型的平面图是由 两个相同的矩形ABCD 和EFGH 构成的面积为200平方米的十字型地域,计划在 正方形MNPQ 上建一座花坛,造价为每平方米4200元,在四个相同的矩形上 (图中阴影部分)铺花岗岩地平,造价为每平方米210元,再在四个角上铺草 坪造价为每平方米80元: (1) 设总造价为S 元,AD 长为x 米,试建立S 关于x 的关系式; (2) 当x 为何值时,S 最小,并求出这个最小值. B。
高二数学天天练(32)

高二数学天天练(32) 姓名 课题:曲线和方程(1)一、选择题:1.若命题“以方程f (x ,y )=0的解为坐标的点都是曲线C 上的点”是正确的,则下列命题中正确的是( )A. 曲线C 上的点的坐标都是方程f (x ,y )=0的解B. 方程f (x ,y )=0的曲线是CC. 坐标不满足f (x ,y )=0的点不在曲线C 上D.不是曲线C 上的点的坐标都不满足方程f (x ,y )=02.设曲线C 的方程为(x-3)2+(y-2)2=2,直线L 的方程为x+y-3=0,点P 的坐标为(2,1),那么以下成立的是( )A. 点P 在直线L 上,但不在曲线C 上B.点P 在曲线C 上,但不在直线L 上C.点P 既在曲线C 上,又在直线L 上D.点P 既不在曲线C 上,又不在直线L 上3.到两坐标轴距离之和为1的点的轨迹围成图形的面积是( ) A.1 B.2 C.2 D.以上都不对4.方程(x 2-1)2+(y 2-1)2=0所表示的曲线是( )A.两条直线B.四条直线C.两个点D.四个点5.过点(2,3)且平行于坐标轴的直线方程是( )A.x=2B.y=3C.x=2且y=3D.(x-2)(y-3)=06.下列各对方程中,表示同一曲线的是( )A.y=-x 与x y=-1 B.y=±x 与y=x C.y=±x 与|y|=|x| D. x 2+y 2=0与xy=07.曲线C 是到两直线x+y=0,x-y=0距离的积等于1的点集合,则曲线C 的方程 是 ( ) A. x 2-y 2=±1 B. x 2-y 2=±2 C. x 2-y 2=0 D. x 2-y 2=1二、填空题:8.方程x 2+xy=x 的曲线是9.若方程x 2+k 2y 2+3x-ky-4=0的曲线经过点(-2,1)则k=10.曲线x 2+y 2=1和直线x+y=0的公共点坐标为11.点M(3cos α,y 0)在曲线4x 2+9y 2=36上,则y 0=三、解答题: 12.(1)方程x 2+2xy+y 2+x+y=0表示什么图形? (2)方程(x-1)2+(y+1)2=0表示什么图形? 13.指出方程x (x-1)=y (y-1)所表示的图形C ,并判断A (0,1),B (-1,-1)是否在曲线C 上. 14.证明:方程4 x 2-y 2+6x-3y=0表示两条相交直线.。
高二数学天天练(16)
高二数学天天练(16) 姓名 课题:含有绝对值不等式一、选择题:1.若A={x||x+2|≤1},B={x|x 2-5x+6≥0},则集合A 、B 的关系是 [ ] A.A ⊆B B.B ⊂A C.A ⊇B D.A ⊂B2.不等式|2x+2log x |<2x+|2log x |的解集为 [ ]A.1<x<2B.0<x<1C.x>1D.x>23.当|x-2|<a 时,不等式|2x -4|<1成立,则正数a 的取值范围是 [ ]A.a≥B.a>-2C.0<a≤上述答案均不正确4.若α∈(54ππ,),M=|sin α|,N=|cos α|,P=12|sin α+cos α|,Q=则它们之间的关系是 [ ]A.M>N>P>QB.M>P>N>QC.M>P>Q>ND.N>P>Q>M5.α,β∈R, α>0,β>0.下式中 : ①|α+β|>|α|; ②|α+β|<|β|; ③|α+β|<|α-β|; ④|α+β|>|α-β|A. ①②B. ①③C. ①④D. ②④6.若ab<0,则下列不等式成立的是 [ ]A.|a+b|>|a-b|B.|a+b|<|a-b|C.|a-b|<|a|-|b|D.|a-b|<|a|+|b|7.若|a-c|<h,|b-c|<h,则下列不等式一定成立的是 [ ]A.|a-b|<2hB.|a-b|>2hC.|a-b|<hD.|a-b|>h8.已知正数a,b,c 满足a+d=b+c,|a-d|<|b-c|,则 [ ]A.ad=bcB.ad<bcC.ad>bcD.ad 与bc 大小不定9.不等式||||||a b a b ++≤1成立的条件是 [ ]A.ab ≠0B.22a b + ≠0C.ab ≥0D.ab ≤0二、填空题:10.不等式|31x x --|<x 的解集是 .11.不等式1122log ||log 32x ππ-≥的解集为 . 12.若M={x||x|≤1,x ∈Z},N={x|≤1,x ∈Z },则M ∩N= 13.若x ∈R,则(1-|x|)(1+x)是正数的充要条件是 三、解答题: 14.若a ∈N,集合P={x||x-a|<a+12,x ∈Z},集合Q={x||x|<2a, x ∈Z }, 求属于P ∩Q 的所有整数之和. 15.求证:|21x x +|≤12,x ∈R. 16.求S=|log log x y y x +| 的最小值,并求取得最小值时,点(x,y)的图形.。
高二数学天天练(06)
高一数学天天练(06) 姓名 课题:算术平均数与几何平均数(3)一、选择题:1、设a 和b 是不相等的正数,则( )A 、2222b a ab b a +<<+ B 、2222b a b a ab +<+<C 、2222ba b a ab +<+< D 、2222ba ab b a +<<+2、已知x>0,y>0且x+y ≤4,则下列不等式中成立的是( )A 11. 2. 111.. 411.≥≥≥+≤+xy D xy C y x B y x3、在下列函数中,最小值是2的是( ))20(s i n 1s i n . ).(33.).101(lg 1lg . )0,(55.π<<+=∈+=<<+=≠∈+=-x x x y D R x y C x x x y B x R x x x y A x x4、下列不等式的证明过程正确的是( )A.22,,=⋅≥+∈b a a b b a a b R b a 则B.若2cos 1cos 2cos 1cos =⋅≥+∈+x x x x R x 则 C 、若4424=⋅≤+∈-x x x x R x 则D 、若2))((2)]()[(0,,-=---≤-+--=+<∈b aa b a b b aa bb aab R b a 则且5、下列不等式,对一切R x ∈恒成立的是( )A 、x x D x x C xB x x 44. .2lg )1lg(. .111. .22sin sin 2222≥+≥+<+≥+6、当a>1,ab<1时a b b a log log +的取值范围是( )A 、[2,++∞)B 、(2,+∞)C 、(-∞,-2)D 、(-∞,-2]二、填空题 7、若x,y ∈R +且x+y=1,当x= y= 时 xy 的最大值是 8、若x>6时函数y=x+61-x 当x= 时,函数有 值是8 9、设a>2,x 22)21(,21,-=-+=∈x N a a M R 则M 、N 的大小关系是 10设a,b ∈R,a+b=2则2a +2b 最小值为 三、解答题 11、求证:lg9lg11<1 12、设lgx+lgy=2求y x 11+的最小值 13、已知x>0,y>0,x+2y=1,求y x 11+的最小值。
高二数学天天练(26)
高二数学天天练(26) 姓名课题:两直线的位置关系(2)一、选择题:1.若直线1l 到直线2l 的角为1θ,2l 到1l 的角为2θ,则cos (1222θθ+)的值为( )A.2B.1C.0D.不能确定2.直线1l 到直线2l 的角为α,tan α的值为 ( )A.正数B.负数C.实数或不存在D.实数3.已知直线1l :x-3y+7=0,2l :x+2y+4=0,下列说法正确的是 ( )A.1l 到2l 的角是34πB.1l 到2l 的角是4πC.2l 到1l 的角是34πD.1l 到2l 的夹角是34π4.两条直线x-y+6=0与x+y+6=0的夹角是 ( ) A.4π B. 34π C.0 D.2π5.直线2x+4y+9=0到直线3x+ay+24=0的角是34π。
则a 等于 ( )A.-9B.1C.-3D.-16.直线x=2和直线x-3y+6=0的夹角是 ( ) A.3π B.6π C. 2π D.23π7.若直线1l ,2l 的斜率分别是62x +x-1=0的两根,则1l 与2l 的夹角是 ( )A.15°B.30°C.45°D.60°8.直线3x+3y+8=0到直线xsin α+ycos α+1=0(4π<α<2π) 的角是 ( )A.α-4πB. 4π-α C.α-34π D.54π-α二、填空题:9.两条直线y=x (x ≥0)和y=-x (x ≤0)的夹角是 .10.若直线y=3x+6与直线y=kx+1的夹角为45°,则k 的值为 .11.x-y+8=0的夹角等于30°,则其方程是 . 三、解答题: 12.直线l 在y 轴上的截距是1,并且l 到直线y+6=0的角为6π,求直线l 的方程. 13.如图,已知△ABC 的一条内角平分线CD 的方程是2x+y-1=0,两个顶点A (1,2),B (-1,-1),求第三个顶点C 的坐标.14.如图,在y 轴上给定两点A (0,a ),B (0,b )(a >b >0),试在x 轴的正半轴上(原ACB 取最大值. 15.已知正方形的中心为(1,4),一个顶点为A (0,2),求过A 的正方形的两边所在直线的方程.。
最新-高二数学期末复习天天练(5、6) 精品
高二数学期末复习天天练(5)姓名 成绩1.已知一个简单多面体的各个顶点都有3条棱.设F,E,V 分别表示多面体的面数,棱数,顶点数,则2F-V 等于 ( )(A)2 (B)4 (C)8 (D)122.如图正方体ABCD -A 1B 1C 1D 1,在它的12条棱及12条面对角线所在直线中,选取若干条直线确定平面。
在所有这些平面中: (1) 过B 1C 且与BD 平行的平面有且只有一个; (2) 过B 1C 且与BD 垂直的平面有且只有一个; (3) BD 与过B 1C 的平面所成的角等于30º.上述命题中是真命题的个数为 ( )(A) 0个 (B)1个 (C)2个 (D)3个3.在空间中,有如下命题:①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线;②若平面α//平面β,则平面α内任意一条直线m//平面β;③若平面α与平面β的交线为m ,平面α内的直线n ⊥直线m ,则直线n ⊥平面β; ④若点P 到三角形三条边的距离相等,则点P 在该三角形内部的射影是该三角形的内心. 其中正确命题的个数为 ( )A .1个B .2个C .3个D .4个4.有6根细木棒,其中较长的两根分别为 3 a , 2 a,其余4根均为a ,用它们搭成三棱锥,则其中两条较长的棱所在的直线所成的角的余弦值为 .5.(本小题满分14分)已知四棱锥P —ABCD (如图),底面是边长为2的正方形. 侧棱PA ⊥底面ABCD ,M 、N 分别为AD 、BC 的中点. MQ ⊥PD 于Q ,直线PC 与平面PBA 所成角的正弦值为.33 (Ⅰ)求证:平面PMN ⊥平面PAD ;(Ⅱ)求PA 的长;(Ⅲ)求二面角P —MN —Q 的余弦值.1 A17.本小题满分14分解法一:(I )∵PA ⊥底面ABCD ,MN ⊂底面ABCD ,∴MN ⊥PA.又MN ⊥AD ,PA ∩AD=A , ∴MN ⊥平面PAD.………………………………3分∵MN ⊂平面PMN ,∴平面PMN ⊥平面PAD.…………………………………4分(Ⅱ)∵BC ⊥BA ,BC ⊥PA ,PA ∩BA=A ,∴BC ⊥平面PBA.∴∠BPC 为直线PC 与平面PBA 所成的角,即sin ∠BPC=33.……………7分 在Rt △PBC 中,PC=32332sin ==∠BPC BC , .2)22()32(2222=-=-=∴AC PC PA …………………………10分(III )由(I ),MN ⊥平面PAD ,知PM ⊥MN ,MQ ⊥MN ,∴∠PMQ 即为二面角P —MN —Q 的平面角.………………………………12分 而.1010522cos ,2222,5===∴===PM MQ PMQ MD MQ PM ……14分高二数学期末复习天天练(6)姓名成绩1、一个凸多面体的顶点数为20,棱数为30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学天天练(01)
姓名
课题:不等式的性质
一、选择题
1、下列不等式:①m-3>m-5 ②5-m>3-m ③5m>3m ④5+m>5-m其中正确的有
A、1 B、2 C、3 D、4 [ ]
2、下列命题不正确的是 [ ]
A、-a2<0 B、a2+(a-1)2>0
C、若a2≤0则a=0 D、若a≤-a则a≤0
3、不等式① a2+2>2a ② a2+b2>2(a-b-1) ③ a2+b2>ab恒成立的个数 [ ]
A、1 B、2 C、3 D、4
4、若a>b+1则下列各式中正确的是 [ ]
A、 a2>b2 B、ba>1 C、lg(a-b)>0 D、lga>lgb
5、若a>b且ba11则有 [ ]
A、a>0且b>0 B、a>0且b<0 C、a<0且b<0 D、a<0且b>0
6、若a
7、若a<0,-1 二、填空(≤,≥,<,>,=) 10、 三、 12、比较)()()(2221222122211bbaababa与的大小
8、设A=21xx,B=43xx,则A与B的大小关系是 [ ]
A、AB C、当x>0时A-2或x<-4时A
9、a不小于b等价于a b
251 561
解答题
11、比较2)23(与626的大小
、
13、比较 )(与)(222224yxxyyxyx的大小
