初三成比例线段典型例题及练习题
初三数学平行线分线段成比例专题练习题

平行线分线段成比例专题练习题
3.如图,l 1∥l 2∥l 3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A.
AD CE BC DF = B. AD BC BE AF = C. AB CD CD EF = D. AD DF BC CE =
5.如图,已知EF CD AB ////,5:3:=AF AD ,12=BE ,那么CE 的长等于( ).
A .536
B .524
C .215
D .29
9.如图所示,△ABC 中,DE ∥BC ,若1
2AD
DB =,则下列结论中
正确的是( )
A .1
2AE
EC = B .1
2DE
BC =
C .1
=3ADE ABC △的周长△的周长 D .1
=3ADE ABC △的面积△的面积
11.如图,已知:△ABC 中,DE ∥BC ,AD=3,DB=6,AE=2,则
EC=_______.
14.在平行四边形ABCD 中,E 为BC 边上的一点.连结AE .
E D
C
B A
(1)若AB=AE , 求证:∠DAE=∠D ;
(2)若点E 为BC 的中点,连接BD ,交AE 于F ,求EF ︰FA 的值.
16.如图,在△ABC 中,已知DE ∥BC ,AD=4,DB=8,DE=3.
(1)求的值;
(2)求BC的长.
19.如图,梯形ABCD中,DC//EF//AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少?
20.如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20㎝,求FC的长.
3。
北师大版九年级上册数学成比例线段同步测试题(解析版)

北师大版九年级上册数学成比例线段同步测试题(解析版)4.1 成比例线段1.四条线段a ,b ,c ,d 中,假设a 与b 的比等于c 与d 的比,即a b =c d,那么这四条线段a ,b ,c ,d 叫做__成比例线段__,简称__比例线段__.2.假设a b =c d ,那么ad =bc .假设ad =bc (a ,b ,c ,d 都不等于0),那么__a b =c d__.假设a b =c d ,那么a ±b b =c ±d d .假设a b =c d =…=m n (b +d +…+n ≠0),那么__a +c +…+m b +d +…+n =a b__. 知识点一:比例线段1.以下各组线段中,成比例线段的一组是( B )A .1,2,3,4B .2,3,4,6C .1,3,5,7D .2,4,6,82.a =0.2,b =1.6,c =4,d =12,那么以下各式中正确的选项是( C ) A .a ∶b =c ∶d B .a ∶c =d ∶bC .a ∶b =d ∶cD .b ∶a =d ∶c3.2021版«中华人民共和国全图»在左下角特别配有一幅缩小的钓鱼岛插图,比例尺为1∶1 500 000,钓鱼岛东西方长约3.5公里,那么在地图上的东西方长约为( B )A .0.002 3 cmB .0.23 cmC .4.29 cmD .0.042 9 cm4.点P 是线段AB 上的点,且AP ∶PB =1∶2,那么AP ∶AB =__1∶3__.5.在同一时辰,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,那么这棵树的高度为__9.6__米.6.a ,b ,c ,d 四条线段依次成比例,其中a =3 cm ,b =(x -1)cm ,c =5 cm ,d =(x +1)cm.求x 的值.解:依题意,得3x -1=5x +1,解得x =4,经检验,x =4是原方程的解,∴x =4 知识点二:比例的性质7.将式子ab =cd (a ,b ,c ,d 都不等于0)写成比例式,错误的选项是( D ) A.a c =d b B.c b =a dC.d a =b cD.a b =c d8.假定a ∶b =2∶3,那么以下式子一定成立的是( D )A .2a =3bB .b -a =1C.a +2b +2=23D.a +b b =53 知识点三:等比的性质 9.a b =c d =e f =23(b +d +f ≠0),那么a +c +e b +d +f=__23__. 10.线段a ,b ,c ,且a 2=b 3=c 4. (1)求a +b b的值; (2)假定线段a ,b ,c 满足a +b +c =27,求a ,b ,c 的值.解:(1)∵a 2=b 3,∴a b =23,∴a +b b =53 (2)设a 2=b 3=c 4=k ,那么a =2k ,b =3k ,c =4k ,∵a +b +c =27,∴2k +3k +4k =27,∴k =3,∴a =6,b =9,c =1211.a b =c d,那么以下式子中正确的选项是( C ) A .a ∶b =c 2∶d 2B .a ∶b =d ∶cC .a ∶b =(a +c )∶(b +d )D .a ∶b =(a -d )∶(b -d )12.假定2a =3b =4c ,且abc ≠0,那么a +b c -2b的值是( B ) A .2 B .-2 C .3 D .-313.两条直角边为6和8的直角三角形斜边与斜边上的高之比为( C )A .3∶4B .4∶3C .25∶12D .12∶2514.在比例尺为1∶2 000 000的地图上,测得A ,B 两地间的图上距离为4.5 cm ,那么A ,B 两地间的实践距离为__90__km.15.△ABC 中,a ,b ,c 区分为它的三边,且a +b +c =60,a ∶b ∶c =3∶4∶5,求△ABC 的面积.解:∵a ∶b ∶c =3∶4∶5,设a =3x ,b =4x ,c =5x ,那么3x +4x +5x =60,∴x =5,∵(3x )2+(4x )2=(5x )2,∴△ABC 是直角三角形,∴S △ABC =12·3x·4x =12×15×20=150 16.三条线段的长区分为1 cm ,2 cm , 2 cm ,假设另外一条线段与它们是成比例线段,试求出另外一条线段的长.解:设另一条线段长为x cm ,有三种状况:①1×2=2x ,解得x =2;②2×2=1·x ,解得x =22;③1×2=2x ,解得x =22.综上所述,另外一条线段的长是2 2 cm 或2 cm 或22cm 17.假定a +23=b 4=c +56,且2a -b +3c =21.试求a ∶b ∶c . 解:令a +23=b 4=c +56=m ,那么a +2=3m ,b =4m ,c +5=6m ,∴a =3m -2,b =4m ,c =6m -5.∵2a -b +3c =21,∴2(3m -2)-4m +3(6m -5)=21,即20m =40,解得m =2,∴a =3m -2=4,b =4m =8,c =6m -5=7.∴a ∶b ∶c =4∶8∶718.如下图,假定点P 在线段AB 上,点Q 在线段AB 的延伸线上,AB =10,AP BP =AQ BQ =32,求线段PQ 的长. 解:设AP =3x ,BP =2x.∵AB =10,∴AB =AP +BP =3x +2x =5x ,即5x =10.∴x=1.∴AP =6,BP =4.∵AQ BQ =32,∴可设BQ =y ,那么AQ =AB +BQ =10+y.∴10+y y =32.解得y =20.∴PQ =PB +BQ =4+20=2419.△ABC 的三边长区分为a ,b ,c ,且(a -c )∶(a +b )∶(c -b )=-2∶7∶1,那么△ABC 是( C )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形20.在△ABC 中,AB =12,点E 在AC 上,点D 在AB 上,假定AE =6,EC =4,且AD DB =AE EC.(1)求AD 的长;(2)试问DB AB =EC AC能成立吗?请说明理由. 解:(1)AD =365 (2)能,由AB =12,AD =365,故DB =245.于是DB AB =25,又EC AC =410=25,故DB AB =EC AC。
成比例线段(原卷版)-九年级数学(北师大版)

第18讲成比例线段1.了解成比例线段;2.掌握比例的性质;3.掌握黄金分割及其应用。
1.成比例线段:对于四条线段a 、b 、c 、d ,如果其中两条线段的比与另两条线段的比相等,如a :b =c :d ,我们就说这四条线段是成比例线段,简称比例线段.2.比例的性质:(1)基本性质:若a :b =c :d ,则ad=bc ;(2)合比性质:如果++==a c a b c d b d b d ,那么如果--==.a c a b c db d b d ,那么(3)等比性质:如果+c c=====k.+da c a ab d b d b k,那么(4)比例中项:若a :b=b :c ,则2b=ac ,b 称为a 、c 的比例中项.要点:通常四条线段a,b,c,d 的单位应该一致,但有时为了计算方便,a,b 的单位一致,c,d 的单位一致也可以。
3.黄金分割如果点P 把线段AB 分割成AP 和PB,(AP>PB)两段,其中AP 是AB 和PB 的比例中项,那么就称这种分割为黄金分割,点P 是线段AB 的黄金分割点.12AP AB -=≈0.618AB(12叫做黄金分割值).要点:线段的黄金分割点有两个.考点1:成比例线段例1.下列各组线段中,成比例线段的组是()A .0.2cm,0.3cm,4cm,6cmB .1cm,3cm,4cm,8cmC .3cm,4cm,5cm,8cmD .1.5cm,2cm,4cm,6cm例①12cma=例A.ab例15例b例考点3:比例中项例34例A.a、bC.c是例(1)求a、(2)若线段例A.50cm例离的比是例考点4:比例的性质综合例A.如果例(1)求代数式(2)如果2例例考点5:分类讨论题例例段能够组成比例线段.例考点6:黄金分割例例A.55例例例例AP =_____.例例考点8:黄金分割的应用例A .(7例作一张“黄金矩形例富的美学价值.例31.“黄金分割”台的黄点分割位置会更自然得体,如图,舞台长例32.在学习“黄金分割”时,的端点B 作BD AB ⊥,使12BD AB =例33.在20世纪70年代,著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做EF 将矩形窗框ABCD 分为上下两部分,其中点E 为边AB 的黄金分割点(AE BE <).已知AB 为2米,则线段BE 的长为______米(结果保留根号).例34.如图,线段1AB =,点C 是线段AB 的黄金分割点()AC BC >,1C 是线段AC 的黄金分割点()111C AC C C >,2C 是线段1AC 的黄金分割点,以此类推,则m AC =__________.考点9:黄金分割难点例35.请阅读下列材料,并完成相应的任务:公元前300年前后,欧几里得撰写的《几何原本》系统地论述了黄金分割,成为最早的有关黄金分割的论著.黄金分割(goldensection )是指把一条线段分割为两部分,使较大部分与全长的比值等于较小部分与较大部分的比值.如图①,在线段AD 上找一个点C ,C 把AD 分为AC 和CD 两段,其中AC 是较小的一段,如果::AC CD CD AD =,那么称线段AD 被C 点黄金分割,点C 叫做线段AD 的黄金分割点,AC 与CD 的比值叫做黄金分割数.为简单起见,设1,AD CD x ==,则1AC x =-.∵::AC CD CD AD =,∴……任务:(3)已知线段例“如图C黄金分割,点C叫做线段另有一点D把线段AB分成两条线段材料二:对于实数:a1<a2<a﹣a)则称a为a,a的黄金数,如图.)实数0<a<b<1,且b为0,)实数k<n<m<t,t=2|k|,m一、单选题二、填空题6.(2021·黑龙江大庆·统考中考真题)已知0234x y z==≠,则2x xy yz+=________7.(2023·四川达州·统考中考真题)如图,乐器上的一根弦80cm AB =,两个端点,A B 固定在乐器板面上,支撑点C 是靠近点B 的黄金分割点,支撑点D 是靠近点A 的黄金分割点,,C D 之间的距离为8.(2022·江苏镇江·统考中考真题)《九章算术》中记载,战国时期的铜衡杆,其形式既不同于天平衡杆,也异于称杆衡杆正中有拱肩提纽和穿线孔,一面刻有贯通上、下的十等分线.用该衡杆称物,可以把被称物与砝码放在提纽两边不同位置的刻线上,这样,用同一个砝码就可以称出大于它一倍或几倍重量的物体.图为铜衡杆的使用示意图,此时被称物重量是砝码重量的_________倍.9.(2022·陕西·统考中考真题)在选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做下两部分,其中E 为边AB 的黄金分割点,即一、单选题1.下列各组线段的长度成比例的是()A .1cm ,2cm ,3cm ,4cm B .3cm ,4cm ,5cm ,6cm C .5cm ,10cm ,15cm ,20cmD .6cm ,4cm ,3cm ,2cmA .1245-11.如果点C 是线段A .512BC AB -=C .512AB AC -=A .12S S >14.“黄金分割”给人以美感,它在建筑、艺术等领域有着广泛的应用.如图(部分,如果BC AC :段AB AC AD 、、的黄金分割点,(A .52-B .522-C .352-D .52-二、填空题15.如果53x y =,那么x x y=-________.16.已知线段AB 长是2,P 是线段AB 上的一点,且满足2·,AP AB BP =那么AP 17.已知点P 是线段AB 上的黄金分割点,且2AB =,AP BP >,那么AP =_____18.已知点P 是线段AB 上的黄金分割点,且4AB =,AP BP >,那么BP 的长度是19.已知线段AB =220.已知点P 把线段的值等于___________21.五角星是我们生活中常见的一种图形,如图五角星中,点割点,已知黄金比为3a c e 三、解答题25.如果234a b c==,且328a b c -+=,求26.(1)已知线段a =2,b =9,求线段(2)已知x :y =4:3,求y xy -的值.27.已知x :y :z =3:5:7,求2353x y x y -+28.已知线段AB=10cm ,点C 是AB 上的黄金分割点,求29.如图,在线段AB 上有一点C ,若点C 是线段AB 的黄金分割点(AC BC <30.(1)已知34b a =,求22a b a b-+的值.(2)已知234x y z==,求23x y z x y z-+++的值.31.一般地,点C 把线段AB 分成两条线段BP AB(1)以图1中的AP 为底,BP 为腰得到等腰APB △(如图2),等腰义为:满足≈0.618=≈+底腰腰底腰的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:(2)如图1,设1AB =,请你说明为什么k 约为0.618;(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“S 的图形分成面积为S 和面积为S 的两部分(设S S <),如果S。
初中数学相似三角形题型归类——成比例线段专项练习5(附答案详解)

初中数学相似三角形题型归类——成比例线段专项练习5(附答案详解) 1.下列四条线段中,不能成比例的是( )A .a=3,b=6,c=2,d=4B .a=1,b= c= ,C .a=4,b=6,c=5,d=10D .a=2,b=c= 2.已知点P 是线段AB 的一个黄金分割点()AP PB >,则:PB AB 的值为( )A .32- B .12C .12D .34- 3.已知点P 是线段AB 的黄金分割点(AP >PB ),AB=4,那么AP 的长是( )A .2B .2C .1D 24.下面四组线段中不能成比例线段的是( )A . 3、6、2、4B . 4、6、5、10C .1?D .、4、5.已知2AB =,点P 是线段AB 上的黄金分割点,且AP BP >,则AP 的长为( )A 1B .12C .352D .36.线段a 、b 、c 、d 是成比例线段,a=4、b=2、c=2,则d 的长为( ) A .1B .2C .3D .47.在比例尺是1:3800的旅游交通图上,A B 、两观光点长约7cm ,则他的实际长度为( ) A .0.266kmB .2.66kmC .26.6kmD .26600km8.四条线段a ,b ,c ,d 成比例,其中b =3cm ,c =8cm ,d =12cm ,则a =( ) A .2cmB .4cmC .6cmD .8cm9.已知线段a 是线段b ,c 的比例中项,则下列式子一定成立的是( )A .a b b c=B .a c b a =C .a cc b = D .b c a b= 10.已知654a b c==≠0且a +b ﹣2c =9,则a 的值为( )A .3B .12C .15D .1811.在比例尺为1:40000的地图上,某条道路的长为7cm ,则该道路的实际长度是_____km .12.已知两地的实际距离为800米,画在图上的距离(图距)为2厘米,在这样的地图上,图距为16厘米的两地间的实际距离为______千米.13.已知线段c 是线段a 和b 的比例中项,且a 、b 的长度分别为2cm 和8cm ,则c 的长度为_____cm .14.已知线段a 、b 、c ,其中c 是a 、b 的比例中项,若a =2cm ,b =8cm ,则线段c =_____cm .15.已知四条线段a 、b 、c 、d 成比例,且线段4cm a =,线段7cm b =,线段2cm c =,则线段d =______cm .16.已知三条线段的长分别是4cm ,6cm 和10cm ,则再加一条__________cm 的线段,才能使之四条线段成比例.17.电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB 长为20m ,试计算主持人应走到离A 点至少_____m 处.(结果精确到0.1m )18.已知线段a =2厘米,c =8厘米,则线段a 和c 的比例中项b 是______厘米. 19.已知a =4,b =9,c 是a b 、的比例中项,则c =____.20.已知线段AB=10,点C 是线段AB 上的黄金分割点(AC<BC),则AC 长是_______(精确到0.01).21.如图,在Rt ABC △中,CD 是斜边AB 上的高线,试猜想线段AC ,AB ,CD ,BC 是否成比例。
初三数学平行线分线段成比例专题习题
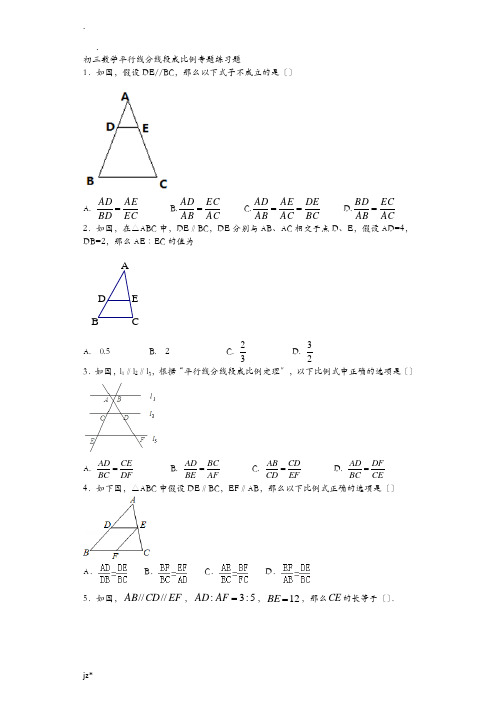
7.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.AB=l,BC=3,DE =2,那么EF'的长为〔〕
A.4 B.5 C.6 D.8
8.如图, ∥ ∥ ,两条直线与这三条平行线分别交于点A、B、C和D、E、F. ,那么 的值为〔〕
考点:平行线分线段成比例.
20.8.
【解析】
试题分析:由DE∥BC,AD:DB=3:2,得到 ,再由EF∥AB, ,可设BF=3k,FC=2k,得到BC=BF+FC=5k=20cm,解出k的值即可得到FC的长.
试题解析:∵DE∥BC,AD:DB=3:2,∴ ,∵EF∥AB, ,设BF=3k,FC=2k,∴BC=BF+FC=3k+2k=5k,又BC=20cm,∴5k=20,k=4,∴FC=2k=8.
求证:〔1〕△ACE≌△BCD;
〔2〕 .
16.如图,在△ABC中,DE∥BC,AD=4,DB=8,DE=3.
〔1〕求 的值;
〔2〕求BC的长.
17.如图,a∥b∥c,
〔1〕假设AC=6cm,EC=4cm,BD=8cm,那么线段DF的长度是多少厘米?
〔2〕假设AE:EC=5:2,DB=5cm,那么线段DF的长度是多少厘米?
〔3〕∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= ,
可得: .
考点:相似形综合题.
19.6cm.
【解析】
试题分析:由平行线的性质可得 , ,进而再由题中条件即可求解BC与GC的长.
试题解析:∵DC∥EF∥AB,∴ =2,又AG=5cm,∴GC=2.5cm. ,CF=2cm,
∴BC=6cm.CB的长是6cm.
成比例线段、平行线分线段成比例测试-简单数学之年九年级下册同步讲练(原卷版)(人教版)

专题27.2.2成比例线段、平行线分线段成比例一、选择题(本大题共14个小题,每题2分,共28分,在每个小题的四个选项中只有一项是符合题目要求的)1.已知线段b 是线段a 、c 的比例中项,3a =,2c =,那么b 的长度等于( )A .B .6CD .1692.已知3x =7y (y ≠0),则下列比例式成立的是( ) A .3x =7yB .7x=3y C .x y =37D .3x =7y 3.如图,在ABC 中,//DE BC ,若3,2AD AE BD ===,则线段CE 的长为( )A .3B .4C .43D .234.已知234a b c ==,则a b c+的值是( ) A .45 B .74C .1D .545.已知:2:3x y =,下列等式中正确的是( )A .():1:3x y y -=B .():2:1x y y -=C .():(1):3x y y -=-D .():(1):2x y y -=-6.在比例尺为1∶5000的地图上,量得甲、乙两地的距离为25cm ,则甲、乙两地的实际距离是( ) A .1250kmB .125kmC .12.5kmD .1.25km7.如果点C 是线段AB 的黄金分割点,那么下列线段比中比值不可为12的是( ) A .ACBCB .BCACC .AB BCD .ACAB8.已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是( ) A .lB .2.25C .4D .29.下列各组线段的长度成比例的是()A.6cm、2cm、1cm、4cm B.4cm、5cm、6cm、7cm C.3cm、4cm、5cm、6cm D.6cm、3cm、8cm、4cm 【答案】D【解析】10.如图l1∥l2∥l3,若32ABBC=,DF=10,则DE=()A.4B.6C.8D.911.如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=6,则CD的长为()A.14B.17C.8D.1212.古希腊时期,≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.某女老师上身长约61.8cm,下身长约96cm,为尽可能达到黄金比的美感效果好,她应穿的高跟鞋的高度大约为(精确到1cm)()A.4cm B.5cm C.6cm D.7cm13.如图所示,BE=3EC,D是线段AC的中点,BD和AE交于点F,已知△ABC的面积是7,求四边形DCEF的面积()A .1B .54C .74D .214.如图,在矩形ABCD 中,将△ABE 沿着BE 翻折,使点A 落在BC 边上的点F 处,再将△DEG 沿着EG 翻折,使点D 落在EF 边上的点H 处. 若点A ,H ,C 在同一直线上,AB=1,则AD 的长为( )A .32B .12C D二、填空题(本题共4个小题;每个小题3分,共12分,把正确答案填在横线上) 15.如图,直线AB ∥CD ∥EF ,已知AC =3,CE =4,BD =3.6,则DF 的长为_____.16.如图所示,乐器上的一根弦80AB cm =,两个端点A B ,固定在乐器面板上,支撑点C 是靠近点B 的黄金分割点(即AC 是AB 与BC 的比例中项),支撑点D 是靠近点A 的黄金分割点,则AC =______cm ,DC =______cm.17.线段a ,b ,c ,d 成比例,即a cb d=,其中a=2cm ,b=4cm ,c=5cm ,则d=______. 18.如图,正方形ABCD 和正方形CEFG 的边长分别为3和2,且B 、C 、E 在一直线上,AE 与CF 交于点P ,则CPFP=__________.三、解答题(本题共8道题,19-21每题6分,22-25每题8分,26题10分,满分60分) 19.已知::3:4:5x y z =.(1)求x yz+的值; (2)若6x y z ++=,求x 、y 、z . 20.已知线段a =0.3m ,b =60cm ,c =12dm . (1)求线段a 与线段b 的比.(2)如果线段a 、b 、c 、d 成比例,求线段d 的长. (3)b 是a 和c 的比例中项吗?为什么?21.如图,四边形ABCD 与四边形ABFE 都是矩形,AB =3,AD =6.5,BF =2. (1)求下列各线段的比:CD BC ,EF CF ,BFAB; (2)指出AB ,BC ,CF ,CD ,EF ,FB 这六条线段中的成比例线段(写一组即可)22.如图,以长为2的线段AB 为边作正方形ABCD ,取AB 的中点P ,连接PD ,在BA 的延长线上取点F ,使PF =PD ,以AF 为边作正方形AMEF ,点M 在AD 上. (1)求AM ,DM 的长; (2)求证:AM 2=AD·DM ;(3)根据(2)的结论你能找出图中的一个黄金分割点吗?23.如图,已知AD ∥BE ∥CF ,它们依次交直线1l 、2l 于点A 、B 、C 和点D 、E 、F ,25DE EF =,14AC =;(1)求AB 、BC 的长;(2)如果7AD =,14CF =,求BE 的长;24.如图是6×6的方格纸,点A 、B 、C 都在格点上,按要求画图:(1)在图1中找到一个格点D ,使以A ,B ,C ,D 为顶点的四边形是平行四边形; (2)在图2中仅用无刻度直尺,在线段AC 取一点P ,使得AP =14AC .(保留作图痕迹,不写画法)25.阅读与计算,请阅读以下材料,并完成相应的问题.角平分线分线段成比例定理,如图1,在△ABC 中,AD 平分∠BAC ,则ABAC =BD CD.下面是这个定理的部分证明过程.证明:如图2,过C 作CE ∥DA .交BA 的延长线于E .… 任务:(1)请按照上面的证明思路,写出该证明的剩余部分;(2)填空:如图3,已知Rt △ABC 中,AB =3,BC =4,∠ABC =90°,AD 平分∠BAC ,则△ABD 的周长是 .26.已知正方形ABCD的对角线相交于O,点P在射线AO上,∠MPN=90°.(1)如图1,当P与点O重合,M、N分别在AD、AB上,AM=2DM,则ANBN=__________;(2)如图2,点P在CO上,AP=2CP,M为AD的中点,求ANBN的值.(3)如图3,P在AC的延长线上,M为AD的中点,AP=nCP,则ANBN=____________(用含n的式子表示)。
初三数学平行线分线段成比例专题练习题
1.如图,若 DE//BC,则下列式子不成立的是(
)
A. AD AE
B.
AD EC C. AD AE DE D. BD EC
BD EC
AB AC
AB AC BC
AB AC
2.如图,在△ ABC中,DE∥BC,DE分别与 AB、AC相交于点 D、E,若 AD=4,DB=2, 则 AE︰EC的值为
)
A.
B.
C.
D.
5.如图, 已知 AB // CD // EF , AD : AF 3 : 5 , BE 12 ,
等于(
).
那么 CE 的 长
A. 36
B
. 24
C
. 15
5
5
2
D. 9 2
6.如图,直线 l 1// l 2// l 3,直线 AC分别交 l 1, l 2, l 3 于点 A, B, C;直线 DF分别交 l 1, l 2, l 3 于点
15.(本小题满分 10 分)如图,已知 B、C、E 三点在同一条直线上,△ ABC与△ DCE都是等边三角形 . 其中 线段 BD交 AC于点 G,线段 AE交 CD于点 F.
D A
G
F
B
C
E
求证:( 1)△ ACE≌△ BCD;
( 2) AG
AF
.
GC FE
16.如图,在△ ABC中,已知 DE∥ BC, AD=4, DB=8, DE=3.
.
13.如图,在△ ABC中, DE∥BC,分别交 AB, AC于点 D,E.若 AD =3, DB =2, BC =6,则 DE的长
为
.
14.在平行四边形 ABCD中, E 为 BC边上的一点.连结 AE.
成比例线段练习题及答案
成比例线段练习题及答案一、判断题请判断下列说法是否正确,正确的在括号内写上“√”,错误的写上“×”。
(×) 1. 成比例线段的比值始终保持不变。
(√) 2. 如果线段AB与线段CD成比例,那么AB与DC也成比例。
(√) 3. 如果线段AB与线段CD成比例,那么AB:BC = CD:DE。
(×) 4. 成比例线段可以有无穷多个比例关系。
二、选择题从每题所给的选项中,选择符合题意的答案,并将其编号填入题前括号内。
1. 已知线段AB与线段CD成比例,若AB=8,CD=20,则BC的长度为:A. 25B. 32C. 5D. 2(√) 2. 线段AB与线段CD成比例,若AB:BC = 3:2,且BC的长度为10 cm,则线段AB的长度为:A. 3 cmB. 10 cmC. 15 cmD. 20 cm(×) 3. 线段AB与线段CD成比例,若AB:BC = 3:4,CD:DE = 2:3,且AD的长度为40 cm,则线段AE的长度为:A. 80 cmB. 120 cmC. 100 cmD. 60 cm(√) 4. 线段AB与线段CD成比例,若AB:BC = 2:3,且BC的长度为15 cm,则线段CD的长度为:A. 5 cmB. 20 cmC. 7.5 cmD. 10 cm三、计算题根据题目中给出的条件,计算出目标线段的长度。
1. 已知线段AB与线段CD成比例,且AB:BC = 5:2,CD:DE = 3:4,且BC的长度为8 cm,求线段DE的长度。
解题过程:根据已知条件,AB:BC = 5:2,CD:DE = 3:4,BC = 8 cm。
根据成比例线段的性质,我们可以得出以下等式:AB/BC = CD/DE5/2 = 3/4通过交叉相乘得到:4 * AB = 2 * CDCD = 2 * AB / 4CD = AB / 2由此可知CD的长度为4 cm。
再根据CD:DE = 3:4,可得:CD / DE = 3 / 44 / DE = 3 / 4通过交叉相乘得到:4 * 4 = 3 * DEDE = 4 * 4 / 3DE = 16 / 3由此可知线段DE的长度为16/3 cm。
初三数学比例线段练习题
初三数学比例线段练习题1. 已知线段AB与线段CD的比为2:5,线段CD的长度为15cm,求线段AB的长度。
解析:设线段AB的长度为x cm。
根据题意,可以列出比例方程:2/5 = x/15。
通过交叉相乘可以得到:5x = 2 * 15。
解方程可知:5x = 30,得到x = 6。
所以,线段AB的长度为6 cm。
2. 若线段EF与线段GH的比为3:4,且线段EF的长度为24 cm,求线段GH的长度。
解析:设线段GH的长度为y cm。
根据题意,可以列出比例方程:3/4 = 24/y。
通过交叉相乘可以得到:3y = 4 * 24。
解方程可知:3y = 96,得到y = 32。
所以,线段GH的长度为32 cm。
3. 已知线段IJ与线段KL的比为7:3,且线段IJ的长度为21 cm,求线段KL的长度。
解析:设线段KL的长度为z cm。
根据题意,可以列出比例方程:7/3 = 21/z。
通过交叉相乘可以得到:7z = 3 * 21。
解方程可知:7z = 63,得到z = 9。
所以,线段KL的长度为9 cm。
4. 两条线段比值为9:7,若线段A的长度为63 cm,求线段B的长度。
解析:设线段B的长度为w cm。
根据题意,可以列出比例方程:9/7 = 63/w。
通过交叉相乘可以得到:9w = 7 * 63。
解方程可知:9w = 441,得到w = 49。
所以,线段B的长度为49 cm。
5. 两条线段比值为3:10,若线段A的长度为12 cm,求线段B的长度。
解析:设线段B的长度为v cm。
根据题意,可以列出比例方程:3/10 = 12/v。
通过交叉相乘可以得到:3v = 10 * 12。
解方程可知:3v = 120,得到v = 40。
所以,线段B的长度为40 cm。
通过以上练习题的解答,我们可以看出在比例问题中,可以用代数方法解决。
根据已知条件,设未知量,并列出比例方程,通过解方程求得未知量的值。
这样的练习题有助于我们加深对比例概念的理解,并提高解决实际问题时的数学能力。
初三数学成比例线段练习
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习必备 欢迎下载
【典型例题】
类型一、比例线段
例题1. (1)求证:如果,那么.
(2)已知线段a、b、c、d,满足acbd ,求证:acabdb.
类型二、相似图形
例题2.(1) 如果两个四边形的对应边成比例,能不能得出这两个四边形相
似?为什么?
(2)下面的四个图案是空心的矩形,正方形,等边三角形,不等边三角形,
其中每个图案的边的宽度都相等,那么每个图案中边的内外边缘所围成的几何
图形不相似的是( )
类型三、相似多边形
例题3.(1) 已知四边形与四边形相似,且
.四边形的周长为26.求四边形
的各边长.
(2)等腰梯形与等腰梯形相似,
,求出的长及梯形各
角的度数.
学习必备 欢迎下载
例题4. 某小区有一块矩形草坪长20米,宽10米,沿着草坪四周要修一宽度
相等的环形小路,使得小路内外边缘所成的矩形相似,你能做到吗?若能,求
出这一宽度;若不能,说明理由.
考点集训 图形的相似和比例线段(提高)
一.选择题
1. 在比例尺为1︰1 000 000的地图上,相距3cm的两地,它们的实际距离为( )
A.3 km B.30 km C.300 km D.3 000 km
2. 已知线段a、b、c、d满足=abcd把它改写成比例式,其中错误的是( )
A.::bcda B.::abcd C.::cbad D.::acdb
3. 已知△ABC的三边长分别为6cm、7.5cm、9cm,△DEF的一边长为4cm,当
△DEF的另两边的长是下列哪一组时,这两个三角形相似( )
A.2cm,3cm B.4cm,5cm C.5cm,6cm D.6cm,7cm
P6
4.△ABC与△A1B1C1相似且相似比为,△A1B1C1与△A2B2C2相似且相似比为,
则△ABC与△A2B2C2的相似比为 ( )
A. B. C.或 D.
5.下列两个图形:① 两个等腰三角形;② 两个直角三角形;③ 两个正方形;
④ 两个矩形;⑤ 两个菱形;⑥ 两个正五边形.其中一定相似的有( )
A. 2组 B. 3组 C. 4组 D. 5组
学习必备 欢迎下载
6.一个钢筋三角架三边长分别是20cm,50cm,60cm,现要做一个与其相似的
三角架,只有长30cm,50cm的两根钢筋,要求以其中一根为一边,从另一
根截下两段(允许有余料)做为其他两边,则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
P7
二. 填空题
7. 小明有一张的地图,他想绘制一幅较小的地图,若新地图宽为
30cm,则新地图长为_________cm.
8. △ABC的三条边长分别为、2、,△A′B′C′的两边长分别为1和
,且△ABC与△A′B′C′相似,那么△A′B′C′的第三边长为
____________
9. 如图:梯形ADFE相似于梯形EFCB,若AD=3,BC=4,则______.AEBE
10.已知若-3=,=____;4xyxyy则若5-4=0,xy则x:y=___.
11.如图:AB:BC=________,AB:CD=_________,BC:DE=________,
AC:CD=__________,CD:DE=________.
P8
12. 用一个放大镜看一个四边形ABCD,若四边形的边长被放大为原来的10倍,
下列结论①放大后的∠B是原来∠B的10倍;②两个四边形的对应边相等;
③两个四边形的对应角相等,
则正确的有 .
三.综合题
学习必备 欢迎下载
13.如果abcdkbcdacdabdabc,一次函数ykxm 经
过点(-1,2),
求此一次函数解析式.
P9
14. 如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以
EM、MF为一边作矩形EMNH、MFGN,使矩形MFGN与矩形ABCD相似.令MN=x,
当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?
15. 从一个矩形中剪去一个尽可能大的正方形,如图所示,若剩下的矩形与原
矩形相似,
求原矩形的长与宽的比.
