三视图中的小正方体计数问题口诀
由三视图确定小正方体的个数的方法

由三视图确定小正方体的个数的方法
通过三视图确定小正方体的个数是一种简单而有效的方法,可以用来解决许多复杂的几何问题。
三视图法是一种几何技术,它使用三个平面图来表示一个物体的形状,其中包括正视图、左视图和俯视图。
这三个视图是从不同的角度来看待物体的,可以清楚地显示出物体的三维形状。
例如,如果要确定小正方体的个数,可以使用三视图法。
首先,先找出三个视图,即正视图,左视图和俯视图,仔细观察每个视图中小正方体的位置,数数它们的个数。
然后,根据三个视图中小正方体的位置和数量,计算出小正方体的总数。
根据三视图法,可以通过观察三个视图来确定小正方体的总数,而不需要真正地计算它们的体积。
这一步骤非常实用,可以节省大量的时间和精力。
当然,在使用三视图法之前,需要先熟悉三视图的概念,然后根据实际情况,灵活地运用这一技术来解决实际问题。
只有掌握了这种几何方法,才能解决复杂的几何问题。
总之,三视图法是一种有效的几何方法,可以用来快速确定小正方体的个数。
它可以节省大量的时间和精力,因此被广泛应用于复杂的几何问题的解决中。
用三视图确定小正方体的块数的简便方法
(2)因为从俯视图可以确定底层有正方体,所以方格中的数字最
小为1,那么只要将每列上的数字留一个,其余的均改为1,这 样就可以确定最少需要的小正方体的块数.举两种情况如图:
321
321
111
32
11
32
32
11
11
所以这个几何体最多需要16块,最少需要10块
上主视图,左视图所看到的小正方体的最高层数.然后,在方 格纸中填入方格所在横,竖上的较小的数字(如果相同取相同的 数字),那么就可确定这个几何体所需最多的小正方体的块数.
(2)在方格纸中寻找所在横、竖方向上的数字一样的方格,取 相同的数字填人方格,这样就可以确定最少需要的小正方体 的块数.
22 3
格,则可得到这个几何体所需最多的小正方体的块数.
(2)因为从俯视图可以确定底层有正方体,所以方格中的数! 字最小为1,那么只要将每横上的数字留一个,其余的均改为1,
这样就可以确定最少需要的小正方体的块数.举两种情况,如
下图:
3
3
3
33
3
1
11
2 222
1
11
2 211
1
11
2ቤተ መጻሕፍቲ ባይዱ21
所以这个几何体最多需要11块,最少需要9块.
2 3
1
1
所以这个几何体最多需要19块,最 少需要8块.
2 13 2
在通过小正方体组合图形的三视图,确定组合图形中小正方 体的个数,在中考或竞赛中经常会遇到.解决这类问题如果没 有掌握正确的方法b呶仅依赖空间想象去解决,不仅思维难度 很大,还很容易出错.通过三视图确定组合图形的小正方体的 个数,关键是要弄清楚这个小正方体组合图形共有多少行、多 少列、每行每列中各有多少层,理清了这些行、列、层的数量, 再按照上面介绍的方法,小正方体的个数就迎刃而解了.
怎样由三视图确定正方体个数

怎样由三视图确定正方体个数山东李浩明三视图不仅是新教材的一大亮点,也是近些年各省市中考的热点•学习视图,不仅会画空间几何体的三视图,还应会根据一个空间几何体的三视图,想象出这个简单几何体的形状,若是由小正方体组成的几何体,则要能确定小正方体的个数例1.由一些大小相同的小正方体组成的几何体的三种视图如图所示,那么组成几何(A) 4(B) 5 (C) 6 (D) 7析解:解决这类问题要做到看俯视图,从左至右共有三列,从上到下共三行;看主视图,共有三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中的一、三列上分别只有一个正方体,分别填 1 (如图1);三看左视图,共三列两行,第一列和第三列上分别只有一层,第二列上有两层,则俯视图中第一行只有一个正方体,填1,第二行有两个正方体,填2,第三行第二列只有一个正方体,填每个小正方体的个数如图1所示,搭成这个几何体的小正方体的个数是本题结果就选(C).相应的几何体如图2 所示.1,所以该俯视图上1+2+1 + 1+1=6,故主视图左视图俯视图图1例2.如图是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是 ___________ 个•主视圉在观图俯視图析解:先看俯视图,从左至右共有两列,从上到下共两行;再看主视图,共有两列两行,第一列上只有一层,第二列上有两层,则俯视图中的第一列的第一行只有一个正方体,填1 (如图3),第二列的第一行、第二行中至少有一行有两个正方体,具体情况再看左视图;左视图共两列两行,第一列有两层,第二列上只有一层,则俯视图中(观察者需站在俯视图的左侧看)第一行的第二列有两个正方体,填2,第二行只有一个正方体,填1,所以该俯视图上每个小正方体的个数如图3所示,搭成这个几何体的小正方体的个数是1+2+仁4,故本题结果就填4.相应的几何体如图4 所示.例3 •一个几何体是由若干个相同正方体组成的,其主视图和左视图如图5所示,则这个几何体最多可由多少个这样的正方体组成()(A) 12 个(B) 13 个(C) 14 个(D) 18 个2121112]_2_正方形,由主视图可知在俯视图第1、3列每个正方形内填2,第2列每个正方形内填1;解析:主视图和左视图都为3列,可知几何体的俯视图有三列三行,最多为又由左视图可知,在俯视图的1、3 行中(观察者需站在俯视图的左侧看)每个小正方形内都填入2,第2行填1,重叠交叉处数字取小,如上图,故最多由13个组成.故选(B).点评:由三视图到确定几何体,应根据主视图和俯视图情况分析,再结合左视图的情况定出几何体,最后便可得出这个几何体组合的小正方体个数.。
由视图确定小正方体的块数的简便方法

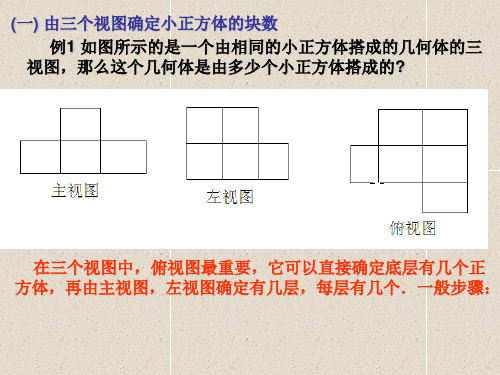
(一) 由三个视图确定小正方体的块数 例1 如图所示的是一个由相同的小正方体搭成的几何体的三
视图,那么这个几何体是由多少个小正方体搭成的?
在三个视图中,俯视图最重要,它可以直接确定底层有几个正 方体,再由主视图,左视图确定有几层,每层有几个.一般步骤:
1.复制一张俯视图,在俯视图的下方、左方分别标上主 视图,左视图所看到的小正方体的最高层数.
2.由左视图,俯视图来确定 方法跟由主视图,俯视图来确定一样.
例3 如图所示的是由一些
3
3
1
11
2 222
解: (1)复制一张俯视图,在俯视图的左方标上左视图所看到 的小正方体的最高层数,将这些数字填人所在横上的每一个方
则可得到这个几何体所需最多的小正方体的块数.
(2)因为从俯视图可以确定底层有正方体,所以方格中的数字最
小为1,那么只要将每列上的数字留一个,其余的均改为1,这 样就可以确定最少需要的小正方体的块数.举两种情况如图:
321
321
111
32
11
32
32
11
11
所以这个几何体最多需要16块,最少需要10块
3 .由主视图,左视图来确定 由这两个视图来确定小正方体的块数是最难的
例4 如图所示的是由一些正方体小木块搭成的几何体的主视 图、左视图,它最多需要多少块?最少需要多少块?
主视图
左视图
22 32
11
1 22 132 11 1
2 13 2
解 (1)取一张3 X4的方格纸,在方格纸的下方,左方分别标
上主视图,左视图所看到的小正方体的最高层数.然后,在方 格纸中填入方格所在横,竖上的较小的数字(如果相同取相同的 数字),那么就可确定这个几何体所需最多的小正方体的块数.
根据三视图求小正方体的个数课件

实例三
要点一
总结词
实际生活中三视图的小正方体个数求解需要结合实际情况 进行,通过观察实际物体的三视图并结合实际尺寸来进行 计算。
要点二
详细描述
在实际生活中,有些物体可能不是规则的几何体,如机器 零件、建筑物等。此时需要结合实际物体的尺寸和三视图 中的投影来进行计算。例如,对于一个建筑物,可以通过 测量其长、宽、高来计算其小正方体的数量。同时,还需 要注意实际物体中的一些细节和特征,如孔洞、凸起等, 这些特征可能会影响小正方体的数量。
下一步学习建议
学习根据多视图计算小正方体个数的方 法
练习常见题型及解题思路 提高空间想象能力和几何思维能力
深入理解多视图的原理及应用 学习立体几何中其他相关知识点
THANKS
感谢观看
在日常生活和生产实践中,很多时候 需要从三视图来观察物体的形状和结 构,因此掌握三视图求解小正方体的 个数是非常重要的技能。
课程目标
理解三视图的基本概 念和原理。
学会求解三视图中小 正方体的个数。
掌握三视图下小正方 体的排列规律。
学习方法
通过实例分析,让学生了解三视 图与立体图之间的转换关系。
通过对不同类型三视图的讲解, 让学生掌握小正方体的排列规律
总结词
理解三视图中的投影关系与小正方体个数的关系是求解小正方体个数的关键。
详细描述
在三视图中,每个视图都是从不同的方向对几何体进行投影得到的。理解投影关系可以帮助我们更好 地理解小正方体的数量。例如,在一个视图中看到的小正方体可能在其他视图中并不能看到,这是因 为其他视图是从不同的方向进行投影的。
06
小正方体的形状由左视图的前后 、左右、上下三个方向确定。
04
CATALOGUE
三视图中的小正方体计数问题.doc

三视图中的小正方体计数问题湖北省黄石市下陆中学宋毓彬通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。
解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。
通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量,小正方体的个数就迎刃而解了。
在三视图中,通过主视图、俯视图可以确定组合图形的列数;通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数。
以上方法可简要地概括为:“主俯看列,俯左看行,主左看层,分清行列层,计数不求人。
”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体货箱共有()。
A.9箱B.10箱C.11箱D.12箱分析:由三视图可知,这堆货箱共有从前到后3行,从左到右3列。
由左视图:第一行均为1层,第二行最高2层,第三行最高3层;由主视图:第一列、第三列均为1层,第二列(中间列)最高为3层。
故第二行、第二列为2层,第三行第二列为3层,其余皆为1层。
各行、各列小正方体的个数如俯视图中所表示。
这堆货箱共有3+1+1+2+1+1=9(箱)。
二、结果不唯一的计数例2(“希望杯”数学邀请赛试题)如图2,是由若干个(大于8个)大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是()。
分析:由给出的主视图、俯视图可以看出,该几何体共有2行,3列。
第1列均为1层,第2列最高2层,第3列最高3层。
左视图为A时,第1行、第2行最高均为3层。
几何体中,第1列第1行为1层;第2列第1行、第2行均可为1层或2层,,但不能同时为1层;第3列两行均为3层。
此时,小正方体的个数如俯视图A所示,最少为1+2+1+3+3=10(个),最多为1+2+2+3+3=11个。
一面、两面、三面小正方体个数的规律

〔4〕没有涂色的在大正方体里面除去外表一层的位置,所以有〔每条棱上小正方体块数-2〕³个,或者用总块数-三面涂色的块数-两面涂色的块数-一面涂色的块数。
课堂练习
〔难点稳固〕
3、将数学形象、数学语言、数学符号一一对应起来,轻松地突破难点;
4、课堂中,学生自主探究,小组合作。
教学环节
教学过程
导入
1、复习正方体相关知识。师:用棱长1cm的小正方体拼成一个棱长为10cm的大正方体,它是由多少个小正方体组成的?把大正方体的6个面分别涂上颜色,随机取出一个小正方体,涂色情况是怎样?
从学生角度分析为什么难
本课具有很强的综合性和实践性,学生需要借助观察,建立表象,发挥想象,发现并总结规律,循序渐进的促进学生空间观念的开展。对于五年级学生来说,探索规律归纳方法,具有一定的难度。
难点教学方法
1、借助直观手段--课前社会实践〔在家切土豆或胡萝卜并涂色〕,丰富表象;
2、多媒体课件演示,帮助学生形象理解;
杨茹
填写时间
8月14日
学科
数学
年级/册
五年级下册
教材版本
人教版
课题名称
第三单元P44《一面、两面、三面小正方体个数的规律》
难点名称
探索规律的归纳方法。
难点分析
从知识角度分析为什么难
学生已经学过的统计和归纳的知识,引导学生在想象、观察后归纳、发现现象后面的本质规律。而没有涂色的小正方体,藏在大正方体的中心,学生看不见摸不着,是本节课学习的重点,更是学习的难点。
2、如果根据涂色的情况给这些小正方体分类,你想怎样分类?
数正方体个数技巧口诀

数正方体个数技巧口诀数正方体可不是小事,有时候看着那些几何图形,像是在玩一场密室逃脱游戏一样。
不过,别怕,今天咱们就来聊聊这个数正方体的技巧口诀,让你秒变“数正方体小能手”。
你得懂得咱们的大原则,那就是从大到小,一层一层来。
别急着踩着点数,先看清楚是不是正方体,是不是从小到大都一样规整。
要有耐心,这玩意可不像面条,乱七八糟的。
来来来,我们先从一层说起。
先数一下底下这层有几个正方体,别漏了角落,每个角都要摸得到。
数完第一层,别松懈,得接着上面那层。
有时候它们藏得特别深,就像找老鼠洞里的猫一样,要动动脑子。
还有个秘密技巧,有时候正方体会连着长得像个积木塔,那就一层一层往上数,别心急,慢慢来,就像泡面一样,急不得。
别以为数数就这么简单,有时候还得靠看它们排列,是不是整整齐齐的,像拍马屁一样,齐齐整整才好看。
咦,别忘了有时候还有些混蛋会躲在一些角落,真是像蚂蚁藏在大象脚底下一样,要仔细找找。
别以为眼睛数不过来就得了事,有时候得用个小工具,像放大镜一样,把每个角度都给照个遍,绝对不能偷懒。
还有个绝招,有时候你看那个形状不对,可能它就不是正方体,那就别浪费时间,扔了它,像脏衣服一样,不要留着它占地方。
记得啊,有时候你数着数着会觉得自己眼花,别怕,歇会儿眼不要逞能,眼花了就眼花了,着急也没用。
还有个经验,有时候一边数一边跟自己念叨,“一二三,四五六”,像是唱小曲儿一样,顺手又不费事。
有时候数数还挺像玩游戏,找宝藏似的,一点一点挖,可能还会有惊喜,就像开心果一样,啃啃还挺有味。
最后别忘了,有时候它们会变着花样,藏在一些看不见的地方,那就得狠下心找,别给它们机会,像老鼠过街,人人喊打。
所以啊,数正方体不是一件简单的事,得有耐心有技巧,像解数学题一样,动动脑筋,一点一滴来,别慌张,就能把它们统统揪出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图中的小正方体计数问题
主俯看列,俯左看行,主左看层。
前上看列,上右看行,前右看层
前面看,上下左右都不变
上面看,左右不变,前下后上
右面看,上下不变,前左后右
左面看,上下不变,前右后左
口诀:主俯定长,俯左定宽,主左定高
俯视图打地基,正视图疯狂盖,左视图拆违章.
1.图形是小华从正面、左面、上面看到的,这个物体
是由______块小方块组成的.
2.一个几何体是由一些大小一样的小立方块摆成的,如下列图是从正面、左面、
上面看这个几何体得到的平面图形,那么组成这个几何体所用的小立方块的个数
是______.
3.如图是某立体图形的俯视图,小正方形中的数字表示在该位置上的小正方体
块的个数,画出这个几何体的主视图和左视图.
4.由一些大小一样的小正方体组成的几何体的俯视图如下图,其中正方形中的
数字表示在该位置上的小正方体的个数,那么,这个几何体的左视图是[ ]
5.如图是一个由多个一样小正方体堆积而成的几何体的俯视图.图中所示数字
为该位置小正方体的个数,那么这个几何体的主视图是〔 〕
6.如下图,是一个由小立方体搭成的几何体的俯视图,小正方形中数字表示该
位置的小立方块的个数,那么它的主视图为〔 〕
7.如图,是一个由小正方体搭成的几何体的俯视图,小正方形中的数字表示在
该位置的小正方体的个数.请你画出它的主视图和左视图.
8.一个由小立方块搭成的几何体如下图.
(1)如图(a)是该几何体的正视图和俯视图,问:这样的几何体的形状确定吗?
如果不确定,那么有多少种情况?
(2)如图(b)是该几何体的正视图、左视图和俯视图,问:这样的几何体的形状
确定吗?如果不确定,那么有多少种情况
9.由一些一样的小正方体搭成的几何体的俯视图如右图所示,其中正方
形中的数字表示该位置上的小正方体的个数,那么该几何体的左视图是
10.如下图的几何体是由一些小立方块搭成的,那么这个几何体的俯视图是
A. B. C. D.
11.如图,由一样的小正方体搭成的几何体的主视图是〔 〕
A. B. C. D.
12.用小正方体搭一个几何体,使它的主视图和俯视图如下图:
〔1〕搭这样的几何体最少需要
个小正方体,最多需要个小正方体;
〔2〕请你在俯视图的小正方体中用数字表示当用最多的小正方体搭起的几何体
时该位置小正方体的个数;
〔3〕画出其中一种搭成的几何体的左视图.
13.画出视图.
14.如图是一个由几块一样的小正方体搭成的立体图形的三视图,那么这堆立
体图形中的小正方体共有( )块.
15.如图,是由一些一样的小正方体搭成的几何体的三视图,搭成这个几何体
的小正方体的个数有〔 〕
