蒙特卡罗反演方法
改进的MCMC方法及其应用

2009年8月水 利 学 报SHUILI XUEBAO 第40卷 第8期收稿日期:2008-06-16基金项目:973课题(2005CB724202);国家自然科学基金项目(50609024);浙江省自然科学基金(Y506138)作者简介:朱嵩(1981-),男,安徽人,博士后,主要从事环境水力学反问题研究。
E -mail:migao@文章编号:0559-9350(2009)08-1019-05改进的MCMC 方法及其应用朱嵩1,毛根海1,刘国华1,黄跃飞2(1.浙江大学建筑工程学院,浙江杭州 310058;2.清华大学水利水电工程系,北京 100084)摘要:概率反演中,马尔科夫链蒙特卡罗是一类重要的后验概率抽样方法,但由于该算法的搜索往往会陷入局部最优解,因而限制了其在具有非唯一解反问题中的应用。
鉴于此,本文对基于Metrop olis -Has tings 算法的多链搜索的方法进行了改进,改进后的方法可以根据搜索结果实时调整链的个数,因而可以在搜索到尽可能多的解的同时节省了多链搜索的时间。
最后将该算法应用于一个地下水污染源反问题的求解,计算结果表明改进后的算法对求解非唯一性反问题具有较好的效果。
关键词:马尔科夫链蒙特卡罗;概率反演;Metropolis -Has tings 算法;非唯一性;环境水力学中图分类号:O242;TV13文献标识码:A1 研究背景一般而言,环境水力学正问题主要研究地表及地下水中污染物的输移、扩散和转化规律,建立相关的分析计算方法,确定污染物浓度的时空分布及其应用[1]。
与此对应,环境水力学反问题是指根据有限且离散的实测水动力、水质数据来估计环境水力学模型参数、边界条件、初始条件以及污染源位置和强度等信息。
与正问题的适定性相反,环境水力学反问题是一种不适定问题,主要表现为解的不唯一性,这给反问题的求解带来了较大的困难[2]。
目前,反问题求解方法主要包括正则化方法、最优化方法、概率统计方法等[3]。
【国家自然科学基金】_马尔可夫链蒙特卡罗方法_基金支持热词逐年推荐_【万方软件创新助手】_20140729
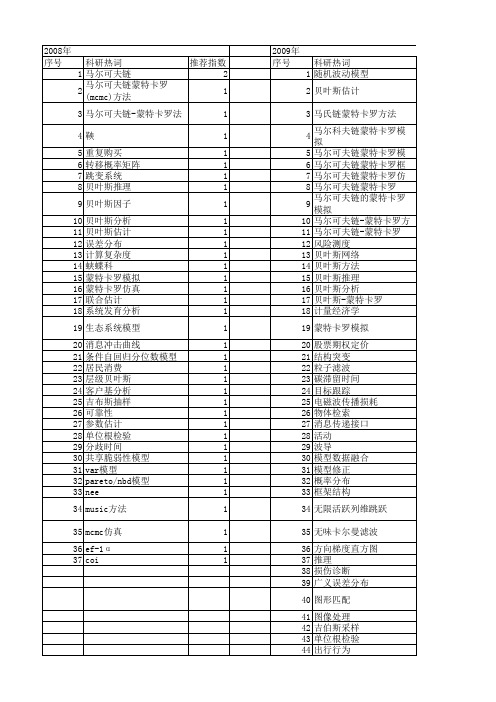
科研热词 推荐指数 参数不确定性 2 马尔可夫链蒙特卡罗模拟 1 马尔可夫链蒙特卡罗方法 1 马尔可夫链蒙特卡洛(mcmc) 1 马尔可夫链 1 马尔可夫 1 遗传算法 1 逆跳mcmc 1 贝叶斯算法 1 贝叶斯理论 1 贝叶斯原理 1 自适应采样 1 粒子滤波 1 稳态可用度 1 洪水概率预报 1 民机 1 概率洪水预报 1 机制转换利率模型 1 时间序列分析 1 平均无故障工作时间 1 图像恢复 1 后验分布 1 利率期限结构 1 分位自回归 1 nash模型 1 bayes 1 am-mcmc 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
53
2011年 科研热词 推荐指数 马尔可夫链蒙特卡罗方法 2 马尔可夫链蒙特卡罗 2 贝叶斯理论 2 高斯粒子滤波 1 马尔可夫链蒙特卡罗法 1 马尔可夫链 1 风险分析 1 非线性系统 1 降深预报 1 重要抽样 1 贝叶斯高分辨 1 贝叶斯法 1 贝叶斯推断 1 贝叶斯后验模型 1 贝叶斯 1 观测数据 1 被动目标方位估计 1 蒙特卡罗方法 1 自适应马尔科夫链蒙特卡罗 1 自适应采样 1 自适应metropolis采样 1 统一模型 1 结构可靠性 1 粒子滤波 1 稳定分布 1 目标跟踪 1 河流污染事故 1 模型阶数检测 1 概率洪水预报 1 暗能量 1 暗物质 1 时域宽带模型 1 数据关联 1 扩散模型 1 扩展卡尔曼滤波 1 快速高斯变换 1 延迟拒绝 1 安全工程 1 宇宙微波背景 1 威尔金森微波各向异性探测器 1 多目标跟踪 1 场景重建 1 地下水模拟 1 含水介质非均质概化 1 可逆跳变马尔可夫链蒙特卡罗(rjmcmc) 1 双边协商 1 参数估计 1 参数不确定性 1 信号处理 1 不确定性 1 snia 1 nash模型 1
地质统计学反演技术专题之三:基于MCMC的StatMod及RockMod

地质统计学反演技术专题之三:基于MCMC的StatMod及RockMod概述在前二期的文章中,我们介绍了HampsonRussell工具包中的地质统计学地震储层表征模块GeoSI(地质统计学随机反演)。
在这篇文章中,我们将介绍CGG GeoSoftware的另外两个地质统计学地震储层表征工具,即Jason地学软件工具包中的StatMod和RockMod。
如同GeoSI,这两个工具也是在地层地质模型框架内精细地整合地质信息和地震数据,生成多个高精度的实现。
这些实现都是对储层的预测,也可用于不确定性分析和风险评估。
StatMod和RockMod紧密融合地球科学领域内所有相关的不同种类数据,从而产生多个储层模型。
这种高度跨学科一致性的特点,确保了油藏模型是符合实际生产开发情况的,并最大限度地挖掘了测量数据和推断信息的价值。
其成果是一系列精确的深度域的储层模型,可用于预测油田储量、流体流动样式和产量估算。
同时,这些模型也为定量估计不确定性提供了可靠的依据;不确定性评估与先验信息、专家知识、井资料和地震具有直接关系。
这些储层模型在远离井点处具有较高预测性,而这恰恰是传统地质统计学建模的痛点。
StatMod使用一个(全)叠加地震数据,所以只在纵波阻抗足以区分岩相时使用。
RockMod同时使用多个(部分)叠加(AVO/AVA)地震数据,因此在需要多个弹性参数组合(如纵波阻抗、横波阻抗和密度)才能区分岩相时使用。
利用地震数据,以及不同领域来源的数据,RockMod可同时得到岩相体、弹性参数体和油藏工程属性体。
图1. RockMod同时反演出弹性属性、岩相和油藏工程属性简要研发历史最早的Jason地质统计学储层表征方法可追溯至1996年。
它始于基于褶积模型的叠后地震反演。
模拟方法包含简单的序贯高斯模拟(SGS)、序贯指示模拟(SIS)和SGS同时模拟、带趋势的序贯指示模拟(SISTR)和序贯高斯协模拟(SGCS)。
sobol序列原理

sobol序列原理
Sobol序列是一种高效的随机数生成方法,常用于蒙特卡罗模拟和数
值计算中。
它可以生成高维度的均匀分布随机数,并且有较好的低差
异特性,使得计算结果更加准确和可靠。
Sobol序列的原理基于Van der Corput序列和Halton序列,利用了一个叫做“数字反演”的技术,在一维情况下,Sobol序列可以看做
是一个Van der Corput序列和一个Halton序列的组合,但是在多维情况下,Sobol序列可以利用数字反演技术构造出一组互不重合的点,使得每个点之间的距离都很均匀,从而实现高维度均匀分布的随机数
生成。
Sobol序列生成的随机数具有低差异性的特点,意味着它们能够更加
均匀地分布在整个随机数空间中。
这种优良特性可以极大地提高随机
数生成的稳定性和准确性,从而使得计算结果更加可靠,尤其对于蒙
特卡罗模拟和数值计算的结果影响更为显著。
另外,Sobol序列的生成速度非常快,使得它能够在计算机上高效地
进行随机数生成和计算,这也是它广泛应用于科学计算和工程仿真的
原因之一。
同时,Sobol序列还能够通过适当的处理和变换来生成多
种分布的随机数,如正态分布、指数分布等,极大地拓展了其实际应
用的范围。
总之,Sobol序列是一种高效、低差异的随机数生成方法,具有生成速度快、可靠性好、适用范围广的优良特性,在蒙特卡罗模拟和数值计算等领域得到了广泛的应用。
【国家自然科学基金】_马尔科夫蒙特卡洛_基金支持热词逐年推荐_【万方软件创新助手】_20140801

科研热词 马尔科夫链-蒙特卡洛 马尔科夫蒙特卡洛模拟 镜质体反射率反演 鄂西渝东 贝叶斯分析 组合预报 不确定性 gibbs抽样
推荐指数 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 mcmc 预测区间 跳跃扩散 覆盖率 缺失数据 双指数分布 区间对称性 区间宽度 mmglue irt glue
推荐指数 3 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 推荐指数 马尔科夫链蒙特卡洛算法 3 粒子滤波 2 mcmc 2 高斯混合模型 1 随机需求 1 随机提前期 1 运动补偿 1 群目标跟踪 1 粒子概率假设密度滤波器 1 检测前跟踪 1 期望最大化算法 1 最小均方误差软干扰消除算法 1 提前期需求 1 微弱目标 1 库存控制 1 多输入输出系统 1 吉布斯采样 1 光流场 1 二次观测模型 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词 推荐指数 马尔科夫蒙特卡罗方法 2 附加质量 2 贝叶斯估计 2 物理参数识别 2 模态参数识别 2 gibbs抽样 2 验证性因子分析模型 1 驾驶仪系统 1 马尔科夫链采样 1 马尔科夫链蒙特卡洛方法 1 马尔科夫蒙特卡洛 1 重要性抽样 1 通货膨胀 1 跳跃随机波动模型 1 贝叶斯网络 1 贝叶斯模型平均 1 贝叶斯层次模型 1 贝叶斯因子 1 贝叶斯 1 蒙特卡洛马尔科夫链 1 蒙特卡洛模拟 1 蒙特卡洛仿真 1 自动推理 1 水文模拟 1 形状参数 1 尺度提升 1 多量测目标跟踪 1 多量测 1 多尺度数据整合 1 基因调控网络 1 土壤水力参数 1 图像重建 1 后验分布 1 吉布斯抽样 1 可靠性分析 1 变分逼近 1 参数不确定性 1 压缩感知 1 动态故障树 1 全国社保基金 1 信息融合 1 上下文建模 1 slurp 1 mc3 1 bayesian推理 1
地球物理反演问题中的贝叶斯方法研究

地球物理反演问题中的贝叶斯方法研究
蒋星达;张伟;杨辉
【期刊名称】《地球与行星物理论评》
【年(卷),期】2022(53)2
【摘要】基于统计理论的贝叶斯反演方法在先验信息和观测数据的约束下,以后验概率分布的形式表征模型参数在不同区间的可能性大小.相对于确定性反演理论,贝叶斯反演通过提取模型参数边缘概率分布、最大后验解、平均解、相关系数等定量评价反演结果的不确定性以及模型参数之间的相互关系,通过模型参数后验概率分布反映观测数据和先验信息对模型参数的约束能力.本文基于贝叶斯方法在地球物理反演中的应用,总结了贝叶斯反演的基本流程,详细介绍了不同背景条件下的先验信息概率分布选择、似然函数建立、后验概率公式求解.在优化参数方面,介绍了模型参数的固定维和变维反演概念,以及超参数的优化方法;在反演方法方面,着重介绍了固定维和变维反演马尔科夫链蒙特卡罗采样方法;在模型参数评价方面,介绍了不同情况下贝叶斯统计参数的求取.然后讨论了贝叶斯反演方法采样效率提升的具体措施.最后对贝叶斯方法在地球物理反演中的应用作出总结.
【总页数】13页(P159-171)
【作者】蒋星达;张伟;杨辉
【作者单位】哈尔滨工业大学航天工程与力学系;南方科技大学深圳市深远海油气勘探技术重点实验室;南方科技大学地球与空间科学系
【正文语种】中文
【中图分类】P315
【相关文献】
1.基于贝叶斯方法的二维大地电磁尖锐边界反演研究
2.统计模拟方法在解地球物理学反演问题中的某些应用
3.地球物理反问题中的随机反演理论
4.地球物理学研究生课程教学改革的探索与思考——以《位场数据处理与反演》课程为例
因版权原因,仅展示原文概要,查看原文内容请购买。
【国家自然科学基金】_最小二乘反演_基金支持热词逐年推荐_【万方软件创新助手】_20140802
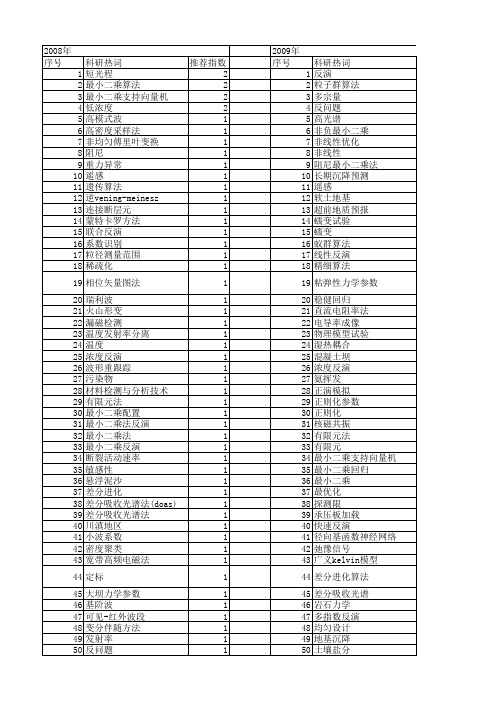
科研热词 反演 粒子群算法 多宗量 反问题 高光谱 非负最小二乘 非线性优化 非线性 阻尼最小二乘法 长期沉降预测 遥感 软土地基 超前地质预报 蠕变试验 蠕变 蚁群算法 线性反演 精细算法 粘弹性力学参数 稳健回归 直流电阻率法 电导率成像 物理模型试验 湿热耦合 混凝土坝 浓度反演 氨挥发 正演模拟 正则化参数 正则化 核磁共振 有限元法 有限元 最小二乘支持向量机 最小二乘回归 最小二乘 最优化 探测限 承压板加载 快速反演 径向基函数神经网络 弛豫信号 广义kelvin模型 差分进化算法 差分吸收光谱 岩石力学 多指数反演 均匀设计 地基沉降 土壤盐分 含水构造 参数反演
1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94
悬浮泥沙 总体最小二乘 微波断层成像 弛豫时间谱 应急监测 应变参数 平面波 层析成像 射线追踪 导热 孔隙度预测 孔隙度 太阳散射光 非参局部多项式回归 太阳掩星法傅里叶变换红外光谱 多项式拟合 多震相走时 多次波射线追踪 多指数反演 基函数拟合 地震层析成像 噪声敏感性试验 同时反演 可控源音频大地电磁法 变分伴随方法 副热带高压 初始模型 几何边界识别 共轭梯度法 光谱导数 偏移成像阴影 偏移 偏最小二乘 假定物理模型 余弦拟合 交流放电 乳腺癌 串联毛管模型 中红外 一维反演 savitzky-golay滤波 lsqr boussinesq方程
推荐指数 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
遥感模型与反演方法

(d)
(e)
(f)
Hale Waihona Puke 不同植被类型的BRDF(GOMS模型)
conifer(a,d) savanna(b,e) shrubland(c,f) 红光波段(a-c) 近红外波段(d-f)
=55º
Li-Strahler几何光学-辐射传输混合模型GORT 由于几何光学模型和辐射传输模型分别在不同的尺度上 具有各自的优势,李小文和 Strahler 充分利用几何光学模型 在解释阴影投射面积和地物表面空间相关性上的基本优势, 在纯 GO 模型和不连续植被间隙率模型的基础上,用辐射传输 方法求解多次散射对各面积分量亮度的贡献,分两个层次来 建立承照面与阴影区反射强度的辐射传输模型,并以间隙率 模型作为联系二者的关键。
(1)辐射传输模型
电磁波从辐射源到目标的传输过程,表示为观测方向 s 上 关于辐亮度I的辐射传输方程:
dI ( s ) K (I J ) ds
K-消光系数,J-源函数。 将辐射传输方程写作微积分形式:
I ( , s ) I ( , s ) ( / 4 ) P( s, s' ) I ( , s' )d' ( r, s ) /
李一 Strahler(1985, 1986) 根据稀疏林的实际情况,抛 弃了“小几何体”假定,直接用森林结构参数计算四个分量随 太阳角和观察角变化,建立了遥感像元尺度的天然林BRDF模型。
典型的几何光学模型为景合成模型:
R(v) ki (v)Ri (v)
其中,R(v) 为冠层的反射率,v 表示为光照方向和观察方向的 函数,Ri(v) 为冠层组分的反射率,Ki(v)表示为冠层结构参数 的函数。
多角度遥感提供多个方向的观测数据,相比单一方向观测 提供了更多的信息,多角度观测信息的利用要求对植被冠层二 向性反射特征的描述 -冠层反射的BRDF 模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蒙特卡罗反演方法
蒙特卡罗反演方法是一种常用于求解各种物理问题的数值计算方法。
它的原理是通过随机抽样来近似计算某一物理量的期望值。
在本文中,我们将介绍蒙特卡罗反演方法的基本原理和应用。
蒙特卡罗反演方法最初是由数学家Metropolis等人在20世纪40年代提出的,用于求解复杂的统计力学问题。
随后,这种方法被推广应用于众多领域,包括物理学、化学、生物学等。
蒙特卡罗反演方法的基本思想是通过随机抽样来模拟某一物理过程,并根据抽样结果进行统计分析。
具体而言,我们首先需要定义一个概率分布函数,用来描述我们想要研究的物理量的概率分布。
然后,我们通过随机抽样的方式来生成一组符合该概率分布的样本。
最后,根据这些样本的统计特征,我们可以近似计算出所研究物理量的期望值。
蒙特卡罗反演方法的核心是如何生成符合给定概率分布的随机样本。
常用的方法有逆变换法和接受-拒绝法。
逆变换法是通过累积分布函数的逆函数来生成符合指定概率分布的随机数。
而接受-拒绝法则是通过比较生成的随机数与目标分布函数的比值来决定是否接受该随机数作为样本。
蒙特卡罗反演方法在实际应用中有着广泛的应用。
例如,在物理学中,我们可以利用蒙特卡罗反演方法来模拟高能物理实验中的粒子
碰撞过程,从而研究粒子的运动轨迹和能量分布等。
在化学领域,我们可以利用蒙特卡罗反演方法来计算复杂分子的能量和构型分布。
在生物学研究中,蒙特卡罗反演方法可以用来分析蛋白质的折叠动力学和相互作用等。
虽然蒙特卡罗反演方法在求解各种物理问题中具有一定的优势,但也存在一些限制。
首先,蒙特卡罗反演方法通常需要大量的样本才能得到准确的结果,这对计算资源和时间要求较高。
其次,蒙特卡罗反演方法在处理高维问题时会面临维度灾难的挑战,即样本数量的指数级增长。
此外,蒙特卡罗反演方法对初始概率分布的选择和参数调节也有一定的要求。
蒙特卡罗反演方法是一种重要的数值计算方法,可以应用于各种物理问题的求解。
它通过随机抽样来近似计算物理量的期望值,具有较好的灵活性和适用性。
然而,蒙特卡罗反演方法也存在一些局限性,需要综合考虑实际问题的特点和计算资源的限制。
因此,在具体应用中需要结合实际情况选择合适的方法和策略,以获得准确可靠的结果。
