分层法D值法ppt课件
合集下载
第四章 框架结构内力计算

4、计算和确定梁、柱弯矩分配系数。 按修正后的刚度计算各结点周围杆件的杆 端分配系数。 5、按力矩分配法计算单层梁、柱弯矩。 6、将每个单层框架的计算结果按相应部分迭 加起来便得到原框架的计算结果,即柱的弯矩 取相邻两个单元中同一柱对应弯矩之和,而梁 的弯矩直接采用。
四、计算例题
作业2
3.2 水平荷载下内力的近似计算—反弯点法
d
i 1
m
V pj
ij
4、柱端弯矩的确定 M j V jY j 柱下端弯矩 柱上端弯矩 M j V j (h j Yj )
5、梁端弯矩的确定 M ml (M mt M m1b ) 对于边柱 ibl 对于中柱
M ml ( M mt M m1b ) M mr ibl ibr ibr ( M mt M m1b ) ibl ibr
第3章 框架结构的内力和位移计算
3.1 竖向荷载下内力的近似计算—分层法 3.2 水平荷载下内力的近似计算—反弯点法 3.3 水平荷载下内力的近似计算—D值法 3.4 水平荷载作用下侧移的近似计算
3.1 竖向荷载下内力近似计算—分层法
一、竖向荷载 自重、活荷、雪荷载及施工检修荷载等。 二、分层法的基本假设 1、忽略侧移的影响; 2、忽略每层梁的竖向荷载对其它各层梁 的影响。 三、分层法计算要点 1、将N层框架划分成N个单层框架,柱 端假定为固端, 用力矩分配法计算。
三、柱的侧移刚度D 12ic D 2 h
—为柱侧移刚度修正系数,表示梁柱刚 度比对柱侧移刚度的影响。
四、剪力计算 有了D值后,与反弯点法类似,计算各柱分 配的剪力 Dij Vij V pj Dij 五、确定柱反弯点高度比 影响柱反弯点高度的主要因素是柱上下端的 约束条件。
高层分层法D值法计算表
-2.79 4.32 18.72
-1.31 -1.31 -51.34 3.60 3.60 48.12 H
4.71 25.58 E EI
0.369
-4.83 -46.62
1.85 50.86
-2.07 -16.14 F
-4.51 -18.57
4.73 -15.60
-5.02 16.15
第三层不平衡分配及弯矩总值
4.16 27.02
-1.98 -42.73
0.77 49.75
0.85 -10.94
-3.60 -18.71
1.97 -19.49
-2.02 19.71
二、D值法
楼层 5 4 3 2 1 柱子
C CG / D DH /
HZ/m
15.55 12.25 8.95 5.65 2.35
ω o/(kN/m^2) 0.50 0.50 0.50 0.50 0.50 ī1 0.91 3.22 3.22 0.91
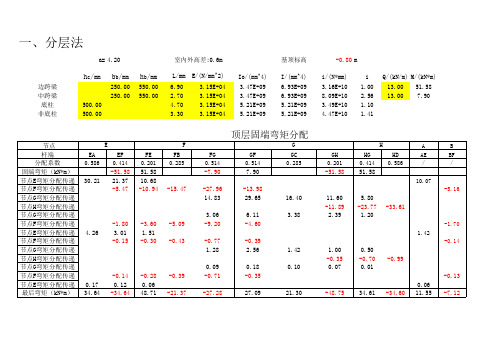
一、分层法
a= 4.20 室内外高差:0.6m 基顶标高 Io/(mm^4) 3.47E+09 3.47E+09 5.21E+09 5.21E+09 I/(mm^4) 6.93E+09 6.93E+09 5.21E+09 5.21E+09 -0.80 m i/(N*mm) 3.16E+10 8.09E+10 3.49E+10 4.47E+10 i 1.00 2.56 1.10 1.41 Q/(kN/m) M/(kN*m) 13.00 13.00 51.58 7.90
0.586
F EF
0.414
FE
0.201
框架结构综述精品PPT课件

1/2 1/2
1/2
1/2
1/2
3. 将各杆端弯矩叠加并绘弯矩图 及不平衡力矩计算
不平衡力矩再次分配后: -4.430-1.149×0.668=-5.198
再作一次弯矩分配,但不再传递
不平衡力矩再次分配后: 5.579-1.149×0.332=5.198
对杆端而言,弯矩以顺时针为正,反之为负。
三、框架内力分析-水平荷载作用
M
A
1 12
ql
2
M
B
1 12
ql
2
反符号分配:
12.1880.3328.142
1/2
1/2
1/2
1/2
(1.1 28 4.8 07 6.1 79 2.5 9)306 .472
1/3
3.081
1/3
1/3
对结点而言,则以逆时针为正,反之为负。
1/3
底 层 计 算 过 程:
1/2 1/2
1/3
1/3
第 13 章 多层框架结构
主要内容:
结构组成和结构布置 框架结构的计算简图及荷载 竖向荷载作用下框架结构内力的近似计算 水平荷载作用下框架结构内力和侧移的近似计算
荷载效应组合和构件设计 框架结构的构造要求
重点:
结构组成和结构布置
框架结构的计算简图及荷载 分层法、反弯点法,D值法
13.1 多层框架结构组成及布置
度之比无限大,各柱上下两端均不发生角位移,或转角近 似为0; (2)确定各柱的反弯点位置时,认为除底层柱以外的其余各 层柱反弯点位于层高的中点; (3)不考虑梁的轴线变形,同一层各节点的水平位移相等。
当梁的线刚度比柱的线刚度大很多时(例如ib/ic>3), 梁柱节点的转角很小。否则,该方法误差较大。
分层法和D值法

(2)影响反弯点高度的具体因素:
a) 侧向外荷载的形式 b) 梁柱线刚度比 c) 结构总层数及该柱所在的层数 d) 柱上下横梁线刚度比 e) 上、下层层高的变化
(3)计算方法 <a> 梁柱线刚度比、层数、层次对反弯点高度的影响 标准反弯点高度比: y0 (反弯点到柱下端距离与柱全高的比值) 条件:框架横梁的线刚度、柱的线刚度和层高沿框架高度保持不变。
2)分配系数——杆AB在结点A的分配系数等于杆AB的转动刚度与交于
A点的各杆的转动刚度之和的比值。以 表示。
Aj
S Aj S
均为固端
Aj
iAj i
A
A
3)固端弯矩 方向 +
4)传递系数——当近端有转角时,远端弯矩与近端弯矩的比值。用C表 示。
M BA CABM AB
3. 计算步骤
解:
边柱:( i1 i3 0 或 i3 i4 0 )
k i2 i4 2ic
梁柱刚度比K和α的关系
楼 层
简图
一 般 柱
边 柱
底 层 柱
固 结
K
k i1 i2 i3 i4 2ic
k
2k
k i1 i2 ic
0.5 k
2k
2. 计算各柱的剪力
➢ 计算方法同反弯点法。 ➢ 则第j层、第k柱的剪力:
M 1上 V1h1 / 3 M 1下 V1 2h1 / 3
5. 根据节点平衡计算梁端弯矩
6. 由梁两端的弯矩,根据梁的平衡条件,可求出梁的剪力。 7. 由梁的剪力,根据结点的平衡条件,可求出柱的轴力。
例题:作下图所示框架的弯矩图,图中括号内数字为各杆的线刚度
解: 当同层各柱h相等时,可直接用柱线刚度计算它们的分配 系数。这里只有第3层中柱与同层其他柱高不同,做如下 变换,即可采用折算线刚度计算分配系数。
分层法质量工具课件

数据分层要合理
数据分层是分层法的关键步骤, 应确保分层的合理性和科学性。
措施制定要具体可行
针对分析出的原因,制定的改 进措施应具体可行,具有可操 作性。
效果评估要客观公正
对改进后的效果进行客观公正 的评估,以便总结经验教训, 持续改进。
05 分层法案例分析
案例一:分层法在生产质量控制中的应用
总结词
质量问题的分析
总结词
深入分析问题
详细描述
在收集到质量数据后,分层法可以帮助我们深入分析质量问题。通过将问题按照不同的层次和维度进行分类,可 以更准确地定位问题的根本原因,为制定有效的改进措施提供依据。
质量改进的措施
总结词
制定针对性措施
详细描述
基于对质量问题的深入分析,分层法可以帮助我们制定针对性的改进措施。这些措施可以针对不同层 次的问题进行解决,从而更有效地提升产品质量和客户满意度。
分层法质量工具课件
目 录
• 分层法概述 • 分层法在质量管理中的应用 • 分层法与其他质量工具的结合 • 分层法实施步骤与注意事项 • 分层法案例分析
contents
01 分层法概述
分层法的定义
01
分层法是一种质量工具,它通过 将复杂问题分解为多个层次,逐 层分析并解决,从而达到全面提 升产品质量的目的。
分层法的应用场景
分层法适用于各种复杂问题的分析和解决,尤其适用于产品、服务、流程等方面 的质量改进。
在制造业、服务业、医疗保健等领域,分层法被广泛应用于质量改进、流程优化、 问题解决等方面,取得了显著的效果。
02 分层法在质量管 理中的应用
质量数据的收集
总结词
分层收集数据
详细描述
在质量管理中,分层法常用于收集质量数据。通过将数据按照不同的特征和属 性进行分类,可以更系统地收集和分析数据,为后续的质量问题分析和改进提 供基础。
分层法D值法课件

(
M
u c
M
d c
)Mr b源自ibr ibl ibr(M
u c
M
d c
)
二、水平荷载作用下的 D 值法
1.反弯点法存在的问题
(1)由于框架各层节点转角不可能相等, 故柱的反弯点位置也不可能 都在 柱中点;
(2)由于梁柱线刚度之比不可能为无穷大, 故柱的抗侧移刚度也不完全取 决于柱本身, 还与梁的刚度由关。
12 14.3 计算方法
第十四章 多层框架结构
2.修正后的柱抗侧移刚度 考虑柱上下端节点的弹性约束作用后,
柱的抗侧移刚度为:
D
12ic h2
13 14.3 计算方法
第十四章 多层框架结构
推导的基本假定为:
(1)柱AB及与其上下相邻的柱的线刚度均为ic; (2) 柱AB及与其上下相邻的柱的层间位移均为Δuj
7 14.3 计算方法
第十四章 多层框架结构
二、水平荷载作用下的反弯点法 P.160
8 14.3 计算方法
第十四章 多层框架结构
基本假定: (1)求各柱剪力时, 假定各柱上下端都不发生角位移, 即认为 梁的线刚度与柱线刚度之比为无限大;(柱按两端嵌固考虑, 因此各柱的抗剪刚度只与柱本身有关)
(2)确定柱反弯点位置时, 假定除底层以外的各层柱的上下端 节点转角均相同, 则除底层外各层框架柱的反弯点均位于柱高 的中点;对于底层柱, 则假定其反弯点距底支座2/3柱高处。 (柱反弯点位置是定值) (3)梁端弯矩可由节点平衡条件求出, 按节点左右梁的线刚度进 行分配。
第十四章 多层框架结构
作业:
P.202: 习题13-1
23
第十四章 多层框架结构
四、框架结构侧移计算及限值
高层建筑结构设计D值法及侧移计算PPT课件
框架的总变形应由这两部分变形组成。但由图3-32可见, 在层数不多的框架中,柱轴向变形引起的侧移很小,常常可 以忽略。
在近似计算中,只需计算由杆件弯曲引起的变形,即所谓 剪切型变形。在高度较大的框架中以剪切型为主,柱轴向力 加大,柱轴向变形引起的侧移不能忽略。一般来说,二者叠 加以后的侧移曲线仍以剪切型为主。
=1 6_E__I h2
=1 M
6_E__I h2
M
D0DD1
柱抗侧刚度修正系数, 按下表计算
柱的部位及 固定情况
一般层
i1
i2
i3 ic i4
底层,下端固定 底层,下端铰支
i1 i2 ic
i1
i2
ic
i
i =i1+i2 +i3 +i4 2ic
i i1 i2 ic
c
i c = 2+i
c
0.5 i 2i
式中各符号意义见表5-4~5-6。
yh h
框架弯矩图 :
反弯点位置确定以后,柱剪力、柱弯矩以及梁端弯矩 的计算与反弯点法相同。
续表
续表
图示为3层框架结构的平面及剖面示意图。受横向水平力 作用时,全部5榀框架参与受力。并给出了楼层标高处的总 水平力及各杆线刚度相对值。计算框架结构内力并画弯矩图。
V D 柱【抗解侧 】刚(1)度D修值正计系算数和31,剪按力下分表配3计1 算 3
查表得反弯点高度比的值。
D 31
D 3j
P3
每一根杆的反弯点位置都不相同,反弯点高j 度系数按下式计算:
V 32 D 32 3
D 32 D 3j
P3
j
V 33 D 33 3
D 33 D 3j
D值法
图12.2 框架体系的布置
(a) 横向布置;(b) 纵向布置;(c) 纵横双向布置
12.1.3 柱网尺寸及层高
(1) 工业厂房
一般采用6m柱距,跨度则随柱网的布置方式不同 分为内廊式和跨度组合式,见图12.3。 厂房的层高一般根据车间的工艺设备、管道布置 及通风采光等因素决定。常用的底层层高有4.2m、 4.5m、4.8m、5.4m、6.0m、7.2m和8.4m。 (2) 民用建筑 民用建筑类型较多,功能要求各有不同,柱网及 层高变化也较大,尺度一般较工业厂房为小。柱网和 层高通常按300mm进级。
沉降缝由于是从基础断开,缝两侧相邻框架的距 离可能较大,给使用带来不便,此时可利用挑梁或搁 置预制梁、板的方法进行建筑上的闭合处理,见图 12.4。
表12.1 钢筋混凝土框架结构伸缩缝最大间距(m) 环境条件
框架类别
装配式 现浇式
室内或土中 75 55
露天 50 35
图12.4 沉降缝做法
(a) 设挑梁(板);(b) 设预制板(梁)
图12.5 框架横梁截面形式
图12.6 框架连系梁截面形式
12.2.1.2 截面尺寸
(1) 框架梁
梁截面尺寸可参考受弯构件来初步确定。梁高hb 一般可取(1/10~1/18)lb(lb为梁的计算跨度),梁净跨 与截面高度之比不宜小于4。梁的宽度bb=(1/2~1/3)hb, 一般不宜小于200mm。
(2) 侧移刚度d的确定
侧移刚度d表示柱上下两端有单位侧移时在柱中 产生的剪力。根据假定(1),梁柱线刚度之比无穷 大,则各柱端转角为零,由结构力学的两端无转角 但有单位水平位移时杆件的杆端剪力方程,柱的侧 移刚度d可写成:
V 12ic d= 2 h EI ic h
D值法ppt
仍设杆端转角为θ,弦转角为φ
i5 J i
i6
M
M JL 4 i5 2 i5 6 i5
K
M JM 4 i6 2 i6 6 i6 MJK4i6i
记,aMJM LJM KJM64ii5 i66i
i i5 i6 (梁柱线刚度比 ) i
得: a 2 3 3i
-
由上式解出 3 3
i1i2i3i4
1
i1 i2
i2 i4
1
反弯点下移,y1取负值
对于底层,不进行该项修正,因为无下梁 -
3.上层柱高 h上与本层柱高h不同时,应加修正值 y 2
令
2
h上 h
据 i 及 2 查相应表格,得修正值 y 2
h上
h上
显然,2 1,反弯点上移,y2取正值;
h
h
2 1,反弯点下移,y2取负值 。
D值法
重 点:D值法原理 知识点:
D值法是修正了侧移 刚度和反弯点位置的剪力分配法 特 点:实用近似计算 应 用:用来计算侧向荷载
-
引言
P3
剪力分配法
P2
1、层间剪力计算-----截面法
P1
2、柱端弯矩与梁端弯矩的计算
P3
B A
MAB
P2
V
V
P1
-
1
P3
B
P2
P1
M AB
4iA
2iB
6EI L2
M BA
2iA
4iB
6EI L2
DAB
VAB
12EI L3
6EI L2
A
6EI L2
B
A
因为杆件两端有转角,所以: 1、各柱侧移刚度不再是12EI/L3 2、反弯点也不一定在柱的中点。
i5 J i
i6
M
M JL 4 i5 2 i5 6 i5
K
M JM 4 i6 2 i6 6 i6 MJK4i6i
记,aMJM LJM KJM64ii5 i66i
i i5 i6 (梁柱线刚度比 ) i
得: a 2 3 3i
-
由上式解出 3 3
i1i2i3i4
1
i1 i2
i2 i4
1
反弯点下移,y1取负值
对于底层,不进行该项修正,因为无下梁 -
3.上层柱高 h上与本层柱高h不同时,应加修正值 y 2
令
2
h上 h
据 i 及 2 查相应表格,得修正值 y 2
h上
h上
显然,2 1,反弯点上移,y2取正值;
h
h
2 1,反弯点下移,y2取负值 。
D值法
重 点:D值法原理 知识点:
D值法是修正了侧移 刚度和反弯点位置的剪力分配法 特 点:实用近似计算 应 用:用来计算侧向荷载
-
引言
P3
剪力分配法
P2
1、层间剪力计算-----截面法
P1
2、柱端弯矩与梁端弯矩的计算
P3
B A
MAB
P2
V
V
P1
-
1
P3
B
P2
P1
M AB
4iA
2iB
6EI L2
M BA
2iA
4iB
6EI L2
DAB
VAB
12EI L3
6EI L2
A
6EI L2
B
A
因为杆件两端有转角,所以: 1、各柱侧移刚度不再是12EI/L3 2、反弯点也不一定在柱的中点。
《d值法,反弯点法》课件
05
CHAPTER
总结与展望
D值法
D值法是一种用于确定结构中节点或单元的相对刚度的方法,通过计算节点或单元的D值,可以评估其刚度对结构整体性能的影响。
D值法广泛应用于各种结构分析中,如桥梁、高层建筑和复杂结构的稳定性分析。
反弯点法
反弯点法是一种用于预测桥梁主梁挠度的简化计算方法。它基于桥梁主梁在荷载作用下的弯矩和剪力分布,通过反弯点位置的弯矩和剪力值来计算挠度。
在土木工程领域,D值法常用于计算高层建CHAPTER
反弯点法介绍
它通过在桥梁的特定位置设置反弯点,以便更好地控制桥梁的施工质量和安全。
反弯点法的名称源于其技术特点,即在桥梁的反弯位置设置控制点。
反弯点法是一种用于确定桥梁施工控制点的技术方法。
反弯点法在铁路轨道设计中的应用
铁路轨道的曲线要素计算对于列车的安全运行至关重要。反弯点法能够计算出轨道曲线的各项参数,为轨道设计提供依据。例如,某铁路线采用反弯点法进行了轨道设计,确保了列车的安全运行。
D值法与反弯点法在跨海大桥设计中的应用:跨海大桥的设计需要考虑风、浪、潮汐等多种因素对桥梁的影响。通过结合D值法和反弯点法,可以计算出桥梁在不同荷载和环境条件下的位移和曲线要素,为跨海大桥的安全设计提供保障。例如,某跨海大桥的设计中,同时采用了D值法和反弯点法进行计算和分析,确保了大桥的安全性和稳定性。
反弯点法的原理基于桥梁结构的力学特性和施工工艺的要求。
通过在反弯点设置控制点,可以有效地控制桥梁的挠度和应力分布,确保施工过程中的安全性和稳定性。
该方法还考虑了施工环境的影响,如温度、风载等因素,以实现更精确的施工控制。
03
CHAPTER
D值法与反弯点法的比较
D值法
D值法是一种基于结构重要性评估的简化计算方法,通过引入重要性系数来考虑结构重要性对极限状态方程的影响。这种方法适用于多跨连续梁和框架结构的分析。
CHAPTER
总结与展望
D值法
D值法是一种用于确定结构中节点或单元的相对刚度的方法,通过计算节点或单元的D值,可以评估其刚度对结构整体性能的影响。
D值法广泛应用于各种结构分析中,如桥梁、高层建筑和复杂结构的稳定性分析。
反弯点法
反弯点法是一种用于预测桥梁主梁挠度的简化计算方法。它基于桥梁主梁在荷载作用下的弯矩和剪力分布,通过反弯点位置的弯矩和剪力值来计算挠度。
在土木工程领域,D值法常用于计算高层建CHAPTER
反弯点法介绍
它通过在桥梁的特定位置设置反弯点,以便更好地控制桥梁的施工质量和安全。
反弯点法的名称源于其技术特点,即在桥梁的反弯位置设置控制点。
反弯点法是一种用于确定桥梁施工控制点的技术方法。
反弯点法在铁路轨道设计中的应用
铁路轨道的曲线要素计算对于列车的安全运行至关重要。反弯点法能够计算出轨道曲线的各项参数,为轨道设计提供依据。例如,某铁路线采用反弯点法进行了轨道设计,确保了列车的安全运行。
D值法与反弯点法在跨海大桥设计中的应用:跨海大桥的设计需要考虑风、浪、潮汐等多种因素对桥梁的影响。通过结合D值法和反弯点法,可以计算出桥梁在不同荷载和环境条件下的位移和曲线要素,为跨海大桥的安全设计提供保障。例如,某跨海大桥的设计中,同时采用了D值法和反弯点法进行计算和分析,确保了大桥的安全性和稳定性。
反弯点法的原理基于桥梁结构的力学特性和施工工艺的要求。
通过在反弯点设置控制点,可以有效地控制桥梁的挠度和应力分布,确保施工过程中的安全性和稳定性。
该方法还考虑了施工环境的影响,如温度、风载等因素,以实现更精确的施工控制。
03
CHAPTER
D值法与反弯点法的比较
D值法
D值法是一种基于结构重要性评估的简化计算方法,通过引入重要性系数来考虑结构重要性对极限状态方程的影响。这种方法适用于多跨连续梁和框架结构的分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图13-11所示,按各开口刚架计算,加强了柱端的约束程度, 即人为增加了柱刚度,由此产生的误差需进行修正:
(1)除底层以外其它各层柱的线刚度均乘以 0.9 的折减系数; (2)除底层以外其它各层柱的弯矩传递系数取为 1/3 。
2
14. 3 计算方法
第十四章 多层框架结构
图13-11 P.159
3
第十四章 多层框架结构
第三节 框架结构内力与侧移的近似计算方法 P.158
工程中常用的平面框架结构内力的近似计算方法:
{ 竖向荷载下的 分层法、迭代法 水平荷载下的反弯点法、D值法
一、竖向荷载作用下的分层法 基本假定:
1、忽略框架在竖向荷载作用下的侧移和由它引起的侧移力矩; 2、忽略本层荷载对其它各层内力的影响。 即:竖向荷载只在本层的梁内以及与本层梁相连的框架柱 内产生弯矩和剪力,而对其它楼层框架梁和隔层框架柱不 产生弯矩和剪力。
12 14. 3 计算方法
第十四章 多层框架结构
2、修正后的柱抗侧移刚度 考虑柱上下端节点的弹性约束作用后,
柱的抗侧移刚度为:
D
12ic h2
13 14. 3 计算方法
第十四章 多层框架结构
推导的基本假定为:
(1)柱AB及与其上下相邻的柱的线刚度均为ic; (2) 柱AB及与其上下相邻的柱的层间位移均为Δuj
7 14. 3 计算方法
第十四章 多层框架结构
二、水平荷载作用下的反弯点法 P.160
8 14. 3 计算方法
第十四章 多层框架结构
基本假定: (1)求各柱剪力时,假定各柱上下端都不发生角位移,即认 为梁的线刚度与柱线刚度之比为无限大;(柱按两端嵌固考虑, 因此各柱的抗剪刚度只与柱本身有关) (2)确定柱反弯点位置时,假定除底层以外的各层柱的上下 端节点转角均相同,则除底层外各层框架柱的反弯点均位于柱 高的中点;对于底层柱,则假定其反弯点距底支座2/3柱高处。 (柱反弯点位置是定值) (3)梁端弯矩可由节点平衡条件求出,按节点左右梁的线刚度进 行分配。
求出D值后则得:
V jk
D jk
m
VFj
D jk
k 1
12i jk
V jk
i jk
m
V h2j Fj m
VFj
i jk
12i jk
h
2 j
k 1
k 1
15
14. 3 计算方法
第十四章 多层框架结构
D值法关键在于求、K,详见表13-2:P.165
16 14. 3 计算方法
2
V1
4
V3
N=V1 +V2 +V3 +V4
4 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
5 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
6 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
框架还原: 梁、柱弯矩同位叠加, 并对框架节点处得不 平衡弯矩进行重分配; 梁柱剪力由其两端弯 矩和承担的其它荷载 根据平衡条件求得; 柱轴力最后计算,为 与其相连上层各梁剪 力之和。
第十四章 多层框架结构
3、修正后的柱反弯点高度 各柱反弯点的位置取决于该柱上下端转角的比值。 若柱上下端转角相同,反弯点则在柱高中点; 若柱上下端转角不同,则反弯点偏向转角大的一端,即偏向约 束刚度较小的一端。 影响柱两端转角大小的因素:侧向外荷载形式;梁柱线刚度比; 结构总层数及该柱所在层数;柱上下横梁线刚度比;上下层层 高变化。
和
修正反弯点法—D值法 的抗侧移刚度:
D
12ic
h2
后者多了一个修正系数 ——反映节点转动降低了柱的抗侧移能力
节点转动大小: 取决于梁对柱节点转动的约束程度,梁越刚 → 对柱 的约束能力越大 → 节点转角越小 → 越接近1。
当框架梁线刚度 K=∞, =1—反弯点法和D值法的抗侧移刚度相等
(3)柱AB两端节点及与其上下左右相邻的各个结点的转角均为i1、i2、i3、i4
推得 j 层 k 柱抗侧移刚度
D jk
V jk u j
12ic
h
2 j
框架柱内的剪力
V jk
D jk
m
VFj
D jk
k 1
14 14. 3 计算方法
第十四章 多层框架结构
比较 反弯点法
12ic h2
求框架的内力步骤:
求出各柱内剪力→ 确定反弯点位置→ 各柱端弯矩→梁端弯矩 → 整个框架内力
9 14. 3 计算方法
第十四章 多层框架结构
设框架有n层,每层有m个柱,以第j层为分析对象,沿柱反弯点切开来,示出
其内力(剪力、轴力,弯矩为零),则按水平力的平衡条件得层间总剪力为:
m
VFj V j1 V j2 V jk V jm V jk
m
k 1
12i j
h
2 j
k
由假定2可求出各柱的杆端弯矩
V jk
i jk
m
VFj
i jk
k 1
对于底层柱
柱顶:M
t c1k
V1k
h1 3
柱底
:
M
b c1k
V1k
2h1 3
对于上部各层柱
M
t cjk
M
b cjk
V jk
hj 2
11 14. 3 计算方法
第十四章 多层框架结构
由假定3 (节点平衡条件)可求出梁端弯矩
M
l b
ibl
ibl ibr
(M
u c
M
d c
)
M
r b
ibr ibl ibr
(M
u cLeabharlann Md c)
二、水平荷载作用下的 D 值法
1、反弯点法存在的问题
(1)由于框架各层节点转角不可能相等,故柱的反弯点位置也不可能 都在 柱中点;
(2)由于梁柱线刚度之比不可能为无穷大,故柱的抗侧移刚度也不完全 取决于柱本身,还与梁的刚度由关。
14. 3 计算方法
第十四章 多层框架结构
梁固端弯矩 梁柱杆端弯矩(节点不平衡弯矩分配) 梁柱杆 端剪力 柱轴力 最后应将各层框架还原为整体框架
框架还原: 梁、柱弯矩同位叠加,并对框架节点 处得不平衡弯矩进行重分配; 梁柱剪力由其两端弯矩和承担的其它 荷载根据平衡条件求得; 柱轴力最后计算,为与其相连上层各 梁剪力之和。
1
14. 3 计算方法
第十四章 多层框架结构
第三节 框架结构内力与侧移的近似计算方法 P.158
基本假定: 1、忽略框架在竖向荷载作用下的侧移和由它引起的侧移力矩; 2、忽略本层荷载对其它各层内力的影响。 即:竖向荷载只在本层的梁内以及与本层梁相连的框架柱内产 生弯矩和剪力,而对其它楼层框架梁和隔层框架柱不产生弯矩 和剪力。
k 1
VFj—层间总剪力
n
VFj Fj Fj1 Fk Fn Fk
k 1
10 14. 3 计算方法
第十四章 多层框架结构
框架受侧向荷载时,框架柱内的剪力:
V jk
12i jk hj2
u j
12i/h2 称为柱的抗侧刚度(抗剪刚度)
由假定1
u j
VFj
(1)除底层以外其它各层柱的线刚度均乘以 0.9 的折减系数; (2)除底层以外其它各层柱的弯矩传递系数取为 1/3 。
2
14. 3 计算方法
第十四章 多层框架结构
图13-11 P.159
3
第十四章 多层框架结构
第三节 框架结构内力与侧移的近似计算方法 P.158
工程中常用的平面框架结构内力的近似计算方法:
{ 竖向荷载下的 分层法、迭代法 水平荷载下的反弯点法、D值法
一、竖向荷载作用下的分层法 基本假定:
1、忽略框架在竖向荷载作用下的侧移和由它引起的侧移力矩; 2、忽略本层荷载对其它各层内力的影响。 即:竖向荷载只在本层的梁内以及与本层梁相连的框架柱 内产生弯矩和剪力,而对其它楼层框架梁和隔层框架柱不 产生弯矩和剪力。
12 14. 3 计算方法
第十四章 多层框架结构
2、修正后的柱抗侧移刚度 考虑柱上下端节点的弹性约束作用后,
柱的抗侧移刚度为:
D
12ic h2
13 14. 3 计算方法
第十四章 多层框架结构
推导的基本假定为:
(1)柱AB及与其上下相邻的柱的线刚度均为ic; (2) 柱AB及与其上下相邻的柱的层间位移均为Δuj
7 14. 3 计算方法
第十四章 多层框架结构
二、水平荷载作用下的反弯点法 P.160
8 14. 3 计算方法
第十四章 多层框架结构
基本假定: (1)求各柱剪力时,假定各柱上下端都不发生角位移,即认 为梁的线刚度与柱线刚度之比为无限大;(柱按两端嵌固考虑, 因此各柱的抗剪刚度只与柱本身有关) (2)确定柱反弯点位置时,假定除底层以外的各层柱的上下 端节点转角均相同,则除底层外各层框架柱的反弯点均位于柱 高的中点;对于底层柱,则假定其反弯点距底支座2/3柱高处。 (柱反弯点位置是定值) (3)梁端弯矩可由节点平衡条件求出,按节点左右梁的线刚度进 行分配。
求出D值后则得:
V jk
D jk
m
VFj
D jk
k 1
12i jk
V jk
i jk
m
V h2j Fj m
VFj
i jk
12i jk
h
2 j
k 1
k 1
15
14. 3 计算方法
第十四章 多层框架结构
D值法关键在于求、K,详见表13-2:P.165
16 14. 3 计算方法
2
V1
4
V3
N=V1 +V2 +V3 +V4
4 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
5 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
6 14. 3 计算方法
第十四章 多层框架结构
P.157例24-1
框架还原: 梁、柱弯矩同位叠加, 并对框架节点处得不 平衡弯矩进行重分配; 梁柱剪力由其两端弯 矩和承担的其它荷载 根据平衡条件求得; 柱轴力最后计算,为 与其相连上层各梁剪 力之和。
第十四章 多层框架结构
3、修正后的柱反弯点高度 各柱反弯点的位置取决于该柱上下端转角的比值。 若柱上下端转角相同,反弯点则在柱高中点; 若柱上下端转角不同,则反弯点偏向转角大的一端,即偏向约 束刚度较小的一端。 影响柱两端转角大小的因素:侧向外荷载形式;梁柱线刚度比; 结构总层数及该柱所在层数;柱上下横梁线刚度比;上下层层 高变化。
和
修正反弯点法—D值法 的抗侧移刚度:
D
12ic
h2
后者多了一个修正系数 ——反映节点转动降低了柱的抗侧移能力
节点转动大小: 取决于梁对柱节点转动的约束程度,梁越刚 → 对柱 的约束能力越大 → 节点转角越小 → 越接近1。
当框架梁线刚度 K=∞, =1—反弯点法和D值法的抗侧移刚度相等
(3)柱AB两端节点及与其上下左右相邻的各个结点的转角均为i1、i2、i3、i4
推得 j 层 k 柱抗侧移刚度
D jk
V jk u j
12ic
h
2 j
框架柱内的剪力
V jk
D jk
m
VFj
D jk
k 1
14 14. 3 计算方法
第十四章 多层框架结构
比较 反弯点法
12ic h2
求框架的内力步骤:
求出各柱内剪力→ 确定反弯点位置→ 各柱端弯矩→梁端弯矩 → 整个框架内力
9 14. 3 计算方法
第十四章 多层框架结构
设框架有n层,每层有m个柱,以第j层为分析对象,沿柱反弯点切开来,示出
其内力(剪力、轴力,弯矩为零),则按水平力的平衡条件得层间总剪力为:
m
VFj V j1 V j2 V jk V jm V jk
m
k 1
12i j
h
2 j
k
由假定2可求出各柱的杆端弯矩
V jk
i jk
m
VFj
i jk
k 1
对于底层柱
柱顶:M
t c1k
V1k
h1 3
柱底
:
M
b c1k
V1k
2h1 3
对于上部各层柱
M
t cjk
M
b cjk
V jk
hj 2
11 14. 3 计算方法
第十四章 多层框架结构
由假定3 (节点平衡条件)可求出梁端弯矩
M
l b
ibl
ibl ibr
(M
u c
M
d c
)
M
r b
ibr ibl ibr
(M
u cLeabharlann Md c)
二、水平荷载作用下的 D 值法
1、反弯点法存在的问题
(1)由于框架各层节点转角不可能相等,故柱的反弯点位置也不可能 都在 柱中点;
(2)由于梁柱线刚度之比不可能为无穷大,故柱的抗侧移刚度也不完全 取决于柱本身,还与梁的刚度由关。
14. 3 计算方法
第十四章 多层框架结构
梁固端弯矩 梁柱杆端弯矩(节点不平衡弯矩分配) 梁柱杆 端剪力 柱轴力 最后应将各层框架还原为整体框架
框架还原: 梁、柱弯矩同位叠加,并对框架节点 处得不平衡弯矩进行重分配; 梁柱剪力由其两端弯矩和承担的其它 荷载根据平衡条件求得; 柱轴力最后计算,为与其相连上层各 梁剪力之和。
1
14. 3 计算方法
第十四章 多层框架结构
第三节 框架结构内力与侧移的近似计算方法 P.158
基本假定: 1、忽略框架在竖向荷载作用下的侧移和由它引起的侧移力矩; 2、忽略本层荷载对其它各层内力的影响。 即:竖向荷载只在本层的梁内以及与本层梁相连的框架柱内产 生弯矩和剪力,而对其它楼层框架梁和隔层框架柱不产生弯矩 和剪力。
k 1
VFj—层间总剪力
n
VFj Fj Fj1 Fk Fn Fk
k 1
10 14. 3 计算方法
第十四章 多层框架结构
框架受侧向荷载时,框架柱内的剪力:
V jk
12i jk hj2
u j
12i/h2 称为柱的抗侧刚度(抗剪刚度)
由假定1
u j
VFj
