【中小学资料】九年级数学下册 27.1 圆的认识练习题 (新版)华东师大版
华东师大版数学九年级下册第27章圆第1节 圆的认识 圆的基本元素专题练习题及答案

华东师大版数学九年级下册第27章圆第1节圆的认识圆的基本元素专题练习题1.下列说法中,正确的是( )A.直径是圆中最长的弦B.弦是圆上任意两点之间的部分C.过圆心的线段是直径D.弦的端点可以不在圆上2.下列说法中正确的个数有( )①大于半圆周的弧叫优弧,小于半圆周的弧叫劣弧;②优弧一定比劣弧长;③任意一条弦都把圆周分成两条弧,一条是优弧,一条是劣弧.A.1个B.2个C.3个D.0个3.下列命题正确的个数有( )①顶点在圆心的角为圆心角;②弦是直径;③直径是弦;④半圆是弧,但弧不一定是半圆.A.1个B.2个C.3个D.4个4.过圆内一点(非圆心)可以作出圆的最长弦有( )A.1条B.2条C.3条D.1条或无数条5.如图,MN为⊙O的弦,∠M=50°,则∠MON等于( )A.50°B.55°C.65°D.80°6.如图,AB是⊙O的直径,AC是弦,若∠A=30°,则∠BOC的度数是( )A.30°B.50°C.60°D.120°7.已知AB,CD是⊙O的两条直径,∠ABC=30°,则∠BAD=___.8. 如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是____.9.把地球看成一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处高出球面16 cm,那么钢丝大约需要加长( )A.102 cm B.104 cm C.106 cm D.108 cm10.下列命题中,正确的个数是( )①圆是由圆心唯一确定的;②半径相等的两个圆是等圆;③一条弦把圆分成的两段弧中,至少有一段是优弧.A.0个B.1个C.2个D.3个11.如图,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )A.a>b>c B.a=b=c C.c>a>b D.b>c>a12.确定一个圆的条件是____和____,____决定圆的位置,____决定圆的大小.13.在同一平面内与已知点P的距离等于2.5 cm的所有点所组成的图形是____.14.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD =____.15.如图所示,两个半径相等的⊙O1和⊙O2相交于A,B两点,且⊙O1经过点O2,则∠O1AB =____.16. 如图,C,D是⊙A的弦BE上的点,且BC=ED.求证:AC=AD.答案:1---6 AACADC7. 30°8. 60°9. A10. B11. B12. 圆心半径圆心半径13. 以点P为圆心,2.5_cm长为半径的圆_14. 40°15. 30°16. 解:连接AB,AE,则AB=AE,∴∠B=∠E.∵BC=ED,∴△ABC≌△AED,∴AC=AD。
九年级数学下册第27章圆27.1圆的认识2圆的对称性第1课时弧、弦、圆心角之间的关系练习华东师大版

九年级数学下册第27章圆27.1 圆的认识2 圆的对称性第1课时弧、弦、圆心角之间的关系同步练习(新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学下册第27章圆27.1 圆的认识2 圆的对称性第1课时弧、弦、圆心角之间的关系同步练习(新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学下册第27章圆27.1 圆的认识2 圆的对称性第1课时弧、弦、圆心角之间的关系同步练习(新版)华东师大版的全部内容。
27.1 2。
第1课时弧、弦、圆心角之间的关系一、选择题1.如图K-13-1,在⊙O中,错误!=错误!,下列结论错误的是( )图K-13-1A.AB=CDB.∠AOC=∠DOBC.∠OCD=∠OBAD。
错误!=错误!2.下列说法中正确的是()①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,圆心到这两条弦的距离也相等;④在等圆中,圆心角不相等,它们所对的弦也不相等.A.①③ B.②④ C.①④ D.②③3.在⊙O和⊙O′中,已知∠AOB=∠CO′D,则()A。
错误!=错误! B。
错误!〈错误! C。
错误!〉错误!D.错误!与错误!的大小无法确定4.在同圆或等圆中,若错误!的长度等于错误!的长度,则下列说法中正确的有( )①错误!的度数=错误!的度数;②错误!所对的圆心角等于错误!所对的圆心角;③错误!和错误!是等弧;④错误!所对的弦的长度等于错误!所对的弦的长度.A.1个 B.2个 C.3个 D.4个5.如图K-13-2,已知AB是⊙O的直径,错误!=错误!=错误!,∠BOC=40°,那么∠AOE的度数为( )图K-13-2A.40° B.60° C.75° D.120°6.如图K-13-3,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论中正确的是( )图K-13-3A.AB=AD B.BC=CDC。
「精品」九年级数学下册第27章圆27.1圆的认识271.1圆的基本元素同步练习新版华东师大版

27.1.1 圆的基本元素知|识|目|标1.通过画圆和表示圆,知道圆的定义以及同心圆、等圆等概念.2.在阅读教材、动手实践、类比思考、例题辨析的基础上,弄清弧、弦、圆心、半径、直径等概念. 3.经历对圆的半径、直径的数量关系的自主探究过程,能计算或证明圆中角或线段的数量关系等.目标一 能画出符合条件的圆例1 教材补充例题 画出符合下列条件的圆:(1)画3个以点O 为圆心的圆;(2)画3个以0.7厘米为半径的圆;(3)画出以点A 为圆心,0.7厘米为半径的圆;(4)画一条线段AB ,再以AB 的中点为圆心,12AB 长为半径画圆.【归纳总结】圆的分类:(1)在同一平面内,圆心相同而半径不同的圆叫做同心圆;(2)半径相等的两个圆称为等圆;(3)圆的位置由圆心确定,圆的大小由半径的长度确定. 目标二 理解圆的相关概念例2 教材补充例题 有以下命题:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的两条弧是等弧;⑥经过圆内一定点的弦有无数条;⑦经过圆内一定点的直径有无数条;⑧等圆的半径相等;⑨弧分为优弧和劣弧;⑩圆心相同而半径不同的两个圆叫做同心圆.其中正确的有( )A .6个B .7个C .8个D .9个 【归纳总结】圆中容易混淆的“两组基本概念”: 1.弦与直径.(1)直径是弦,是圆中最长的弦,但弦不一定是直径;(2)弦是连结圆上任意两点的线段,而直径是经过圆心的弦. 2.弧与半圆.(1)半圆是弧,但弧不一定是半圆;(2)圆上任意两点把圆分成两条弧,圆上任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.目标三 能进行圆中的计算或证明例3 高频考题 如图27-1-1,已知CD 是⊙O 的直径,∠DOE =78°,A 是DC 延长线上的一点,AE交⊙O 于点B ,且AB =OC ,求∠A 的度数.图27-1-1【归纳总结】解决此类问题的一般方法是作出圆的半径,利用同圆的半径相等解题.知识点一 圆的定义 圆的定义有两种:(1)如图27-1-2所示,在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆.固定的端点O 叫做圆心,线段OA 是圆的半径.图27-1-2(2)圆是到定点的距离等于定长的点的集合,此定点为圆心,定长为半径.如图27-1-2所示,这个以点O 为圆心,以OA 的长为半径的圆叫做“圆 O ”,记作“________”. (3)圆把平面分成三部分,分别是圆内、圆上和圆外.[点拨]圆是指到圆心的距离等于半径的所有点的集合,也就是封闭的曲线,而不是指圆面. 知识点二 与圆有关的概念(1)弦和直径:连结圆上任意两点的________叫做弦.如图27-1-3中的线段AC ,CD ,BD ,AB 都是⊙O 的弦.经过________的弦叫做直径,弦AB 是⊙O 的直径,直径是圆中最长的弦.圆心到弦的距离叫做此弦的弦心距,图27-1-3中线段OM 的长表示弦CD 的弦心距.图27-1-3(2)弧和半圆:圆上任意两点间的部分叫做弧,弧用符号“⌒”表示,以A ,B 为端点的弧记作“AB ︵”,读作“弧AB ”.一条直径把圆分成了两个半圆,小于半圆周的圆弧叫做劣弧,如图27-1-3中的AC ︵,BC ︵.大于半圆周的圆弧叫做优弧,在表示优弧时,用三个字母表示,如图27-1-3中的BAC ︵.[点拨]等弧是指能够互相重合的弧,等弧只能在同圆或等圆中出现.已知在半径为5的⊙O中,弦AB=5 2,弦AC=5,求∠BAC的度数.解:如图27-1-4,连结OA,OB,OC.∵AC=OA=OC=5,∴△OAC是等边三角形,∴∠OAC=60°.∵OA2+OB2=52+52=50,AB2=(5 2)2=50,∴OA2+OB2=AB2,图27-1-4 ∴△OAB是直角三角形.又∵OA=OB,∴△OAB是等腰直角三角形,∴∠OAB=45°,∴∠BAC=∠OAB+∠OAC=45°+60°=105°.以上解答过程完整吗?若不完整,请进行补充.教师详解详析【目标突破】例1解:根据题目中的条件,分别画出符合条件的圆:例2[解析] A①③④⑥⑧⑩正确.例3[解析] 已知∠DOE=78°,与未知角∠A构成了内、外角关系,而∠E也未知,且AB=OC这一条件不能直接使用,因此想到同圆的半径相等,需连结OB,从而得到OB=AB.解:如图,连结OB.∵AB=OC,OB=OC,∴AB=OB,∴∠A=∠1.又∵OB=OE,∴∠E=∠2=∠1+∠A=2∠A,∴∠DOE=∠E+∠A=3∠A.又∵∠DOE=78°,∴3∠A=78°,∴∠A=26°.【总结反思】[小结] 知识点一(2)⊙O知识点二(1)线段圆心[反思] 不完整.补充如下:若点B,C在直线OA的异侧,则∠BAC=∠OAB+∠OAC=45°+60°=105°;若点B,C在直线OA的同侧,如图所示,则∠BAC=∠OAC-∠OAB=60°-45°=15°.综上可得,∠BAC的度数是105°或15°.。
九年级数学下册第27章圆27.1圆的认识27.1.2.1弧、弦、圆心角之间的关系练习华东师大版(2

2018-2019学年九年级数学下册第27章圆27.1 圆的认识27.1.2.1 弧、弦、圆心角之间的关系同步练习(新版)华东师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年九年级数学下册第27章圆27.1 圆的认识27.1.2.1 弧、弦、圆心角之间的关系同步练习(新版)华东师大版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年九年级数学下册第27章圆27.1 圆的认识27.1.2.1 弧、弦、圆心角之间的关系同步练习(新版)华东师大版的全部内容。
27. 2.圆的对称性第1课时弧、弦、圆心角之间的关系知|识|目|标1.通过旋转一个圆心角,发现圆的旋转不变性,知道弧、弦、圆心角之间的关系.2.通过阅读、讨论、动手实践,能运用弧、弦、圆心角之间的关系解决问题.目标一探究弧、弦、圆心角之间的关系例1 教材补充例题圆是旋转对称图形,围绕着圆心旋转________角度,它都能与自身重合.例2 教材补充例题如图27-1-5,两个等圆中有两个圆心角∠AOB,∠A′O′B′,连结AB,A′B′,请你添加一个条件,使得△AOB≌△A′O′B′。
请你试一试有几种添加方法.图27-1-5(1)同学甲:我添加∠AOB=∠A′O′B′,根据________可判定△AOB≌△A′O′B′。
这样你还能得到哪些相等关系?(2)同学乙:我添加AB=A′B′,根据________可判定△AOB≌△A′O′B′.这样你还能得到哪些相等关系?【归纳总结】在同圆或等圆中,圆心角越大,它所对应的弧就越长,所对应的弦也越长.目标二能运用弧、弦、圆心角之间的关系解题例3 教材例1针对训练如图27-1-6,在⊙O中,若C是错误!的中点,∠A=50°,则∠BOC 的度数是()图27-1-6A.40° B.45°C.50° D.60°例4 [教材例1针对训练]如图27-1-7,AB,CD,EF都是⊙O的直径,AC=EB=DF,求∠1,∠2,∠3的度数.图27-1-7【归纳总结】弧、弦、圆心角之间关系的应用:(1)充分利用弧、弦、圆心角之间的关系进行转化,如将弦相等转化为它们所对的圆心角相等;(2)弧、弦、圆心角之间的关系定理适用的前提条件是在同圆或等圆中.知识点一圆的旋转不变性圆是一个中心对称图形,对称中心为________.圆又是一个旋转对称图形,一个圆绕其圆心旋转任意一个角度,都能与自身重合,圆的这个性质称为圆的旋转不变性.知识点二弧、弦、圆心角之间的关系在同圆或等圆中,如果圆心角相等,那么它们所对的弧________,所对的弦________;在同圆或等圆中,如果弧相等,那么它们所对的圆心角________,所对的弦______;在同圆或等圆中,如果弦相等,那么它们所对的圆心角________,所对的弧________.[点拨]不能去掉“在同圆或等圆中”这个前提条件.如图27-1-8,在⊙O中,若错误!=2错误!,试判断AB与2CD之间的大小关系,并说明理由.图27-1-8解:∵在同圆或等圆中,相等的弧所对的弦相等,∴当错误!=2错误!时,AB=2CD。
人教版2020九年级数学下册 27.1 圆的认识 27.1.3 圆周角配套练习(无答案)(新版)华东师大版
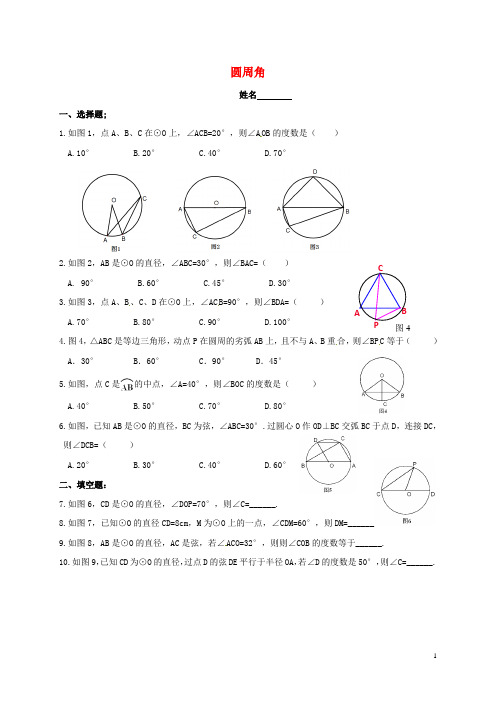
圆周角姓名一、选择题;1.如图1,点A、B、C在⊙O上,∠ACB=20°,则∠A OB的度数是()A.10°B.20°C.40°D.70°2.如图2,AB是⊙O的直径,∠ABC=30°,则∠BAC=()A. 90°B.60°C.45°D.30°3.如图3,点A、B、C、D在⊙O上,∠AC B=90°,则∠BDA=()A.70°B.80°C.90°D.100°4.图4,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BP C等于()A.30° B.60° C.90° D.45°5.如图,点C是的中点,∠A=40°,则∠BOC的度数是()A.40°B.50°C.70°D.80°6.如图,已知AB是⊙O的直径,BC为弦,∠ABC=30°.过圆心O作OD⊥BC交弧BC于点D,连接DC,则∠DCB=()A.20°B.30°C.40°D.60°二、填空题:7.如图6,CD是⊙O的直径,∠DOP=70°,则∠C=______.8.如图7,已知⊙O的直径CD=8cm,M为⊙O上的一点,∠CDM=60°,则DM=______.9.如图8,AB是⊙O的直径,AC是弦,若∠ACO=32°,则则∠COB的度数等于______.10.如图9,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C=______.CA BP 图411.如图10,AB是⊙O的直径,C、D、E是⊙O上的点,则∠1+∠2=______.三、解答题:12.如图11,AB是⊙O的直径,∠B=45°,BC=2cm,求半径AO的长.13.如图12,点A、B、C是⊙O上的点,∠C=30°,试判断△ABO的形状.14.如图14,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,连结BD,求∠ABD的度数.15.如图15,已知是⊙O的半径为2,弦AB的长为32,点C与点D分别是劣弧AB与优弧ADB上的任一点(点C、D均不与A、B重合).(1)求∠ACB;(2)求△ABD的最大面积.。
九年级数学下册第27章圆27.1圆的认识2圆的对称性第2课时垂径定理同步练习新版华东师大版

27.1 2. 第 2 课时垂径定理一、选择题1.圆是轴对称图形,它的对称轴有()A.1条B.2条C.4 条D.无数条2.在半径为 3 的圆中,一条弦的长度为4,则圆心到这条弦的距离是链接听课例2归纳总结()A.3B.4 C.5 D.73.2018·张家界如图K- 14- 1,AB是⊙O的直径,弦CD⊥ AB于点 E, OC=5 cm, CD=8 cm,则 AE等于()图 K-14-1A. 8 cm B.5 cmC. 3 cm D.2 cm4.过⊙O内一点M的最长的弦长为 4 cm,最短的弦长为 2 cm,则OM的长为 ()A. 3 cmB. 2 cm C.3 cm D.2 cm5.2017·金华如图K- 14- 2,在半径为 13 cm的圆形铁片上切下一块高为8 cm 的弓形铁片,则弓形弦 AB的长为()图 K-14-2A. 10 cm B.16 cmC. 24 cm D.26 cm6.在直径为200 cm 的圆柱形油槽内装入一些油此后,截面如图K-14- 3 所示.若油面AB = 160 cm ,则油的最大深度为()图 K-14-3A. 40 cm B.60 cm C.80 cm D.100 cm7.如图 K- 14- 4,正方形ABCD的四个极点在⊙ O上,⊙ O的直径为 2 dm,若往这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是()图 K-14-42π1A. πB.9C.2πD.2π二、填空题8.如图 K- 14- 5,在⊙O中,弦AB=6,圆心O到AB的距离OC= 2,则⊙O的半径为 ________.图 K-14-59.如图 K- 14- 6,在 5×5的正方形网格中,一条圆弧经过A,B, C三点,那么这条圆弧所在圆的圆心是点________.图 K-14-610.如图K- 14- 7,在⊙ O中, AB,AC为相互垂直且相等的弦,OD⊥ AB,OE⊥AC,垂足分别为 D,E. 若 AC=2 cm,则⊙ O的半径为 ________.图 K-14-711.如图K- 14- 8,在△ ABC中,已知∠ ACB=130°,∠ BAC= 20°, BC= 2,以点 C 为圆心,CB长为半径的圆交 AB于点 D,则 BD的长为 ________.图 K-14-812.如图K- 14- 9 所示,若⊙ O的半径为13 cm, P 是弦 AB 上的一个动点,且到圆心的最短距离为 5 cm,则弦 AB的长为 ________cm.图 K-14-913.工程上常用钢珠来丈量部件上小圆孔的宽口,假设钢珠的直径是10 mm,测得钢珠顶端离部件表面的距离为8 mm,如图K-14-10所示,则这个小圆孔的宽口AB 的长度为________mm.图 K-14-10三、解答题14.如图K- 14- 11,在以点O为圆心的两个齐心圆中,大圆的弦AB 交小圆于C,D 两点.求证: AC= BD.图 K-14-11︵15.如图K-14- 12,已知 AB是⊙ O的弦, C 是 AB的中点, AB= 8,AC= 2 5,求⊙ O的半径.图 K-14-1216.如图K- 14- 13,已知⊙ O的弦 CD垂直于直径AB于点 F,点 E 在 CD上,且 AE= CE.2(1) 求证: CA=CE·CD;(2) 已知 CA= 5, AE= 3,求sin∠ EAF的值.图 K-14-1317.如图K- 14- 14,在一块残缺的轮片上,量得弓形的弦AB= 24 cm,弓形的高为8 cm,求残缺的轮片的直径.图 K-14-141.[答案]D2.[答案]C13.[ 解析 ] A∵弦CD⊥AB于点E,CD=8cm,∴ CE=CD=4cm.在Rt△ OCE中,∵ OC=5cm,222CE= 4 cm,∴ OE=OC-CE= 3 cm,∴ AE= AO+ OE= 5+ 3= 8 ( cm) .应选A.4.[ 解析 ] A过圆内一点最长的弦为直径,最短的弦为与这条直径垂直的弦,由垂径定理和勾股定理可求得OM= 3 cm.22 5.[ 解析 ] C如图,在Rt△ OCB中,OC=5cm,OB=13cm,依据勾股定理,得BC=OB-OC=132- 52= 12( cm) .∵OC⊥AB,∴ AB= 2BC= 24 cm.6.[答案]A7.[答案]A8.[ 答案 ]139.[答案]Q[ 解析 ] 依据垂径定理的推论,则作弦AB和 BC的垂直均分线,交点Q即为圆心.10.[ 答案 ] 2 cm11.[ 答案 ] 23[ 解析 ]如图,过点 C 作 CE⊥AB 于点 E.由题意易知∠ B= 180°-∠ BAC-∠ ACB= 180°- 20°- 130°= 30° .在 Rt△BCE中,∵∠CEB= 90°,∠ B=30°, BC= 2,1∴CE=2BC= 1,BE= 3CE= 3.∵CE⊥BD,∴ DE= BE,∴BD=2BE= 2 3.故答案为 2 3.12.[ 答案 ] 24[解析]连结 OA,当 OP⊥AB 时, OP最短,此时 OP=5 cm,且 AB= 2AP.在Rt△AOP中, AP=2222= 12() ,因此 AB= 24 .OA- OP=13 -5cm cm 13.[ 答案 ] 814.证明:过点O作 OE⊥AB 于点 E,则 AE= BE, CE= DE,∴AE-CE= BE-DE,即 AC= BD.15.解:如图,连结OA, OC, OC交 AB 于点 D.设⊙O的半径为r.︵∵ C 是AB的中点,︵︵∴AC=BC,∴ OC⊥ AB,1∴ AD=DB=2AB=4.在 Rt△ACD中,CD =22AC- AD= 2,222在 Rt△ADO中,∵OA=AD+OD,∴ r 2=16+ (r -2) 2,解得 r =5.∴⊙ O的半径为 5.16.解: (1) 证明:∵弦CD垂直于直径AB,︵︵∴AC=AD,∴ AC= AD,∴∠ D=∠ C.又∵ AE= CE,∴∠ CAE=∠ C,∴∠ CAE=∠ D.又∵∠ C=∠ C,∴△ CEA∽△ CAD,CA CE2∴ =,即 CA=CE·CD.CD CA(2) ∵CA2=CE·CD, CA= 5, CE= AE= 3,∴52=3CD,∴ CD=25.3∵弦 CD垂直于直径AB于点 F,∴ CF= FD,112525257∴CF=2CD=2×3=6,∴ EF= CF- CE=6- 3=6.7EF67在 Rt△AFE中, sin ∠EAF=AE=3=18.17.解:如图,设残缺的轮片的圆心为O,过点 O作 OC⊥AB 于点 C,延长 OC交⊙O于点 D,则 CD= 8,AC= BC=1AB= 12. 连结 OB.设⊙O的半径为 R,由勾股定理,得R2= 122+ (R-8) 2,解得 R= 13,∴残缺的轮片的直径为26 cm.。
2018-2019学年九年级数学下册 第27章 圆 27.1 圆的认识 27.1.1 圆的基本元素同步练习 (新版)华东师大版
27.1.1 圆的基本元素知|识|目|标1.通过画圆和表示圆,知道圆的定义以及同心圆、等圆等概念.2.在阅读教材、动手实践、类比思考、例题辨析的基础上,弄清弧、弦、圆心、半径、直径等概念.3.经历对圆的半径、直径的数量关系的自主探究过程,能计算或证明圆中角或线段的数量关系等.目标一 能画出符合条件的圆例1 教材补充例题 画出符合下列条件的圆:(1)画3个以点O 为圆心的圆;(2)画3个以0.7厘米为半径的圆;(3)画出以点A 为圆心,0.7厘米为半径的圆;(4)画一条线段AB ,再以AB 的中点为圆心,12AB 长为半径画圆.【归纳总结】圆的分类:(1)在同一平面内,圆心相同而半径不同的圆叫做同心圆;(2)半径相等的两个圆称为等圆;(3)圆的位置由圆心确定,圆的大小由半径的长度确定.目标二 理解圆的相关概念例2 教材补充例题 有以下命题:①直径是弦;②弦是直径;③半圆是弧,但弧不一定是半圆;④半径相等的两个半圆是等弧;⑤长度相等的两条弧是等弧;⑥经过圆内一定点的弦有无数条;⑦经过圆内一定点的直径有无数条;⑧等圆的半径相等;⑨弧分为优弧和劣弧;⑩圆心相同而半径不同的两个圆叫做同心圆.其中正确的有( )A .6个B .7个C .8个D .9个【归纳总结】圆中容易混淆的“两组基本概念”:1.弦与直径.(1)直径是弦,是圆中最长的弦,但弦不一定是直径;(2)弦是连结圆上任意两点的线段,而直径是经过圆心的弦.2.弧与半圆.(1)半圆是弧,但弧不一定是半圆;(2)圆上任意两点把圆分成两条弧,圆上任意一条直径的两个端点把圆分成两条弧,每一条弧叫做半圆.目标三 能进行圆中的计算或证明例3 高频考题 如图27-1-1,已知CD 是⊙O 的直径,∠DOE =78°,A 是DC 延长线上的一点,AE 交⊙O 于点B ,且AB =OC ,求∠A 的度数.图27-1-1【归纳总结】解决此类问题的一般方法是作出圆的半径,利用同圆的半径相等解题.知识点一 圆的定义圆的定义有两种:(1)如图27-1-2所示,在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆.固定的端点O 叫做圆心,线段OA 是圆的半径.图27-1-2(2)圆是到定点的距离等于定长的点的集合,此定点为圆心,定长为半径.如图27-1-2所示,这个以点O 为圆心,以OA 的长为半径的圆叫做“圆 O ”,记作“________”.(3)圆把平面分成三部分,分别是圆内、圆上和圆外.[点拨]圆是指到圆心的距离等于半径的所有点的集合,也就是封闭的曲线,而不是指圆面. 知识点二 与圆有关的概念(1)弦和直径:连结圆上任意两点的________叫做弦.如图27-1-3中的线段AC ,CD ,BD ,AB 都是⊙O 的弦.经过________的弦叫做直径,弦AB 是⊙O 的直径,直径是圆中最长的弦.圆心到弦的距离叫做此弦的弦心距,图27-1-3中线段OM 的长表示弦CD 的弦心距.图27-1-3(2)弧和半圆:圆上任意两点间的部分叫做弧,弧用符号“⌒”表示,以A ,B 为端点的弧记作“AB ︵”,读作“弧AB ”.一条直径把圆分成了两个半圆,小于半圆周的圆弧叫做劣弧,如图27-1-3中的AC ︵,BC ︵.大于半圆周的圆弧叫做优弧,在表示优弧时,用三个字母表示,如图27-1-3中的BAC ︵.[点拨]等弧是指能够互相重合的弧,等弧只能在同圆或等圆中出现.已知在半径为5的⊙O中,弦AB=5 2,弦AC=5,求∠BAC的度数.解:如图27-1-4,连结OA,OB,OC.∵AC=OA=OC=5,∴△OAC是等边三角形,∴∠OAC=60°.∵OA2+OB2=52+52=50,AB2=(5 2)2=50,∴OA2+OB2=AB2,图27-1-4 ∴△OAB是直角三角形.又∵OA=OB,∴△OAB是等腰直角三角形,∴∠OAB=45°,∴∠BAC=∠OAB+∠OAC=45°+60°=105°.以上解答过程完整吗?若不完整,请进行补充.教师详解详析【目标突破】例1解:根据题目中的条件,分别画出符合条件的圆:例2[解析] A①③④⑥⑧⑩正确.例3[解析] 已知∠DOE=78°,与未知角∠A构成了内、外角关系,而∠E也未知,且AB =OC这一条件不能直接使用,因此想到同圆的半径相等,需连结OB,从而得到OB=AB. 解:如图,连结OB.∵AB=OC,OB=OC,∴AB=OB,∴∠A=∠1.又∵OB=OE,∴∠E=∠2=∠1+∠A=2∠A,∴∠DOE=∠E+∠A=3∠A.又∵∠DOE=78°,∴3∠A=78°,∴∠A=26°.【总结反思】[小结] 知识点一(2)⊙O知识点二(1)线段圆心[反思] 不完整.补充如下:若点B,C在直线OA的异侧,则∠BAC=∠OAB+∠OAC=45°+60°=105°;若点B,C在直线OA的同侧,如图所示,则∠BAC=∠OAC-∠OAB=60°-45°=15°.综上可得,∠BAC的度数是105°或15°.。
华师大版九年级下册数学(圆)单元练习题课件精选全文
8.如图,已知⊙O 中,AB,CD 是弦,根据条件填空: (1)若 AB=CD,则_A︵_B__=__C︵_D___,__∠__A_O_B_=__∠__C__O_D___;
13.如图,在⊙E 中,如果A︵B=2C︵D,那么( C )
A.AB=2CD B.AB>2CD C.AB<2CD D.以上答案都不对 14.如图,AB 是⊙O 的直径,BC,CD,DA 是⊙O 的弦,且 BC =CD=DA,则∠BCD=__1_2_0_°____.
15.如图,AB,CD 是⊙O 的两条直径,CE∥AB.求证:B︵C=A︵E =A︵D.
18.如图,在△ABC中,∠ACB=90°,∠A=40°,以点C为圆 心,CB长为半径的圆交AB于点D,求∠ACD的度数. 解:∵∠A=40°,∠ACB=90°,∴∠B=50°,∵CD=CB, ∴∠CDB=∠B=50°,∴∠ACD=∠CDB-∠A=50°-40° =10°
19.如图,AB,AC为⊙O的弦,连结CO,BO并延长分别交弦 AB,AC于点E,F,∠B=∠C. 求证:CE=BF. 解 : 先 用 “ ASA” 证 △ BOE≌△COF , 从 而 得 到 OE = OF , 由 于 OB=OC,则可证得CE=BF
华东师大版九年级下册 精品课件
使络本 用只课
供件 免来 费源 交于 流网
第27章 圆
27.1 圆的认识 27.1.1 圆的基本元素
1.如图: (1)以点O为圆心的圆叫做“____圆__O_”,记为“_____⊙__O”. (2)半径:线段____O_A_,_____O_B_,_____O__C都是⊙O的半径. (3)直径:线段____A_B_是⊙O的直径. (4)弦:线段____A__B_,_____A_C,_____B__C都是⊙O的弦.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中小学最新教育资料
中小学最新教育资料
27.1圆的认识练习题
一、选择题
1、到P点的距离小于5cm的范围是( )
A、以P为圆心,5cm为半径的圆的外部; B、以P为圆心,5cm为半径的圆的内部;
C、以P为圆心,5cm为半径的圆上; D、以上说法都不正确;
2、已知⊙P的半径是3cm,则下列说法错误的是()
A、⊙P的直径是6cm B、⊙P的的周长为6cm
C、⊙P的的面积是9cm2 D、⊙P的弧长是9cm2
3、如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.3 B.2.5 C.4 D.3.5
4、如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为5cm,则圆心O
到弦CD的距离为( )
A.cm B.3cm C.3cm D.6cm
5、如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=65°,∠D=60°,则
的度数为何?( )
A.25 B.40 C.50 D.55
6、如图,在⊙O中,=,∠AOB=40°,则∠ADC的度数是( )
A.40° B.30° C.20° D.15°
中小学最新教育资料
中小学最新教育资料
7、如图,线段AB是⊙O的直径,弦CD⊥AB,∠CAB=40°,则∠ABD与∠AOD分别等于
( )
A.40°,80° B.50°,100° C.50°,80° D.40°,100°
8、如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
A.75° B.60° C.45° D.30°
二、填空题
1、如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE= .
2、如图,⊙O的直径CD=20cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM=6cm,则AB的长
为 cm.
3、如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径
为 .
中小学最新教育资料
中小学最新教育资料
4、如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆
盖这个平面图形的圆面的最小半径是 mm.
5、如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC= .
6、如图,A,B,C,D是⊙O上的四个点,∠C=110°,则∠BOD= 度.
三、解答题
1、如图,在⊙O中,弦AC=2,点B是圆上一点,且∠ABC=45°,求⊙O的半径
2、如图,扇形OAB的圆心角为122°,C是上一点,求∠ACB的度数。
中小学最新教育资料
中小学最新教育资料
3、如图,点P是四边形ABCD外接圆上任意一点,且不与四边形顶点重合,若AD是⊙O的
直径,AB=BC=CD.连接PA、PA、PC,若PA=a,求点A到PB和PC的距离之和。
4、如图,AB是⊙O的直径,AC、BC是⊙O的弦,直径DE⊥AC于点P.若点D在优弧
上,AB=8,BC=3,求DP的长度 .
华师大版九年级下册27.1圆的认识练习题答案
一、选择题
BDCAB CBD
二、填空题
1、4﹣
2、16
3、10
中小学最新教育资料
中小学最新教育资料
4、50
5、35°
6、140
三、解答题
1、解:∵∠ABC=45°,
∴∠AOC=90°,
∵OA=OC=R,
∴R2+R2=2,
解得R=.
2、解:如图所示,在⊙O上取点D,连接AD,BD,
∵∠AOB=122°,
∴∠ADB=∠AOB=×122°=61°.
∵四边形ADBC是圆内接四边形,
∴∠ACB=180°﹣61°=119°.
3、解:如图,连接OB、OC.
∵AD是直径,AB=BC=CD,
∴==,
∴∠AOB=∠BOC=∠COD=60°,
∴∠APB=∠AOB=30°,∠APC=∠AOC=60°,
在Rt△APE中,∵∠AEP=90°,
∴AE=AP•sin30°=a,
在Rt△APF中,∵∠AFP=90°,
∴AF=AP•sin60°=a,
∴AE+AF=a.
4、解:∵AB和DE是⊙O的直径,
∴OA=OB=OD=4,∠C=90°,
又∵DE⊥AC,
∴OP∥BC,
∴△AOP∽△ABC,
∴,
即,
中小学最新教育资料
中小学最新教育资料
∴OP=1.5.
∴DP=OD+OP=5.5,
