(2.6) 第六节 变化率问题举例及相关变化率(少学时简约版)
变化率ppt

类似地,y f(x2) f (x1)
于是,平均变化率可表示为 y . x
注:
1)x是一个整体符号 ,而不是与x相乘; 2)x可看作是相对于x1的一个“增量”, 即,x2 x x1
那么,函数的平均变化率还可以表示为:
f (x Δx) f (x ) x
二、函数的平均变化率的几何意义
y
fx2 fx1
我们知道,气球的体积V 单位 : L与半径r(单
位:
dm)之间的函数关系是V
r
4 3
r3,
如果把半径r表示为体积V的函数,那么
rV
3
3V
4
.
当空气容积V从0增加到1 L时, 气球半径增加了
r1 r0 0.62cm,
气球的平均膨胀率为
r1
1
r0
0
0.62dm
/
L.
类似地,当空气容量从1 L增加到2 L时, 气球半径
思考:
如果上述两个问题中的 函数关系用 f x表示,
那么问题中变化率该如 何表示?
f x2 f x1 ,
x2 x1
新授:
一、函数的平均变化率
若有
f x2 f x1 ,
x2 x1
我们把这个式子称为函数 f x从 x1到 x2的
平均变化率
习惯上用 x表示 x2 x1,即x Байду номын сангаасx2 x1,
增加了r2 r1 0.16dm,
气球的平均膨胀率为
r2
2
r1
1
0.16dm
/
L.
可以看出,随着气球体积逐渐变大,它的平均膨
胀率逐渐变小了.
思考 : 当空气的容量从V1增加到V2时,气球的平
变化率问题
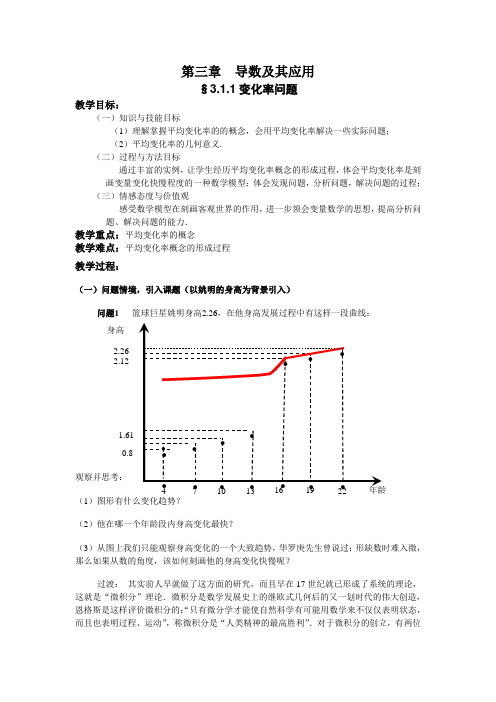
第三章 导数及其应用§3.1.1变化率问题教学目标:(一)知识与技能目标(1)理解掌握平均变化率的的概念,会用平均变化率解决一些实际问题;(2)平均变化率的几何意义.(二)过程与方法目标通过丰富的实例,让学生经历平均变化率概念的形成过程,体会平均变化率是刻 画变量变化快慢程度的一种数学模型;体会发现问题,分析问题,解决问题的过程;(三)情感态度与价值观感受数学模型在刻画客观世界的作用,进一步领会变量数学的思想,提高分析问 题、解决问题的能力.教学重点:平均变化率的概念教学难点:平均变化率概念的形成过程 教学过程:(一)问题情境,引入课题(以姚明的身高为背景引入)问题1 篮球巨星姚明身高2.26,在他身高发展过程中有这样一段曲线:观察并思考: (1)图形有什么变化趋势? (2)他在哪一个年龄段内身高变化最快?(3)从图上我们只能观察身高变化的一个大致趋势,华罗庚先生曾说过:形缺数时难入微,那么如果从数的角度,该如何刻画他的身高变化快慢呢?过渡: 其实前人早就做了这方面的研究,而且早在17世纪就已形成了系统的理论,这就是“微积分”理论.微积分是数学发展史上的继欧式几何后的又一划时代的伟大创造,恩格斯是这样评价微积分的:“只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程、运动”,称微积分是“人类精神的最高胜利”.对于微积分的创立,有两位2.26 2.12 ● ● ● ● ● ● 年龄身高 4 710 13 16 ● 19 22 0.8 1.61 ● ● ●● ● ● ●科学家做出了重大的贡献:牛顿和莱布尼兹。
今天我们一起来学习微积分的基础:导数的概念第一课——变化率问题.(板书课题) 变化率问题主要是研究变量变化快慢程度(二)实例分析,探究概念 1、身高变化率我们先来看看有没有什么办法解决问题1中的最后一个问题:如何从数的角度刻画他身高 变化快慢,也就是身高的变化率?刚才通过我们对图形的观察发现,在[13,16]里曲线最陡,其他两段比较平缓如果我们将这段曲线近似的看成直线段,我们是如何刻画直线的倾斜程度的?——直线的斜率,那么我们是否可以用同样的方法来刻画一下身高的变化率呢?计算:在[13,16]这个年龄段里,身高的变化率:17.0131661.112.2=--=年龄的差值身高的差值(米/年) 那么这个年龄段的最陡,比值算出来是0.17(米/年),其他两端稍微平缓一些,也请同学们计算一下[4,13]这个年龄段里,比值是09.04-138.0-61.1=(米/年) [16,22]这个年龄段里,比值是023.061-22.122-.262≈(米/年) 从三个比值可以看出,13—16岁这个年龄段比值最大,从图形上看这个是最陡的,所以我们从形和数两个方面都予以了刻画,形上,这个年龄段最陡;数上,这个年龄段比值最大。
变化率问题与导数的概念ppt课件

y 2x (x)2 2 x
x
x
lim y lim (2 x) 2
x x0
x0
y | 2 ' x1
ppt课件.
14
小结:
1.平均速度
瞬时速度;
2.平均变化率
瞬时变化率;
3.导数
f’(x0)=
lim
△x 0
f(x0+△x)-f(x0)
△x
ppt课件.
15
此课件下载可自行编辑修改,供参考! 感谢您的支持,我们努力做得更好!
变化率问题 与导数的概念
ppt课件.
1
问题1.气球平均膨胀率.
吹气球时,会发现:随着气球内空气容量的
增加,气球的半径增加得越来越慢,能从数
学的角度解释这一现象吗?
解:可知:V(r)= 4 πr3 即:r(V)= 3 3V
3
4
当空气容量V从0增加1L时,半径增加了
r(1)-r(0)= 0.62气球平均源自胀率:r(1) r(0) 0.62
(平均速度的极限为瞬时速度)
即:lim △t 0
S(3+△t)-S(3)
△t
=
29.4
思考:在t0时刻的瞬时速度呢?
lim S(t0+△t)-S(t0)
△t 0
△t
ppt课件.
10
瞬时变化率:
思考:我们利用平均速度的极限求得
瞬时速度,那么如何求函数f(x)在
x=x0点的瞬时变化率呢?
可知:函数f(x)在x=x0处的瞬时变化率为:
ppt课件.
5
平均变化率
如果上述的两个函数关系用f(x)表示 那么当自变量x从x1变化到x2时,
【最新】课件-变化率问题PPT

∵x2=x1 +△x
∴平均变化率也可表示为
y x
f (x1 x) x
f (x1)
课堂小结
1、函数y=f(x)平均变化率
=
函数值差 自变量差
y x
f (x2) f (x1) x2 x1
2、平均变化率的几何意义就是两
y y f (x)
点(x1,y1),(x2,y2)间连线(曲线的一条
割线)的斜率。
什么是导数呢?.
问题1:气球膨胀率 新知探究——变化率 在吹气球的过程中可以发现,随着气球内空气容量的增加, 气球的 半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢?
气球的体积V(单位:L)与半径r (单位:dm)之间的函数关系是
若将半径
r
V
4 3
r
3
表示为体积V的函数,
那么
r(V )
3
3v
4
思思考考1::当当空空气气容容量量r(从V11)从V100r增L(0r增加)(V加到20到)V.621时2Lr(d,(,气Vm气1球/)球L的)的平平均均膨膨胀胀率率是是多多少少??
类比:当空气气球容平量均Vr膨(从22)胀1L率增1r(表1加) 示到V0特22.L1征6,V(—气d1m—球/半的L)径平差均/膨体胀积率差是多少?
知识回顾与新知引入
1、函数单调性的定义—— 已知x1,x2∈D,且x1<x2; 若f(x1)<f(x2),则函数f(x)是D上的单调增函数; 若f(x1)>f(x2),则函数f(x)是D上的单调减函数;
2、函数单调性的性质—— 若函数f(x)与g(x)在区间D上有相同的单调性,则和函数f(x)+g(x)
f (0) f (1) 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当 t = 2 时,
v( 2 )=[ 3t 2 - 12 t + 9 ]t=2 = 32 2 - 12 2 + 9 = -3 m /s,
当 t = 4 时,
v( 4 )=[ 3t 2 - 12 t + 9 ]t=4 = 34 2 - 12 4 + 9 = 9 m /s y dx
?
dx
dy
dt
dt
(2) 相关变化率问题分析
设已知变量 x,y 间的关系满足方程 F( x ,y )= 0 . 若变量 x、y 还和另一变量 t 之间存在函数关系:
x = ( t ),y = ( t ),
则三变量 x、y 、t 间的关系满足方程
F( x ,y )= F[( t ),( t )]= 0 .
而在 x = 1 处的线密度为
d dm x21x
0.50kgm .
x1
(1) 相关变化率问题的一般概念
如果有一固定的条件联系着几个变量,这些变量又
都随着另一个变量的改变而改变,那么它们的变化率之
间必然也有一定的关系。具有这种连带关系的变化率就
叫做相关变化率。在这种相关变化率问题中,一个变化
率往往能由其它变化率计算出来。
• 求质点运动过程中的瞬间静止不动点 质点的静止不动点就是速度为零的点,于是令:
v( t )= 3t 2 - 12 t + 9 = 3( t 2 - 4 t + 3 )= 3( t - 1 )( t - 3 )= 0, 解得 t = 1 和 t = 3 是质点的静止不动点。
• 求质点沿数轴正向运动的时间段 质点沿数轴正向运动的时间段就是速度方向与数轴
质量关于长度的变化率或导数。 用符号表示就是
l i x m 0m x l i x m 0f x 1 x x f x 1 d d m x .
例如:设 m = f( x )= x , 则杆在[1,1.2 ]上的平均线密
度为 m x f 1 1 .2 .2 1 f 1 1 0 .2 .2 1 0 .4 8 k g m .
应用问题中的函数关系所涉及的变量往往 不止一个,这些变量及变化率之间都有着某种 依赖关系和联系,这就是所谓相关变量及相关 变化率问题。
根据导数的物理意义进行计算 • 求质点的速度表达式及 2s,4s 时的速度导数
速度函数是位置函数对时间的导数,给定位置函数 s = f( t )= t 3 - 6 t 2 + 9 t, 故求得速度函数为
其平均线密度为
m xfxx22 xf1x1.
x
6 7 x8
这部分质量为 f( x )
x1 x2
随着 x →0 ( 即 x 2 → x 1 ) ,平均线密度
m x f x 1 x x f x 1 f x x 2 2 x f 1 x 1
的极限就是金属杆在 x = x 1 处的线密度 ,即线密度是
容器内水位高度 x 显然是时间 t 的函数,记为
x = x( t ),于是问题归结为求
dx dt
. x
h 2
由于 x = x( t )难以写出,直
接求 x 对时间的变化率有困难。
注意到水注入速率,即容器
内水的体积 V 的变化速率 d V 是
dt
已知的,故考虑先求出体积 V 与
x
t 的函数关系,再间接求
方向一致的时间段,即 v( t )> 0 的情形,于是令: v( t )= 3t 2 - 12 t + 9 = 3( t - 1 )( t - 3 )> 0,
解得 t < 1 和 t > 3 .
• 作质点运动草图 作质点运动的图形通常就是作质点运动的轨迹图,
而不是位移函数的二维图形。 由前几问的讨论知: 当 t < 1 和 t > 3 时,质点沿数轴正向运动, 当 1< t < 2 时,质点沿数轴反向运动。
dx dt
. x
h 2
利用相关变化率关系求解
设圆锥形容器的容积为V 0,容器内尚未被水填充
部分的体积为 V 1,则有 V = V 0 - V 1 . 易求得
V 01 3R 2 h ,V 11 3r2h x,
由图可得
A 每秒
R rh hx,即 rh hxR ,
故有 V113r2hx
1 3 h hxR2hx
• 线密度问题
例:如果金属杆是均匀的,则其线密度 是不变的,此
时可用单位长度的质量来定义其密度,其单位为kg/m .
现考虑不均匀杆的密度定义,假设从左端算起长度
为 x 的一段杆的质量为 m = f( x ),杆位于 x = x 1 和 x = x 2
之间部分的质量为 m = f( x 2 )- f( x 1),
R2
3h2
hx3,
V0
V1
r
h
V
x
R
求得容器中水的体积 V 与液面高度 x 的函数关系为
V x V 0 V 1 1 3R 2 h 3 h R 2 2h x 3.
于是可作出质点运动的轨迹图如下:
t 3 s 0
t 0
t1
s
s 0
s 4
• 求质点在 5s 内走过的路程 因为当 t < 1 时,质点沿数轴正向运动,当 1< t < 2
时,质点沿数轴反向运动,当 t > 3 时,质点又沿数轴 正向运动。因此质点在 5s 内走过的路程应逐段考察。
质点从 t = 0 到 t = 1 内走过的路程为 f( 1 )- f( 0 )= 4 - 0 = 4( m ); 质点从 t = 1 到 t = 2 内走过的路程为 f( 2 )- f( 1 )= 0 - 4 = 4( m ); 质点从 t = 2 到 t = 5 内走过的路程为 f( 5 )- f( 2 )= 20 - 0 = 20( m ); 于是求得质点在 5s 内走过的路程为 4 + 4 + 20 = 28( m ) .
将此方程两边对变量 t 求导可得方程
G[ x ,y , ( t ), ( t )]= 0 . 由于已知 x = ( t ),y = ( t ),故只要知道了( t ) ( t )中的一个,解方程就可求得另一个,由此还可进
一步求得 d y .
dx
例:有一底半径为 R( cm ),高为 h( cm )的圆锥形容器, 今以每秒 A( cm 3 )的速率自顶部向容器内注水,试求: 当容器内水位达到锥高一半时,水面上升的速率?
