初四数学测试题及答案
初四数学专题测试练习
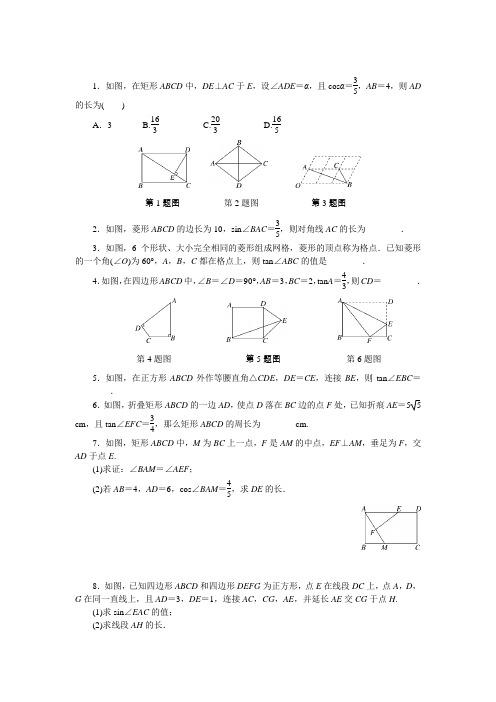
1.如图,在矩形ABCD 中,DE ⊥AC 于E ,设∠ADE =α,且cos α=35,AB =4,则AD的长为( )A .3 B.163 C.203 D.165第1题图 第2题图 第3题图2.如图,菱形ABCD 的边长为10,sin ∠BAC =35,则对角线AC 的长为________.3.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O )为60°,A ,B ,C 都在格点上,则tan ∠ABC 的值是________.4.如图,在四边形ABCD 中,∠B =∠D =90°,AB =3,BC =2,tan A =43,则CD =________.第4题图 第5题图 第6题图5.如图,在正方形ABCD 外作等腰直角△CDE ,DE =CE ,连接BE ,则tan ∠EBC =________.6.如图,折叠矩形ABCD 的一边AD ,使点D 落在BC 边的点F 处,已知折痕AE =55cm ,且tan ∠EFC =34,那么矩形ABCD 的周长为________cm.7.如图,矩形ABCD 中,M 为BC 上一点,F 是AM 的中点,EF ⊥AM ,垂足为F ,交AD 于点E .(1)求证:∠BAM =∠AEF ;(2)若AB =4,AD =6,cos ∠BAM =45,求DE 的长.8.如图,已知四边形ABCD 和四边形DEFG 为正方形,点E 在线段DC 上,点A ,D ,G 在同一直线上,且AD =3,DE =1,连接AC ,CG ,AE ,并延长AE 交CG 于点H .(1)求sin ∠EAC 的值; (2)求线段AH 的长.9.如图,直线y =34x +3与x 、y 轴分别交于A 、B 两点,则cos ∠BAO 的值是( )A.45B.35C.43D.54第9题图 第10题图10.如图,P (12,a )在反比例函数y =60x 图象上,PH ⊥x 轴于H ,则tan ∠POH 的值为________.11.如图,AB 是⊙O 的直径,C 是⊙O 上的点,过点C 作⊙O 的切线交AB 的延长线于点E ,若∠A =30°,则sin E 的值为( )A.12B.22C.32D.33第11题图 第12题图 第13题图12.如图,四边形BDCE 内接于以BC 为直径的⊙A ,若BC =10,cos ∠BCD =35,∠BCE=30°,则线段DE 的长是( )A.89 B .73 C .4+3 3 D .3+4 313.如图,已知⊙O 的半径为6cm ,弦AB 的长为8cm ,P 是AB 延长线上一点,BP =2cm ,则tan ∠OP A 的值是________.14.如图,圆O 的直径AB =8,AC =3CB ,过C 作AB 的垂线交圆O 于M ,N 两点,连接MB ,则∠MBA 的余弦值为________.第14题图 第15题图15.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,若⊙O 的半径是4,sin B =14,则线段AC 的长为________.16.如图,在△ABC 中,∠C =90°,D 是BC 边上一点,以DB 为直径的⊙O 经过AB 的中点E ,交AD 的延长线于点F ,连接EF .(1)求证:∠1=∠F ;(2)若sin B =55,EF =25,求CD 的长.17.如图,AB 为⊙O 的直径,CO ⊥AB 于O ,D 在⊙O 上,连接BD ,CD ,延长CD 与AB 的延长线交于E ,F 在BE 上,且FD =FE .(1)求证:FD 是⊙O 的切线;(2)若AF =8,tan ∠BDF =14,求EF 的长.。
初四数学试题及答案

初四数学试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项不是有理数?A. πB. -3C. 0.5D. √42. 如果一个数的平方等于它本身,那么这个数可能是:A. 1B. -1C. 0D. 以上都是3. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 15厘米4. 以下哪个表达式是正确的?A. (-2)^2 = -4B. √16 = 4C. (-3)^3 = -27D. √9 = -35. 如果a > b,且b > 0,那么下列哪个不等式是正确的?A. a + b < bB. a - b > 0C. a * b < 0D. a / b < 16. 下列哪个是二次根式?A. √2xB. 3x + 2C. 4x^2D. 5x^37. 一个三角形的三边长分别为3, 4, 5,这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形8. 一个数的绝对值是其本身,这个数可能是:A. 正数B. 负数C. 零D. 以上都是9. 以下哪个表达式是正确的?A. 2x + 3y = 5xB. 3x - 2y = 5x + 2yC. 4x^2 - 9y^2 = (2x + 3y)(2x - 3y)D. x^2 - y^2 = (x + y)(x - y)10. 一个数的倒数是1/4,这个数是:A. 4B. 1/4C. 1/2D. 4/1二、填空题(每题2分,共20分)11. 如果一个数的相反数是-5,那么这个数是________。
12. 一个数的立方等于它本身,这个数可能是________、________、________。
13. 一个数的平方根是4,那么这个数是________。
14. 如果a + b = 10,且a - b = 2,那么2a的值是________。
15. 一个圆的周长是2πr,其中r是圆的半径,如果周长是12.56厘米,那么半径是________。
初四数学试题参考答案

②① 2014—2015学年度下学期期中质量检测初四数学试题参考答案评卷说明:1.选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分. 2.解答题每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.每小题只给出一种或两种解法,对考生的其它解法,请参照评分意见进行评分.3.如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.一、选择题(本大题共12小题,每小题4分,共48分.错选、不选或选出的答案超13.±22;14.1;15.20cm ;16.k =2;17 三、解答题 (本大题共7小题,共52分) :18.(本题满分5分)解:⎩⎨⎧≥+->+x x x 33)1(203 由①得,x >-3,由②得,x ≤1, ………………….………2分 所以原不等式组的解集为:-3<x ≤1, ……………….………4分 ,∴x ………………… .………5分 19.(本题满分5分)(1)证明:∵AE 是∠BAC 的平分线,EC ⊥AC ,EF ⊥AF ,∴CE =EF , ………………… .………1分在Rt △ACE 与Rt △AFE 中,⎩⎨⎧==AEAE EF CE , …………2分 ∴Rt △ACE ≌Rt △AFE (HL ); ……………….………3分(2)解:由(1)可知△ACE ≌△AFE ,∴AC =AF ,CE =EF , ………………….………4分 设BF =a ,则AC =AF =2a ,AB =3a ,∴BC==,∴在Rt △ABC 中,tan ∠B =AC BC在Rt △EFB 中,tan ∠B =EF BF =AC BC∴EF,∴CE =EF, ∴在Rt △ACE 中,tan ∠CAE=CE AC .………….………5分 20.(本题满分8分) 解:(1)表中a 的值是:a =50-4-8-16-10=12; ………………… .………2分 (2)图略; .………4分 (3)本次测试的优秀率是501012 =0.44=44%; 答:本次测试的优秀率是44%; ………………… .………6分 (4)p=412=13树状图的第一种画法DC ABAC CB CD AB CB AD CA BD BD ACBC AD BA CD AD BCACBD ABCD 分组情况:第二个第一个A C………………… 8分p=26=13树状图的第二种画法………………… 8分21.(本题满分8分)(1)证明:∵AC 为直径,∴∠ADC =90°, ……………… .………1分第21题∴∠A +∠DCA =90°, …………… .………2分 ∵∠ACB =90°,∴∠DCB +∠DCA =90°,………… .………3分 ∴∠A =∠BCD ; …………………4分(2)当MC =MD (或点M 是BC 的中点)时, 直线DM 与⊙O 相切;…………………5分 证明:连接DO ,……………… .………6分∵DO =CO , ∴∠1=∠2, ∵DM =CM , ∴∠4=∠3, ∵∠2+∠4=90°,∴∠1+∠3=90°, …… .………7分 ∴直线DM 与⊙O 相切. ……… 8分22.(本题满分8分) 解:(1)△ABC 是等腰三角形; …………………………1分 理由:∵x =-1是方程的根, ∴(a +c )×(-1)2-2b +(a -c )=0, ∴a +c -2b +a -c =0,∴a -b =0, …………………………2分 ∴a =b ,∴△ABC 是等腰三角形; …………………3分 (2)△ABC 是直角三角形; …………………………4分 理由:∵方程有两个相等的实数根, ∴(2b )2-4(a +c )(a -c )=0,∴4b 2-4a 2+4c 2=0,∴a 2=b 2+c 2, …………………………5分 ∴△ABC 是直角三角形; …………………………6分 (3)∵当△ABC 是等边三角形,a= b =c∴(a +c )x 2+2bx +(a -c )=0,可整理为: 2ax 2+2ax =0,∴x 2+x =0, …………………………7分 解得:x 1=0,x 2=-1. ………………….………8分 23.(本题满分9分) 解:(1)①四边形DECF 是平行四边形; …………………1分∵DE ∥AC ,DF ∥BC ,∴四边形DECF 是平行四边形.……………………2分②作AG ⊥BC ,交BC 于点G ,交DF 于点H , ………………3分 ∵∠ACB =45°,AC =24cm∴AG=, 设DF =EC =x ,平行四边形的高为h , 则AH=-h , ∵DF ∥BC ,∴DF BC = ∵BC =20cm ,即:20x =∴x×20,∵S =xh =h×20=20h-6h 2. …………………………4分∴当h =-2ba=AG==, …………………………5分 ∴AH=AH =GH ,∴AF =FC ,∴在AC 中点处剪四边形DECF ,能使它的面积最大.……………6分(2)第一步,沿∠ABC 的平分线对折,使点C 与点C 1重合,得到三角形ABB 1,第二步,对折BB 1,得到DA 1⊥BB 1. …………………………7分理由:对角线互相垂直平分的四边形是菱形. ………………………9分 24.(本题满分9分)(1)解:∵二次函数图象的顶点在原点O ,∴设二次函数的解析式为y =ax 2, ……………1分将点A (1,14)代入y =ax 2得:a =14, ∴二次函数的解析式为y =14x 2; ……………3分(2)证明:∵点P 在抛物线y =14x 2上,第23题GHB 1A 1C 1第24题∴可设点P 的坐标为(x ,14x 2), 过点P 作PB ⊥y 轴于点B ,则BF =14x 2-1,PB =x ,∴在Rt △BPF 中, PF14x 2+1, ∵PM ⊥直线y =-1, ∴PM =14x 2+1, ∴PF =PM ,∴∠PFM =∠PMF ,……………… 4分 又∵PM ∥y 轴,∴∠MFH =∠PMF ,………………5分 ∴∠PFM =∠MFH ,∴FM 平分∠OFP ;………………6分(3)解:当△FPM 是等边三角形时,∠PMF =60°,∴∠FMH =30°,在Rt △MFH 中,MF =2FH =2×2=4, ∵PF =PM =FM ,∴14x 2+1=4, 解得:x =±…………………………7分 ∴14x 2=14×12=3, …………………………8分 ∴满足条件的点P 的坐标为(3)或(-3).…………9分。
初四数学测试题及答案

初四数学测试卷桓台县实验中学命题人:刘桂兰分)分,共48(每个一、选择题:47.四个命题:①三角形的一条中线能将三角形分成面积相等的两部分;②有两边和2 +3的结果是1.计算-2其中一边的对角对应相等的两个三角形全等;③点P(1,2)关于原点的对称点坐标为D.A.7 B.5 C.51??(-1,-2);④两圆的半径分别是3和4,圆心距为d,若两圆有公共点,则其中正确的是下面所给的交通标志图中是轴对称图形的是 2..7?d?1A. ①②B.①③C.②③D.③④8.如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点.连结MP,MQ,PQ.在整个运动过8题第9-),用科学计数法表示这个病毒纳M=10M(病毒直径为H3.如图,7N930纳M1△MPQ的面积大小变化情况是()程中,正确的是直径的大小,A.一直增大B.一直减小C.先减小后增大D.先增大后减小89--M MB. 3.0×A.30×1010910--M MD. 0.3×C. 3.0×10109. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此项工作,且下列计算正确的是4.甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是22263 A. B.a22(?a)?a?aa?A.8 B.7C.6D.5人数10. 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接111022 C. D.aaa??a2?21a2?(?)?9BD、DE.若BD平分∠ABC,则下列结论不一定成立的是26=2AB·ACAE A.BD⊥ACB.4下图是某学校全体教职工年龄的频数分布直方5.C.△ADE是等腰三角形 D. BC=2AD.的原则,如年龄图(统计中采用“”上限不在内2.二次函数1134 36 38 40 42 44 46 48年龄bax?y?bxax?y?的图象大致是的图象如图所示,那么一次函数<<x38x小组,而不在34≤36≤36为岁统计在().yyyyy的是()36小组),根据图形提供的信息,下列说法中错误..A人.该学校教职工总人数是50xxxxx00000小组的教职工人数占该学校全体教职工4240≤x.年龄在B<(D)20%总人数的题10第(C)(A)(B)y1142<.教职工年龄的中位数一定落在C40≤x这一组22.如图,在平面直角坐标系中,抛物线12?2xxxyy??,经过平移得到抛物线22 40<这一组38≤x.教职工年龄的众数一定在D其对称轴与两段抛物线弧所围成的阴影部分的面积为().816 D C BA....42x0的取值范围在数+6,x2(P.如果点6)在平面直角坐标系的第四象限内,那么4-xx 轴上可表示为()204:二、填空题(每个分,共分)1 / 4在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白.、(8分)20x.13.要使式子的取值范围是有意义,则x2?台电脑3.5万元,购买2板,经过市场考察得知,购买1台电脑和2台电子白板需要32已知,则4m=_________.分解因式:m﹣14.6m?m?2.1____________2m??2m?.2.5万元和1台电子白板需要、某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下:15?(1)求每台电脑、每台电子白板各多少万元22m69x?1.0315.s?0.0006s?0,则这两名运动员中的,,,m.69x?1万元,但不(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30乙甲乙甲的成绩更稳定。
初四数学模拟试题及答案

N MD CBA初四数学模拟试题(全卷共五个大题,满分150分,考试时间120分钟)注意事项:1.试题的答案书写在答题卡上,不得在试卷上直接作答.2.作答前认真阅读答题卡上的注意事项.参考公式:抛物线y=ax 2+bx+c (a ≠0)的顶点坐标为(2b a -,244ac b a-),对称轴公式为2b x a =-.一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的.请将答题卡...上对应题目的正确答案标号涂黑. 1. 下列各数中,既不是正数也不是负数的数是( )新- 课 -标- 第 -一- 网A .-1B .0C .1D 2. 下列运算正确的是( )A .23a a a += B .23a a a ⋅= C .22a a ÷= D .2(2)4a a =3. 如图,直线a b c 、、,//a b ,150∠=°,则2∠为( )A .130°B .150°C .75°D .25°4. 下列四个几何体中,三视图(主视图、左视图、俯视图)相同的几何体是()A .B .C .D .5. 2014年4月13日,某中学初三650名学生参加了中考体育测试,为了了解这些学生的体考成绩,现从中抽取了50名学生的体考成绩进行了分析,以下说法正确的是( ) A .这50名学生是总体的一个样本 B .每位学生的体考成绩是个体 C .50名学生是样本容量D .650名学生是总体6. 已知x y -=7,xy =2,则22x y +的值为( ) A .53 B .45 C .47D .517. 二元一次方程组233x y x y ⎧⎨⎩+=-=的解为( ) A .21x y ⎧⎨⎩==B .21x y ⎧⎨⎩==-C .21x y ⎧⎨⎩=-=-D .21x y ⎧⎨⎩=-=(第8题图) (第9题图)21cba (第3题图)8. 如图,P 是⊙O 外一点,P A 是⊙O 的切线,A 为切点,PO 与⊙O 相交于 B 点,已知∠P =28°,C 为⊙O 上一点,连接CA ,CB ,则∠C 的值为( ) A .28°B .62°C .31°D .56°9. 如图,四边形ABCD 是平行四边形,点N 是AB 上一点,且BN = 2AN ,AC 、DN 相交于点M ,则ADM CMNB S S ∆四边形∶的值为( ) A .3∶11 B .1∶3C .1∶9D .3∶1010. 如图,某同学在沙滩上用石子摆小房子,观察图形的变化规律,写出第⑨个小房子用的石子总数为( )① ② ③ ④A .155B .147C .145D .14611. 3月20日,小彬全家开车前往铜梁看油菜花,车刚离开家时,由于车流量大,行进非常缓慢,十几分钟后,汽车终于行驶在高速公路上,大约三十分钟后,汽车顺利到达铜梁收费站,停车交费后,汽车驶入通畅的城市道路,二十多分钟后顺利到达了油菜花基地,在以上描述中,汽车行驶的路程s (千米)与所经历的时间t (分钟)之间的大致函数图像是( )12. 如图,四边形ABCD 是平行四边形,顶点A 、B 的坐标分别是A (1,0),B (0,﹣2),顶点C 、D 在双曲线(0)ky k x=≠上,边AD 与y 轴相交于点E ,5ABE BEDC S S =△四边形=10,则k 的值是( )A .-16B .-9C .-8D .-12(第12题图)二、填空题(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上.13. 2013年,全重庆市参加中考的考生有36.4万人,则36.4万人用科学计数法表示为____人. 14. 使函数y =有意义的x 的取值范围是____________. 15. 离中考还有20天,为了响应“还时间给学生”的号召,学校领导在全年级随机的调查了20名tt学生每天作业完成时间,绘制了如下表格:则这20个学生每天作业完成的时间的中位数为____________. 16. 如图,△ABC 是边长为2的等边三角形,D 为AB 边的中点,以CD 为直径画圆,则图中影阴部分的面积为____________(结果保留π). 17. 有5张正面分别写有数字1-,14-,0,1,3的卡片,它们除数字不同外全部相同.将它们背面朝上,洗匀后从中随机的抽取一张,记卡片上的数字为a ,则使以x 为自变量的反比例函数37a y x -=经过二、四象限,且关于x 的方程2221111a x x x +=-+-有实数解的概率是_____________.18. 如图,以Rt ABC △的斜边AB 为一边在ABC ∆同侧作正方形ABEF .点O 为AE与BF 的交点,连接CO ,若CA = 2,CO =,那么CB 的长为______________.三、解答题(本大题共2个小题,每小题7分,共14分) 19.()()12014141tan 602π-⎛⎫---+---- ⎪⎝⎭°20. 如图,在Rt ABC △中,已知90C ∠=°,4sin 5B =,AC = 8,D 为线段BC 上一点,并且CD = 2.(1) 求BD 的值; (2) 求cos DAC ∠的值.四、解答题(本大题4个小题,每小题10分,共40分)(第16题图)OFECBA(第18题图)D BC A (第20题图)CB DA图(2)图(1)项目21. 先化简,再求值:22151()939x x x x x x --÷----,其中x 是不等式组35157332x x x x -≤+⎧⎪⎨+≤+⎪⎩的整数解.22. 西大附中的“周末远道生管理”是学校的一大特色,为了增强远道生的体质,丰富远道生的周末生活,学校决定开设以下体育活动项目:A .篮球 B .乒乓球C .羽毛球 D .足球.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1) 这次被调查的学生共有 人; (2) 请你将条形统计图 (2) 补充完整;(3) 在平时的乒乓球活动项目中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).23. 直辖市之一的重庆,发展的速度是不容置疑的.很多人把重庆作为旅游的首选之地.“不览夜景,(第22题图)NM FEDCBA未到重庆”.乘游船夜游两江,犹如在星河中畅游,是一个近距离认识重庆的最佳窗口.“两江号”游轮经过核算,每位游客的接待成本为30元.根据市场调查,同一时间段里,票价为40元时,每晚将售出船票600张,而票价每涨1元,就会少售出10张船票. (1) 若该游轮每晚获得10000元利润,则票价应定为多少元?(2) 端午节期间,工商管理部门规定游轮船票单价不能低于42元,同时该游轮为提高市场占有率,决定每晚售出船票数量不少于560张,则票价应定为多少元,才能使每晚获得的利润最大?最大利润是多少?24. 如图,在等腰三角形ABC 中,CA = CB ,∠ACB = 90°,点D 、E 是直线BC 上两点且CD = BE ,过点C 作CM ⊥AE 交AE 于点M ,交AB 于点F ,连接DF 并延长交AE 于点N . (1) 若AC = 2,CD = 1,求CM 的值; (2) 求证:∠D =∠E .五、解答题:(本大题2个小题,每小题12分,共24分)25. 如图,抛物线2y ax bx =+-2与x 轴交于A 、B 两点,与y 轴交于点C ,已知A (–1,0),且tan∠ABC = 12,作垂直于x 轴的直线x m =,与抛物线交于点F ,与线段BC 交于点E .(1) 求抛物线的解析式和直线BC 的解析式; (2) 若△CEF 为等腰三角形,求m 的值;(3) 点P 为y 轴左侧抛物线上的一点,过点P 作PM BC ⊥BPM ABC ∠=∠,求P 点的坐标.(第24题图)26. 如图,在矩形ABCD 中,AB=,BC = 8,M 是BC 的中点,P 、Q 两点同时从M 点出发,其中点P 以每秒1个单位的速度向B 运动,到达点B 后立即按原来的速度反向向M 点运动,到达M 点后停止,点Q 以每秒1个单位的速度沿射线MC 运动,当点P 停止时点Q 也随之停止.以PQ 为边长向上作等边三角形PQE .(1) 求点E 落在线段AD 上时,P 、Q 两点的运动时间;(2) 设运动时间为t 秒,矩形ABCD 与PQE △重叠的面积为S ,求出S 与t 之间的函数关系式,并写出t 的取值范围;(3) 在矩形ABCD 中,点N 是线段BC 上一点,并且CN = 2,在直线CD 上找一点H (H 点在D 点的上方)连接HN ,DN ,将HDN △绕点N 逆时针旋转90°,得到''H D N △,连接'HH ,得到四边形''HH D N ,四边形''HH D N的面积能否是312HD 的长;若不能,请说明理由.(第26题图)B DCBADCBA图(2)项目第二次第一次丁丁丁丙丙丙乙乙乙甲甲甲丁丙乙甲开始数学试题参考答案一、选择题(本大题12个小题,每小题4分,共48分) 1—5 BBADB 6—10 ABCAC 11—12 AD二、填空题(本大题6个小题,每小题4分,共24分)13.53.6410⨯14.22x x ≥-≠且15.2.75 164π17.2518.三、解答题:(本大题共2个小题,每小题7分,共14分)19.解:原式112=---5分=4- .............................................................................................................. 7分 20.(1) Rt ABC 在△中,4sin 8105AC B AC AB AB ====∴,, 6BC =2BD BC CD CD =-=又,624BD =-=∴ ....................................................................................................... 4分 (2) Rt ACD 在△中AD cos AC DAC AD ∠=== ............................................................................. 7分 四、解答题(本大题4个小题,每小题 10分,共40分) 21.解:原式1(3)(51)=3)(3)(3)(3)x x x x x x x x -+--÷+-+-(2121=3)(3)(3)(3)x x x x x x x --+÷+-+-(213)(3)=3)(3)(1)x x x x x x -+-⋅+--(( 11x =- ........................................................................................................... 6分 解得不等式组35157332x x x x -≤+⎧⎪⎨+≤+⎪⎩的解集为13x ≤≤123x x =∴又为整数,,, 13x x ≠≠又且 2x =∴ ............................ 8分 12121x ===-当时,原式 ................................................................................10分 22.(1) 200 ............................................................................................................................ 2分(2)(2分) (3) (6分)解:画树状图如下:NM F ED CBA21122126P ==∴∴共种,满足题意的种。
初四数学练习试题_22

初四数学练习题(1)一、选择题:1、抛物线322-+=x x y 与x 轴的交点坐标是 ( )A .(-3,0),(1,0)B .(3,0),(1,0)C .(-4,0),(1,0)D .(4,0),(1,0) 2.在△ABC 中,∠C=90°,BC :AC=1:2,则sinB 等于 ( )A .55B .552C .21D .2 3、已知二次函数的图像如图所示,那么此函数的解析式可能是( )A .122++-=x x yB .122---=x x yC .122+--=x x yD .122++=x x y4、在Rt △ABC 中,︒=∠90C 。
若sinA ︰tanA 2=︰3,则cosA 等于( )A .31B .32C .94D .3325.6、抛物线122+--=m mx x y 的图象过原点,则m 为( ) A .0 B .1 C .-1 D .±17、一人乘雪橇沿倾斜角是︒30的斜坡滑下,滑下的路程S (米)与时间t (秒)间的关系式为210t t S +=,若滑到坡底的时间为2秒,则此人下滑的高度为( )A .24米B .12米C .312米D .6米 8.若抛物线c bx x y ++=2经过点(3,-8)和(-5,-8),则此抛物线的对称轴是 ( )A .x = 5B .x =3C .x =4D .x =-l9.在△ABC 中,∠C=90°,两条直角边的和为12,tanB=3,则AB 的长度为( )A .103B .33C .310D .6210.已知二次函数c bx ax y ++=2的图象如图所示,则下列四个结论:①a <0 ②abc <0③b +2a =0 ④042<-ac b 中,正确的个数为 ( )A .4个 B .3个 C .2个D .1个 11、抛物线y=-x 2+bx+c 的的部分图象如图所示,若y>0,则x 取值范围是( ) A.-4<x<1 B.-3<x<1C.x<-4或x>1 D.x<-3或x>112、如图,在Rt ABC △中,CD 是斜边AB 上的中线,已知2CD =,3AC =,则sin B 的值是( ) ADA .23B .32C .34D .43二、填空题:1.=︒+︒60cos 30sin。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
个人收集整理资料, 仅供交流学习, 勿作商业用途
初四数学测试题
桓台县实验中学 命题人:刘桂兰
一、选择题:<每个4分,共48分)
1.计算-22+3的结果是
A.7 B.5 C.1 D.
5
2.下面所给的交通标志图中是轴对称图形的是
3.如图,H7N9
病毒直径为30
纳M<1纳M=10-9M),用科学计数法表示这个病毒直径的
大小,正确的是mNbQwqpO0H
A.30×10-9M B. 3.0×10-8M
C. 3.0×10-10M D. 0.3×10-9M
4.下列计算正确的是
A.222)2(aa B.
C.aa22)1(2 D.
22
aaa
5. 下图是某学校全体教职工年龄的频数分布直方图<统 计中采用“上限
不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x
<36小组),根据图形提供的信息,下列说法中错误的是< )
mNbQwqpO0H
A.该学校教职工总人数是50人
B.年龄在40≤x<42小组的教职工人数占该学校全体教职工
总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
6.如果点P<2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取
值范围在数轴上可表示为< )mNbQwqpO0H
7.四个命题: ①三角形的一条中线能将三角形分成面积相等的两部分;
②有两边和其中一边的对角对应相等的两个三角形全等; ③点P<1,2)
关于原点的对称点坐标为<-1,-2); ④两圆的半径分别是3和4,
圆心距为d,若两圆有公共点,则.71d其中正确的是mNbQwqpO0H
A. ①② B.①③ C.②③ D.③④
8.如图,在△ABC中,∠C=90°,M是AB的中点,动点P
从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方
向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点.连结MP,
MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是< )
mNbQwqpO0H
632
aaa
34 36 38 40 42 44 46 48
4
6
9
10
11
人数
年龄
第8题
个人收集整理资料, 仅供交流学习, 勿作商业用途
2 / 6
A.一直增大 B.一直减小 C.先减小后增大 D.先增大
后减小
9. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此
项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成
此项工作的天数是mNbQwqpO0H
A.8 B.7 C.6 D.5
10. 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,
连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是
mNbQwqpO0H
A.BD⊥AC B.AC2=2AB·AE
C.△ADE是等腰三角形 D. BC=2AD.
11.二次函数2yaxbx的图象如图所示,那么一次函数yaxb的图象大
致是< ).
12.如图,在平面直角坐标系中,抛物线212yx经过平移得到抛物线
2
1
22yxx
,其对称轴与两段抛物线弧所围成的阴影部分的面积为
< ).mNbQwqpO0H
A.2 B.4 C.8 D.
16
二、填空题:<每个4分,共20分)
13.要使式子2x有意义,则x的取值范围是 .
14.已知62mm,则 .____________2212mm分解因式:m3﹣4m=
_________ .
15、某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如
下:mx69.1甲,mx69.1乙,0006.02甲s,0315.02乙s,则这两名运动
员中的____的成绩更稳定。mNbQwqpO0H
某企业2010年底缴税40万元,2018年底缴税48.4万元,设这两年该
企业缴税的年平均增长率为x,根据题意,可得方程
___________mNbQwqpO0H
16.已知一个扇形的半径为60厘M,圆心角为0150.用它围成一个圆锥的
侧面,那么圆锥的底面半径为_____________厘M.
17.一项“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子<六
个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数
之和大于n2,则算过关;否则不算过关,则能过第二关的概率是
< )IungKozQZB
三、解答题
18. <1)计算<3分): 001)3(30tan2)21(3.
(A)
(B)
(C)
(D)
0yx0yxxy0xy0
0
y
x
0
y
x
0题
个人收集整理资料, 仅供交流学习, 勿作商业用途
3 / 6
<2) 先化简,再求值<5分):÷,其中a=﹣
1.
<3)<5分)一元二次方程25x2x04的某个根,也是一元二次方程
2
9
x(k2)x04
的根,求k的值
19、<6分)某校学生捐款支援地震灾区,第一次捐款总额为6600元,第
二次捐款总额为7260元,第二次捐款人数比第一次多30人,而且两
次人均捐款额恰好相等,求第一次的捐款人数IungKozQZB
20、<8分).在东营市中小学标准化建设工程中,某学校计划购进一批电
脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要
3.5万元,购买2台电脑和1台电子白板需要2.5万元.IungKozQZB
<1)求每台电脑、每台电子白板各多少万元?
<2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万
元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费
用最低.IungKozQZB
21、<8分).如图,△ABC中,∠ACB=90°,D是边AB上的一点,且
∠A=2∠DCB.E是BC上的一点,以EC为直径的⊙O经过点D。
IungKozQZB
<1)求证:AB是⊙O的切线;
<2)若CD的弦心距为1,BE=ED.求BD的长.
第22题 第23题
22、<8分).如图,某海监船向正西方向航行,在A处望见一艘正在作
业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东
45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,
若海监船的速度为50海里/小时,求A,B之间的距离<取,结果
精确到0.1海里).IungKozQZB
23、<9分)如图,已知抛物线y=﹣x2+bx+4与x轴相交于A、B两点,
与y轴相交于点C,若已知A点的坐标为A<﹣2,0).IungKozQZB
<1)求抛物线的解读式及它的对称轴;
<2)求点C的坐标,连接AC、BC并求线段BC所在直线的解读式;
<3)试判断△AOC与△COB是否相似?并说明理由;
测试题答案
一、 选择题:
第22题图
A
B
C
O
E
D
第21题
个人收集整理资料, 仅供交流学习, 勿作商业用途
4 / 6
1---5 C A B C D 6---10 C B C A D 11 C 12
BIungKozQZB
二、 填空:
13、x≤2 14、-11, m(m+2>(m-2> 15、甲 40<1+x)
2=48.4 IungKozQZB
16、25 17、1813
三、解答题:
18、<1) 33-1 (2>2)a(a1 代入结果=1
19、
20、
<3)
个人收集整理资料, 仅供交流学习, 勿作商业用途
5 / 6
23、
个人收集整理资料, 仅供交流学习, 勿作商业用途
6 / 6
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
