高二数学期末测试题
(完整word版)高二上学期数学期末测试题.doc

高 中 学 生 学 科 素 质 训 练高二 上 学 期 数学期末测试题题号一 二三总分171819202122得分一、选择题(本大题共 12 小题,每题 5 分,共 60 分)1.设会合 A{ x | x 2 10}, B { x | log 2 x 0 |}, 则 AB 等于()A . { x | x 1}B . { x | x 0}C . { x | x1}D . { x | x1或 x 1}2.若不等式 | ax2 | 6 的解集为(- 1, 2),则实数 a 等于()A . 8B . 2C .- 4D .- 83.若点( a , b )是直线 x +2y+1=0 上的一个动点,则 ab 的最大值是()A .11C .1 D .12B .81644.求过直线 2x - y - 10=0 和直线 x+y+1=0 的交点且平行于3x - 2y+4=0 的直线方程()A . 2x+3y+6=0B . 3x - 2y - 17=0C . 2x -3y - 18=0D . 3x - 2y -1=05.圆 (x1)2y21的圆心到直线 y3x 的距离是()3A .13C . 1D .32B .26.假如双曲线的实半轴长为2,焦距为 6,那么该双曲线的离心率为 ()A . 36C . 3D . 7B .2 227.过椭圆x2y21的焦点且垂直于x 轴的直线 l 被此椭圆截得的弦长为()43A .3B .3C. 3D.223 x 4 5cos ,8.椭圆3sin (为参数)的焦点坐标为()yA .( 0, 0),( 0,- 8)B.(0, 0),(- 8, 0)C.( 0, 0),( 0, 8)D.( 0, 0),( 8, 0)9.点P(1,0)到曲线x t 2(此中参数 t R )上的点的最短距离为()y2tA .0B .1C.2D.210.抛物线的极点在原点,对称轴为坐标轴,焦点在直线3x 4 y12 0 上,则抛物线的方程为()A .y216x B.x212 yC.y216x或 x 212 y D.以上均不对11.在同一坐标系中,方程a2 x2b2 y 21与 ax by 20(a b0) 的曲线大概是()12.在直角坐标系 xOy 中,已知△ AOB 三边所在直线的方程分别为x 0, y 0,2 x 3 y30 ,则△ AOB 内部和边上整点(即横、纵坐标均为整数的点)的总数是()A.95B.91C.88D. 75二、填空题(本大题共 4 小题,每题 4 分,共 16 分)13.椭圆5x2ky 2 5 的一个焦点是(0,2) ,那么k.14.已知直线 x =a (a>0) 和圆( x -1)2+ y 2 = 4 相切,那么 a 的值是15.如图, F1,F2分别为椭圆x2y21的左、右焦点,点 P 在椭圆上,△ POF2是面积为3 a 2b2的正三角形,则b2的值是.16.函数y lg(| x |x)的定义域是__.1x 2三、解答题(本大题共 6 小题,共74 分)17.解对于x的不等式:log a(4 3x x2) log a(2x 1) log a2,(a0,a 1) .(12分) 18.设A( c,0), B(c,0)(c0) 为两定点,动点P到A点的距离与到 B 点的距离的比为定值a(a 0) ,求P点的轨迹.(12分)19.某厂用甲、乙两种原料生产 A 、 B 两种产品,已知生产1t A 产品, 1t B 产品分别需要的甲、乙原料数,可获取的收益数及该厂现有原料数以下表所示.问:在现有原料下, A 、B产品应各生产多少才能使收益总数最大?列产品和原料关系表以下:产品所需原料原料甲原料( t)乙原料( t)收益(万元)(12 分)A 产品 B 产品总原料( 1t)( 1t)( t)2510 5318 43知抛物线的极点在原点,它的准线经过曲线x2y2x 轴垂直,a1 的右焦点,且与2b2抛物线与此双曲线交于点(3,6 ),求抛物线与双曲线的方程.(12分)221.已知点P到两个定点M ( 1,0) 、N (1,0) 距离的比为 2 ,点N到直线PM的距离为1,求直线 PN 的方程.(12分)y22.已知某椭圆的焦点是F1 ( 4,0) 、 F2 (4,0) ,过并垂直于x 轴的直线与椭圆的一个交点为B,F1O A点 F2 BC且F2x|F1B||F2B| 10,椭圆上不一样的两点B'A( x1 , y1 ) 、 C (x2 , y2 ) 知足条件: | F2 A |、 | F2 B | 、 | F2 C | 成等差数列.(I )求该椭圆的方程;(II )求弦 AC 中点的横坐标.( 14 分)参照答案一.选择题(本大题共12 小题,每题 5 分,共 60 分)题号123456789101112答案A C C B A C C D B C D B 二.填空题(本大题共 4 小题,每题 4 分,共 16 分)13. 114. 315.2316.(-1,0)三.解答题(本大题共 6 小题,共 74分)17. (12分 )[ 分析 ] :原不等式可化为log a( 4 3 x x2 ) log a 2(2x1)2x10x 1 2当 a>1 时有43x x20141x2x43x x22(2x1)3x22(中间一个不等式可省)2 x10x 1 2当 0<a<1 时有43x x201x42x 443x x 22(2 x1)x或x23∴当 a>1 时不等式的解集为12;x2当 0<a<1 时不等式的解集为2x4 18.( 12 分)[分析 ]:设动点 P 的坐标为( x, y).由 |PA|a(a0),得(x c)2y2.|PB|( x c)2a y 2化简得(1a 2)x22 (1a2)x c2(1a2)(1a2)y20.c22c(1a2)221 2a2( 2ac2当a 1时,得x x c y0 ,整理得( x)2.1a2c)2y 2a1 a 1当 a=1 时,化简得 x=0.因此当 a1时,P点的轨迹是以(a21c,0)为圆心,|22ac|为半径的圆;2a1a1当 a=1 时, P 点的轨迹为y 轴.19.( 12 分)[分析 ]:设生产 A 、B 两种产品分别为xt,yt,其收益总数依据题意,可得拘束条件为2x5y10 6x3y18作出可行域如图:x0, y0为 z 万元 ,y25P( -,1)2352x+5y=10 x 6x+3y=18目标函数z=4x+3y,作直线 l0:4x+3y=0,再作一组平行于 l0的直线 l : 4x+3 y =z ,当直线 l 经过 P 点时 z=4x+3y 获得最大值,由2x 5 y 10,解得交点 P (5,1) 6x3y182因此有z P53113(万元 )42因此生产 A 产品 2. 5t, B 产品 1t 时,总收益最大,为13 万元.12 分)[ 分析 ] :由题意可知抛物线的焦点到准线间的距离为2C(即双曲线的焦距).设抛物线的方程为y24cx.∵抛物线过点(3, 6 )64c3c1即a 2 b 2 1①22又知(3) 2( 6)213 2196 1②由①②可得a 2, b 2a 2b 24a 2 b 244∴所求抛物线的方程为y 24x ,双曲线的方程为 4 x24y21321.( 12 分)[ 分析 ] :设点P的坐标为( x, y),由题设有| PM |2 |PN |即(x 1)2y 22(x 1) 2y 2整理得 x2y 26x10 ①由于点 N 到 PM 的距离为1,|MN |2因此∠ PMN30 ,直线PM的斜率为33直线 PM 的方程为y3( x 1)②3将②式代入①式整理得x 24x10解得 x 2 3 , x23代入②式得点P 的坐标为( 23,13)或 (23,13);(23,13)或 (23,13)直线 PN 的方程为y x1或 y x122.( 14 分)[分析 ]:( I)由椭圆定义及条件知2a|F1B| |F2B|10(完好word 版)高二上学期数学期末测试题.doc得 a 5,又 c4 ,因此 b a 2 c 2 3y故椭圆方程为x 2 y 2 1A B259C( II )由点 B (4, y B ) 在椭圆上,得OFF 12| F 2 B | | y B |9B'5解法一:x由于椭圆右准线方程为x 25 ,离心率为 4 .4 54 25 依据椭圆定义,有 | F 24 25x 1 ) , | F 2C |A | (5 (5 44由 | F 2A |, | F 2B |, | F 2C |成等差数列,得4 25x 1 ) (45由此得出 x 1x 2 8.设弦 AC 的中点为 P (x 0 , y 0 ) ,x 1 x 28 4 .则 x 022解法二:x 2 )4 25 x 29 ,5() 245由 | F 2A |,| F 2B |, ||F 2C 成等差数列,得(x 1 4) 2y 12( x 24)2 y 222 9 ,5由 A ( x 1 , y 1 ) 在椭圆x 2y 21上,得 y 129(25 x 12 )25 925因此( x 1 2228x 1 1692)(54 214)y 1x 1(25x 1x 1 )( 25 4x 1 )2555同理可得 (x 2 4)2y 221(25 4x 2 )5将代入式,得 1(25 4 x 1 )1(25 4 x 2 )18 . 5 55因此 x 1 x 2 8 设弦 AC 的中点为 P (x 0 , y 0 )则x ax 1 x 2824 .2。
2023-2024学年四川省绵阳市高二上学期期末教学质量测试数学检测试卷(有解析)

EF F 两点,求 S△PAB 的最大值.
1.A
【分析】求出给定直线的斜率即可得该直线的一个方向向量 a ,再求与 a 共线的向量即可.
【详解】直线
2x
3
y
1
0
的斜率为
k
2 3
,则直线
2x
3
y
1
0
的一个方向向量
a
1,
2 3
,
对于
A,因
3
2 3
1
2
0
,即向量
(3,
2)
与
1,
2 3
共线,A
是;
对于Biblioteka 2 3rrr abc
r b
r c
2
3
rrr abc
1
r b
1
r c
2
r a
3 3 3.
故选:A.
7.C
【分析】连接 QA 、 OA ,由题意可得 QA QP ,所以 QA QO QP QO OP r , 根据双曲线的定义,即可得答案. 【详解】连接 QA 、 OA ,如图所示:
因为 l 为 PA 的垂直平分线,所以 QA QP ,
(1)求 a 的值; (2)估计家庭消费总支出的平均值及第 80 百分位数.(结果保留一位小数)
18.已知直线 l : kx y 2k 1 0 ( k R ),圆 C : x 12 y 12 9 . (1)试判断直线 l 与圆 C 的位置关系,并加以证明; (2)若直线 l 与圆 C 相交于 A , B 两点,求 AB 的最小值及此时直线 l 的方程.
.
-3-
15.已知 F1 、 F2 是双曲线 C :
x2 a2
y2 b2
江西省上饶市2023-2024学年高二上学期期末教学质量测试数学试题

C. 0.7
D. 0.8
7. 6 名学生参加数学建模活动,有 3 个不同的数学建模小组,每个小组分配 2 名学生,
则不同的分配方法种数为( )
A. 45
B. 90
C.180
D. 360
8.已知抛物线
y2
8x ,弦
AB
过抛物线的焦点
F
且满足
uuur AF
uuur 3FB
,则弦
AB
的长为(
)
A. 8 3
A.1
B.2
C.4
D.8
6.某大学有 A, B 两家餐厅,某同学第 1 天午餐时随机地选择一家餐厅用餐,如果第一
天去 A 餐厅,那么第 2 天去 A 餐厅的概率是 0.4 ;如果第一天去 B 餐厅,那么第二天去 A
餐厅的概率是 0.8;则该同学第 2 天去 A 餐厅用餐的概率是( )
A. 0.5
B. 0.6
12.已知双曲线 C : x2
y2 b2
1b
0 的左、右焦点分别为 F1 、F2 ,左、右顶点分别为 A1 、
A2 , P 为双曲线右支上的一点,且直线 PA1 与 PA2 的斜率之积等于 2 ,过点 P 的切线与
双曲线的渐近线交于 M 、 N 两点,则下列说法正确的有( )
A.双曲线 C 的渐近线方程为 y 3x B. PM PN
呈阳性,则对剩下的 5 只小白鼠再逐个化验,直到查出患病小白鼠.
(1)若用方案甲,求化验次数为 5 次的概率;
(2)若平均化验次数少的方案好,请你确定方案甲、方案乙哪个更好.
22.已知椭圆 E :
x2 a2
y2 b2
1a
b
0 的两焦点分别为 F1 1,0 、 F2 1,0 ,且椭圆的离
高二下期期末数学测试题及答案解析
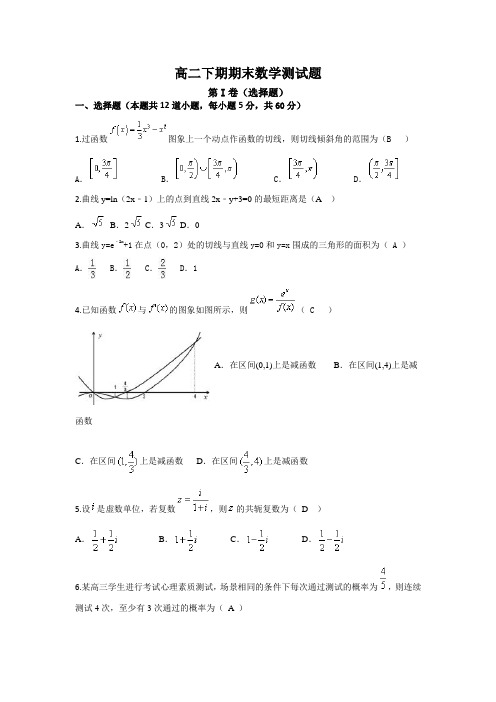
高二下期期末数学测试题第I卷(选择题)一、选择题(本题共12道小题,每小题5分,共60分)1.过函数图象上一个动点作函数的切线,则切线倾斜角的范围为(B )A. B. C. D.2.曲线y=ln(2x﹣1)上的点到直线2x﹣y+3=0的最短距离是(A)A.B.2 C.3 D.03.曲线y=e﹣2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为( A )A.B.C.D.14.已知函数与的图象如图所示,则(C)A.在区间(0,1)上是减函数B.在区间(1,4)上是减函数C.在区间上是减函数D.在区间上是减函数5.设是虚数单位,若复数,则的共轭复数为(D )A.B.C.D.6.某高三学生进行考试心理素质测试,场景相同的条件下每次通过测试的概率为,则连续测试4次,至少有3次通过的概率为(A )A.B. C.D.7.将某选手的7个得分去掉1个最高分,去掉1个最低分,剩余5个分数的平均数为91,现场作的7个分数的茎叶图有一个数据模糊,无法辨认,在图中以表示,则5个剩余分数的方差为(C )A.B. C. 6 D.308.在的展开式中,常数项是(D)A.B.C.D.9.由数字0,1,2,3组成的无重复数字的4位数,比2018大的有( B )个A.10 B.11 C.12 D.1310.已知,在的图象上存在一点,使得在处作图象的切线,满足的斜率为,则的取值范围为(A )A.B.C.D.11.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:连续剧连续剧播放时长/min 广告播放时长/min 收视人次/万人甲70 5 60乙60 5 25电视台每周安排的甲、乙连续剧的总播放时长不多于600min,广告的总播放时长不少于30min,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用,表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为(A )A.6,3 B.5,2 C. 4,5 D.2,712.若直线()和曲线()的图象交于,,()三点时,曲线在点,点处的切线总是平行,则过点可作曲线的(C )条切线A.0 B.1 C.2 D.3第II卷(非选择题)二、填空题(本题共4道小题,每小题5分,共20分)13.将原油精炼为汽油、柴油、塑胶等各种不同的产品,需要对原油进行冷却和加热,若在第xh时,原油的温度(单位:℃)为f(x)=x2﹣7x+15(0≤x≤8),则在第1h时,原油温度的瞬时变化率为 -5℃/h.14.随机变量服从正态分布,若,则0.259 .15.口袋中有形状和大小完全相同的4个球,球的编号分别为1,2,3,4,若从袋中一次随机摸出2个球,则摸出的2个球的编号之和大于4的概率为.16.若直线与曲线满足下列两个条件:()直线在点处与曲线相切;()曲线在点附近位于直线的两侧,则称直线在点处“切过”曲线.下列命题正确的是___①③_____.(写出所有正确命题的编号)①直线在点处“切过”曲线;②直线在点处“切过”曲线;③直线在点处“切过”曲线;④直线在点处“切过”曲线.①∵,,∴,∴曲线在点处切线为,当时,,当时,,即曲线在点附近位于直线的两侧,①正确;②设,,当时,,在是减函数,当时,,在是增函数,∴,即在上恒成立,∴曲线总在直线下方,不合要求,②不正确;③∵,,∴,∴曲线在点处切线为,设,,∴是减函数,又∵,∴当时,,即,曲线在切线的下方,当,,即,曲线在切线的上方,③正确;④设,,当时,,当时,,函数在区间上是减函数,当时,,函数在区间上是增函数,∴,即在上是恒成立,∴总在直线上方,不合要求,④不正确.综上,正确命题有①③.三、解答题(本题共6道小题,第1题10分,第2题12分,第3题12分,第4题12分,第5题12分,第6题12分,,共70分)17.已知函数f(x)=(2x﹣1)2+5x(1)求f′(x)(2)求曲线y=f(x)在点(2,19)处的切线方程.解:(1)f′(x)=4(2x﹣1)+5=8x+1;(2)f′(2)=17,故切线方程是:y﹣19=17(x﹣2),即17x﹣y﹣15=0.18.为了解今年某校高三毕业班准备报考飞行员学生的身体素质,学校对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.(1)求该校报考飞行员的总人数;(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的学生中(人数很多)任选2人,设表示体重超过60公斤的学生人数,求的分布列和数学期望.解:(1)设报考飞行员的人数为,前3个小组的频率分别为,则由条件可得:解得,又因为,所以.(2)由(1)可得,一个报考学生体重超过60公斤的概率为,由题意知服从二项分布,,所以随机变量的分布列为.19某超市在元旦期间开展优惠酬宾活动,凡购物满100元可抽奖一次,满200元可抽奖两次…依此类推.抽奖箱中有7个白球和3个红球,其中3个红球上分别标有10元,10元,20元字样.每次抽奖要从抽奖箱中有放回地....任摸一个球,若摸到红球,根据球上标注金额奖励现金;若摸到白球,没有任何奖励.(Ⅰ)一次抽奖中,已知摸中了红球,求获得20元奖励的概率;(Ⅱ)小明有两次抽奖机会,用表示他两次抽奖获得的现金总额,写出的分布列与数学期望.解:(Ⅰ)设事件,事件则所求概率为(Ⅱ)的可能取值为0,10,20,30,40∴的分布列为所以,.20.已知函数,(其中为自然对数的底数,). (1)若函数的图象与函数的图象相切于处,求的值;(2)当时,若不等式恒成立,求的最小值.解(1),.(过程略)(2)令,则,当时,单调递增,而,∴时,不合题意当时,令,则,∵为减函数,∴时,,单调递增,时,,单调递减,∴,即.(△)但,等号成立当且仅当且.故(△)式成立只能即.21.第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,这是2017年我国重要的主场外交活动,对推动国际和地区合作具有重要意义.某高中政数处为了调查学生对“一带一络"的关注情况,在全校组织了“一带一路知多少”的知识问卷测试,并从中随机抽取了12份问卷,得到其测试成绩(百分制),如茎叶图所示.(1)写出该样本的众数、中位数,若该校共有3000名学生,试估计该校测试成绩在70分以上的人数;(2)从所轴取的70分以上的学生中再随机选取4人.①记表示选取4人的成绩的平均数,求;②记表示测试成绩在80分以上的人数,求的分布列和数学期望.(1)众数为76,中位数为76.抽取的12人中,70分以下的有4人,不低于70分的有8人,故从该校学生中人选1人,这个人测试成绩在70分以上的概率为,故该校这次测试成绩在70分以上的约有(人)(2)①由题意知70分以上的有72,76,76,76,82,88,93,94.当所选取的四个人的成绩的平均分大于87分时,有两类.一类是82,88,93,94,共1种;另一类是76,88,93,94,共3种.所以.②由题意可得,的可能取值为0,1,2,3,4,,,,.的分别列为0 1 2 3 422.已知函数.(1)若,函数在其定义域内是增函数,求的取值范围;(2)的图像与轴交于,两点,中点为,求证:.(1)依题意:,在上递增,对恒成立,即对恒成立,只需.,,当且仅当时取“”,,的取值范围为.(2)由已知得两式相减,得. 由及,得令,,在上递减,.则有,又,.。
高中数学选择性必修二 高二数学上学期期末测试卷01()(含答案)

2021-2022学年上学期期末卷01高二数学·全解全析【解析由214y x =化为24x y =,抛物线焦点在y 轴正半轴,且2p =, 则准线方程为1y =-. 故选:A .2.【答案】D【解析】当4k =时,直线1l 的斜率不存在,直线2l 的斜率存在,两直线不平行;当4k ≠时,两直线平行的一个必要条件是334kk k-=--,解得3k =或5k =,但必须满足截距不相等,经检验知3k =或5k =时两直线的截距都不相等. 故选:D . 3.【答案】C【解析】联立2010x y x y -=⎧⎨--=⎩得12x y =-⎧⎨=-⎩. 把12x y =-⎧⎨=-⎩代入280x ky ++=得3k =.故选:C4.【答案】B【解析】①当0b =时,a 与c 不一定共线,故①错误;②当a ,b ,c 共面时,它们所在的直线平行于同一平面,或在同一平面内, 故②错误;由空间向量基本定理知③正确;④当a ,b 不共线且c a b λμ=+时,a ,b ,c 共面,故④错误. 故选:B . 5.【答案】B【解析】在等差数列{}n a 中573a a =,所以7723a d a -=,所以()72+0a d =,即80a =, 又等差数列{}n a 中10a >,公差0d <,所以等差数列{}n a 是单调递减数列,所以1278910...0...a a a a a a >>>>=>>,所以等差数列{}n a 的前n 项和为n S 取得最大值,则n 的值为7或8. 故选:B .6.【答案】D【解析】设该高阶等差数列的第8项为x , 根据所给定义,用数列的后一项减去前一项得到一个数列,得到的数列也用后一项减去前一项得到一个数列,即得到了一个等差数列,如图:由图可得341295y x y -=⎧⎨-=⎩,则14146x y =⎧⎨=⎩. 故选:D 7.【答案】B【解析】设P 为第一象限的交点,1||PF m =、2||PF n =, 则12m n a +=、22m n a -=,解得12m a a =+、12n a a =-,在12PF F ∆中,由余弦定理得:2221241cos 22m n mn F c F P +-∠==,∴2224m n mn c +-=,∴22212121212()()()()4a a a a a a a a c ++--+-=,∴2221234a a c +=,∴22122234a a c c+=,∴2221314e e +=,设112sin e α=,21e α,则12112sin )6e e πααα+==+,当3πα=时,1211e e +,此时1e =2e,12e e +=故选:B8.【答案】D【解析】在①中,∵1111AC B D ⊥,111A C BB ⊥,1111B D BB B ⋂=, 且111,B D BB ⊂平面11BB D ,∴11A C ⊥平面11BB D ,1BD ⊂平面11BB D , ∴111AC BD ⊥, 同理,11DC BD ⊥, ∵1111AC DC C ⋂=,且111,A C DC ⊂平面11AC D , ∴直线1BD ⊥平面11AC D ,正确; 在②中,∵11//A D B C ,1A D ⊂平面11AC D ,1B C ⊄平面11AC D ,∴1//B C 平面11AC D ,∵点P 在线段1B C 上运动,∴P 到平面11AC D 的距离为定值,又11A C D 的面积是定值, ∴三棱锥11P AC D -的体积为定值,正确; 在③中,∵11//A D B C ,∴异面直线AP 与1A D 所成角为直线AP 与直线1B C 的夹角. 易知1AB C 为等边三角形, 当P 为1B C 的中点时,1AP B C ⊥;当P 与点1B 或C 重合时,直线AP 与直线1B C 的夹角为3π.故异面直线AP 与1A D 所成角的取值范围是,32ππ⎡⎤⎢⎥⎣⎦,错误;在④中,以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设正方体1111ABCD A B C D -的棱长为1,则(),1,P a a ,()10,1,1C ,()1,1,0B ,()10,0,1D , 所以()1,0,1C P a a =-,()11,1,1D B =-.由①正确:可知()11,1,1D B =-是平面11AC D 的一个法向量,∴直线1C P 与平面11AC D所成角的正弦值为:1111C P D B C P D Ba ⋅==⋅, ∴当12a =时,直线1C P 与平面11AC D ,正确. 故选:D9.【答案】CD【解析】对于A :在平行六面体1111ABCD A B C D -中,有11B B BC BC +=,()11//B B BC A D ∴+,故A 错误;对于B :111111A A A D A B A D A B BD +-=-=,1AB AD ==,60BAD ︒∠=,21BD =,又2111A B =,∴()22111111A A A D A BA B +-=,故B 错误;对于C :11A B AD AB AD DB -=-=,()111AC A B AD ⋅-=()11()()()()AB AD AA AB AD AB AD AB AD AA AB AD ++⋅-=+⋅-+⋅-,由题知,1AB AD ==,12AA =,1145BAA DAA ∠=∠=︒,60BAD ∠=︒,所以,()221111AC A B AD AB AD AA ⋅-=-+10AB AA AD ⋅-⋅=,故C 正确; 对于D:AC AB AD =+,111AC AC AA AB AD AA =+=++,21AC =()21AB AD AA ++222111||||222AB AD AA AB AD AB AA AD AA =+++⋅+⋅+⋅112211cos6021cos 45︒︒+⨯⨯⨯+⨯21cos 459︒+⨯=.所以13AC =.故D 正确,故选:CD. 10.【答案】ABC【解析】由圆22:4O x y +=可得圆心()0,0O ,半径2r ,对于A :因为2PQ OP OQ ===,所以POQ △是边长为2的等边三角形, 若PQ 中点为M ,则OM PQ ⊥,且OM =所以点M 的轨迹是以()0,0O所以点M 的轨迹方程为223x y +=,故选项A 正确;对于B :设()00,P x y ,BP 中点为(),x y ,则00222x x y y +⎧=⎪⎪⎨⎪=⎪⎩,所以00222x x y y =-⎧⎨=⎩,因为()00,P x y 在圆22:4O x y +=上,所以22004x y +=,所以()()222224x y -+=,所以()2211x y -+=即BP 中点轨迹方程为()2211x y -+=,故选项B 正确; 对于C :设()00,P x y ,CP 的中点(),x y ,则00322x x y y +⎧=⎪⎪⎨⎪=⎪⎩,所以00232x x y y =-⎧⎨=⎩,因为()00,P x y 在圆22:4O x y +=上,所以22004x y +=,所以()()222324x y -+=,即22312x y ⎛⎫-+= ⎪⎝⎭,所以CP 的中点轨迹方程为22312x y ⎛⎫-+= ⎪⎝⎭,故选项C 正确;对于D :设AP 的中垂线与OP 的交点为M ,由垂直平分线的性质可得MA MP =,所以21MO MA MO MP OP OA +=+==>=,所以点M 的轨迹是以O ,A 为焦点,长轴长为2的椭圆,故选项D 不正确; 故选:ABC .11.【答案】ACD 【解析】对于选项A ,令2y t x+=,则2y tx =-, 因为点(),P x y 在圆22:(1)(1)2C x y -+-=上,所以直线2y tx =-与圆22:(1)(1)2C x y -+-=有交点,因此圆心到直线的距离d =≤7k ≤-或1k ,故A 正确; 对于选项B ,由10kx y k ---=,得()()110k x y --+=,因此直线10kx y k ---=过定点()1,1P -,因为213312PM k +==-,111312PN k +==---,且313-<<,所以12k ≤-或32k ≥,故B 错误;对于选项C ,圆222(0)x y r r +=>的圆心直线l的距离2d =因为点(),P a b 是圆222(0)x y r r +=>外一点,所以222a b r +>,因此2d r =<,即直线与圆相交,故C 正确;对于选项D ,到点()1,0N 的距离为1点在圆()2211x y -+=上, 由题意可知,圆()2211x y -+=与圆222:(4)(4)(0)M x y r r -+-=>相交, 故圆心距5d MN ==,且11r d r -<<+,解得46r <<,故D 正确. 故选:ACD .12.【答案】BCD【解析】22:21n n C x y a n +=++的圆心为()0,0,半径为r =所以圆心到直线:n l y x =d ==则()()2224421n n n A B r d a =-=+,所以121n n a a +=+,则()1121n n a a ++=+所以()111122n n n a a -+=+=,得21n n a =- ,故A 错,B 正确;前n 项和为()12122212n n n S n n +-=-=---,故C 正确;由()()11111111122111221212121212121ii n nnni i n n i i i i i i i a a +++++===+-⎛⎫==-=-= ⎪------⎝⎭∑∑∑,故D 正确. 故选:BCD13.【答案】1【解析】圆C :()()22211x k y k -++-=的圆心为()21,k k -因为圆C 与x 轴和y 轴均相切,所以211k k -== 解得1k = 故答案为:114.【答案】14【解析】因为四面体ABCD 的每条棱长都等于1,点G 是棱CD 的中点,所以AG AC CG =+,且12CG =,1AC =,1BC =,所以()AC CG A BC AG BC BC BC C CG ⋅=⋅⋅+=+⋅ 111cos60cos120244AC BC G BC C ⋅=-⋅⋅+⋅==, 故答案为:1. 15.-【解析】如图,取1PF 的中点A ,连接OA ,12OA OF OP ∴=+,212OA F P =, ∴12OFOP F P +=,11()0PF OF OP +=,∴120PF F P =,∴12PF F P ⊥,12||2||PF PF =,不妨设2||PF m =,则1||PF , 21||||2PF PF a m +==,1)ma ∴==,12||2F F c =,2222242334(3cm m m a∴=+==⨯-,∴2229c a=-=,e ∴=-16.【答案】20202021-【解析】由题意可知,对任意的n *∈N ,0n a >且22n n n S a a =+.当1n =时,则21112a a a =+,解得11a =.当2n ≥时,由22n n n S a a =+可得21112n n n S a a ---=+,上述两式作差得22112n n n n n a a a a a --=-+-,可得()()1110n n n n a a a a --+--=, 所以,11n n a a --=,所以,数列{}n a 是等差数列,且首项和公差均为1,则11n a n n =+-=,()12n n n S +=, 则()()()()211211111112nn n n n n a c n n n n n S +⎛⎫=+ ⎪++=--⎝+=⎭-, 因此,数列{}n c 的前2020项之和为202011111111202011223342020202120212021T ⎛⎫⎛⎫⎛⎫⎛⎫=-+++-++++=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 故答案为:20202021-. 17.【解析】(1)因为11n n n S S a +=++,所以11n n n S S a +-=+,即11n n a a +=+, 所以数列{}n a 是首项为1a ,公差为1的等差数列.选①.由4713a a +=,得113613a d a d +++=,即12139a d =-, 所以1213914a =-⨯=,解得12a =.所以()()112111n a a n d n n =+-=+-⨯=+, 即数列{}n a 的通项公式为1n a n =+.选②.由1a ,3a ,7a 成等比数列,得()()211126a d a a d +=+,则2221111446a a d d a a d ++=+,所以12a =.所以()()112111n a a n d n n =+-=+-⨯=+.选③.因为10111091010452S a d a d ⨯=+⨯=+, 所以11045165a +⨯=,所以12a =.所以()()112111n a a n d n n =+-=+-=+.(2)由题可知122n n na n +=,所以2323412222n n n T +=+++⋅⋅⋅+, 所以234112*********n n n n n T ++=+++⋅⋅⋅++,两式相减,得23411111111222222n n n n T ++=++++⋅⋅⋅+-2311111111112222222n n n -++⎛⎫=+⨯++++⋅⋅⋅+- ⎪⎝⎭ 111111133212222212nn n n n ++-++=+⨯-=--, 所以332n n n T +=-.18.【解析】(1)在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,则,,AB AD AP 两两垂直,以A 为原点,射线,,AB AD AP 分别为x ,y ,z 轴非负半轴建立空间直角坐标系,如图:则(0,0,0)A ,()2,0,0B ,()0,0,4P ,()2,4,0C ,()0,4,0D ,连BD,则BD =BP =BD BP ,PBD △是等腰三角形,而M 是PD 上一点,且BM PD ⊥,于是得M 是PD 的中点,即()0,2,2M , 因此,()2,4,0AC =,()0,2,2AM =,()2,0,0AB =,设平面ACM 的一个法向量为(,,)n x y z =,则240220n AC x y n AM y z ⎧⋅=+=⎨⋅=+=⎩,令1z =,得()2,1,1n =-,所以点B 到平面ACM的距离为46AB n h n⋅===. (2)由(1)知,()2,2,2BM =-,()2,4,4PC =-,则4cos ,||||12BMPC BM PC BM PC ⋅-〈〉===所以异面直线BM 与PC 19.【解析】(1)证明:因为直线()():2129120l k x k y k ++-+-=,所以()()292120k x y x y -+++-=.令2902120x y x y -+=⎧⎨+-=⎩解得36x y =⎧⎨=⎩,所以不论k 取何值,直线l 必过定点()3,6P .(2)由(1)知:直线l 经过圆C 内一定点()3,6P ,圆心()2,3C , 设圆心C 到直线l 的距离为d ,则12ABCSAB d=== 因为(0,d∈,所以d =ABC 面积的最大值为4. 20.【解析】(1)证明:连接BO ,AB BC ==O 是AC 的中点,BO AC ∴⊥,且 2BO =, 又 2PA PC PB AC ====,,PO AC PO ∴⊥=222PB PO BO =+,则PO OB ⊥, OB AC O =,OB ⊂平面ABC ,AC ⊂平面ABC ,PO ∴⊥平面ABC, (2)解:建立以 O 为坐标原点,,,OB OC OP 分别为,,x y z 轴的空间直角坐标系如图所示,则()0,2,0A -,(0,0,P ,()0,2,0C ,()2,0,0B ,设(2,2,0)BM BC λλλ==-()01λ≤≤,则()()(2,2,0)2,2,022,22,0AM BM BA λλλλ=-=----=-+, 则平面PAC 的法向量为()1,0,0m =, 设平面MPA的法向量(,,),n x y z = 则(0,2,PA =-- 20,n PA y ⋅=--= ()()22220n AM xy λλ⋅=-++=,令1z =,则y =(11x λλ+=-,二面角M PA C --为30︒,∴3cos302m n m n︒⋅==⋅, 即31=+⨯13λ= 或 3λ=( 舍 ),设平面MPA 的法向量(23,n =,(0,2,PC =-, 设PC 与平面PAM 所成的角为θ,则|sin |cos ,|12PC n θ-=<>===+所以PC 与平面P AM21.【解析】(1)由题意,从今年起每年生活垃圾的总量(单位:万吨)构成数列{}n a ,每年以环保方式处理的垃圾量(单位:万吨)构成数列{}n b ,∴{}n a 是以20(1+5%)为首项,1+5%为公比的等比数列;{}n b 是以6 1.57.5+=为首项,1.5为公差的等差数列,∴()2015%nn a =+,6 1.5n b n =+.(2)设今年起n 年内通过填埋方式处理的垃圾总量为n S , ∴()()11n n n S a b a b =-++-()()1212n n a a a b b b =+++-+++()()220 1.0520 1.0520 1.057.596 1.5n n =⨯+⨯++⨯-++++()()()20 1.051 1.057.56 1.51 1.052n n n +⨯-=-++-2327420 1.0542044n n n =⨯---, 当5n =时,63.5n S ≈.∴今年起5年内通过填埋方式处理的垃圾总量约为63.5万吨.22.【解析】(1)12c e a ==,1AF a c =-=,∴2a =,1c =,2223b a c =-=,∴22143x y +=; (2)设()11,C x y ,()22,D x y ,则()11,B x y --,CF :1x my =-联立221143x my x y =-⎧⎪⎨+=⎪⎩ ∴()234690m y my +--=,∴122122934634y y m m y y m -⎧=⎪⎪+⎨⎪+=⎪+⎩()()()()()()22121211212212121212121121232321212y y x y my y my k x my y y y k y x y my y my my y y x ----+-=====+-+++-1221211229627333434343993434m m m y y m m m m my y m m -⎛⎫---+ ⎪++⎝⎭+===--++++。
高二(下)期末数学试卷

高二(下)期末数学试卷一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)复数z 在复平面内对应点的坐标为(3,6),则|2|(z i -= ) A .3B .4C .5D .62.(5分)5人排成一行,其中甲、乙两人相邻的不同排法共有( ) A .24种B .48种C .72种D .120种3.(5分)52()x x-的展开式中3x 的系数为( )66666666666666A .10B .10-C .5D .5-4.(5分)某铁球在0C ︒时,半径为1dm .当温度在很小的范围内变化时,由于热胀冷缩,铁球的半径会发生变化,且当温度为C t ︒时铁球的半径为(1)at dm +,其中a 为常数,则在0t =时,铁球体积对温度的瞬时变化率为( )(参考公式:34)3V R π=球A .0B .a πC .43a πD .4a π5.(5分)长时间玩手机可能影响视力.据调查,某校学生大约有40%的人近视,而该校大约有20%的学生每天玩手机超过1小时,这些人的近视率约为50%.现从每天玩手机不超过1小时的学生中任意调查一名学生,则他近视的概率约为( ) A .0.125B .0.25C .0.375D .0.46.(5分)正四面体ABCD 中,M ,N 分别是BC ,AD 的中点,则直线AM 和CN 夹角的余弦值为( ) A .33B .63C .22D .237.(5分)如图,一个质点在随机外力的作用下,从原点O 出发,每次等可能地向左或向右移动一个单位.若质点移动6次,则回到原点O 的概率为( )A .0B .14C .516 D .588.(5分)已知函数()f x xlnx =,()24g x x =-,若12()()f x g x =,则21x x -的最小值为()A .22e -B .3e -C .2e -D .1二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分. 9.(5分)随机变量~(2,4)X N ,则( ) A .()2E X =B .()2D X =C .(4)(1)P X P X >><D .(1)(3)1P X P X >+>=10.(5分)已知函数()y f x =的导函数()y f x '=的图象如图所示,则(A .12()()f x f x <B .32()()f x f x <C .()f x 在(,)a b 内有2个极值点D .()f x 的图象在点0x =处的切线斜率小于011.(5分)把4个编号为1,2,3,4的球放入4个编号为1,2,3,4的盒子中,则()A .不同的放法有64种B .每个盒子放一个球的不同放法有24种C .每个盒子放一个球,且球的编号和盒子的编号都不相同的不同放法有9种D .恰有一个盒子不放球的不同放法有72种12.(5分)在棱长为1的正方体1111ABCD A B C D -中,点E ,F 分别满足AE AB λ=,BF BC μ=,其中[0λ=,1],[0μ∈,1],则( )A .当1μ=时,三棱锥11AB EF -的体积为定值 B .当12λ=时,点A ,B 到平面1B EF 的距离相等C .当12μ=时,存在λ使得1BD ⊥平面1B EF D .当λμ=时,11A F C E ⊥三、填空题:本题共4小题,每小题5分,共20分. 13.(5分)若31iz i-=+,则z z += . 14.(5分)已知(1A ,0,0),(0B ,1,0),(0C ,0,1),若点(P x ,1,1)在平面ABC 内,则x = .15.(5分)由0,1,2,3,4,5组成没有重复数字的三位数,其中偶数有 个.(用数字作答)16.(5分)函数,(),x xe x a f x x x a⎧=⎨>⎩,当0a =时,()f x 零点的个数是 ;若存在实数0x ,使得对于任意x R ∈,都有0()()f x f x ,则实数a 的取值范围是 .四、解答题:本题共6小题,共70分.解答应写出文字说明证明过程或演算步骤. 17.(10分)已知函数32()f x x ax b =++在2x =处有极值2-. (1)求()f x 的解析式;(2)求()f x 在[2-,3]上的最值.18.(12分)在国家政策扶持下,近几年我国新能源汽车产业迅速发展.某公司为了解职工购买新能源汽车的意愿,随机调查了30名职工,得到的部分数据如表所示:(1)请将上述22⨯列联表补充完整,并判断能否有99%的把握认为“该公司职工购买新能源汽车的意愿与性别有关”;(2)为进一步了解职工不愿意购买新能源汽车的原因,从不愿意购买新能源汽车的被调查职工中随机抽取3人进行问卷调查,求至少抽到2名女职工的概率. 附:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.20()P K k0.100 0.050 0.010 0.001 0k2.7063.8416.63510.82819.(12分)如图,在三棱锥P ABC -中,PBC ∆是正三角形,AC BC ⊥,D 是AB 的中点. (1)证明:BC PD ⊥;(2)若2AC BC ==,22PA =,求二面角D PA C --的余弦值.20.(12分)为了解某地区未成年男性身高与体重的关系,对该地区12组不同身高i x (单位:)cm 的未成年男性体重的平均值i y (单位:)(1kg i =,2,,12)数据作了初步处理,得到下面的散点图和一些统计量的值.xyω1221()ii xx =-∑121()()ii i xx y y =--∑121()()ii i xx ωω=--∑11524.3582.95814300 6300 286表中(1i i lny i ω==,2,,12),112i i ωω==∑.(1)根据散点图判断y ax b =+和cx d y e +=哪一个适宜作为该地区未成年男性体重的平均值y 与身高x 的回归方程类型?(给出判断即可,不必说明理由). (2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)如果体重高于相同身高的未成年男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该地区的一位未成年男性身高为175cm ,体重为78kg ,他的体重是否正常?附:对于一组数据1(u ,1)v ,2(u ,2)v ,⋯⋯,(n u ,)n v ,其回归直线v u αβ=+的斜率和截距的最小二乘估计分别为121()()ˆ()nii i nii uu v v uu β==--=-∑∑,ˆˆv u αβ=-,20.693ln ≈. 21.(12分)一个袋子中有10个大小相同的球,其中有4个白球,6个黄球,从中随机地摸4个球作为样本,用X 表示样本中黄球的个数,Y 表示样本中黄球的比例. (1)若有放回摸球,求X 的分布列及数学期望;(2)(ⅰ)分别就有放回摸球和不放回摸球,求Y 与总体中黄球的比例之差的绝对值不超过0.2的概率.(ⅱ)比较(ⅰ)中所求概率的大小,说明其实际含义. 22.(12分)已知函数()(1)()f x ln x ax a a R =++-∈. (1)讨论()f x 的单调性;(2)若()x a f x xe ax -+,求a 的取值范围.高二(下)期末数学试卷一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)复数212iz i=-的实部与虚部之和为( ) A .25-B .25C .45D .652.(5分)已知函数32()2f x x x =+,()f x '是()f x 的导函数,则f '(2)(= ) A .24B .26C .32D .283.(5分)函数()23x f x x =-在[0,2]上的平均变化率为( ) A .32 B .32-C .1D .2-4.(5分)4(23)x -展开式中的第3项为( ) A .216-B .216x -C .216D .2216x5.(5分)某学校高三年级总共有800名学生,学校对高三年级的学生进行一次体能测试.这次体能测试满分为100分,已知测试结果ξ服从正态分布2(70,)N σ.若ξ在[60,70]内取值的概率为0.2,则估计该学校高三年级体能测试成绩在80分以上的人数为( ) A .160B .200C .240D .3206.(5分)从1,2,3,4,5,6,7,8中不放回地依次取2个数,事件A 为“第一次取到的数是偶数”,事件B 为“第二次取到的数是偶数”,则(|)(P B A = ) A .12B .25 C .37D .387.(5分)已知复数1cos sin ()z i R θθθ=+∈,2z i =,且12z z 在复平面内对应的点在第一,三象限的角平分线上,则tan (θ= )A .2-B .2-+CD .8.(5分)某学校安排甲、乙,丙、丁、戊五位同学参加数学、物理、化学竞赛,要求每位同学仅报一科,每科至少有一位同学参加,且甲不参加数学竞赛,则不同的安排方法有()A .86种B .100种C .112种D .134种二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.(5分)已知复数(2)(1)z i i =+-,则( ) A .1z i =+B .||z =C .z 在复平面内对应的点在第四象限D .13zi i=- 10.(5分)已知~(4X B ,)(01)p p <<,则下列结论正确的有( )A .若13p =,则8()9E X =B .若13p =,则16(0)81P X ==C .()1maxD X =D .若(1)()3P x P X =>=,则102p <<11.(5分)下面四个结论中正确的有( )A .43)+展开式中各项的二项式系数之和为16B .用4个0和3个1可以组成35个不同的七位数C .0.290.251()x x+的展开式中不存在有理项D .方程10x y z ++=有36组正整数解12.(5分)已知函数2()(2)(2)f x x x a a =->,若函数()(()1)g x f f x =+恰有4个零点,则a 的取值可以是( ) A .52B .3C .4D .92三.填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.(5分)若随机变量ξ的分布列为.ξ0 1 2 Pa0.2a +0.3则a = .14.(5分)写出一个恰有1个极值点,且其图象经过坐标原点的函数()f x = . 15.(5分)某电影院的一个放映室前3排的位置如图所示,甲和乙各自买了1张同一个场次的电影票,已知他们买的票的座位都在前3排,则他们观影时座位相邻(相邻包括左右相邻和前后相邻)的概率为 .16.(5分)若221a lna c b d--==,则22()()a c b d -+-的最小值是 . 四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)马拉松赛事是当下一项非常火爆的运动项目,受到越来越多人的喜爱.现随机在“马拉松跑友群”中选取100人,记录他们在某一天马拉松训练中的跑步公里数,并将数据整理如下: 跑步公里数 性别 [5,10) [10,15) [15,20) [20,25) [25,30) [30,35]男 4 6 10 25 10 5 女2581762(1)分别估计“马拉松跑友群”中的人在一天的马拉松训练中的跑步公里数为[5,15),[15,25),[25,35]的概率;(2)已知一天的跑步公里数不少于20公里的跑友被“跑友群”评定为“高级”,否则为“初级”,根据题意完成给出的22⨯列联表,并据此判断能否有95%的把握认为“评定级别”与“性别”有关.附:2K =,n a b c d =+++.2)k18.(12分)已知函数()f x 的导函数是()f x ',且21()(1)24f x f x f '=+(1)4x -. (1)求()f x 的解析式;(2)求经过点(0,6)-且与曲线()y f x =相切的直线方程. 19.(12分)已知6621201212(1)(1)x x a a x a x a x -+=+++⋯+.(1)求2221311a a a ++⋅⋅⋅+的值;(2)求2412a a a ++⋯+的值; (3)求46a a +的值.20.(12分)某小型企业在开春后前半年的利润情况如表所示:设第i 个月的利润为y 万元.(1)根据表中数据,求y 关于i 的回归方程ˆˆˆ(22)i yb i a =-+(系数精确到0.01); (2)由(1)中的回归方程预测该企业第7个月的利润是多少万元?(结果精确到整数部分,如98.1万元~98万元)(3)已知y 关于i 的线性相关系数为0.8834.从相关系数的角度看,y 与i 的拟合关系式更适合用ˆˆˆypi q =+还是ˆˆˆ(22)i y b i a =-+,说明你的理由. 参考数据:62221()1933.5,22523188,1418.5259ii yy =-=+=⨯=∑,1140.96109.44⨯=,取2005.4=.附:样本(i x ,)(1i y i =,2,⋯,)n的相关系数()()nii xx y y r --=∑线性回归方程ˆˆˆybx a =+中的系数1122211()()ˆ()nnii i ii i nniii i xx y y x ynxy b xx xnx ====---==--∑∑∑∑,ˆˆay bx =-. 21.(12分)在一个不透明的盒中,装有大小、质地相同的两个小球,其中1个是黑色,1个是白色,甲、乙进行取球游戏,两人随机地从盒中各取一球,两球都取出之后再一起放回盒中,这称为一次取球,约定每次取到白球者得1分,取到黑球者得0分,一人比另一人多3分或取满9次时游戏结束,并且只有当一人比另一人多3分时,得分高者才能获得游戏奖品.已知前3次取球后,甲得2分,乙得1分. (1)求甲获得游戏奖品的概率;(2)设X 表示游戏结束时所进行的取球次数,求X 的分布列及数学期望.22.(12分)已知函数234()sin 3f x x sin x m =-+.(1)求()f x 在[0,]π上的单调区间;(2)设函数4()2(2)(16)x g x x e ln x =--,若(0,)α∀∈+∞,[0β∀∈,]π,()()f g βα,求m 的取值范围.。
2024-2025学年高二上学期数学期末模拟卷B卷(含解析)
高二上学期数学人教A 版(2019)期末模拟测试卷B 卷【满分:150分】一、选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知圆C :,P 为直线上一点,过点P 作圆C 的两条切线,切点分别为A 和B ,当四边形PACB 的面积最小时,直线AB 的方程为( )A. B. C. D.2.如图,已知点P 在正方体的对角线上,.设,则的值为( )D.3.已知椭圆E ()的左焦点为F ,过焦点F 作圆的一条切线l 交椭圆E 的一个交点为A ,切点为Q ,且(O 为坐标原点),则椭圆E 的离心率为( )4.牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法——牛顿法.设是的根,选取作为的初始近似值,过点做曲线的切线l ,l 与x 轴的交点的横坐标为,称是r 的一次近似值;过点做曲线的切线,则该切线与x 轴的交点的横坐标为,称是r 的二次近似值.则222440x y x y +---=:20l x y ++=5530x y ++=5530x y -+=5530x y +-=5530x y --=ABCD A B C D -''''BD '60PDC ∠=︒D P D B λ''=λ1-3-221y b+=0a b >>222x y b +=2OA OF OQ +=r ()2f x x =+()100x x -=>01x =r ()()00,x f x ()y f x =1x 1x ()()11,x f x ()y f x =2x 2x( )的右顶点为圆心,焦点到渐近线的距离为半径的圆交抛物线6.数列的前n 项和为,,,设,则数列的前51项之和为()A.-149B.-49C.49D.1497.已知函数的定义域为R ,其导函数为,且满足,,则不等式A. B. C. D.8.设曲线的直线l 与C 交于A ,B 两点,线段的垂直平分线分别交直线二、选择题:本题共3小题.每小题6分.共18分.在每小题给出的选项中,有多项符合题目要求全部选对的得6分.部分选对的得部分分,有选错的得0分.9.已知实数x ,y 满足圆C 的方程,则下列说法正确的是( )A.圆心,半径为1B.过点作圆C 的切线,则切线方程为2x =219y =22y px=()0p >{}n a n S 11a =-*(1)()n n na S n n n =+-∈N (1)nn n b a =-{}n b ()f x ()f x '()()e xf x f x -+'=()00f =()()2e 1e xf x -<11,e ⎛⎫- ⎪⎝⎭1e ,e ⎛⎫ ⎪⎝⎭()1,1-()1,e -:C x =)AB x =+2220x y x +-=()1,0-()2,02x =D.的最大值是410.已知等差数列的前n 项和为,,,则下列说法正确的是( )A. B.C.为递减数列 D.11.已知函数,对于任意实数a ,b ,下列结论成立的有( )A.B.函数在定义域上单调递增C.曲线在点处的切线方程是D.若,则三、填空题:本题共3小题,每小题5分,共15分.12.已知等比数列中,,,公比,则__________.13.在正方体中,点P 、Q 分别在、上,且,,则异面直线与所成角的余弦值为___________.14.已知定点,动点P满足方程为__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或者演算步骤.15.已知圆心为的圆经过点,直线.(1)求圆M 的方程;(2)写出直线l 恒过定点Q 的坐标,并求直线l 被圆M 所截得的弦长最短时m 的值及最短弦长.16.如图,四棱锥中,底面为正方形,平面,E 为的中点.22x y +{}n a n S 24a =742S =54a =21522n S n n =+n a n ⎧⎫⎨⎬⎩⎭11n n a a +⎧⎨⎩e ()x x f x =-min ()1f x =e ()x x f x =-e ()x x f x =-(0,1)1y =0a b =->()()f a f b >{}n a 47512a a ⋅=-38124a a +=q ∈Z 10a =1111ABCD A B C D -11A B 11C D 112A P PB =112C Q QD =BP DQ ()()4,0,1,0M N MN MP ⋅ ()2,1M --()1,3:0l x my m ++=P ABCD -ABCD PA ⊥ABCD PD(1)证明:平面;(2)若,,求平面与平面夹角的余弦值.17.已知函数(a 为实常数).(1)若,求证:在上是增函数;(2)当时,求函数在上的最大值与最小值及相应的x 值;(3)若存在,使得成立,求实数a 的取值范围.18.已知数列的前项和为,且.(1)求的通项公式;(2)求数列的前项和.19.已知双曲线C 的中心为坐标原点,左焦点为(1)求双曲线C的方程:(2)记双曲线C 的右顶点为A ,过点A 作直线,与C 的左支分别交于M ,N 两点,且,,为垂足.(i )证明:直线恒过定点P ,并求出点P 坐标[1,e]()(2)f x a x ≤+n 24n n S a =-{}n nS n T //PB AEC 2AB AD ==4AP =ADE ACE 2()ln f x a x x =+2a =-()f x (1,)+∞4a =-()f x [1,e]x ∈{}n a n S {}n a n (-MA NA MA NA ⊥AD MN ⊥D MN答案以及解析1.答案:A解析:由,得圆C 的圆心,半径.因.故PC 的方程为,即.联立,,解得.所以直线AB 的方程为,化简,得.2.答案:C解析:以D 为原点,以,,的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系.不妨设,则,,,,所以,,,所以,因为,解得,由题可知,所以.故选:C3.答案:A解析:由题意可知:圆的圆心为点O ,半径为b ,,设椭圆E 的右焦点为,连接,因为,可知点Q 为的中点,且点O 为的中点,则()()22222440129x y x y x y +---=⇒-+-=()1,2C 3r =122S AP AC =⨯⋅=l ⊥21y x -=-10x y -+=1020x y x y -+=⎧⎨++=⎩x =y =31,22P ⎛⎫-- ⎪⎝⎭()()311122922x y ⎛⎫⎛⎫---+---= ⎪ ⎪⎝⎭⎝⎭5530x y ++=DA DC DD '1AD =()0,0,0D ()1,1,0B ()0,0,1D '()0,1,0C ()0,0,1DD '=()1,1,1D B =-' ()0,1,0DC = ()()0,0,11,1,1DP DD D P DD D B λλ'''=+=+=+-='(),,1λλλ-60PDC ∠=cos 60=︒=2210λλ+-=1λ=-1=-01λ≤≤1λ=-222x y b +=c b >2F 2AF 2OA OF OQ +=AF 2FF,因为Q为切点,可知,则,解得4.答案:C解析:由题意可得,,由导数的几何意义得过点做曲线的切线的斜率,所以,整理得,所以做曲线的切线的斜率该切线为,则,整理得5.答案:A的右顶点坐标为,焦点为,渐近线方程为,即,焦点到渐近线,所以题中圆的方程为,因为圆和抛物线的图象都关于轴对称,所以A,B两点关于x轴对称,不妨设点A,在第一象限,设,则,上,所以,//OQ AF222AF OQ==2222a AF a b-=-OQ AF⊥2AF AF⊥2222AF AF F+=()()2222242244b a bc a b+-==-23a==cea====()1f x=()21f x x'=+()1,1()y f x=l()113k f='=():131l y x-=-:32l y x=-1x=()2122133f x⎛⎫=+-=⎪⎝⎭21,39⎫⎪⎭()y f x=223k f⎛⎫'==⎪⎝⎭2l2172:933l y x⎛⎫-=-⎪⎝⎭73y x=2x=219y-=()2,0()32y x=±320x y±=)32x y+=3()2229x y-+=()2229x y-+=()220y px p=>x()()1111,0,0A x y x y>>()11,B x y-12y=1y=)2229x y-+=()21289x-+=解得或3,所以或,当,则,解得,当,则,解得故选:A.6.答案:B解析:因为,当时,,即,所以是以-1为首项,1,则,当时,所以,当时也成立,所以,可得数列的前51项之和为.故选:B.7.答案:C解析:由得,即,可设,当时,因得,所以,,因为,故为偶函数,,当时,因,,故,所以在区间上单调递增,因为,所以当时,又因为11x =(1,A (3,A (1,A 82p =4p =(3,A 86p =p =*(1)()n n na S n n n =+-∈N 2n ≥1()(1)n n n n na n S S S n n -=-=+-1(1)(1)n n n S nS n n ---=-11n S n --=-11a ==-n S n ⎧⎫⎨⎬⎩⎭112n n =-+-=-(2)n S n n =-2n ≥()11(3)n S n n -=--()()121(3)23n n n a S S n n n n n -==----=--1n =23n a n =-()()()1123nnn n b a n =-=--{}n b (11)(35)...(9597)99++-+++-+-2259949=⨯-=-()()e x f x f x -+'=()()e e 1x x x f x f +'=()e 1x f x '⎡⎤=⎣⎦()e xf x x m =+0x =()00f =0m =()e xf x x -=()()2e 1e x f x -<-()2e e 1e x x x --<-e e e x x x x --<()e e x xg x x x -=-()()e e x x g x x x g x --=-+=()g x ()e e e e x x x x g x x x --'=++-0x ≥e e 0x x x x -+≥e e 0x x --≥()e e e x x xg x x x -'=++e 0x --≥()g x [)0,+∞()11e e g -=-0x ≥()e x g x x =-e e xx -<-)0,1为偶函数,故.故选:C8.答案:D解析:因为曲线,,所以C是双曲线的右支,其焦点为,渐近线为.由题意,设(故A选项可排除),联立得,,所以,,解得.故选:D.9.答案:BD解析:对选项A:,即,圆心为,半径为,A错误;对选项B:在圆上,则和圆心均在x轴上,故切线与x轴垂直,为,B正确;对选项C:表示圆上的点到点的斜率,如图所示::1C x=≥()2211x y x-=≥221x y-=)F y x=±(:l y k x=(,y k xx⎧=-⎪⎨⎪=⎩()22221210k x x k--++=()2Δ410k=+>A Bx x+=A Bx x=Bx-==()g x()eg x<)1,1-=2A BNx x+==NMN x=-==(2k=±+2220x y x+-=22(1)1x y-+=(1,0)1r=(2,0)(2,0)2x=1yx+(,)x y(1,0)A-当与圆相切时,斜率最大,此时,,故,故此时斜率最大为C 错误;对选项D :表示圆上的点到原点距离的平方,故最大值为,D 正确.故选:BD.10.答案:BC解析:等差数列中,,解得,而,因此公差,通项,对于A ,,A 错误;对于B ,,B 正确;为递减数列,C 正确;的前5项和为11.答案:ACD解析:对A ,对求导,,令,即,解得.当时,,函数单调递减;当时,,函数单调递增.所以函数在处取得最小值,即,所以,A 选项正确.AB ||2AC =||1BC =AB BC ⊥tan 30︒=22x y +(,)x y 2(1)4r +={}n a ()177477422a a S a +===46a =24a =42142a a d -==-2(2)2n a a n d n =+-=+57a =2(32)15222n n n S n n ++==+1=n a n ⎧⎫⎨⎬⎩⎭11(2)(3)2n n n ==-+++11n n a a +⎫⎬⎭1111134457-+-++ 111838-=-=e ()x x f x =-)1(e x f x =-'()0f x '=e x -1=00x =0x <()0f x '<()f x 0x >()0f x '>()f x ()f x 0x =(0)1f =()min 1f x =对B ,由上述分析可知,上函数单调递减,上函数单调递增,B 选项错误.对C ,由于切线斜率为0,在点,切线方程为,C 选项正确.对D ,因为,则.则.令,则,则在单调递增.故.即,即.D 选项正确.故选:ACD 12.答案:512解析:,,,,则得,或者,,公比q 为整数,,,,解得,即,故答案为:512.解析:设正方体中棱长为3,以D 为原点,为x 轴,为y 轴,为z 轴,建立如图所示空间直角坐标系,则,,,,,,设异面直线(,0)-∞()f x (0,)+∞()f x ()()000e 010e 10.f f '=-==-=,()0,11y =0,0a b b a =->=-<()e ,()()e a a f a a f b f a a -=-=-=+()()f a f b -=e (e )e e 2a a a a a a a ----+=--()e e 2x x g x x -=--()e e 220x x g x -=+-'≥-=()g x (0,)+∞()(0)0g x g >=()()0f a f b ->()()f a f b >47512a a ⋅=- 38124a a +=3847512a a a a ∴⋅=⋅=-38124a a +=34a =-8128a =3128a =44a =- 34a ∴=-8128a =54128q ∴-=2q =-22108128(2)1284512a a q ==⨯-=⨯=1111ABCD A B C D -DA DC 1DD ()0,0,0D ()0,1,3Q ()3,3,0B ()3,2,3P ()0,1,3BP =- ()0,1,3DQ =与所成角为,则与所成角的余解析:设动点,则.又.化简得,动点P 的轨迹E的方.15.答案:(1)(2)最小值为.解析:(1)圆M的半径,圆M 的方程为.(2)直线l 的方程为,,令解得:,定点Q 的坐标为.,点Q 在圆M 的内部,故直线l 恒与圆M 相交.又圆心M 到直线l 的距离l 被圆M 截得的弦长为当d 取得最大值2时,弦长有最小值,最小值为.16.答案:(1)证明见解析;BP DQ θcos BP DQ BP DQθ⋅===⋅ BP DQ 213y =(),P x y ()()()4,,3,0,1,MP x y MN PN x y =-=-=-- MN MP ⋅ ()34x ∴--=2234x y +=213y +=∴23y +=213y =()()222125x y +++=0= 5r ==∴()()222125x y +++= 0x my m ++=(1)0x m y ∴++=010x y =⎧⎨+=⎩01x y =⎧⎨=-⎩∴()0,1-()()220211425++-+=< ∴2d ≤∴=0=解析:(1)证明:如图所示,连接,设,连接,因为四边形为正方形,则O 为的中点,因为E 是的中点,所以.又因为平面,平面,所以平面.(2)因为平面,四边形为正方形,以A 为坐标原点,分别以、、所在直线为x 、y 、z 轴建立如图所示空间直角坐标系,因为,,则、、、、、,设平面的法向量为,,,则,取,可得,又为平面的一个法向量,则所以,平面与平面BD AC BD O = OE ABCD BD PD //EO PB EO ⊂AEC PB ⊄AEC //PB AEC PA ⊥ABCD ABCD AB AD AP 2AB AD ==4AP =()0,0,0A ()2,0,0B ()0,0,4P ()0,2,0D ()0,1,2E ()2,2,0C AEC (),,m x y z = ()0,1,2AE = ()2,2,0AC = 20220m AE y z m AC x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩ 1z =()2,2,1m =- ()1,0,0n =ADE 2cos ,31m n m n m n ⋅===⋅⨯ ADE17.答案:(1)答案见解析(2)当有最小值为,当时,函数有最大值为(3)解析:(1)由题可知函数的定义域,因为,所以,所以令解得,所以在上是增函数(2)因为,所以,所以令解得解得所以在上单调递减,在上单调递增,所以在上单调递减,在上单调递增,所以当时,函数有最小值为,因为,所以当时,函数有最大值为.(3)由得,即,因为,所以,所以,且当时,所以在恒成立,所以即存在时,令()0f x'>()0f x'<()f x)+∞⎡⎣x=22ln2f=-2(e)e41f=->()f x()(2)f x a x≤+x=()f x22ln2f=-ex=()f x2(e)e4f=-[)1,-+∞(0,)+∞2a=-2()2lnf x x x=-+2()2f x xx'=-+=()0f x'>1x>()f x(1,)+∞4a=-2()4lnf x x x=-+4()2f x xx'=-+=x>0x<()f x⎤⎦()f x(1)1f=ex=2(e)e4f=-2(ln2)a x x a x≤++()2ln2a x x x x-≤-[1,e]x∈1,ln ln e1x x≥≤=lne lnx x≥≥1x=ln0x= lnx x>[1,e]x∈a≥[1,e]x∈a≥()g x=()g x'=令,令,解得,令,解得,所以在单调递减,单调递增,所以,所以时,恒成立,所以,所以实数a 的取值范围是.18.答案:(1)(2)答案见解析解析:(1),当时,,两式相减,得,整理得,即时,,又当时,,解得,数列是以4为首项,2为公比的等比数列,.(2)由(1)知,,令,易知,,设数列的前n 项和为,则,,n K 456321222322n n K n +=⨯+⨯+⨯++⋅ ②()22ln h x x x =+-22()1x h x x x-'=-=2()0x h x x -'=>2e x <≤2()0x h x x-'=<12x ≤<()h x [)1,2(]2,e ()(2)2(2ln 2)0h x h ≥=->[1,e]x ∈()2(1)(22ln )()0ln x x x g x x x -+-'=≥-min ()(1)1g x g ==-[)1,-+∞12n +24n n S a =- ∴2n ≥1124n n S a --=-()112424n n n n S S a a ---=---12n n a a -=2n ≥12n n a a -=1n =11124S a a ==-14a =∴{}n a 11422n n n a -+∴=⨯=1222424n n n S ++=⨯-=-224n n nS n n +∴=⋅-22,4n n n b n c n +=⋅=-()()1214212n n n c c c n n ++++=-⨯=-+ {}n b 34521222322n n K n +=⨯+⨯+⨯++⋅ ①由,得,即.(2)见解析解析:(1)由题意,双曲线C 的中心为坐标原点,左焦点为可得,解得,.(2)证明:(i )由(1)知,当直线斜率存在时,设直线方程为,联立方程组,整理得,,即,3456231222222n n n K n ++-=⨯+++++-⋅ ()()413332122212812n n n n K n n -++-∴=+-⋅=-⋅+--①②()4133332122222812n n n n n K n n -+++--=+-⋅=-⋅--()()()32112218n n n T K n n n n n +∴=-+=-⋅-++2116y =(-222c c e a b c a ⎧=⎪⎪==⎨⎪=-⎪⎩2,4a b ==2116y -=()2,0A MN MN y kx m =+221416y kx m x y =+⎧⎪⎨-=⎪⎩()22242160k x kmx m ----=()()2222444160k m k m ∆=+-+>22416k m -<设,,由韦达定理可得.因为,可得,即,即,整理得,即,即,可得,解得将代入直线,此时直线过定点,不合题意;将,此时直线过定点,当直线的斜率不存在时,不妨设直线方程为,因为,所以为等腰直角三角形,此时M 点坐标为,所以(舍)或此时过定点,综上可知,直线恒过定点(ii )因为,此时存在以为斜边的直角三角形,()11,M x y ()22,N x y 122212224,164km x x k m x x k ⎧+=⎪⎪-⎨+⎪=⎪-⎩MA ⊥2212y x =--()()1212220y y x x +--=()121212240y y x x x x +-++=()()()121212240kx m kx m x x x x +++-++=()()()2212121240k x x mk x x m ++-+++=()()22222162124044m km k mk m k k +++-++=--2234200m km k --=()()23100m k m k +-=2m km =-=2m k =-()2y kx m y k x =+⇒=-MN ()2,0A m =103y kx m y k x ⎛⎫=+⇒=+ ⎪⎝⎭MN 10,03P ⎛⎫-⎪⎝⎭MN x t =MA NA ⊥AMN (,t 22342002t t t t =-⇒+-=⇒=t =MN 10,03P ⎛⎫- ⎪⎝⎭MN 10,0,3P ⎛⎫- ⎪⎝⎭AD MN ⊥AP1 2AP=2,03⎛⎫-⎪⎝⎭所以存在定点Q为.AP。
高二数学上学期期末测试试题(共10页)
高二年级期末(q ī m ò)测试上学期数学试卷〔考试时间是是:120分钟 总分:160分〕一、填空题:本大题一一共14小题,每一小题5分,一共70分.请把答案填.....写上在答题纸相应位置上............ 的准线方程是 .2.命题“〞的否认是 .中,双曲线:〔〕的一条渐近线与直线:垂直,那么实数.4.在等差数列中,,那么 .5.假设△的内角所对的边满足,且角C=60°,那么的值是 .6.原命题:“设>bc 〞那么它的逆命题的真假为 .7.假设方程表示焦点在轴上的椭圆,那么的取值范围是 .8.在数列}{n a 中,,,其中为常数,那么B A ,的积等于 .中,为上底面的中心(zh ōngx īn),且每两条的夹角都是60º,那么向量的长.10.,假设是真命题,那么实数a 的取值范围是___.11.椭圆x 2a 2+y 2b2=1(a >b >0)的右焦点为F ,其右准线与x 轴的交点为A .在椭圆上存在点P 满足线段AP 的垂直平分线过点F ,那么椭圆离心率的取值范围是 .12.在算式“1×口+4×口=30”的两个口中,分别填入两个自然数,使它们的倒数之和最小,那么这两个数的和为________.13.给出以下四个命题:①假设a >b >0,那么1a >1b;②假设a >b >0,那么a -1a >b -1b;③假设a >b >0,那么2a +b a +2b >a b ;④假设a >0,b >0,且2a +b =1,那么2a +1b的最小值为9.其中正确命题的序号是______.(把你认为正确命题的序号都填上)14.将n 个正整数1, 2, 3, …,n (N *)分成两组,使得每组中没有两个数的和是一个完全平方数,且这两组数中没有一样的数. 那么n 的最大值是 .二、解答题:〔本大题一一共6小题,计90分.请把答案填写上在答题纸相............应位置上...., .解容许写出必要的文字说明、证明过程或者演算步骤.......................〕15.(此题满分是14分〕公比(ɡōnɡ bǐ)为3的等比数列与数列满足,且,〔1〕判断{}n a是何种数列,并给出证明;〔2〕假设,求数列的前项和16.(此题满分是14分〕△ABC 中,在边上,且o ,o.〔1〕求的长;〔2〕求△ABC的面积.17.(此题满分是14分〕如图,正三棱锥ABC—A1B1C1的底面边长为a ,侧棱长为a,M是A1B1的中点.〔I 〕求证:是平面ABB1A1的一个法向量;MA1 B1C1〔II〕求AC1与侧面ABB1A1所成的角.18.(此题满分(mǎn fēn)是16分〕椭圆C:x2a2+y2b2=1(a>b>0)的离心率为12,且经过点P(1,32)。
江苏南京六校联合体2024年高二下学期期末调研测试数学试卷
2023-2024学年第二学期六校联合体期末调研测试高二数学2024.6.24注意事项:1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷.2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.对于x ,y 两个变量,有四组样本数据,分别算出它们的线性相关系数r (如下),则线性相关性最强的是A .-0.87B .0.72C .-0.78D .0.852.在空间直角坐标系O -xyz 中,点(-1,2,3)关于x 轴的对称点坐标是A .(1,2,3)B .(-1,-2,3)C .(-1,-2,-3)D .(1,-2,-3)3.已知(x -2)8=a 0+a 1(x -1)+…+a 8(x -1)8,则a 0+a 1+…+a 8=A .-1B .0C .1D .24.3个男生2个女生站成一排,其中女生相邻的排法个数是A .24B .48C .96D .1205.已知函数f (x )=tan x ,那么f '(π3)的值是A.33B.3C.2D.46.已知随机变量X ,Y 满足:X ~B (4,p ),P (X =0)=1681,X +2Y =1,则A .E (X )=23B .E (Y )=-13C .D (X )=49D .D (Y )=297.给出下列四个命题,其中真命题是A .若向量a 与向量b ,c 共面,则存在实数x ,y ,使a =x b +y cB .若存在实数x ,y ,使MP →=xMA →+yMB →,则点P ,M ,A ,B 共面C .直线a 的方向向量为a =(1,0,-1),平面α的法向量为m =(1,1,1),则a ⊥αD .若平面β经过三点P (-1,2,0),Q (1,0,-1),T (0,1,0),向量n =(1,x ,y )是平面β的法向量,则x +y =28.若函数2)(x ae x f x -=有两个极值点21,x x ,且21x x <,则下列结论中不正确的是A .12>x B .112x e x <C .a 的范围是2,0(eD .0ln ln 21<+x x 二.选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对得部分分,不选或有选错的得0分.9.A -,B -分别为随机事件A ,B 的对立事件,下列命题正确的是A .P (A |B )+P (A -|B )=1B .若P (A )>0,P (B )>0,则P (A )+P (B )=P (A +B )C .若P (A |B )=P (A ),则A 与B 独立D .P (A |B )P (B )+P (A |B -)P (B -)=P (A )10.已知函数f (x )=13x 3-ax 2-x ,下列选项正确的是A .若f (x )在区间(0,2)上单调递减,则a 的取值范围为(34,+∞)B .若f (x )在区间(0,2)上有极小值,则a 的取值范围为(-∞,34)C .当a =0时,若经过点M (2,m )可以作出曲线y =f (x )的三条切线,则实数m 的取值范围为(-2,23)D.若曲线y =f (x )的对称中心为(1,-53),则a =111.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,点F 在底面ABCD 内运动(含边界),点E 是棱CC 1的中点,则A.若F 在棱AD 上时,存在点F 使cos ∠D 1B 1F =56B.若F 是棱AD 的中点,则EF //平面AB 1CC.若EF ⊥平面B 1D 1E ,则F 是AC 上靠近C 的四等分点D.若F 在棱AB 上运动,则点F 到直线B 1E 的距离最小值为255三、填空题:本题共3小题,每小题5分,共15分.12.平面α过点A (0,1,0),其法向量为m =(0,2,1),则点B (1,1,1)到平面α的距离为▲________.13.从集合U={a 1,a 2,a 3,a 4}的子集中选出2个不同..的子集A ,B ,且A ⊆B ,则一共有▲________种选法.14.现有甲、乙两个盒子,甲盒有2个红球和1个白球,乙盒有1个红球和1个白球.先从甲盒中取出2个球放入乙盒,再从乙盒中取出2个球放入甲盒.记事件A 为“从甲盒中取出2个红球”,事件B 为“乙盒还剩1个红球和1个白球”,则P (B |A )=▲________,P (-A -B )=▲________.四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分)为了研究学生的性别与喜欢运动的关联性,随机调查了某中学的100名学生,整理得到如下,左表数据:(1)求a ,b 的值,并判断是否有90%的把握认为“学生的性别与喜欢运动有关联”?(2)经调查,学生的学习效率指数y 与每天锻炼时间x (单位:拾分钟)呈线性相关关系,统计数据见右下表,求y 关于x 的线性回归方程.附:(1)()()()()()22n ad bc a b c d a c b d χ-=++++(2)()()()1122211ˆ,ˆˆnni iiii i n niii i x x yy x ynx y ba y bxx x xnx ====---===---∑∑∑∑16.(本小题满分15分)已知),3()2()(*N n n x x f n ∈≥+=的展开式中,第2,3,4项的二项式系数成等差数列.(1)求n 的值;(2)求)001.0(f 的近似值(精确到0.01);(3)求n x )2(+的二项展开式中系数最大的项.男学生女学生合计喜欢运动a b 60不喜欢运动b b合计60100x 23456y 2.533.556α0.10.050.01x α2.7063.8416.63517.(本小题满分15分)如图,所有棱长均为2的正四棱锥P -ABCD ,点M ,N 分别是PA ,BD 上靠近P ,B 的三等分点.(1)求证:MN ⊥BC ;(2)求二面角M -CN -B 的余弦值.18.(本小题满分17分)某校举行投篮趣味比赛,甲、乙两位选手进入决赛,每位选手各投篮4次,选手在连续投篮时,第一次投进得1分,并规定:若某次投进,则下一次投进的得分比本次得分多1分;若某次未投进,则该次得0分,且下一次投进得1分.已知甲同学每次投进的概率为13,乙同学每次投进的概率为23,且甲、乙每次投篮相互独立.(1)求甲最后得3分的概率;(2)记甲最后得分为X ,求X 的概率分布和数学期望;(3)记事件B 为“甲、乙总分之和为7”,求P (B ).19.(本小题满分17分)定义:如果函数y =f (x )与y =g (x )的图象上分别存在点M 和点N 关于x 轴对称,则称函数y =f (x )和y =g (x )具有“伙伴”关系.(1)判断函数f (x )=9x -4与g (x )=3x +1是否具有“伙伴”关系;(2)已知函数f (x )=ln x -ax -1,x ∈(1,+∞),a >0,g (x )=1-a x +2a .①若两函数具有“伙伴”关系,求a 的取值范围;②若两函数不具有“伙伴”关系,求证:1n +1+1n +2+1n +3+…+1n +n +14n >ln2,其中n 为正整数.。
高二数学试卷期末题及答案
一、选择题(每题5分,共50分)1. 已知函数f(x) = x^2 - 2x + 1,则f(x)的图像是:A. 一个开口向上的抛物线,顶点在(1, 0)B. 一个开口向下的抛物线,顶点在(1, 0)C. 一个开口向上的抛物线,顶点在(0, 1)D. 一个开口向下的抛物线,顶点在(0, 1)2. 若a, b, c是等差数列,且a + b + c = 12,a + c = 8,则b的值为:A. 4B. 6C. 8D. 103. 在△ABC中,若∠A = 30°,∠B = 45°,则∠C的度数是:A. 105°B. 120°C. 135°D. 150°4. 下列哪个方程的解集是空集:A. x^2 + 1 = 0B. x^2 - 4 = 0C. x^2 - 2x + 1 = 0D. x^2 + 2x + 1 = 05. 若复数z满足|z - 1| = |z + 1|,则z在复平面上的轨迹是:A. 以(0, 0)为圆心,1为半径的圆B. 以(0, 0)为圆心,2为半径的圆C. x = 0的直线D. y = 0的直线6. 下列函数中,是奇函数的是:A. f(x) = x^2B. f(x) = x^3C. f(x) = |x|D. f(x) = x^47. 若等比数列{an}的首项为2,公比为3,则第5项an是:A. 24B. 27C. 81D. 2438. 在平面直角坐标系中,点P(2, 3)关于直线y = x的对称点是:A. (3, 2)B. (2, 3)C. (3, 3)D. (2, 2)9. 下列哪个数是等差数列1, 3, 5, ...的第10项:A. 19B. 20C. 21D. 2210. 若log2x + log2(4x) = 3,则x的值是:A. 2B. 4C. 8D. 16二、填空题(每题5分,共50分)11. 已知等差数列{an}的首项a1 = 3,公差d = 2,则第10项an = ________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学期末第1页(共6页)
高二数学期末测试题
题号 一 二 三 总分
16 17 18 19 20 21 22
一、选择题(本大题共12小题,每小题5分,共60分)
1.已知Rcba,,,下列命题正确的是 ( )
A.22bcacba B.bacbca
C.baabba11033 D.baabba11022
2.过点M(-4,3)和N(-2,1)的直线方程是 ( )
A.03yx B.01yx C.01yx D.03yx
3.圆01)4()3(22yxyx关于直线对称的圆的方程是 ( )
A.1)4()3(22yx B.1)3()4(22yx
C.1)3()4(22yx D.1)4()3(22yx
4.过椭圆13422yx的焦点且垂直于x轴的直线l被此椭圆截得的弦长为 ( )
A.23 B.3 C.32 D.3
5.若0,0ba,则与不等式axb1等价的是 ( )
A.axbx11或 B.bxa11
C.axxb1001或 D.bxxa1001或
6.若a、1||||,baRb成立的充分不必要条件 ( )
A.1||ba B.21||21||ba且
C.1a D.1b
高二数学期末第2页(共6页)
7.与椭圆1251622yx共焦点,且两准线间的距离为310的双曲线方程为 ( )
A.14522xy B.14522yx C.13522xy D.13522yx
8.不等式)310)(31(xxxy的最大值是 ( )
A.2434 B.121 C.641 D.721
9.两定点A(-2,-1),B(2,-1),动点P在抛物线2xy上移动,则△PAB重心G
的轨迹方程是 ( )
A.312xy B.3232xy C.3222xy D.41212xy
10.直线220323yxyx截圆=4得的劣弧所对的圆心角为 ( )
A.6 B.4 C.3 D.2
11.不等式2|2|xxxx的解集是 ( )
A.(-2,0) B.]0,2( C.R D.),0()2,(
12.定长为)2(2abll的线段AB的端点在双曲线222222bayaxb的右支上,则AB中
点M的横坐标的最小值为 ( )
A.222baal B.222bala C.222)2(baala D.222)2(baala
二、填空题(本大题共4小题,每小题4分,共16分)
13.若不等式}213|{0342xxxxxax或的解集为,则a= .
14.设椭圆)0(12222babyax的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦长等
于F1到l1的距离,则椭圆的离心率为 .
15.F1,F2是双曲线145422yx的两个焦点,P是双曲线上的点,已知|PF1|,|PF2|,|F1F2|
依次成等差数列,且公差大于0,则∠F1PF2= .
16.给出下列命题:
高二数学期末第3页(共6页)
(1)角2tanxy是的倾斜角
(2)若x、|"|||||""0",yxyxxyRy是则的充要条件
(3)若xxRx22,则的最小值为2
(4)若定义1*)1(*)1(,1)1)(1(*xxxxyxyx则
其中正确命题的序号是 .
三、解答题(本大题共6小题,共74分)
17.已知不等式}1|{2)63(log22bxxxxax或的解集是.
(1) 求a,b的值,(2)解不等式0baxxc(c为常数).(12分)
18.求过点P(1,6)与圆25)2()2(22yx相切的直线方程.(12分)
19.已知椭圆12222byax,其长轴长是短轴长的2倍,右准线方程为334x.
(1)求该椭圆方程,
(2)如过点(0,m),且倾斜角为4的直线l与椭圆交于A、B两点,当△AOB(O为
原点)面积最大时,求m的值.(12分)
20.已知抛物线的顶点在原点,它的准线经过曲线12222byax的右焦点,且与x轴垂直,
抛物线与此双曲线交于点(6,23),求抛物线与双曲线的方程.(12分)
高二数学期末第4页(共6页)
21.已知抛物线xy42的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线
l交抛物线于A、B两点,弦AB的中点为P,AB的垂直平分线与x轴交于点E(,0xO).
(1)求k的取值范围
(2)求证:30x
(3)△PEF能否成为以EF为底的等腰三角形?若能,求出k的值,若不能,请说明理
由.(14分)
高二数学期末测试题参考答案
一、1. C 2.B 3.B 4.D 5.A 6.D 7.A 8.B 9.B 10.C 11.A 12.D
二、13.-2 14.21 15.120° 16.(4)
三、17.(1)a=1, b=2 (3)c<-2时,解集为(c,-2); c=-2时空集;c>-2时,
解集为(-2,c)
18.解:∵圆心为(-2,2) ∴|OP|=5 则P在圆上,且切线的斜率存在.
设切线方程为06)1(6kykxxky即
由0274343,51|622|2yxkkkk切线方程为解得
19.解(1)2343,22222aceabacba.
又141,3,2334222yxbcaca椭圆方程为
(2)设mxyl:,代入椭圆方程得0448522mmxx
令550)44(206422mmm得.设544,58),(),(221212221mxxmxxyxByxA则
2212
2121
55244)(2||2||mxxxxxxAB
原点O到l的距离2||md
425)25(525||52||2
1
222
mmmdABS
OAB
时当252m
,S取得最大值. 即当△AOB的面积最大时,.210m
20.解:由题意可知抛物线的焦点到准线间的距离为2C(即双曲线的焦距).
高二数学期末第5页(共6页)
设抛物线的方程为.42cxy∵抛物线过点112346)6,23(22bacc即①
又知16491)6()23(222222baba② 由①②可得43,4122ba
∴所求抛物线的方程为xy42,双曲线的方程为134422yx
21.解:设安排生产产品Z、Y的件数分别为x,y,利润总额为S元.
由题意得约束条件为0,01563125321004yxyxyxyx 如图,作出可行域.
若市场情况如(I),则目标函数yxS10002000
作直线02010002000:1yxyxl即.
把l1向右上方平移到l1′的位置时,直线经过可行域
上的点C,且与原点距离最大,此
时S取得最大值. 解9,49.156312532yxcyxyx点坐标得.此即所求最优解.
若市场情况如(II)则目标函数030001000:,300010002yxlyxS作直线
即03yx,把l2向右上方平移至l2′的位置时,直线经过可行域上的点B,且与原点距
离最大,此时S取得最大值,解方程组.1540100412532yxByxyx点坐标得此即所求最优解.
答:若市场情况如(I),应生产Z、Y各49件和9件.
若市场情况如(II),应生产Z、Y各40件和15件.
22.解:由题设有)0,1(),0,1(MF(1)设0)2(24)1(),1(:22222kxkxkxyxkyxkyl得由
令11016164)2(42422kkkk得
(2)设AB中点为kxkykkxxxyxPPPPP2)1(,22),,(2221则
∴AB的垂直平分线的方程为)2(1222kkxkky
令322121002220xkkkxy得
(3)
PEFkkPkEF).2,21(),0,21(),0,1(
22
是以EF为底的等腰三角形.
C
高二数学期末第6页(共6页)
)1,1(22,21221121222kkkk则
∴△PEF能构成以EF为底的等腰三角形,此时22k
