华师一附中自主招生数学试题
华师一附中自招考试数学试题
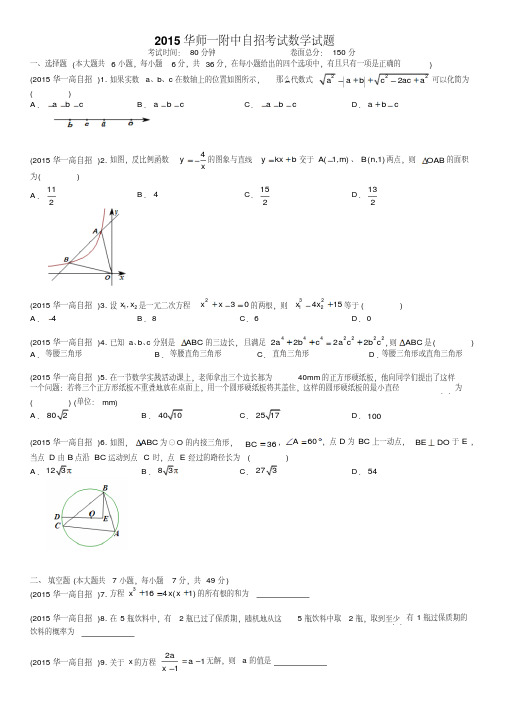
2015华师一附中自招考试数学试题考试时间:80分钟卷面总分:150分一、选择题(本大题共6小题,每小题6分,共36分,在每小题给出的四个选项中,有且只有一项是正确的)(2015华一高自招)1.如果实数a 、b 、c 在数轴上的位置如图所示,那么代数式2222aa bcac a 可以化简为()A .a b c B .a b cC .a b c D .ab c(2015华一高自招)2.如图,反比例函数4yx的图象与直线y kx b 交于(1,)A m 、(,1)B n 两点,则OAB 的面积为()A .112B .4C .152D .132(2015华一高自招)3.设12,x x 是一元二次方程230xx 的两根,则3212415x x 等于()A .4B .8C .6D .0(2015华一高自招)4.已知a 、b 、c 分别是ABC 的三边长,且满足44422222222a b c a cb c ,则ABC 是()A .等腰三角形B .等腰直角三角形C .直角三角形D .等腰三角形或直角三角形(2015华一高自招)5.在一节数学实践活动课上,老师拿出三个边长都为40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径..为()(单位:mm)A .802B .4010C .2517D .100(2015华一高自招)6.如图,ABC 为⊙O 的内接三角形,36BC,60A,点D 为BC 上一动点,BEDO 于E ,当点D 由B 点沿BC 运动到点C 时,点E 经过的路径长为()A .123B .83C .273D .54二、填空题(本大题共7小题,每小题7分,共49分)(2015华一高自招)7.方程3164(1)xx x 的所有根的和为(2015华一高自招)8.在5瓶饮料中,有2瓶已过了保质期,随机地从这5瓶饮料中取2瓶,取到至少..有1瓶过保质期的饮料的概率为(2015华一高自招)9.关于x 的方程211a a x 无解,则a 的值是。
华中师大一附中2015年自主招生考试数学试题(word版附答案)

华中师大一附中2015年高中招生考试数学试题考试时间:80分钟 卷面满分:150分说明:所有答案一律书写在答题卡上,写在试卷上作答无效.一、选择题 (本大题共6小题,每小题6分,共36分.在每小题给出的四个选项中,有且只有一项是正确的.)1.如果实数a ,b ,c a b +可以化简为( )....A a b c B a b cC a b cD a b c--+-----+-2.反比例函数4y x=-的图象与直线y kx b =-+交于 ()()1,,,1A m B n -两点,则△OAB 的面积为( )111513..4..222A B C D 3.设12,x x 是一元二次方程230x x +-=的两根,则3212415x x -+等于( )A .-4B .8C .6D .04.已知a ,b ,c 分别是△ABC 的三边长,且满足44422222222a b c a c b c ++-+=0,则△ABC 是( )A .等腰三角形B .等腰直角三角形C .直角三角形D .等腰三角形或直角三角形5.在一节数学实践活动课上,老师拿出三个边长都为40mm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径为(单位:mm )( ).100A B C D6.如图,△ABC 内接于圆O ,BC =36,∠A =60°,点D 为弧BC 上一动点,BE ⊥直线OD 于E ,当点D 由B 点沿弧BC 运动到点C 时,点E 经过的路线长为( ).54A B C D二、填空题(本大题共7小题,每小题7分,共49分) 7.方程()31641x x x +=+的所有根的和为8.在5瓶饮料中,有2瓶已过了保质期,随机地从这5瓶饮料中取2瓶,取到至少有1瓶过保质期饮料的概率为 9.关于x 的方程211aa x =--无解,则a 的值是10.一辆快车从甲地开往乙地,一辆慢车从乙地开往甲地,两车同时出发,分别以各自的速度在甲乙两地间匀速行驶,1小时后,快车司机发现有重要文件遗忘在出发地,便立即返回拿上文件(取文件时间不计)后再从甲地开往乙地,结果快车先到达乙地.慢车继续行驶到甲地.设慢车行驶速度为x(h ),两车之间的距离为y (km ),y 与x 的函数图象如图所示,则a = 11.已知24,13,234a x y x ax ≥≤≤=-+当时函数的最小值为-23,则a = 12.如图,在单位为1的正方形的网格纸上,123345567A A A ,A A A ,A A A ,,∆∆∆都是斜边在x 轴上,且斜边长分别为2,4,6,…的等腰直角三角形.若123A A A ∆的顶点分别为()()()123A 2,0,A 1,-1,A 0,0,则依图中的规律,2015A 的坐标为13.有一张矩形风景画,长为90cm ,宽为60cm ,现对该风景画进行装裱,得到一个新的矩形,要求其长,宽之比与原风景画的长,宽之比相同,且面积比原风景画的面积大44%.若装裱后的上,下边衬的宽都为a cm ,左,右边衬都为b cm ,那么ab = 三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程和演算步骤) 14.(14分)已知m ,n 是方程2310x x ++=的两根,(1)求162102553m m m m m -⎛⎫+-⋅- ⎪--⎝⎭的值;(215.(15分)如图,△ABC 中,AC =BC ,I 为△ABC 的内心,O 为BC 上一点,过B ,I 两点的圆O 交BC 于D 点,1tan ,6,3CBI AB ∠== (1)求线段BD 的长; (2)求线段BC 的长.16.(18分)如图,四边形ABCD 中,AD ∥BC ,∠BCD =90°,AD =6,BC =3,DE ⊥AB 于E ,AC 交DE 于F , (1)求AE ·AB 的值; (2)若CD =4,求AFFC的值; (3)若CD =6,过A 点作AM ∥CD ,交CE 的延长线于M , 求MEEC的值.17.(18分)二次函数242y x mx n =-+的图象与x 轴交于()()()1212,0,,A x B x o x x <两点,与y 轴交于c 点.(1)若AB =2,且抛物线的顶点在直线y =-x -2上,试确定m ,n 的值;(2)在(1)中,若点P 为直线BC 下方抛物线上一点,当△PBC 的面积最大时,求P 点坐标;(3)是否存在整数m ,n ,使得1212,12,x x <<<<同时成立?请证明你的结论.参考答案一.选择题(6分×6=36分) 1.【解析】由图知0b c a <<<,(),a a a b a b c a a c ==-+=-+=-=-a b +()()a a b a c a b c =-+++-=+-,选D .2.【解析】(补形)()4.1,:-4,4;xy A m m m =--=-∴=代入(),1:4B n n =-代入.故有A (-1,4),B (-4,1). 作AE ⊥y 轴于E ,BD ⊥x 轴于D .可知: △AOE ≌△BOD .且11422AOE BOD S S ∆∆==⨯⨯=. 延长EA ,DB 交于C ,则四边形CDOE 是边长为4的正方形, 且2416,CDOES==△ABC 是腰长为3的等腰直角三角形,且219322ABC S ∆=⨯=.于是△OAB 的面积为915162222ABC S ∆=-⨯-= 3.【解析】(降次)由韦达定理:221212112211.3,3x x x x x x x x +=-⇒=--+=+=()()()2322212111111141534115341215x x x x x x x x x ∴-+=----+=--+++()2115344x x =-+--=-,故选A .4.【解析】由条件得: 4442222442440,a b c a c b c ++--=()()222222222222220,22,a c b c c a b a b a b c -+-=∴===+=即或且.故△ABC 是等腰直角三角形,选B . 5.【解析】当3个正方形按如图排列时,其外接圆直径最小.显然,这个圆是等腰梯形ABCD 的外接圆O ,这里AB ∥CD 且CD =40,AB =80. 设此等腰梯形的对称轴交AB 于M ,交CD 于N ,则MN =80. ∵AB >CD ,∴OM <ON .设OM =40-x ,ON =40+x ,圆半径为r .△AOM 中,()()22240401r x =+-; △DON 中,()()22220402r x =++(1)-(2):1512001600,2x x -=∴=,代入(2)290251062562517400,444r r ⨯=+==∴=故所求最小圆的直径为2r =C .6.【解析】(轨迹法)如解图,连结OB ,分别在弧BC 上取123,,,,,B D D D C 其中2OD BC ⊥,则相应的动点依次为123,,,,.B E E E N 12390BE O BE O BE O BNO ∠=∠=∠=∠=︒.故点E 的轨迹是OB 为直径的优弧BE 2N .已知BC =36,∴2218.BE BOE =∆是含30°角的直角三角形,∴OB =.设M 为OB 的中点(优弧圆心),连MN . 则圆M 的半径MB=注意到∠BOC =120°,∴∠BON =60°,∠BMN =120°, 优弧BE 2N 之长为圆M周长的222,2.33BE N l π∴=⨯⋅=,故选B .二.填空题(7×7=49分)7.【解析1】3244160x x x --+=.根据广义韦达定理,此方程3根之和为4.即123,1,4b x x x a b a ⎛⎫++=-==- ⎪⎝⎭这里 【解析2】由原方程得:()()()124220,4,2,x x x x x -+-=∴==-31232.4x x x x =++=. 8.【解析】(正繁则反)由于从这5瓶饮料中任取2瓶,没有过期饮料的概率为3,5故取2瓶,取到至少有1瓶过保质期饮料的概率为32155-=, 9.【解析】由原方程得:()()()2111a a x =--,关于x 的方程(1)只有唯一解1x =,代入(1)得0a =,此时原方程无解;又在方程(1)中令1,a =得0a =.矛盾.此时方程(1)无解,从而原方程无解.故若原方程无解,则必01a =或. 10.【解析】慢车12.5小时走完全程,()12.5100080x x km =⇒=设快车速度为t (h )∵1小时后两车相距800km ,即1小时两车共行200km ,∴t =120km (h )∵a 小时后两车相遇,此时慢车走80akm ,快车走120(a -1)km , 故有:()()80120110002001120, 5.6a a a a h +-=⇒=∴=11.【解析】原式配方得:2392448y x a a ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭,抛物线开口向上且对称轴为34x a =.当34,34a a ≥≥时,故当13x ≤≤时,y 随x 增大而减小.故当x =3时有: 22333423945, 5.a a a ⨯-⋅+=-⇒=∴=12.【解析】注意到点13521,,,,n A A A A +全在x 轴上,设其横坐标依次为1352015,,,,x x x x ..继续分析.点41A n +都在原点右边,其横坐标取正值,点41A n -都在原点左边(其中3A 为原点),其横坐标取0或负值(其中仅3A 横坐标为0).∵2015=4×504-1,故2015A 必在原点左边,其横坐标必为负值.易求()()34117421114310,021,0224,x x x x x x ⨯-⨯-⨯-====+-⨯==+-⨯=-()201545041025031006x x ⨯-==+-⨯=-,故所求点A 的坐标为:()20151006,0A -.13.【解析】依题意有:9029032360260222a ab b +==⇒=+(据等比定理)故()231a b =又:()()1449026029060100a b ++=⨯⨯()120180454442a b ab ⇒++=⨯,(1)代入(2):2260318065444603960.b b b b b ⋅++=⨯⇒+-=解得:()666b b ==-或舍,从而9,54a ab =∴=. 三.解答题14.【解析】(1)∵2310,m m ++=故()()()()551625162102255353m m m m m m m m m m m +-+--⎛⎫+-⋅-=⋅- ⎪-----⎝⎭ ()()2229223123203m m m m m m m m-++=--=-+-=-⋅=-. (2)m ,n 是方程2310x x ++=的两根,31m n mn +=-⎧∴⎨=⎩设x =,则33442m n m n x n m mn +=++=+()()()2222222221,2229249mn x m nm n m n mn ⎡⎤=∴=+-+=+-=-=⎣⎦7,x ∴=即=7.15.【解析】(1)如解图,I 为△ABC 内心,故BI 平分∠ABC . 设∠ABI =∠CBI =α.连CI ,并延长交AB 于E ,∵CA =CB ,∴CE ⊥AB ,且AE =BE =3.于是1IE=BE tan 31,3BI α⋅=⨯===连DI ,∵BD 为圆O 的直径,∴∠BID =90°.于是10tan 3DI BI BD α=⋅===. (2)连OI ,∵OI =OB =53,∴∠DOI =2α,故OI ∥AB , △COI ∽△CBE ,5533,539353OI CO CO CO BE CB CO CO =⇒=⇒=++2525515,121234CO BC ∴==+=. 16.【解析】(1)如解图1,作AG ∥BC ,交 CB 延长线于G ,则四边形AGCD 为矩形. ∴GC =AD =6,但BC =3,∴GB =3. 已知DE ⊥AB 于E ,∴△AGB ∽△DEA . 于是18.AB BG AB AE AD BG AD AE=⇒⋅=⋅= (2)延长AB ,DC 交于H .∵AD ∥BC ,且 AD =2BC ,∴BC 为△AHD 的中位线,故 CH =DC =4.由勾股定理知AH =10,AB =BH =5. 沿DE ,CB 交于T ,有△AED ∽△BTE .Rt △ADH 中,DE ⊥AH ,23618,105AD AE AH ∴=== 187555BE AB AE =-=-=.于是 775,186185BT BE BT AD AE =⇒==7716,3333BT CT ∴==+=由△AFD ∽△CFT ,知691638AF AD FC CT ===. (3)如解图3有AB BH ==AE EH==∴==∵△AEM∽△HEC,1.4ME AEEC EH∴===17.(18分)二次函数242y x mx n=-+的图象与x轴交于()()()1212,0,,A xB x o x x<两点,与y轴交于c点.(1)若AB=2,且抛物线的顶点在直线y=-x-2上,试确定m,n的值;(2)在(1)中,若点P为直线BC下方抛物线上一点,当△PBC的面积最大时,求P点坐标;(3)是否存在整数m,n,使得1212,12,x x<<<<同时成立?请证明你的结论.【解析】(1)()2212121AB=2244x x x x x x⇒-=⇒+-=.由韦达定理:121224mx xnx x⎧+=⎪⎪⎨⎪=⎪⎩,故有:()2414mn-=抛物线的顶点为24,44m n m⎛⎫-⎪⎝⎭,代入y=-x-2:()2242224444n m m m mn-=--⇒=--代入(1):20,8,4mm-=∴=从而12n=.(2)在(1)的条件下,有:241612y x x=-+此抛物线的顶点为(2,-4),交x轴于A(1,0),B(3,0),交y轴于C(0,12)易求直线BC的解析式为412y x=-+.为使△PBC面积最大,只需点P与直线BC距离最远.设过P且平行于BC的直线解析式为4y x b=-+,代入抛物线解析式;22416124412120.x x x b x x b-+=-+⇒-+-=()14416120912,3b b b ∆=--=⇒=-∴=令.此时有33,43 3.22x y ==-⨯+=-即所求点的坐标为3,32P ⎛⎫-⎪⎝⎭. (3)(反证法)假如存在这样的整数m ,n ,使得方程2420x mx n -+=之2根满足121,2x x <<.那么:()122<<4,4<8,,5,6,7;12mx x m m m +=∴<∴=为整数()121<<4,416,,5,6,7,,15;24nx x n n n =∴<<∴=为整数()224160,34m m n n ∆=->∴<方程之2根为:x ==()22148164244m m m m n n m >⇒->⇒-+>-⇒>-()2228464164165m m n m m n m <⇒-⇒-<-+⇒>-当m =5时,2m -4=6>4m -16=4,根据(3),(4),取2m -4<24m n <,即1664n <<,无整数解,舍去;当m =6时, 2m -4=8=4m -16, 根据(3),(4),取2m -4<24m n <,即89,n <<无整数解,舍去;当m =7时, 2m -4=10<4m -16=12. 根据(5),(4),取2416,4m m n -<<即112124n <<无整数解,舍去.据上分析,不存在整数m ,n ,使得1212,12,x x <<<<同时成立.。
2020年华中师范一附中(自主招生)预录考试数学模拟测试题(无答案)

2020年华中师范一附中(自主招生)预录考试数学模拟测试题一、选择题。
(5分×8=40分,每小题只有一个正确选项)1、已知531,251x x x x +++=则,的值等于( ) A 、215- B 、25 C 、21 D 、352、已知△ABC 中,AD 、BE 是两边BC 、AC 上的高,。
D 、E 为垂足,若CE+CD=AB , 则∠C 为 ( )A 、锐角B 、直角C 、钝角D 、均有可能3、如图,已知AB 和CD 分别是半圆O 的直径和弦,AD 和BC 交于E ,∠AEC=α, 则S △CDE :S △ABE 等于 ( )A 、sin 2∂B 、cos 2∂C 、tan 2∂D 、cot 2∂4、和抛物线,1182+-=ox x y 只有一个公共点(1,-1)的直线解析式为( )A 、76--=x yB 、1=xC 、176=-=x x y 或D 、1=y5、设关于x 的方程o a x a ax =+++9)2(2,有两个不等的实根21211x x ,、x x <<且那么a 的取值范围是 ( ) A 、5272<<-a B 、52>a C 、72<a D 、o a <<-726、一个退休工人每年获得一笔退休金,钱数的平方正比于他工作的年数,如果他多工作a 年,退休金将比现在多P 元;如果他多工作b 年(a ≠b ,a 、b>0),退休金会比现在多q 元,那么,他现在的退休金是( )元。
A 、)(222b a q p --B 、abq p 2)(2- C 、)(222bq ap bq ap -- D 、)(222aq bp bp aq -- 7、两平面镜OM 、ON 的夹角为30度(图示),光源S 放在两平面镜之间,S 距交点O 为20厘米,它分别在两平面镜中第一次所成的两个象之间的距离为 ( ) A.40厘米 B.20厘米 C.15厘米 D.大于15厘米而小于20厘米8、某汽车在平直的道路上做直线运动。
湖北省华师一附中2011年高中自主招生数学试题(word含答案)

师大附中2011年高一自主招生考试数学测试题本卷满分150分 考试时间120分钟题号一 二 三总 分复 核1 2 3 4 5 得分 阅卷教师一、选择题(每小题6分,共30分。
每小题均给出了代号为A 、B 、C 、D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填均得0分)1、下列图中阴影部分面积与算式2131242-⎛⎫-++ ⎪⎝⎭的结果相同的是………………【 】2、下列命题中正确的个数有……………………………………………………………【 】① 实数不是有理数就是无理数;② a <a +a ;③121的平方根是 ±11;④在实数范围内,非负数一定是正数;⑤两个无理数之和一定是无理数A. 1 个B. 2 个C. 3 个D. 4 3、某家庭三口人准备在“五一”期间参加旅行团外出旅游。
甲旅行社告知:父母买全票,女儿按半价优惠;乙旅行社告知:家庭旅行可按团体票计价,即每人均按八折收费。
若这两家旅行社每人的原标价相同,那么……………………………………………………………………【 】A 、甲比乙更优惠B 、乙比甲更优惠C 、甲与乙相同D 、与原标价有关 4、如图,∠ACB =60○,半径为2的⊙O 切BC 于点C ,若将⊙O 在CB 上向右则3121455x x ++= 。
8、小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多道。
三、解答题(本大题6小题,共72分)1、(10分)在ABC ∆中,AC AB =, 45=∠A 。
AC 的垂直平分线分别交AB 、AC 于D 、E 两点,连结CD ,如果1=AD ,求:BCD ∠tan 的值。
2、(12分)某公司为了扩大经营,决定购买6台机器用于生产活塞。
现有甲、乙两种机器供选择,其中每种机器的价格和每台机器的日生产活塞数量如下表所示。
华中师大一附中2016年高中招生考试数学试题(word版附答案)

华中师大一附中2016年高中招生考试数学试题考试时间:80分钟 卷面满分:150分说明:所有答案一律书写在答题卡上,写在试卷上作答无效.一、选择题 (本大题共6小题,每小题7分,共42分.在每小题给出的四个选项中,有且只有一项是正确的.)1.已知方程1x ax =+有一个负根,而且没有正根,则a 的取值范围是( ) A .1a >- B .1a ≥C .1a =D .1a >2.关于x 的方程21212x x ax x x x +-=+-+-的根为负数,则a 的值为( ) A .3a ≠-B .3a ≠C .1a <-且3a ≠-D .1a >-且3a ≠3.如图,抛物线21(0)y ax bx c a =++≠的顶点为(1,3)A ,且与x 轴有一个交点为(4,0)B ,直线2y mx n =+与抛物线交于A 、B 两点,下列结论: ①20a b +=;②0abc >;③方程23ax bx c ++=有两个相等的实数根; ④抛物线与x 轴的另一个交点坐标是(1,0)-,⑤当14x <<时,有21y y <.其中正确的是( ) A .①②③B .①③④C .①③⑤D .②④⑤4.已知,αβ是方程2260x ax a -++=的两实数根,那么22(1)(1)αβ+++的最小值为( ) A .414-B .2C .10D .325.设S ⋅⋅⋅+S 最接近的整数是( ) A .2015B .2016C .2017D .20186.如图,菱形ABCD 中,60A ∠=︒,6AB =,⊙A 、⊙B 的半径分别为4和2,P 、E 、F 分别是线段CD 、⊙A 和⊙B 上的动点,则PE PF +的最大值是( ) A.12 B.16 C .18D .6CBD二、填空题(本大题共6小题,每小题7分,共42分).7.如图,四边形ABCD 是菱形,E 、F 、G 、H 分别是各边的中点,随机地向菱形ABCD 内掷一粒米,则米粒落在阴影区域内的概率是 . 8.已知222x y z x y z x y z z y x +--+-++==且0xyz ≠,则()()()x y y z z x xyz+++= .9.满足1mx m n +-=的整数对(,)m n 共有 对.10.已知22(1)56p q p p q pq ++=⎧⎨+=⎩,则以p 、q 为实数根的一元二次方程为 . 11.函数3max{4,,}y t t t =-+表示对于给定的t 的值,代数式4t -+、t 、3t的值中最大的数,例如当1t =-时,max{5,1,3}5y =--=,当1t =时,max{3,1,3}3y ==,则当t = 时函数y 的值最小.12.在平面直角坐标系中,同时满足下列两个条件的点的坐标为 . (1)直线23y x =-+通过这样的点;(2)不论m 取何非零实数值,抛物线2(21)3y mx m x m =+--都不通过这样的点. 三、解答题(本大题共4小题,共66分.解答应写出文字说明、证明过程和演算步骤) 13. (本小题满分16分)对于任意实数k ,方程2222(1)2()40k x k a x k k b +-++++=总有一个根是1.(1)求实数a 、b ; (2)求另一个根的范围.14. (本小题满分16分)如图,在平面直角坐标系中,直线y =-12x +4与x 轴交于A 点,与y 轴交于B 点,以AB 为直径作⊙1O ,过B 作⊙1O 的切线交x 轴于点C . (1)求C 点的坐标;(2)设点D 为BC 延长线上一点,CD BC =,P 为线段BC 上的一个动点(异于B 、C ),过P 点作x 轴的平行线交AB 于M ,交DA 的延长线于N ,试判断PM PN +是否为定值,如果是,求出这个值,若不是,说明理由.15. (本小题满分16分)在四边形ABCD 中,AD ∥BC ,BAC D ∠=∠,点E 在边BC (点C 除外)上运动,点F 在边CD 上运动,且AEF ACD ∠=∠.(1)如图1,若AB kBC =(k 为常数),则AE 与EF 之间是否存在某种确定的数量关系?若存在,请证明,若不存在,请说明理由; (2)如图2,若5AB AC ==,2425sin BAC ∠=,BAC ∠为锐角,设EF 的长度为m ,当E 、F 点运动时,求m 的变化范围.16. (本小题满分16分)已知抛物线2:24C y x x =-+,其顶点为E ,与y 轴交于点D . (1)直线2:(0)l y kx k =>与抛物线C 交于不同两点P 、Q ,并与直线1:28l y x =-+交于点R ,分别过P 、Q 、R 作x 轴的垂线,其垂足依次为1P 、1Q 、1R ,若11111u OP OQ OR +=,求u 的值; (2)若直线31:83l y x =-+与抛物线C 在第一象限交于点B ,交y 轴于点A ,求ABD DBE∠-∠的值; (3)若13(1,)4F 、(0,8)A ,请在抛物线C 上找一点K ,使得KFA ∆的周长最小,并求出周长的最小值.EDBB华中师大一附中2016年高中招生考试数学试题参考答案及评分标准考试时间:80分钟 卷面满分:150分说明:所有答案一律书写在答题卡上,写在试卷上作答无效.一、选择题(本大题共6小题,每小题7分,共42分.在每小题给出的四个选项中,有且只有一项是正确的.)7.128.-1或8(只填对一个只得3分) 9.6 10.x 2-3x +2 =0 (填了x 2-2x +3 =0给4分)11.212.(-3,9),(1,1),(3,-3)[(正确答案个数-错误答案个数)×2。
2021年华师大一附中自主招生数学试题含详解

2021年华师大一附中自主招生数学试题含详解XXX高中数学招生考试详解本文为XXX高中数学招生考试的题目解析。
考试时间为80分钟,卷面满分为150分。
一、选取题(共6题,每题6分,共36分)1.如果实数a、b、c在数轴上的位置如图所示,那么代数式a-a+b+c-2ac+a可以化简为什么?解析:由图可知b<c<a,因此a=a'=-a,a+b=-(a+b'),c-2ac+a=c-a。
将代数式代入化简得到a^2-a+b+c^2-2ac+a^2=-a+(a+b)+(a-c)=a+b-c,因此选D。
2.反比例函数y=-4x的图像与直线y=-kx+b交于A(-1,m)和B(n,1)两点,那么△OAB的面积是多少?解析:将A(-1,m)代入y=-4x得到-m=-4,因此m=4;将B(n,1)代入y=-4x得到n=-4,因此A(-1,4)、B(-4,1)。
作AE⊥y 轴于E,BD⊥x轴于D,则△AOE≌△BOD,且S△AOE=S△BOD=1×4/2=2.延长EA、DB交于C,则四边形CDOE是边长为4的正方形,且SCDOE=4×4=16.△ABC是腰长为3的等腰直角三角形,且S△ABC=3×2/2=3.因此,△OAB的面积为S△OAB=16-2×2-3/22=323/22.3.设x1、x2是一元二次方程x^2+x-3的两根,那么x1-4x2+15等于多少?解析:由韦达定理,x1+x2=-1,因此x1=-1-x2.又因为x1x2=-3,所以x2^2+(-1-x2)x2-3=0,即x2^2-x2-3=0.解得x2=(1-√13)/2或x2=(1+√13)/2.代入x1=-1-x2得到x1=-(3+√13)/2或x1=-(3-√13)/2.因此,x1-4x2+15=-5(x2+x1^2+x1x2)-4=-4,因此选A。
4.已知a、b、c分别是△ABC三边长,且满足2a+2b+c-2ac+2bc,那么△ABC是什么?解析:将2a+2b+c-2ac+2bc分解得到2(a+b)+c(1-2a+2b),由于a、b、c为三角形的三条边长,因此a+b>c,即2(a+b)>c。
华师一附中自招考试数学试题
2016华师一附中自招考试数学试题一、选择题(2016华一高自招)1.已知方程1x ax =+有一个负根,而且没有正根,则a 的取值范围是( )A .1a >-B .1a ≥C .1a =D .1a >(2016华一高自招)2.关于x 的方程21212x x a x x x x +-=+-+-的根为负数,则a 的值为( ) A .3a ≠- B .3a ≠C .1a <-且3a ≠-D .1a >-且3a ≠(2016华一高自招)3.如图,抛物线21(0)y ax bx c a =++≠的顶点为(1,3)A ,且与x 轴有一个交点为(4,0)B ,直线2y mx n =+与抛物线交于A 、B 两点,下列结论:①20a b +=; ②0abc >; ③方程23ax bx c ++=有两个相等的实数根;④抛物线与x 轴的另一个交点坐标是(1,0)-, ⑤当14x <<时,有21y y <其中正确的是( )A .①②③B .①③④C .①③⑤D .②④⑤(2016华一高自招)4.已知,αβ是方程2260x ax a -++=的两实数根,那么22(1)(1)αβ+++的最小值为( )A .414-B .2C .10D .32(2016华一高自招)5.设S =⋅⋅⋅+S 最接近的整数是( ) A .2015 B .2016C .2017D .2018(2016华一高自招)6.如图,菱形ABCD 中,60A ∠=︒,6AB =,⊙A 、⊙B 的半径分别为4和2,P 、E 、F 分别是线段CD 、⊙A 和⊙B 上的动点,则PE PF +的最大值是( )A .12B .16C .18D .6二、填空题 (2016华一高自招)7.如图,四边形ABCD 是菱形,E 、F 、G 、H 分别是各边的中点,随机地向菱形ABCD 内掷一粒米,则米粒落在阴影区域内的概率是(2016华一高自招)8.已知222x y z x y z x y z z y x +--+-++==且0xyz ≠,则()()()x y y z z x xyz+++=(2016华一高自招)9.满足1mx m n +-=的整数对(,)m n 共有 对(2016华一高自招)10.已知22(1)56p q p p q pq ++=⎧⎨+=⎩,则以p 、q 为实数根的一元二次方程为(2016华一高自招)11.函数3max{4,,}y t t t =-+表示对于给定的t 的值,代数式4t -+、t 、3t的值中最大的数,例如当1t =-时,max{5,1,3}5y =--=,当1t =时,max{3,1,3}3y ==,则当t = 时函数y 的值最小(2016华一高自招)12.在平面直角坐标系中,同时满足下列两个条件的点的坐标为(1)直线23y x =-+通过这样的点(2)不论m 取何非零实数值,抛物线2(21)3y mx m x m =+--都不通过这样的点三、解答题(2016华一高自招)13.对于任意实数k ,方程2222(1)2()40k x k a x k k b +-++++=总有一个根是1(1)求实数a 、b(2)求另一个根的范围(2016华一高自招)14.如图,在平面直角坐标系中,直线142y x =+与x 轴交于A 点,与y 轴交于B 点,以AB 为直径作⊙1O ,过B 作⊙1O 的切线交x 轴于点C (1)求C 点的坐标(2)设点D 为BC 延长线上一点,CD BC =,P 为线段BC 上一动点(异于B 、C ),过P 点作x 轴的平行线交AB 于M ,交DA 的延长线于N ,试判断PM PN +是否为定值,如果是,求出这个值,若不是,说明理由(2016华一高自招)15.在四边形ABCD 中,AD ∥BC ,BAC D ∠=∠,点E 在边BC (点C 除外)上运动,点F 在边CD 上运动,且AEF ACD ∠=∠(1)如图1,若AB kBC =(k 为常数),则AE 与EF 之间是否存在某种确定的数量关系,若存在,请证明,若不存在,请说明理由(2)如图2,若5AB AC ==,2425sin BAC ∠=,BAC ∠为锐角,设EF 的长度为m ,当E 、F 点运动时,求m 的变化范围(2016华一高自招)16.已知抛物线2:24C y x x =-+,其顶点为E ,与y 轴交于点D(1)直线2:(0)l y kx k =>与抛物线C 交于不同两点P 、Q ,并与直线1:28l y x =-+交于点R ,分别过P 、Q 、R 作x 轴的垂线,其垂足依次都1P 、1Q 、1R ,若11111u OP OQ OR +=,求u 的值(2)若直线31:83l y x=-+与抛物线C在第一象限交于点B,交y轴于点A,求ABD DBE∠-∠的值(3)若13(1,)4F、(0,8)A,请在抛物线C上找一点K,使得KFA∆的周长最小,并求出周长的最小值。
