回归分析作业答案1
回归分析考试试题及答案

回归分析考试试题及答案一、单项选择题(每题2分,共20分)1. 回归分析中,自变量和因变量之间的关系是()。
A. 确定性关系B. 函数关系C. 相关关系D. 因果关系答案:C2. 简单线性回归模型中,回归系数的估计值是通过()方法得到的。
A. 最小二乘法B. 最大似然法C. 贝叶斯方法D. 决策树方法答案:A3. 在多元线性回归分析中,如果自变量之间存在完全相关关系,则会导致()。
A. 多重共线性B. 异方差性C. 自相关D. 非线性答案:A4. 回归分析中,残差平方和(SSE)是用来衡量()的。
A. 模型的拟合优度B. 模型的预测能力C. 模型的解释能力D. 模型的预测误差答案:D5. 回归方程的显著性检验中,F检验的零假设是()。
A. 所有回归系数都等于0B. 所有回归系数都不等于0C. 至少有一个回归系数等于0D. 至少有一个回归系数不等于0答案:A6. 回归分析中,调整后的R平方(Adjusted R-squared)用于()。
A. 调整模型的复杂性B. 调整样本量的大小C. 调整自变量的数量D. 调整因变量的范围答案:C7. 在回归分析中,如果自变量的增加导致因变量的增加,则称自变量和因变量之间存在()。
A. 正相关B. 负相关C. 无相关D. 完全相关答案:A8. 回归分析中,残差的标准差(S)是用来衡量()的。
A. 模型的拟合优度B. 模型的预测能力C. 模型的解释能力D. 模型的预测误差答案:D9. 在多元线性回归中,如果一个自变量的t统计量显著,那么我们可以得出结论()。
A. 该自变量对因变量有显著影响B. 该自变量对因变量没有显著影响C. 该自变量对因变量的影响不明确D. 该自变量对因变量的影响是正的答案:A10. 回归分析中,Durbin-Watson统计量用于检测()。
A. 多重共线性B. 异方差性C. 自相关D. 非线性答案:C二、多项选择题(每题3分,共15分)11. 以下哪些因素可能导致回归模型中的异方差性?()A. 模型中遗漏了重要的解释变量B. 模型中包含了不应该包含的变量C. 模型中的误差项不是独立同分布的D. 模型中的误差项具有非恒定的方差答案:CD12. 在回归分析中,以下哪些方法可以用来处理多重共线性问题?()A. 增加样本量B. 移除相关性高的自变量C. 使用岭回归D. 增加更多的自变量答案:BC13. 以下哪些是回归分析中常用的诊断图?()A. 残差图B. 正态Q-Q图C. 散点图D. 杠杆值图答案:ABD14. 在回归分析中,以下哪些因素可能导致模型的预测能力下降?()A. 模型过拟合B. 模型欠拟合C. 模型中的误差项具有自相关性D. 模型中的误差项具有异方差性答案:ABCD15. 以下哪些是回归分析中常用的模型选择标准?()A. AIC(赤池信息准则)B. BIC(贝叶斯信息准则)C. R平方D. 调整后的R平方答案:ABCD三、简答题(每题10分,共30分)16. 简述简单线性回归模型的基本形式。
《应用回归分析》部分课后习题答案-何晓群版

《应用回归分析》部分课后习题答案第一章回归分析概述1.1 变量间统计关系和函数关系的区别是什么?答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么?在回归变量设置时应注意哪些问题?答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
回归分析练习题及参考答案
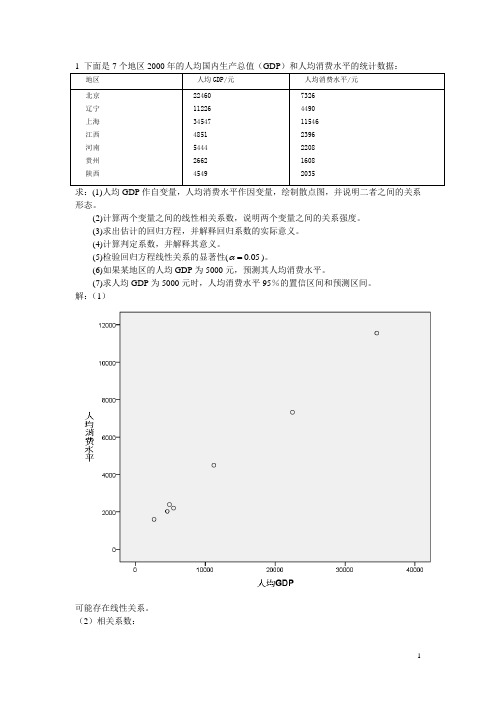
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
回归分析考试试题及答案

回归分析考试试题及答案一、单项选择题(每题3分,共30分)1. 回归分析中,因变量Y对自变量X的依赖关系可以用以下哪种模型表示?A. 线性模型B. 指数模型C. 对数模型D. 所有以上模型答案:D2. 在简单线性回归分析中,回归系数β1表示什么?A. 自变量X每变化一个单位,因变量Y平均变化β1个单位B. 自变量X每变化一个单位,因变量Y变化β1%个单位C. 自变量X每变化一个单位,因变量Y变化β1倍D. 自变量X每变化一个单位,因变量Y变化β1的平方答案:A3. 回归分析中,残差平方和(SSE)是用来衡量什么的?A. 模型的拟合优度B. 模型的预测能力C. 模型的解释能力D. 模型的预测误差答案:D4. 多元线性回归中,如果自变量之间存在完全相关关系,会导致什么问题?A. 模型无法估计B. 模型估计不准确C. 模型估计不稳定D. 模型估计无意义答案:A5. 回归分析中,R平方(R²)值越接近1,说明什么?A. 模型的解释能力越强B. 模型的预测能力越强C. 模型的拟合优度越差D. 模型的预测误差越大答案:A6. 在回归分析中,如果自变量的值增加,而因变量的值减少,那么回归系数β1应该是:A. 正数B. 负数C. 零D. 不确定答案:B7. 多元线性回归中,如果增加一个自变量,R平方值增加,但调整后的R平方值减少,这说明什么?A. 新增的自变量对模型没有贡献B. 新增的自变量对模型有贡献C. 新增的自变量增加了模型的复杂度D. 新增的自变量减少了模型的复杂度答案:A8. 回归分析中,F检验是用来检验什么的?A. 模型的整体显著性B. 单个自变量的显著性C. 模型的预测能力D. 模型的解释能力答案:A9. 回归分析中,如果残差图显示残差随自变量的增加而系统性增加,这可能表明什么?A. 模型是合适的B. 存在异方差性C. 模型中遗漏了重要的自变量D. 自变量与因变量之间存在非线性关系答案:D10. 在回归分析中,如果一个自变量的t检验的p值大于0.05,这通常意味着什么?A. 自变量对因变量有显著影响B. 自变量对因变量没有显著影响C. 自变量对因变量的影响不确定D. 自变量对因变量有非常显著的影响答案:B二、多项选择题(每题4分,共20分)11. 以下哪些因素可能导致回归模型的异方差性?A. 模型中遗漏了重要的自变量B. 模型中存在非线性关系C. 模型中存在异常值D. 自变量之间存在完全相关关系答案:ABC12. 在多元线性回归中,以下哪些方法可以用来提高模型的预测能力?A. 增加更多的自变量B. 使用交叉验证来选择模型C. 应用变量选择技术,如向前选择或向后剔除D. 对自变量进行变换,如对数变换或平方答案:BCD13. 以下哪些是回归分析中常用的诊断图?A. 残差图B. 正态概率图C. 残差与预测值图D. 散点图答案:ABC14. 以下哪些是回归分析中可能遇到的问题?A. 多重共线性B. 异方差性C. 自变量之间的完全相关D. 模型过拟合答案:ABCD15. 在回归分析中,以下哪些是模型拟合优度的度量指标?A. R平方B. 调整后的R平方C. F统计量D. AIC(赤池信息准则)答案:ABCD三、简答题(每题10分,共40分)16. 简述简单线性回归模型的基本形式,并解释回归系数β0和β1的意义。
《应用回归分析》课后题答案解析

.
《应用回归分析》部分课后习题答案
第一章 回归分析概述
1.1 变量间统计关系和函数关系的区别是什么? 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量 唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另 外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么? 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。区别有 a. 在回归分析中,变量 y 称为因变量,处在被解释的特殊地位。在相关分析中,变 量 x 和变量 y 处于平等的地位,即研究变量 y 与变量 x 的密切程度与研究变量 x 与变量 y 的密切程度是一回事。b.相关分析中所涉及的变量 y 与变量 x 全是随机 变量。而在回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量也可以 是非随机的确定变量。C.相关分析的研究主要是为了刻画两类变量间线性相关的 密切程度。而回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归 方程进行预测和控制。
1 3
即为:(2.49,11.5)
33,7+2.353 1 3
33)
0
N
(0
,
(
1 n
(x)2 Lxx
)
2
)
t
0 0
0 0
(
1
(
x)2
)
2
1 (x)2
n Lxx
n Lxx
服从自由度为 n-2 的 t 分布。因而
P |
0 0
1 (x)2
| t /2 (n 2) 1
n Lxx页脚源自 ..1330 6.1
3
(5)由于 1
N
(1,
《应用回归分析》课后习题答案

答:选择模型的数学形式的主要依据是经济行为理论,根据变量的样本数据作出解释变量与被解释变量之间关系的散点图,并将由散点图显示的变量间的函数关系作为理论模型的数学形式。对同一问题我们可以采用不同的形式进行计算机模拟,对不同的模拟结果,选择较好的一个作为理论模型。
df
均方
F
显著性
组间
(组合)
1231497.500
7
175928.214
5.302
.168
线性项
加权的
1168713.036
1
1168713.036
35.222
.027
偏差
62784.464
6
10464.077
.315
.885
组内
66362.500
2
33181.250
总数
1297860.000
9
由于 ,拒绝 ,说明回归方程显著,x与y有显著的线性关系。
.212
.586
1.708
a.因变量: y
(6)可以看到P值最大的是x3为0.284,所以x3的回归系数没有通过显著检验,应去除。
去除x3后作F检验,得:
Anovab
模型
平方和
df
均方
F
Sig.
1
回归
12893.199
2
6446.600
11.117
.007a
残差
4059.3.500
.724
.433
.212
.586
1.708
a.因变量: y
(2)
所以三元线性回归方程为
模型汇总
模型
R
回归分析练习试题和参考答案解析
1 下面是7个地区2000年的人均国生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元22460 11226 34547 4851 5444 2662 4549 7326 4490 11546 2396 2208 1608 2035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规排版。
应用回归分析课后习题参考答案 全部版 何晓群,刘文卿
第一章回归分析概述1.2 回归分析与相关分析的联系与区别是什么?答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有 a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3回归模型中随机误差项ε的意义是什么?答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么?答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2…. Cov(εi,εj)={σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.第二章一元线性回归分析思考与练习参考答案2.1一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=σ2i=1,2, …,nCov(εi,εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(X i, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, σ2) i=1,2, …,n2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
《应用回归分析》课后题答案解析
(8) t
1
2
/ Lxx
1
Lxx
2
其中
1 n2
n i1
ei 2
1 n2
n i1
( yi
2
yi )
0.0036 1297860 8.542 0.04801
t /2 1.895
t 8.542 t /2
接受原假设 H 0: 1 0, 认为 1 显著不为 0,因变量 y 对自变量 x 的一元线性回归成立。
( yi
2
yi )
1 n-2
n i=1
( yi
( 0 1
2
x))
=
1 3
( 10-(-1+71))2 (10-(-1+7 (20-(-1+7 4))2 (40-(-1+7
2))2 (20-(-1+7 5))2
3))2
1 16 9 0 49 36
3
110 / 3
1
330 6.1
《应用回归分析》部分课后习题答案
第一章 回归分析概述
变量间统计关系和函数关系的区别是什么 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量 唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另 外一个变量的确定关系。
回归分析与相关分析的联系与区别是什么 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。区别有 a. 在回归分析中,变量 y 称为因变量,处在被解释的特殊地位。在相关分析中,变 量 x 和变量 y 处于平等的地位,即研究变量 y 与变量 x 的密切程度与研究变量 x 与变量 y 的密切程度是一回事。b.相关分析中所涉及的变量 y 与变量 x 全是随机 变量。而在回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量也可以 是非随机的确定变量。C.相关分析的研究主要是为了刻画两类变量间线性相关的 密切程度。而回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归 方程进行预测和控制。
回归分析期末试题及答案
回归分析期末试题及答案一、简答题1. 请解释回归分析的基本思想。
回归分析是一种统计学方法,用于研究变量之间的关系。
其基本思想是通过建立一个数学模型来描述一个或多个自变量对因变量的影响,并根据观察数据对模型进行拟合和推断。
2. 请解释简单线性回归和多元线性回归的区别。
简单线性回归是建立在一个自变量和一个因变量之间的基础上的回归模型。
多元线性回归则是在两个或更多个自变量和一个因变量之间建立的回归模型。
3. 请解释残差的含义。
残差是指建立回归模型后,观测值与模型预测值之间的差异。
残差可以用来评估模型的拟合程度,如果残差较大,则说明模型无法很好地解释观察数据的变化。
4. 请解释R平方的含义及其优缺点。
R平方是一个用来衡量回归模型拟合程度的指标,其值介于0和1之间。
R平方越接近1,说明模型对观察数据的拟合越好;而R平方越接近0,则说明模型对观察数据的拟合越差。
R平方的优点是简单直观,易于理解,但其缺点是不适用于比较不同自变量的模型。
5. 请简要说明什么是多重共线性问题。
多重共线性问题指的是在多元线性回归中,自变量之间存在高度相关性的情况。
多重共线性会导致回归系数的估计不准确,难以解释自变量与因变量之间的关系。
二、计算题1. 已知一个简单线性回归模型为:Y = 2 + 3X,回归系数的解释是什么?回归系数3表示自变量X每增加1个单位,因变量Y会增加3个单位。
而常数项2表示当自变量X为0时,因变量Y的取值为2。
2. 使用最小二乘法求解简单线性回归模型的参数估计值。
最小二乘法是一种常用的回归分析方法,用于估计回归模型中的参数值。
以简单线性回归模型Y = β0 + β1X 为例,最小二乘法通过最小化观测值Y与模型预测值之间的平方差来估计β0和β1。
3. 请计算多元线性回归模型的回归系数。
多元线性回归模型可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn。
回归系数β1、β2、...、βn可以使用最小二乘法来估计,通过最小化观测值Y与模型预测值之间的平方差来得出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 、教材 p87 习题 3.11
研究货运总量 y(万吨)与工业总产值 x1(亿元)、农业总产值 x2 (亿元)、
居民非商品支出 x3(亿元)的关系。数据见表
3.9
表 3.9
编号
货运总量 y(万吨 ) 工业总产值 x1(亿元) 农业总产值
x2( 亿元 ) 居民非商品支 出x3(亿元 )
1 160 70 35 1.0
2 260 75 40 2.4
3 210 65 40 2.0
4 265 74 42 3.0
5 240 72 38 1.2
6 220 68 45 1.5
7 275 78 42 4.0
8 160 66 36 2.0
9 275 70 44 3.2
10 250 65 42 3.0
本题全部代码如下:
1)计算出 y,x1, x2,x3
的相关系数矩阵。
1.000 0.556 0.731 0.724
0.556 1.000 0.113 0.398
0.724 0.398 0.547 1.000
2)求出 y 与 x1 ,x2, x3
的三元线性回归方程。
y? 348.38 3.754x1 7.101x2 12.447x
3
3
)对所求的方程作拟合优度检验。
由上表可知,调整后的决定系数为 0.7083 ,说明回归方程对样本观测值的
拟合程度较好。
4)
对回归方程作显著性检验。
从( 2)题表格中最后一行 p-value=0.01487<0.05 ,说明在置信水平为
95%
下,回归方程显著。
r
则相关系数矩阵为:
0.731 0.113 1.000 0.547
从 coefficients 中可以看出回归方程为:
5
)对每一个回归系数作显著性检验。
原假设为 H0: i 0 ,给定显著性水平 0.05,从上表中可以看到,X1的t值
=1.942, p值>0.05, 处在接受域;X2的t值=2.465,p值<0.05
,拒绝
原假设;X3的t 值=1.178, p值>0.05, 处在接受域。所以,在显著性水平
0.05
时,只有 x2 的回归系数较
为显著, x1,x2的系数均不显著。
6
)如果有的回归系数没有通过显著性检验,将其剔除,重新建立回归方
程,
并作回归方程的显著性检验和回归系数的显著性检验。
用后退法对数据重新做回归分析,代码如上图,结果如下: 重新建立的回归
方程为: y? 459.624 4.676 x1 8.971x2 对新的回归方程做显著性检验:
从表格中最后一行 p-value=0.006718<0.05 ,说明在置信水平为
95%
下, x1, x2 整体上对 y有显著的线性影响,即回归方程是显著的。 对每
一个回归系数做显著性检验:
给定显著性水平 0.05 ,从上表中可以看到, X1的t 值=2.575,p值
<
0.05, 拒 绝原假设; X2的 t 值= 3.643 ,p 值<0.05
,拒绝原假设。所
以,在显著性水平 0.05时, 1和β2都通过检验,可认为对 x1,x2 分别对
y
都有显著的影响。
7)求出每一个回归系数的置信水平为 95%
置信区间
由回归系数表可以看到, β1 置信水平为 95%的置信区间
[0.381,8.970] , β2 置信水平为 95%
的置信区间
[3.134,14.808]
。
8
)求标准化回归方程。
由回归系数表(上表)可得,标准化后的回归方程为:
y?* 0.479x1* 0.676x2*
( 9)求当 x01=75 ,x02=42 ,x03=3.1 时的 y0 的预测值,并请给出置
信水平 为 95% 的预测区间。
由输出结果可知,当 x01 75, x02 42,x03 3.1 时, y?0 267.829 y0 的置信度为
95%的精确预测区间为( 204.4,331.2
)
y0
的置信度为 95%的近似预测区间为 (y?0 2 ?),
手工计算得:( 267.829-2*24.08 ,267.829+2*24.08 )即
( 219.6,316.0 )。 (10)结合回归方程对问题做一些基本分析。
由回归方程 y? 459.624 4.676 x1 8.971x2 可知农业总产值固定的时
候, 工业总产值每增加 1 亿元,货运总量平均增加 4.676 万吨;工业总
产值固定的时候,农业总产值每增加 1 亿元,货运总量平均增加 8.971 万
吨。而居民非商品支出对货运总量没有显著的线性影响。
由标准化回归方程 y? 0.479x1 0.676x2 可知: 工业总产值、农业总产值与 Y都是正相
关关系, 比较回归系数的大小可知农业总 产值 X2对货运总量 Y 的影响程
度大一些。
2
、思考:理论上,残差之间并不独立,为何可用来检验独立性?请计算、检
验 第 1 题中残差的相关性 / 独立性。
答:残差确实是相关的,并不独立。但是我们这里谈残差分析,残差分析是
通过 残差所提供的信息,分析模型是否正确,残差蕴含着的是有关模型的重
要信息, 若模型正确, 则可将残差看作误差的观测值, 符合模型的假设条
件, 具有误差的 一些性质, 即可用残差来检验模型误差是否相互独立。
但是残差图具有很强的主 观性,所以实际中最好将其和其他检验方法结合起
来使用
方法一:残差序列图
方法二:计算自相关系数
自相关系数用于测定序列自相关强弱,其取值范围为 -1 到 1 ,接近 1 表明序列 存在
正自相关性。
从图中可以看出一阶自相关系数为 -0.057 ,可以认为序列不存在自相关性。
方法三: DW 检验。
DW 值用来检验回归分析中的残差项是否存在自相关现象, DW 值的取值介于 0
和 4 之间:残差一阶正相关时, DW≈ 0 ;残差一阶负相关时, DW≈ 4 ;残差
从图上可以看出,残差在 0 附件随机变化,认为残差独立。
独
立时, DW≈ 2 。用r 语言实现,结果如下:
DW=1.9353 ,p 值 >0.05 ,认为残差独立
