电磁场理论课件 静电场二.ppt
合集下载
第11章 静电场精品PPT课件

第11章 静电场
(electrostatic field)
§11.1 电荷
1.电荷的定义及种类: 电荷有正、负两种。
+-
注意:(1)电荷不是物质而是物体的属性。
(2)电量(Q, q):表示物体所带电荷多少的物理量。 2. 电荷守恒定律 在一个孤立系统内发生的任何的变化过程中,电荷总 数(电荷的代数和)保持不变。
3. 电荷的量子性: qne
e1.6012 0 1C 9 -----基本电荷量
§11.2
一、库仑定律
库仑定 律与+叠q 加原r理+q
1.点电荷模型
F2 1
P
F1 2
当带电体的形状、大小与它们之间的距离相比可以忽略时,
可以把带电体看作点电荷。
2.库仑定律 ----静电力所服从的规律 真空中两个静止点电荷之间相互作用力的大小与这两个点
电荷所施静电力的矢量和--------电场力的叠加原理。
q2
-
FF01F02
+
Fo2
q1
+
F
F Fi
qo
Fo1
i
连续带电体对点电荷的作用
FdF
dq
+
q dF
F x dF x F y dF y
§11.3 电场和电场强度
一、电场 —— 电荷周围存在着的特殊物质
产生
电场
EA
作用
电荷A
电荷B
作用
P
n
E Ei
i
3.连续带电体的场强
dE
1
4 0
dr2qer
Y
E
q
dE
q
1
4 0
电磁场与电磁波静电场PPT精选文档

q(
4
r
0
r' ) r r' 3
图1.1.2 点电荷的电场
q
4 0R2
eR
V/m
Slide 7
b) n个点电荷产生的电场强度 (注意:矢量叠加)
Slide 8
E (r) 4 1 0k N 1r q r k k '2r r r r k k '' 4 1 0k N 1R q k k 2 e k
图1.2.4 点电荷与接地导体的电场
图1.2.5 点电荷与不接地导体的电场
2) 已知电荷分布,求电位:
以点电荷为例推导电位:
E(r)4q0
rr' rr' 3
1
rr'
rr'
rr' 3
点电荷群
(r)410 iN 1
qi rri'
C
连续分布电荷
E (r) 40q rr' (r)
(r)410 v'
dqC rr'
(r)40qrr' C
d:qd,Vd,Sdl
Slide 20
3) E与的微分关系
E
在静电场中,任意一点的电场强度E的方向总是沿着电位减少的最快 方向,其大小等于电位的最大变化率。
在直角坐标系中:
E[ xex yey zez]
根据 E 与的微分关系,试问静电场中的某一点
• 0 E0 ?
(
)
• E0 0 ?
(
)
Slide 21
4) E与 的积分关系
Edl dl
Slide 14
Slide 15
u uv eR
Slide 15
电磁场与电磁波之静电场分析课件

静电场可以用于药物传 递和基因治疗,提高药 物靶向性和治疗效果。
静电场可以用于肿瘤热 疗和免疫治疗等领域, 为肿瘤治疗提供新的手 段。
静电场的安全防护
1.A 为了避免静电场对生物体的负面影响,需要采 取有效的安全防护措施。
1.B 安全防护措施包括控制电场强度、减少作
用时间和优化作用方式等。
1.C 在生物医学应用中,需要严格控制电场参数 ,确保安全性和有效性。
静电场的解法通常包括解析法和数值 法。
数值法适用于复杂形状和电荷分布的 情况,通过离散化电荷分布和电场, 使用数值计算方法求解微分方程和边 界条件,得到近似解。
解析法适用于简单的物理特性
电场线与电通量密度
电场线
表示电场分布的假想曲线,线上每一点的切线方向与该点的 电场方向一致。电场线的疏密程度表示电场强度的大小。
电磁场与电磁波之静 电场分析课件
目录
• 静电场的基本概念 • 静电场的数学描述 • 静电场的物理特性 • 静电场的工程应用 • 静电场的测量技术 • 静电场的生物效应
01 静电场的基本概念
电场与电场强度
电场
带电体周围存在的一种特殊物质 ,由正负电荷产生,其基本特性 是对其中运动的电荷施加力。
电场强度
02
高斯定理
在静电场中,穿过任意闭合曲面的电场强度通量等于该 曲面内包围的电荷量。
03
静电场的边界条件
在两种不同介质分界面上,电场强度和电位满足一定的 连续性条件。
02 静电场的数学描述
静电场的微分方程
静电场的基本微分方程是高斯定 理和泊松方程。
高斯定理描述了电场线在封闭曲 面内的电荷量总和,而泊松方程 则描述了电荷分布如何产生电场
静电除尘与静电喷涂
电磁场理论课件 2-1静电场的标势及其微分方程

P r
(P)
Q
4 0
(1 r
1 r
)
r2 R 2 l 2 2Rl cos
Q
2l
x -Q
求近似值:
r R
1
l2 R2
2l
cos
/
R
R
1 2l cos / R
R(1 1 2l cos ) R l cos
2R
R r
y
(l R)
同理
r R l cos
1 1 r r 2l cos 2l cos
R02 R2
20
ln
R R0
若选P0为参考点,则
(P)
ln R
ER
R
20
,
2 0 R
R0 E EZ 0
解2:
z
电荷源
dq dz z' o
r
场点
p
R
选取柱坐标:源点的坐标为(0, z'),场点的坐标为
(R, 0),考虑到导线是无限长,电场强度显然与z
无关。
这里,先求场强 E
,后求电势
E 0
D
E
这两方程连同介质的 电磁性质方程是解决 静电问题的基础。
静电场的无旋性是它的一个重要特 性,由于无旋性,我们可以引入一 个标势来描述静电场。
无旋性的积分形式是电场 沿任一闭合回路的环量等 于零,即
E dl 0
设C1和C2为P1和P2点的两 条不同路径。C1与C2合成 闭合回路,因此
量与存在着电荷分布的空间有关。真实的静电能量是以
密度 w 1 E D的形式在空间连续分布,场强大的地方 2
能量也大;
(4)W 1 dV中的 是由电荷分布 激发的电势; 2
(P)
Q
4 0
(1 r
1 r
)
r2 R 2 l 2 2Rl cos
Q
2l
x -Q
求近似值:
r R
1
l2 R2
2l
cos
/
R
R
1 2l cos / R
R(1 1 2l cos ) R l cos
2R
R r
y
(l R)
同理
r R l cos
1 1 r r 2l cos 2l cos
R02 R2
20
ln
R R0
若选P0为参考点,则
(P)
ln R
ER
R
20
,
2 0 R
R0 E EZ 0
解2:
z
电荷源
dq dz z' o
r
场点
p
R
选取柱坐标:源点的坐标为(0, z'),场点的坐标为
(R, 0),考虑到导线是无限长,电场强度显然与z
无关。
这里,先求场强 E
,后求电势
E 0
D
E
这两方程连同介质的 电磁性质方程是解决 静电问题的基础。
静电场的无旋性是它的一个重要特 性,由于无旋性,我们可以引入一 个标势来描述静电场。
无旋性的积分形式是电场 沿任一闭合回路的环量等 于零,即
E dl 0
设C1和C2为P1和P2点的两 条不同路径。C1与C2合成 闭合回路,因此
量与存在着电荷分布的空间有关。真实的静电能量是以
密度 w 1 E D的形式在空间连续分布,场强大的地方 2
能量也大;
(4)W 1 dV中的 是由电荷分布 激发的电势; 2
电磁场理论-2011-2[1]
![电磁场理论-2011-2[1]](https://img.taocdn.com/s3/m/9b8462c7bb4cf7ec4afed0be.png)
q ne , (n , ,) 1 2
静电场—静电场的基本规律
上式中,基元电荷电量在数值上等于一个电子所带 的电量。即
密立根油滴实验说明:物体所带电量是不连续的, 即自然界中的电荷是量子化的。 现代科学实验证明,任何物体都由大量的原子构 成,而原子则由带正电的原子核和带负电的电子组 成。 通常,同一个原子中正负电量数值相等,因而整 个物体呈现电中性。当它们因为某种原因,例如摩 擦、受热、化学变化等失去一部分电子时,则表现 为正电性;当获得额外电子时,则呈现负电性。
静电场的保守力性质也可以用另一个等价形式表 示,即
上式表明:在静电场中,电场强度沿任意闭合环 路的线积分恒等于零。 通常,将某一个量沿任意闭合环路的线积分称为 该物理量的环流。于是上式又可以表述为:在静电 场中,电场强度的环流为零。这一结论称为静电场 的环路定理,它是静电场的基本规律之一。
静电场—静电场的基本规律
静电场—静电场的基本规律
例题5 半径为a 的球中充满密度为ρ(r)的体分布电 荷,已知
求:电荷密度为ρ(r)。 解:由高斯定理,在球内有
静电场—静电场的基本规律
解得
(r ) 5 0 r 4 0 Ar
2
又考虑在球外,有
0
0
r
2
a r
5
Ar 4 0 Ar
4
即求得电荷密度
(r ) 5 0 r
2
静电场—电势及静电势能
电势
§2.2 电势及静电势能
电势差
静电场环路定理说明:电场力移动电荷所作的功 只与电荷的始末位置有关,而与具体的路径无关。 因此可以用一个位置函数φ(x,y,z)描述电场力电荷 所作的功,即
电磁场静电场ppt
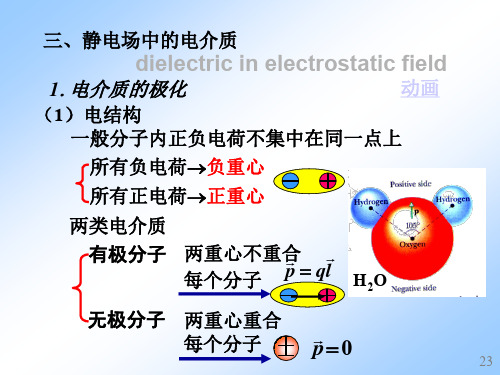
P
1º P
的定义
P
pi
V
单位体积内所有分子 的电偶极矩矢量和
单位 C/m2
显然
E外=0
2ºP与E成正比
pi 0
P0
实验结论: 对各项同性的电介质有
P e0E E E外 E
e r 1
e —电极化率
真空 r 1
r 相对介电常数
空气 其他
r 1 r 1
27
(4)电极穿——电介质t]
t
r
d
C
q
V r 0 S rd (r
讨论
1与)t 介 质d 板0的rSr 位1 t置无关d0S
电容C 介质板的厚度t、C
t =d 时 C r0S
d
41
例6. 半径都是a 的两根平行长直导线相距为d
求 单位长度的电容。 (其中d >>a)
C
Q
V
d
解:设导线单位长度带电+, –
S内
3º求出两导体间电势差V (定义法)
VAB
B
A
E
dl
4º根据 C = Q/V 求出电容
43
5.电容器的串、并联
一个电容器的电容量或耐压能力不够时
可采用多个电容连接:
C1
如增大电容, 可将多个电容 并联
C2
C C1 C2 Ck
…
Ck
若增强耐压, 可将多个电容 串联
C
U1 U2 … Uk U
E0
位移极化 有极分子电介质的极化
E0
F
束缚电荷
可见:E外强, p 排列越整齐
取向极化 端面上束缚电荷越多,电极化程度越高。
24
电磁场与电磁波 第2章静电场
如果电场由点电荷q单独产生
如果是一个闭合路径,则W=0 电场强度的环路线积分恒为零,即
应用斯托克斯定理
因此,静电场的电场强度 可以用一个标量函数 的梯度来表示,即定义
单位正实验电荷在电场中移动电场力做功
两点间的电位差定义为两点间的电压U,即
单位:V
电位函数不唯一确定,取
故可选空间某点Q作为电位参考点,空间任一点P的电位为 通常选取无限远作为电位参考点,则任一P点的电位为
在交界面上不存在 时,E、D满足折射定律。
D 1 n D 2 n 1 E 1 c1 o 2 E s 2 c2 os
E 1 t E 2 t E 1 si1 n E 2 si2n
图2.3.3 分界面上E线的折射
t电位函数 表示分界面上的衔接条件
Ax Ay Az
对应静电场的基本方程 E 0 ,矢量 A 可以表示一个静电场。
能否根据矢量场的散度来判断该矢量场是否是静电场?
2.3.2 分界面上的边界条件
1、 电位移矢量D的衔接条件 以分界面上点P作为观察点,作一
小扁圆柱高斯面( L 0)。
图2.3.1 在电介质分界面上应用高斯定律
根据 DdSq
V ' P d ' V S 'P e n d ' S 0
• 在均匀极化的电介质内,极化电荷体密度 p 0。
• 有电介质存在的场域中,任一点的电位及电场强度表示为
(r) 4 1 0 V '( r f r 'p )d' V S '( r f r 'p )d' S E (r ) 4 1 0 V '( f r p r )'3 r( r ')d' V S '( f r p r ) '3 r( r ')d' S
如果是一个闭合路径,则W=0 电场强度的环路线积分恒为零,即
应用斯托克斯定理
因此,静电场的电场强度 可以用一个标量函数 的梯度来表示,即定义
单位正实验电荷在电场中移动电场力做功
两点间的电位差定义为两点间的电压U,即
单位:V
电位函数不唯一确定,取
故可选空间某点Q作为电位参考点,空间任一点P的电位为 通常选取无限远作为电位参考点,则任一P点的电位为
在交界面上不存在 时,E、D满足折射定律。
D 1 n D 2 n 1 E 1 c1 o 2 E s 2 c2 os
E 1 t E 2 t E 1 si1 n E 2 si2n
图2.3.3 分界面上E线的折射
t电位函数 表示分界面上的衔接条件
Ax Ay Az
对应静电场的基本方程 E 0 ,矢量 A 可以表示一个静电场。
能否根据矢量场的散度来判断该矢量场是否是静电场?
2.3.2 分界面上的边界条件
1、 电位移矢量D的衔接条件 以分界面上点P作为观察点,作一
小扁圆柱高斯面( L 0)。
图2.3.1 在电介质分界面上应用高斯定律
根据 DdSq
V ' P d ' V S 'P e n d ' S 0
• 在均匀极化的电介质内,极化电荷体密度 p 0。
• 有电介质存在的场域中,任一点的电位及电场强度表示为
(r) 4 1 0 V '( r f r 'p )d' V S '( r f r 'p )d' S E (r ) 4 1 0 V '( f r p r )'3 r( r ')d' V S '( f r p r ) '3 r( r ')d' S
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9
三、唯一性定理的意义
1. 唯一性定理给出了确定静电场的条件,为求电 场强度指明了方向。
2. 更重要的是它具有十分重要的实用价值。无论 采用什么方法得到解,只要该解满足泊松方程、 边值关系和给定边界条件,则该解就是唯一的 正确解。因此对于许多具有对称性的问题,可 以不必用繁杂的数学去求解泊松方程,而是通 过提出尝试解,然后验证是否满足方程、边值 关系和边界条件。满足即为唯一解,若不满足, 可以加以修改。
平行双电轴电场是一个平行平面场,在垂直于电 轴的各个平面上,场有完全相同的分布图形。
静电场唯一性定理的简明表述:
若区域V内给定电介质分布和自由电荷分布ρ(x) ,
在V的边界S上给定
(i)电位 S
或
(ii)电位的法向导数
n S
若区域内有导体存在,还要给定各导体的电位或各
导体所带的自由电量,则V内的电场唯一地确定。
(如果V的边界面上和内部的导体上没有一处给定 电位,那么V内 的电场强度唯一确定,但电位ϕ不 能完全确定,可以相差一个常量。)
的内表面为S2,对于壳内区域而言它是一 个边界面。首先,S2是一个等位面。其次, 若在壳内紧贴S2作一高斯面S,则有
S
dS
n
q1
即电位移矢量 D的通量为q1。因此以S2作为导体壳内
电场的一个边界面,通过它的电通量仅仅决定于导体
壳内的电荷,而与壳外的电荷分布是无关的。根据唯
一性定理,当导体壳内带电导体都是给定电荷量时,
电位函数可以相差一个常数,但是电场强度是唯一确
定的。它不受导体壳外电荷q2的影响。如果导体壳接 地,这时甚至壳内的电位函数也是唯一确定的。总之,
在第二种情况下,导体壳内的电场不受壳外电荷的影
响。
14
§2-2 平 行 双 电 轴 法
平行双电轴电场法
如图2-7所示,两平行输电线表面电荷分布是不 均匀的。为了计算它们在周围空间激发的电场,人 们找到了平行双电轴法。
7
也就是说,存在唯一的解,它在导体以外满足泊松
方程
2
在两均匀区域分界面上满足i 边值关系,
i
,
j
i
n
i
j
n
j
在第i个导体上满足总自由电荷条件:
Si
dS
n
Qi
和等势面条件:
Si i 常量
以及在V的边界S上具有给定的ϕ |s 或(∂ ϕ /∂n)|s值。 8
值。
5
二、有导体存在时的唯一性定理
当有导体存在时,由实践经
验我们知道,为了确定电场,所
需要条件有两种类型:一类是给
定每个导体上的电位i ;另一类
是给定每个导体上的总自由电量
Qi。 如图,设在某区域V内有一些导体,扣除导体外
表面内所围区域以后剩下的区域为V ’。设V ’内给定
电介质分布、给定自由电荷分布ρ,S上给定了
第二章 静 电 场(二)
§2-1 静电场的唯一性定理及其应用 §2-2 §2-3 §2-4 §2-5 无限大介质交界平面的镜象 §2-6 §2-7 §2-8 §2-9 带电导体系统的电场能量及其分布 §2-10 虚位移法计算电场力
2
§2-1 静电场的唯一性定理及其应用
处理静电问题总是根据一定条件去解泊松方程。 静电学中许多问题都涉及到有限空间区域,在 区域内可以有电荷,也可以没有电荷,但都具 有确定的边界条件。现在有这样一个问题:要 使区域内存在唯一的、合理的解,问适合泊松 方程的边界条件是什么?唯一性定理回答了这 个问题。
或
S
n S
6
当每个导体上的电位ϕi 给定时(即给出了V’所有边 界上的ϕ或∂ϕ/∂n值),因而由唯一性定理可知, V’ 内的电场唯一地被确定。
对于第二种类型的问题,唯一性定理表述如下: 设区域V内有一些导体,给定导体之外的电介质分 布和自由电荷分布,给定各导体上的总自由电量 Qi以及V的边界S上的ϕ 或∂ϕ/∂n 值,则V’内的电场 唯一地确定。
定理,另一侧的场没有变化。由于这一方法是沿等位面
填充介质,因而称之为等位面法。
12
例2-1 静电场唯一性定理在解静电 屏蔽现象中的应用。
解 在物理学中,已知静电屏蔽现象: (1)接地的封闭导体壳内的电荷不影 响壳外的电场;(2)封闭导体壳无论 是否接地,壳内的电场都不受壳外电 荷的影响。作为唯一性定理的应用,
图2-5 沿场的等位面一侧, 填充导电媒质后的电场 11
因为这样处理之后:
1.它保持了另一侧场的边界形状及介质分布不变,且对
另一侧场而言,边界仍为等位面。填充导电媒质后,边
界上的总电荷量等于填充导电媒质前边界上所穿过的总
电通量,即
D dS
dS
n
,亦即边界条件没有变化。
2.它保持了另一侧场的电荷分布不变。因而根据唯一性
或混合边界条件,
则V内的电场唯一地确定。
4
也就是说,在V内存在唯一的解 ,它在每个Байду номын сангаас匀区
域Vi内满足泊松方程, 2 / i
在两均匀区域分界面上满足边值关系,
i
,
j
i
n
i
j
n
j
并在V的边界S上满足给定的
或
S
n S
3
一、静电问题的唯一性定理 下面研究可以均匀分区的区域V,即V可以分为若
干个均V内匀有区给域定Vi,的每自一由均电匀荷区分域布的(电x)容。率为εi 。
可以证明 若给定V的边界S上
(i)电位 ,第一类边值问题 “狄利克莱”边界条件 S 或(ii)电位的法向导数 ,第二类边值问题 n S “诺伊曼”边界条件
10
唯一性定理的应用——等位面法 根据唯一性定理,若沿 场的等位面的任意一侧,填充导电媒质,则等位面另一 侧的电场保持不变。如图2-4为两平行输电线的电场,若 沿场中任一等位面k之一侧(这里我们沿其内侧)填充导电 媒质(见图2-5),则导电媒质以外之另一侧,其电场不变。
图2-4 两平行输电线的电场
图2-6(a)表示一种情形。设封闭导体
壳的外表面为S1,对于壳外区域而言, 它是一个边界面。无论壳内电荷q1在
数量上增减或作位置上的移动,由于 导体壳接地,恒有 s,1 始0 终没有 改变壳外区域边界面上的边界条件。 因此在这种情况下,壳内的电荷不影 图2-6 例2-1图
13
图2-6(b)表示第二种情形。设封闭导体壳
三、唯一性定理的意义
1. 唯一性定理给出了确定静电场的条件,为求电 场强度指明了方向。
2. 更重要的是它具有十分重要的实用价值。无论 采用什么方法得到解,只要该解满足泊松方程、 边值关系和给定边界条件,则该解就是唯一的 正确解。因此对于许多具有对称性的问题,可 以不必用繁杂的数学去求解泊松方程,而是通 过提出尝试解,然后验证是否满足方程、边值 关系和边界条件。满足即为唯一解,若不满足, 可以加以修改。
平行双电轴电场是一个平行平面场,在垂直于电 轴的各个平面上,场有完全相同的分布图形。
静电场唯一性定理的简明表述:
若区域V内给定电介质分布和自由电荷分布ρ(x) ,
在V的边界S上给定
(i)电位 S
或
(ii)电位的法向导数
n S
若区域内有导体存在,还要给定各导体的电位或各
导体所带的自由电量,则V内的电场唯一地确定。
(如果V的边界面上和内部的导体上没有一处给定 电位,那么V内 的电场强度唯一确定,但电位ϕ不 能完全确定,可以相差一个常量。)
的内表面为S2,对于壳内区域而言它是一 个边界面。首先,S2是一个等位面。其次, 若在壳内紧贴S2作一高斯面S,则有
S
dS
n
q1
即电位移矢量 D的通量为q1。因此以S2作为导体壳内
电场的一个边界面,通过它的电通量仅仅决定于导体
壳内的电荷,而与壳外的电荷分布是无关的。根据唯
一性定理,当导体壳内带电导体都是给定电荷量时,
电位函数可以相差一个常数,但是电场强度是唯一确
定的。它不受导体壳外电荷q2的影响。如果导体壳接 地,这时甚至壳内的电位函数也是唯一确定的。总之,
在第二种情况下,导体壳内的电场不受壳外电荷的影
响。
14
§2-2 平 行 双 电 轴 法
平行双电轴电场法
如图2-7所示,两平行输电线表面电荷分布是不 均匀的。为了计算它们在周围空间激发的电场,人 们找到了平行双电轴法。
7
也就是说,存在唯一的解,它在导体以外满足泊松
方程
2
在两均匀区域分界面上满足i 边值关系,
i
,
j
i
n
i
j
n
j
在第i个导体上满足总自由电荷条件:
Si
dS
n
Qi
和等势面条件:
Si i 常量
以及在V的边界S上具有给定的ϕ |s 或(∂ ϕ /∂n)|s值。 8
值。
5
二、有导体存在时的唯一性定理
当有导体存在时,由实践经
验我们知道,为了确定电场,所
需要条件有两种类型:一类是给
定每个导体上的电位i ;另一类
是给定每个导体上的总自由电量
Qi。 如图,设在某区域V内有一些导体,扣除导体外
表面内所围区域以后剩下的区域为V ’。设V ’内给定
电介质分布、给定自由电荷分布ρ,S上给定了
第二章 静 电 场(二)
§2-1 静电场的唯一性定理及其应用 §2-2 §2-3 §2-4 §2-5 无限大介质交界平面的镜象 §2-6 §2-7 §2-8 §2-9 带电导体系统的电场能量及其分布 §2-10 虚位移法计算电场力
2
§2-1 静电场的唯一性定理及其应用
处理静电问题总是根据一定条件去解泊松方程。 静电学中许多问题都涉及到有限空间区域,在 区域内可以有电荷,也可以没有电荷,但都具 有确定的边界条件。现在有这样一个问题:要 使区域内存在唯一的、合理的解,问适合泊松 方程的边界条件是什么?唯一性定理回答了这 个问题。
或
S
n S
6
当每个导体上的电位ϕi 给定时(即给出了V’所有边 界上的ϕ或∂ϕ/∂n值),因而由唯一性定理可知, V’ 内的电场唯一地被确定。
对于第二种类型的问题,唯一性定理表述如下: 设区域V内有一些导体,给定导体之外的电介质分 布和自由电荷分布,给定各导体上的总自由电量 Qi以及V的边界S上的ϕ 或∂ϕ/∂n 值,则V’内的电场 唯一地确定。
定理,另一侧的场没有变化。由于这一方法是沿等位面
填充介质,因而称之为等位面法。
12
例2-1 静电场唯一性定理在解静电 屏蔽现象中的应用。
解 在物理学中,已知静电屏蔽现象: (1)接地的封闭导体壳内的电荷不影 响壳外的电场;(2)封闭导体壳无论 是否接地,壳内的电场都不受壳外电 荷的影响。作为唯一性定理的应用,
图2-5 沿场的等位面一侧, 填充导电媒质后的电场 11
因为这样处理之后:
1.它保持了另一侧场的边界形状及介质分布不变,且对
另一侧场而言,边界仍为等位面。填充导电媒质后,边
界上的总电荷量等于填充导电媒质前边界上所穿过的总
电通量,即
D dS
dS
n
,亦即边界条件没有变化。
2.它保持了另一侧场的电荷分布不变。因而根据唯一性
或混合边界条件,
则V内的电场唯一地确定。
4
也就是说,在V内存在唯一的解 ,它在每个Байду номын сангаас匀区
域Vi内满足泊松方程, 2 / i
在两均匀区域分界面上满足边值关系,
i
,
j
i
n
i
j
n
j
并在V的边界S上满足给定的
或
S
n S
3
一、静电问题的唯一性定理 下面研究可以均匀分区的区域V,即V可以分为若
干个均V内匀有区给域定Vi,的每自一由均电匀荷区分域布的(电x)容。率为εi 。
可以证明 若给定V的边界S上
(i)电位 ,第一类边值问题 “狄利克莱”边界条件 S 或(ii)电位的法向导数 ,第二类边值问题 n S “诺伊曼”边界条件
10
唯一性定理的应用——等位面法 根据唯一性定理,若沿 场的等位面的任意一侧,填充导电媒质,则等位面另一 侧的电场保持不变。如图2-4为两平行输电线的电场,若 沿场中任一等位面k之一侧(这里我们沿其内侧)填充导电 媒质(见图2-5),则导电媒质以外之另一侧,其电场不变。
图2-4 两平行输电线的电场
图2-6(a)表示一种情形。设封闭导体
壳的外表面为S1,对于壳外区域而言, 它是一个边界面。无论壳内电荷q1在
数量上增减或作位置上的移动,由于 导体壳接地,恒有 s,1 始0 终没有 改变壳外区域边界面上的边界条件。 因此在这种情况下,壳内的电荷不影 图2-6 例2-1图
13
图2-6(b)表示第二种情形。设封闭导体壳
