第三章 空间向量与立体几何 复习技巧
第3章 空间向量与立体几何 §3.2 立体几何中的向量方法.pdf

uuur
uuur
EF =(0,-1,-1), EG =(0,-1,-1),
设平面 EFG 的法向量是 n=(x,y,z),
uuur
uuur
则有 n⊥ EF ,n⊥ PA ,
∴
y x
+z= −y−
uuur
0, z=
0,
令
y=1,得
z=-1,x=0,即
ቤተ መጻሕፍቲ ባይዱ
n=(0,1,-1).
而显然 PA =(3,0,0)是平面 PBC 的一个法向量.
方法一 ∵△AMN,△BMN 为等腰三角形,
∴AG⊥MN,BG⊥MN.
∴∠AGB 为二面角的平面角或其补角.
∵AG=BG= 6 ,
uuur uuur 4uuur
uuur uuur
AB = AG + GB, ,设〈 AG , GB 〉=θ, uuur uuur uuur uuur uuur
AB 2= AG 2+2 AG ·GB + GB 2,
系 C-xyz.
由题意知 C(0,0,0),A(4,4,0),
B(4,0,0),D(0,4,0),E(4,2,0),
Fu(u2ur,4,0),G(0,0,u2u)u.r
BE =(0,2,0), BF =(-2,4,0), uuuur
设向量
BM
⊥平面
GEF,垂足为
uuuur
M,则
uuur
Mu、uurG、E、uuFur
2 2
y − 2z
= 0,
−
2 x+ 2
2 y − 2z = 0, 2
取 z=
2 ,解得 uuur
n
=
(0,4,
2 ).设点 B 到平面 OCD 的距离为 d,
高考数学空间向量与立体几何总复习
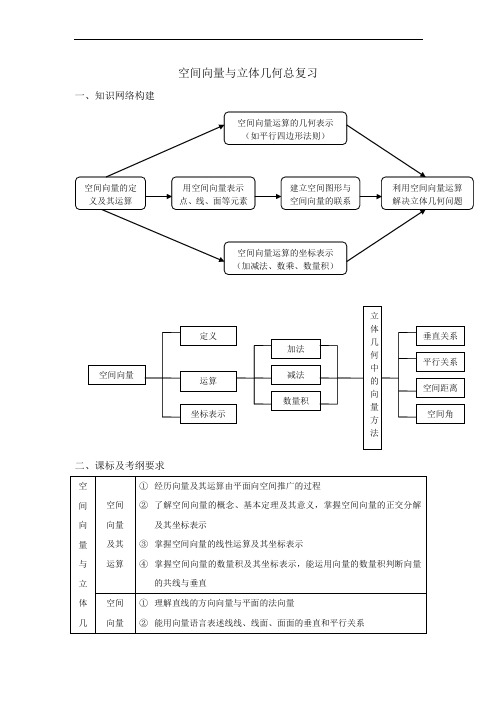
空间向量与立体几何总复习 一、知识网络构建
二、课标及考纲要求 空间向量与立体几
空间 向量 及其 运算 ① 经历向量及其运算由平面向空间推广的过程 ② 了解空间向量的概念、基本定理及其意义,掌握空间向量的正交分解及其坐标表示 ③ 掌握空间向量的线性运算及其坐标表示 ④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直 空间 向量 ① 理解直线的方向向量与平面的法向量 ② 能用向量语言表述线线、线面、面面的垂直和平行关系
空间向量的定义及其运算 空间向量运算的几何表示(如平行四边形法则) 用空间向量表示点、线、面等元素 建立空间图形与空间向量的联系 利用空间向量运算解决立体几何问题
空间向量运算的坐标表示(加减法、数乘、数量积)
空间向量 定义 运算 坐标表示 加法 减法 数量积
立体几何中的向量方法
垂直关系 平行关系 空间距离 空间角 何 的运 用 ③ 能用向量方法证明有关线、面位置关系的一些定理 ④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用 三、知识要点及考点精析 (一)空间向量及其运算 1.空间向量的概念 在空间,我们把具有大小和方向的量叫做空间向量,向量的大小叫做向量的长度或模. 还需要掌握的几个相关的概念包括相等向量、零向量、共线向量等. 2.空间向量的线性运算 (1)空间向量的加法、减法和数乘运算 平面向量中的三角形法则和平行四边形法则同样适用于空间向量的加(减)法运算.加法运算对于有限个向量求和,交换相加向量的顺序其和不变.三个不共面的向量的和等于以这三个向量为邻边的平行六面体的对角线所表示的向量.加法和数乘运算满足运算律: ①交换律,即a+b=b+a; ②结合律,即()()a+bcab+c; ③分配律,即()a=a+a及()a+bab(其中,均为实数). (2)空间向量的基本定理 ① 共线向量定理:对空间向量,ab(0),bab∥的充要条件是存在实数,使a=b
空间向量与立体几何例题和知识点总结

空间向量与立体几何例题和知识点总结在高中数学的学习中,空间向量与立体几何是一个重要且具有一定难度的板块。
通过空间向量的方法,我们能够更加简便地解决立体几何中的许多问题。
接下来,让我们一起通过一些例题来深入理解,并总结相关的知识点。
一、空间向量的基本知识点1、空间向量的概念:空间中具有大小和方向的量称为空间向量。
2、空间向量的表示:可以用有向线段表示,也可以用坐标表示。
3、空间向量的运算:包括加法、减法、数乘以及数量积。
加法和减法满足三角形法则和平行四边形法则。
数乘:λ(a + b) =λa +λb数量积:a·b =|a|·|b|·cosθ(θ为两向量的夹角)二、空间向量在立体几何中的应用1、证明线线平行设直线 l₁和 l₂的方向向量分别为 a 和 b,如果 a =λb(λ 为非零实数),则 l₁∥ l₂。
例 1:在长方体 ABCD A₁B₁C₁D₁中,E,F 分别为棱 AA₁,CC₁的中点,求证:BE ∥ DF 。
解:以 D 为原点,分别以 DA,DC,DD₁所在直线为 x,y,z 轴,建立空间直角坐标系。
设长方体的长、宽、高分别为 a,b,c 。
则 B(a,b,0),E(a,0,c/2),D(0,0,0),F(0,b,c/2)BE =(0,b,c/2),DF =(0,b,c/2)因为 BE = DF ,所以 BE ∥ DF 。
2、证明线线垂直设直线 l₁和 l₂的方向向量分别为 a 和 b,如果 a·b = 0,则 l₁⊥l₂。
例 2:在正方体 ABCD A₁B₁C₁D₁中,M,N 分别为棱 AB,CC₁的中点,求证:DM ⊥ MN 。
解:以 D 为原点,分别以 DA,DC,DD₁所在直线为 x,y,z 轴,建立空间直角坐标系。
设正方体的棱长为 2。
则 D(0,0,0),M(2,1,0),N(0,2,1)DM =(2,1,0),MN =(-2,1,1)DM·MN =-4 + 1 + 0 =-3 ≠ 0 ,所以 DM 与 MN 不垂直。
空间向量与立体几何例题和知识点总结

空间向量与立体几何例题和知识点总结一、空间向量的基本知识点在立体几何中,空间向量是一个非常有力的工具。
首先,我们来了解一下空间向量的一些基本概念。
空间向量是具有大小和方向的量,它可以用有向线段来表示。
如果两个空间向量的大小和方向都相同,那么这两个向量就是相等的。
向量的加法和减法遵循三角形法则和平行四边形法则。
例如,对于向量\(\overrightarrow{a}\)和\(\overrightarrow{b}\),它们的和\(\overrightarrow{a} +\overrightarrow{b}\)可以通过将两个向量首尾相连得到,而差\(\overrightarrow{a} \overrightarrow{b}\)则是\(\overrightarrow{a}\)加上\(\overrightarrow{b}\)的相反向量。
空间向量的数量积\(\overrightarrow{a} \cdot \overrightarrow{b}\)等于\(\vert\overrightarrow{a}\vert \vert\overrightarrow{b}\vert \cos\theta\),其中\(\theta\)是\(\overrightarrow{a}\)和\(\overrightarrow{b}\)之间的夹角。
数量积的结果是一个标量。
空间向量的坐标表示:在空间直角坐标系中,向量\(\overrightarrow{a} =(x, y, z)\),其中\(x\)、\(y\)、\(z\)分别是向量在\(x\)轴、\(y\)轴、\(z\)轴上的分量。
二、空间向量在立体几何中的应用接下来,通过一些具体的例题来看看空间向量是如何解决立体几何问题的。
例 1:证明线线平行已知直线\(l_1\)和\(l_2\)的方向向量分别为\(\overrightarrow{v_1} =(2, -1, 3)\)和\(\overrightarrow{v_2} =(4, -2, 6)\),证明\(l_1 \parallel l_2\)。
知识讲解_《空间向量与立体几何》全章复习与巩固_提高
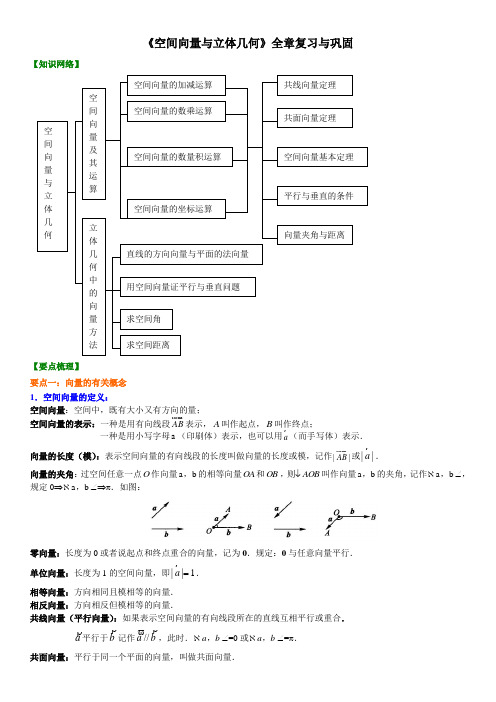
《空间向量与立体几何》全章复习与巩固【知识网络】【要点梳理】要点一:向量的有关概念1.空间向量的定义:空间向量:空间中,既有大小又有方向的量;空间向量的表示:一种是用有向线段AB u u u r表示,A 叫作起点,B 叫作终点;一种是用小写字母a (印刷体)表示,也可以用a r(而手写体)表示.向量的长度(模):表示空间向量的有向线段的长度叫做向量的长度或模,记作||AB uuu r或||a r .向量的夹角:过空间任意一点O 作向量a b ,的相等向量OA 和OB ,则↓AOB 叫作向量a b ,的夹角,记作ℵa b ,∠,规定0⇒ℵa b ,∠⇒π.如图:零向量:长度为0或者说起点和终点重合的向量,记为0.规定:0与任意向量平行.单位向量:长度为1的空间向量,即||1a =r.相等向量:方向相同且模相等的向量. 相反向量:方向相反但模相等的向量. 共线向量(平行向量):如果表示空间向量的有向线段所在的直线互相平行或重合.a ρ平行于b ρ记作b a ρϖ//,此时.ℵa b ,∠=0或ℵa b ,∠=π.共面向量:平行于同一个平面的向量,叫做共面向量.空间向量与立体几何空间向量及其运算立体几何中的向量方法空间向量的加减运算空间向量的数乘运算空间向量的数量积运算 空间向量的坐标运算共线向量定理共面向量定理空间向量基本定理平行与垂直的条件向量夹角与距离直线的方向向量与平面的法向量用空间向量证平行与垂直问题求空间角 求空间距离要点诠释:(1)数学中讨论的向量是自由向量,即与向量的起点无关,只与大小和方向有关. 只要不改变大小和方向,空间向量可在空间内任意平移;(2)当我们说向量a ρ、b ρ共线(或a ρ//b ρ)时,表示a ρ、b ρ的有向线段所在的直线可能是同一直线,也可能是平行直线.(3)对于任意一个非零向量a ,我们把aa叫作向量a 的单位向量,记作0a .0a 与a 同向. (4)当ℵa b ,∠=0或π时,向量a b ,平行,记作a ⎩b ;当 ℵa b ,∠=2π时,向量a b ,垂直,记作a ⊥b .要点二:空间向量的基本运算 空间向量的基本运算: 运算类型几何方法运算性质向 量 的 加 法1平行四边形法则: OC OA ABa b=+=+u u u r u u u r u u u r rr加法交换率:.a b b a ρρρρ+=+加法结合率:()()a b c a b c ++=++r r r r rr()a b a b -=+-r r r r AB BC=AC +u u u r u u u r u u u r 0AB BA=+u u u r u r r2三角形法则: OB OA ABa b=+=+u u u r u u u r u u u r rr向 量 的 减 法三角形法则: BA OA OBa b=-=-u u u r u u u r u u u r rrAB OA OB =-向 量 的 乘 法 a λ是一个向量,满足:λ>0时,a λr 与a r同向;λ<0时,a λr 与a r异向;λ=0时, a λr=0()()a a λμλμ=r r()a a a λμλμ+=+r r r()a b a b λλλ+=+r r r ra r∥b a b λ⇔=r r r向 量 的 数 量 积 1.a b r rg是一个数:||||cos()a b a b a b =r r r r r r g ,; 2.0a =r ,0b=r或a b ⊥ ⇔b a •=0.a b b a =r r r r g g ()()()a b a b a b λλλ==r r r r r r g g g ()a b c a c b c +=+r r r r r r rg g g 22||a a =r r ||||||a b a b ≤r r r r g g共线共面共线定理:空间任意两个向量a 与b (b ≠0)共线的充要条件是存在实数λ,使a ≠b λ.共面向量定理:如果两个向量,a b r r 不共线,p r 与向量,a b r r 共面的充要条件是存在唯一的有序实数对(,x y ),使p xa yb =+r r r.推论:空间一点P 位于平面MAB 内的充要条件是存在有序实数对x y ,使得MP xMA yMB =+u u u r u u u r u u u r,或对空间任意一点O 有OP OM xMA yMB =++u u u r u u u u r u u u r u u u r 或OP xOM yOA zOM =++u u u r u u u u r u u u r u u u u r(其中1x y z ++=).要点诠释:(1)可以用共线定理来判定两条直线平行(进而证线面平行)或证明三点共线. (2)可以用共面向量定理证明线面平行(进而证面面平行)或证明四点共面. 要点三:空间向量基本定理空间向量基本定理:如果123e e e ,,是空间三个不共面的向量,a 是空间任一向量,那么存在唯一一组实数123λλλ,,,使得112233=++λλλa e e e .空间中不共面的三个向量123e e e ,,称为这个空间的一个基底. 当向量123e e e ,,两两垂直时,就得到这个向量的一个正交分解.要点诠释:(1)空间任意三个不共面的向量都可以作为空间向量的一个基底;(2)由于零向量可视为与任意一个非零向量共线,与任意两个非零向量共面,所以,三个向量不共面,就隐含着它们都不是零向量0.(3)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.要点四:空间向量的直角坐标运算 1. 空间直角坐标系及坐标在空间选定一点O 和一个单位正交基底()i j k ,,,以点O 为原点,分别以i j k ,,的方向为正方向建立三条数轴:x 轴、y 轴、z 轴,它们都叫坐标轴.我们称建立了一个空间直角坐标系O xyz ,点O 叫原点,向量i j k ,,都叫坐标向量.给定一个空间直角坐标系O xyz -中,对于空间任一点A ,对应一个向量OA ,若=x +y +z OA i j k ,则有序数组()x y z ,,叫点A 在此空间直角坐标系中的坐标,记为()A x y z ,,,其中x 叫做点A 的横坐标,y 叫点A 的纵坐标,z 叫点A 的竖坐标.2. 空间两点的距离公式若111(,,)A x y z ,222(,,)B x y z ,则①222111212121(,,)(,,)(,,)AB OB OA x y z x y z x x y y z z =-=-=---u u u r u u u r u u u r;②||AB ==u u u r ;③ AB 的中点坐标为121212222x +x y +y z +z ⎛⎫⎪⎝⎭,,.3. 空间向量运算的的坐标运算设111(,,)a x y z =r ,222(,,)b x y z =r,则 ① 121212(,,)a b x x y y z z +=+++r r; ② 121212(,,)a b x x y y z z -=---r r; ③ 111(,,)()a x y z R λλλλλ=∈r; ④ 121212a b x x y y z z ⋅=++r r;⑤ 222111a a a x y z ==++r r r g ,222222b b b x y z ==++r r r g ; ⑥ ()121212222222111222cos 00x x y y z z a ba b a b a bx y z x y z ++==≠≠++++r rr r r rg r r g g ,,.4. 空间向量平行和垂直的条件若111(,,)a x y z =r ,222(,,)b x y z =r,则①12//a b a b x x λλ⇔=⇔=r r r r ,12y y λ=,12()z z R λλ=∈⇔111222x y zx y z ==222(0)x y z ≠;②12121200a b a b x x y y z z ⊥⇔⋅=⇔++=r r r r.要点诠释:(1)空间任一点P 的坐标的确定:过P 作面xOy 的垂线,垂足为'P ,在面xOy 中,过'P 分别作x 轴、y 轴的垂线,垂足分别为A C 、,则|'|||||x P C y AP z PP ===,,''.如图: (2)夹角公式可以根据数量积的定义推出:a b a b |a ||b|cos a b cos a b |a ||b|⋅⋅=<⋅>⇒<⋅>=⋅r rr r r r r r r rr r ,其中θ的范围是[0,]π.(3)0r与任意空间向量平行或垂直.要点五:用空间向量讨论垂直与平行图示向量证明方法线线平行 (a b î)a b î(a b ,分别为直线a b ,的方向向量)线线垂直 (a b ⊥)⊥a b(a b ,分别为直线a b ,的方向向量)线面平行 (l αî)⊥a n ,即0=⋅a n(a 是直线l 的方向向量,n 是平面α的法向量).线面垂直(l α⊥)a n î(a 是直线l 的方向向量,n 是平面α的法向量) 面面平行 (αβî)//u v(u v ,分别是平面α,β的法向量)面面垂直 (αβ⊥)⊥u v ,即0=u v g(u ,v 分别是平面α,β的法向量)要点诠释:(1)直线的方向向量:若A 、B 是直线l 上的任意两点,则AB u u u r 为直线l 的一个方向向量;与AB u u u r平行的任意非零向量也是直线l 的方向向量.(2)平面的法向量:已知平面α,直线l α⊥,取l 的方向向量a ,有α⊥a ,则称为a 为平面α的法向量. 一个平面的法向量不是唯一的.要点六:用空间向量求夹角图示向量证明方法异面直线的夹角||cos ||||AC BD AC BD θ⋅=⋅u u u r u u u r u u ur u u u r(A ,C 是直线a 上不同的两点,B ,D 是直线b 上不同的两点)直线和平面的夹角||sin |cos |||||θϕ⋅==⋅a u a u(其中直线l 的方向向量为a ,平面α的法向量为u ,直线与平面所成的角为θ,a 与u 的角为ϕ)平面间的夹角121212cos =cos =.θ⋅n n n n n n ,(平面1π与2π的法向量分别为1n 和2n ,平面1π与2π的夹角为θ)(1)空间两直线所成的角可以通过这两直线的方向向量的夹角来求得,但二者不完全相等,当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角. 即设直线1l 与2l 的方向向量分别为1s ,2s .当0≤12s s ,≤2π时,直线1l 与2l 的夹角等于12s s ,;当2π<12s s ,≤π时,直线1l 与2l 的夹角等于π 12s s ,. (2)最小角定理:斜线和射影所成的角,是斜线和这个平面内所有直线所成角中最小的角,其范围是02π⎡⎤⎢⎥⎣⎦,.(3)两平面的夹角范围是02π⎡⎤⎢⎥⎣⎦,,已知平面1π和2π的法向量分别为1n 和2n ,则当0≤12n n ,≤2π时,平面1π和2π的夹角等于12n n ,; 当2π<12n n , ≤π时,平面1π和2π的夹角等于π12n n , .要点七:用空间向量求距离图示向量证明方法两点之间的距离设()()111222M x y z N x y z ,,,,,,则()()()222121212d MN x x y y z z ==++u u u u r点到直线的距离22PA d=PA s su u u r g u u u r(l 是过点P 平行于向量s 的直线) 点到平面的距离PA d=AA'=n nu u u r g(n 为平面π的法向量)两条异面直线的距离CD d=n nu u u r g(n 是直线12l l ,的公共法向量)与平面平行的直线到平面的距离PA d=AA'=n nu u u r g(n 是平面π的公共法向量)两平行平面间的距离PA d=AA'=n nu u u r g(n 是平面α,β的一个公共法向量)(2)空间距离不只有向量法一种方法,比如点面距还有一种重要的求法为等积转化法.(3)各种距离之间有密切联系,有些可以相互转化,如两条平行线的距离可转化为求点到直线的距离,平行线面间的距离或平行平面间的距离都可转化成点到平面的距离.而且我们在求解时往往又转化为空间向量的处理方法.要点八:立体几何中的向量方法用空间向量解决立体几何问题的“三步曲”1.建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题)2.通过向量运算研究点、线、面之间的位置关系及它们之间的距离和夹角等问题;(进行向量运算) 3.把向量的运算结果“翻译”成相应的几何意义.(回到图形问题)用坐标法解决立体几何中问题的一般步骤 1.建立适当的空间直角坐标系; 2.写出相关点的坐标及向量的坐标; 3.进行相关的计算;4.写出几何意义下的结论.【典型例题】类型一:空间向量的概念及运算例1. 如图,在平行六面体1111ABCD A B C D -中,M 为11A C 与11B D 的交点. 若AB a =u u u r r ,AD b =u u u r r ,1AA c =u u u r r,则下列向量中与BM u u u u v相等的向量是( )A . 1122a b c -++r r rB . 1122a b c ++r r rC . 1122a b c --+r r rD . 1122a b c -+r r r【思路点拨】本题以向量的加减法为前提,考查了向量相等的概念:(1)相等向量指的是方向相同且模相等的向量;(2)注意向量加法的三角形法则和平行四边形法则、减法的三角形法则的正确运用;注意公式AB BC=AC +u u u r u u u r u u u r,AB AC=CB u u u r u u u r u u u r的灵活应用.【答案】A 【解析】M CB1D1A1B D法一: 1111()2BM BB B M AD AB AA =+=-+=u u u u r u u u r u u u u r u u u r u u u r u u u r 1122a b c -++r r r .法二:()11111111111=++=++=D+=+=222222a b c AB AD AA BA AD AA B AA B M BB BM -++-u u ur u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u u r u u u r u u u u r r r r ; ()11111111111=++=++=+=+=222222a b c AB AD AA AB AD AA AC AA A M AA AM ++u u ur u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u u r u u u r u u u u r r r r ; ()11111111=++=+==2222a b c AB AD AA AC AA C M CC CM ++u u ur u u u r u u u r u u u r u u u r u u u u u r u u u u r u u u u r r r r ; ()11111111=+==+2222a b c AB AD AA DB AA D M DD DM -+-=+=u u ur u u u r u u u r u u u r u u u r u u u u u r u u u u r u u u u r r r r . 故选A .【总结升华】类比平面向量表达平面位置关系过程,掌握好空间向量的用途. 用向量的方法处理立体几何问题,使复杂的线面空间关系代数化,本题考查的是基本的向量相等与向量的加减法,考查学生的空间想象能力.【变式1】如图,在三棱柱111ABC A B C -中,M 是1BB 的中点,化简下列各式: (1)1CB BA +u u u r u u u r ;(2)112AC CB AA ++u u u r u u u r u u u r ;(3)1AA AC CB --u u u r u u u r u u u r . 【答案】(1)11CB BA CA +=u u u r u u u r u u u u r;(2)112AC CB AA AM ++=u u u r u u u r u u u r u u u u r;(3)11AA AC CB BA --=u u u r u u u r u u u r u u u u r .【变式2】在四边形ABCD 中,−→−AB =−→−DC ,且−→−AC ·−→−BD =0,则四边形ABCD 是( ) A . 矩形 B . 菱形 C .直角梯形 D .等腰梯形 【答案】B类型二:空间向量的直角坐标运算例2.已知空间三点()202A -,,,()112B -,,,()304C -,,.设a =AB u r u u u r ,b=AC u r u u u r. (1)求3-2a b r r;(2)求a r 和b r的夹角θ的余弦值;(2)若向量ka r +与ka r -2b r互相垂直,求k 的值.【思路点拨】根据空间向量直角坐标的相关公式进行运算.【解析】∵()202A -,,,()112B -,,,()304C -,,, ∴a =AB u r u u u r =(1,1,0),b=AC u r u u u r=(-1,0,2).(1)()3330a=r ,,,()2204b=r-,,,∴()3-2534a b =r r,,. (2)cos θ== ∴和的夹角的余弦值为 (2)ka r+=(k ,k ,0)+(-1,0,2)=(k -1,k ,2),ka r -2b r=(k +2,k ,-4), ∵(ka r +)⊥(ka r-2),∴(ka r +)⎡(ka r-2)=(k -1,k ,2)·(k +2,k ,-4)()22(1)282100=k k k k k ++=+=---∴52k =-或2k =.【变式1】已知A B C 、、三点坐标分别为()()()212451223---,,,,,,,,,求点P 的坐标使得=()12AB AC u u ur u u u r . 【答案】1502P ⎛⎫⎪⎝⎭,, 【变式2】已知向量()=24a x r ,,,()=22b y r,,,若=6a r ,a r ⊥b r ,则x y +的值是( ) A .3-或1 B .3或1- C . 3-D .1 【答案】A由题意可知2416364420.x y x ⎧++=⎨++=⎩, 解得43x y =⎧⎨=⎩, 或41.x y =⎧⎨=⎩,【变式3】已知空间四点(2,3,1)A -,(2,5,3)B -,(10,0,10)C 和(8,4,9)D ,试判断四边形ABCD 的形状. 【答案】矩形类型三:共线和共面向量定理的应用例3. 已知平行四边形ABCD ,从平面AC 外一点O 引向量OE kOA =u u u r u u u r ,OF kOB =u u u r u u u r ,OG kOC =u u u r u u u r ,OH kOD =u u u u r u u u r. 求证:(1)四点E F G H 、、、共面; (2)平面AC //平面EG . 【思路点拨】(1)利用共面向量定理证明四点E F G H 、、、共面; (2)由向量共线得到线线平行,利用平面平行的判定定理证明. 【证明】(1)()()()===OE kOA k OB BA k OB CD k OB OD OC kOB kOD kOC OF OH OG =+=+=+++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u u r u u u r ,∵1111+-=,由共线向量定理可知,点E F G H 、、、共面. (2)()EF OF OE kOB kOA k OB OA k AB ====u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,∴EF AB î,又∵EF ⊄平面AC ,AB ⊂平面AC , ∴EF ∥平面AC . 同理FG ∥平面AC , ∵=EF FG F I ,∴平面AC //平面EG .【总结升华】在求一个向量由其他向量来表示的时候,通常是利用向量的三角形法则、平行四边形法则和共线向量的特点,把要求的向量逐步分解,向已知向量靠近,进行求解. 若要证明两直线平行,只需判断两直线所在的向量是否满足线性关系a b λ=r r即可.在本题第(1)题的解析中运用了共面向量定理的推论,其实利用共面向量定理也可以给予证明,同学们试一试.【变式1】已知3240a m n p =--≠r v v v v ,(1)82b x m n yp =+++v v v v ,且,,m n p v v v不共面. 若a b v v î,求y x ,的值. 【答案】13,8x y =-=由题意列等式:182324x y+==--,解得13,8x y =-=. 【变式2】下列各组向量共面的是( )A . a =(1,2,3),b =(3,0,2),c =(4,2,5)B . =(1,0,0),=(0,1,0),=(0,0,1)C . =(1,1,0),=(1,0,1),=(0,1,1)D . =(1,1,1),=(1,1,0),=(1,0,1) 【答案】D类型四:空间向量在立体几何中的应用例4. 四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,4PA AD ==,2AB =. 以AC 的中点O 为球心、AC 为直径的球面交PD 于点M ,交PC 于点N .DB(1)求证:平面ABM ⊥平面PCD ;(2)求直线CD 与平面ACM 所成的角的正弦值; (3)求点N 到平面ACM 的距离.【思路点拨】建立适当的空间直角坐标系,将立体几何问题转化为空间向量问题,再通过向量运算判断向量的平行、垂直及计算向量的夹角,最后再翻译成图形语言.(1)将证明平面ABM ⊥平面PCD 转化为证明平面ABM 的法向量与平面PCD 的法向量垂直;(2)直线CD 与平面ACM 的夹角的正弦值就是直线CD 的方向向量与平面ACM 的法向量的夹角的余弦值的绝对值;(3)由于N 点坐标不确定,故将求点N 到平面ACM 的距离,转化为求求点P 到平面ACM 的距离. 【解析】(1)方法一:∵AC 是所作球面的直径,∴AM MC ⊥。
(完整)空间向量与立体几何知识总结(高考必备),推荐文档

为平面ABCD外一点,且PA⊥平面分成定,求满足的实数
结合图形,从向量出发,利用向量运算法则不断进行分解,直到全部向量都用、、表示出来,
,则。
点评:选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决立体几何问题的一项基本
求的向量当作新的所需向量,如此继续下去,直到所有向量都符合目标要求为止,这就是向量的分解。
有分解才有组合,组合是分解的表现形式。
空间向量基本定理恰好说明,用空间三个不共面的向量组可以表示出空间任意一个向
)证明两条直线平行,只需证明这两条直线的方向向量是共线向量.
【用空间向量求空间角】
—中,分别是,的中点,求:
)两条异面直线所成的角可以借助这两条直线的方向向量的夹角求得,即。
(2)直线与平面所成的角主要可以通过直线的方向向量与平面的法向量的夹角求得,即或
(3)二面角的大小可以通过该二面角的两个面的法向量的夹角求得,它等于两法向量的夹角或其补角。
【用空间向量求距离】
—中,,,
热点。
现列出几类问题的解决方法。
)平面的法向量的求法:设,利用
是平面的一个法向量,是平面的斜线的一个方向向量,则直线与平面所
(3)二面角的求法:①分别是二面角的两个面内与棱。
②设分别是二面角的两个平面的法向量,则就是二面角的平
)异面直线间距离的求法:是两条异面直线,是的公垂线段
上的任意两点,则。
是平面的法向量,AB是平面的一条斜线,则点到平面的距离为。
空间向量与立体几何知识点推荐文档
立体几何空间向量知识点总结知识网络:知识点拨:1、空间向量的概念及其运算与平面向量类似,向量加、减法的平行四边形法则,三角形 法则以及相关的运算律仍然成立.空间向量的数量积运算、 共线向量定理、共面向量定理都是平面向量在空间中的推广,空间向量基本定理则是向量由二维到三维的推广.量研究线线、线面、 面面垂直的关键,通常可以与向量的运算法则、有关运算律联系来解决 垂直的论证问题.r r r ra b cos a, br r3、 公式3 b是应用空间向量求空间中各种角的基础,用这个公式可以求两异面直线所成的角(但要注意两异面直线所成角与两向量的夹角在取值范围上的区别), 再结合平面的法向量,可以求直线与平面所成的角和二面角等.4、 直线的方向向量与平面的法向量是用来描述空间中直线和平面的相对位置的重要概念, 通过研究方向向量与法向量之间的关系, 可以确定直线与直线、 直线与平面、平面与平面等 的位置关系以及有关的计算问题.5、用空间向量判断空间中的位置关系的常用方法(1) 线线平行证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2) 线线垂直证明两条直线垂直,只需证明两条直线的方向向量垂直,即2、当a 、b 为非零向量时.0 a b 是数形结合的纽带之一,这是运用空间向r br ao rb r空间向tt与立悔几柯(3) 线面平行用向量证明线面平行的方法主要有:① 证明直线的方向向量与平面的法向量垂直;② 证明可在平面内找到一个向量与直线方向向量是共线向量;③ 利用共面向量定理,即证明可在平面内找到两不共线向量来线性表示直线的方向向 量. (4) 线面垂直用向量证明线面垂直的方法主要有: ① 证明直线方向向量与平面法向量平行; ② 利用线面垂直的判定定理转化为线线垂直问题. (5) 面面平行① 证明两个平面的法向量平行(即是共线向量); ② 转化为线面平行、线线平行问题. (6) 面面垂直① 证明两个平面的法向量互相垂直; ② 转化为线面垂直、线线垂直问题. 6、运用空间向量求空间角(1) 求两异面直线所成角(2) 求线面角求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量, 通过数量积求出直线与平面所成角; 另一种方法是借助平面的法向量, 先求出直线方向向量与平面法向量的夹角0,即可求出直线与平面所成的角其关系是sin | cos ©(3) 求二面角用向量法求二面角也有两种方法: 一种方法是利用平面角的定义, 在两个面内先求出与 棱垂直的两条直线对应的方向向量, 然后求出这两个方向向量的夹角, 由此可求出二面角的 大小;另一种方法是转化为求二面角的两个面的法向量的夹角, 它与二面角的大小相等或互补.7、运用空间向量求空间距离空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离. (1) 点与点的距离点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模. (2) 点与面的距离 点面距离的求解步骤是: ① 求出该平面的一个法向量;② 求出从该点出发的平面的任一条斜线段对应的向量;③ 求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得要求的点面距cos a,b利用公式但务必注意两异面直线所成角B 的范围是0,—2故实质上应有: cos cos a,b离.备考建议:1、 空间向量的引入,把平面向量及其运算推广到空间,运用空间向量解决有关直线、平 面位置关系的问题,应体会向量方法在研究几何图形中的作用, 进一步发展空间想像能力和几何直观能力.2、 灵活选择运用向量方法与综合方法,从不同角度解决立体几何问题.3、 在解决立体几何中有关平行、垂直、夹角、距离等问题时,直线的方向向量与平面的法向量有着举足轻重的地位和作用, 它的特点是用代数方法解决立体几何问题, 无需进行繁、 难的几何作图和推理论证,起着从抽象到具体、化难为易的作用. 因此,应熟练掌握平面法 向量的求法和用法.4、 加强运算能力的培养,提高运算的速度和准确性.第一讲空间向量及运算一、空间向量的有关概念 1、 空间向量的定义在空间中,既有大小又有方向的量叫做空间向量. 注意空间向量和数量的区别.数量是只有大小而没有方向的量. 2、 空间向量的表示方法空间向量与平面向量一样, 也可以用有向线段来表示, 用有向线段的长度表示向量的大r小,用有向线段的方向表示向量的方向.若向量a 对应的有向线段的起点是 A ,终点是B ,3、零向量r长度为零的向量称为零向量,记为° •零向量的方向不确定,是任意的•由于零向量的这一特殊性,在解题中一定要看清题目中所指向量是“零向量”还是“非零向量”. 4、 单位向量模长为1的向量叫做单位向量.单位向量是一种常用的、重要的空间向量,在以后的学 习中还要经常用到. 5、 相等向量r rr r长度相等且方向相同的空间向量叫做相等向量•若向量a与向量b 相等,记为a =b .零向量与零向量相等,任意两个相等的非零向量都可以用空间中的同一条有向线段来表示, 并且与有向线段的起点无关. 6、 相反向量rr长度相等但方向相反的两个向量叫做相反向量. a的相反向量记为一a二、共面向量 1、 定义平行于同一平面的向量叫做共面向量. 2、 共面向量定理r r u r r若两个向量a 、b 不共线,则向量 P 与向量a 、b 共面的充要条件是存在实数对x 、y,ruuu则向量a 可以记为AB ,其模长为ur r r 使得 P = xa yb 。
空间向量与立体几何知识点
空间向量与立体几何知识点第一篇:空间向量1. 空间向量的表示方法空间向量可以用有向线段、坐标和向量分量等多种方式进行表示。
其中,有向线段表示空间向量的长度、方向和起点,坐标表示空间向量的左端点和右端点的坐标,向量分量表示空间向量在三个坐标轴上的投影。
2. 空间向量的加减法空间向量的加减法与二维向量的加减法类似,可以通过将两个向量的分量逐一相加或相减得到结果向量的分量。
也可以通过平移法、三角法、正交分解等方法进行计算。
3. 空间向量的数量积和向量积空间向量的数量积和向量积都具有几何意义和物理意义。
数量积表示两个向量之间的夹角余弦值和向量长度的乘积,通常用于计算向量的投影和求解平面或直线的方程。
向量积表示两个向量所在平行四边形的面积和法向量,通常用于计算向量的叉积、平面或直线的法向量以及计算空间中两个平面的夹角。
4. 空间向量的共线、垂直和平行空间向量的共线、垂直和平行是三种基本关系。
当两个向量共线时,它们所在直线相交或重合;当两个向量垂直时,它们的数量积为0,而向量积为一个与它们垂直的向量;当两个向量平行时,它们的向量积为0,而数量积为它们长度的乘积。
5. 应用举例空间向量广泛应用于物理、工程、计算机图形学等领域。
例如,通过计算物体的重心和质量分布情况,可以求解物体的转动惯量和稳定性问题;通过计算矢量场中的散度和旋度,可以分析流体的运动状态和变化规律;通过计算三维空间中的距离和夹角,可以在计算机图形学中进行三维模型的建模和渲染。
第二篇:立体几何1. 立体几何的基本概念立体几何是研究三维空间中的基本几何对象和它们的性质、关系的数学分支。
它包括点、线、面、体和空间角等多个基本概念,用于描述和分析三维物体的形状、大小和位置关系。
2. 立体几何的基本公理立体几何的基本公理是欧几里得几何的扩展,是指空间中的点、线、面、体和空间角等基本几何对象应满足的性质和约束。
这些公理包括点的唯一性、直线的唯一性、平面的唯一性、线段长度的可加性、平面的无限性、等角推移原理等。
高中数学知识点总结大全空间向量与立体几何
高中数学知识点总结空间向量与立体几何一、考点概要:1、空间向量及其运算〔1〕空间向量的根本知识:①定义:空间向量的定义和平面向量一样,那些具有大小和方向的量叫做向量,并且仍用有向线段表示空间向量,且方向相同、长度相等的有向线段表示相同向量或相等的向量。
②空间向量根本定理:ⅰ定理:如果三个向量不共面,那么对于空间任一向量,存在唯一的有序实数组x、y、z,使。
且把叫做空间的一个基底,都叫基向量。
ⅱ正交基底:如果空间一个基底的三个基向量是两两相互垂直,那么这个基底叫正交基底。
ⅲ单位正交基底:当一个正交基底的三个基向量都是单位向量时,称为单位正交基底,通常用表示。
ⅳ空间四点共面:设O、A、B、C是不共面的四点,那么对空间中任意一点P,都存在唯一的有序实数组x、y、z,使。
③共线向量〔平行向量〕:ⅰ定义:如果表示空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量,记作。
ⅱ规定:零向量与任意向量共线;ⅲ共线向量定理:对空间任意两个向量平行的充要条件是:存在实数λ,使。
④共面向量:ⅰ定义:一般地,能平移到同一平面内的向量叫做共面向量;空间的任意两个向量都是共面向量。
ⅱ向量与平面平行:如果直线OA平行于平面或在α内,那么说向量平行于平面α,记作。
平行于同一平面的向量,也是共面向量。
ⅲ共面向量定理:如果两个向量、不共线,那么向量与向量、共面的充要条件是:存在实数对x、y,使。
ⅳ空间的三个向量共面的条件:当、、都是非零向量时,共面向量定理实际上也是、、所在的三条直线共面的充要条件,但用于判定时,还需要证明其中一条直线上有一点在另两条直线所确定的平面内。
ⅴ共面向量定理的推论:空间一点P在平面MAB内的充要条件是:存在有序实数对x、y,使得,或对于空间任意一定点O,有。
⑤空间两向量的夹角:两个非零向量、,在空间任取一点O,作,〔两个向量的起点一定要相同〕,那么叫做向量与的夹角,记作,且。
⑥两个向量的数量积:ⅰ定义:空间两个非零向量、,那么叫做向量、的数量积,记作,即:。
高考数学复习-空间向量与立体几何
空间向量与立体几何【核心考点】空间向量应用1.线线关系证明设直线l 的方向向量为a =(a 1,b 1,c 1),平面α,β的法向量分别为μ=(a 2,b 2,c 2),v =(a 3,b 3,c 3)则有: (1)线面平行l ∥α⇔a ⊥μ⇔a ·μ=0⇔a 1a 2+b 1b 2+c 1c 2=0. (2)线面垂直l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2,b 1=kb 2,c 1=kc 2. (3)面面平行α∥β⇔μ∥v ⇔μ=λv ⇔a 2=λa 3,b 2=λb 3,c 2=λc 3. (4)面面垂直α⊥β⇔μ⊥v ⇔μ·v =0⇔a 2a 3+b 2b 3+c 2c 3=0. 2.夹角和距离设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同). (1)线线夹角设l ,m 的夹角为θ(0≤θ≤π2),则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21a 22+b 22+c 22. (2)线面夹角设直线l 与平面α的夹角为θ(0≤θ≤π2),则sin θ=|a ·μ||a ||μ|=|cos 〈a ,μ〉|.(3)面面夹角设平面α、β的夹角为θ(0≤θ<π), 则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|. (4)距离问题①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α的距离为||n .②.异面直线间的距离d =(12,l l 是两异面直线,其公垂向量为n r,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).【补充】空间向量基础知识点1、空间向量的坐标及基本运算空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵坐标),z 轴是竖轴(对应为竖坐标).=(a 1,a 2,a 3),),,(321b b b =,),,(332211b a b a b a ±±±=+,))(,,(321R a a a a ∈=λλλλλ,332211b a b a b a ++=⋅ ,向量平行:a ∥)(,,332211R b a b a b a ∈===⇔λλλλ332211b a b a b a ==⇔ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 空间向量加减法运用的三个层次空间向量是处理立体几何问题的有力工具,但要用好向量这一工具解题,必须熟练运用加减法运算.第1层 用已知向量表示未知向量例1 如图所示,在平行六面体ABCD -A 1B 1C 1D 1中,设AA 1→=a ,AB →=b ,AD →=c ,M ,N ,P 分别是AA 1,BC ,C 1D 1的中点,试用a ,b ,c 表示以下各向量:(1)AP →;(2)A 1N →;(3)MP →+NC 1→. 解 (1)∵P 是C 1D 1的中点,∴AP →=AA 1→+A 1D 1→+D 1P →=a +AD →+12D 1C 1→=a +c +12AB →=a +c +12b .(2)∵N 是BC 的中点,∴A 1N →=A 1A →+AB →+BN →=-a +b +12BC →=-a +b +12AD →=-a +b +12c .(3)∵M 是AA 1的中点, ∴MP →=MA →+AP →=12A 1A →+AP →=-12a +⎝⎛⎭⎫a +c +12b =12a +12b +c ,又NC 1→=NC →+CC 1→=12BC →+AA 1→=12AD →+AA 1→=12c +a , ∴MP →+NC 1→=⎝⎛⎭⎫12a +12b +c +⎝⎛⎭⎫a +12c =32a +12b +32c . 点评 用已知向量来表示未知向量,一定要结合图形,以图形为指导是解题的关键.要正确理解向量加法、减法与数乘运算的几何意义.首尾相接的若干向量之和,等于由起始向量的始点指向末尾向量的终点的向量,我们可把这个法则称为向量加法的多边形法则.在立体几何中要灵活应用三角形法则,向量加法的平行四边形法则在空间仍然成立. 第2层 化简向量例2 如图,已知空间四边形ABCD ,连接AC 、BD .设M 、G 分别是BC 、CD 的中点,化简下列各表达式,并标出化简结果的向量. (1)AB →+BC →+CD →;(2)AB →+12(BD →+BC →);(3)AG →-12(AB →+AC →).解 (1)AB →+BC →+CD →=AC →+CD →=AD →. (2)AB →+12(BD →+BC →)=AB →+12BC →+12BD →=AB →+BM →+MG →=AG →. (3)AG →-12(AB →+AC →)=AG →-AM →=MG →. AD →、AG →、MG →如图所示.点评 要求空间若干向量之和,可以通过平移,将它们转化为首尾相接的向量,如果首尾相接的若干向量构成一个封闭图形,则它们的和为0.两个向量相加的平行四边形法则在空间仍成立,求始点相同的两个向量之和时,可以考虑运用平行四边形法则. 第3层 证明立体几何问题例3 如图,已知M 、N 分别为四面体ABCD 的面BCD 与面ACD 的重心,且G 为AM 上一点,且GM ∶GA =1∶3.求证:B 、G 、N 三点共线.证明 设AB →=a ,AC →=b ,AD →=c , 则BG →=BA →+AG →=BA →+34AM →=-a +14(a +b +c )=-34a +14b +14c ,BN →=BA →+AN →=BA →+13(AC →+AD →)=-a +13b +13c =43BG →.∴BN →∥BG →,即B 、G 、N 三点共线.2 空间向量易错点扫描 易错点1 对向量夹角与数量积的关系理解不清例1 “a·b <0”是“〈a ,b 〉为钝角”的________条件. 错解 a·b <0⇔cos 〈a ,b 〉=a·b|a||b |<0⇔〈a ,b 〉为钝角,所以“a·b <0”是“〈a ,b 〉为钝角”的充要条件.错因分析 错解中忽略了两个向量共线且反向的情况.剖析 当〈a ,b 〉=π时,a·b <0,但此时夹角不为钝角,所以“a·b <0”是“〈a ,b 〉为钝角”的必要不充分条件. 正解 必要不充分总结 a·b <0⇔a 与b 夹角为钝角或a 与b 方向相反,a·b >0⇔a 与b 夹角为锐角或a 与b 方向相同.易错点2 忽略两向量的夹角的定义例2 如图所示,在120°的二面角α—AB —β中,AC ⊂α,BD ⊂β,且AC ⊥AB ,BD ⊥AB ,垂足分别为A ,B .已知AC =AB =BD =6,试求线段CD 的长. 错解 ∵AC ⊥AB ,BD ⊥AB , ∴CA →·AB →=0,BD →·AB →=0,∵二面角α—AB —β的平面角为120°,∴〈CA →,BD →〉=120°.∴CD 2=CD →2=(CA →+AB →+BD →)2=CA →2+AB →2+BD →2+2CA →·AB →+2CA →·BD →+2BD →·AB →=3×62+2×62×cos 120°=72,∴CD =6 2.错因分析 错解中混淆了二面角的平面角与向量夹角的概念.向量CA →,BD →的夹角与二面角α—AB —β的平面角互补,而不是相等. 正解 ∵AC ⊥AB ,BD ⊥AB , ∴CA →·AB →=0,BD →·AB →=0,∵二面角α—AB —β的平面角为120°, ∴〈CA →,BD →〉=180°-120°=60°. ∴CD 2=CD →2=(CA →+AB →+BD →)2=CA →2+AB →2+BD →2+2CA →·AB →+2CA →·BD →+2BD →·AB →=3×62+2×62×cos 60°=144,∴CD =12. 易错点3 判断是否共面出错例3 已知O 、A 、B 、C 为空间不共面的四点,a =OA →+OB →+OC →,b =OA →+OB →-OC →,则与a 、b 不能构成空间的一个基底的是( ) A.OA → B.OB → C.OC → D.OA →或OB →错解 a =OA →+OB →+OC →,b =OA →+OB →-OC →, 相加得:OA →+OB →=12(a +b ),所以OA →、OB →都与a 、b 共面,不能构成空间的一个基底,故选D.剖析 OA →+OB →=12(a +b ),说明OA →+OB →与a 、b 共面,但不能认为OA →、OB →都与a 、b 共面.对A 、B :设OA →=x a +y b ,因为a =OA →+OB →+OC →,b =OA →+OB →-OC →,代入整理得(x +y -1)OA →+(x +y )OB →+(x -y )OC →=0,因为O 、A 、B 、C 不共面, 所以OA →、OB →、OC →不共面,所以x +y -1=0,x +y =0,x -y =0,此时,x 、y 不存在,所以a 、b 与OA →不共面, 故a 、b 与OA →可构成空间的一个基底. 同理a 、b 与OB →也可构成空间的一个基底.对C :因为a =OA →+OB →+OC →,b =OA →+OB →-OC →,相减有OC →=12(a -b ),所以OC →与a 、b 共面,故不能构成空间的一个基底. 正解 C易错点4 混淆向量运算和实数运算 例4 阅读下列各式,其中正确的是( ) A .a ·b =b ·c (b ≠0)⇒a =c B .a ·b =0⇒a =0或b =0 C .(a ·b )·c =a ·(b ·c )D.OA →·BO →=|OA →||BO →|cos(180°-∠AOB ) 错解 A(或B 或C)剖析 想当然地将向量的数量积运算和实数运算等价,以致出错.向量的数量积运算不满足消去律、结合律 ,故A 、C 错误;若a ·b =0⇒a =0或b =0或a ⊥b ,故B 错误;OA →·BO →的夹角是180°-∠AOB . 正解 D易错点5 忽略建系的前提例5 四边形ABCD 是边长为2的菱形,∠ABC =60°,AE ⊥平面ABCD ,AE =2,F 为CE 中点,试合理建立坐标系,求AF →、BC →所成角的余弦值.错解 以A 为坐标原点,以AB →、AD →、AE →的方向分别为x 、y 、z 轴的正方向,建立空间直角坐标系Axyz .此时AF →=(1,1,1),BC →=(0,2,0),所以cos 〈AF →,BC →〉=33.剖析 空间直角坐标系的建立的前提是三条直线两两垂直,而本题中直线AB 与AD 不垂直. 正解 设AC 、BD 交于点O ,则AC ⊥BD . 因为F 为CE 中点,所以OF ∥AE , 因为AE ⊥平面ABCD ,所以OF ⊥平面ABCD ,OF ⊥AC ,OF ⊥BD ,以O 为坐标原点,以OC →、OD →、OF →的方向分别为x 、y 、z 轴的正方向,建立空间直角坐标系Oxyz .此时AF →=(1,0,1),BC →=(1,3,0), 所以cos 〈AF →,BC →〉=24.3 空间直角坐标系构建三策略利用空间向量的方法解决立体几何问题,关键是依托图形建立空间直角坐标系,将其它向量用坐标表示,通过向量运算,判定或证明空间元素的位置关系,以及空间角、空间距离问题的探求.所以如何建立空间直角坐标系显得非常重要,下面简述空间建系的三种方法,希望同学们面对空间几何问题能做到有的放矢,化解自如. 1.利用共顶点的互相垂直的三条棱例1 已知直四棱柱中,AA 1=2,底面ABCD 是直角梯形,∠DAB 为直角,AB ∥CD ,AB =4,AD =2,DC =1,试求异面直线BC 1与DC 所成角的余弦值.解 如图以D 为坐标原点,分别以DA ,DC ,DD 1所在的直线为x 轴,y 轴,z 轴,建立空间直角坐标系,则D (0,0,0),C 1(0,1,2),B (2,4,0),C (0,1,0), 所以BC 1→=(-2,-3,2), CD →=(0,-1,0).所以cos 〈BC 1→,CD →〉=BC 1→·CD →|BC 1→||CD →|=31717.故异面直线BC 1与DC 所成角的余弦值为31717.点评 本例以直四棱柱为背景,求异面直线所成角.求解关键是从直四棱柱图形中的共点的三条棱互相垂直关系处着眼,建立空间直角坐标系,写出有关点的坐标和相关向量的坐标,再求两异面直线的方向向量的夹角即可. 2.利用线面垂直关系例2 如图,在三棱柱ABC -A 1B 1C 1中,AB ⊥面BB 1C 1C ,E 为棱C 1C 的中点,已知AB =2,BB 1=2,BC =1,∠BCC 1=π3.试建立合适的空间直角坐标系,求出图中所有点的坐标.解 过B 点作BP 垂直BB 1交C 1C 于P 点, 因为AB ⊥面BB 1C 1C ,所以BP ⊥面ABB 1A 1,以B 为原点,分别以BP ,BB 1,BA 所在的直线为x ,y ,z 轴,建立空间直角坐标系. 因为AB =2,BB 1=2,BC =1,∠BCC 1=π3,所以CP =12,C 1P =32,BP =32,则各点坐标分别为B (0,0,0),A (0,0,2),B 1(0,2,0),C (32,-12,0),C 1(32,32,0),E (32,12,0),A 1(0,2,2). 点评 空间直角坐标系的建立,要尽量地使尽可能多的点落在坐标轴上,这样建成的坐标系,既能迅速写出各点的坐标,又由于坐标轴上的点的坐标含有0,也为后续的运算带来了方便.本题已知条件中的垂直关系“AB ⊥面BB 1C 1C ”,可作为建系的突破口. 3.利用面面垂直关系例3 如图1,等腰梯形ABCD 中,AD ∥BC ,AB =AD =2,∠ABC =60°,E 是BC 的中点.将△ABE 沿AE 折起,使平面BAE ⊥平面AEC (如图2),连接BC ,BD .求平面ABE 与平面BCD 所成的锐角的大小.解 取AE 中点M ,连接BM ,DM .因为在等腰梯形ABCD 中,AD ∥BC ,AB =AD ,∠ABC =60°,E 是BC 的中点, 所以△ABE 与△ADE 都是等边三角形, 所以BM ⊥AE ,DM ⊥AE .又平面BAE ⊥平面AEC ,所以BM ⊥MD .以M 为原点,分别以ME ,MD ,MB 所在的直线为x ,y ,z 轴, 建立空间直角坐标系Mxyz ,如图,则E (1,0,0),B (0,0,3),C (2,3,0),D (0,3,0),所以DC →=(2,0,0),BD →=(0,3,-3), 设平面BCD 的法向量为m =(x ,y ,z ),由⎩⎪⎨⎪⎧m ·DC →=2x =0,m ·BD →=3y -3z =0.取y =1,得m =(0,1,1),又因平面ABE 的一个法向量MD →=(0,3,0), 所以cos 〈m ,MD →〉=m ·MD →|m ||MD →|=22,所以平面ABE 与平面BCD 所成的锐角为45°.点评 本题求解关键是利用面面垂直关系,先证在两平面内共点的三线垂直,再构建空间直角坐标系,然后分别求出两个平面的法向量,求出两法向量夹角的余弦值,即可得所求的两平面所成的锐角的大小.用法向量的夹角求二面角时应注意:平面的法向量有两个相反的方向,取的方向不同求出来的角度就不同,所以最后还应该根据这个二面角的实际形态确定其大小.4 用向量法研究“动态”立体几何问题“动态”立体几何问题是在静态几何问题中渗透了一些“动态”的点、线、面等元素,同时由于“动态”的存在,使得问题的处理趋于灵活.本文介绍巧解“动态”立体几何问题的法宝——向量法,教你如何以静制动. 1.求解、证明问题例1 在棱长为a 的正方体OABC —O 1A 1B 1C 1中,E 、F 分别是AB 、BC 上的动点,且AE =BF ,求证:A 1F ⊥C 1E .证明 以O 为坐标原点建立如图所示的空间直角坐标系, 则A 1(a,0,a ),C 1(0,a ,a ). 设AE =BF =x ,∴E (a ,x,0),F (a -x ,a,0). ∴A 1F →=(-x ,a ,-a ),C 1E →=(a ,x -a ,-a ).∵A 1F →·C 1E →=(-x ,a ,-a )·(a ,x -a ,-a ) =-ax +ax -a 2+a 2=0, ∴A 1F →⊥C 1E →,即A 1F ⊥C 1E . 2.定位问题例2 如图,已知四边形ABCD ,CDGF ,ADGE 均为正方形,且边长为1,在DG 上是否存在点M ,使得直线MB 与平面BEF 的夹角为45°?若存在,求出点M 的位置;若不存在,请说明理由.解题提示 假设存在点M ,设平面BEF 的法向量为n ,设BM 与平面BEF 所成的角为θ,利用sin θ=|BM →·n ||BM →||n |解出t ,若t 满足条件则存在.解 因为四边形CDGF ,ADGE 均为正方形, 所以GD ⊥DA ,GD ⊥DC .又DA ∩DC =D ,所以GD ⊥平面ABCD .又DA ⊥DC ,所以DA ,DG ,DC 两两互相垂直,如图,以D 为原点建立空间直角坐标系,则B (1,1,0),E (1,0,1),F (0,1,1). 因为点M 在DG 上,假设存在点M (0,0,t ) (0≤t ≤1)使得直线BM 与平面BEF 的夹角为45°. 设平面BEF 的法向量为n =(x ,y ,z ). 因为BE →=(0,-1,1),BF →=(-1,0,1),则⎩⎪⎨⎪⎧n ·BE →=0,n ·BF →=0,即⎩⎪⎨⎪⎧-y +z =0,-x +z =0,令z =1,得x =y =1,所以n =(1,1,1)为平面BEF 的一个法向量.又BM →=(-1,-1,t ),直线BM 与平面BEF 所成的角为45°,所以sin 45°=|BM →·n ||BM →||n |=|-2+t |t 2+2×3=2,2解得t=-4±3 2.又0≤t≤1,所以t=32-4.故在DG上存在点M(0,0,32-4),且DM=32-4时,直线MB与平面BEF所成的角为45°. 点评由于立体几何题中“动态”性的存在,使有些问题的结果变得不确定,这时我们要以不变应万变,抓住问题的实质,引入参量,利用空间垂直关系及数量积将几何问题代数化,达到以静制动的效果.5向量与立体几何中的数学思想1.数形结合思想向量方法是解决问题的一种重要方法,坐标是研究向量问题的有效工具,利用空间向量的坐标表示可以把向量问题转化为代数运算,从而沟通了几何与代数的联系,体现了数形结合的重要思想.向量具有数形兼备的特点,因此,它能将几何中的“形”和代数中的“数”有机地结合在一起.例1如图,在四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,∠BAD=90°,AD∥BC,且A1A=AB=AD=2BC=2,点E在棱AB上,平面A1EC与棱C1D1相交于点F.(1)证明:A1F∥平面B1CE;(2)若E是棱AB的中点,求二面角A1-EC-D的余弦值;(3)求三棱锥B1-A1EF的体积的最大值.(1)证明因为ABCD-A1B1C1D1是棱柱,所以平面ABCD∥平面A1B1C1D1.又因为平面ABCD∩平面A1ECF=EC,平面A1B1C1D1∩平面A1ECF=AF,所以A1F∥EC.又因为A1F⊄平面B1CE,EC⊂平面B1CE,所以A1F∥平面B1CE.(2)解因为AA1⊥底面ABCD,⊥BAD=90°,所以AA1,AB,AD两两垂直,以A为原点,以AB,AD,AA1分别为x轴、y轴和z轴,如图建立空间直角坐标系.则A 1(0,0,2),E (1,0,0),C (2,1,0),所以A 1E →=(1,0,-2),A 1C →=(2,1,-2).设平面A 1ECF 的法向量为m =(x ,y ,z ),由A 1E →·m =0,A 1C →·m =0,得⎩⎪⎨⎪⎧x -2z =0,2x +y -2z =0. 令z =1,得m =(2,-2,1).又因为平面DEC 的法向量为n =(0,0,1),所以cos 〈m ,n 〉=m ·n |m |·|n |=13, 由图可知,二面角AA 1-EC -D 的平面角为锐角,所以二面角A 1-EC -D 的余弦值为13. (3)解 过点F 作FM ⊥A 1B 1于点M ,因为平面A 1ABB 1⊥平面A 1B 1C 1D 1,FM ⊂平面A 1B 1C 1D 1,所以FM ⊥平面A 1ABB 1,所以VB 1-A 1EF =VF -B 1A 1E =13×S △A 1B 1E ×FM =13×2×22×FM =23FM . 因为当F 与点D 1重合时,FM 取到最大值2(此时点E 与点B 重合),所以当F 与点D 1重合时,三棱锥B 1-A 1EF 的体积的最大值为43. 2.转化与化归思想空间向量的坐标及运算为解决立体几何中的夹角、距离、垂直、平行等问题提供了工具,因此我们要善于把这些问题转化为向量的夹角、模、垂直、平行等问题,利用向量方法解决.将几何问题化归为向量问题,然后利用向量的性质进行运算和论证,再将结果转化为几何问题.这种“从几何到向量,再从向量到几何”的思想方法,在本章尤为重要.例2 如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=AB =2AD =2,E 为AB 的中点,F 为D 1E 上的一点,D 1F =2FE .(1)证明:平面DFC ⊥平面D 1EC ;(2)求二面角A -DF -C 的平面角的余弦值.分析 求二面角最常用的办法就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角.解 (1)以D 为原点,分别以DA 、DC 、DD 1所在的直线为x 轴、y 轴、z 轴建立如图所示空间直角坐标系,则A (1,0,0),B (1,2,0),C (0,2,0),D 1(0,0,2).∵E 为AB 的中点,∴E 点坐标为E (1,1,0),∵D 1F =2FE ,∴D 1F →=23D 1E →=23(1,1,-2) =(23,23,-43), ∴DF →=DD 1→+D 1F →=(0,0,2)+(23,23,-43) =(23,23,23), 设n =(x ,y ,z )是平面DFC 的法向量,则⎩⎪⎨⎪⎧ n ·DF →=0,n ·DC →=0, ∴⎩⎪⎨⎪⎧23x +23y +23z =0,2y =0.取x =1得平面FDC 的一个法向量为n =(1,0,-1).设p =(x ,y ,z )是平面ED 1C 的法向量,则⎩⎪⎨⎪⎧ p ·D 1F →=0,p ·D 1C →=0, ∴⎩⎪⎨⎪⎧ 23x +23y -43z =0,2y -2z =0,取y =1得平面D 1EC 的一个法向量p =(1,1,1), ∵n ·p =(1,0,-1)·(1,1,1)=0,∴平面DFC ⊥平面D 1EC .(3)设q =(x ,y ,z )是平面ADF 的法向量,则⎩⎪⎨⎪⎧ q ·DF →=0,q ·DA →=0, ∴⎩⎪⎨⎪⎧ 23x +23y +23z =0,x =0,取y =1得平面ADF 的一个法向量q =(0,1,-1),设二面角A -DF -C 的平面角为θ,由题中条件可知θ∈(π2,π),则cos θ=|n ·q |n |·|q ||=-0+0+12×2=-12, ∴二面角A -DF -C 的平面角的余弦值为12. 3.函数思想例3 已知关于x 的方程x 2-(t -2)x +t 2+3t +5=0有两个实根,且c =a +t b ,a =(-1,1,3),b =(1,0,-2).问|c |能否取得最大值?若能,求出实数t 的值及对应的向量b 与c 夹角的余弦值;若不能,说明理由.分析 写出|c |关于t 的函数关系式,再利用函数观点求解.解 由题意知Δ≥0,得-4≤t ≤-43, 又c =(-1,1,3)+t (1,0,-2)=(-1+t,1,3-2t ),∴|c |=(-1+t )2+(3-2t )2+1 =5⎝⎛⎭⎫t -752+65.当t ∈⎣⎡⎦⎤-4,-43时,f (t )=5⎝⎛⎭⎫t -752+65是单调递减函数,∴y max =f (-4),即|c |的最大值存在, 此时c =(-5,1,11).b·c =-27,|c |=7 3.而|b |=5,∴cos 〈b ,c 〉=b·c |b||c |=-275×73=-91535. 点评 凡涉及向量中的最值问题,若可用向量坐标形式,一般可考虑写出函数关系式,利用函数思想求解.4.分类讨论思想例4 如图,矩形ABCD 中,AB =1,BC =a ,P A ⊥平面ABCD (点P 位于平面ABCD 上方),问BC 边上是否存在点Q ,使PQ →⊥QD →?分析 由PQ →⊥QD →,得PQ ⊥QD ,所以平面ABCD 内,点Q 在以边AD为直径的圆上,若此圆与边BC 相切或相交,则BC 边上存在点Q ,否则不存在.解 假设存在点Q (Q 点在边BC 上),使PQ →⊥QD →,即PQ ⊥QD ,连接AQ .∵P A ⊥平面ABCD ,∴P A ⊥QD .又PQ →=P A →+AQ →且PQ →⊥QD →,∴PQ →·QD →=0,即P A →·QD →+AQ →·QD →=0.又由P A →·QD →=0,∴AQ →·QD →=0,∴AQ →⊥QD →.即点Q 在以边AD 为直径的圆上,圆的半径为a 2. 又∵AB =1,由题图知,当a 2=1,即a =2时,该圆与边BC 相切,存在1个点Q 满足题意; 当a 2>1,即a >2时,该圆与边BC 相交,存在2个点Q 满足题意; 当a 2<1,即a <2时,该圆与边BC 相离,不存在点Q 满足题意.综上所述,当a≥2时,存在点Q;当0<a<2时,不存在点Q.。
