非线性半参数EV模型的经验似然置信域
MA(∞)误差下部分线性模型的经验似然统计推断

MA(∞)误差下部分线性模型的经验似然统计推断于卓熙;王德辉【摘要】应用经验似然方法,针对误差为不可观测无穷阶滑动平均过程的部分线性模型,构造了回归参数的对数经验似然比检验统计量,并证明了统计量在参数取真值时渐近地服从X2分布,构造了参数的置信区间.模拟计算表明,经验似然方法优于最小二乘方法.【期刊名称】《吉林大学学报(理学版)》【年(卷),期】2011(049)004【总页数】10页(P615-624)【关键词】部分线性模型;MA(∞)误差过程;经验似然【作者】于卓熙;王德辉【作者单位】吉林财经大学管理科学与信息工程学院,长春130117;吉林大学数学学院,长春130012【正文语种】中文【中图分类】O212.70 引言考虑如下部分线性模型:(1)其中: yi是反应变量; xi=(xi1,…,xip)T是非随机设计点; β=(β1,…,βp)T是未知参数向量; ti∈[0,1]; g(·)是定义在[0,1]上的未知有界实值函数; εi是不可观测的误差项. 文献[1]应用模型(1)拟合了公用事业行业的早期消费曲线. 在误差变量是i.i.d的情形下, 文献[2-6]分别用不同的方法获得了模型(1)未知量的估计.在实际问题中, 误差独立同分布的假设并不总合适. 近年来, 具有序列相依误差的部分线性回归模型的研究已引起人们广泛关注. 用于误差建模的一种无穷阶滑动平均过程即为MA(∞)过程, 假设{εi}具有如下形式:(2)这里{ei}是i.i.d.随机变量列, 满足文献[7]应用文献[8]给出的线性过程多项式分解方法获得了参数β的半参数最小二乘估计(SLSE)的重对数律和渐近正态性. 文献[9]应用MA(∞)过程截断方法在更一般的情形下证明了参数β的SLSE的重对数律.经验似然是一类重要的构造非参数置信区间和检验的方法, 文献[10]对此方法的一般性质进行了系统研究. 文献[11-12]研究表明, 经验似然有类似于参数似然法的优良性, 特别是对数形式类似于Wilk’s理论, 趋于χ2分布. 文献[13-14]给出了用分组经验似然方法处理强相依的数据.本文在误差由式(2)定义的MA(∞)过程下应用经验似然方法构造了MA(∞)误差下模型(1)回归系数的经验似然比检验统计量, 并讨论了该统计量的渐近性质.1 方法与主要结果假设随机误差{εi,1≤i≤n}构成由式(2)定义的MA(∞)过程, 且令则假设0<|C(1)|<∞.给定β时g(·)的一个非参数估计量为这里Wni(·)(1≤i≤n)是一些定义在[0,1]上的权函数.令β的对数经验似然比统计量定义为(3)这里λ(β)∈Rp定义如下:(4)假设:(H1) 存在定义在[0,1]上的函数hj(·), 使得xij=hj(ti)+uij, i=1,2,…,n, j=1,2,…,p,(5)这里(ui1,…,uip)T=ui是实值向量, 满足(6)(7)其中: B为正定矩阵; (j1,…, jn)是(1,2,…,n)的任意置换; ‖·‖表示欧氏模;(8)C是不依赖于n的常数.(H2) 函数g(·), hj(·)(j=1,2,…,n)满足一阶Lipschitz条件.(H3) 权函数Wni(·)满足:∀t∈[0,1];这里bn=o(n-2/3(log n)-2);这里dn=O(n-1/3(log n)-1);对s,t∈[0,1]一致成立, 这里c2是一个常数.(H4) 由式(2)所定义的误差过程{εi}满足如下条件:(ii) {εi}的谱密度函数ψ(ω)有界非零, 即0<c3≤ψ(ω)≤c4<∞, ω∈(-π,π],这里c3和c4是常数.定理1 令β0为参数的真值, 假设(H1)~(H4)成立, 则当n→∞时,这里表示依分布收敛.由定理1, 可以建立β的α-水平置信域:这里cα满足2 模拟计算下面通过模拟计算比较经验似然方法和渐近正态方法. 为简单, 只考虑β为标量的情况.应用模型yi=xiβ+g(ti)+εi, εi=θεi-1+ei, 这里g(ti)=sin(2πti), β=1.5, 设计点从固定种子10的U[0,1]分布中产生, 设计点产生于这里vi是i.i.d.的且服从T(3)分布, ei是i.i.d.的且服从N(0,1)分布.由文献[7]中定理1知, β的最小二乘估计渐近服从正态分布, 即这里: 所以, β的水平为1-α的双侧置信区间为这里Zα满足Φ(Zα)=α, Φ(·)是标准正态分布的分布函数. 权函数具有如下形式:其中核函数K(t)是高斯核, 由最小平方交叉核实方法(LSCV)选取带宽hn. 样本容量分别取50,100和200; α=0.10, α=0.05. 基于500次模拟, 计算经验似然(EL)和渐近正态方法(LS)的覆盖率, 结果列于表1. 由表1可见, 两种方法在θ>0时结果较好. 由于由两种方法构造置信区间时都有C(1)=1/(1-θ), 因此在考虑的所有情形下, EL 方法比LS方法结果更好.表1 β的覆盖率Table 1 Coverage probabilities for β样品容量n参数α方法θ-0.5-0.3-0.1500.150.30.5500.10LS0.556 40.668 80.746 00.809 80.86640.925 20.978 0EL0.639 20.734 20.829 40.883 60.922 60.968 00.99220.05LS0.563 80.678 80.767 00.833 80.902 40.958 20.994 4EL0.646 60.774 80.861 20.913 40.959 00.987 40.999 21000.10LS0.564 60.667 60.763 60.826 80.888 80.938 60.983 8EL0.653 00.758 20.842 80.896 40.940 60.971 40.995 40.05LS0.568 40.674 80.773 40.843 20.912 40.957 60.992 6EL0.656 80.770 20.860 60.918 40.958 40.986 80.998 82000.10LS0.580 00.669 00.767 20.828 40.888 00.934 00.983 0EL0.661 80.756 40.841 80.896 20.942 40.970 60.996 80.05LS0.577 60.685 40.779 60.845 00.906 80.952 80.992 6EL0.668 80.778 80.861 20.914 60.958 60.983 00.998 43 定理的证明引理1 1) 假设(H2)和(H3)中(iv)成立, 则当n→∞时,这里G0(·)=g(·), Gj(·)=hj(·)(1≤j≤p);2) 假设(H1)~(H3)成立, 则当n→∞时,这里引理1的证明与文献[7]中引理2的证明类似.引理2 假设(H1)~(H3)成立, 则引理2的证明与文献[7]中引理3(i)的证明类似.引理3 对于式(2)中的线性过程, 假设(H3)中(iii)和(v)、 (H4)中(i)成立, 则证明参见文献[9]中引理2.引理4 对于式(2)中的线性过程, 假设(H4)中(i)成立, 则这里(j1, j2,…, jn)是(1,2,…,n)的任意置换.证明参见文献[9]中引理4.引理5 假设(H1)~(H4)成立, 则证明:这里:下面证明(9)由于故由Chebychev不等式, 得从而, 由Borel-Cantelli引理可得(10)令由和三级数定理, 有而注意到同理可得应用Bernstein’s不等式, 存在c5>0, 使得这里:是一个正的常数. 所以, 正确选择c6, 并应用Borel-Cantelli引理, 可得由以上证明可得(11)结合式(10)和(11), 即可得式(9). 应用引理1中1)、引理2和引理3、 (H1)和(H2), 即可完成引理5的证明.引理6 假设(H1)~(H4)成立, 则有证明: 由Zi的定义, 有对于1≤k≤p, 用表示的第k个元素, 应用假设(H1)和引理1, 有这里类似于以上证明, 应用引理1和引理3, 可得下面证明注意到对于1≤k≤p, (j1, j2,…, jn)是(1,2,…,n)的任意置换, 应用引理4, 有由文献[8], 有这里所以由假设(H1), 有应用Abel不等式, 有由假设(H4), 类似于文献[7]中引理5的证明, 有这里表示依概率收敛.结合以上证明并应用引理2, 即可完成引理6的证明. 引理7 假设(H1)~(H4)成立, 则∀a∈Rp.证明: 由引理6直接可得.引理8 假设(H1)~(H4)成立, 令则证明:应用引理2和引理3, 可得应用引理1, 有‖Rn3‖=O(n-2/3(log n)-2).由引理3和可得同理可证‖Rn5‖=O(n-1/3(log n)-1)O(n1/4log n)=O(n-1/12) a.s., ‖Rn6‖=O(n-1/3log n)O(n-1/3(log n)-1)=O(n-2/3) a.s. 下面证明(12)由文献[8], 有这里:为证明式(12), 只需证(13)(14)注意到这里:从而有故有应用Abel不等式, 可以证明对任意的矩阵A, 用Ahl表示A的第h行、第l列元素(h,l=1,2,…,p).下面证明(15)(16)若则式(15)成立. 而由假设(H4)中(i)可知式(15)成立.式(16)等价于对∀c>0,(17)若则式(17)成立;若则式(16)成立, 从而式(13)成立.由文献[8], 有这里:≜令则由文献[8]中引理3.6(b), 可得由及可知从而有注意到为证明(18)只需证(19)(20)若则式(19)成立. 又由文献[8]中引理5.9知, 若则由假设(H4)中(i)可知式(19)成立.式(20)等价于(21)对∀c>0, 由于从而式(21)成立.而式(18)得证.综上可见, 引理8成立.下面证明定理1. 由引理5~引理8, 类似于文献[10]中定理1的证明, 有结合引理6和引理8, 即可证得定理1.参考文献【相关文献】[1] Shiller R J. Smoothness Priors and Nonlinear Regression [J]. J Amer Statist Assoc, 1984, 79: 605-615.[2] Speckman P. Kernel Smoothing in Partial Linear Models [J]. J Royal Statist Soc B, 1988, 50(3): 413-436.[3] Chen H, Shiau J. A Two-Stage Spline Smoothing Method for Partial Linear Models [J]. J Statist Plann Inference, 1991, 27(2): 187-201.[4] Donald S G, Newey W K. Series Estimation of Semilinear Models [J]. J Multivariate Anal, 1994, 50(1): 30-40.[5] Hamilton S A, Truong Y K. Local Linear Estimation in Partial Linear Models [J]. J Multivariate Anal, 1997, 60(1): 1-19.[6] Härdle W, Liang H, Gao J. Partial Linear Models [M]. Heidelberg: Physica-Verlag, 2000.[7] Gao J T, Anh V V. Semiparametric Regression under Long-Range Dependent Errors [J]. J Statist Plann Inference, 1999, 80(1/2): 37-57.[8] Philips P C B, Solo V. Asymptotics for Linear Processes [J]. Ann Statist, 1992, 20(2): 971-1001.[9] Sun X Q, You J H, Chen G, et al. Convergence Rate of a Class of Estimators in Partially Linear Regression Models with Serially Correlated Errors [J]. Communications Statist: Theory Methods, 2002, 31(12): 2251-2252.[10] Owen A B. Empirical Likelihood Confidence Regions [J]. Ann Statist, 1990, 18(1): 90-120.[11] Owen A B. Empirical Likelihood for Linear Models [J]. Ann Statist, 1991, 19(4): 1725-1747.[12] QIN Jin, Lawless J. Empirical Likelihood and General Estimating Equations [J]. Ann Statist, 1994, 22(1): 300-325.[13] Kitamura Y. Empirical Likelihood Methods with Weakly Dependent Processes [J]. Ann Statist, 1997, 25(5): 2084-2102.[14] ZHANG Jun-jian, WANG Cheng-ming, WANG Wei. Empirical Likelihood Ratio Confidence Regions for Dependent Samples [J]. Appl Math J Chines Univ: Ser A, 1999,14(1): 63-72. (张军舰, 王成名, 王炜. 相依样本情形时的经验似然比置信区间 [J]. 高校应用数学学报: A辑, 1999, 14(1): 63-72.)。
协变量缺失下线性EV模型中参数的经验似然推断

定条件下 , 明了构造 的估计 函数其经验似 然比趋 于一个标准的卡方分布。利用这个结果可 以构造参数的置信域。 证 估计 函数 经验似然 A 置信域
关键词 线性 E V模 型 中图法分类号 O 1. ; 2 2 1
文献 标志码
E (r Y i- r be) V er s nv i l 模型 、 o— aa s 缺失数据下的回归模 型都是当今统计界研究 的热 点模型 。不论是 E V模 型
断, 文献 [ ] 2 考虑 了没有核实数据响应变量随机缺失 的 线性 E V模型 , 利用 回归 借补方法 , 构造 了未知参数 的
尸 6=1 l W)=P =1 Y ( , l, ( )=叮 1 。 2 I r , () ()
MA R条件表 明在 给定 l 的条件 下 , 与 条 , , 6 件独 立 。 现仅 考虑 测量误 差 U的方差 V r U a( )= ∑ 已知 时 , 构造 口的经验似 然置信 域 。 如何 在协变 量没有 缺失 而仅有 测量误 差时 , 令
[ I) 一 I )】 卢 +∑ ;
() 4 i=12… , ,, n
M1 II , ≤ ≤ K( )≤ M2 I 且 ¨ , I
f( d= ,M “ u 0fK ) ≠ 。 M M 1f (d= ,u (d 0 ) K)
C :当 5 ∞ 时 , +0 n h_ ,h ∞ ,h n 0 。
考虑 如下 的线性 E V模 型
21 0 0年 5月 1 1日收到 山东省 自然科学基金 ( 2 0 A 4) Q 0 8 0 资助
式( ) 3 中 = 6 Y)=1 )但 式 ( ) P( =1 i f T ( 。 3 不能
直接 作 为估 计 函数 ,因为式 中的 耵 , ( l ) , E
部分线性变系数EV模型估计的渐近正态性

部分线性变系数EV模型估计的渐近正态性冯三营;牛惠芳【摘要】研究非参数部分带有测量误差(EV)的部分线性变系数模型,综合局部纠偏方法和Profile最小二乘估计方法定义了模型中未知参数和系数函数的估计,并在适当条件下证明了它们的渐近性质,最后通过数值模拟研究了所提估计方法在有限样本下的实际表现.【期刊名称】《河南科技大学学报(自然科学版)》【年(卷),期】2011(032)002【总页数】5页(P83-87)【关键词】部分线性变系数模型;测量误差;局部纠偏;profile最小二乘;渐近正态性【作者】冯三营;牛惠芳【作者单位】洛阳师范学院数学科学学院,河南洛阳471022;洛阳师范学院数学科学学院,河南洛阳471022【正文语种】中文【中图分类】O212.70 前言考虑部分线性变系数模型:其中,Y为一维响应变量;X为p维协变量;Z为q维协变量;T为一维协变量;β为p维未知参数向量; α(T)=(α1(T),…αq(T))τ是q维未知函数向量;ε是不可观测的随机误差。
作为变系数模型和部分线性模型的推广,模型(1)最近得到了广泛的关注,已有大量学者进行了深入的研究,例如,文献[1]基于局部多项式方法最早研究了该模型;文献[2]利用小波方法估计了模型中的参数部分和非参数部分;文献[3]基于局部线性方法提出了一种新的有效估计;文献[4]提出了Profile最小二乘估计并且基于广义似然比检验方法研究了该模型的检验问题。
但在实际操作中,协变量X,Z往往带有测量误差。
对协变量X带有测量误差的部分线性变系数模型,文献[5]在测量误差向量协方差阵已知的情形下,获得了模型中参数和非参数部分的估计,并证明了估计量的相合性和渐近正态性。
文献[6]运用经验似然方法构造了模型中参数的最大经验似然估计及其经验似然置信域,并证明了估计量的渐近正态性。
对于协变量Z带有测量误差的部分线性变系数模型尚未见到相关文献。
本文考虑协变量Z带有测量误差的部分线性变系数模型,运用局部纠偏方法和Profile最小二乘估计方法得到了模型中未知参数和未知系数函数的估计,并在适当条件下研究了它们的渐近性质,并对本文所提估计方法在有限样本下的实际表现进行了数值模拟研究。
【国家自然科学基金】_非线性半参数模型_基金支持热词逐年推荐_【万方软件创新助手】_20140802
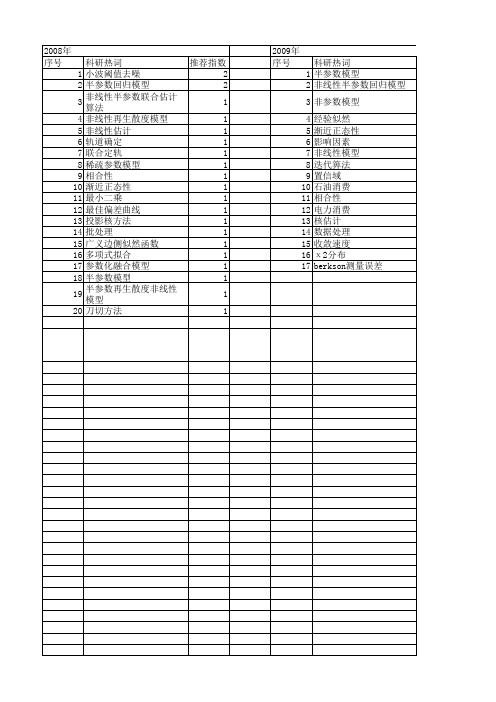
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 半参数模型 非线性半参数回归模型 非参数模型 经验似然 渐近正态性 影响因素 非线性模型 迭代箅法 置信域 石油消费 相合性 电力消费 核估计 数据处理 收敛速度 χ 2分布 berkson测量误差
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 推荐指数 小波阈值去噪 2 半参数回归模型 2 非线性半参数联合估计算法 1 非线性再生散度模型 1 非线性估计 1 轨道确定 1 联合定轨 1 稀疏参数模型 1 相合性 1 渐近正态性 1 最小二乘 1 最佳偏差曲线 1 投影核方法 1 批处理 1 广义边侧似然函数 1 多项式拟合 1 参数化融合模型 1 半参数模型 1 半参数再生散度非线性模型 1 刀切方法 1
2014年 科研热词 推荐指数 贸易开放 1 碳排放 1 半参数面板空间滞后模型 1 内生性 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 非参数随机前沿面 载体磁场 补偿 级数估计 相合性 渐近正态性性 技术效率 平滑转换回归模型 局部线性估计 地磁导航 半参数模型 tobit模型
推荐指数 1 1 1 1 1 1荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2011年 科研热词 风险管理 风险价值 面板结构 非线性系统 非线性 遗传算法 超越对数生产函数 误差分析 自助法 线性模型 神经网络 指向误差 广义似然比检验 局部线性估计 小波分析 多尺度分析 多体系统建模 半参数模型 半参数有效估计 半参数回归模型 半参数变系数模型 光电探测系统 var模型 gmm估计 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
部分函数型EV回归模型的经验似然推断①

部分函数型EV回归模型的经验似然推断①方连娣【期刊名称】《《佳木斯大学学报(自然科学版)》》【年(卷),期】2019(037)006【总页数】4页(P1013-1016)【关键词】函数型数据; 测量误差; 经验似然; 卡方分布; 渐近置信域【作者】方连娣【作者单位】铜陵学院数学与计算机学院安徽铜陵244000; 江苏大学电气信息工程学院江苏镇江212013【正文语种】中文【中图分类】O212. 70 引言近年来,函数型数据分析成为统计研究领域的一个热点问题,受到诸多学者的广泛关注。
实际中,通常观测到的数据既有函数型的,又有矢量型的,称之为混合数据。
鉴于此,文献[1]提出了包含这样混合数据的部分函数型线性回归模型。
自该模型被提出后,人们对该模型在无误差情形下进行了充分研究,比如文献[2]给出了其系数函数的估计量及其渐近性质。
文献[3]构造了模型中未知参数和未知斜率函数的岭估计。
文献[4]在相依模型误差下,给出了未知参数和斜率函数的估计量。
而现实中,解释变量的观测值可能存在测量误差,如由于医学仪器的精密度而使得在医学研究中对某项指标的观测往往含有测量误差等。
而对文献[1]提出的部分函数型线性模型在解释变量有测量误差下统计推断的研究尚少。
因此,参考面板数据下误差模型的研究成果[5-7],采用经验似然方法对部分函数型线性模型进行统计推断。
首先构造出未知参数的经验似然比统计量,并证明该统计量是渐近卡方的,给出了未知参数的置信域,以及未知参数和系数函数的极大经验似然估计及其收敛速度。
1 方法与主要结果考虑带有测量误差的部分函数型线性回归模型:(1)其中,Y是实值响应变量,Z是q维随机向量且EZ=0,E(ZτZ)<;真实变量Z不能被观测,只能观测到替代变量W的值;X(t)∈L2[0,1]是随机过程且EX=0,E(‖X‖2)=EX2(t)dt<;θ和β(t)分别是q维未知回归参数和未知系数函数,且β(t)∈L2[0,1],‖β‖2<;e和υ分别是独立于(X,W,Z)的模型误差和测量误差向量,e和υ也相互独立,且E(e)=E(υ)=0,var(e)=σ2<,cov(υ)=Λ已知。
【国家自然科学基金】_右删失_基金支持热词逐年推荐_【万方软件创新助手】_20140730
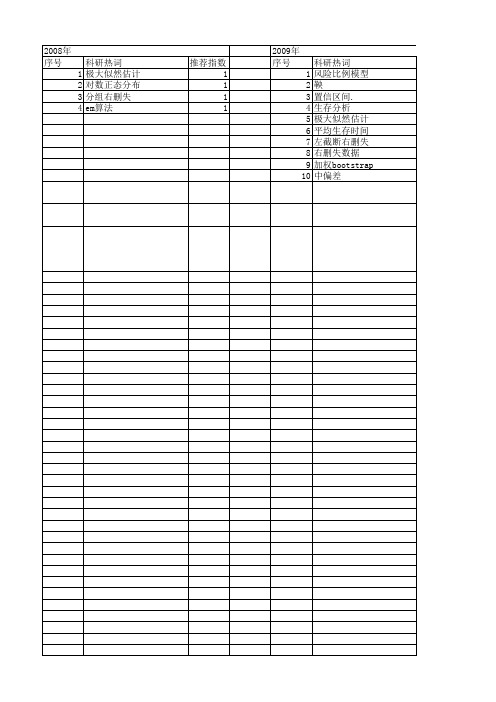
科研热词 极大似然估计 对数正态分布 分组右删失 em算法
推荐指数 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10
科研热词 风险比例模型 鞅 置信区间. 生存分析 极大似然估计 平均生存时间 左截断右删失 右删失数据1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2014年 科研热词 推荐指数 非线性回归 1 经验分布函数 1 满条件分布 1 影响函数 1 广义 m估计 1 完全数据似然函数 1 右删失数据 1 右删失 1 单一插补法 1 区间删失数据 1 sc(self-consistent)算法 1 metropolis-hastings 算法 1 mcmc 方法 1 kaplan-meier权 1 gibbs 抽样 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 推荐指数 零膨胀poisson回归 1 随机效应 1 经验似然估计 1 线性 1 混合物 1 极限分布 1 有限样本性质 1 最大边际似然估计 1 指标模型 1 应用程序 1 右删失数据 1 删失数据 1 censored data, regression model, 1 empirical likeli
推荐指数 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4
科研热词 非线性模型 调整的经验似然 置信域 删失数据
推荐指数 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9
2011年 科研热词 随机删失 经验bayes检验 线性模型 纵向数据 相合性 渐进最优性 无偏转换 收敛速度 删失 推荐指数 1 1 1 1 1 1 1 1 1
响应变量存在缺失时部分线性模型的经验似然推断
响应变量存在缺失时部分线性模型的经验似然推断杨宜平; 薛留根; 程维虎【期刊名称】《《高校应用数学学报A辑》》【年(卷),期】2010(025)001【总页数】10页(P43-52)【关键词】部分线性模型; 借补; 经验似然; 缺失数据; 置信区间【作者】杨宜平; 薛留根; 程维虎【作者单位】北京工业大学应用数理学院北京100124【正文语种】中文【中图分类】O212.7考虑如下部分线性模型其中Y是响应变量,X是p维协变量,Z为标量协变量,v(·)是未知函数,ε为随机误差且对模型(1.1)的研究已有许多文献,Engle等[1]在研究天气与电力需求的关系时首次引入该模型,随后得到了广泛的应用.Liang等[2]考虑了模型(1.1),其中协变量X含有测量误差,提出了参数β的修正估计,研究了估计的相合性和渐近正态性;Liang等[3]考虑了模型(1.1)中X随机缺失的情况,给出了β和函数v(·)的估计;Wang等[4]考虑了模型(1.1)中Y随机缺失,提出了Y的均值的几种估计;Liang等[5]考虑了响应变量带有缺失而协变量带有测量误差的部分线性模型,给出了基于观测数据下参数β的估计及总体均值E(Y)的估计;Wang和Sun[6]仍考虑了模型(1.1)中响应变量缺失的情况,对缺失数据借补后,给出了估计β和函数v(·)的方法及估计的性质.本文感兴趣的是模型(1.1)中响应变量Y缺失的情形,即当δ=1时,表示Y能观测;δ=0时,表示Y缺失.本文的目的是估计模型(1.1)中参数部分和函数部分的置信域和逐点置信区间.注意到Y缺失,很自然的想到,当Y的缺失很大时,基于观测的数据估计参数β和函数v(z)会影响估计的精度.为了处理缺失数据,本文采用了借补的思想.先对缺失值进行借补,然后估计参数β和函数v(z)的置信域和逐点置信区间.对参数β,文献[6]中定理2.1给出了参数β的估计的渐近正态性,但从该定理可看出估计的极限方差的形式很复杂且含有未知部分需要估计,基于正态性去构造置信区间会影响区间的精度.这促使本文考虑用Owen[7-8]提出的经验似然方法去构造参数β的置信区间,避免了估计极限方差且有较高的精度.对函数v(z),构造了函数的逐点置信区间.2.1 参数部分的经验似然推断设是来自模型(1.1)一个不完全随机样本,其中可以完全观测.当δi=1时,Yi可以观测;当δi=0时,Yi缺失.在本文中,我们假定Y为随机缺失,即:其中π(X,Z)未知.(2.1)式表明了在给定X和Z的条件下,δ和Y条件独立.该假定在实际应用中是合理的[4,6].l(β)不能直接应用于β的统计推断,因为它包含未知函数以及Hi,解决这个问题的一个自然的想法就是用它们的估计去代替.考虑Hi的估计,其中分别为基于观测数据下β和v(Zi)的估计.记据文献[4]可知这里分别为mx(z)和my(z)的估计,即其中为核函数,h1为带宽.µ1(z),µ2(z)的核估计分别为其中且M(·)为核函数,为带宽.在中分别用代替得到一个估计的辅助向量,并记之为则可以定义一个估计的对数似然比函数其中对任意给定的β,假设0在点所构成的凸集的内部,则存在唯一的解.用Lagrange乘子法,可以表示为这里λ由下式确定:对(2.4)式进行Taylor展开,并结合4中的引理2和引理3,可得(参见定理1的证明) 为了给出的渐近分布,需引入一些记号:由引理1可知,依分布收敛到均值为0,方差为V(β)的正态分布.进一步,由引理2,其中表示依概率收敛.因此,不再渐近于标准分布,而是依分布收敛到自由度为1的标准分布的加权和.定理1将给出渐近分布.定理1假设在4中的条件成立,如果β是参数真值,则其中表示依分布收敛,的特征值,为相互独立的自由度为1的χ2随机变量.利用定理1构造β的置信域需要估计权重ωi,这样会降低置信域的精度.下面给出一个调整的对数经验似然比,使得调整的对数经验似然比渐近于标准χ2分布.令根据Rao和Scott[9]的结果,可以定义一个调整的对数经验似然比其中定理2给出了渐近于自由度为p的标准χ2分布.定理2假设在4中的条件成立,如果β是参数真值,基于定理2,可以构造β的置信域,以的1−α分位数,0<α<1.由定理2可以得到β的近似1−α置信域为2.2非参数部分的经验似然推断对给定的β,令则模型(2.2)变为其中E(e|X=x,Z=z)=0.利用与文献[10]中2.2节的方法,构造辅助随机向量但中含有未知参数β和Hi,为此用的估计代替,则得到ηi(v(z))的估计则可以定义v(z)的被估计的经验对数似然比函数,即用Lagrange乘子法,可以表示为这里λ1由下式确定:下面的定理给出的渐近性质:定理3假设在4中的条件成立,对任意给定的(A是Z的有界支撑集),如果v(z0)为参数真值,则基于定理3,可以构造v(z0)的置信域,以的1−α分位数,0<α<1.由定理3可以得到v(z0)的近似1−α逐点置信域为考虑部分线性模型数据产生如下:核函数带宽的选取采用文献[6]带宽选取的方法.基于上述模型,我们考虑如下三种缺失机制:(1)当|x−1|+|z−0.5|≤1时,否则,以上三种情况的均值分别为下面模拟中,我们取样本容量分别为n=60,100,200.显著水平为0.05.各自做了1000次模拟.对参数部分,用本文的经验似然(IEL)方法得到的β的置信区间与正态逼近(INA)方法构造β的置信区间进行了比较,其中正态逼近方法基于Wang和Sun[6]定理2.1中β的渐近分布.在模拟过程中,也与未借补(忽略缺失值)的经验似然(NIEL)方法构造β的置信区间进行了比较,模拟结果在表1中给出.从表1可以得到如下结论:(1)本文提出的基于经验似然构造置信区间的方法(IEL)优于正态逼近方法(INA)和未借补的经验似然方法(NIEL).IEL方法给出了更小的置信区间,且覆盖概率大. (2)对任意固定的缺失概率,随着样本量的增加,三种方法得到的β的置信区间的平均长度在减少,覆盖概率越接近置信水平0.95.同时,缺失概率也影响β的置信区间,对任意固定的样本容量,随着缺失概率的增加,置信区间的平均长度增加.对函数v(z),模拟了v(z)的置信水平为95%的逐点置信区间.我们仅列出了n=100的结果,模拟结果见图1.从图1可以看出本文的方法构造的逐点置信区间大体上令人满意.在证明本文的结论之前,首先给出一些正则化条件.(C1)Z的密度函数fZ(z)具有有界的二阶连续偏导数,且满足∞,这里A是Z的有界支撑集.(C2)是正定矩阵,是正定矩阵,V(β)是正定矩阵,其中V(β)在2节中定义.(C4)核K(·)和M(·)是有界的2阶核函数且具有紧支撑.(C5)µ1(·)和µ2(·)具有有界的二阶连续偏导数;mx(·)和my(·)具有有界的二阶连续偏导数, v(·)具有有界的二阶连续偏导数.为了证明定理1,需要先证明以下几个引理:引理1在定理1的条件下,如果β是参数真值,则证通过简单的计算可得其中由文献[5]中的(A.2)式可知利用大数定律及(4.4)式可得由文献[6]中的(A.14)式可知其中π(z)=P(δ=1|Z=z).类似文献[6]中(A.18)和(A.19)式的证明可得注意到结合(4.2)-(4.3)和(4.5)-(4.7)式,可得由文献[6]中的(A.21)-(A.26)式可得由中心极限定理,结合(4.1),(4.8)和(4.9)式可得引理1.引理2在定理1的条件下,如果β是参数真值,则证利用引理2并类似文献[8]中(2.14)式的论证可以证明第二式.下证明第一式,仍使用引理1证明中的记号.显然利用文献[8]中的引理3可得B1=op(n1/2).结合引理1中的证明可以推出B2=op(n1/2).第1个等式证毕.定理1的的证明对(2.4)式进行Taylor展开,利用引理2和3得由(2.5)式可得利用引理1-3得由此式结合(4.10)式可证得结合引理3可得由引理1可得其中1p是p×p的单位阵.而具有相同的特征值,因此,由(4.11)和(4.12)式可证得定理1.定理2的的证明令显然,类似引理2的证明可得结合引理1,可证得定理2.为了证明定理3,需下面引理:引理4在定理3的条件下,如果v(z0)是参数真值,则有证经简单的计算可得又由文献[6]中的定理2.1可知则类似文献[11]中引理1的证明可得结合(4.13)-(4.16),可得引理4.引理5在定理3的条件下,如果v(z0)是参数真值,则有证我们仍采用引理4的记号,令Si=J2i+J3i+J4i+J5i,则有由大数定律可得结合引理4用类似引理2的证法可得引理证毕.定理3的的证明通过类似于定理1的证法可得【相关文献】[1]Engle R F,Granger C W J,Rice J,et al.Semiparametric estimates of the relation between weather and electricity sales[J].J Amer Statist Assoc,1986,80:310-319.[2]Liang H,H¨ardle H,Carroll R J.Estimation in a semiparametric partially linear error-invariables model[J].Ann Statist,1999,27:1519-1535.[3]Liang H,Wang S,Robins J M,et al.Estimation in partially linear models with missing covariates[J].J Amer Statist Assoc,2004,99:357-367.[4]Wang Q H,Linton O,H¨ardle W.Semiparametric regression analysis with missing response at random[J].J Amer Statist Assoc,2004,99:334-345.[5]Liang H,Wang S,Carroll R J.Partially linear models with missing response variables and error-prone covariates[J].Biometrika,2007,94:185-198.[6]Wang Qihua,Sun Zhihua.Estimation in partially linear models with missing responses at random[J].J Multivariate Anal,2007,98:1470-1493.[7]Owen A B.Empirical likelihood ratio confidence intervals for a singlefunction[J].Biometrika, 1988,75:237-325.[8]Owen A B.Empirical likelihood ratio confidence regions[J].Ann Statist,1990,18:90-120.[9]Rao J,Scott A.The analysis of categorical data from complex sample surveys:Chi-squared tests for goodness-of-fit and independence in two-way tables[J].J Amer Statist Assoc,1981, 76:221-230.[10]Xue Liugen,Zhu Lixing.Empirical likelihood-based inference in a partially linear model for longitudinal data[J].Sci China Ser A,2008,51:115-130.[11]Wu C O,Chiang C T,Hoover D R.Asympotic confidence regions for kernel smoothing ofa varying-coefficient model with longitudinal data[J].J Amer Statist Assoc,1998,93: 1388-1402.。
经验似然介绍和研究状况
❖ 非参数统计又称为非参数检验,是指在不考 虑原总体分布或者不做有关参数假定旳前提 下,尽量从数据或样本本身取得所需要旳信 息,经过估计而取得分布旳构造,并逐渐建 立对事物旳数学描述和统计模型旳措施,更 为稳健。
❖ 非参数统计措施一般称为“分布自由”旳措施,即 非参数数据分析措施对产生数据旳总体旳分布不做 假设,或者仅给出很一般旳假设,例如连续型分布、 对称分布等某些简朴旳假设,成果一般有很好旳稳 定性。所以合用范围非常宽泛。 在经典旳统计框架
❖ Wang与Jing(2023),Wang与 `Vang(2023),Wang与Li(2023), Wang 与 Rao(2023),Wang与Rao(2023a,b,c)推广 Owen在完全样本下旳经验似然措施到上面所 提到旳三种不完全数据类型旳统计推断
❖ Wang与Jing(2023), Qin与Jing(2023), Wang 与Li(2023)及Li与Wang(2023)在随机删失下 发展了生存分布一类泛函、处理差别、随机 删失线性及部分线性模型旳统计推断.
❖ 经验 似 然 是Owen(1988)在完全样本下提出 旳一种非参数统计推断措施,它有类似于 bootstrap旳抽样特征.这一措施与经典旳或当 代旳统计措施比较有诸多突出旳优点,如:用 经验似然措施构造置性区间除有域保持性、 变换不变性及置信域旳形状由数据自行决定 等诸多优点外,还有Bartlett纠偏性及无需构 造轴统计量等优点。
y xT ,i 1,..., n x p维协变量,y 反映变量, -p维未知参数, -独立同服从均值0的随机变量误差
广义线性模型
y g(xT )
使E[( y xT )2 ]达到最小的 =(E(xT x))1E ( xT y)
【国家自然科学基金】_经验似然比_基金支持热词逐年推荐_【万方软件创新助手】_20140731
科研热词 经验似然 置信域 置信区间 缺失数据 部分线性模型 线性模型 分位数 黄麂 鹿科 非线性模型 非线性半参数模型 随机缺失 随机回归插补 辅助信息 调整的经验似然 纵向数据 测量误差 正选择 普通光滑 插值 局部纠偏 多态性 变系数ev模型 单指标模型 半参数模型 删失数据 分数线性回归填补 分数填补法 分块经验似然 借补 χ 2分布 wilks定理 mhc-drb
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
科研热词 推荐指数 经验似然 5 删失数据 3 置信区间 2 单指标模型 2 分组经验似然 2 非线性半参数回归模型 1 随机距离 1 随机微分方程 1 递推型估计 1 边际密度函数 1 负相协样本 1 试用 1 肌肉收缩 1 肌电信号 1 置信区间. 1 治疗效果 1 概率密度函数 1 极限分布 1 期望型检验 1 推理过程 1 拟合优度检验 1 强混合 1 广义似然比检测法 1 判决阈值 1 分块经验似然 1 分位点型检验 1 似然法 1 似然比检验统计量 1 估计方差 1 二阶扩散过程 1 χ ~2分布 1 x~2分布 1 x2分布 1 rubin的随机经验分布函数 1 na样本 1 na sample, probability density1 function, recursiv empirical likelihood, pretest-posttest 1 trial, tre
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 推荐指数 经验似然 4 缺失数据 2 附加信息 1 自回归条件久期(acd)模型 1 自回归条件 1 置信区域 1 条件分位数 1 最不利点集 1 拟似然函数 1 广义线性模型 1 两样本中位数 1 不等式约束 1
半参EV模型和缺失数据下估计方程的经验似然推断的开题报告
半参EV模型和缺失数据下估计方程的经验似然推断的开题报告1. 研究背景和目的随着大数据时代的到来,数据缺失问题已经成为许多研究领域中的一个重要挑战。
在实际应用中,经常会出现数据缺失的情况,这就要求研究者需要采用合适的方法来处理缺失数据,以确保研究结果的准确性和可靠性。
因此,本文旨在探讨缺失数据下估计方程的经验似然推断方法,并应用在半参EV模型中。
2. 研究方法本文主要采用以下方法进行研究:(1)分析半参EV模型,并应用缺失数据下估计方程的经验似然推断方法进行参数估计。
(2)通过模拟实验,验证缺失数据下估计方程的经验似然推断方法在参数估计上的有效性和稳定性。
(3)通过实际数据应用,验证缺失数据下估计方程的经验似然推断方法在实际问题中的应用价值。
3. 研究内容(1)缺失数据下估计方程的经验似然推断方法在缺失数据下,如果简单地忽略缺失数据,将会导致参数估计的偏差和方差的增大。
此时,我们可以采用经验似然推断方法来处理缺失数据,将缺失数据看作隐变量,利用EM算法进行参数估计,并通过Bootstrap方法进行标准误估计。
(2)半参EV模型半参EV模型是一种在经济学和金融学领域中广泛使用的统计模型,在风险管理和金融衍生品定价中有着重要的应用。
该模型的特点是同时考虑了风险中性和实际中性的假设,并通过随机过程中的期望值、方差和协方差等统计量来分析模型的性质和参数。
(3)模拟实验和实证分析本文将通过模拟实验来验证缺失数据下估计方程的经验似然推断方法的有效性和稳定性,并通过实际数据应用来证明该方法在实际问题中的应用价值。
4. 研究意义本文提出的缺失数据下估计方程的经验似然推断方法和半参EV模型相结合的方法,不仅可以有效地处理缺失数据问题,在参数估计和标准误估计上有较高的精度,而且可广泛应用于风险管理、金融衍生品定价等领域。
因此,该研究具有重要的理论和实际意义。
5. 研究计划(1)文献综述和理论分析(2个月)对半参EV模型和缺失数据下估计方程的经验似然推断方法进行文献综述,并进行相关理论分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
