证明(一)练习题精选

合集下载

第十八章平行四边形正方形证明专项习题2021-2022学年人教版八年级数学下册

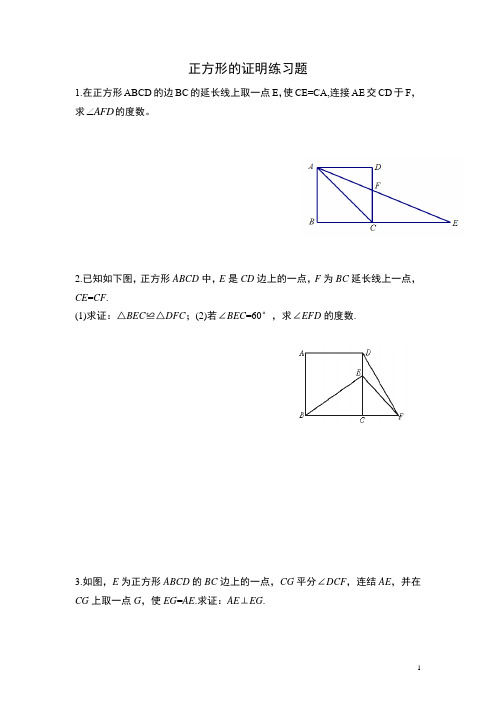
正方形的证明练习题1.在正方形ABCD的边BC的延长线上取一点E，使CE=CA,连接AE交CD于F，求AFD的度数。

2.已知如下图，正方形ABCD中，E是CD边上的一点，F为BC延长线上一点，CE=CF.(1)求证：△BEC≌△DFC；(2)若∠BEC=60°，求∠EFD的度数.3.如图，E为正方形ABCD的BC边上的一点，CG平分∠DCF，连结AE，并在CG上取一点G，使EG=AE.求证：AE⊥EG.4.P为正方形ABCD内一点，PA=1，PB=2，PC=3，求∠APB的度数.5.如图，在正方形ABCD中，P为BC上一点，Q为CD上一点，(1)若PQ=BP+DQ，求PAQ∠。

（2）若45∠=︒,求证：PQ=BP+DQ.PAQ6.如图，已知正方形ABCD的对角线相交于O，点E.F分别在AB与BC边上的点，且BE=CF.求证：OE⊥OF.7．如图，正方形ABCD的面积为1，则以相邻两边中点连线EF为边正方形EFGH的周长为多少？8．如图，有一平行四边形ABCD与一正方形CEFG，其中E点在AD 上．若∠ECD=35°，∠AEF=15°，则∠B的度数为何？9．如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90°，AE=CF=5，BE=DF=12，求EF的长。

10．如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH．若BE：EC=2：1，求线段CH的长。

11．如图，在正方形ABCD中，对角线AC，BD相交于点O，E，F分别在OD，OC上，且DE＝CF，连接DF，AE，AE的延长线交DF于点M.求证：AM⊥DF.12．如图，P，Q，R，S四个小球分别从正方形的四个顶点A，B，C，D同时出发，以同样的速度分别沿AB，BC，CD，DA的方向滚动，其终点分别是B，C，D，A.不管滚动多长时间，求证：连接四个小球所得的四边形PQRS总是正方形．13．如图，在正方形ABCD中，G是BC上任意一点，连接AG，DE⊥AG于E，BF∥DE交AG于点F，探究线段AF，BF，EF三者之间的数量关系，并说明理由．14．如图1，在正方形ABCD中，E.F分别是边AD.DC上的点，且AF⊥BE．（1）求证：AF=BE；（2）如图2，在正方形ABCD 中，M.N.P.Q 分别是边AB.BC.CD.DA 上的点，且MP ⊥NQ ．MP 与NQ 是否相等？并说明理由．15.如图，正方形ABCD 与正方形OMNP的边长均为10，点O 是正方形ABCD 的中心，正方形OMNP 绕O 点旋转，证明：无论正方形OMNP 旋转到何种位置，这两个正方形重叠部分的面积总是一个定值，并求这个定值．16.如图，P 是边长为1的正方形ABCD 对角线AC 上一动点（P 与A .C 不重合），点E 在射线BC 上，且PE=PB .（1）求证：① PE=PD ； ② PE ⊥PD ；17.如图1，四边形ABCD 是正方形，G 是CD 边上的一个动点(点G 与C.D 不重合)，以CG 为一边在正方形ABCD 外作正方形CEFG ，连结BG ，DE ．我们探究下列图中线段BG .线段DE 的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG .线段DE 的长度关系及所在直线的位置关系；ABCPDE②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度，得到如图2.如图3情形．请你通过观察.测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．18.如图，点E是正方形ABCD内一点，△CDE是等边三角形，连接EB，EA，延长BE交边AD于点F．（1）求证：△ADE≌△BCE；（2）求∠AFB的度数．19.数学课上，张老师出示了问题：如图1，四边形ABCD 是正方形，点E 是边BC 的中点．90AEF ∠=，且EF 交正方形外角DCG ∠的平行线CF 于点F ，求证：AE =EF ．经过思考，小明展示了一种正确的解题思路：取AB 的中点M ，连接ME ，则AM =EC ，易证AME ECF △≌△，所以AE EF =．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．ADFC GE B图1ADF C GE B 图2 ADFC GE B图3。

命题与证明的综合练习

命题与证明的综合练习一、选择题1．下列命题的逆命题不正确的是（）A．全等三角形的对应边相等B．两直线平行，同位角相等C．等腰三角形的两个底角相等D．矩形的对角线相等．【答案】D【解析】【分析】根据求逆命题的原则，把原命题的结论作为条件，原命题的条件作为结论得到的命题是原命题的逆命题，逐一判断逆命题的正误即可．【详解】解：A的逆命题是：对应边相等的三角形是全等三角形，正确；B的逆命题是：同位角相等，两直线平行，正确；C的逆命题是：两底角相等的三角形是等腰三角形，正确；D的逆命题是：对角线相等的四边形是矩形，错误故选：D【点睛】本题考查逆命题、全等三角形的判定、平行线的判定、等腰三角形的判定、矩形的判定，解题的关键是正确找出各选项的逆命题．2．下列命题中逆命题是假命题的是（）A．如果两个三角形的三条边都对应相等，那么这两个三角形全等B．如果a2=9，那么a=3C．对顶角相等D．线段垂直平分线上的任意一点到这条线段两个端点的距离相等【答案】C【解析】【分析】首先写出各命题的逆命题（将每个命题的题设与结论调换），然后再证明各命题的正误．因为相等的角不只是对顶角，所以此答案是假命题，继而得到正确答案．【详解】解：A、逆命题为：如果两个三角形全等，那么这两个三角形的三条边都对应相等．是真命题；B、逆命题为：如果a=3，那么a2=9．是真命题；C、逆命题为：相等的角是对顶角．是假命题；D、逆命题为：到线段两个端点的距离相等的点在这条线段垂直平分线上．是真命题．故选C．【点睛】此题考查了命题与逆命题的关系．解题的关键是找到各命题的逆命题，再证明正误即可．3．下列命题是假命题的是（）A．有一个角为60︒的等腰三角形是等边三角形B．等角的余角相等C．钝角三角形一定有一个角大于90︒D．同位角相等【答案】D【解析】【分析】【详解】解：选项A、B、C都是真命题；选项D，两直线平行，同位角相等，选项D错误，是假命题，故选：D．4．下列命题是假命题的是( )A．对顶角相等B．两直线平行，同旁内角相等C．平行于同一条直线的两直线平行D．同位角相等，两直线平行【答案】B【解析】解：A．对顶角相等是真命题，故本选项正确，不符合题意；B．两直线平行，同旁内角互补，故本选项错误，符合题意；C．平行于同一条直线的两条直线平行是真命题，故本选项正确，不符合题意；D．同位角相等，两直线平行是真命题，故本选项正确，不符合题意．故选B．5．下列命题：①两条直线被第三条直线所截，同位角相等；②两点之间，线段最短；③相等的角是对顶角；④直角三角形的两个锐角互余；⑤同角或等角的补角相等．其中真命题的个数是（）A．2个B．3个C．4个D．5个【答案】B【解析】【分析】【详解】解：命题①两条平行线被第三条直线所截，同位角相等，错误，为假命题；命题②两点之间，线段最短，正确，为真命题；命题③相等的角是对顶角，错误，为假命题；命题④直角三角形的两个锐角互余，正确，为真命题；命题⑤同角或等角的补角相等，正确，为真命题，故答案选B ．考点：命题与定理．6．下列命题的逆命题成立的是（）A ．对顶角相等B ．全等三角形的对应角相等C ．如果两个数相等，那么它们的绝对值相等D ．两直线平行，同位角相等【答案】D【解析】【分析】写出各个命题的逆命题，然后判断是否成立即可．【详解】解：A 、逆命题为相等的角为对顶角，不成立；B 、逆命题为对应角相等的三角形全等，不成立；C 、逆命题为绝对值相等的两个数相等，不成立；D 、逆命题为同位角相等，两直线平行，成立，故选：D ．【点睛】本题考查了命题与定理的知识，解题的关键是能够正确的写出各个命题的逆命题，难度不大．7．下列命题中：①；②在同一平面内，若a ⊥b ，a ⊥c ，则b ∥c ；③若ab ＝0，则P(a ，b)表示原点；9．是真命题的有（）A ．1 个B ．2 个C ．3 个D ．4 个【答案】A【解析】【分析】根据立方根、平行线的判定和算术平方根判断即可．【详解】解：①≥0≤0不一定成立，错误； ②在同一平面内，若a b ⊥r r ，a c ⊥，则//b c ，正确； ③若0ab =，则(,)P a b 表示原点或坐标轴，错误；3，错误；故选：A ．【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．8．下列命题的逆命题正确的是（）A ．如果两个角是直角，那么它们相等B ．全等三角形的面积相等C ．同位角相等，两直线平行D ．若a b =，则22a b =【答案】C【解析】【分析】交换原命题的题设与结论得到四个命题的逆命题，然后分别根据直角的定义、全等三角形的判定、平行线的性质和平方根的定义判定四个逆命题的真假．【详解】解：A 、逆命题为：如果两个角相等，那么它们都是直角，此逆命题为假命题； B 、逆命题为：面积相等的两三角形全等，此逆命题为假命题；C 、逆命题为：两直线平行，同位角相等，此逆命题为真命题；D 、逆命题为，若a 2＝b 2，则a ＝b ，此逆命题为假命题．故选：C ．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．也考查了逆命题．9．下列命题是真命题的是（）A ．若两个数的平方相等，则这两个数相等B ．同位角相等C ．同一平面内，垂直于同一直线的两条直线平行D ．相等的角是对顶角【答案】C【解析】【分析】根据平方的意义，同位角的概念，平行线的判定，对顶角的概念逐一进行判断即可得．【详解】A ．若两个数的平方相等，则这两个数不一定相等，如22=（-2）2，但2≠-2，故A 选项错误；B ．只有两直线平行的情况下，才有同位角相等，故B 选项错误；C ．同一平面内，垂直于同一直线的两条直线平行，真命题，符合题意；D ．相等的角不一定是对顶角，如图，∠1=∠2，但这两个角不符合对顶角的概念，故D 选故选C．【点睛】本题考查了命题真假的判定，涉及了乘方、同位角、对顶角、平行线的判定等知识，熟练掌握相关知识是解题的关键．10．下列四个命题中：①在同一平面内，互相垂直的两条直线一定相交②有且只有一条直线垂直于已知直线③两条直线被第三条直线所截，同位角相等④从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．其中真命题的个数为（）A．1个 B．2 个 C．3个 D．4个【答案】A【解析】分析：利用平行公理及其推论和垂线的定义、点到直线的距离的定义分别分析求出即可．详解：①在同一平面内，互相垂直的两条直线一定相交，正确；②在同一个平面内，有且只有一条直线垂直于已知直线，此选项错误；③两条平行直线被第三条直线所截，同位角相等，错误；④从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离，错误；真命题有1个.故选A.点睛：本题考查了命题与定理.其中真命题是由题设得出结论，如果不能由题设得出结论则称为假命题.题干中②、③、④，均不能由题设得出结论故不为真命题.11．下列命题是真命题的是（）A．同位角相等B．对顶角互补C．如果两个角的两边互相平行，那么这两个角相等=-的图像上．D．如果点P的横坐标和纵坐标互为相反数，那么点P在直线y x【答案】D【分析】根据平行线的性质定理对A 、C 进行判断；利用对顶角的性质对B 进行判断；根据直角坐标系下点坐标特点对D 进行判断．【详解】A ．两直线平行，同位角相等，故A 是假命题；B ．对顶角相等，故B 是假命题；C ．如果两个角的两边互相平行，那么这两个角相等或互补，故C 是假命题；D ．如果点的横坐标和纵坐标互为相反数，那么点P 在直线y x =-的图像上，故D 是真命题故选：D【点睛】本题考查了真命题与假命题，正确的命题称为真命题，错误的命题称为假命题．利用了平行线性质、对顶角性质、直角坐标系中点坐标特点等知识点．12．下列命题中，是假命题的是( )A ．任意多边形的外角和为360oB ．在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C VC ．在一个三角形中，任意两边之差小于第三边D ．同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析．【详解】解：A. 任意多边形的外角和为360o ,是真命题；B. 在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C V ，根据HL ，是真命题；C. 在一个三角形中，任意两边之差小于第三边，是真命题；D. 同弧所对的圆周角等于圆心角的一半，本选项是假命题.故选D ．【点睛】本题考核知识点：判断命题的真假. 解题关键点：熟记相关性质或定义．13．已知下列命题：①若a ＞b ，则ac ＞bc ；②若a=1；③内错角相等；④90°的圆周角所对的弦是直径．其中原命题与逆命题均为真命题的个数是（）A．1个B．2个C．3个D．4个【答案】A【解析】【分析】先对原命题进行判断，再判断出逆命题的真假即可．【详解】解:①若a＞b，则ac＞bc是假命题，逆命题是假命题；②若a=1是真命题，逆命题是假命题；③内错角相等是假命题，逆命题是假命题；④90°的圆周角所对的弦是直径是真命题，逆命题是真命题；其中原命题与逆命题均为真命题的个数是1个；故选A．点评：主要考查命题与定理，用到的知识点是互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题，判断命题的真假关键是要熟悉课本中的性质定理．14．对于命题“若a2＞b2，则a＞b”，下面四组关于a，b的值中，能说明这个命题是假命题的是（）A．a=3，b=2 B．a=﹣3，b=2 C．a=3，b=﹣1 D．a=﹣1，b=3【答案】B【解析】试题解析：在A中，a2=9，b2=4，且3＞2，满足“若a2＞b2，则a＞b”，故A选项中a、b 的值不能说明命题为假命题；在B中，a2=9，b2=4，且﹣3＜2，此时虽然满足a2＞b2，但a＞b不成立，故B选项中a、b 的值可以说明命题为假命题；在C中，a2=9，b2=1，且3＞﹣1，满足“若a2＞b2，则a＞b”，故C选项中a、b的值不能说明命题为假命题；在D中，a2=1，b2=9，且﹣1＜3，此时满足a2＜b2，得出a＜b，即意味着命题“若a2＞b2，则a＞b”成立，故D选项中a、b的值不能说明命题为假命题；故选B．考点：命题与定理．15．下列命题的逆命题成立的有( )①勾股数是三个正整数②全等三角形的三条对应边分别相等③如果两个实数相等，那么它们的平方相等 ④平行四边形的两组对角分别相等 A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】先写出每个命题的逆命题，再分别根据勾股数的定义、三角形全等的判定、平方根的定义、平行四边形的判定逐个判断即可．【详解】①逆命题：如果三个数是正整数，那么它们是勾股数反例：正整数1,2,3，但222123+?，即它们不是勾股数，则此逆命题不成立 ②逆命题：三条对应边分别相等的两个三角形全等由SSS 定理可知，此逆命题成立③逆命题：如果两个实数的平方相等，那么这两个实数相等反例：222(2)4=-=，但22≠-，则此逆命题不成立④逆命题：两组对角分别相等的四边形是平行四边形由平行四边形的判定可知，此逆命题成立综上，逆命题成立的有2个故选：B ．【点睛】本题考查了命题的相关概念、勾股数的定义、三角形全等的判定、平方根的定义、平行四边形的判定，正确写出各命题的逆命题是解题关键．16．已知：在ABC V 中，AB AC ≠，求证：.B C ∠≠∠若用反证法来证明这个结论，可以假设( )A ．AB ∠=∠B ．AB BC = C ．B C ∠=∠D ．A C ∠=∠【答案】C【解析】【分析】反证法的步骤:1、假设命题反面成立;2、从假设出发,经过推理得出和反面命题矛盾,或者与定义、公理、定理矛盾;3、得出假设命题不成立是错误的,即所求证命题成立.【详解】已知：在ABC V 中，AB AC ≠，求证：.B C ∠≠∠若用反证法来证明这个结论，可以假设B C ∠=∠,由“等角对等边”可得AB=AC,这与已知矛盾，所以.B C ∠≠∠故选C【点睛】本题考核知识点：反证法. 解题关键点：理解反证法的一般步骤.17．下列命题中，真命题的序号为（）①相等的角是对顶角；②在同一平面内，若//a b ，//b c ，则//a c ；③同旁内角互补；④互为邻补角的两角的角平分线互相垂直.A ．①②B ．①③C ．①②④D ．②④【答案】D【解析】【分析】根据对顶角的性质、平行线的判定、平行线的性质、角平分线的性质判断即可．【详解】①相等的角不一定是对顶角，是假命题；②在同一平面内，若a ∥b ，b ∥c ，则a ∥c ，是真命题；③两直线平行，同旁内角互补；是假命题；④互为邻补角的两角的角平分线互相垂直，是真命题；故选：D ．【点睛】此题考查命题的真假判断，解题关键在于掌握正确的命题叫真命题，错误的命题叫做假命题．18．下列命题错误的是（）A ．平行四边形的对角线互相平分B ．两直线平行，内错角相等C ．等腰三角形的两个底角相等D ．若两实数的平方相等，则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义，分别进行判断，即可得到答案.【详解】解：A 、平行四边形的对角线互相平分，正确；B 、两直线平行，内错角相等，正确；C 、等腰三角形的两个底角相等，正确；D 、若两实数的平方相等，则这两个实数相等或互为相反数，故D 错误；故选：D.【点睛】本题考查了判断命题的真假，以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义，解题的关键是熟练掌握所学的性质进行解题.19．下列命题中哪一个是假命题（）A ．8的立方根是2B ．在函数y ＝3x 的图象中，y 随x 增大而增大C ．菱形的对角线相等且平分D ．在同圆中，相等的圆心角所对的弧相等【答案】C【解析】【分析】利用立方根的定义、一次函数的性质、菱形的性质及圆周角定理分别判断后即可确定正确的选项．【详解】A 、8的立方根是2，正确，是真命题；B 、在函数3y x 的图象中，y 随x 增大而增大，正确，是真命题；C 、菱形的对角线垂直且平分，故错误，是假命题；D 、在同圆中，相等的圆心角所对的弧相等，正确，是真命题，故选C ．【点睛】考查了命题与定理的知识，能够了解立方根的定义、一次函数的性质、菱形的性质及圆周角定理等知识是解题关键．20．下列说法正确的是（）A ．两锐角分别相等的两个直角三角形全等B ．两条直角边分别相等的两直角三角形全等C ．一个命题是真命题，它的逆命题一定也是真命题D ．经过旋转，对应线段平行且相等【答案】B【解析】【分析】A,B 利用斜边和一条直角边对应相等的两个直角三角形全等，判定直角三角形全等时，也可以运用其它的方法．C 利用命题与定理进行分析即可，D.利用旋转的性质即可解答；【详解】A 、两个锐角分别相等的两个直角三角形不一定全等，故A 选项错误；B 、根据SAS 可得，两条直角边分别相等的两个直角三角形全等，故B 选项正确；C 、一个命题是真命题，它的逆命题不一定是真命题．故C 选项错误；D 、经过旋转，对应线段相等，故D 选项错误；故选：B ．【点睛】此题考查命题与定理，解题关键在于掌握判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．。

初一英语几何证明方法练习题20题(带答案)

初一英语几何证明方法练习题20题(带答案)1. In a triangle ABC, angle A is 50 degrees and angle B is 60 degrees. What is the measure of angle C?A. 60 degreesB. 70 degreesC. 80 degreesD. 90 degrees答案：B。

解析：三角形内角和为180 度，已知角A 是50 度，角B 是60 度，那么角C 的度数为180 减去50 再减去60 等于70 度。

A 选项不符合计算结果；C 选项是错误计算结果；D 选项也不符合实际情况。

2. A triangle has sides of lengths 5 cm, 6 cm, and 7 cm. Which statement is true?A. It is an equilateral triangle.B. It is an isosceles triangle.C. It is a scalene triangle.D. It is a right triangle.答案：C。

解析：因为三条边长度都不相等，所以是不等边三角形即scalene triangle。

A 选项等边三角形三条边相等，不符合；B 选项等腰三角形至少有两条边相等，不符合；D 选项直角三角形需要满足勾股定理等条件，这里无法判断是直角三角形。

3. If two angles of a triangle are equal, what kind of triangle is it?A. Acute triangleB. Obtuse triangleC. Right triangleD. Isosceles triangle答案：D。

解析：有两个角相等的三角形是等腰三角形。

A 选项锐角三角形是三个角都是锐角的三角形，不符合；B 选项钝角三角形是有一个角是钝角的三角形，不符合；C 选项直角三角形是有一个角是直角的三角形，不符合。

证明不等式的基本方法练习题(基础、经典、好用)

证明不等式的基本方法一、选择题1．设t ＝a ＋2b ，s ＝a ＋b 2＋1，则s 与t 的大小关系是( )A ．s ≥tB ．s >tC ．s ≤tD ．s <t2．设0<x <1，则a ＝2x ，b ＝1＋x ，c ＝11－x 中最大的一个是( ) A ．a B ．b C ．c D ．无法判断3．设a 、b ∈(0，＋∞)，且ab －a －b ＝1，则有( )A ．a ＋b ≥2(2＋1)B ．a ＋b ≤2＋1C ．a ＋b ＜2＋1D ．a ＋b ＞2(2＋1)4．已知a 、b 、c 是正实数，且a ＋b ＋c ＝1，则1a ＋1b ＋1c 的最小值为( )A ．5B ．7C ．9D ．115．(2012·湖北高考)设a ，b ，c ，x ，y ，z 均为正数，且a 2＋b 2＋c 2＝10，x 2＋y 2＋z 2＝40，ax ＋by ＋cz ＝20，则a ＋b ＋c x ＋y ＋z 等于( ) A.14 B.13C.12D.34 二、填空题6．设a ＞b ＞0，m ＝a －b ，n ＝a －b ，则m 与n 的大小关系是________．7．以下三个命题：①若|a －b |＜1，则|a |＜|b |＋1；②若a 、b ∈R ，则|a ＋b |－2|a |≤|a －b |；③若|x |＜2，|y |＞3，则|x y |＜23，其中正确命题的序号是________．8．若x ＋y ＋z ＝1，且x ，y ，z ∈R ，则x 2＋y 2＋z 2与13的大小关系为________．三、解答题9．设a ＞0，b ＞0，a ＋b ＝1，求证：1a ＋1b ＋1ab ≥8.10．(2013·深圳调研)已知a ，b 为正实数．(1)求证：a 2b ＋b 2a ≥a ＋b ；(2)利用(1)的结论求函数y ＝（1－x ）2x ＋x 21－x(0＜x ＜1)的最小值．11．(1)设x ≥1，y ≥1，证明x ＋y ＋1xy ≤1x ＋1y ＋xy .(2)1≤a ≤b ≤c ，证明log a b ＋log b c ＋log c a ≤log b a ＋log c b ＋log a c .解析及答案一、选择题1．【解析】 ∵s －t ＝b 2－2b ＋1＝(b －1)2≥0，∴s ≥t .【答案】 A2．【解析】 ∵0<x <1，∴1＋x >2x ＝4x >2x ， ∴只需比较1＋x 与11－x的大小， ∵1＋x －11－x ＝1－x 2－11－x ＝－x 21－x<0， ∴1＋x <11－x. 因此c ＝11－x 最大．【答案】 C3．【解析】 ∵ab －a －b ＝1，∴1＋a ＋b ＝ab ≤(a ＋b 2)2.令a ＋b ＝t (t ＞0)，则1＋t ≤t 24(t ＞0)．解得t ≥2(2＋1)，则a ＋b ≥2(2＋1)．【答案】 A4．【解析】把a ＋b ＋c ＝1代入1a ＋1b ＋1c 得a ＋b ＋c a ＋a ＋b ＋c b ＋a ＋b ＋c c＝3＋(b a ＋a b )＋(c a ＋a c )＋(c b ＋b c )≥3＋2＋2＋2＝9.【答案】 C5．【解析】由题意可得x 2＋y 2＋z 2＝2ax ＋2by ＋2cz ，又a 2＋b 2＋c 2＝10相加可得(x －a )2＋(y －b )2＋(z －c )2＝10，所以不妨令⎩⎨⎧x －a ＝a ，y －b ＝b ，z －c ＝c (或⎩⎨⎧x －a ＝b ，y －b ＝c ，z －c ＝a)，则x ＋y ＋z ＝2(a ＋b ＋c )，∴a ＋b ＋c x ＋y ＋z ＝12. 【答案】 C二、填空题6．【解析】 ∵a ＞b ＞0，∴m ＝a －b ＞0，n ＝a －b ＞0.∵m 2－n 2＝(a ＋b －2ab )－(a －b )＝2b －2ab ＝2b (b －a )＜0，∴m 2＜n 2，从而m ＜n .【答案】 m ＜n7．【解析】 ①|a |－|b |≤|a －b |＜1，所以|a |＜|b |＋1； ②|a ＋b |－|a －b |≤|(a ＋b )＋(a －b )|＝|2a |，所以|a ＋b |－2|a |≤|a －b |；③|x |＜2，|y |＞3，所以1|y |＜13，因此|x ||y |＜23.∴①②③均正确．【答案】 ①②③8．【解析】 ∵(x ＋y ＋z )2＝1，∴x 2＋y 2＋z 2＋2(xy ＋yz ＋zx )＝1，又2(xy ＋yz ＋zx )≤2(x 2＋y 2＋z 2)，∴3(x 2＋y 2＋z 2)≥1，则x 2＋y 2＋z 2≥13.【答案】 x 2＋y 2＋z 2≥13三、解答题9．【证明】 ∵a ＞0，b ＞0，a ＋b ＝1， ∴2ab ≤a ＋b ＝1.因此ab≤12，1ab≥4.则1a＋1b＋1ab＝(a＋b)(1a＋1b)＋1ab≥2ab·2 1ab＋4＝8.故1a＋1b＋1ab≥8成立．10．【解】(1)证明∵a2b＋b2a－(a＋b)＝a3＋b3－a2b－ab2ab＝a2（a－b）－b2（a－b）ab＝（a－b）2（a＋b）ab.又∵a＞0，b＞0，∴（a－b）2（a＋b）ab≥0，当且仅当a＝b时等号成立．∴a2b＋b2a≥a＋b.(2)∵0＜x＜1，∴1－x＞0，由(1)的结论，函数y＝（1－x）2x＋x21－x≥(1－x)＋x＝1.当且仅当1－x＝x即x＝12时等号成立．∴函数y＝（1－x）2x＋x21－x(0＜x＜1)的最小值为1.11．【证明】(1)由于x≥1，y≥1，则x＋y＋1xy≤1x＋1y＋xy⇔xy(x＋y)＋1≤y＋x＋(xy)2，将上式中右式减左式得[y＋x＋(xy)2]－[xy(x＋y)＋1]＝[(xy)2－1]－[xy(x＋y)－(x＋y)]＝(xy－1)(xy－x－y＋1)＝(xy－1)(x－1)(y－1)，由x≥1，y≥1易知(xy－1)(x－1)(y－1)≥0，即原不等式成立．(2)设log a b＝x，log b c＝y，由对数换底公式得log c a＝1xy，log b a＝1x，log c b＝1y，log a c＝xy，则所证不等式可化为x＋y＋1xy≤1x＋1y＋xy，由1≤a≤b≤c知x＝log a b≥1，y＝log b c≥1，由(1)知所证不等式成立．。

2021-2022学年基础强化北师大版八年级数学下册第一章三角形的证明专题练习试卷(名师精选)

北师大版八年级数学下册第一章三角形的证明专题练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在△ABC中，∠BAC＝45°，E是AC中点，连接BE，CD⊥BE于点F，CD＝BE．若AD则BD的长为（）A．2 B．C．D．2、△ABC中，∠A,∠B,∠C所对的边分别是a,b,c下列条件中不能说明△ABC是直角三角形的是（）A．b2- c2=a2B．a:b:c= 5:12:13C．∠A:∠B:∠C =3:4:5 D．∠C =∠A -∠B3、已知等腰三角形的两条边长分别为4和9，则它的周长为（）A．17 B．22 C．23 D．17或224、如图，直线a∥b，直线AB⊥AC，若∠1＝52°，则∠2的度数是（）A ．38°B ．42°C ．48°D ．52°5、等腰三角形的一个顶角是80°，则它的底角是（）．A ．40°B ．50°C ．60°D ．70°6、如图，在ABC ∆中，90C ∠=︒，AC BC =，AD 平分BAC ∠交BC 于点D ，DE AB ⊥，垂足为E ，且12cm AB =，则DEB ∆的周长是（）A ．6cmB ．8cmC ．10cmD ．12cm7、如图，在△ABC 中，AB ＝AC ＝6cm ，AD ，CE 是△ABC 的两条中线，CE ＝4cm ，P 是AD 上的一个动点，则BP +EP 的最小值是（）A ．3cmB ．4cmC ．6cmD ．10cm8、如图点,,A B C 在同一条直线上，△CCC ,△CCC 都是等边三角形，,AE BD 相交于点O ，且分别与,CD CE 交于点,M N ，连接,M N ，有如下结论：①△CCC ≅△CCC ；②AM DN =；③△CCC 为等边三角形；④60EOB ∠=︒.其中正确的结论个数是（）A．1个B．2个C．3个D．4个9、我们称网格线的交点为格点．如图，在4×4的长方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，则满足条件的格点C的个数是（）A．3 B．4 C．5 D．610、如图，在三角形ABC，222AB AC BC+=，AB AC且，H是BC上中点，F是射线AH上一点．E=是AB上一点，连接EF，EC，BF FE=，点G在AC上，连接BG，2∠=∠，AE=ECG GBCAG=CF的长为（）A．B．C．D．9第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、在△ABC中，∠C=90°，AD是△ABC的角平分线，BC=6、AC=8、AB=10，则点D到AB的距离为_______．2、如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DF⊥AC于点F，S△ABC＝21，DE＝3，AB＝9，则AC长是_____．3、如图，在等边△ABC中，E为AC边的中点，AD垂直平分BC，P是AD上的动点．若AD=6，则EP+CP的最小值为_______________．4、在△ABC中，AB=AC，BD平分∠ABC交AC于D，DE垂直平分AB，垂足为E，则∠C=______．=，线段AB的垂直平分线分别交AB、AC于点D、E，如果5、已知：如图，在△CCC中，AB AC∠=︒，那么A42EBC∠=______．三、解答题（5小题，每小题10分，共计50分）1、如图，已知在平面直角坐标系中，点A（0，n）是y轴上的一点，且n使得√C−4+√4−C有意义，以OA为边在第一象限内作等边三角形△OAB．（1）求点B的坐标；（2）若点C是在射线BO上第三象限内的一点，连接AC，以AC为边在y轴右侧画等边三角形△ACD，连接BD，OD．①请先依题意补全图形后，求∠ABD的度数；②当OD最小时，求△ACD的边长．2、下面是小丽同学设计的“作30°角”的尺规作图过程．已知：如图1，射线OA．求作：∠AOB，使∠AOB＝30°．作法：如图2，①在射线OA上任取一点C；②分别以O，C为圆心，OC长为半径作弧，两弧在射线OA的上方交于点D，作射线OD，并连接CD；③以O为圆心，任意长为半径作弧，分别交射线OA，OD于点E，F；④分别以E，F为圆心，以大于12EF的同样长为半径作弧，两弧在∠AOD内部交于点B；⑤作射线OB；∴ ∠AOB就是所求的角．根据小丽设计的尺规作图过程，解答下列问题：（1）使用直尺和圆规，依作法补全图2（保留作图痕迹）；（2）补全下面证明过程：证明：连接BE，BF．∵ OC＝OD＝CD，∴ △OCD是等边三角形．∴∠COD＝°．又∵ OE＝OF，BE＝BF，OB＝OB，∴ △OEB≌△OFB（）（填推理依据）．∴ ∠EOB＝∠FOB（）（填推理依据）．∴ ∠AOB＝12COD＝30°．∴∠AOB就是所求的角．3、如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．（1）求对角线AB所在直线的函数关系式；（2）对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；（3）若点P是直线AB上的一个动点，当△PAM的面积与长方形OACB的面积相等时，求点P的坐标．4、如图，等边△ABC中，点D在BC上，CE=CD，∠BCE=60°，连接AD、BE．（1）如图1，求证：AD=BE；（2）如图2，延长AD交BE于点F，连接DE、CF，在不添加任何辅助线和其它字母的情况下，请直接写出等于120°的角．5、如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点，点A，B，C均落在格点上．（1）计算线段AB的长度；（2）判断△ABC的形状；（3）写出△ABC的面积；（4）画出△ABC关于直线l的轴对称图形△A1B1C1．-参考答案-一、单选题1、B【分析】过点C作CN⊥AB于点N，连接ED，EN，利用SAS证明△DCE≌△BEN，可得ED＝NB，∠CED＝∠ENB＝135°，得△ADE是等腰直角三角形，可得AD＝DN＝BN，进而可得结果．【详解】解：如图，过点C作CN⊥AB于点N，连接EN，∴∠CNA＝90°，∵∠BAC＝45°，∴∠NCA＝∠A＝45°，∴AN＝CN，∵点E是AC的中点，∴∠ANE＝∠CNE＝45°，∠CEN＝∠AEN＝90°，∴∠CEF+∠FEN＝90°，∵CD⊥BE，∴∠CFE＝90°，∴∠CEF+∠FCE＝90°，∴∠DCE＝∠BEN，在△DCE和△BEN中，CE EN DCE BEN CD EB =⎧⎪∠=∠⎨⎪=⎩， ∴△DCE ≌△BEN （SAS ），∴ED ＝NB ，∠CED ＝∠ENB ＝135°，∴∠AED ＝45°＝∠A ＝∠ACN ，∴AD ＝DE ，∵AE ＝CE ，∴AE =EN ，∴AD ＝DN ，∴AD ＝DN ＝BN ，∴BD ＝2AD ＝故选B ．【点睛】本题主要考查了全等三角形的性质与判定，等腰直角三角形的性质与判定，解题的关键在于能够正确作出辅助线，构造全等三角形求解．2、C【分析】由三角形内角和定理及勾股定理的逆定理进行判断即可．【详解】A. b 2- c 2=a 2，根据勾股定理逆定理可以判断，△ABC 是直角三角形，故不符合题意；B. a :b :c= 5:12:13，设5,12,13a k b k c k ===，则2222222169,25144169c k a b k k k =+=+=，则222c a b =+，根据勾股定理逆定理可以判断，△ABC 是直角三角形，故不符合题意；C. ∠A :∠B :∠C = 3:4:5，设∠A 、∠B 、∠C 分别是3,4,5x x x ，则12180x =︒，15x =︒，则45,60,75A B C ∠=︒∠=︒∠=︒，所以△ABC 是不直角三角形，故符合题意；D. ∠C =∠A -∠B ，又∠A +∠B +∠C =180°，则∠A =90°，是直角三角形，故不符合题意，故选C.【点睛】本题考查了直角三角形的判定，涉及了勾股定理的逆定理、三角形内角和定理等知识，注意在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．3、B【分析】题目给出等腰三角形有两条边长为4和9，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【详解】解：（1）如果腰长为4，则三边是：4，4，9；不满足三角形两边之和大于第三边的性质，不成立；（2）如果腰长为9，则三边是：4，9，9；满足三角形两边之和大于第三边的性质，成立；周长=9+9+4=22．故选：B ．【点睛】本题主要考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．4、A【分析】利用直角三角形的性质先求出∠B，再利用平行线的性质求出∠2．【详解】解：∵AB⊥AC，∠1＝52°，∴∠B＝90°﹣∠1＝90°﹣52°＝38°∵a∥b，∴∠2＝∠B＝38°．故选：A．【点睛】本题考查平行线的性质、两直线平行同位角相等，直角三角形两个锐角互余等知识，在基础考点，掌握相关知识是解题关键．5、B【分析】依据三角形的内角和是180°以及等腰三角形的性质即可解答．【详解】解：（180°-80°）÷2=100°÷2=50°；答：底角为50°．故选：B．【点睛】本题主要考查三角形的内角和定理及等腰三角形的两个底角相等的特点．6、D【分析】根据角平分线的性质可得DC DE =，再证Rt ACD Rt AED ∆≅∆，可得AE AC =，最后根据三角形的中周长公式计算即可．【详解】解：AD 平分BAC ∠，90C ∠=︒，DE AB ⊥，DC DE ∴=，在Rt ACD ∆和Rt AED ∆中，DC DE AD AD =⎧⎨=⎩， Rt ACD Rt AED(HL)∴∆≅∆，AE AC ∴=，AC BC =，BC AE ∴=，DEB ∴∆的周长()12cm DE BD BE CD BD BE BC BE AE BE AB =++=++=+=+==．故选：D ．【点睛】本题主要考查了角平分线的性质、直角三角形全等的判定等知识点，掌握角平分线的性质成为解答本题的关键．7、B【分析】连接CE 交AD 于点P ，则BP +EP 的最小值为CE 的长．【详解】如图，连接CE 交AD 于点P ，∵AB ＝AC ，AD 是BC 的中线，∴AD ⊥BC ，∴BP ＝CP ，∴BP +EP ＝CP +EP ≥CE ，∴BP +EP 的最小值为CE 的长，∵CE ＝4cm ，∴BP +EP 的最小值为4cm ，故选：B ．【点睛】本题是典型的将军饮马问题，考查了等腰三角形三线合一的性质和两点间线段最短知识，关键是把BP +EP 的最小值转化为CP +EP 的最小值，从而根据两点间线段最短解决最小值的问题．8、D【分析】由SAS 即可证明DCB ACE ∆≅∆，则①正确；有∠CAE =∠CDB ，然后证明△ACM ≌△DCN ，则②正确；由CM =CN ，∠MCN =60°，即可得到∆CMN 为等边三角形，则③正确；由AD∥CE ，则∠DAO =∠NEO =∠CBN ，由外角的性质60EOB OAC CBN ∠=∠+∠=︒，即可得到答案．【详解】解：∵△DAC 和△EBC 均是等边三角形，∴AC =CD ，BC =CE ，∠ACD =∠BCE =60°，∴∠ACD +∠DCE =∠BCE +∠DCE ，即∠ACE =∠BCD ，∠MCN =180°-∠ACD -∠BCE =60°，在△ACE 和△DCB 中，AC CD ACE BCD BC CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△DCB （SAS ），则①正确；∴AE =BD ，∠CAE =∠CDB ，在ACM 和△DCN 中，ACM DCN AC CD CAM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ACM ≌△DCN （ASA ），∴CM =CN ，AM DN =；则②正确；∵∠MCN =60°，∴∆CMN 为等边三角形；则③正确；∵∠DAC =∠ECB =60°，∴AD∥CE ，∴∠DAO =∠NEO =∠CBN ，∴60EOB OAC CBN OAC DAO ∠=∠+∠=∠+∠=︒；则④正确；∴正确的结论由4个；故选D ．【点睛】本题考查了等边三角形的性质与判定，全等三角形的判定与性质，平行线的性质与判定，综合性较强，但难度不是很大，准确识图找出全等三角形是解题的关键．9、A【分析】根据题意，结合图形，分两种情况讨论：①AB 为等腰直角△ABC 底边；②AB 为等腰直角△ABC 其中的一条腰．【详解】解：如图：分情况讨论：①AB 为等腰直角△ABC 底边时，符合条件的格点C 点有0个；②AB 为等腰直角△ABC 其中的一条腰时，符合条件的格点C 点有3个．故共有3个点，故选：A ．【点睛】本题考查了等腰三角形的性质和判定；解答本题关键是根据题意，画出符合实际条件的图形，数形结合的思想是数学解题中很重要的解题思想．10、D【分析】延长EA 到K ，是的AK =AG ，连接CK ，先由勾股定理的逆定理可以得到△ABC 是等腰直角三角形，∠BAC =90°，∠ACB =∠ABC =45°，由BF =FE ，得到∠FBE =∠FEB ，设∠BFE =x ，则()11=180=9022EBF BFE x ︒-︒-∠∠，然后证明CB =FC =FE ，得到∠FBC =∠FCA ，∠AFB =∠AFC 则1902FCA x ∠=︒-，()11=180=9022EBF BFE x ︒-︒-∠即可证明==90EFC AFE AFC +︒∠∠∠，推出CF =；设22ECG GBC y ==∠∠，证明△ABG ≌△ACK ，得到==45K AGB ACB GBC y =+︒+∠∠∠∠，==45ACK ABG ABC GBC y -=︒-∠∠∠∠，即可推出∠ECK =∠K ，得到EK =EC ，则EK AE AK AE AG =+=+=【详解】解：延长EA 到K ，是的AK =AG ，连接CK ，∵在三角形ABC ，222AB AC BC +=，AB AC =且，∴△ABC 是等腰直角三角形，∠BAC =90°，∴∠ACB =∠ABC =45°，∵BF =FE ，∴∠FBE =∠FEB ，设∠BFE =x ，则()11=180=9022EBF BFE x ︒-︒-∠∠， ∵H 是BC 上中点，F 是射线AH 上一点，∴AH ⊥BC ，∴AH 是线段BC 的垂直平分线，∠FAC =45°，∴CB =FC =FE ，∴∠FBC =∠FCA ，∠AFB =∠AFC ∴1902FCA x ∠=︒-，()11=180=9022EBF BFE x ︒-︒-∠∴1180452AFB AFC FAC FCA x ∠=∠=︒-∠-∠=︒+， ∴1==452AFE AFB BFE x -︒-∠∠∠， ∴==90EFC AFE AFC +︒∠∠∠，∴222EF CF CE +=，∴2CF =，设22ECG GBC y ==∠∠，∵AG =AK ，AB =AC ，∠KAC =∠GAB =90°，∴△ABG ≌△ACK （SAS ），==45K AGB ACB GBC y =+︒+∠∠∠∠，==45ACK ABG ABC GBC y -=︒-∠∠∠∠，∴==45ECK ACE ACK a +︒+∠∠∠，∴∠ECK =∠K ，∴EK =EC ，∵EK AE AK AE AG =+=+=∴EF EK ==∴9CF =，故选D ．【点睛】本题主要考查了勾股定理和勾股定理的逆定理，等腰三角形的性质与判定，线段垂直平分线的性质与判定，全等三角形的性质与判定，三角形内角和定理等等，熟知相关知识是解题的关键．二、填空题1、83##【分析】作DE⊥AB于E，如图，先根据勾股定理计算出BC=8，再利用角平分线的性质得到DE=DC，设DE=DC=x，利用面积法得到10x=6（8-x），然后解方程即可．【详解】解：作DE⊥AB于E，如图，∵AD是△ABC的一条角平分线，DC⊥AC，DE⊥AB，∴DE=DC，设DE=DC=x，S△ABD=12DE•AB=12AC•BD，即10x=8（6-x），解得x=83，即点D到AB边的距离为83．故答案为：83．【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，由已知能够注意到D到AB 的距离即为DE长是解决的关键．2、5【分析】根据角平分线上的点到角的两边距离相等可得DE=DF，再根据三角形的面积公式列式计算即可得解．【详解】解：∵AD是△ABC中∠BAC的角平分线，DE⊥AB，DF⊥AC，∴DE=DF，∴S△ABC=12×9×3+12AC•3 =21，解得AC=5．故答案为：5．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．3、6【分析】要求EP+CP的最小值，需考虑通过作辅助线转化EP，CP的值，从而找出其最小值求解．【详解】解：作点E关于AD的对称点F，连接CF，∵△ABC是等边三角形，AD是BC边上的中垂线，∴点E关于AD的对应点为点F，∴CF就是EP+CP的最小值．∵△ABC是等边三角形，E是AC边的中点，∴F是AB的中点，∴CF=AD=6，即EP+CP的最小值为6，故答案为6．【点睛】本题考查了等边三角形的性质和轴对称等知识，熟练掌握等边三角形和轴对称的性质是本题的关键．4、72°72度【分析】由角平分线的定义可知∠ABC=2∠1，由等腰三角形的性质得∠C=∠ABC，由垂直平分线的性质得∠A=∠1，然后根据三角形内角和求解即可．【详解】解：∵BD平分∠ABC，∴∠ABC=2∠1．∵AB=AC，∴∠C=∠ABC=2∠1．∵DE垂直平分AB，∴AD=BD，∴∠A=∠1．∵∠A+∠ABC+∠C=180°，∴∠1+2∠1+2∠1=180°，∴∠1=36°，∴∠C=2∠1=72°．故答案为：72°．【点睛】本题考查了角平分线的定义，等腰三角形的性质，以及线段垂直平分线的性质等知识，熟练掌握相关性质是解答本题的关键．5、32°32度【分析】先根据等腰三角形的性质求出∠ABC＝∠ACB，再根据线段垂直平分线的性质求出∠A与∠ABE的关系，根据三角形内角和定理列方程解答即可．【详解】解：∵△ABC中，AB＝AC，∴∠ABC＝∠ACB，∵DE是线段AB的垂直平分线，∴∠A＝∠ABE，设∠A＝x°，则∠ABC＝∠ACB＝x°＋42°，∴∠A＋∠ABC＋∠ACB＝180°，即x°＋x°＋42°＋x°＋42°＝180°，解得，x＝32°．故∠A＝32°．故答案为：32°．【点睛】此题主要考查线段的垂直平分线的性质等几何知识．①线段的垂直平分线上的点到线段的两个端点的距离相等；②可得到等腰三角形，再利用等腰三角形的知识解答．三、解答题1、（1）B的坐标为2)；（2）①见解析，120ABD︒∠=；②△ACD的边长为【详解】（1）利用非负数的性质求解即可．（2）①根据要求作出图形即可．证明△AOC≌△ABD（SAS），可得结论．②由图可知，点D在与AB夹角为120°的直线上运动，推出当OD⊥BD时OD最短，此时点D在x轴上．【解答】解：（1有意义∴40 40nn-≥⎧⎨-≥⎩，∴n＝4，∴等边△OAB的边长为4，过点B作BC⊥x轴，垂足为点C，∵∠BOC＝30°，∴122BC OB==，∴CC=√CC2−CC2=2√3，点B的坐标为2)．（2）①△ACD如图所画：∵△AOB与△ACD是等边三角形，∴∠CAD＝∠OAB＝∠AOB＝60°，AC＝AD，AB＝AO，∴∠CAO＝60°﹣∠OAD＝∠DAB，∴△AOC≌△ABD（SAS），∴∠ABD＝∠AOC＝180°﹣∠AOB＝120°．②∵∠ABD＝120°，∴由图可知，点D在与AB夹角为120°的直线上运动，∴当OD⊥BD时OD最短，此时点D在x轴上，∴点B的坐标为2)，∴OD=在Rt△AOD中，根据勾股定理AD=∴等边△ACD的边长为【点睛】本题属于三角形综合题，考查了等边三角形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形解决问题．2、（1）见解析；（2）60°，SSS，全等三角形对应角相等【分析】（1）根据题意，③以O为圆心，任意长为半径作弧，分别交射线OA，OD于点E，F；④分别以E，F为圆心，以大于12EF的同样长为半径作弧，两弧在∠AOD内部交于点B；⑤作射线OB；则∠AOB就是所求的角．（2）根据等边三角形的性质，三角形全等的性质与判定推理即可【详解】（1）补全作图如下，（2）证明：连接BE，BF．∵ OC＝OD＝CD，∴ △OCD是等边三角形．∴∠COD＝60°．又∵ OE＝OF，BE＝BF，OB＝OB，∴ △OEB≌△OFB（SSS）（填推理依据）．∴ ∠EOB＝∠FOB（全等三角形对应角相等）（填推理依据）．∴ ∠AOB＝12COD∠＝30°．∴∠AOB就是所求的角．故答案为：60°，SSS，全等三角形对应角相等【点睛】本题考查了基本作图-作角平分线，三角形全等的性质与判定，掌握基本作图是解题的关键．3、（1）142y x=-+；（2）5；（3）点P的坐标为（1285，－445）或（－1285，845）【分析】（1）由坐标系中点的意义结合图形可得出A、B点的坐标，设出对角线AB所在直线的函数关系式，由待定系数法即可求得结论；（2）由勾股定理求出AB的长，再结合线段垂直平分线的性质，可得AM＝BM，OM＝OB−BM，再次利用勾股定理得出AM的长；（3）（方法一）先求出直线AM的解析式，设出P点坐标，由点到直线的距离求出AM边上的高h，再结合三角形面积公式与长方形面积公式即可求出P点坐标；（方法二）由△PAM的面积与长方形OACB的面积相等可得出S△PAM的值，设点P的坐标为（x，−12x＋4），分点P在AM的右侧及左侧两种情况，找出关于x的一元一次方程，解之即可得出点P的坐标，此题得解．【详解】解：（1）∵四边形AOBC为长方形，且点C的坐标是（8，4），∴AO＝CB＝4，OB＝AC＝8，∴A点坐标为（0，4），B点坐标为（8，0）．设对角线AB所在直线的函数关系式为y＝kx＋b，则有408bk b=⎧⎨=+⎩，解得：124kb⎧=-⎪⎨⎪=⎩，∴对角线AB所在直线的函数关系式为y＝－12x＋4．（2）∵∠AOB＝90°，∴勾股定理得：AB＝∵MN垂直平分AB，∴BN＝AN＝12AB＝∵MN为线段AB的垂直平分线，∴AM＝BM设AM＝a，则BM＝a，OM＝8－a，由勾股定理得，a2＝42＋（8－a）2，解得a＝5，即AM＝5．（3）（方法一）∵OM＝3，∴点M坐标为（3，0）．又∵点A坐标为（0，4），∴直线AM的解析式为y＝－43x＋4．∵点P在直线AB：y＝－12x＋4上，∴设P点坐标为（m，－12m＋4），点P到直线AM：43x＋y－4＝0的距离h2m．△PAM的面积S△PAM＝12AM•h＝54|m|＝S OABC＝AO•OB＝32，解得m＝±1285，故点P的坐标为（1285，－445）或（－1285，845）．（方法二）∵S长方形OACB＝8×4＝32，∴S△PAM＝32．设点P的坐标为（x，－12x＋4）．当点P在AM右侧时，S△PAM＝12MB•（y A－y P）＝12×5×（4＋12x－4）＝32，解得：x＝1285，∴点P的坐标为（1285，－445）；当点P在AM左侧时，S△PAM＝S△PMB－S△ABM＝12MB•y P－10＝12×5（－12x＋4）－10＝32，解得：x＝－1285，∴点P的坐标为（－1285，845）．综上所述，点P的坐标为（1285，－445）或（－1285，845）．【点睛】本题考查了坐标系中点的意、勾股定理、点到直线的距离、三角形和长方形的面积公式，解题的关键：（1）根据坐标系中点的意义，找到A、B点的坐标；（2）由线段垂直平分线的性质和勾股定理找出BM的长度；（3）（方法一）结合点到直线的距离、三角形和长方形的面积公式找到关于m的一元一次方程；（方法二）利用分割图形求面积法找出关于x的一元一次方程．本题属于中等题，难度不大，运算量不小，这里尤其要注意点P有两个．4、（1）见解析；（2）等于120°的角有∠BFC、∠BDE、∠DFE=120°．【分析】（1）利用SAS证明△ADC≌△BEC，即可证明AD=BE；（2）证明△CDE为等边三角形，可求得∠BDE=120°；利用全等三角形的性质可求得∠BFD=∠BCA=60°，推出∠DFE=120°；同理可推出∠BFC=∠AFC+∠BFD=120°．【详解】（1）证明：等边△ABC中，CA=CB，∠ACB=60°，∵CE=CD，∠BCE=60°，∴△ADC≌△BEC(SAS)，∴AD=BE；（2）等于120°的角有∠BFC、∠BDE、∠DFE=120°．∵CE=CD，∠BCE=60°，∴△CDE为等边三角形，∴∠CDE=60°，∴∠BDE=120°；∵△ADC≌△BEC，∴∠DAC=∠EBC，又∠BDF=∠ADC，∴∠BFD=∠BCA=60°，∴∠DFE=120°；同理可求得∠AFC=∠ABC=60°，∴∠BFC=∠AFC+∠BFD=120°；综上，等于120°的角有∠BFC、∠BDE、∠DFE=120°．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，熟记各图形的性质并准确识图是解题的关键．5、（1（2）直角三角形（3）5（4）图形见解析【分析】（1）根据勾股定理计算即可；（2）求出BC、AC的长即可判断△ABC的形状；（3）由（2）可知△ABC 是直角三角形，直接利用公式求面积；（4）分别画出A 、B 、C 关于直线l 的轴对称点111A B C 、、，再依次链接111A B C 、、即可．（1）AB （2）AC BC =∴22220AB AC BC +==∴△ABC 的形状是一个直角三角形（3）由（2）可知△ABC 是直角三角形∴11==22ABC S AB AC ∆⋅ （4）图形如图所示：【点睛】本题考查网格中作对称及利用勾股定理求边长，属于常规题，解题的关键是熟练在网格中找到线段所在的直角三角形．。

综合解析鲁教版(五四制)七年级数学下册第八章平行线的有关证明同步测评练习题(精选)

七年级数学下册第八章平行线的有关证明同步测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下列四个命题是真命题的是（）A ．两条直线被第三条直线所截，同位角相等．B ．三角形的一个外角大于任何一个内角．C ．同角的余角相等．D ．若∠3＝∠4，则∠3和∠4是对顶角．2、对于命题“若22x y >，则x y >”，能说明它是假命题的反例是（）A ．2x =-，1y =-B ．1x =-，2y =-C ．2x =，1y =D ．1x =，2y = 3、下列语句中，属于命题的是（）A ．将27开立方B ．画线段AB CD =C ．正数都小于零D ．任意三角形的三条高线交于一点吗？4、如图，将△ABC 沿着DE 减去一个角后得到四边形BCED ，若∠BDE 和∠DEC 的平分线交于点F ，∠DFE ＝α，则∠A 的度数是（）A ．180°﹣αB ．180°﹣2αC ．360°﹣αD ．360°﹣2α5、如图，在ABC 中，∠A ＝55°，∠B ＝45°，那么∠ACD 的度数为（）A ．110B ．100C ．55D ．456、如图，下列四个选项中不能判断AD ∥BC 的是（）A ．13∠=∠B ．180B BAD ∠+∠=°C ．5D ∠=∠ D ．24∠∠=7、下列命题中真命题的个数有（）①有公共顶点且相等的两个角叫对顶角；②过直线外一点有且只有一条直线与已知直线平行；③平行于同一条直线的两条直线平行；④过一点有且只有一条直线与已知直线垂直；⑤直线外一点到已知直线的垂线段就是该点到直线的距离．A ．1个B ．2个C ．3个D ．4个8、下列命题，是真命题的是（）A ．两条直线被第三条直线所截，内错角相等B ．邻补角的角平分线互相垂直C ．相等的角是对顶角D ．若a b ⊥，b c ⊥，则a c ⊥9、下列说法正确的是（）A ．同位角相等B ．在同一平面内，如果a ⊥b ，b ⊥c ，则a ⊥cC ．相等的角是对顶角D ．在同一平面内，如果a ∥b ，b ∥c ，则a ∥c10、△ABC 中，∠A ，∠B ，∠C 的对边分别是a ，b ，c ，下列命题中的假命题是（）A ．如果∠C -∠B =∠A ，则△ABC 是直角三角形B ．如果c 2=b 2-a 2，则△ABC 是直角三角形，且∠C =90°C ．如果（c +a ）（c -a ）=b 2，则△ABC 是直角三角形D ．如果∠A ：∠B ：∠C =5：2：3，则△ABC 是直角三角形第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，四边形ABCD 为一条长方形纸带，AB ∥CD ，将四边形ABCD 沿EF 折叠，A 、D 两点分别为A '、D '对应，若∠1＝∠2，则∠AEF 的度数为______．2、同一平面内，两条直线相交有__________个交点，两条直线相交的特殊位置关系是__________．3、如图，在△ABC 中，∠ACB ＝90°，点D 在AB 上，将△ABC 沿CD 折叠，点A 落在BC 边上的点A '处，若∠B ＝35°，则BDA '∠的度数为___________．4、将命题“两个全等三角形的面积相等”写成“如果_______，那么________”．5、如图，在直线l 1∥l 2，把三角板的直角顶点放在直线l 2上，三角板中60°的角在直线l 1与l 2之间，如果∠1=35°，那么∠2=___度．三、解答题（5小题，每小题10分，共计50分）1、如图，点E ，F 分别在直线AB ，CD 上，//AB CD ，60CFE ∠=︒．射线EM 从EA 开始，绕点E 以每秒3度的速度顺时针旋转至EB 后立即返回，同时，射线FN 从FC 开始，绕点F 以每秒2度的速度顺时针旋转至FD 停止．射线FN 停止运动的同时，射线EM 也停止运动，设旋转时间为t （s ）．(1)当射线FN 经过点E 时，直接写出此时t 的值；(2)当3045t <<时，射线EM 与FN 交于点P ，过点P 作KP FN ⊥交AB 于点K ，求KPE ∠；（用含t 的式子表示）(3)当EM //FN 时，求t 的值．2、如图，已知直线EF GH ∥，AC BC ⊥，BC 平分DCH ∠．(1)求证：ACD DAC ∠=∠；(2)若ACG ∠比BCH ∠的2倍少3度，求DAC ∠的度数．3、如图，ABC 的三个顶点A 、B 、C 在正方形网格中，每小方格的边长都为1cm ．请在方格纸上画图并回答下列问题：(1)延长线段AB 到点D ，使BD AB =；(2)过C 点画AB 的垂线，垂足为点E ；(3)过A 点画直线AF BC ∥，交直线CE 于点F ；(4)点C 到直线AB 的距离为线段的长度．4、如图，,,12AB BF CD BF ⊥⊥∠=∠，试说明3E ∠=∠．证明：∵,AB BF CD BF ⊥⊥（己知），∴90ABD CDF ∠=∠=︒（___________________）， ∴____________（同位角相等，两直线平行），∵12∠=∠（已知），∴AB EF ∥（___________________），∴CD EF ∥（___________________），∴3E ∠=∠（两直线平行，同位角相等）．5、如图，ABC 中，BE 为AC 边上的高，CD 平分ACB ∠，CD 、BE 相交于点F ．若70A ∠=︒，60ABC ∠=︒，求BFC ∠的度数．-参考答案-一、单选题1、C【解析】【详解】解：A 、两条直线被第三条平行直线所截，同位角相等，故原命题错误，是假命题，不符合题意；B 、三角形的一个外角大于任何一个不相邻的内角，故原命题错误，是假命题，不符合题意；C 、同角的余角相等，正确，是真命题，符合题意；D 、若∠3=∠4，则∠3和∠4不一定是对顶角，故原命题错误，是假命题，不符合题意．故选：C【点睛】考查了命题与定理的知识，解题的关键是了解平行线的性质、三角形的外角的性质、余角的定义及对顶角的性质，难度不大．2、A【解析】【分析】要证明一个结论不成立，可以通过举反例的方法来证明一个命题是假命题．【详解】解：当x=-2，y=-1时，x2＞y2，但x＜y，选项A符合题意；当x=-1，y=-2时，x2＜y2，选项B不符合题意；当x=2，y=1时，x2＞y2，则x＞y，选项C不符合题意；当x=1，y=2时，则x2＜y2，选项D不符合题意；故选：A．【点睛】本题考查的是命题与定理，要说明数学命题的错误，只需举出一个反例即可这是数学中常用的一种方法．3、C【解析】【分析】根据命题的定义对各选项进行判断．【详解】解：A．“将27开立方”为陈述句，它不是命题，所以选项不符合题意；”为陈述句，它不是命题，所以选项不符合题意；B．“画线段AB CDC．“正数都小于零”为命题，所以选项符合题意；D．“等任意三角形的三条高线交于一点吗？”为疑问句，它不是命题，所以选项不符合题意．故选：C．【点睛】本题考查了命题，解题的关键是掌握判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成．4、B【解析】【分析】根据∠DFE=α得到∠FDE+∠FED，再根据角平分线的性质求出∠BDE+∠CED=360°-2α，利用外角的性质得到∠ADE+∠AED=2α，最后根据三角形内角和求出结果．【详解】解：∵∠DFE=α，∴∠FDE+∠FED=180°-α，由角平分线的定义可知：∠BDF=∠FDE，∠CEF=∠FED，∴∠BDE+∠CED=2∠FDE+2∠FED=360°-2α，∴∠ADE+∠AED=180°-∠BDE+180°-∠CED=2α，∴∠A=180°-（∠ADE+∠AED）=180°-2α，故选B．【点睛】本题考查了角平分线的定义，三角形内角和，三角形外角的性质，解题的关键是利用角平分线得到相等的角，根据内角和进行计算．5、B【解析】【分析】根据三角形的外角的性质计算即可．【详解】解：由三角形的外角的性质可知，∠ACD ＝∠A +∠B ＝100°，故选：B ．【点睛】本题考查了三角形外角的性质，熟练掌握三角形外角的性质是解答本题的关键．三角形的一个外角等于与它不相邻的两个内角的和，三角形的一个外角大于任何一个与它不相邻的内角．6、D【解析】【分析】直接利用平行线的判定定理分析得出答案．【详解】解：A 、已知13∠=∠，那么AD ∥BC ，故此选项不符合题意；B 、已知180B BAD ∠+∠=°，那么AD ∥BC ，故此选项不符合题意；C 、已知5D ∠=∠，那么AD ∥BC ，故此选项不符合题意；D 、已知24∠∠=，那么AB ∥CD ，不能推出AD ∥BC ，故此选项符合题意；故选：D ．【点睛】本题主要考查了平行线的判定，正确掌握平行线的判定方法是解题关键．平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．7、A【解析】【分析】根据对顶角的定义（有公共顶点且两条边都互为反向延长线的两个角称为对顶角）可判断①；同一平面内，过直线外一点有且只有一条直线与已知直线平行，可判断②；平行于同一条直线的两条直线平行，根据平行线的判定可判断③；同一平面内，过一点有且只有一条直线与已知直线垂直，可判断④；直线外一点到已知直线的垂线段长度就是该点到直线的距离，可判断⑤，综合即可得出选项．【详解】解：根据对顶角的定义（有公共顶点且两条边都互为反向延长线的两个角称为对顶角）判断①错误，是假命题；同一平面内，过直线外一点有且只有一条直线与已知直线平行，故②错误，是假命题；平行于同一条直线的两条直线平行，根据平行线的判定可得③正确，是真命题；同一平面内，过一点有且只有一条直线与已知直线垂直，故④错误，是假命题；直线外一点到已知直线的垂线段长度就是该点到直线的距离，故⑤错误，是假命题；综上可得只有③正确，是真命题，故选：A ．【点睛】题目主要考查真假命题的判断，包括对顶角，平行线和垂线的性质，点到直线的距离等，理解题意，熟练掌握各个定理是解题关键．8、B【解析】【分析】利用平行线的性质、邻补角的定义及性质、对顶角的定义等知识分别判断后即可确定正确的选项．【详解】解：A 、两条平行直线被第三条直线所截，内错角相等，故原命题错误，是假命题，不符合题意； B 、邻补角的角平分线互相垂直，正确，是真命题，符合题意；C 、相等的角不一定是对顶角，故错误，是假命题，不符合题意；D 、平面内，若a b ⊥，b c ⊥，则//a c ，故原命题错误，是假命题，不符合题意，故选：B ．【点睛】考查了命题与定理的知识，解题的关键是了解平行线的性质、邻补角的定义及性质、对顶角的定义等知识，难度不大．9、D【解析】【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断．【详解】解：A. 同位角不一定相等，故该项不符合题意；B. 在同一平面内，如果a⊥b，b⊥c，则a∥c，故该项不符合题意；C. 相等的角不一定是对顶角，故该项不符合题意；D. 在同一平面内，如果a∥b，∥bc，则a∥c，故该项符合题意；故选：D．【点睛】此题考查了语句的判断，正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键．10、B【解析】【分析】利用三角形内角和可对A、D选项进行判断；根据勾股定理的逆定理可对B、C选项进行判断．【详解】解：A、因为∠C-∠B=∠A，即∠A+∠B=∠C，∠A+∠B=180°-∠C，所以∠C=90°，则△ABC是直角三角形，所以A选项为真命题；B 、因为c 2=b 2-a 2，即c 2+a 2=b 2，则△ABC 是直角三角形，且∠B =90°，所以B 选项为假命题；C 、因为（c +a ）（c -a ）=b 2，即c 2=a 2+b 2，则△ABC 是直角三角形，且∠C =90°，所以C 选项为真命题；D 、因为∠A ：∠B ：∠C =5：2：3，所以∠A =510×180°=90°，则△ABC 是直角三角形，所以D 选项为真命题．故选：B ．【点睛】本题考查了命题与定理：命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．二、填空题1、60°##60度【解析】【分析】由题意知2AEF FEA '∠=∠=∠，1180AEF FEA '∠+∠+∠=︒，角度等量替换，然后求解即可．【详解】解：由翻折的性质可知：AEF FEA '∠=∠∵AB CD∴2AEF FEA '∠=∠=∠∵1180AEF FEA '∠+∠+∠=︒，12∠=∠∴260AEF ∠=︒=∠故答案为：60°．【点睛】本题考查了翻折的性质，平行的性质，平角．解题的关键在于确定角的数量关系．2、 1 垂直【解析】略3、20°##20度【解析】【分析】先根据三角形内角和求出∠A ，利用翻折不变性得出55CA D A ∠'=∠=︒，再根据三角形外角的性质即可解决问题．【详解】解：90ACB ∠=︒，∠B ＝35°，180180903555A ACB B ∴∠=︒-∠-∠=︒-︒-︒=︒，CDA '△是由CDA 翻折得到，55CA D A ∴∠'=∠=︒，20CA D B BDA B ∠'=∠+∠'=∠+︒，553520BDA CA D B ''∴∠=∠-∠=︒-︒=︒．故答案为：20°．【点睛】本题考查三角形内角和定理和三角形外角的性质，翻折变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．4、两个三角形全等这两个三角形的面积相等【解析】【分析】根据如果的后面是条件，那么的后面是结论，即可求解．【详解】解：将命题“两个全等三角形的面积相等”写成“如果……，那么……”形式为如果两个三角形全等，那么这两个三角形的面积相等．故答案为：两个三角形全等；这两个三角形的面积相等【点睛】本题主要考查了命题的“如果……，那么……”形式，熟练掌握如果的后面是条件，那么的后面是结论是解题的关键．5、65【解析】【分析】根据三角形外角性质即可求得∠3的度数，再依据平行线的性质，可求得∠3=∠2．【详解】解：∵∠3是△ABC的外角，∠1=∠ABC=35°，∴∠3=∠C+∠ABC=30°+35°=65°，∵直线l1∥l2，∴∠2=∠3=65°，故答案为：65．【点睛】本题主要考查平行线的性质，掌握平行线的性质和判定是解题的关键，即①同位角相等⇔两直线平行，②内错角相等⇔两直线平行，③同旁内角互补⇔两直线平行．三、解答题1、 (1)t 的值为30(2)90KPE t ∠=︒-(3)72t =【解析】【分析】（1）∠CFE 的度数除以射线FN 旋转的速度即可求得t 的值；（2）过点P 作直线//HQ AB ，则由已知可得////HQ AB CD ，由平行线的性质可得∠KPF ，再由垂直关系即可求得∠KPE ；（3）当060t <时，EM 与FN 不平行；当6090t <时，EM 与FN 可能平行，当//EM FN 时，设FN 与AB 交于点G ，由平行线的性质建立方程，即可求得t 的值．(1) FN 的速度为每秒2︒，60CFE ∠=︒，∴当射线FN 经过点E 时，所用的时间t 为：60230t =︒÷︒=；(2)过点P 作直线//HQ AB ，如图所示：//AB CD ，////HQ AB CD ∴，2FPQ CFP t ∴∠=∠=，3EPQ KEP t ∠=∠=，32EPF EPQ FPQ t t t ∴∠=∠-∠=-=，KP FN ⊥，90KPF ∴∠=︒，9090KPE EPF t ∴∠=︒-∠=︒-；(3) EM 与FN 的速度不相等，∴当060t <时，EM 与FN 不平行；当6090t <时，EM 与FN 可能平行，当//EM FN 时，设FN 与AB 交于点G ，如图所示：//EM FN ，AGF MEB ∴∠=∠，由题意可得：3180MEB t ∠=-︒，3180AGF t ∴∠=-︒，//AB CD ，180AGF CFN ∴∠+∠=︒，2CFN t ∠=，31802180t t ∴-︒+=︒，解得：72t =．【点睛】本题是与平行线有关的综合问题，它考查了平行线的性质、垂直的性质、角的和差运算，运用了方程思想．2、 (1)见解析(2)59︒【解析】【分析】（1）根据平行线的性质，角平分线的定义，直角三角形的两锐角互余可得12∠=∠，23∠∠=，25=9034=90∠+∠︒∠+∠︒，，进而即可得45∠=∠，即ACD DAC ∠=∠；（2）根据题意，由（1）的角度之间关系可得1590∠+∠=︒，结合已知条件建立二元一次方程组，解方程组即可求解．(1)如图，BC 平分DCH ∠12∠∠∴=EF GH ∥13∠∠∴=23∴∠=∠AC BC ⊥，25=9034=90∴∠+∠︒∠+∠︒，45∴∠=∠即ACD DAC ∠=∠(2)如图，EF GH ∥4ACG ∴∠=∠45,12∠=∠∠=∠5,1ACG BCH ∴∠=∠∠=∠由ACG ∠比BCH ∠的2倍少3度，即5213∠=∠-︒①5290∠+∠=︒，又12∠=∠即5190∠+∠=︒②213190∴∠-︒+∠=︒解得131∠=︒45213231359DAC ∠=∠=∠=∠-︒=⨯︒-︒=∴︒59DAC ∴∠=︒【点睛】本题考查了平行线的性质，直角三角形的两锐角互余，二元一次方程组，数形结合是解题的关键．3、 (1)AB =BD ，见详解；(2)CE ⊥AD 于E ，见详解；(3)AF∥BC ；见详解；(4)CE ．【解析】【分析】（1）根据网格的性质，线段中点定义，得出BD =3，延长即可；（2）根据网格的性质，利用点平移方法即可画出CE ⊥AD ；（3）根据网格中小正方形对角线的性质，即可画出AF∥BC ；（4）根据网格的性质， CE ⊥AB ，根据点到直线的距离得出CE 的长即可得(1)解：根据题意，得AB=3cm，在AB的延长线上，截取BD=3则AB=BD，如图所示：(2)解：如图所示：点C向下平移2个单位取点E，连结CE，则CE⊥AD于E；(3)解：如图所示：∵BE=2=CE，AB=3，∴AE=AB+BE=3+2=5，∴点C向上平移3个格到点F，连结AF，则AF∥BC，∵AF是正方形网格的对角线，CB是正方形网格的对角线，∴∠FAB=45°，∠CBE=45°，∵∠FAB=∠CBE=45°，∴AF∥BC；(4)点C到直线AB的距离为线段CE的长度．故答案为CE．【点睛】此题主要考查正方形网格中的作图综合问题，熟练掌握网格的性质，中点定义，垂线定义，平行线判定与性质，点到直线的距离是解题关键．4、垂直定义；AB；CD；内错角相等，两直线平行；平行于同一条直线的两条直线平行【解析】【分析】根据垂直定义求出∠B=∠CDF=90°，根据平行线的判定得出AB∥EF，EF∥CD，即可得出答案．【详解】证明：∵,AB BF CD BF ⊥⊥（己知），∴90ABD CDF ∠=∠=︒（垂直定义），∴AB CD （同位角相等，两直线平行），∵12∠=∠（已知），∴AB EF ∥（内错角相等，两直线平行），∴CD EF ∥（平行于同一条直线的两条直线平行），∴3E ∠=∠（两直线平行，同位角相等）．故答案为：垂直定义；AB ；CD ；内错角相等，两直线平行；平行于同一条直线的两条直线平行【点睛】本题考查了平行线的判定的应用，能正确运用判定定理进行推理是解此题的关键，注意：平行线的判定定理有：①同位角相等，两直线平行，②内错角相等，两直线平行，③同旁内角互补，两直线平行，④平行于同一直线的两直线平行．5、115︒．【解析】【分析】先根据三角形的内角和定理可得50∠=°ACB ，再根据角平分线的定义可得25ECF ∠=︒，然后根据垂直的定义可得90CEF ∠=︒，最后根据三角形的外角性质即可得．【详解】解：在ABC 中，70A ∠=︒，60ABC ∠=︒，18050AB B C AC A ∴∠=︒-∠=∠-︒， CD 平分ACB ∠，1252ECF ACB ∠=∠=∴︒，BE为AC边上的高，∴∠=︒，CEF90∴∠=∠+∠=︒+︒=︒．9025115BFC CEF ECF【点睛】本题考查了三角形的内角和定理、角平分线的定义、三角形的外角性质等知识点，熟练掌握三角形的内角和定理是解题关键．。

(易错题精选)初中数学命题与证明的技巧及练习题含答案

（易错题精选）初中数学命题与证明的技巧及练习题含答案一、选择题1．下列命题是真命题的是（）A．若x＞y，则x2＞y2B．若|a|=|b|，则a=b C．若a＞|b|，则a2＞b2D．若a＜1，则a＞1a【答案】C【解析】【分析】根据实数的乘方，绝对值的性质和倒数的意义等，对各选项举反例分析判断后利用排除法求解．【详解】A. x＞y，如x=0，y=-1，02<(-1)2，此时x2<y2，故A选项错误；B. |a|=|b|，如a=2，b=-2，此时a≠b，故B选项错误；C. 若a＞|b|，则a2＞b2，正确；D. a＜1，如a=-1，此时a=1a，故D选项错误，故选C.【点睛】本题考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题，本题主要利用了实数的性质．2．下列各命题的逆命题是真命题的是A．对顶角相等B．全等三角形的对应角相等C．相等的角是同位角D．等边三角形的三个内角都相等【答案】D【解析】【分析】分别写出四个命题的逆命题：相等的角为对顶角；对应角相等的两三角形全等；同位角相等；三个角都相等的三角形为等边三角形；然后再分别根据对顶角的定义对第一个进行判断；根据三角形全等的判定方法对第二个进行判断；根据同位角的性质对第三个进行判断；根据等边三角形的判定方法对第四个进行判断．【详解】A、“对顶角相等”的逆命题为“相等的角为对顶角”，此逆命题为假命题，所以A选项错误；B、“全等三角形的对应角相等”的逆命题为“对应角相等的两三角形全等”，此逆命题为假命题，所以B选项错误；C、“相等的角是同位角”的逆命题为“同位角相等”，此逆命题为假命题，所以C选项错误；D、“等边三角形的三个内角都相等”的逆命题为“三个角都相等的三角形为等边三角形”，此逆命题为真命题，所以D选项正确．故选D.【点睛】本题考查了命题与定理：判断事物的语句叫命题；题设与结论互换的两个命题互为逆命题；正确的命题叫真命题，错误的命题叫假命题；经过推论论证得到的真命题称为定理．3．下列三个命题：①对顶角相等；②全等三角形的对应边相等；③如果两个实数是正数，它们的积是正数.它们的逆命题成立的个数是( )A．0个 B．1个 C．2个 D．3个【答案】B【解析】【分析】把一个命题的条件和结论互换就得到它的逆命题，再把逆命题进行判断即可．【详解】①对顶角相等的逆命题是相等的角是对顶角，逆命题错误；②全等三角形的对应边相等的逆命题是对应边相等的两个三角形全等，正确；③如果两个实数是正数，它们的积是正数的逆命题是如果两个数的积为正数，那么这两个数也是正数，逆命题错误，也可以有都是负数，所以逆命题成立的只有一个，故选B.【点睛】本题考查了互逆命题，真命题与假命题，真命题要运用相关知识进行推导，假命题要通过举反例来进行否定.4．下列命题中，正确的命题是（）A．度数相等的弧是等弧B．正多边形既是轴对称图形，又是中心对称图形C．垂直于弦的直径平分弦D．三角形的外心到三边的距离相等【答案】C【解析】【分析】根据等弧或垂径定理，正多边形的性质一一判断即可；【详解】A、完全重合的两条弧是等弧，错误；B、正五边形不是中心对称图形，错误；C、垂直于弦的直径平分弦，正确；D、三角形的外心到三个顶点的距离相等，错误；故选：C．【点睛】此题考查命题与定义，正多边形的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．5．下列命题中，是真命题的是（）A ．将函数y ＝12x +1向右平移2个单位后所得函数的解析式为y ＝12x B ．若一个数的平方根等于其本身，则这个数是0和1 C ．对函数y ＝2x，其函数值y 随自变量x 的增大而增大 D ．直线y ＝3x +1与直线y ＝﹣3x +2一定互相平行【答案】A【解析】【分析】利用一次函数的性质、平方根的定义、反比例函数的性质等知识分别判断后即可确定正确的选项．【详解】解：A 、将函数y ＝12x +1向右平移2个单位后所得函数的解析式为y ＝12x ，正确，符合题意；B 、若一个数的平方根等于其本身，则这个数是0，故错误，是假命题，不符合题意；C 、对函数y ＝2x，其函数值在每个象限内y 随自变量x 的增大而增大，故错误，是假命题，不符合题意； D 、直线y ＝3x +1与直线y ＝﹣3x +2因比例系数不相等，故一定不互相平行，故错误，是假命题，故选：A ．【点睛】本题考查了判断命题真假的问题，掌握一次函数的性质、平方根的定义、反比例函数的性质等知识是解题的关键．6．下列选项中，可以用来说明命题“若22a b ＞，则a b ＞”是假命题的反例是（） A ．2,a =b=-1B ．2,1a b =-=C ．3,a =b=-2D ．2,0a b ==【答案】B【解析】分析：根据要证明一个结论不成立，可以通过举反例的方法来证明一个命题是假命题．详解：∵当a =﹣2，b =1时，（﹣2）2＞12，但是﹣2＜1，∴a =﹣2，b =1是假命题的反例．故选B ．点睛：本题考查的是命题与定理，要说明数学命题的错误，只需举出一个反例即可．这是数学中常用的一种方法．7．下列命题中是真命题的是（）A ．两个锐角的和是锐角B ．两条直线被第三条直线所截，同位角相等C ．点(3,2)-到x 轴的距离是2D ．若a b >，则a b ->-【答案】C【解析】【分析】根据角的定义、平行线的性质、点的坐标及不等式的性质对各选项进行分析判断，即可得解．【详解】A. 两个锐角的和是锐角是假命题，例如80°+80°=160°，是钝角，不是锐角，故本选项错误；B. 两条直线被第三条直线所截，同位角相等是假命题，两条平行线被第三条直线所截，同位角才相等，故本选项错误；C. 点(3,2)-到x 轴的距离是2是真命题，故本选项正确；D. 若a b >，则a b ->-是假命题，正确结果应为a b -<-，故本选项错误．故选：C ．【点睛】本题考查真假命题的判断，解题关键是认真判断由条件是否能推出结论，如果能举出一个反例，或由条件推出的结论与题干结论不一致，则为假命题．8．下列命题中：①；②在同一平面内，若a ⊥b ，a ⊥c ，则b ∥c ；③若ab ＝0，则P(a ，b)表示原点；9．是真命题的有（）A ．1 个B ．2 个C ．3 个D ．4 个【答案】A【解析】【分析】根据立方根、平行线的判定和算术平方根判断即可．【详解】解：①≥0≤0不一定成立，错误； ②在同一平面内，若a b ⊥r r ，a c ⊥，则//b c ，正确； ③若0ab =，则(,)P a b 表示原点或坐标轴，错误；3，错误；故选：A ．【点睛】本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．9．下列命题中:①等腰三角形底边的中点到两腰的距离相等；②等腰三角形的高、中线、角平分线互相重合； ③若ABC V 与'''A B C V 成轴对称，则ABC V 一定与'''A B C V 全等；④有一个角是60度的三角形是等边三角形；⑤等腰三角形的对称轴是顶角的平分线．正确命题的个数是（）A ．2B ．3C ．4D ．5【答案】A【解析】【分析】利用轴对称的性质、等腰三角形的性质、等边三角形的判定等知识分别判断后即可确定正确的选项．【详解】解:①等腰三角形底边的中点到两腰的距离相等；正确； ②等腰三角形的底边上的高、底边上的中线、顶角的平分线互相重合；不正确: ③若ABC V 与'''A B C V 成轴对称，则ABC V 一定与'''A B C V 全等；正确； ④有一个角是60度的等腰三角形是等边三角形；不正确；⑤等腰三角形的对称轴是顶角的平分线所在的直线，不正确．正确命题为:2①③，个；故选：A【点睛】本题考查了命题与定理的知识，解题的关键是了解轴对称的性质、等腰三角形的性质、等边三角形的判定等知识，属于基础知识，难度不大．10．下列说法正确的是( )A ．相等的角是对顶角B ．在平面内,经过一点有且只有一条直线与已知直线平行C ．两条直线被第三条直线所截,内错角相等D ．在平面内,经过一点有且只有一条直线与已知直线垂直【答案】D【解析】【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．【详解】解：相等的角不一定是对顶角，故A 错误；在平面内,经过直线外一点有且只有一条直线与已知直线平行，故B 错误；两直线平行，内错角相等，故C 错误；在平面内，经过一点有且只有一条直线与已知直线垂直，故D 正确；故答案为D.【点睛】此题主要考查了命题的真假判断，掌握定理并灵活运用是解题的关键.11．已知：在ABC V 中，AB AC ≠，求证：.B C ∠≠∠若用反证法来证明这个结论，可以假设( )A ．AB ∠=∠B ．AB BC = C ．B C ∠=∠D ．A C ∠=∠【答案】C【解析】【分析】反证法的步骤:1、假设命题反面成立;2、从假设出发,经过推理得出和反面命题矛盾,或者与定义、公理、定理矛盾;3、得出假设命题不成立是错误的,即所求证命题成立.【详解】已知：在ABC V 中，AB AC ≠，求证：.B C ∠≠∠若用反证法来证明这个结论，可以假设B C ∠=∠,由“等角对等边”可得AB=AC,这与已知矛盾，所以.B C ∠≠∠故选C【点睛】本题考核知识点：反证法. 解题关键点：理解反证法的一般步骤.12．下列说法正确的是( )A ．若a ＞b ，则a 2＞b 2B ．若三条线段的长a 、b 、c 满足a +b ＞c ，则以a 、b 、c 为边一定能组成三角形C ．两直线平行，同旁内角相等D ．三角形的外角和为360°【答案】D【解析】【分析】利用特例对A 进行分析，利用三角形三边关系、平行线的性质、三角形外角的性质分别对B 、C 、D 进行分析判断．【详解】A 、若a ＞b ，则不一定有a 2＞b 2，比如a ＝0,b ＝﹣1，故本选项错误；B 、若三条线段的长a 、b 、c 满足a +b ＞c ，则以a 、b 、c 为边不一定能组成三角形，故本选项错误；C 、两直线平行，同旁内角互补，故本选项错误；D 、三角形的外角和为360°，故本选项正确；故选：D【点睛】本题考查真假命题的判断，解题的关键是根据相关知识对命题进行分析判断．13．下列命题中正确的有（）个①平分弦的直径垂直于弦；②经过半径的外端且与这条半径垂直的直线是圆的切线；③在同圆或等圆中，圆周角等于圆心角的一半；④平面内三点确定一个圆；⑤三角形的外心到三角形的各个顶点的距离相等．A．1 B．2 C．3 D．4【答案】B【解析】【分析】根据垂径定理的推论对①进行判断；根据切线的判定定理对②进行判断；根据圆周角定理对③进行判断；根据确定圆的条件对④进行判断；根据三角形外心的性质对⑤进行判断．【详解】①平分弦（非直径）的直径垂直于弦，错误；②经过半径的外端且与这条半径垂直的直线是圆的切线，正确；③在同圆或等圆中，同弧所对的圆周角等于圆心角的一半，错误；④平面内不共线的三点确定一个圆，错误；⑤三角形的外心到三角形的各个顶点的距离相等，正确；故正确的命题有2个故答案为：B．【点睛】本题考查了判断命题真假的问题，掌握垂径定理的推论、切线的判定定理、圆周角定理、确定圆的条件、三角形外心的性质是解题的关键．14．下列命题：①直线外一点到这条直线的垂线段，叫做点到直线的距离；②两点之间线段最短；③相等的圆心角所对的弧相等；④平分弦的直径垂直于弦．其中，真命题的个数是（）A．1 B．2 C．3 D．4【答案】A【解析】【分析】根据点到直线的距离，线段的性质，弧、弦、圆心角之间的关系以及垂径定理判断即可．【详解】①直线外一点到这条直线的垂线段，叫做点到直线的距离；假命题；②两点之间线段最短；真命题；③相等的圆心角所对的弧相等；假命题；④平分弦的直径垂直于弦；假命题；真命题的个数是1个；故选：A．【点睛】考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．15．用反证法证明命题：“在三角形中，至多有一个内角是直角”，正确的假设是（） A ．在三角形中，至少有一个内角是直角B ．在三角形中，至少有两个内角是直角C ．在三角形中，没有一个内角是直角D ．在三角形中，至多有两个内角是直角【答案】B【解析】【分析】反证法即假设结论的反面成立，“最多有一个”的反面为“至少有两个”.【详解】解：∵“最多有一个”的反面是“至少有两个”，反证即假设原命题的否命题正确， ∴应假设：在三角形中，至少有两个内角是直角.故选：B.【点睛】此题主要考查了反证法，解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，不需要一一否定，只需否定其一即可.16．39．下列命题中，是假命题的是（）A ．同旁内角互补B ．对顶角相等C ．直角的补角仍然是直角D ．两点之间，线段最短【答案】A【解析】同旁内角不一定互补，同旁内角互补的条件是两直线平行，故选A.17．下列命题中，是假命题的是( )A ．任意多边形的外角和为360oB ．在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C VC ．在一个三角形中，任意两边之差小于第三边D ．同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析．【详解】解：A. 任意多边形的外角和为360o ,是真命题；B. 在ABC V 和'''A B C V 中，若''AB A B =，''BC B C =，'90C C ∠=∠=o ，则ABC V ≌'''A B C V ，根据HL ，是真命题；C. 在一个三角形中，任意两边之差小于第三边，是真命题；D. 同弧所对的圆周角等于圆心角的一半，本选项是假命题.故选D ．【点睛】本题考核知识点：判断命题的真假. 解题关键点：熟记相关性质或定义．18．下列选项中，能说明命题“若22a b >，则a b >”是假命题的反例是( )A ．1a =-，2b =B ．2a =，1b =-C ．1a =，2b =-D ．2a =-，1b =【答案】D【解析】【分析】根据要证明一个结论不成立，可以通过举反例的方法来证明一个命题是假命题，作答本题直接利用选项中数据代入求出答案．【详解】A. 当1a =-，2b =时，2a ＜2b ，a ＜b ，则此选项不是假命题的反例；B. 当2a =，1b =-时，2a ＞2b ，a ＞b ，则此选项不是假命题的反例；C. 当1a =，2b =-时，2a ＜2b ，a ＞b ，则此选项不是假命题的反例；D. 当2a =-，1b =时，2a ＞2b ，a ＜b ，则此选项是假命题的反例，故选：D ．【点睛】本题考查真命题与假命题．要说明数学命题的错误，只需举出一个反例即可，反例就是符合已知条件但不满足结论的例子．19．下列命题是真命题的是（）A ．同旁内角相等，两直线平行B ．对角线互相平分的四边形是平行四边形C ．相等的两个角是对顶角D ．圆内接四边形对角相等【答案】B【解析】【分析】由平行线的判定方法得出A 是假命题；由平行四边形的判定定理得出B 是真命题；由对顶角的定义得出C 是假命题；由圆内接四边形的性质得出D 是假命题；综上，即可得出答案.【详解】A.同旁内角相等，两直线平行；假命题；B.对角线互相平分的四边形是平行四边形；真命题；C.相等的两个角是对顶角；假命题；D.圆内接四边形对角相等；假命题；故选：B.【点睛】本题考查了命题与定理、平行线的判定、平行四边形的判定、对顶角的定义、圆内接四边形的性质；熟练掌握相关性质和定理、定义是解题关键.20．下列命题中真命题是（）A．若a2=b2,则a=b B．4的平方根是±2C．两个锐角之和一定是钝角 D．相等的两个角是对顶角【答案】B【解析】【分析】利用对顶角的性质、平方根的性质、锐角和钝角的定义分别判断后即可确定正确的选项．【详解】A、若a2=b2,则a=±b，错误，是假命题；B、4的平方根是±2，正确，是真命题；C、两个锐角的和不一定是钝角，故错误，是假命题；D、相等的两个角不一定是对顶角，故错误，是假命题.故选B．【点睛】考查了命题与定理的知识，解题的关键是了解对顶角的性质、平方根的性质、锐角和钝角的定义，难度不大．。

难点详解鲁教版(五四制)七年级数学下册第十章三角形的有关证明专项测试练习题(精选含解析)

鲁教版（五四制）七年级数学下册第十章三角形的有关证明专项测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、在△ABC 中，AB =AC ，AC 边上的中线BD 把△ABC 的周长分为24 cm 和30 cm 的两部分，则BC 的长为 ( )cmA ．14B ．16或22C ．22D ．14或222、如图，直线DE 是ABC 边AC 的垂直平分线，且与AC 相交于点E ，与AB 相交于点D ，连接CD ，已知BC ＝8cm ，AB ＝12cm ，则BCD 的周长为（）A ．16cmB ．18cmC ．20cmD ．22cm3、如图，点P ，D 分别是∠ABC 边BA ，BC 上的点，且4BD =，60ABC ∠=︒．连结PD ，以PD 为边，在PD 的右侧作等边△DPE ，连结BE ，则△BDE 的面积为（）A．B．2 C．4 D．4、如图，△ABD≌△ECB，若5AD=，6DE=，则BC的长为（）A．11 B．10 C．9 D．85、等腰三角形的顶角为80°，则其底角的度数是（）A．100°B．80°C．50°D．40°6、已知：如图，在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°．其中正确的个数有（）A．1个B．2个C．3个D．4个7、下列命题为假命题的是（）A．三角形的三个内角的和等于180度B ．三角形的任意两边之和大于第三边C ．三角形的角平分线是一条射线D ．三角形的面积等于一条边上的长与该条边上的高的乘积的一半8、在ABC 中，线段AP ，AQ ，AR 分别是BC 边上的高线，中线和角平分线，则（）A ．AP AQ ≤B ．AQ AR ≤C ．AP AR >D ．AP AQ >9、如图，点D 为ABC 的边BC 上一点，且满足AD DC =，作DE AB ⊥于点E ，若68BAC ∠=︒，36C ∠=︒，则ADE ∠的度数为（）A ．56°B ．58°C ．60°D ．62°10、如图，在△ABC 中，∠C ＝90°，D ，E 是AC 上两点，且AE ＝DE ，BD 平分∠EBC ，那么下列说法中不正确的是（）A ．BE 是△ABD 的中线B ．BD 是△BCE 的角平分线C ．∠1＝∠2＝∠3D ．S △AEB ＝S △EDB第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在ABC 中，5AB AC ==，6BC =，AD 是BAC ∠的平分线，4=AD ．若P ，Q 分别是AD 和AC 上的动点，则PC PQ +的最小值是______．2、等边三角形的边长为a ，则该等边三角形的面积为________．（用含a 的代数式表示）3、如图，△ABC 是等边三角形．在AC ，BC 边上各取一点P ，Q ，使AP ＝CQ ，且∠ABP ＝20°，AQ ，BP 相交于点O ，则∠AQB ＝_____．4、已知ABC DEF ≌△△，若5AB =，6BC =，7AC =，则DEF 的周长是______． 5、如图，D 是等边三角形ABC 外一点．若BD ＝8，CD ＝6，则AD 的最大值与最小值的差为 _____．三、解答题（5小题，每小题10分，共计50分）1、如图，在△ABC 中，AB AC =，AD 为BC 边上的中线，E 为AC 上一点，且AE AD =，∠=︒，求∠CDE的度数．BAD502、在△ABC中，AB＝AC，CD⊥AB于D．(1)若∠A＝40°，求∠DCB的度数；(2)若BC＝15，CD＝12，求AC的长．3、如图，△ACB 和△DCE 都是等腰直角三角形，∠ACB=∠DCE=90°．AC=41，DE=18，将△DCE 绕着顶点C 旋转，连接AD，BE．(1)求证：△ACD≌△BCE；(2)在△DCE 的旋转过程中，探求：点A，D，E 在同一直线上时，AE 的长．4、已知OM是∠AOB的平分线，点P是射线OM上一点，点C、D分别在射线OA、OB上，连接PC、PD．(1)如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是．(2)如图②，点C、D在射线OA、OB上滑动，且∠AOB＝90°，当PC⊥PD时，PC与PD在（1）中的数量关系还成立吗？说明理由．5、如图，CD是△ABC的角平分线，DE，DF分别是△ACD和△BCD的高．(1)求证CD⊥EF；(2)若AC＝6，BC＝4，S△ABC＝10，∠ACB＝60°，求CG的长．-参考答案-一、单选题1、D【解析】【分析】根据点D为AC中点，得出AD=DC=12AC，根据AB=AC，得出AB=2AD，分两种情况当AB+AD=24cm时，2AD+AD=24cm，可求BC=30cm-CD=30cm-8cm=22cm，当AB+AD=30cm时，2AD+AD=30cm，可求BC=24cm-CD=24cm-10cm=14cm即可．【详解】解：∵点D为AC中点，∴AD=DC=12 AC，∵AB=AC，∴AB=2AD，分两种情况，当AB+AD=24cm时，2AD+AD=24cm，解得AD=8cm，∵BC+CD=30cm，∴BC=30cm-CD=30cm-8cm=22cm，当AB+AD=30cm时，2AD+AD=30cm，解得AD=10cm，∵BC+CD=24cm，∴BC=24cm-CD=24cm-10cm=14cm，∴BC的长为14cm或22cm．故选D．【点睛】本题考查等腰三角形性质，中线性质，一元一次方程，线段和差，分类思想的应用，掌握等腰三角形性质，中线性质，一元一次方程，线段和差，分类思想的应用是解题关键．2、C【解析】【分析】根据线段垂直平分线的性质得出AD＝CD，求出△BCD的周长＝BC+CD+BD＝BC+AB，再代入求出答案即可．【详解】解：∵直线DE是AC的垂直平分线，∴AD＝CD，∵BC＝8cm，AB＝12cm，∴△BCD的周长＝BC+CD+BD＝BC+AD+BD＝BC+AB＝8+12＝20（cm），故选：C．【点睛】本题考查了线段垂直平分线的性质，能熟记线段垂直平分线上的点到线段两个端点的距离相等是解此题的关键．3、A【解析】【分析】要求BDE ∆的面积，想到过点E 作EF BC ⊥，垂足为F ，因为题目已知60ABC ∠=︒，想到把ABC ∠放在直角三角形中，所以过点D 作DG BA ⊥，垂足为G ，利用勾股定理求出DG 的长，最后证明GPD FDE ∆≅∆即可解答．【详解】解：过点E 作EF BC ⊥，垂足为F ，过点D 作DG BA ⊥，垂足为G ，在Rt BGD 中，4BD =，60ABC ∠=︒，30BDG ∴∠=︒，122BG BD ∴==，GD ∴PDE ∆是等边三角形，60PDE ∴∠=︒，PD DE =，180120PDB EDF PDE ∴∠+∠=︒-∠=︒，60ABC ∠=︒，180120PDB BPD ABC ∴∠+∠=︒-∠=︒，BPD EDF ∴∠=∠，90PGD DFE ∠=∠=︒，()GPD FDE AAS ∴∆≅∆，GD EF ∴==，BDE∴∆的面积12BD EF=⋅，142=⨯⨯=故选：A．【点睛】本题考查了等边三角形的性质，全等三角形、勾股定理，解题的关键是根据题目的已知条件并结合图形添加适当的辅助线．4、A【解析】【分析】由三角形全等的性质可知AD=BE，BD=BC，故可得BC=BD=BE+DE=11．【详解】∵△ABD≌△ECB∴AD=BE，BD=BC∴BE=5∵BD=BE+DE=5+6=11∴BC=BD=11故选：A．【点睛】本题考查了全等三角形的性质，全等三角形的对应边相等，对应角相等，可以进一步推广到全等三角形对应边上的高相等，对应角的平分线相等，对应边上的中线相等，周长及面积相等．5、C【解析】【分析】根据等腰三角形两底角相等即可得解．【详解】解：∵等腰三角形的顶角为80°，∴它的底角度数为12（180°-80°）=50°．故选：C．【点睛】本题考查了等腰三角形两底角相等的性质，关键是根据等腰三角形的性质解答．6、D【解析】【分析】①由AB=AC，AD=AE，利用等式的性质得到夹角相等，利用SAS得出三角形ABD与三角形AEC全等，由全等三角形的对应边相等得到BD=CE，本选项正确；②由三角形ABD与三角形AEC全等，得到一对角相等，由等腰直角三角形的性质得到∠ABD+∠DBC=45°，等量代换得到∠ACE+∠DBC=45°，本选项正确；③再利用等腰直角三角形的性质及等量代换得到BD垂直于CE，本选项正确；④利用周角减去两个直角可得答案．【详解】解：①∵∠BAC=∠DAE=90°，∴∠BAC+∠CAD=∠DAE+∠CAD，即∠BAD=∠CAE，∵在△BAD和△CAE中，AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAD≌△CAE（SAS），∴BD=CE，本选项正确；②∵△ABC为等腰直角三角形，∴∠ABC=∠ACB=45°，∴∠ABD+∠DBC=45°，∵△BAD≌△CAE，∴∠ABD=∠ACE，∴∠ACE+∠DBC=45°，本选项正确；③∵∠ABD+∠DBC=45°，∴∠ACE+∠DBC=45°，∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°，则BD⊥CE，本选项正确；④∵∠BAC=∠DAE=90°，∴∠BAE+∠DAC=360°-90°-90°=180°，故此选项正确，综上，四个选项都是正确的，故选：D．【点睛】本题考查了全等三角形的判定与性质，以及等腰直角三角形的性质，熟练掌握全等三角形的判定与性质是解本题的关键．7、C【解析】【分析】分别根据三角形内角和定理、三角形三边的关系、三角形角平分线定义以及三角形面积公式对各个命题进行判断．【详解】解：A.三角形三个内角的和等于180°，所以此选项为真命题；B.三角形两边之和大于第三边，所以此选项为真命题；C.三角形的角平分线是一条线段，所以此选项为假命题；D.三角形的面积等于一条边的长与该边上的高的乘积的一半，所以此选项为真命题．故选：C ．【点睛】本题考查了命题：判断事物的语句叫命题；正确的命题叫真命题，错误的命题叫假命题；经过推理论证的真命题叫定理．8、A【解析】【分析】根据垂线段最短解答即可．【详解】解：∵线段AP 是BC 边上在的高线，∴根据垂线段最短得：PA ≤AQ ，P A ≤AR ，故选：A ．【点睛】本题考查三角形的高、中线和角平分线、垂线段最短等知识，熟练掌握垂线段最短是解答的关键．9、B【解析】【分析】首先根据等边对等解救出36DAC ∠=︒，再求出32DAE ∠=︒，最后根据“直角三角形两锐角互余”得58ADE ∠=︒，从而得到结论．【详解】解：∵AD DC =，且36C ∠=︒∴36DAC C ∠=∠=︒又68BAC ∠=︒∴683632BAD BAC DAC ∠=∠-∠=︒-︒=︒∵DE AB ⊥∴90DEA ∠=︒∴90903258ADE BAD ∠=︒-∠=︒-︒=︒故选：B【点睛】本题主要考查了等腰三角形的性质，以及直角三角形两锐角互余等知识，利用等腰三角形的性质“等边对等角”求出36DAC ∠=︒是解答本题的关键．10、C【解析】【分析】根据三角形中线、角平分线的定义逐项判断即可求解．【详解】解：A 、∵AE ＝DE ，∴BE 是△ABD 的中线，故本选项不符合题意；B 、∵BD 平分∠EBC ，∴BD 是△BCE 的角平分线，故本选项不符合题意；C 、∵BD 平分∠EBC ，∴∠2＝∠3，但不能推出∠2、∠3和∠1相等，故本选项符合题意；D、∵S△AEB＝12×AE×BC，S△EDB＝12×DE×BC，AE＝DE，∴S△AEB＝S△EDB，故本选项不符合题意；故选：C【点睛】本题主要考查了三角形中线、角平分线的定义，熟练掌握三角形中，连接一个顶点和它的对边的中点的线段叫做三角形的中线；三角形的一个角的平分线与这个角的对边相交，连接这个角的顶点和交点的线段叫三角形的角平分线是解题的关键．二、填空题1、4.8【解析】【分析】作点Q关于AD的对称点E，连接PE，过点C作CF⊥AB于点F，则当C、P、E三点共线且与CF重合时，PC+PQ取得最小值；由等腰三角形的性质及勾股定理可求得AD的长，再利用面积关系即可求得最小值CF的长．【详解】如图，作点Q关于AD的对称点E，连接PE，过点C作CF⊥AB于点F∵AB =AC ，AD 是BAC ∠的平分线∴AD ⊥BC ，△ABC 关于直线AD 对称，132BD CD BC ===∵点Q 、点E 关于AD 对称∴PQ =PE∴PC +PQ =PC +PE ≥CF当C 、P 、E 三点共线且与CF 重合时，PC +PQ 取得最小值，且最小值为线段CF 的长在Rt △ABD 中，由勾股定理得：4AD = ∵1122ABC S BC AD AB CF =⨯=⨯△ ∴64 4.85BC AD CF AB ⨯⨯=== 即PC +PQ 的最小值为4.8故答案为：4.8【点睛】本题考查了等腰三角形的性质，垂线段最短，勾股定理等知识，作点Q 的对称点是本题的关键与难点所在．22 【解析】【分析】求出等边三角形的高，根据三角形面积公式即可得出答案．【详解】如图所示，ABC 是等边三角形，过点A 作AD BC ⊥交于点D ，∵ABC 的边长为a ，∴AB BC a ==，122a BD BC ==，∴AD ===，∴212ABC S a =⨯=，2．【点睛】本题考查等边三角形的性质，掌握等边三角形“三线合一”求长度是解题的关键．3、80︒##80度【解析】【分析】先证明,BAP ACQ ≌ 再利用全等三角形的性质可得20,ABP CAQ 再利用三角形的外角的性质可得结论.【详解】解： △ABC 是等边三角形，,60,AB AC ABC C BAC,AP CQ,BAP ACQ ≌20,ABP CAQ 602080.AQB C CAQ故答案为：80︒【点睛】本题考查的是三角形的外角的性质，全等三角形的判定与性质，等边三角形的性质，证明20ABP CAQ 是解本题的关键.4、18【解析】【分析】根据全等三角形的性质，即可求解．【详解】解：∵ABC DEF ≌△△， ∴5,6,7DE AB EF BC DF AC ====== ，∴DEF 的周长为56718DE EF DF ++=++= ．故答案为：18【点睛】本题主要考查了全等三角形的性质，熟练掌握全等三角形的对应边相等，对应角相等是解题的关键． 5、12【解析】【分析】以CD 为边向外作等边△CDE ，连接BE ，可证得△ECB ≌△DCA 从而得到BE ＝AD ，再根据三角形的三边关系即可得出结论．【详解】解：如图，以CD为边向外作等边△CDE，连接BE，∵△CDE和△ABC是等边三角形，∴CE＝CD，CB＝CA，∠ECD＝∠BCA＝60°，∴∠ECB＝∠DCA，在△ECB和△DCA中，CE CDECB DCACB CA=⎧⎪∠=∠⎨⎪=⎩，∴△ECB≌△DCA（SAS），∴BE＝AD，∵DE＝CD＝6，BD＝8，∴BD﹣DE≤BE≤BD+DE，即8﹣6≤BE≤8+6，∴2≤BE≤14，∴2≤AD≤14．则当B、D、E三点共线时，如图所示：可得BE 的最大值与最小值分别为14和2．∴AD 的最大值与最小值的差为14﹣2＝12．故答案为：12．【点睛】本题考查了全等三角形的判定与性质、等边三角形的性质以及三角形的三边关系，解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解，是一道较好的中考题．三、解答题1、25°【解析】【分析】由题意知AD BC ⊥，50CAD BAD ∠=∠=︒，根据等边对等角，三角形内角和定理求出ADE ∠的值，进而可求出CDE ∠的值．【详解】解：∵AB AC =，AD 是中线，50BAD ∠=︒∴AD BC ⊥，50CAD BAD ∠=∠=︒∵AE AD = ∴18050652ADE ︒-︒∠==︒ ∴25CDE ADC ADE ∠=∠-∠=︒∴CDE ∠的值为25°．【点睛】本题考查了等腰三角形的性质，三角形的内角和定理．解题的关键在于熟练掌握等腰三角形的性质．2、 (1)∠DCB ＝20°(2)AC ＝12.5【解析】【分析】（1）利用等腰三角形的性质，求出∠B ，然后根据直角三角形中的互余关系求出∠DCB ；（2）利用勾股定理，用一个未知数表示出直角三角形的未知边长，解方程求出边长．(1)∵AB ＝AC ，∴∠B ＝∠ACB ，∵∠A ＝40°，∴∠B ＝∠ACB ＝70°，∵CD ⊥AB ，∴∠BDC ＝90°．∴∠DCB ＝90°－∠B ＝20°；(2)在Rt △BCD 中，BD ＝9，设AC ＝AB ＝x ，则AD ＝x －9，∵在Rt △ACD 中，22AD CD +＝2AC ，∴22(9)12x -+＝2x ，解得x ＝22518＝12.5， ∴AC ＝12.5．【点睛】本题主要考查等腰三角形的性质，勾股定理的知识点，解答本题的关键是熟练掌握勾股定理去求边长．3、 (1)见解析(2)AE 的长为49或31【解析】【分析】（1）根据△ACB 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．得出∠ACD =∠BCE ，再证△ACD ≌△BCE （SAS ）即可；（2）过点C 作CF ⊥DE 于F ，根据△CDE 为等腰直角三角形，CF ⊥DE ，求出DE =DF =EF =1118922DE =⨯=，分两种情况，点E 在AD 延长线上，在Rt△ACF 中，根据勾股定理AF=40=，点E 在AD 上利用线段和差求出AE 即可．(1)证明：∵△ACB 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．∴AC =BC ，DC =EC ，∠ACD +∠DCB =∠DCB +∠BCE ，∴∠ACD =∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BCE （SAS ），(2)解：过点C作CF⊥DE于F，∵△CDE为等腰直角三角形，CF⊥DE，∴DE=DF=EF=11189 22DE=⨯=，分两种情况点E在AD延长线上，在Rt△ACF中，根据勾股定理AF40，∴AE=AF+EF=40+9=49；点E在AD上，在Rt△ACF中，根据勾股定理AF40，∴AE=AF-EF=40-9=31；∴点A，D，E 在同一直线上时，AE 的长为49或31．【点睛】本题考查等腰直角三角形性质，三角形全等判定，图形旋转性质，勾股定理，线段和差，掌握等腰直角三角形性质，三角形全等判定，图形旋转性质，勾股定理，线段和差是解题关键．4、 (1)PC＝PD(2)成立，理由见解析【解析】【分析】（1）根据角平分线性质可知PC＝PD；（2）过点P点作PE⊥OA于E，PF⊥OB于F，根据垂直的定义得到∠PEC＝∠PFD＝90°，由OM是∠AOB的平分线，根据角平分线的性质得到PE＝PF，利用四边形内角和定理可得到∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，而∠PDO+∠PDF＝180°，则∠PCE＝∠PDF，然后根据“AAS”可判断△PCE≌△PDF，根据全等的性质即可得到PC＝PD．(1)解：PC＝PD，理由：∵OM是∠AOB的平分线，∴PC＝PD（角平分线上点到角两边的距离相等），故答案为：PC＝PD；(2)证明：过点P点作PE⊥OA于E，PF⊥OB于F，如图，∴∠PEC＝∠PFD＝90°，∵OM是∠AOB的平分线，∴PE＝PF，∵∠AOB＝90°，∠CPD＝90°，∴∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，而∠PDO+∠PDF＝180°，∴∠PCE＝∠PDF，在△PCE和△PDF中，PCE PDFPEC PFD PE PF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PCE≌△PDF（AAS），∴PC＝PD．【点睛】本题考查角平分线的性质，全等三角形的证明，能够在图中构造适合的辅助线是解决本题的关键．5、 (1)见解析(2)3【解析】【分析】根据角平分线的性质定理可得DE =DF ，从而得到Rt CDE Rt CDF ≅，进而得到CE =CF ，即可求证；（2）先证得△CEF 是等边三角形，可得EF =CE ，∠ACD =30°，1122EG EF CE ==，再由ABC ACD BCD S S S =+△△△，可得DE =2，再根据直角三角形的性质可得CD =2DE =4，然后由勾股定理，即可求解．(1)∵CD 是△ABC 的角平分线，DE ⊥AC ，DF ⊥BC ，∴DE =DF ，△CDE 和△CDF 是直角三角形，∵CD =CD ，∴()Rt CDE Rt CDF HL ≅，∴CE =CF ，∴CD 垂直平分EF ，即CD ⊥EF ．(2)∵CE =CF ，∠ACB ＝60°，∴△CEF 是等边三角形，∴EF =CE ，∠ACD =30°，∵CD ⊥EF ， ∴1122EG EF CE ==， ∵AC ＝6，BC ＝4，S △ABC ＝10，DE =DF ，ABC ACD BCD S S S =+△△△， ∴ ()11110222DE AC DF BC DE AC BC ⨯+⨯=⨯+=，解得：DE =2，在Rt CDE △ 中，∠ACD =30°，∴CD =2DE =4，∴CE ==∴1122EG EF CE ===∴3CG =．【点睛】本题主要考查了全等三角形的判定和性质，角平分线的性质定理，直角三角形的性质，勾股定理、等边三角形的判定和性质，熟练掌握全等三角形的判定和性质，角平分线的性质定理，直角三角形的性质，勾股定理、等边三角形的判定和性质是解题的关键．。

数学分析部分习题参考解答

数学分析上册第三版华东师范大学数学系部分习题参考解答P.4 习题1．设a 为有理数，x 为无理数，证明：（1）a + x 是无理数；（2）当0≠a 时，ax 是无理数.证明（1）（反证）假设a + x 是有理数，则由有理数对减法的封闭性，知 x = a +x – a 是有理数. 这与题设“x 为无理数”矛盾，故a + x 是无理数.（2）假设ax 是有理数，于是aax x =是有理数，这与题设“x 为无理数”矛盾，故ax 是无理数.3．设R b a ∈,，证明：若对任何正数ε有ε<-||b a ，则 a = b .证明由题设，对任何正数ε有0||+<-εb a ，再由教材P.3 例2，可得0||≤-b a ，于是0||=-b a ，从而 a = b .另证（反证）假设0||>-b a ，由实数的稠密性，存在 r 使得0||>>-r b a . 这与题设“对任何正数ε有ε<-||b a ”矛盾，于是0||=-b a ，从而 a = b .5．证明：对任何R x ∈有（1）1|2||1|≥-+-x x ；（2）2|3||2||1|≥-+-+-x x x证明（1）|2||1||)2()1(|1-+-≤---=x x x x（2）因为|2||1||1||)3(2||3|2-+-≤-=-+≤--x x x x x ，所以2|3||2||1|≥-+-+-x x x6．设+∈R c b a ,,证明 ||||2222c b c a b a -≤+-+证明建立坐标系如图，在三角形OAC 中，OA 的长度是22b a +，OC 的长度是22c a +，AC 的长度为||c b -. 因为三角形两边的差小于第三边，所以有 ||||2222c b c a b a -≤+-+7．设 b a b x ≠>>,0,0，证明x b x a ++介于1与ba 之间. 证明因为1||1-=-<+-=-++ba b b a x b b a x b x a ，1||)()(-=-<+-=-++b a b b a x b b x a b b a x b x a 所以x b x a ++介于1与ba 之间. 8．设 p 为正整数，证明：若 p 不是完全平方数，则p 是无理数. 证明（反证）假设p 为有理数，则存在正整数 m 、n 使得m n p =，其中m 、n 互素. 于是22n p m =，因为 p 不是完全平方数，所以 p 能整除 n ，即存在整数 k ，使得kp n =. 于是222p k p m =，p k m 22=，从而 p 是 m 的约数，故m 、n 有公约数 p .这与“m 、n 互素”矛盾. 所以p 是无理数.P.9 习题2．设S 为非空数集，试对下列概念给出定义：（1）S 无上界；若M ∀，S x ∈∃0，使得M x >0，则称S 无上界.（请与S 有上界的定义相比较：若M ∃，使得S x ∈∀，有M x ≤，则称S 有上界）（2）S 无界.若0>∀M ，S x ∈∃0，使得M x >||0，则称S 无界.（请与S 有界的定义相比较：若0>∃M ，使得S x ∈∀，有M x ≤||，则称S 有界）3．试证明数集},2|{2R x x y y S ∈-==有上界而无下界.证明 S y ∈∀，有222≤-=x y ，故2是S 的一个上界.而对0>∀M ，取M x +=30，S M x y ∈--=-=12200，但M y -<0. 故数集S 无下界.4．求下列数集的上、下确界，并依定义加以验证：（1）},2|{2R x x x S ∈<=解 2sup =S ，2inf -=S . 下面依定义加以验证2sup =S （2inf -=S 可类似进行）. S x ∈∀，有22<<-x ，即2是S 的一个上界，2-是S 的一个下界.2<∀α，若2-≤α，则S x ∈∀0，都有α>0x ；若22<<-α，则由实数的稠密性，必有实数 r ，使得22<<<-r α，即S r ∈，α不是上界，所以2sup =S .（2）},!|{+∈==N n n x x S解 S 无上界，故无上确界，非正常上确界为+∞=S sup .下面证明：1inf =S .① S x ∈∀，有1!≥=n x ，即 1 是S 的一个下界；② 1>∀β，因为 S ∈=!11，即β不是S 的下界. 所以 1inf =S .(3)})1,0(|{内的无理数为x x S =解仿照教材P .6例2的方法，可以验证：1sup =S . 0inf =S⑷ },211|{+∈-==N n x x S n 解 1sup =S ，21inf =S 首先验证1sup =S .① S x ∈∀，有1211≤-=n x ，即 1 是S 的一个上界； ② 0>∀ε，取正整数0n ，使得ε<021n ，于是取02110n x -=. 从而S x ∈0，且ε->-=121100n x . 所以1sup =S5．设S 为非空有下界数集，证明：S S S min inf =⇔∈=ξξ证明：⇒）设S S ∈=ξinf ，则对一切S x ∈，有ξ≥x ，而S ∈ξ，故ξ是数集S 中的最小的数，即S min =ξ.⇐）设S min =ξ，则S ∈ξ；下面验证S inf =ξ；⑴ 对一切S x ∈，有ξ≥x ，即ξ是数集S 的下界；⑵ 对任何ξβ>，只须取ξ=0x ，则β<0x . 所以S inf =ξ.6．设S 为非空数集，定义}|{S x x S∈-=-. 证明： ⑴ S S sup inf -=- ⑵ S S inf sup -=-证 ⑴ 设-=S inf ξ，下面证明：S sup =-ξ.① 对一切S x ∈，有-∈-S x . 因为-=S inf ξ，所以有ξ≥-x ，于是ξ-≤x ，即ξ-是数集S 的上界；② 对任何ξα-<，有ξα>-. 因为-=S inf ξ，所以存在-∈S x 0，使得α-<0x .于是有S x ∈-0，使得α>-0x .由①，②可知S sup =-ξ.7．设A 、B 皆为非空有界数集，定义数集},,|{B y A x y x z z B A ∈∈+==+ 证明：（1）B A B A sup sup )sup(+=+；（2）B A B A inf inf )inf(+=+证明（1）因为A 、B 皆为非空有界数集，所以A sup 和B sup 都存在.B A z +∈∀，由定义分别存在B y A x ∈∈,，使得y x z +=. 由于A x sup ≤，B y sup ≤，故B A y x z sup sup +≤+=，即B A sup sup +是数集B A +的一个上界.B A sup sup +<∀α，（要证α不是数集B A +的上界），A B sup sup <-α，由上确界A sup 的定义，知存在A x ∈0，使得B x sup 0->α. 于是B x sup 0<-α，再由上确界B sup 的定义，知存在B y ∈0，使得00x y ->α. 从而α>+=000y x z ，且B A z +∈0. 因此B A sup sup +是数集B A +的上确界，即B A B A sup sup )sup(+=+另证 B A z +∈∀，由定义分别存在B y A x ∈∈,，使得y x z +=. 由于A x sup ≤，B y sup ≤，故B A y x z sup sup +≤+=，于是B A B A sup sup )sup(+≤+. ①由上确界的定义，0>∀ε，A x ∈∃0，使得2sup 0ε->A x ，B y ∈∃0，使得2sup 0ε->B y ，从而ε-+>+≥+B A y x B A sup sup )sup(00，由教材P.3 例2，可得 B A B A sup sup )sup(+≥+ ②由①、②，可得 B A B A sup sup )sup(+=+类似地可证明：B A B A inf inf )inf(+=+P.15 习题9．试作函数)arcsin(sin x y =的图象解 )arcsin(sin x y =是以2π为周期，定义域为),(∞+-∞，值域为]2,2[ππ-的分段线性函数，其图象如图.11．试问||x y =是初等函数吗？解因为2||x x y ==，可看成是两个初等函数u y =与2x u =的复合，所以||x y =是初等函数.12．证明关于函数[]x y =的如下不等式：（1）当0>x 时，111≤⎥⎦⎤⎢⎣⎡<-x x x （2）当0<x 时，x x x -<⎥⎦⎤⎢⎣⎡≤111 证明（1）因为 1111+⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡x x x ，所以当0>x 时，有x x x x x +⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡111，从而有111≤⎥⎦⎤⎢⎣⎡<-x x x .（2）当0<x 时，在不等式1111+⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡x x x 中同时乘以x ，可得⎥⎦⎤⎢⎣⎡≤<+⎥⎦⎤⎢⎣⎡x x x x x 111，从而得到所需要的不等式x x x -<⎥⎦⎤⎢⎣⎡≤111. P.20 习题1．证明1)(2+=x x x f 是R 上的有界函数. 证明因为对R 中的任何实数x 有21212=≤+x x x x )||21(2x x ≥+ 所以 f 在R 上有界.2．（1）叙述无界函数的定义；（2）证明21)(x x f =为（0，1）上的无界函数；（3）举出函数 f 的例子，使 f 为闭区间 [0，1] 上的无界函数. 解（1）设函数D x x f ∈)(，若对任何0>M ，都存在D x ∈0，使得M x f >|)(|0，则称 f 是D 上的无界函数.（2）分析：0>∀M ，要找)1,0(0∈x ，使得M x >201. 为此只需Mx 10<. 证明 0>∀M ，取110+=M x ，则)1,0(0∈x ，且M M x >+=1120，所以f 为区间（0，1）上的无界函数. （3）函数⎪⎩⎪⎨⎧=≤<=00101)(x x x x f 是闭区间 [0，1] 上的无界函数.7．设f 、g 为定义在D 上的有界函数，满足)()(x g x f ≤，D x ∈证明：⑴ )(sup )(sup x g x f D x D x ∈∈≤；⑵ )(inf )(inf x g x f Dx D x ∈∈≤证 ⑴ D x ∈∀，有)(sup )()(x g x g x f D x ∈≤≤，即)(sup x g Dx ∈是f 在D 上的一个上界，所以)(sup )(sup x g x f Dx D x ∈∈≤.⑵ D x ∈∀，有)()()(inf x g x f x f D x ≤≤∈，即)(inf x f Dx ∈是g 在D 上的一个下界，所以)(inf )(inf x g x f Dx D x ∈∈≤. 8．设f 为定义在D 上的有界函数，证明：⑴ )(inf )}({sup x f x f D x D x ∈∈-=-； ⑵ )(sup )}({inf x f x f Dx D x ∈∈-=-证 ⑴ D x ∈∀，有)}({sup )(x f x f D x -≤-∈，于是)}({sup )(x f x f Dx --≥∈，即)}({sup x f D x --∈是f 在D 上的一个下界，从而)}({sup )(inf x f x f Dx D x --≥∈∈，所以)(inf )}({sup x f x f Dx D x ∈∈-≥- ①反之，D x ∈∀，有)(inf )(x f x f D x ∈≥，于是)(inf )(x f x f D x ∈-≤-，即)(inf x f Dx ∈-是f -在D 上的一个上界，从而)(inf )}({sup x f x f Dx D x ∈∈-≤- ②由①，②得，)(inf )}({sup x f x f Dx D x ∈∈-=-.9．证明：x tan 在)2,2(ππ-上无界，而在)2,2(ππ-内任一闭区间],[b a 上有界.证 0>∀M ，取)1arctan(0+=M x ，于是)2,2(0ππ-∈x . 则有M M x >+=1tan 0，所以x tan 在)2,2(ππ-上无界. 在)2,2(ππ-内任一闭区间],[b a 上，取|}tan ||,tan max{|b a M =，则],[b a x ∈∀，必有M x ≤|tan |，所以x tan 在],[b a 上有界.10．讨论狄利克雷函数⎩⎨⎧=为无理数当为有理数当x ，x x D 0,1)(，的有界性，单调性与周期性. 解函数)(x D 是有界函数：1|)(|≤x D . 不是单调函数.)(x D 是周期函数，任何一个正有理数都是它的周期，故它没有最小周期. 证明如下：设 r 是任一正有理数. 若 x 是有理数，则r x ±是有理数，于是)(1)(x D r x D ==±；若 x 是无理数，则r x ±是无理数，于是)(0)(x D r x D ==±.任何无理数都不是)(x D 的周期.11．证明：x x x f sin )(+=在R 上严格增.证设21x x <，于是2sin 2cos2sin sin )()(121212112212x x x x x x x x x x x f x f -++-=--+=- 因为0>∀x ，有x x <sin ，所以12121212|2sin |2|2sin 2cos 2|x x x x x x x x -<-≤-+，从而121212212sin 2cos 2x x x x x x x x -<-+<-. 所以有 02sin 2cos2)()(211212121212=-+->-++-=-x x x x x x x x x x x f x f 即x x x f sin )(+=在R 上严格增.P.21 总练习题1．设R b a ∈,，证明：⑴ |)|(21},max{b a b a b a -++=证若b a ≥，则a b a =},max{，a b a b a b a b a =-++=-++)(21|)|(21，这时有|)|(21},max{b a b a b a -++=；若b a <，则b b a =},max{，=-++|)|(21b a b a b b a b a =+-+)(21，也有|)|(21},max{b a b a b a -++=，所以|)|(21},max{b a b a b a -++= 2．设f 和g 都是初等函数，定义)}(),(max{)(x g x f x M =，)}(),(min{)(x g x f x m =，D x ∈试问)(x M 和)(x m 是否为初等函数？解由第1题有|))()(|)()((21)}(),(max{)(x g x f x g x f x g x f x M -++==，因为f 和g 都是初等函数，于是)()(x g x f -是初等函数，再由212})]()({[|)()(|x g x f x g x f -=-，知|)()(|x g x f -是初等函数，所以)(x M 是初等函数.8．设f 、g 和h 为增函数，满足)()()(x h x g x f ≤≤，R x ∈，证明：))(())(())((x h h x g g x f f ≤≤证因为f 、g 为增函数，再由)()(x g x f ≤，得))(())((x g f x f f ≤，))(())((x g g x g f ≤，所以有))(())((x g g x f f ≤. 同理可得))(())((x h h x g g ≤.9．设f 、g 为区间),(b a 上的增函数，证明)}(),(max{)(x g x f x =ϕ，)}(),(min{)(x g x f x =ψ也都是区间),(b a 上的增函数.证 ⑴ 先证)}(),(max{)(x g x f x =ϕ是区间),(b a 上的增函数.设21x x <，于是有)()()}(),(m ax {)(12222x f x f x g x f x ≥≥=ϕ，)()()}(),(m ax {)(12222x g x g x g x f x ≥≥=ϕ，从而)()}(),(m ax {)(1112x x g x f x ϕϕ=≥，所以)(x ϕ是增函数.⑵ 其次证明)}(),(min{)(x g x f x =ψ是区间),(b a 上的增函数设21x x <，于是有)()()}(),(m in{)(21111x f x f x g x f x ≤≤=ψ)()()}(),(m in{)(21111x g x g x g x f x ≤≤=ψ从而 )()}(),(m in{)(2221x x g x f x ψψ=≤12．设f 、g 为D 上的有界函数，证明：⑴ )(sup )(inf )}()({inf x g x f x g x f Dx D x D x ∈∈∈+≤+ ⑵ )}()({sup )(inf )(sup x g x f x g x f Dx D x D x +≤+∈∈∈证 ⑴ 由p.17例2 (i)，有)(inf )}({inf )}()({inf x f x g x g x f Dx D x D x ∈∈∈≤-++ ① 再由p.20习题8，有)(sup )}({inf x g x g Dx D x ∈∈-=- ② 结合①、②可得)(sup )(inf )}()({inf x g x f x g x f Dx D x D x ∈∈∈+≤+ 13．设f 、g 为D 上的非负有界函数，证明：⑴ )}()({inf )(inf )(inf x g x f x g x f Dx D x D x ⋅≤⋅∈∈∈ ⑵ )(inf )(sup )}()({sup x g x f x g x f Dx D x D x ∈∈∈⋅≤⋅证 ⑴ D x ∈∀，有)()(inf x f x f D x ≤∈，)()(inf x g x g D x ≤∈，从而)()()(inf )(inf x g x f x g x f Dx D x ⋅≤⋅∈∈. 即)(inf )(inf x g x f Dx D x ∈∈⋅是)()(x g x f ⋅在D 上的一个下界，所以有 )}()({inf )(inf )(inf x g x f x g x f Dx D x D x ⋅≤⋅∈∈∈ 15．设f 为定义在R 上以h 为周期的函数，a 为实数. 证明：若f 在 [ a , a +h ] 上有界，则f 在R 上有界.证设f 在 [ a , a +h ] 上有界，即存在0>M ，使得],[h a a x +∈∀，有M x f ≤|)(|.R x ∈∀，必存在整数m 和实数],[0h a a x +∈，使得0x mh x +=. 于是M x f mh x f x f ≤=+=|)(||)(||)(|00，所以f 在R 上有界.16．设f 在区间I 上有界. 记)(sup x f M I x ∈=，)(inf x f m Ix ∈=，证明m M x f x f Ix x -=''-'∈'''|)()(|sup ,证 I x ∈∀，有M x f ≤)(，m x f ≥)(. 于是I x x ∈'''∀,，有m M x f x f -≤''-'|)()(|，即m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的一个上界. 下面证明：m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的最小上界.由上确界，下确界的定义知，0>∀ε，I x x ∈'''∃,，使得2)(ε->'M x f ，2)(ε+<''m x f ，从而εεε--=+-->''-'m M m M x f x f )2(2)()(. 所以m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的最小上界.所以m M x f x f Ix x -=''-'∈'''|)()(|sup ,部分重点高校历年研究生入学考试试题选（供参考）1．（北京科技大学，1999年）叙述数集A 的上确界的定义，并证明：对任意有界数列}{n x ，}{n y ，总有}sup{}sup{}sup{n n n n y x y x +≤+证明定义参考教材.由上确界的定义，有}sup{n n x x ≤，}sup{n n y y ≤，（ ,2,1=n ）. 于是}sup{}sup{n n n n y x y x +≤+，即实数}sup{}sup{n n y x +是数列}{n n y x +的一个上界，所以有}sup{}sup{}sup{n n n n y x y x +≤+2．（中国人民大学）设249)3lg(1)(x x x f -+-=，求)(x f 的定义域和)]7([-f f . 解由049,13,032≥-≠->-x x x 解得)(x f 的定义域为)3,2()2,7[⋃-110lg 1)7(==-f ，所以342lg 1)]7([+=-f f 3．（华中理工大学）设1)(-=x x x f ，试验证x x f f f f =))]}(([{，并求])(1[x f f （0≠x ，1≠x ）.解由x x x x xx f x f x f f =---=-=1111)()()]([，得x x f f x f f f f ==)]([))]}(([{. x xx x x x x f x f f -=---=-=1111]1[])(1[ 4．（同济大学）设⎩⎨⎧≥<+=010,1)(x x x x f ，求)]([x f f . 解当0≥x 时，1)1()]([==f x f f ，当01<≤-x 时，1)1()]([=+=x f x f f ，当1-<x 时，2)1()]([+=+=x x f x f f ，所以⎩⎨⎧-≥-<+=111,2)]([x x x x f f 5．（西北工业大学）设2)(x x x f +=，求 ⑴ )(x f 的定义域⑵2)]}([{21x f f ⑶ x x f x )(lim 0→ 解 ⑴ ⎩⎨⎧>≤=+=0,20,0||)(x x x x x x f ，所以)(x f 的定义域为),(∞+-∞. ⑵ 因为)(22)()]([2222x f x x x x x x x f f =+=+++=，所以22)()]}([{21x x x f x f f +== ⑶ 因为00lim )(lim 00==--→→x x x f x x ，+∞==-+→→x x x x f x x 2lim )(lim 00，所以x x f x )(lim 0→不存在6．（清华大学）设函数)(x f 在),(∞+-∞上是奇函数，a f =)1(且对任何x 值均有)2()()2(f x f x f =-+⑴ 试用a 表示)2(f 与)5(f⑵ 问a 取什么值时，)(x f 是以2为周期的周期函数.解 ⑴ 因为对任何x 值均有)2()()2(f x f x f +=+，令1-=x 得a f f f f f f f a -=-=-+=+-==)2()1()2()1()2()21()1(，所以a f 2)2(=.a f f f 3)2()1()3(=+=，a f f f 5)3()2()5(=+=⑵ 由)2()()2(f x f x f +=+知当且仅当0)2(=f ，即0=a 时，)(x f 是以2为周期的周期函数.7．（合肥工业大学）证明：定义在对称区间),(l l -内的任何函数)(x f ，必可表示成偶函数)(x H 与奇函数)(x G 之和的形式，且这种表示法是唯一的.证明令)]()([21)(x f x f x H -+=，)]()([21)(x f x f x G --=，则)()()(x G x H x f +=，且容易证明)(x H 是偶函数，)(x G 是奇函数.下证唯一性. 若还有偶函数)(1x H 与奇函数)(1x G ，满足)()()(11x G x H x f +=，则有)()()()(11x G x G x H x H -=-， ①用x -代入①式，得)()()()(11x G x G x H x H -=- ②①+② 得 )()(1x H x H =，再代入②式得)()(1x G x G =8．（内蒙古大学）作函数||2|2|x y --=的图形解 ⎪⎪⎩⎪⎪⎨⎧>-≤≤-<≤<-=44424200x x x x x x x x y 9．（上海师范大学）是否存在这样的函数，它在区间]1,0[上每点都取有限值，但在此区间的任何点的任何邻域内都无界.答存在，例如⎩⎨⎧>==1000,,)(或为无理数或为且互质x ，n ，n m n m x n ，x f 10．（武汉大学，1994年）设}{n x 为一个正无穷大数列，E 为}{n x 的一切项组成的数集，试证：必存在自然数p ，使得E x p inf =证明因为}{n x 为一个正无穷大数列，所以存在自然数N ，使得当N n >时，1x x n >. 于是},,,m in{inf 21N x x x E =，由于},,,{21N x x x 为有限集，所以存在p x ，使得E x x x x N p inf },,,min{21== .11．（天津大学）证明：2是满足不等式22>r 的一切正有理数的下确界；证设}0,2,|{2>>∈=r r Q r r A . 要证2是数集A 的下确界. A r ∈∀，有22>r ，所以2>r ，即2是数集A 的一个下界.0>∀ε，由有理数的稠密性，在)2,2(ε+上存在无穷多个有理数，于是可取)2,2(1ε+∈r ，即A r ∈1且ε+<21r . 所以2inf =A12．（华中师范大学）设函数)(x f 定义在区间I 上，如果对于任何I x x ∈21,，及)1,0(∈λ，恒有)()1()())1((2121x f x f x x f λλλλ-+≤-+，证明：在区间I 的任何闭子区间上)(x f 有界.证 I b a ⊂∀],[，要证)(x f 在],[b a 有界. ),(b a x ∈∀，存在)1,0(∈λ，使 )(a b a x -+=λ，即a b x )1(λλ-+=.M M M a f b f a b f x f =-+≤-+≤-+=)1()()1()())1(()(λλλλλλ ① 其中)}(),(max{b f a f M =],[b a x ∈∀，令x b a y -+=)(，则22y x b a +=+， M x f y f x f y x f b a f 21)(21)(21)(21)22()2(+≤+≤+=+，所以 M b a f x f -+≥)2(2)( ② 由①、②可得，],[b a x ∈∀，有M x f M b a f ≤≤-+)()2(2，所以)(x f 在],[b a 有界.。

第一章可测函数.§1.1第四章可测函数练习题.习题1.1.1证明f（x）

第一章可测函数§1.1 第四章可测函数练习题习题1.1.1 证明： f x在E 上为可测函数的充要条件是对任一有理数r集E f gtr可测.如果集E f r可测，问 f x是否可测？证明分析：根据可测函数的定义t ∈R E f gt t为可测集，则函数 f 为可测函数.由题意知道，对于有理数r集E f gt r可测那么问题就是如何将已知的有理数转化到未知的实数上，那么就可以采用有理数在实数中稠密的特征，任何一个实数都可以用有理数进行逼近的办法然后利用可测集的运算性质的到想要的结果. 证明中的等式可以参考课本P80 的引理中的集证明：若对任意有理数r E f gt r可测，则对任意实数α记rn 为大于α的一切合论等式的证明E f gt ∞ ∪∪∞ g E f gt有理数，则有E f gt α E f gt rn 由E f gt rn 可测得E f gt α是可测的，所rn ∩ n1 Eg lt rn 在n1 这个式子中仅仅可以以f x 是E 上的可测函数. 取g a a lt rn 即可. 若对于任意的有理数r E f r可测，则 f x不一定是可测的.例如，E √ √∞ ∞ z为E 中的不可测集. 对于任意x ∈z f x 3 x z f x 2则对任意√有理数r E f r 是可测的.而E f gt 2 z为不可测的.因此 f 是不可测的.习题 1.1.2 设fn 为E 上的可测函数列，证明它的收敛点集和发散点集都是可测的. 证明分析：写出收敛点集和发散点集的组成结构，结果一目了然.证明：由P82定理6 lim fn x和lim fn x都是E 上的可测函数，显然，n→∞ n→∞Elimn→∞ fn x ∞是收敛到∞的点组成的集，而E lim fn x ∞是收敛n→∞到∞的点组成的集合.E lim fn gt limn→∞ fn 是fn 的不收敛点组成的集.因此fn x在E 上n→∞的收敛的点组成的集为E E lim fn x ∞ E lim fn x ∞ E lim fn gt n→∞ n→∞ n→∞lim fn 因而，由可测集的运算规律知，收敛点集为可测集.n→∞ ∪同样，对于发散点组成的集合为E lim fn x ∞ E lim fn x ∞ n→∞ n→∞∪ E lim fn gt lim fn 也是可测集. n→∞ n→∞ 1第一章可测函数2习题1.1.3 设E 为0 1中的不可测集，令x x ∈ E f x x x ∈0 1 E. 问 f x在0 1上是否可测？ f x是否可测？证明： f x不可测.若0 ∈E则E f ≥ 0 E 不可测.若0 E则E f gt 0 E 不可测.综上，f x为不可测函数. 当x ∈0 1时，f x x是连续函数，所以 f x在0 1上是可测的.习题 1.1.4 设fn xn 1 是E 上a.e.有限的可测函数列，而fn a.e.收敛于有限函数f则对于任意的gt 0 存在常数c与可测集E0 E mE E0 lt 使在E0 上对一切n有f x ≤ c.这里mE lt ∞.证明：由题意， E fn ∞ E fn 都是空集n 0 1 .令E1 E fn ∪∪∞f E fn ∞ 则mE1 0.而在EE1 上fn x都是有限函数，且收敛于 f x.令E2 n0E E1 则任意x ∈E2 sup fn x lt ∞.因此∪∞ E2 E2sup fn ≤ k 1.1 k1 n E2 sup fn ≤ k E2 sup fn ≤ k 1 1.2 n n所以mE2 lim mE2 sup fn ≤ k.因此存在k0 使mE2 mE2 sup fn ≤ k0 lt .令E0 n→∞ n nE2 sup fn ≤ k0 c k0 .在E0 上，对任意n fn x ≤ c而n mE E0 mE E2 mE2 E0 lt . 1.3证明：使用叶戈洛夫定理和鲁津定理来证明.这个证明较为详细. 由题意显然有mE gt 0不妨设mE lt ∞否则任取E 中满足0 lt mE1 lt ∞的子集E1 来代替E. 依题意设fn x在E 上几乎处处收敛，且其极限函数为f x即fn x → f x a.e.于En → ∞. 1.4从而由叶戈洛夫定理，δ 对mE 4 gt 0 Eδ E使得mE 3 imE Eδ lt δ 即mEδ gt mE 1.5 4 4第一章可测函数3 ii在Eδ 上一致收敛于 f x. 1.6另外，Eδ 上使用鲁津定理，在对mE 4 gt 0由鲁津定理，存在闭集F Eδ 使得mE mE imFδ F lt 即mF gt 1.7 4 2 ii f x在F 连续，于是M gt 0 s.t. f x ≤ Mx ∈ F. 1.8由于 f x在F 上一致收敛到 f x故fn 在F 上也一致收敛于 f F Eδ 所以存在自然数N当n gt N 时，有fn x f x ≤ 1x ∈ F. 1.9从而有fn x ≤ f x 1 n gt N x ∈F. 1.10 即x ∈F当n gt N 时，fn x ≤ M 1. 在考虑fn x中的前N 个f1 x f2 x fN x.因为fi xi 1 N几乎处处有限，mE fi ∞ 0i 1 N. 而故∪∞ E fi ∞ E fi gt k 1.11 k1且 E fi gt k E fi gt k 1.i 1 N 1.12从而，lim mE fi gt k mE fi ∞ 0. 1.13 k→∞故对于每一个ii 1 N ki 使得mF mE fi gt k lt . 1.14 2N取k0 maxk1 kN 则mF mE fi gt k0 lt i 1 N 1.15 2N于是N ∑ ∑N m E fi gt k0 ≤ mE fi gt k0 i1 i1 1.16 mF ˙ mF lt N 2N 2第一章可测函数4故只需令∑ N E0 F E fi gt c c maxM 1 k0 1.17 i1则mF 1 1 mE0 gt mF mF gt mE gt 0 1.18 2 2 4且在E0 F 上，对一切n 均有fn x ≤ c.习题1.1.5 设mE lt ∞若 f x是E 上a.e.有限的可测函数证明对任意δ gt 0存在EδE 和M gt 0使得mE Eδ lt δ且对任意x ∈Eδ f x ≤ M.命题1.1.1 设mE lt ∞若fn x是E 上a.e.有限的可测函数证明对任意δ gt 0存在EδE 和M gt 0使得mE Eδ lt δ且对任意x ∈Eδ fn x ≤ M.证明：不妨设E 为有界集合，mE lt ∞且fn xn ∈N皆为实值.因为即∪∞ E x ∈ E : sup fn x ≤ k 1.19 k1 n≥1 lim m x ∈ E : sup fn x ≤ k mE 1.20 k→∞ n≥1所以存在k0 使得m x ∈ E : sup fn x ≤ k0 gt mE δ 1.21 n≥1从而令Eδ x ∈ E : sup fn x ≤ k0 M k0 1.22 n≥1则mE Eδ lt δ fn x ≤ M n ∈N x ∈E0 . 在习题1.1.4和命题1.1.1的提示下，解决习题1.1.5证明：利用前一题的结论将fn x取成同一个函数采用相同的方法即可. 不妨设E 为有界集合，mE lt ∞且 f x 为实值.因为即∪∞ ∪∞ E x ∈ E : sup f x ≤ k Ek sup f x ≤ k 1.23 k1 k1由于关于变量k Ek sup f x ≤ k Ek1 sup f x ≤ k 1 1.24第一章可测函数5从而说明集合列Ek 单调递增的，且存在极限为lim m x ∈ E : sup f x ≤ k mE 1.25 k→∞所以存在k0 使得m x ∈ E : sup f x ≤ k0 gt mE δ 1.26从而令Eδ x ∈ E : sup f x ≤ k0 M k0 1.27则mE Eδ lt δ f x ≤ M x ∈E0 . 这是证法2 δ证明：由鲁津定理知，闭集Fδ E mE Fδ lt 2 s.t. f x在Fδ 上是连续函数. ∩记Fk Fδ k kn n为空间的维数.则说明集合列Fk 随着k的增加而逐渐的趋∪∞于Fδ . 从而有Fδ F k 且k1 lim mFdelta Fk lim mFδ mFk k→∞ k→∞ mFδ lim mFk k→∞ 1.28 mFδ mFδ 0由等式1.28知k0 s.t. δ mFδ Fk0 lt 1.29 2 ∩从而由等式1.28、§1.1知，k0 Fδ k0 k0 n 为闭集且有F mE Fk0 mE Fδ mFδ Fk0 lt δ 1.30且M gt 0 s.t. f x在Eδ Fk0 上有f x ≤ M 成立.习题1.1.6 设 f x是∞ ∞上的连续函数，为a b上的可测函数，f gx也gx 则是可测函数.第一章可测函数6证明：记E1 ∞ ∞ E2 a b.由于 f x在E1 上连续，故对于任意的实数c E1 f gt ∪∞c是直线上的开集. 设E1 f gt c αn βn 其中αn βn 是其构成区间（可能是n1 ∪∞有限个，αn 可能是∞ βn 可能为∞）. 因此E2 f g gt c E2 αn lt g lt βn n1∪∞ ∪E2 αn lt g E2 g lt βn 由于g在E2 上可测，因此E2 g gt αn E2 g lt βn 都可n1测，E f g gt c 可测. 故习题1.1.7 设函数列fn x n 1 在有界集上E 上“基本上”一致收敛于 f x证明fn a.e.收敛于 f. 证明分析：“基本上”一致收敛是“对于任意的δ gt 0存在可测集Eδ E使mE Eδ ltδ而fn 在Eδ 上一致收敛于 f x.” a.e.收敛除掉一个零测度集命题成立.证明：因为fn x 在有界集上E 上“基本上”一致收敛于 f x所以对于任意的δ gt0存在可测集Eδ E使mE Eδ lt δ而fn 在Eδ 上一致收敛于 f x.设E0 是E 中不收敛点的全体，则对任意δ E0 E Eδ 因为Eδ 上fn 收敛，所以mE0 ≤ mE Eδ ltδ令δ → 0得mE0 0.所以fn x在E 上a.e.收敛于 f x不必有有界的条件.习题 1.1.8 试证鲁津定理的逆定理. 证明分析：首先描述一下鲁津定理的逆定理是说的什么？f x是E 上的函数，对任意的δ gt 0存在闭子集Eδ E 使 f x在Eδ 上是连续函数，且mE Eδ ltδ则 f x是E 上a.e.有限可测函数.证明：对任意的 1 存在闭子集En E使 f x在En 上连续且n mE En lt δ 1.31 ∪∞ ∪∞ 令E0 E En 则对任意的n 有mE0 m E En ≤ mE En lt 1 .令n → n n1n1 ∪∪∞ ∪∪∞∞得mE0 0.且E E E0 E0 En E0 En .对任意实数a E f gt a n1 n0 ∪∪∞E0 f gt a En f gt a 由于 f 在En 上连续，可知En f gt a可测，而m E0 f gt n0第一章可测函数7a ≤ m E0 0所以E0 f gt a亦可测，从而E f gt a是可测的.因此f 是可测的.因∪∞为 f 在En 上有限，故在En 上有限，所以 f x a.e.有限. n0习题1.1.9 设函数列fn 在E 上依测度收敛于f且fn x ≤ gx a.e.于E n 1 2 试证f x ≤ gx在E 上几乎处处成立. 证明.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学习解题的最好方法之一就是研究例题
初二北师大版数学第六章证明（一）练习题
祁家河初中主笔：陈全安审阅：姓名__________
练习目标：⒈加深理解本章所学各个知识点，在证题过程中能娴熟灵活地运用之。
⒉学会分析证明思路，初步掌握综合法证明的步骤和格式。
知识提炼：㈠、关于命题、定理及公理
⒈对名称和术语的含义加以描述，作出明确的规定，也就是给出它们
的定义。
⒉判断一件事情的句子，叫做命题，每个命题都由条件和结论两部分
组成。
⒊正确的命题称为真命题，不正确的命题称为假命题。
⒋ 公认的真命题称为公理（书P225 6条公理）（等量代换）
⒌ 推理的过程称为证明，经过证明的真命题称为定理。
㈡、平行线的性质及判定
判定：⒈同位角相等，两直线平行。⒉同旁内角互补，两直线平行。
⒊内错角相等，两直线平行。
性质：⒈两直线平行，同位角相等。⒉两直线平行，同旁内角互补。
⒊两直线平行，内错角相等。
㈢、三角形的内角和外角的定理
⒈如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
⒉如果两条直线都和第三条直线垂直，那么这两条直线也互相平行。
⒊如果一条直线垂直于两条平行线中的一条，那么它也垂直于另一条。
⒋三角形内角和定理：三角形三个内角的和等于180°
⒌三角形一个外角等于和它不相邻的两个内角的和。
⒍三角形的一个外角大于任何一个和它不相邻的内角。
提升训练：
一、填空题：

⒈把命题“对顶角相等”改写成“如果„那么„”的形式____________________。
⒉把“等角的余角相等”改写成 “如果„，那么„”的形式_________________。

⒊命题“任意两个直角都相等”的条件是___________，结论是_________________，
它是______（真或假）命题。
⒋如图所示，∠1＋∠2=180°，若∠3=50°，则∠4=
⒌如图所示：已知∠1 = 20°，∠2 = 25°，∠A = 3°，
则∠BDC 的度数为。
⒍、如图所示：AB∥CD，∠1 = 100°，∠2 = 120°，
则 ∠α= 。
⒎如图所示：已知DB平分∠ADE，DE∥AB，∠CDE=82º，
则∠EDB= ， ∠A=_______。
⒏如图所示：平行四边形ABCD中，E为AB上一点，
DE与AC交于点F，AF∶FC=3∶7，则AE∶EB= 。
⒐在△ABC中，∠ABC和∠ACB的平分线交于点I,
若∠A=60 则∠BIC=__________。
⒑在三角形中，最多有个锐角，至少有个锐角，
最多有个钝角（或直角）。
二、选择题：
⒈下列语句不是命题的是（）
A、 2008年奥运会的举办城是北京。
B、如果一个三角形三边a，b，c满足a2＝b2＋c2，则这个
三角形是直角三角形。
C、同角的补角相等。
D、过点P作直线l的垂线。

2
B
C

A
D
1
2

A
2
1

C
F


E
D
CB

A
学习解题的最好方法之一就是研究例题
⒉下列命题是真命题的是（）
A、－a一定是负数。

B、a＞0
C、平行于同一条直线的两条直线平行。
D、有一角为80°的等腰三角形的另两个角为50°与50°。
⒊“两条直线相交，有且只有一个交点”的题设是（）
A、两条直线。 B.、交点。 C、两条直线相交。 D、只有一个交点。
⒋命题“垂直与同一条直线的两条直线互相平行”的题设是（）
A、垂直。B、两条直线。C、同一条直线。 D、两条直线垂直于同一条线。

⒌如图所示：AB⊥EF ，CD⊥ EF，∠1=∠F=30°，那么与FCD相等的角
有（）A、 1个 B、2 C、3个 D、4个
⒍如图所示：AD平分CAE，∠ B=30°，CAD=65°， ∠ACD=（） A、50° B、 65° C、80° D、95° ⒎如图所示：∠A+∠B+∠C+∠D+∠E+∠F等于（） A、180° B、360° C、540° D、720° ⒏如图所示：如果AB∥CD，则角α、β、γ之间的关系式为（） A、α＋β＋γ=360° B、α－β＋γ=180° C、α＋β＋γ=180° D、α＋β－γ=180° 三、完型填空： ⒈如图所示：直线AB∥MN，分别交直线EF于点C、D，∠BCD、∠CDN的角平分线交于点G，求∠CGD的度数。解：∵AB∥MN（_______） ∴∠BCD＋∠CDN＝180°（_____________________） ∵CG、DG是角平分线（_______) ∴∠1=21∠BCD ∠2=21∠CDN (__________________) ∴∠1＋∠2＝90° ∵∠1＋∠2＋∠CGD＝180°（___________________）
∴∠CGD＝90°

⒉已知：如图所示：在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC
的平分线。
求证：∠A= 2∠H
证明： ∵∠ACD是△ABC的一个外角，
∴∠ACD=∠ABC+∠A （________________）
∠2是△BCD的一个外角，
∴∠2=∠1+∠H （__________________）
∵CH是外角∠ACD的平分线，BH是∠ABC的平分线，
∴∠1= 21∠ABC ，∠2= 21∠ACD（_____________________）

E
D
C

B
A




E

D
C

B
A

E
A C B
G
M D N

1
2
学习解题的最好方法之一就是研究例题
∴∠A =∠ACD-∠ABC= 2 （∠2 －∠1）（____________）
而 ∠H=∠2 - ∠1 （等式的性质）
∴∠A= 2∠H （____________）

四、解答题：
⒈如图所示：已知：AD∥EF，∠1＝∠2。求证：AB∥DG。

⒉．如图所示：已知：AB∥CD，∠1＝∠B，∠2＝∠D。求证：BE⊥DE。

⒊. 如图所示：在△ABC中，∠B、∠C的平分线相交于点P，∠BPC＝130°，
求：∠A的度数。

⒋如图所示：已知：直线AB∥MN，分别交直线EF于点C、D，
∠BCD、∠CDN的角平分线交于点G。
求∠CGD的度数。

⒌如图所示：已知：CF⊥AB于F，ED⊥AB于D，∠1＝∠2，
求证：FG∥BC

⒍如图所示：O是四边形ABCD的两条对角线的交点，过点
O作OE∥CD，交AD于E，作OF∥ BC，交AB于F，连接
EF。求证：EF∥BD

A
P
1 2
B C

E
A C B
G
M D N

1
2

2
1
G
F
E

A
学习解题的最好方法之一就是研究例题
⒎如图所示：已知：AB∥DE。
⑴猜测∠A、∠ACD、∠D有什么关系？并
证明你的结论。
⑵若点C向右移动到线段AD的右侧，此时∠A、∠ACD、∠D之间的关系，
仍然满足⑴中的结论吗？若符合，请你证明，若不符，请你写出正确的结论
并证明。要求画出相应的图形。

⒏如图所示：已知∠BED = ∠B + ∠D，求证：AB∥CD。（两种方法）
A
B

C D
E