代数知识点整理
数学数与代数知识点整理

数学数与代数知识点整理数学数与代数知识点整理在我们上学期间,说起知识点,应该没有人不熟悉吧?知识点就是一些常考的内容,或者考试经常出题的地方。
还在苦恼没有知识点总结吗?以下是店铺收集整理的数学数与代数知识点整理,希望对大家有所帮助。
数学数与代数知识点整理篇1认识计数单位“百”和“千”,知道相邻两个计数单位之间的十进关系。
掌握万以内的数位顺序,会读、写万以内的数。
知道万以内数的组成。
会比较万以内数的大小,能用符号和词语描述万以内数的大小。
理解并认识万以内的近似数。
会口算百以内的两位数加、减两位数。
会口算整百、整千数加、减法。
会计算几百几十加、减几百几十,能结合实际进行估算。
知道除法的.含义和除法各部分名称以及乘法与除法的关系。
熟练进行用乘法口诀求商。
会从生活中发现和提出数学问题,能用所学知识(两步计算)加以解决。
知道小括号的作用,会使用小括号。
会探索给定图形或数的排列中的简单规律。
有发现和欣赏数学美、运用数学去创造美的意识。
初步形成观察、分析和推理能力。
认识质量单位克和千克。
初步建立1克和1千克的质量观念,知道1千克=1000克。
建立质量观念,培养学生估算物体质量的意识。
数学数与代数知识点整理篇21、小数乘整数:意义求几个相同加数的和的简便运算。
如:1.53表示1.5的3倍是多少或3个1.5的和的简便运算。
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
2、小数乘小数:意义就是求这个数的几分之几是多少。
如:1.50.8就是求1.5的十分之八是多少。
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
3、规律:一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小。
初中代数方程解法知识点整理

初中代数方程解法知识点整理代数方程是数学中重要的概念之一,它是由数字、字母和运算符组成的等式。
解方程是求出使等式成立的未知数的值的过程。
在初中阶段,学习代数方程的解法是非常重要的基础知识,本文将整理初中代数方程解法的知识点,帮助初中学生更好地理解和掌握。
一、一元一次方程的解法1. 移项法:一元一次方程的一般形式为ax + b = 0,其中a、b为已知数,x为未知数。
通过移项将方程化简为形如x = c的形式,其中c为常数。
2. 消元法:如果一个方程中含有未知数的两个或多个倍数,可通过消去这些倍数,将方程化简为一元一次方程。
常用的消元法有加减法消元和代入法消元。
3. 倒数法:一元一次方程中,有时可以通过将等式两边同时除以未知数的系数,将方程转化为更简单的形式。
二、一元二次方程的解法1. 因式分解法:将一元二次方程转化为两个一元一次方程,并求解每个一元一次方程的根。
2. 公式法:一元二次方程的一般形式为ax² + bx + c = 0。
其中,Δ = b² - 4ac称为判别式。
当Δ > 0时,方程有两个不相等的实数根;当Δ = 0时,方程有两个相等的实数根;当Δ < 0时,方程没有实数根。
根据一元二次方程的求根公式x = (-b ± √Δ) / 2a,可以求解一元二次方程。
三、分式方程的解法1. 通分法:分式方程中,通过找到等式两边的最小公倍数,将分母通分,将分式方程转化为整式方程。
2. 交叉乘法:分式方程中,通过交叉相乘法将方程中的分式进行乘法运算,将分式方程转化为整式方程。
3. 求最小公倍数法:分式方程中,通过先求出等式两边的最小公倍数,再进行乘法运算,将分式方程转化为整式方程。
四、绝对值方程的解法1. 判断法:绝对值方程解的个数与等式中绝对值的取值范围相关,通过对绝对值的取值范围进行分析,可以判断绝对值方程的解的个数。
2. 分段法:对绝对值表达式进行绝对值符号的两种可能取值进行讨论,然后求解得到绝对值方程的解。
《高等代数》知识点梳理

高等代数知识点梳理第四章 矩阵一、矩阵及其运算 1、矩阵的概念(1)定义:由n s ×个数ij a (s i ,2,1=;n j ,2,1=)排成s 行n 列的数表sn s n a aa a 1111,称为s 行n 列矩阵,简记为n s ij a A ×=)(。
(2)矩阵的相等:设n m ij a A ×=)(,k l ij a B ×=)(,如果l m =,k n =,且ij ijb a =,对m i ,2,1=;n j ,2,1=都成立,则称A 与B 相等,记B A =。
(3)各种特殊矩阵:行矩阵,列矩阵,零矩阵,方阵,(上)下三角矩阵,对角矩阵,数量矩阵,单位矩阵。
2、矩阵的运算(1)矩阵的加法:++++= +sn sn s s n n sn s n sn s n b a b a b a b a b b b b a a a a 1111111111111111。
运算规律:①A B B A +=+②)()(C B A C B A ++=++③A O A =+ ④O A A =−+)((2)数与矩阵的乘法:= sn s n sn s n ka ka ka ka a a a a k 11111111运算规律:①lA kA A l k +=+)( ②kB kA B A k +=+)(③A kl lA k )()(= ④O A A =−+)((3)矩阵的乘法:= sm s m nm n m sn s n c c c c b b b b a a a a 111111111111其中nj in i i i i ij b a b a b a c +++= 2211,s i ,2,1=;m j ,2,1=。
运算规律:①)()(BC A C AB = ②AC AB C B A +=+)( ③CA BA A C B +=+)( ④B kA kB A AB k )()()(==一般情况,①BA AB ≠②AC AB =,0≠A ,⇒C B =③0=AB ⇒0=A 或0=A(4)矩阵的转置: =sn s n a a a a A 1111,A 的转置就是指矩阵=ns n s a a a a A 1111'运算规律:①A A =)''( ②'')'(B A B A +=+③'')'(A B AB = ④')'(kA kA =(5)方阵的行列式:设方阵1111n n nn a a A a a= ,则A 的行列式为1111||n n nn a a A a a = 。
初中数学代数知识点大全

初中数学代数知识点大全代数是数学的一个重要分支,它研究数与数之间的关系以及运算规律。
在初中数学学习中,代数是一个重要的内容,通过代数的学习,学生可以学会运用符号和代数表达式描述问题,进行算式的变形和计算,培养逻辑思维和解决问题的能力。
下面将给大家介绍初中数学代数知识点大全。
一、代数式与项的概念1. 代数式:由数、字母和数学符号(如+、-、×、÷等)组成的有意义的表达式。
2. 项:代数式中的基本单位,由数与字母的积组成,或者只是单独一个数或字母。
二、代数式的加减法1. 代数式的加法:对应项相加,合并同类项。
2. 代数式的减法:对应项相减,合并同类项。
三、代数式的乘法与因式分解1. 代数式的乘法:将每一个项相乘得到的新的代数式。
2. 因式分解:将代数式中的项用括号括起来,根据因式的乘法规则进行合并。
四、代数式的除法与分式1. 代数式的除法:将代数式相除,可以通过因式分解的方式进行。
2. 分式:含有分子和分母的代数式,分母不能为零。
五、方程与等式1. 方程:由等号连接的两个代数式构成,含有未知数的代数式。
求解方程即求解未知数的值。
2. 等式:由等号连接的两个代数式。
六、一次方程与二次方程1. 一次方程:未知数的最高次数为1的方程,如ax+b=0。
2. 二次方程:未知数的最高次数为2的方程,如ax²+bx+c=0。
七、函数与图像1. 函数:表示两个变量之间依赖关系的关系式。
2. 图像:函数在平面直角坐标系上的表示。
八、线性函数与一次函数1. 线性函数:函数的表达式为y=kx+b,k和b为常数,表示直线函数。
2. 一次函数:最高次数为一次的函数。
九、整式与分式1. 整式:只含有加减乘幂四种运算的代数式。
2. 分式:含有除法运算的代数式。
十、因式分解与最大公因数1. 因式分解:将代数式中的各个项写成最简单的乘积形式的过程。
2. 最大公因数:能整除多个整数的最大正整数。
十一、一次函数与二次函数的图像1. 一次函数的图像:直线。
代数基础知识点总结

代数基础知识点总结代数作为数学的一个重要分支,主要研究数与变量之间的关系以及运算规律。
它是其他数学分支的基础,也是解决实际问题的有力工具。
在学习代数时,我们需要掌握一些基础知识点,下面对这些知识点进行总结。
一、代数符号及表达式1. 代数符号:代数中常用的符号包括字母、数字符号以及运算符号等。
字母常用来表示变量,数字符号则表示特定的数值,运算符号用于表示各种运算关系。
2. 代数表达式:代数表达式是由数字符号、字母和运算符号按照一定规则组成的式子。
代数表达式中的字母常用来表示未知数或变量,用于表示具有普遍性的情况。
二、代数运算1. 代数运算符号:包括加法、减法、乘法、除法、指数、根号、阶乘等运算符号。
这些运算符号具有特定的运算规则,掌握这些规则对于进行正确的代数运算至关重要。
2. 代数运算法则:- 加法和乘法的交换律:a + b = b + a,a × b = b × a;- 加法的结合律:(a + b) + c = a + (b + c);- 乘法的结合律:(a × b) × c = a × (b × c);- 分配律:a × (b + c) = a × b + a × c;- 指数运算法则:a^m × a^n = a^(m+n),(a^m)^n = a^(m×n)。
三、代数方程1. 代数方程定义:代数方程是用等号连接的两个代数表达式构成的式子。
等号左边称为方程的左边,等号右边称为方程的右边。
2. 一元一次方程:形如ax + b = 0的方程,其中a、b为已知数,x为未知数。
解一元一次方程可用等式的等价变形和运算法则。
3. 一元二次方程:形如ax^2 + bx + c = 0的方程,其中a、b、c为已知数,x为未知数。
一元二次方程的求解可以通过配方法、因式分解法、根公式等方法进行。
四、代数函数1. 代数函数定义:代数函数是变量间关系的一种特殊表示方式,用f(x)表示。
代数公式的知识点总结

代数公式的知识点总结一、整式的加减。
1. 单项式。
- 定义:由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
例如:3x,-2y,5,a等都是单项式。
- 系数:单项式中的数字因数叫做这个单项式的系数。
例如在单项式3x中,系数是3;在单项式-(2)/(3)y中,系数是-(2)/(3)。
- 次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如单项式x^2y的次数是2 + 1=3。
2. 多项式。
- 定义:几个单项式的和叫做多项式。
例如2x+3y,x^2-2x + 1等都是多项式。
- 项:在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项。
例如在多项式x^2-2x+3中,x^2、-2x、3都是它的项,3是常数项。
- 次数:多项式里次数最高项的次数,叫做这个多项式的次数。
例如多项式x^3-x^2+2的次数是3。
3. 整式。
- 单项式和多项式统称为整式。
4. 同类项。
- 定义:所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如3x^2y与-5x^2y是同类项,2与-7是同类项。
- 合并同类项:把多项式中的同类项合并成一项,叫做合并同类项。
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
例如3x^2y - 5x^2y=(3 - 5)x^2y=-2x^2y。
二、一元一次方程。
1. 方程。
- 定义:含有未知数的等式叫做方程。
例如2x+3 = 7,x - y=5等都是方程。
2. 一元一次方程。
- 定义:只含有一个未知数(元),未知数的次数都是1,等号两边都是整式的方程叫做一元一次方程。
一般形式是ax + b = 0(a≠0),例如3x+5 = 0就是一元一次方程。
- 解方程的步骤:- 去分母(若方程中有分母时):根据等式的性质2,在方程两边同时乘以各分母的最小公倍数,将分母去掉。
例如对于方程(x+1)/(2)+(x - 1)/(3)=1,先找出2和3的最小公倍数6,然后方程两边同时乘以6得到3(x + 1)+2(x - 1)=6。
(完整版)数与代数的知识点
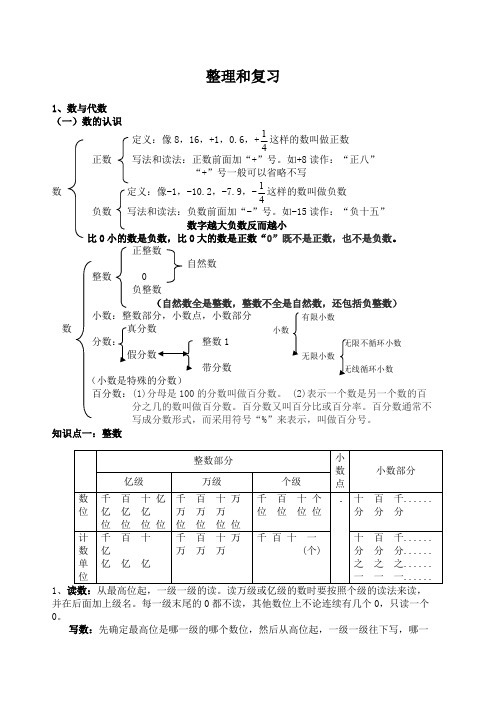
整理和复习1、数与代数(一)数的认识定义:像8,16,+1,0.6,+这样的数叫做正数41正数 写法和读法:正数前面加“+”号。
如+8读作:“正八” “+”号一般可以省略不写数 定义:像-1,-10.2,-7.9,-这样的数叫做负数41负数 写法和读法:负数前面加“-”号。
如-15读作:“负十五” 数字越大负数反而越小比0小的数是负数,比0大的数是正数“0”既不是正数,也不是负数。
正整数自然数 整数 0 数 (小数是特殊的分数)百分数:(1)分母是100的分数叫做百分数。
(2)表示一个数是另一个数的百分之几的数叫做百分数。
百分数又叫百分比或百分率。
百分数通常不写成分数形式,而采用符号“%”来表示,叫做百分号。
知识点一:整数1、读数:从最高位起,一级一级的读。
读万级或亿级的数时要按照个级的读法来读,并在后面加上级名。
每一级末尾的0都不读,其他数位上不论连续有几个0,只读一个0。
写数:先确定最高位是哪一级的哪个数位,然后从高位起,一级一级往下写,哪一整数部分亿级万级个级小数点小数部分数位千 百 十 亿亿 亿 亿位 位 位 位千 百 十 万万 万 万位 位 位 位千 百 十 个位 位 位 位十 百 千......分 分 分计数单位千 百 十 亿亿 亿 亿千 百 十 万万 万 万千 百 十 一 (个).十 百 千......分 分 分......之 之 之......一 一 一......位一个单位也没有,就在哪个数位上写0。
2、数的改写与求近似数:为了读写方便,常把较大的数简写成用“万”或“亿”作单位的数。
如:2365500=236.55万(改写用“万”作单位的数)。
如:2365500≈237万(省略万位后面的尾数,写成近似数),如:7.62983≈7.6(保留一位小数)。
知识点二:小数1、小数的意义: 把整数“1”平均分成10份,100份,1000份……这样的1份或几份是十分之几,百分之几,千分之几…可以用小数来表示。
初一数学《代数式》知识点精讲

初一数学《代数式》知识点精讲知识点总结一、代数式的定义:用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
注意:(1)单个数字与字母也是代数式;(2)代数式与公式、等式的区别是代数式中不含等号,而公式和等式中都含有等号;(3)代数式可按运算关系和运算结果两种情况理解。
三、整式:单项式与多项式统称为整式。
1.单项式:数与字母的积所表示的代数式叫做单项式,单项式中的数字因数叫做单项式的系数;单项式中所有字母的指数的和叫做单项式的次数。
特别地,单独一个数或者一个字母也是单项式。
2.多项式:几个单项式的和叫做多项式,在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项;在多项式里,次数最高项的次数就是这个多项式的次数。
四、升(降)幂排列:把一个多项式按某一个字母的指数从小到大(或从大到小)的顺序排列起来,叫做把多项式按这个字母升(降)幂排列。
五、代数式书写要求:1.代数式中出现的乘号通常用“·”表示或者省略不写;数与字母相乘时,数应写在字母前面;数与数相乘时,仍用“×”号;2.数字与字母相乘、单项式与多项式相乘时,一般按照先写数字,再写单项式,最后写多项式的书写顺序.如式子(a+b)·2·a应写成2a(a+b);3.带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘;4.在代数式中出现除法运算时,按分数的写法来写;5.在一些实际问题中,有时表示数量的代数式有单位名称,如果代数式是积或商的形式,则单位直接写在式子后面;如果代数式是和或差的形式,则必须先把代数式用括号括起来,再将单位名称写在式子的后面,如2a 米,(2a-b)kg。
六、系数与次数单项式的系数和次数,多项式的项数和次数。
1.单项式的系数:单项式中的数字因数叫做单项式的系数。
注意:(1)单项式的系数包括它前面的符号;(2)若单项式的系数是"1”或-1“时,"1"通常省略不写,但“-”号不能省略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代数知识点整理
1. 代数的基本概念
代数是数学的一个重要分支,它研究各种数学结构之间的关系和运算规律。
在代数中,我们使用符号来表示未知量和运算符号来表示运算规则。
以下是一些代数的基本概念:
•变量:代数中常用字母表示未知量,这些字母称为变量。
例如,x、y、z等都可以作为变量。
•常数:代数中不变化的值称为常数。
例如,2、3.14、-5等都是常数。
•表达式:由变量、常数和运算符组成的式子称为表达式。
例如,2x + 3y是一个表达式。
•方程:包含一个或多个未知量,并且等号连接左右两边的表达式称为方程。
例如,2x + 3 = 7是一个方程。
2. 一元一次方程
一元一次方程是指只含有一个未知量,并且该未知量的最高次幂为1的方程。
一元一次方程的一般形式为ax + b = c,其中a、b、c都是已知常数。
解一元一次方程的步骤如下:
1.将方程转化为标准形式:将未知量的系数移到方程的一边,常数移到方程的
另一边,使得方程左边为0。
例如,2x + 3 = 7可以转化为2x - 4 = 0。
2.消去未知量的系数:通过将方程两边同时除以未知量的系数,消去未知量的
系数,使得未知量的系数变为1。
例如,2x - 4 = 0可以变为x - 2 = 0。
3.求解未知量:将方程中等号左边为1的项求解出来即可得到未知量的值。
例
如,x - 2 = 0可以求解出x = 2。
3. 多元一次方程组
多元一次方程组是指含有多个未知量,并且每个未知量的最高次幂都为1的一组方程。
多元一次方程组的一般形式如下:
a₁x₁ + a₂x₂ + ... + aₙxₙ = b₁
a₁'x₁ + a₂'x₂ + ... + aₙ'xₙ = b₂
...
a₁''x₁ + a₂''x₂ + ... + aₙ''xₙ = bₙ
其中a₁, a₂, …, aₙ, b₁, …, bₙ都是已知常数。
解多元一次方程组的步骤如下:
1.将方程组转化为增广矩阵形式:将方程组的系数和常数写成一个矩阵,形如
[A|B],其中A是系数矩阵,B是常数矩阵。
2.初等行变换:通过初等行变换将增广矩阵化简为行阶梯形式或最简形式。
3.回代求解:从最后一行开始,依次回代求解出未知量的值。
4. 二次函数
二次函数是指未知量的最高次幂为2的函数。
二次函数的一般形式为f(x) = ax²
+ bx + c,其中a、b、c都是已知常数且a ≠ 0。
二次函数的图像可以表示为抛物线。
当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。
抛物线的顶点坐标为(-b/2a, f(-b/2a))。
二次函数的性质包括:
•零点:即方程ax² + bx + c = 0的解,可以通过求解方程得到。
•对称轴:即过顶点和焦点中垂直于x轴的直线。
•最值:当抛物线开口向上时,最小值为顶点坐标对应y值;当抛物线开口向下时,最大值为顶点坐标对应y值。
5. 等差数列和等比数列
等差数列是指相邻两项之差为常数的数列,常用字母a表示首项,d表示公差。
等
差数列的通项公式为an = a + (n-1)d。
等比数列是指相邻两项之比为常数的数列,常用字母a表示首项,r表示公比。
等
比数列的通项公式为an = ar^(n-1)。
等差数列和等比数列有许多重要性质:
•公式求和:可以通过特定的公式求解等差数列和等比数列的前n项和。
•递归定义:可以通过递归定义来表示等差数列和等比数列。
•常用性质:例如,对于等差数列来说,第n项与倒数第n项之和是一个常量;
对于等比数列来说,任意一项与它后面一项之商都是一个常量。
总结
代数知识点是学习高中及以上级别的重要基础。
本文介绍了代数的基本概念、一元一次方程、多元一次方程组、二次函数以及等差数列和等比数列这些核心知识点。
掌握了这些知识点,可以帮助我们解决实际问题,推导出更复杂的代数关系。
因此,对于学习数学和解决实际问题来说,代数知识是不可或缺的一部分。
