材料力学2013
武汉理工大学2012-2013-2学期材料力学C历年试卷
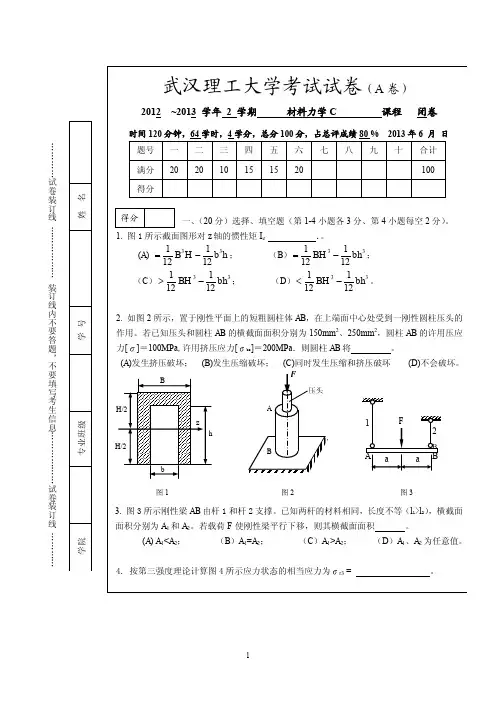
… … 60° … 60 … 60 试 卷 装 订 线 图9 … … … … … … 装 订 线 内 不 得分 3 六、 (20 分) 如图 10 所示结构中, 梁 AB 为 14 号普通热轧工字钢, WZ=102cm , 要 答 CD 为等截面圆直杆,直径 d=20mm,两者材料均为 Q235 钢, E=206GPa,λp =100。结构 题 , 受力如图所示,F 铅垂向下;A、C、D 三处均为铰接。若已知 l=1.25m,a=0.55m,强度许用 不 要 应力[σ] =160MPa,规定的稳定安全因数[n]st=2.0。试求结构的许可载荷[F]。 填 写 考 l l 生 z B 信 A B C 息 … … F … … D … … 试 卷 图 10 装 订 线 … … … …
MeA MeB MeC
A
B 图6
C
2
得分
三、 (10 分)作图 7 所示梁的剪力图和弯矩图 (可求得 A、B 处的约束力
FA qa , FB 5qa )。
2qa2 A a
B
q B 2a 图7 a
B
2qa
得分
四、 (15 分)承受轴向偏心载荷的矩形截面杆如图 8 所示,已知 F = 200kN, 作用在对称轴 y 上一点处,弹性模量 E = 40GPa,矩形截面尺寸 h = 30cm,
题号 满分 姓 名 得分 得分
一 20
二 20
三 10
四 15
五 15
六 20
七
八
九
十
合计 100
一、 (20 分)选择、填空题(第 1-4 小题各 3 分、第 4 小题每空 2 分) 。 . 。 (B)
1. 图 1 所示截面图形对 z 轴的惯性矩 Iz
2013年青岛大学考研真题819材料力学
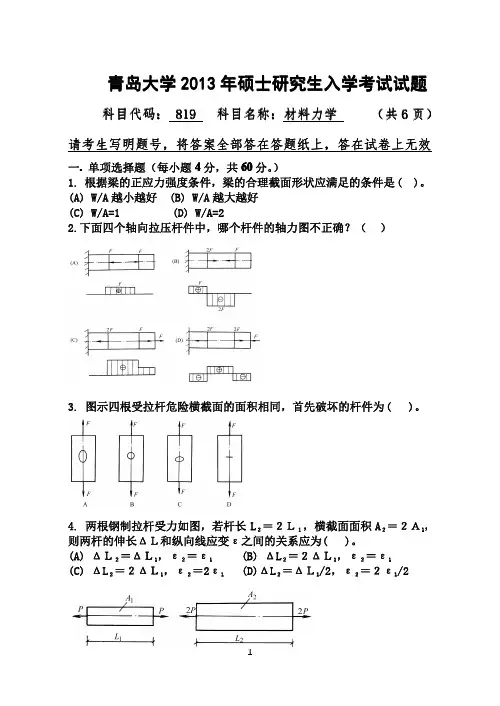
青岛大学2013年硕士研究生入学考试试题科目代码:819科目名称:科目名称:材料力学材料力学(共6页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一.单项选择题(每小题4分,共60分。
)1.根据梁的正应力强度条件,梁的合理截面形状应满足的条件是()。
(A)W/A 越小越好(B)W/A 越大越好(C)W/A=1(D)W/A=22.下面四个轴向拉压杆件中,哪个杆件的轴力图不正确?()3.图示四根受拉杆危险横截面的面积相同,首先破坏的杆件为()。
4.两根钢制拉杆受力如图,若杆长L 2=2L1,横截面面积A 2=2A1,则两杆的伸长ΔL和纵向线应变ε之间的关系应为()。
(A)ΔL2=ΔL1,ε2=ε1(B)ΔL 2=2ΔL1,ε2=ε1 (C)ΔL 2=2ΔL1,ε2=2ε1(D)ΔL 2=ΔL1/2,ε2=2ε1/25.图示等截面直杆的抗拉刚度为EA,其变形能应为下列式中的()。
(A)U=5P2l/(6EA)(B)U=3P2l/(2EA)(C)U=9P2l/(4EA)(D)U=13P2l/(4EA)6.在图示受扭圆轴横截面上的切应力分布图中,正确的结果是()。
7.空心圆轴,其内外径之比为α,扭转时轴内的最大切应力为τ,这时横截面上内边缘处的切应力为()。
(A)O(B)ατ(C)τ/α(D)(1-α4)τ8.请选择正确结论:图形对其对称轴的()。
(A)静矩为零,惯性矩不为零,惯性积为零(B)静矩不为零,惯性矩和惯性积均为零(C)静矩、惯性矩及惯性积均为零(D)静矩、惯性矩及惯性积均不为零9.梁的弯矩图如右图所示,则梁上的最大剪力为()。
(A)P(B)5P/2(C)3P/2(D)7P/210.图示两根简支梁,一根材料为钢,另一根材料为铝。
已知它们的抗弯刚度EI 相同,在相同外力作用下,二者的不同之处为()。
(A)弯曲最大正应力(B)剪力图(C)最大挠度(D)最大转角11.插销穿过水平放置的平板上的圆孔,在其下端受有一拉力P.该插销的剪切面面积和挤压面积分别等于()(A)πdh ,πD 2/4;(B)πDh ,πD 2/4;(C)πdh ,π(D 2-d 2)/4;(D)πDh ,π(D 2-d 2)/4。
北航2013材料力学第二学期小测验1(答案)
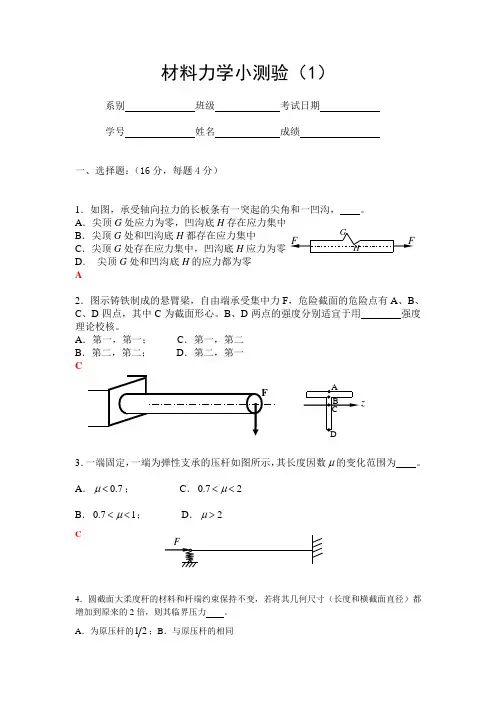
材料力学小测验(1)系别 班级 考试日期学号 姓名 成绩一、选择题:(16分,每题4分)1.如图,承受轴向拉力的长板条有一突起的尖角和一凹沟, 。
A .尖顶G 处应力为零,凹沟底H 存在应力集中B .尖顶G 处和凹沟底H 都存在应力集中C .尖顶G 处存在应力集中,凹沟底H 应力为零D . 尖顶G 处和凹沟底H 的应力都为零 A2.图示铸铁制成的悬臂梁,自由端承受集中力F ,危险截面的危险点有A 、B 、C 、D 四点,其中C 为截面形心。
B 、D 两点的强度分别适宜于用 强度理论校核。
A .第一,第一; C .第一,第二B .第二,第二; D .第二,第一 C3.一端固定,一端为弹性支承的压杆如图所示,其长度因数μ的变化范围为 。
A .0.7μ<; C .0.72μ<< B .0.71μ<<; D .2μ>C4.圆截面大柔度杆的材料和杆端约束保持不变,若将其几何尺寸(长度和横截面直径)都增加到原来的2倍,则其临界压力 。
A .为原压杆的12;B .与原压杆的相同zC.为原压杆的2倍;D.为原压杆的4倍D二、填空题:(24分,每个空2分)1、第一强度理论认为引起材料断裂的主要因素是最大拉应力;第二强度理论认为引起材料断裂的主要因素是最大拉应变;第三强度理论认为引起材料屈服的主要因素是最大切应力;第四强度理论认为引起材料屈服的主要因素是畸变能。
2、某点的应力状态如图所示,已知材料的弹性模量E和泊松比μ,则该点沿α=45°方向的正应力为σ45°=___τ______,切应力为τ45°=___-τ______;正应变、τ2,切应变分别为ε45°=__(1+μ)τ/E__,γ45°=__-2(1+μ)τ/E___。
主应力为σ1=σ2=__0__,σ3=τ2-,最大切应力为τmax=τ2。
Array题 1图三、计算题:1、(20分)圆钢杆受力如图,已知直径d=20mm,力F=8kN,[σ]=170MPa。
《材料力学教学课件》b 05 20130402 第四章

根据已知条件,主传动轴横截面上的扭矩Mx=Me=1.5 kN·m,轴的内直径与外直径之比
= d =D-2 =90mm-2 2.5mm =0.944
DD
90mm
因为轴只在两端承受外加力偶,所以轴各横截面的危险 程度相同,轴的所有横截面上的最大剪应力均为
=
max
Mx WP
M
M
M
截面尺寸突变
M
配置过渡圆角
Page8
BUAA
MECHANICS OF MATERIALS
扭转强度设计
例 题 1 (教材3-4类似)
已知:汽车发动机将功率通过主 传动轴AB传给后桥,驱动车轮行 驶。设主传动轴所承受的最大外力 偶矩为Me=1.5 kN·m,轴由45号钢 无缝钢管制成,外直径D
脆性材料: = (0.8-1.0)st
Page4
BUAA
MECHANICS OF MATERIALS
强度条件
max
T
WP
max
[ ]
根据强度条件可以解决以下几类强度问题
max
T WP
max
?[
]
WP
Tmax
[ ]
Tmax WP [ ]
T
T 2M x a
M
x
B
2M
A
可能危险截面A、B
Page22
BUAA
MECHANICS OF MATERIALS
2、总扭转角 (分4段计算)
m 2M a
A
BM
3M
dD
a
x
T
材料力学期末试卷答案
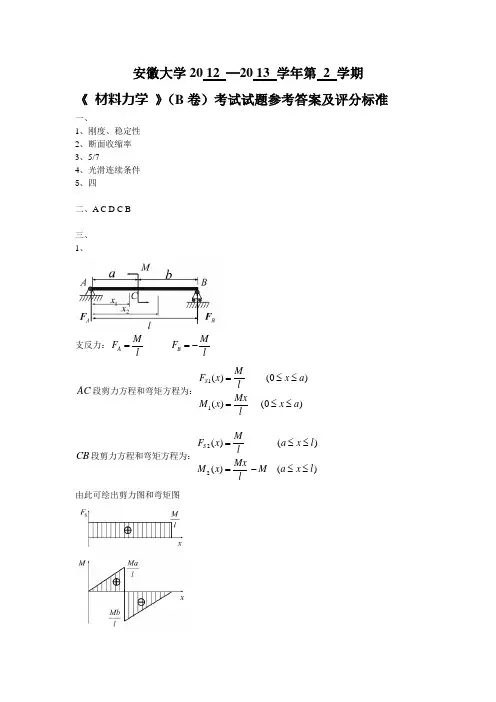
安徽大学20 12 —20 13 学年第 2 学期《 材料力学 》(B 卷)考试试题参考答案及评分标准 一、1、刚度、稳定性2、断面收缩率3、5/74、光滑连续条件5、四二、A C D C B三、1、支反力:A B MM F F l l==- AC 段剪力方程和弯矩方程为:11()(0)()(0)S M F x x a l Mx M x x a l=≤≤=≤≤ CB 段剪力方程和弯矩方程为:22()()()()S MF x a x l l Mx M x M a x l l=≤≤=-≤≤ 由此可绘出剪力图和弯矩图2、应力圆方程2222()()22x yx yxy αασσσσσττ+--+=+ 圆心坐标为,02x y σσ+⎛⎫ ⎪⎝⎭,半径R =单向受力状态下,圆心为,02x σ⎛⎫⎪⎝⎭,半径为2x σ,应力圆为:四:1:解:3根杆的受力及变形如图示:(1):平衡条件: 123230,00,20y N N N A N N F FF F F M F a F a =++-==⨯+⨯=∑∑(2):变形几何关系:1322l l l ∆+∆=∆(3):物理关系:1,2,3Ni ii F l l i EA ∆==(4):补充方程物理关系与几何关系联立:1322N N N F l F l F l EA EA EA+=得补充方程:1322N N N F F F += 上式与平衡条件联立,得:123511,,636N N N F F F F F F ===- 2、边界条件: 2200,0x ωθ=⎧=⎨=⎩ 2121,2l x ωωθθ=⎧=⎨=⎩ ()1=-F l x EI ω- 211=-2Flx Flx C EI EIθ++ 23111=-26Flx Flx C x D EI EIω+++ ()2=-2F l x EI ω- 2322=-26Flx Flx C EI EI θ++ 23222=-412Flx Flx C x D EI EIω+++ 以上式子联立并结合边界条件得1122320031624C D Fl C EI Fl D EI=⎧⎪=⎪⎪⎨=⎪⎪⎪=-⎩ 又因为最大挠度和转角均发生在C 端,所以 32max max 35,1616Fl Fl EI EI ωθ=-=- 3、在立柱任一截面上有187.2FN F kNM M Fa kN m ====⋅ 所以有[]max 23432N t F M F M A W d d σσππ=+=+≤ 得3362341810327.210 3.510Pa Pa d d ππ⎛⎫⨯⨯⨯⨯+≤⨯ ⎪⎝⎭解得128d mm ≥4、解:单独取一根立柱进行研究,如图所示: '2504FF kN =='42501000cr st F N F kN =⋅=⨯= 假设欧拉公式成立,则有34222()64cr EI Ed F l l ππμ==97d mm ==而:92.94123.7p Pl li d λμλλ=====>故假设是正确的,所以97d mm =。
2013春材料力学II 26-第十一章材料失效及强度理论
第四强度理论的屈服线
19 s 0.577 s 两个强度理论,在纯切
应力状态时差别最大 。
第11章 材料失效及强度理论
11-3 关于屈服的强度理论
工程构件的强度达到极限状态(即发生强度失效)的条件 是什么?怎样才能保证构件安全可靠的工作? 以最大切应力理论为例,来回 答这个问题。 现有材料相同的四个构件,其 危险点应力状态如图所示。
r 3 1 3 [ ]
21
第11章 材料失效及强度理论
例11-1 直径为d=0.1m的圆杆受力如图,T=7kNm,F=50kN, 为铸
铁构件,[]=40MPa,试用第一强度理论校核杆的强度。
T F A T F
解:危险点A的应力状态如图:
F 4 50 103 6.37MPa A 0.12
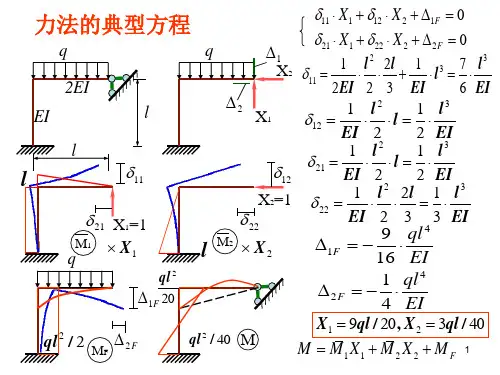
11 X1 12 X 2 1F 0 力法的典型方程 21 X1 22 X 2 2F 0 q q 1 1 l 2 2l 1 3 7 l 3 X2 11 l 2 EI 2 3 EI 6 EI 2EI 2 1 l2 1 l3 l EI X1 12 l EI 2 2 EI 2 l 1 l 1 l3 21 l 11 12 EI 2 2 EI l 2 1 l 2l 1 l 3 X2=1 22 EI 2 3 3 EI 22 21 X1=1 9 ql 4 M2 M1 X 1F X2 l 1 16 EI q ql2 1 ql 4 2 F 1F 20 4 EI X1 9ql / 20, X 2 3ql / 40 2 ql / 40 M ql 2 / 2 MF 2F M M1 X1 M2 X 2 M F 1
拉伸实验(材料力学课程实验)2013
拉伸新国家标准-GB228-2002
拉伸问题说明(2) -断口位置对断后延伸率影响及修正
实验报告要求(每人一份)
1 按照拉伸试验报告要求独立完成实验报告。 (见实验教材P31,注:第7题改为选作题) 2 实验报告要有低碳钢(或铝合金)和铸铁两种材料的实验数 据、曲线和结果。 3 认真总结几种典型材料力学性能特点,完成分析讨论题。 4 曲线要求每人一份,并做修正和说明。 5 要将实验原始数据记录(有老师和本组同学签名,每组至少一 份 )附在实验报告后面。 6 实验报告下次实验时带来交给老师。 7 实验报告要求手写。
复合材料断裂特点
在纤维增强复合材料中,每平方厘米的 纤维数有几千~几万根。由于有大量独立的 纤维,过载时复合材料中即使有少量纤维断 裂,载荷会迅速重新分配到未被破坏的纤维 上,不至于造成构件在瞬间完全丧失承载能 力而断裂。 问题: 与一般脆性材料断裂过程比较,最大区别?
常用材料性能比较
材料 弹性模量 GPa 屈服强度 MPa 强度极限 MPa 延伸率 % 低碳钢 200 280 380 40 铝合金 70 420 590 14 铸铁 180 / 100~ 300 0 纤维复 合材料 20~50 / 1600 0 高分子 材料 1~5 30~53 / 1~500
增强材料:碳纤维,基体:环氧树脂 碳纤维含量:60% 试件尺寸:12.6x1.5
玻璃纤维增强复合材料 拉伸过程(1)
玻璃纤维增强复合材料 拉伸过程(2)
玻璃纤维增强复合材料 拉伸过程(3)
玻璃纤维增强复合材料 拉伸过程(4)
纤维性能: S型玻璃纤维: 抗拉强度4.6GPa, 弹性模量84GPa T-300型碳纤维: 抗拉强度3.5GPa, 弹性模量230GPa B(W)型硼纤维: 抗拉强度3.6GPa, 弹性模量400GPa
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学2013
第一章绪论
强度:抵抗破坏的能力。
刚度:抵抗变形的能力
材料力学研究变形固体的内部效应(构件受到的内力)及变形
弹性变形
塑性变形
材料力学的研究对象(杆件)
杆件变形的基本形式:轴向拉伸及压缩
剪切
扭转
平面弯曲
第二章轴向拉伸与压缩
杆件发生纵向伸长或缩短
内力——由于物体受外力作用而引起的其内部各质点间相互作用的力的改变量
求内力的一般方法——截面法
轴力FN:杆件任一横截面上的内力,其作用线均与杆件的轴线重合,引起伸长变形的轴力为正
引起压缩变形的轴力为负
轴力图:用平行于杆轴线的坐标表示横截面的位置,用垂直于杆轴线的坐标表示横截面上轴力的数值
拉压杆的强度=材料的强度+轴力+横截面尺寸
应力:杆件截面上的分布内力的集度
总应力 p=正应力δ 法向分量, 引起长度改变
切应力ζ 切向分量,引起角度改变
正应力:拉为正,压为负
切应力:对截面内一点产生顺时针力矩的切应力为正,反之为负 内力与应力间的关系:⎰=A A F d N σ
⎰=A
A F d S τ 拉(压)杆横截面上的应力A F N
=σ (由A F σ=N )
圣维南原理: 力作用于杆端方式的不同,只会使与杆端距离不大于杆的横向尺寸的范围内受到影响
极限应力δu 塑性材料: δs 或δp0.2 ns 一般取 1.25 ~ 2.5 脆性材料 δb nb 一般取 2.5 ~ 3.0,甚至 4 ~ 14 许用应力
拉(压)杆的纵向变形
绝对变形l l l -1=∆
相对变形(线应变)l l ∆=
ε
横向变形 ασσα2
0cos =αστα2sin 20=n
u ][σσ=
绝对变形d d d -1=∆ 线应变d d
∆='ε 拉(压)杆的胡克定律EA l
F l N =∆
E — 弹性模量
EA — 杆的拉伸(压缩)刚度
EA l F l N =∆ A F
E l l N
1=∆ E σ
ε=
横向变形εεν-='
v ----- 横向变形因数或泊松比
拉(压)杆内的应变能=εV l F ∆⋅21
)(EA Fl
l =∆
EA l F 22=EA
l
F 22
N
= 或l l EA 2)(2
∆= 应变能密度V V v εε=Al l
F ∆⋅=2
1
σε21
=)(εσE =
E 22σ=22
εE =
第三章 扭 转。
