2010年云南省第二次高中毕业生复习统一检测
高考英语语法词汇专项突破:代词要点全解读+巩固训练(含高考真题)

高考英语语法词汇专项突破:代词考点专题全突破+巩固训练养成良好的答题习惯,是决定高考英语成败的决定性因素之一。
做题前,要认真阅读题目要求、题干和选项,并对答案内容作出合理预测;答题时,切忌跟着感觉走,最好按照题目序号来做,不会的或存在疑问的,要做好标记,要善于发现,找到题目的题眼所在,规范答题,书写工整;答题完毕时,要认真检查,查漏补缺,纠正错误。
总之,在最后的复习阶段,学生们不要加大练习量。
在这个时候,学生要尽快找到适合自己的答题方式,最重要的是以平常心去面对考试。
英语最后的复习要树立信心,考试的时候遇到难题要想“别人也难”,遇到容易的则要想“细心审题”。
越到最后,考生越要回归基础,单词最好再梳理一遍,这样有利于提高阅读理解的效率。
另附高考复习方法和考前30天冲刺复习方法。
[命题热点]代词结构种类很多,有人称代词、反身代词、物主代词、疑问代词、指示代词、连接代词、关系代词、不定式代词、替代词以及it等。
从命题角度看主要考查代词词义的区别,如that/one/it;代词功能的区别,如me, oneself, she, ours;含有代词的固定短语,如make it/give me five; 反身代词的用法,如help oneself, enjoy oneself; 比较中的代词用法;反义疑问句中的代词;不定代词用法;疑问代词与疑问副词辨析。
从历年高考题来看,不定代词和替代词的考查是重点。
试题设置了一定情景干扰,题干句的语法结构十分重要,重点考查考生在语境中灵活运用代词的能力。
考点1 人称代词的主格与宾格_____(I), too. I was a little stressed out about this new store, but now I'm feeling much more confident.详解:Me。
根据答句后面的I看出前面是第一人称单数,再根据单独使用得出用宾格代词代替主格代词,用Me。
昆明市2010年高中(中专)招生统一考试答案
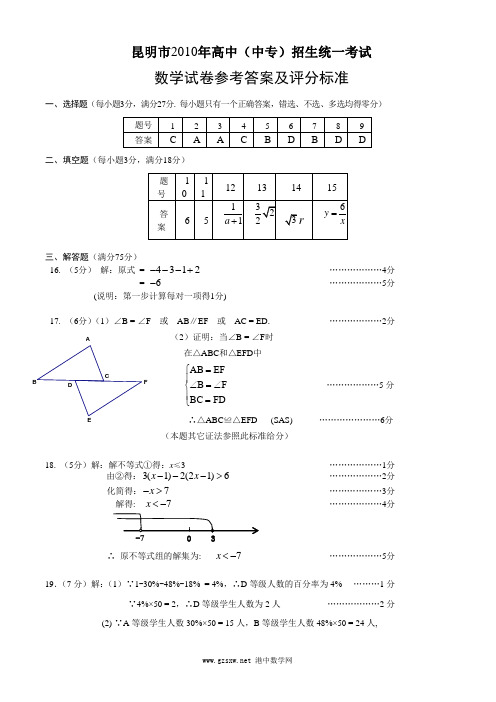
3.-7昆明市2010年高中(中专)招生统一考试数学试卷参考答案及评分标准一、选择题(每小题3分,满分27分. 每小题只有一个正确答案,错选、不选、多选均得零分)题号 123456789答案C A A C BD B D D二、填空题(每小题3分,满分18分)题号 10 11 121314 15答案6511a +3223r6y x=三、解答题(满分75分)16. (5分) 解:原式 = 4312---+………………4分= 6-………………5分(说明:第一步计算每对一项得1分)17. (6分)(1)∠B = ∠F 或 AB ∥EF 或 AC = ED .………………2分(2)证明:当∠B = ∠F 时 在△ABC 和△EFD 中A B E FB F BC FD =⎧⎪∠=∠⎨⎪=⎩………………5分∴△ABC ≌△EFD (SAS) …………………6分 (本题其它证法参照此标准给分)18. (5分)解:解不等式①得:x ≤3 ………………1分由②得:3(1)2(21)6x x ---> ………………2分 化简得:7x ->………………3分 解得: 7x <-………………4分∴ 原不等式组的解集为: 7x <-………………5分19.(7分)解:(1)∵1-30%-48%-18% = 4%,∴D 等级人数的百分率为4%………1分∵4%×50 = 2,∴D 等级学生人数为2人………………2分(2) ∵A 等级学生人数30%×50 = 15人,B 等级学生人数48%×50 = 24人,FEDCBAB 1 C1C 等级学生人数18%×50 = 9人,D 等级学生人数4%×50 = 2人……………3分 ∴中位数落在B 等级. ………………4分 (3)合格以上人数 = 800×(30%+48%+18%)= 768 ………………6分 ∴ 成绩达合格以上的人数大约有768人. ………………7分20. (8分) 解:(1)A(2,0),B(-1,-4)………………2分 (2)画图正确……………………4分(3)设线段B 1A 所在直线 l 的解析式为:(0)y kx b k =+≠ ∵B 1(-2,3),A (2,0)∴2320k b k b -+=⎧⎨+=⎩………………5分33,42k b =-=………………6分∴线段B 1A 所在直线 l 的解析式为:3342y x =-+………………7分 线段B 1A 的自变量 x 的取值范围是:-2 ≤ x ≤ 2 ……………8分21.(8分) 解:过点A 作BC 的垂线,垂足为D 点 ……………1分由题意知:∠CAD = 45°, ∠BAD = 60°, AD = 60m在Rt △ACD 中,∠CAD = 45°, AD ⊥BC∴ CD = AD = 60 ……………………3分 在Rt △ABD 中, ∵BDtan BAD AD∠=……………………4分 ∴ BD = AD·tan ∠BAD= 603 ……………………5分∴BC = CD+BD= 60+603 ……………………6分开始(6,6) 1361 3 6 1 3 6 1 3 6 (1,1)(1,3) (1,6) (3,1) (3,3) (3,6) (6,1)(6,3) ≈ 163.9 (m) …………………7分答:这栋高楼约有163.9m . …………………8分 (本题其它解法参照此标准给分)22.(8分) 解:(1)列表如下: 树形图如下:备注:此小题4分,画对表1(或图1)得2分,结果写对得2分. 表1: 图1:(2)数字之和分别为:2,4,7,4,6,9,7,9,12.算术平方根分别是:2,2,7,2,6,3,7,3,23 ………………5分 设两数字之和的算术平方根为无理数是事件A∴5()9P A =………………8分23.(7分)解:设原计划每天修水渠 x 米. ………………1分 根据题意得:36003600201.8x x-= ………………3分解得:x = 80 ………………5分经检验:x = 80是原分式方程的解 ………………6分答:原计划每天修水渠80米. ………………7分24.(9分) (1)证明:∵AD ∥BC∴∠OBP = ∠ODE ……………1分 在△BOP 和△DOE 中 ∠OBP = ∠ODE13 6 1 (1 ,1) (1 ,3) (1 ,6) 3 (3 ,1) (3 ,3) (3 ,6) 6 (6 ,1)(6 ,3)(6 ,6)1 3 6 1 3 6开始13613 6 13 6 13 6∠BOP = ∠DOE …………………2分 ∴△BOP ∽△DOE (有两个角对应相等的两三角形相似) ……………3分(2)① 平行四边形 …………………4分② 直角梯形 …………………5分③ 等腰梯形 …………………6分证明:∵k = 2时,BP2DE= ∴ BP = 2DE = AD又∵AD ︰BC = 2︰3 BC = 32AD PC = BC - BP =32AD - AD =12AD = ED ED ∥PC , ∴四边形PCDE 是平行四边形 ∵∠DCB = 90°∴四边形PCDE 是矩形 …………………7分 ∴ ∠EPB = 90° …………………8分 又∵ 在直角梯形ABCD 中 AD ∥BC, AB 与DC 不平行 ∴ AE ∥BP, AB 与EP 不平行四边形ABPE 是直角梯形 ………………………9分(本题其它证法参照此标准给分)25.(12分) 解:(1)设抛物线的解析式为:2(0)y ax bx c a =++≠由题意得:0164023933⎧⎪=⎪⎪++=⎨⎪⎪++=-⎪⎩c a b c a b c……………1分解得:2383,,099a b c ==-= ………………2分 ∴抛物线的解析式为:2238399y x x =- ………………3分(2)存在 ………………4分抛物线2238399y x x =-的顶点坐标是83(2,)9-,作抛物线和⊙M (如图), 设满足条件的切线 l 与 x 轴交于点B ,与⊙M 相切于点C 连接MC ,过C 作CD ⊥ x 轴于D∵ MC = OM = 2, ∠CBM = 30°, CM ⊥BC∴∠BCM = 90° ,∠BMC = 60° ,BM = 2CM = 4 , ∴B (-2, 0) 在Rt △CDM 中,∠DCM = ∠CDM - ∠CMD = 30° ∴DM = 1, CD =22CM DM -=3 ∴ C (1, 3)设切线 l 的解析式为:(0)y kx b k =+ ,点B 、C 在 l 上,可得:320k b k b ⎧+=⎪⎨-+=⎪⎩ 解得: 323,33k b == ∴切线BC 的解析式为:32333y x =+∵点P 为抛物线与切线的交点由223839932333y x x y x ⎧=-⎪⎪⎨⎪=+⎪⎩ 解得:111232x y ⎧=-⎪⎪⎨⎪=⎪⎩ 226833x y =⎧⎪⎨=⎪⎩∴点P 的坐标为:113(,)22P -, 283(6,)3P ………………8分 ∵ 抛物线2238399y x x =-的对称轴是直线2=x 此抛物线、⊙M 都与直线2=x 成轴对称图形 于是作切线 l 关于直线2=x 的对称直线 l ′(如图) 得到B 、C 关于直线2=x 的对称点B 1、C 1l ′满足题中要求,由对称性,得到P 1、P 2关于直线2=x 的对称点:393 (,) 22P,483 (2,)3P-即为所求的点.∴这样的点P共有4个:113 (,)22P-,283 (6,)3P,393 (,) 22P,483 (2,)3P-………12分(本题其它解法参照此标准给分)。
2021年云南省高三第二次复习统一检测理综生物试题 word(含答案)

秘密★启用前【考试时间:4月21日 9:00-11:30】2021年云南省第二次高中毕业生复习统一检测理科综合能力测试注意事项:1.答卷前,考生务必用黑色碳素笔将自己的学校、姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的学校、准考证号、姓名、考场号、座位号,在规定的位置贴好条形码及填涂准考证号。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
可能用到的相对原子质量:H-1 C-12 N-14 O-16 F-19 C1-35.5 Fe-56 Ga-70第I卷(选择题,共126分)本卷共21小题,每小题6分,共126分。
一、选择题:本大题共13小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关膜蛋白的叙述,正确的是A.膜蛋白都分布在磷脂双分子层的表面B.细胞膜的功能与膜蛋白的种类和数量有关C.物质的跨膜运输都需要膜蛋白来协助完成D.膜蛋白均能与糖类结合形成糖蛋白2.下列有关生态系统物质循环和能量流动的叙述,错误的是A.生态系统中能量的输入几乎都是通过生产者的光合作用完成B.能量作为动力,使物质能够在生物群落内部不断循环往返C.能量的固定、储存、转移和释放,离不开物质的合成和分解等过程D.生态系统的能量输出大于输入,可能会破坏生态系统的稳定性3.下列关于生物学实验的叙述,错误的是A.可用抽样检测的方法调查培养液中酵母菌数目B.可用同位素标记法探究T2噬菌体的遗传物质C.可用黑藻叶观察线粒体和叶绿体的形态和分布D.可用过氧化氢酶探究pH对酶活性的影响4.下列关于细胞呼吸的叙述,正确的是A.放置时间过长的牛奶发生胀袋,是乳酸菌污染导致的B.细胞呼吸是葡萄糖在线粒体内氧化分解、释放能量的过程C.剧烈运动时,骨骼肌细胞吸收O2的速率小于释放CO2的速率D.血浆的HCO3-能与细胞呼吸产生的乳酸反应,维持血浆PH值稳定5.下图为脱落酸对某种水稻的种子萌发率影响的实验结果。
【省级联考】云南省2024届高三第二次高中毕业生复习统一检测理科综合全真演练物理试题

【省级联考】云南省2024届高三第二次高中毕业生复习统一检测理科综合全真演练物理试题一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题医用防病毒口罩的熔喷布经过驻极处理可增加静电吸附作用,某驻极处理后的口罩可以简化为下图均匀带正电竖直绝缘板。
一颗有一定质量的飞行带电颗粒在重力和静电力作用下由a点运动到b点,轨迹如图所示。
忽略空气阻力,关于该颗粒的电势能与机械能的变化情况,下列说法正确的是()A.电势能先减小后增大,机械能先减小后增大B.电势能先增大后减小,机械能先减小后增大C.电势能先减小后增大,机械能先增大后减小D.电势能先增大后减小,机械能先增大后减小第(2)题如图所示,在原点O处有一个波源,从时刻位于波源处的质点从平衡位置开始沿y轴正方向做简谐运动,振幅为4cm,产生的简谐横波在均匀介质中沿x轴正向传播。
时,平衡位置坐标为的质点P开始运动,此时波源质点的振动位移为2cm,对该简谐波,下列说法错误的是( )A.该列简谐横波在介质中传播的最大波长为36mB.该列简谐横波的传播速度为C.周期可能为6sD.周期为可能第(3)题如图,实线表示某固定场源点电荷电场中的三条电场线,虚线为一正离子仅在电场力作用下从P点运动到Q点的轨迹,下列判定正确的是( )A.场源点电荷带正电B.正离子在P点的加速度大于在Q点的加速度C.正离子在P点的速度小于在Q点的速度D.正离子在P点的电势能大于在Q点的电势能第(4)题某行星的密度为地球的,半径为地球的,那么在此行星上的“第一宇宙速度”与在地球上的第一宇宙速度大小之比为( )A.4∶1B.1∶4C.6∶1D.1∶6第(5)题一列向右传播的简谐横波在时刻的波形图如图所示,A、B两质点间距为,B、C两质点的平衡位置间距为,时质点C恰好向下通过平衡位置,则该波的最小波速为()A.B.C.D.第(6)题近年来,人们在探索月球、火星的同时,开始关注金星,它是太阳系的八大行星中从太阳向外的第二颗行星,也是距离地球最近的行星,如图所示。
2024届云南省红河州高中毕业生第二次复习统一检测英语试卷

2024届云南省红河州高中毕业生第二次复习统一检测英语试卷一、听力选择题1. What are the speakers mainly talking about?A.A flight.B.A vacation.C.The sunset.2. What did Alicia do?A.Received a call.B.Had an interview.C.Got a job.3. When did Lucy get to school?A.At 2:00.B.At 2:15.C.At 2:30.4. How long will the registration last?A.One hour.B.One and a half hours.C.One hour and forty minutes.5. What is the probable relationship between the speakers?A.Patient and nurse.B.Hostess and audience.C.Airline passenger and air hostess.二、听力选择题6. 听下面一段较长对话,回答以下小题。
1. Where did the woman see the guest speaker?A.In the gym.B.In the hallway.C.In the classroom.2. How many presentations will the speakers listen to?A.One.B.Two.C.Three.3. What will the final speaker talk about?A.Travel safety.B.Road safety.C.Classroom safety.4. Which class did the woman take?A.Wood Working.B.Metal Working.C.Cooking.7. 听下面一段较长对话,回答以下小题。
云南省大理州2024届高中毕业生第二次复习统一检测数学试卷(附答案)

云南省大理州2024届高中毕业生第二次复习统一检测数 学(全卷四个大题,共22个小题,共6页;满分150分,考试用时120分钟)考生注意:1.答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.第I 卷(选择题共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题所给的四个选项中,只有一项是符合题目要求的)1.已知,i x R ∈是虚数单位,则不等式1i 2x +<的解集为( )A.(B.()1,1-C.(D.()2,2-2.已知{}{}2410xax x b -+==∣,其中,a b R ∈,则b =( ) A.0 B.14或12 C.12 D.143.已知向量,,a b c均为单位向量,且0a b +=,则a与b的夹角为( ) A.π6 B.π4 C.π3 D.2π34.已知12π,cos,lgπ3a ebc -===,则( ) A.a b c << B.c b a << C.b a c << D.c a b <<5.函数()()πsin 0,0,2f x A x h A ωϕωϕ⎛⎫=++>>< ⎪⎝⎭的部分图象如图所示,则函数()π16g x f x ⎛⎫=+- ⎪⎝⎭的单调递减区间为( )A.ππ,π,2k k k Z ⎛⎫+∈ ⎪⎝⎭ B.ππ,π,2k k k Z ⎛⎫-+∈ ⎪⎝⎭C.πππ,π,22k k k Z ⎛⎫-++∈ ⎪⎝⎭D.()()()1π,1π,k k k Z -+∈6.如图,圆锥的高SO =2,AB C =是圆O 上一点,且1AC =,若SA 与BC 所成角为θ,则22sin cos 22θθ-=( )A.4 B.4- C.58 D.4-7.已知,a b 为实数,则直线0ax by -=与圆220x y ax by ++-=的位置关系是( ) A.相交且过圆心 B.相交但不过圆心 C.相离 D.相切8.若m 为函数()()2()f x m x m n x =--(其中0m ≠)的极小值点,则( )A.0m n >>B.0m n <<C.2mn m >D.2mn m <二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题所给的四个选项中,有多项符合题目要求,全部选对得5分,部分选对得2分,有选错的得0分)9.下列四个选项中,说法正确的是( )A.从人群中随机选出一人,设事件A =“选出的人患有心脏病”,B =“选出的人是年龄大于60岁的心脏病患者”,则有:()()P A P B >B.抛一枚骰子,设事件A =“掷出2点”,B =“掷出的点数不大于4点”,则有:()56P A B ⋃=C.分别抛掷两枚质地均匀的硬币,设A =“第一枚正面朝上”,B =“第二枚反面朝上”,则有:()()P B A P B =∣ D.两批同种规格的产品,第一批占50%,次品率为6%;第二批的次品率为4%,从混合产品中任取1件,设事件A =“取出的产品为合格品”,则有:()0.95P A =10.如图所示,在平行六面体1111A B C D ABCD -中,O 为正方形ABCD 的中心,11,,A A AC AB M N ==分别为线段11,A A A B 的中点,下列结论正确的是( )A.1C C∥平面OMNB.平面1A CD ∥平面OMNC.直线MN 与平面1A BD 所成的角为45D.1OM D D ⊥11.激活函数是神经网络模型的重要组成部分,是一种添加到人工神经网络中的函数.tanh 函数是常用的激活函数之一,其答案解析式为()221e 1exxf x ---=+,则( ) A.tanh 函数是奇函数 B.tanh 函数是减函数C.对于实数a ,当01a <<时,函数()y f x a =-有两个零点D.曲线()y f x =存在与直线20x y +=垂直的切线12.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为12F F 、,离心率为2,.过2F 作直线l 交双曲线C 的右支于A B 、两点,若H G 、分别为12AF F 与12BF F 的内心,则( )A.双曲线C的焦距为B.点H 与点G 均在同一条定直线上 C.直线HG 不可能与l 平行D.HG的取值范围为3⎡⎫⎪⎢⎪⎣⎭第II 卷(非选择题共90分)三、填空题(本大题共4小题,每小题5分,共20分)13.已知某种商品的广告费支出x (单位:万元)与销售额y (单位:万元)之间有如下表对应数据:x 1 3 4 5 7 y1520304045根据表中数据得到y 关于x 的经验回归方程为5ˆˆ5.yx a =+,则当7x =时,残差为__________.(残差=观测值-预测值)14.已知抛物线()2:,0C y mxm R m =∈≠过点()1,2P ,则拋物线C 的准线方程为__________.15.函数()12ln f x x x =--的最大值为__________.16.我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.已知长度为PQ ,取PQ 的中点1M ,以1PM 为边作等边三角形(如图1),该等边三角形的面积为1S ,再取1M Q 的中点2M ,以12M M 为边作等边三角形(如图2),图2中所有的等边三角形的面积之和为2S ,以此类推,则3S =__________,11114nk k k kS S +=+=∑__________.四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)如图,在四棱锥O ABCD -中,OA ⊥底面ABCD ,底面ABCD 是边长为2的正方形,2OA =,点M N Q 、、分别为OA BC CD 、、的中点.(1)证明:DN OQ ⊥; (2)求点D 到平面AMN 的距离. 18.(本小题满分12分)如图所示,在平行四边形ABCD 中,有:()cos 2cos AC BAC AB BC ABC ∠∠=-.(1)求ABC ∠的大小;(2)若3,BC AC ==,求平行四边形ABCD 的面积.19.(本小题满分12分)学校进行足球专项测试考核,考核分“定位球传准”和“20米运球绕杆射门”两个项目.规定:“定位球传准”考核合格得4分,否则得0分;“20米运球绕杆射门”考核合格得6分,否则得0分.现将某班学生分为两组,一组先进行“定位球传准”考核,一组先进行“20米运球绕杆射门”考核,若先考核的项目不合格,则无需进行下一个项目,直接判定为考核不合格;若先考核的项目合格,则进入下一个项目进行考核,无论第二个项目考核是否合格都结束考核.已知小明“定位球传准”考核合格的概率为0.8,“20米运球绕杆射门”考核合格的概率为0.7,且每个项目考核合格的概率与考核次序无关.(1)若小明先进行“定位球传准”考核,记X 为小明结束考核后的累计得分,求X 的分布列; (2)为使累计得分的期望最大,小明应选择先进行哪个项目的考核?并说明理由. 20.(本小题满分12分)在数列{}n a 中,1232,6,12a a a ===,且数列{}1n n a a +-是等差数列. (1)求{}n a 的通项公式;(2)若(1)nn n b a =-,设数列{}n b 的前n 项和为n T ,求20T .21.(本小题满分12分)已知函数()2ln ,f x ax x a R =-∈.(1)讨论函数()f x 的单调性;(2)设()()0,a g x f x bx >=+,且1x =是()g x 的极值点,证明: (i )1x =时,()g x 取得极小值; (ii )ln 20a b +<. 22.(本小题满分12分)已知点()()1,0,1,0A B -,点D 是圆22:4O x y +=上一动点,动点E 满足2BE BD = ,线段BE 的中垂线与直线AE 交于点P .(1)求点P 的轨迹C 的标准方程;(2)已知点Q 在直线:40l x -=上,过点Q 作曲线C 的两条切线,切点分别为M N 、,若四边形OMQN 的面积S ,求MN S的最大值,并求出此时Q 点的坐标.参考答案一、单选题(本大题共8小题,每小题5分,共40分)题号 1 2 3 4 5 6 7 8 答案ABCBABDC1.【答案解析】由于1i 2x +<2<,解得:x <<.故选A.2.【答案解析】由题意知:b 为方程2410ax x -+=的根,当0a =时,14b =;当0a ≠时,有24101640ab b a ⎧-+=⎨-=⎩,此时12b =,故选B.3.【答案解析】因为||||||1a b c === ,且0a b ++= ,则a b += ,两边平方可得222||||23||a b a b c ++⋅= ,即21a b ⋅=,所以1,2a b a ⋅= 与b 的夹角为π3,故选C.4.【答案解析】因为1212a eb -==>=,所以a b >;又1lgπ2c =<=即b c >,故c b a <<,故选B.5.【答案解析】依题意可得31A h A h +=⎧⎨-+=-⎩,解得21A h =⎧⎨=⎩,又311ππ3π41264T =-=,所以2ππT ω==,解得2ω=,所以()()2sin 21f x x ϕ=++,又函数过点π,36⎛⎫⎪⎝⎭, 所以ππ2sin 21366f ϕ⎛⎫⎛⎫=⨯++=⎪ ⎪⎝⎭⎝⎭,即πsin 13ϕ⎛⎫+= ⎪⎝⎭,所以ππ2π,Z 32k k ϕ+=+∈,所以π2π,Z 6k k ϕ=+∈,又π2ϕ<,所以π6ϕ=,所以()π2sin 216f x x ⎛⎫=++ ⎪⎝⎭.故()2cos2g x x =,其单调递减区间为ππ,π,2k k k Z ⎛⎫+∈ ⎪⎝⎭.故选A. 6.【答案解析】建立如图所示的空间直角坐标系得:()()0,1,0,0,1,0A B -,(1,,,022S C ⎛⎫- ⎪ ⎪⎝⎭,而,AS BC 的夹角为π,02θθ<≤又(3,,,022AS BC ⎛⎫==- ⎪ ⎪⎝⎭则cos 4||||AS BC AS BC θ⋅== ,由于22sin cos cos 224θθθ-=-=-,故选B.7.【答案解析】圆()222200x y ax by a b ++-=+>,可化为2222224a b a b x y +⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭, 故圆心为,22a b ⎛⎫-⎪⎝⎭,半径r =,而圆心到直线0ax by -=的距离d r ===, 所以直线0ax by -=与圆220x y ax by ++-=相切,故选D.8.【答案解析】若m n =,则()3()f x m x m =--为单调函数,无极值点,不符合题意,故m n ≠.由于()()()32f x m x m x m n =--++',且m n ≠,故()0f x '=有两根为x m =或23m nx +=①当0m>时,若m 为极小值点,则需满足:23m nm +<,故有0m n << ②当0m<时,若m 为极小值点,则需满足:23m nm +>,故有:0m n >>,故A ,B 选项错误,综合①②有:2mn m >,故选C.二、多选题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)题号 9 10 11 12 答案ACDBCDACBD9.【答案解析】对于A ,设事件C =“选出的人年龄大于60岁”,则有:()()()()()1P AC P B P CA P A P A ==<∣故()()P A P B >,故A 正确;对于B ,事件A 与B 不互斥,故()()()()23P A B P A P B P AB ⋃=+-=,故B 不正确; 对于C ,事件,A B 相互独立,则()()P BA PB =∣,所以C 正确; 对于D ,根据全概率公式可得()0.50.940.50.960.95P A =⨯+⨯=,故D 正确故选ACD.10.【答案解析】如图所示,对于A ,若1C C ∥平面OMN ,因为1C C ∥1A A ,则1A A ∥平面OMN ,或1A A ⊂平面OMN ,而1A A 和平面OMN 相交,故A 错;对于B ,因为,M N 分别为线段11,A A A B 的中点,所以MN∥AB ∥,CD MN ⊄平面1,ACD CD ⊂平面1A CD ,所以MN ∥平面1A CD ,因为,O N 分别为线段1,BD A B 的中点,所以ON ∥1,A D ON ⊄平面11,ACD A D ⊂平面1A CD ,所以ON ∥平面1,,ACD MN ON N MN ⋂=⊂平面OMN ,ON ⊂平面OMN ,所以平面1A CD ∥平面OMN ,故B 正确;对于C ,由于AC BD ⊥,且11A A A C =,故1AC A O ⊥,而1A O BD O ⋂=,故AO ⊥平面1A BD ,而MN∥AB ,故MN 与平面1A BD 所成的角即为AB 与平面1A BD 所成的角,即为45ABO ∠= ,故C 正确.对于D ,设11A A AC AB a ===,则AC =,显然22211A A A C AC +=,故11AC A A ⊥,由MO ∥1A C ,所以1MO A A ⊥,而1D D ∥1A A ,所以1OM D D ⊥,故D 正确.故选BCD.11.【答案解析】()2211e x f x -=-+定义域为()()2222R,1101e 1ex xf x f x --+=-+-=++, 所以()2211e xf x -=-+为奇函数,A 正确;()()2224e 01e xxf x --=>+'恒成立,所以tanh 函数是增函数,故B 错误;当0x >时,()22111e xf x -=-<+恒成立,所以()y f x =在(),0∞-上单调递减,在()0,∞+上单调递增,且()[)0,1y f x =∈,故当01a <<时,()y f x =与直线y a =有两个交点,故函数()y f x a =-有两个零点. C 正确;()()222224e 41e e 21e xx x xf x ---'==≤=+++,且()(]0,1f x '∈, 所以()2f x '≠,故曲线()y f x =不存在与直线20x y +=垂直的切线.D 错误. 故选AC.12.【答案解析】设双曲线C 半焦距为c ,双曲线C 的渐近线方程为by x a=±,即0bx ay ±=,双曲线C 的右焦点()2,0F cb ==,由题意知2c e a ====,所以22,a c ===,故双曲线C 的方程为22126x y -=, 故双曲线C的焦距为,故A 不正确;对于B 选项,记12AF F 的内切圆在边1212AF AF F F 、、上的切点分别为M N E 、、,由切线长定理可得1122,,AM AN F M F E F N F E ===, 由122AF AF a -=,即()122AM MF AN NF a +-+=, 得122MF NF a -=,即122F E F E a -=,记H 的横坐标为0x ,则()0,0E x ,于是()002x c c x a +--=,得0x a =,同理内心G 的横坐标也为a ,故HG x ⊥轴,即H G 、均在直线x a =上,故B 正确; 对于C 选项,当l 与x 轴垂直时,HG ∥l ,故C 错误; 对于D 选项,设直线AB 的倾斜角为θ,则22OF G θ∠=,2902HF O θ∠=- (O 为坐标原点),在2HF G 中,()()sin 90sin 22tan tan 9022cos cos 9022HG EG HE c a c a θθθθθθ⎡⎤⎛⎫- ⎪⎢⎥⎡⎤⎛⎫⎝⎭⎢⎥=+=-+-=-+ ⎪⎢⎥⎛⎫⎝⎭⎢⎥⎣⎦- ⎪⎢⎥⎝⎭⎣⎦ ()()()sin cos 1222sin sin cos sin sin cos2222c a c a c a θθθθθθθθ⎛⎫ ⎪-+=-=-⋅= ⎪ ⎪⎝⎭ 由于直线l 与C 的右支交于两点,且C的一条渐近线的斜率为ba=60 , 结合图形可知60120θ<<,即sin 12θ<≤,所以,sin 3HG θ⎡⎫=∈⎪⎢⎪⎣⎭,故D 正确.故选BD. 三、填空题(本大题共4小题,每小题5分,共20分)题号1314151613.【答案解析】()()11134574,15203040453055x y =⨯++++==⨯++++=, 故回归直线方程过点()4,30,代入5ˆˆ5.yx a =+,可得ˆˆ30 5.54,8a a =⨯+=, 当7x =时, 5.57838.5846.5ˆy=⨯+=+=, 所以残差为4546.5 1.5-=-,故答案为:-1.5.14.【答案解析】由题可得,2212m m =⋅⇒=,故221:22C y x x y =⇒=. 故拋物线C 的准线方程为18y =-.故答案为:18y =- 15.【答案解析】由题可得,当1x ≥时,()()112ln ,20f x x x f x x=--∴--'=< ()f x ∴在[)1,∞+为减函数,()max ()11f x f ∴==-;当01x <<时,()()12112ln ,2x f x x x f x x x-+=-+∴=-+=', ∴当10,2x ⎛⎫∈ ⎪⎝⎭时,()0f x '>,当1,12x ⎛⎫∈ ⎪⎝⎭时,()0f x '<,max 11()ln ln222f x f ⎛⎫∴===- ⎪⎝⎭,综上可知,max ()ln2f x =-.故答案为:ln2-.16.【答案解析】由题可得,11sin6024S ==, 从第2个等边三角形起,每个三角形的面积为前一个三角形面积的14, 故可构成一个以1S 为首项,14为公比的等比数列,则12111141111111444414n n nn S S S -⎡⎤⎛⎫-⎢⎥ ⎪⎡⎤⎤⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫⎣⎦=++++==-⎢⎥⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎥⎣⎦⎣⎦- ,所以3311464S ⎡⎤⎛⎫=-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦. 1441nn n S =-11111111114414144414134141n n n n n n n n n n n S S ++++++∴⋅⋅==⨯⨯---- 111194141n n +⎛⎫=⨯- ⎪--⎝⎭112231111111111149414141414141nk n n k k k S S ++=+⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-++- ⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦∑ 11119341n +⎛⎫=⨯- ⎪-⎝⎭故答案为:364S =, 1111111149341nk n k k k S S ++=+⎛⎫=⨯- ⎪-⎝⎭∑ 四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.【答案解析】(1)证明:由题意可知AO AB AD 、、两两垂直,以点A 为坐标原点,AB AD 、、AO 所在直线分别为x y z 、、轴,建立如图所示的空间直角坐标系A xyz -,从而可得以下各点的坐标.()()()()()()0,0,0,2,0,0,0,2,0,0,0,2,0,0,1,2,1,0A B D O M N , ()1,2,0Q ,则()()2,1,0,1,2,0DN OQ =-=()211200,DN OQ DN OQ ∴⋅=⨯+-⨯+=∴⊥所以DN OQ ⊥(2)解:设平面AMN 的法向量为(),,n x y z =,则00n AM n AN ⎧⋅=⎪⎨⋅=⎪⎩ ,即020z x y =⎧⎨+=⎩,令1x =,可得平面DMN 的法向量()1,2,0n =-,故点D 到平面AMN的距离5DN n d n ⋅===. 18.【答案解析】(1)由()cos 2cos AC BAC AB BC ABC ∠∠=-,由正弦定理得,2sin cos sin cos sin cos ACB ABC BAC ABC ABC BAC ∠∠∠∠∠∠=+()()2sin cos sin sin πsin ACB ABC BAC ABC ACB ACB ∠∠∠∠∠∠∴=+=-=,又()0,πACB ∠∈ ,则1sin 0,cos 2ACB ABC ∠∠≠∴=, ()π0,π,;3ABC ABC ∠∠∈∴=(2)在平行四边形ABCD中,π,3,3ABC BC AC ∠===, 在ABC 中,由余弦定理得,2222cos AC AB BC AB BC ABC ∠=+-⨯,即2179232AB AB ⎛⎫=+-⨯⨯⨯ ⎪⎝⎭解得:1AB =或2AB =,当1AB =时,平行四边形ABCD 的面积:1π122sin 21323222ABC S S AB BC ==⨯⨯=⨯⨯⨯⨯= 当2AB =时,平行四边形ABCD 的面积:1π122sin 2232322ABC S S AB BC ==⨯⨯=⨯⨯⨯⨯= . 19.【答案解析】(1)由已知可得,X 的所有可能取值为0,4,10,则()()()010.80.2,40.810.70.24P X P X ==-===⨯-=,()100.80.70.56P X ==⨯=,所以X 的分布列为:X 0 4 10 P0.20.240.56(2)小明应选择先进行“定位球传准”考核,理由如下: 由(1)可知小明先进行“定位球传准”考核,累计得分的期望为()00.240.24100.56 6.56,E X =⨯+⨯+⨯=若小明先进行“20米运球绕杆射门”考核,记Y 为小明的累计得分,则Y 的所有可能取值为0,6,10,()()()010.70.3,60.710.80.14P Y P Y ==-===⨯-=, ()100.70.80.56P Y ==⨯=,则Y 的期望为()00.360.14100.56 6.44E Y =⨯+⨯+⨯=,因为()()E X E Y >,所以为使累计得分的期望最大,小明应选择先进行“定位球传准”考核. 20.【答案解析】(1)因为21324,6a a a a -=-=,所以()32212a a a a ---=.所以数列{}1n n a a +-是首项为4,公差为2的等差数列,所以()142122n n a a n n +-=+-=+.当2n …时, ()()()()2112211221222n n n n n a a a a a a a a n n n n ---=-+-++-+=+-++⨯+=+⋅当1n =时,12a =也满足上式.所以2n a n n =+.(2)由(1)知,()()2(1)(1)1nn n b nn n n =-+=-+.当*2,n k k N =∈时,()()()()21223344511224;2n n n T n n n n n +=-⨯+⨯-⨯+⨯---++=+++=()20202022202T ⨯+∴==21.【答案解析】(1)由函数()2ln f x ax x =-知,定义域为()0,∞+,()21212ax f x ax x x-=-='∴, 当0a …时,()0f x '<恒成立,()f x 在()0,∞+单调递减,当0a >时,()00,()022f x x f x x a a''<⇒<<>⇒>,所以()f x 在0,2a ⎛⎫⎪ ⎪⎝⎭单调递减,在,2a ∞⎛⎫+ ⎪ ⎪⎝⎭单调递增;(2)()()2ln g x f x bx ax x bx =+=-+,()12g x ax b x=-+',由条件()1210g a b =-+=',所以12b a =-, (i )()()()()221212111212ax a x ax x g x ax a x x x'+--+-=-+-==, 由于0a >,故01x <<时,()()0,g x g x '<单调递减, 当1x >时,()()0,g x g x '>单调递增, 所以1x =时,()g x 取极小值成立,(ii )设()()1ln 2ln 24,4h a a b a a h a a '+=+=-=-,易知()h a 在10,4⎛⎫⎪⎝⎭单调递增, 1,4∞⎛⎫+ ⎪⎝⎭递减. 故()11ln404h a h ⎛⎫=-<⎪⎝⎭…,故ln 20a b +<. 22.【答案解析】(1)由2BE BD =,可知D 为线段EB 的中点, 所以PD 是线段EB 的垂直平分线,故PE PB =因为点P 在直线AE 上,所以242PA PB PA PE AE OD AB +=+===>=.由椭圆的定义可知,P 点轨迹是以()()1,0,1,0A B -为焦点,以4为长轴长的椭圆,即24,1a c ==,解得2,a b ==,另当D 点坐标为()2,0±时,P 与D 重合,不符合题意,故C 的标准方程为()221243x y x +=≠±(2)设()()()1122,,,,4,M x y N x y Q t ,所以曲线22:143x y C +=点()11,M x y 处的切线QM 的方程为11143x x y y ⋅⋅+=,又因为切线QM 过()4,Q t ,所以1113t y x ⋅+=. 同理可得2213t y x ⋅+=,故直线MN 的方程为13tyx +=.所以12MN y =-.设点,M N 到直线OQ 的距离分别为12,d d 因为直线OQ 的方程为40tx y -=,所以12d d ==又因为,M N 在直线OQ 的两侧, 所以()121122114422S OQ d d tx y tx y =+=+=--+ 由于点,M N 的坐标满足方程13ty x +=,即有:11221313ty x ty x ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得:()12123tx x y y -=-,故可得: 211222111444223t S tx y tx y y y ⎛⎫=--+=+- ⎪⎝⎭,所以2221223121423MN S t t y y ====++- ⎪⎝⎭,令3u =≥,则23MNSu u=+, 令()33y u u u =+≥,故可知()33y u u u=+≥的最小值为4, 当且仅当3u =时,等号成立,此时0t =故2132MNSu u=≤+,其最大值为12,此时Q 点的坐标为()4,0.。
云南省高三数学第二次毕业生复习统一检测理
2011年云南省第二次高中毕业生复习统一检测理科数学本试卷分第I卷(选择题)和第I I卷(非选择题)两部分。
第I卷1至3页,第I I卷4至6页。
考试结束后,将本试卷和答题卡一并交回。
满分150分,考试用时120分钟。
第I卷(选择题,共60分)注意事项.1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
答在试卷上的答案无效。
参考公式:如果事件A、B互斥,那么球的表面积公式P(A+B)=P(A) + P(B)如果事件A、B相互独立,那么其中R表示球的半径P(A • B) = P(A) • P(B)球的体积公式如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中事件A恰好发生k次的概率其中R表示球的半径本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一.选择题(1)已知的定义域为实数集如果=2011,那么=(A)3(B) 2011(C)3 x (D)2011x(2)在的展开式中,的系数等于(A)80(B)-80(C)40(D)-40(3) 已知数列是公差等于2的等差数列,如果a4是a2与a5的等比中项,那么的值等于(A)4(B)-2(C)-8(D)-14(4) 已知n是正整数,实数a是常数,若,则a的值是(A)(B)(C)和(D)和(5) 曲线在点(一1,-)处的切线的倾斜角等于(A) (B)(C)(D)一(6) 如果点(,-2)在椭圆上,那么椭圆的离心率等于(A) (B)(C)(D)(7) 如果,那么等于(A) -2(B) - 1(C)1(D)2(8) 己知直线把圆分成两段弧,这两段弧长之差的绝对值等于(A) (B)(C) (D)(9) 在下列给出的四个函数中,与互为反函数的是(A)(B)(C)(D)(10)以抛物线X2=8y上的一点M为圆心作圆M ,如果圆M经过抛物线的顶点和焦点,那么圆M的半径等于(A) 1/2 (B) 2(C) 5/2 (D) 3(11)己知球O在一个棱长为的正四面体内,如果球0是该正四面体内的最大球,那么球O的表面积等于(A) (B)(C) (D)(12)己知N是自然数集,常数a,b都是自然数,集合,集合,如果,那么以(a,b)为坐标的点一共有(A) 42 个(B) 30个(C) 25 个(D) 20 个2011年云南省第二次高中毕业生复习统一检测理科数学(非选择题,共90分)注意事项:本卷共3页,10小题,用黑色碳素笔将答案答在答题卡上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年云南省第二次高中毕业生复习统一检测 文科综合能力测试•地理学科质量分析
云南省2010年云南省第二次高中毕业生复习统一检测文科综合能力测试,地理学科基本情况及教学建议如下: 一、基本情况 表1:全省基本情况及分数段统计
分数段 人数 分数段 人数 100~90 297 49~40 15822 89~80 3163 39~30 8435 79~70 9877 29~20 3156 69~60 18255 19~10 698 59~50 19597 9~0 130
实考人数:79430 满分值:100 最低分: 0 平均分:54.02 最高分:100 及格率: 39.77 本次统测的统计直方图如下: 高中毕业生复习统一检测文综之地理抽样分数段分布表050100150200250300
0-910-1920-2930-3940-4950-5960-6970-7980-8990-100分数段学生数
二、试题分析 (一)试题结构、知识点分布、考查内容及能力要求
表2: 题型 问 题 题号 分 值 呈 现 方 式 考 查 内 容 能 力
要 求
选 择 题
交通运输线判读 1—3 12分 某地交通运输线路示意图及图例 交通运输线的分布规律、交通运输线与地形的关系 读图分析能力、空间想象能力、区域定位能力、分
析推理和综合判断能力。
极地地区天气图判读 4—6 12分 极地地区天气图 及图例 锋面气旋对天气的影响、天气图的判读、不同季节各区域地理现象的呈现、气旋运动规律及半球判断 从图中提炼和获取信息的能力、区域空间定位能力、读图分析能力、整合地理信息的能力、分析推理和综合判断的能力
黑海附近区域 7—9 12分 黑海附近区域 示意图及图例、 区域定位、盐度分布规律、文化与文化景观、黑海附近区域特征分析 读图观察能力、区域定位能力、知识的迁移运用能
力、调动和运用知识的能力、区域特征描述能力。 日影的计算与运用
10—11 8分 文字材料、太阳历广场示意图 正午太阳高度角的计算与运用、位置及方向的判断、地球公转的地理意义 读图观察与分析能力、从图文材料中提炼和获取信息的能力、调动和运用知
识的能力、分析推理和综合判断的能力、整合地理信息的能力。
综 合 题 澳大利亚水资源、农业、人口分布特点分析 36 (1) 10分 (2) 8分 (3) 10分 (4) 8分 共36分 澳大利亚降水、地表水与地下水局部分布图及图例,澳大利亚农牧业局部分布图及图例 空间定位、区域分析(1)根据澳大利亚东南部及中部的降水、地表水、地下水分布图来分析极干旱时会带来的问题。 (2)根据澳大利亚局部农牧业分布图分析农业带类型及农业发展的区位因素。 (3)农业可持续发展的可行性分析。 (4)根据降水、地表水与地下水分布状况分析该地人口、城市分布特点及原因。 空间定位能力、区域特征描述能力、从图文材料中提炼和获取信息的能力、区域分析能力、知识整合归纳能力、分析推理和综合判断能力、阐释地理问题的能力
中国气象灾害和地质灾害空间分布特点及成灾自然原因
39 (1)10分 (2)10分 共20分 季风区与非季风区、内外流区、半干旱与半湿润地区分界线示意图 (1)中国地质灾害多发地区成灾自然原因。 (2)沙尘暴天气空间分布特点及其成灾的自然原因。 记忆能力、读图观察与分析能力、从图文材料中提炼和获取信息的能力、调动和运用知识的能力
表3: 自然地理 人文地理 通过对表2与表3的分析,本套试卷符合“文综综合能力测试”的考核目标与要求:以能力测试为主导,考查考生地理基础知识、基本技能的掌握程度和综合运用所学知识分析、解决实际问题的能力。考查了获取和解读信息;调动和运用知识;描述和阐释事物;论证和探讨问题四个能力层次要求。
(二)试题特点 1.知识抽样,能力覆盖。 试题考核内容涉及交通运输线的布局、天气图的判读、海水盐度分布特征、区域特征分析、正午太阳高度角的计算与运用、农业区位因素分析及区位因素的发展变化、城市人口分布的区位因素、可持续发展、水资源对人类活动的影响、自然灾害的分布与成因。对于备考多时的学生来说,考到的知识点不算多,但试卷对高考考纲要求的四个考核目标的体现却一个不少。从宏观上掌握知识体系,注意知识的综合以及对结构的把握。 2.图像简明、题干精炼。 本卷题目选材围绕中学地理主干知识进行设计,使用7幅图,类型有:示意图、等值线图、区域图、景观图等。试题内容的时间性、空间性、综合性强,相对于文字表述来说,以图表形式提供信息更具有直观、形象的特点。不仅便于阅读,而且能考查学生的读图、用图能力,注意空间地理事物的结构联系,发展变化。培养学生掌握图形语言所承载的信息(如某地位置),提取定性和定量的信息并找出相关联系(如从位置联系到地形、气候、经济等),实现图形语言的基本技能训练。
选择题 第3、4、5、6、7、10、11题,共28分 第1、2、8、9题, 共16分 综合题 36题(1)、39题(3)、(4),共30分 36题(2)、(3)、(4), 共26分 比 例 58% 42% 3.凸显课改,能力立意。 “学习生活中的地理,学习地理中的生活”。本卷提供给学生与其生活和周围世界密切相关的地理知识,侧重基础性的地理知识和技能,增强学生的生存能力。材料新颖,切入巧妙,创设解题情境,考查学生的能力。将知识与能力、过程与方法、情感态度价值观的三维目标灵活运用到试题的考查中。 材料来源广泛,且是密切同现实联系在一起,为学生展开广阔的想象和思维能力空间提供平台。如4~6题,从天气图的阅读来分析天气状况,考查了学生知识迁移和运用能力,并考查学生对新问题的应变能力、审题能力、对问题的思维能力、表述能力和稳定的心态。重视学生推理假设能力的培养。 4.切中薄弱,强化思维。 结合学生平时学习中较容易出现的问题,如审题粗心、不重基础、不求甚解等问题,试题设计予以关注。本卷以高考四项能力,即获取和解读信息,调动和运用知识,描述和阐释事物,论证和探讨问题入手,利用图文材料,引导学生分析每一个细节和隐藏信息,分析每一个选项涉及的知识内容,分析试题内容与教材知识的联系、分析参考答案体现的知识和原理,帮助学生在所给材料和教材内容之间快速搭建思维通道。 5.隐含热点,关注拓展。 如分析澳大利亚干旱区水资源利用及农业可持续发展等问题,关注到当前西南地区的严重旱情。对我国自然灾害的考查,与当前全球灾害频发相关。
三、学生答题情况抽样分析 1.选择题答题情况抽样分析 表4: 题 号 题中有效 信 息 正确 答案 各选项选 答率(%) 平均分 难度 错 因 分 析 1 图例显示两条公路,用图显示一条为之字形路线,一条为直线形。 A A:82.06 B:9.09 C:5.33 D:3.52 未(多)选:0 3.28 0.82 本题做答较好。出错的原因主要是对公路布局情况掌握不好,不了解道路建设和布局原则。 2 B A:0.73 B:94.67 C:1.94 D:2.67 未(多)选:0
3.79 0.95 本题做答较好,少数考生出错是不了解“之”字型道路的地形特点。
3 D A:40.97 B: 6.67 C: 15.27 D:36.97 未(多)选:0.12 1.48 0.37 该题出错率较高。主要原因是考生不能根据图中公路和隧道的分布特点推知各处地形的特点,没有掌握乡村公路的修建不会通过山顶,山谷不用修建隧道,所以错选A、C。
4 题干显示:某日极地附近风向示意图。图中有经度,等压线、风向和锋面。由图中的等压线和风向可推知该地为北极点附近。考查天气系统 A A:57.58 B:3.76 C: 5.09 D:33.45 未(多)选:0.12 2.3 0.58 本题属于锋面气旋的基础知识题。考生出错在于:(1)没有掌握天气系统的判读规律,不会由风向推知所在半球的位置;(2)不了解锋面气旋的运动规律。
5 C A:11.76 B:16.85 C:51.03 D:20.24 未(多)选:0.12 2.04 0.51 本题考查锋面系统的天气状况,也属于基础知识题,出错的原因主要在于没有掌握冷锋和暖锋的运动特点及其对天气的影响。 A:5.58 B:13.7 C:65.94
2.64 0.66 本题是常规题目,出错原因在于区域定
位的不准确,以及对此季节题中各地区 6 图的阅读。 C D:14.67 未(多)选:0.12 域特征掌握不清楚。 7 利用经纬度判读,示意图显示为黑海附近地区。 B A:7.76 B:63.27 C:13.33 D:15.64 未(多)选:0 2.53 0.63 出错原因在于:(1)考生对示意图中的有效信息提取和获取不好,如该处是相对封闭海域,没有暖流;(2)不会运用所学的盐度的知识对陌生区域进行推理、分析。
8 A A:85.09 B:7.39 C:1.09 D:6.18 未(多)选:0.24 3.4 0.85 本题做答较好。主要是迁移考查文化景观、文化区及文化扩散的理解。出错原因主要是考生对上述概念和特征没有一个清晰的了解。
9 D A:5.82 B:22.18 C:13.21 D:58.55 未(多)选:0.24 2.34 0.59 本题考查该区域的特征。考生主要是对附近地区没有一个清晰的认识,以及不能根据附近区域特征来推理、分析本区域的特征。
10 题干显示太阳历广场中间的雕像柱高及影子的方向、长度。北京时间为当地的正午。图示显示太阳历广场的 D A:24.97 B:21.7 C:26.67 D:26.55 未(多)选:0.12 1.06 0.27 本题出错率较高。出错原因主要是:(1)对太阳视运动知识掌握不牢;(2)从题目中分析、提取信息能力薄弱;(3)不能综合运用上述知识解决问题;(4)对区域位置掌握不好。可根据“影长从不超过雕像高”和影长最短时间推算出该地经纬度,再判断该地位于哪个省区。
A A:30.06 B:8.85 1.2 0.3 本题出错率较高。出错原因主要是:(1)对太阳视运动的知识没有清晰的认识,
