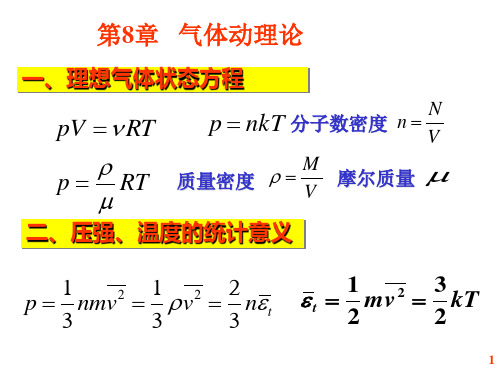
理想气体状态方程与分子动理论
理想气体的分子动理论气体分子的运动与理想气体定律

理想气体的分子动理论气体分子的运动与理想气体定律理想气体的分子动理论与气体分子的运动气体是一种物质的形态,也是我们生活中经常接触到的物质。
了解气体分子的运动和理论,能够帮助我们更好地理解气体的性质和行为。
本文将介绍理想气体的分子动理论,并探讨气体分子在空间中的运动方式以及与理想气体定律的关系。
一、理想气体的分子动理论理想气体的分子动理论是描述气体分子运动行为的理论模型。
根据分子动理论,气体分子是以高速无规则的方式在空间中运动的。
以下是气体分子的运动特征:1. 气体分子运动无规则性:气体分子在空间中以高速运动,并且没有固定的运动轨迹。
分子之间相互碰撞,这种碰撞是弹性碰撞,没有能量的损失。
2. 气体分子间的相互作用力可忽略不计:气体分子之间的相互作用力非常微弱,可以忽略不计。
这个假设的前提是气体分子之间的距离相对较远,而且气体分子体积相对较小。
3. 气体分子的速度服从麦克斯韦速度分布定律:根据麦克斯韦速度分布定律,气体分子的速度符合高斯分布(也称为正态分布),其中大多数分子具有平均速度,速度分布呈现钟形曲线。
二、气体分子的运动方式理想气体分子的运动方式可以通过分子运动学理论进行研究。
以下是气体分子的运动方式:1. 直线运动:气体分子在空间中以直线的方式运动。
当碰撞到容器壁或其他分子时,会发生反弹,继续直线运动。
2. 碰撞运动:由于气体分子之间的无规则运动,分子之间会发生碰撞现象。
这种碰撞是弹性碰撞,即碰撞后没有能量损失。
3. 自由平均路径:气体分子在碰撞之间的平均路径称为自由平均路径。
自由平均路径受气体分子的浓度和温度的影响。
三、气体分子的运动与理想气体定律的关系理想气体定律是描述理想气体状态的数学表达式,包括波义耳定律、查理定律和盖-吕萨克定律。
这些定律可以通过气体分子的运动来解释。
1. 波义耳定律:波义耳定律描述了气体压强与温度之间的关系。
根据理论分析,当气体分子碰撞容器壁时会产生压力,而压强与温度成正比。
第四章气体动理论总结

第四章⽓体动理论总结第四章⽓体动理论单个分⼦的运动具有⽆序性布朗运动⼤量分⼦的运动具有规律性伽尔顿板热平衡定律(热⼒学第零定律)实验表明:若 A 与C 热平衡 B 与C 热平衡则 A 与B 热平衡意义:互为热平衡的物体必然存在⼀个相同的特征--- 它们的温度相同定义温度:处于同⼀热平衡态下的热⼒学系统所具有的共同的宏观性质,称为温度。
⼀切处于同⼀热平衡态的系统有相同的温度。
理想⽓体状态⽅程: 形式1:mol M PV =RT =νRTM形式2:222111T V p T V p =形式3: nkT P =n ----分⼦数密度(单位体积中的分⼦数) k = R/NA = 1.38*10 –23 J/K----玻⽿兹曼常数在通常的压强与温度下,各种实际⽓体都服从理想⽓体状态⽅程。
§4-2 ⽓体动理论的压强公式VNV N n ==d d 1)分⼦按位置的分布是均匀的2)分⼦各⽅向运动概率均等、速度各种平均值相等kj i iz iy ix iv v v v ++=分⼦运动速度单个分⼦碰撞器壁的作⽤⼒是不连续的、偶然的、不均匀的。
从总的效果上来看,⼀个持续的平均作⽤⼒。
2213212()323p nmvp n mv n ω===v----摩尔数R--普适⽓体恒量描述⽓体状态三个物理量: P,V T 压强公式122ω=mv理想⽓体的压强公式揭⽰了宏观量与微观量统计平均值之间的关系,说明压强具有统计意义;压强公式指出:有两个途径可以增加压强 1)增加分⼦数密度n 即增加碰壁的个数2)增加分⼦运动的平均平动能即增加每次碰壁的强度思考题:对于⼀定量的⽓体来说,当温度不变时,⽓体的压强随体积的减⼩⽽增⼤(玻意⽿定律);当体积不变时,压强随温度的升⾼⽽增⼤(查理定律)。
从宏观来看,这两种变化同样使压强增⼤,从微观(分⼦运动)来看,它们有什么区别?对⼀定量的⽓体,在温度不变时,体积减⼩使单位体积内的分⼦数增多,则单位时间内与器壁碰撞的分⼦数增多,器壁所受的平均冲⼒增⼤,因⽽压强增⼤。
5.分子动理论 大学物理习题答案

vp
.099v p时,x 0.99 ; v v p
vp
(2) 由归一化条件
0
v0
1 f (v) d v 1 , c d v cv 0 1 ,得 c v0 0
v0
f (v)
C
(3) v vf (v) d v v c d v
大学物理练习册—分子动理论
理想气体状态方程 5-1 一容器内储有氧气,其压强为 1.01105Pa,温度为 270C,求: (1)气体分子的数密度; (2)氧气的质 量密度; (3)氧分子的质量; (4)分子间的平均距离(设分子均匀等距分布) 。 解:(1) p nkT , n
p 1.01 105 2.44 1025 /m 3 kT 1.38 1023 (273 27)
5-4 体积 V 10 3 m 3 ,压强 p 10 5 Pa 的气体分子平均平动动能的总和为多少? 解: t N
N 3 pV kT ,其中 N 为总分子数。 p nkT kT , N 2 kT V pV 3 3 3 t kT pV 105 103 150 J kT 2 2 2
m M pV RT ,T mol M mol mR
t
3 3 M pV 3 2 10 3 3.9 105 4.0 103 kT k mol 1.38 10 23 3.88 1022 J 2 2 mR 2 2 102 8.31
2 RT 可知,在相同温度下, M mol 大的气体 v p 小, M mol
f(v) I II
所以曲线 对应氢气的分布,即 v p H 2000 m/s
理想气体状态方程及应用

理想气体状态方程及应用理想气体状态方程是描述理想气体行为的基本方程,它在物理、化学、工程等领域中得到广泛的应用。
本文将介绍理想气体状态方程的定义、推导以及常见的应用。
一、理想气体状态方程的定义理想气体状态方程又称为理想气体定律,用来描述理想气体的体积、压力和温度之间的关系。
它可以表示为以下形式:P V = n R T其中,P是气体的压力,V是气体的体积,n是气体的物质的量,R是气体常数,T是气体的温度。
二、理想气体状态方程的推导理想气体状态方程的推导基于理想气体的特性和分子动理论。
根据分子动理论,气体分子之间几乎没有相互作用力,可以看作是质点自由运动,与容器壁碰撞的过程可以看作是碰撞弹性的。
在此基础上,可以通过以下推导得到理想气体状态方程。
首先,根据牛顿第二定律可以得到气体的压力公式:P = F/A其中,F是气体分子对容器壁的作用力,A是容器壁的面积。
其次,根据分子动理论,气体分子碰撞容器壁的次数与气体的分子数成正比:F = Δp/Δt其中,Δp是气体分子对容器壁的动量变化,Δt是碰撞的时间。
再次,根据动理论的平均定理,气体分子碰撞容器壁的平均动量变化可以表示为:Δp = 2mΔv其中,m是气体分子的质量,Δv是气体分子碰撞前后速度的差值。
将以上三个式子联立可得到:P = 2mΔv/ΔtA根据体积的定义V = A Δx其中,Δx为单位时间内气体分子与容器壁碰撞的平均距离。
进一步推导可得到:P V = 2mΔv/Δt Δx A由于Δv/Δt 为气体分子碰撞容器壁的平均速度v,Δx 为气体分子碰撞容器壁的平均自由程λ,上述方程可以进一步简化为:P V = 2m v λ根据动理论的假设可以得到,气体分子的平均动能与温度成正比,即2m v^2 = 3 k T其中,k是玻尔兹曼常数。
将上两个式子联立得到:P V = N k T其中,N为气体分子的数目。
进一步推导可得到理想气体状态方程的标准形式:P V = n R T其中,n = N/N0为气体的物质的量,N0为阿伏伽德罗常数。
气体分子动理论的基本概念

F rs rt
s t
r :两个分子的中心距离 、、 s、t :正数,由实验确定。
1.第一项是正的,代表斥力; 2.第二项是负的,代表引力; 3.s,t都比较大,所以随着分子间距r的增大,分子力急剧减小。 4.有一定的有效作用距离,超出此距离,作用力可忽略。 5.s>t,所以斥力的有效作用距离比引力小。
第二章 气体分子动理论的基本概念
2.1 物质的微观模型
一、物质由大量分子所组成的论点是指宏观物体是不连续 的,它由大量分子或原子(离子)所组成的。
利用扫描隧道显微镜技术 把一个个原子排列成 IBM 字 母的照片.
分子的数密度和线度
NA 6.0221367(36) 1023 mol1
分子数密度( n ):单位体积内的分子数目.
二、物体内的分子在不停地做着无规则热运动,其剧烈程度 与物体的温度有关
由于分子之间的相互碰撞,每个 分子的运动方向和速率都在不断 地改变;任何时刻,在液体或 气体内部,沿各个方向运动的分 子都有,而且分子运动的速率有 大有小。
与物体的温度有关,温度越高,分子 的无规则运动越剧烈
扩散现象说明:一切物体(气 体、液体、固体)的分子都在不
停地运动着。
布朗运动并非分子的运动, 但它能间接反映出液体(或 气体)内分子运动的无规则 性。
为什么?
1. 为什么固体和液体的分子不会散开而能保持一定的体积? 2. 为什么固体和液体的分子不会散开而能保持一定的体积?铅 柱被切成两段,然后把两个断面对上,在两头加上不大的压力就 能使两段铅柱重新接合起来。
N NA
m
RT
RT
1 m
R M
T
12.1 理想气体的描述及其状态方程

2 T2 T2 p2 ,V1 , T p p 21 , V1 , T1 2 1 , V1 , T1
Chapter . 气体动理论 §12. 1 理想气体的描述及其状态方程 作者:杨茂田
P. 1
一、理想气体的状态参量
平衡态下,可用三个宏观状态参量描述: m-2), 帕(Pa) ) 1. 压强 p:(国际单位:牛顿/米2(N· 1 Pa = 1 N· m-2 另:大气压(atm)
pV m RT M
m M pV RT
原氧气瓶内质量: m1 M p1V1 RT 氧气瓶剩余质量: m2 M p2V2 RT M pV m 每天使用氧气质量: 3 RT 3 3
Chapter . 气体动理论 §12. 1 理想气体的描述及其状态方程 作者:杨茂田
P. 2
m1 m2 ( p1 p2 ) V1 (130 10) 30 使用的天数: n m3 p3V3 1 40 90 (天 )
1atm 1.013 10 Pa
5
温 p ,V , T 度
计 泡 水
水汽
2. 体积V:(国际单位:米3 (m3)
冰
1 m 1 10 L
3
3
Chapter . 气体动理论 §12. 1 理想气体的描述及其状态方程 作者:杨茂田
P. 1
3. 温度T: 宏观上反映物体的冷热程度,微观上反映 物质分子热运动的剧烈程度。 温度的数值方法称作温标。 绝对温标T:水的三相点温度为273.16 K 。
2 2 2 v v v 2 N v 2 v 1 N N 2 2 2 2 2 2 (v12x v12y v12z ) (v2 v v ) ( v v v x 2y 2z Nx Ny Nz ) N N 2 2 2 2 2 2 2 2 2 v v v v1 x v2 x v Nx v v v 1y 2y Ny Nz 1z 2 z N N N
气体分子运动论

但因 cos cos cos 1
2 2 2
故只需
r = 2 个转动自由度
故只需
r = 2 个转动自由度
所以,直线需要的自由度数为: i t r 3 2 5
(3)对刚体 确定刚体一轴线5个自由度 t 3, r 2
确定刚体绕轴转动加一个自由度 r 1 刚体的自由度数: i t r 3 3 6
1T1 2T2 由于 P 所以有: 1V1 P 2V2 混合前的总内能为: 3 5
8 E 0 E1 E 2 1 RT1 2 RT 2 1 RT1 2 2 2
混合后,气体的温度变为T,总内能为: 3 5 3 5T1 E 1RT 2 RT ( )1RT 2 2 2 2T2 由于混合前后总内能相等,即E0=E,所以有 8T1 8 3 5T1 284K 1 RT1 ( ) 1 RT T 3 5T1 / T2 2 2 2T2
2
3RT 3 8.31 273 = m / s 493m / s 3 M mol 28 10
5 一容器内贮有氧气,其压强 P 1 . 013 10 Pa,温 例3: t 27 ℃,求: 度 (1)分子的平均平动动能和平均转动动能; (2)1mol气体的总能量; (3)1千克气体的内能。
3
3 3 3
2
2 3 3
0
1 0
5
6 6 难以确定
非刚性
复杂
3. 能量按自由度均分定理 (1)分子平均平动动能
1 3 2 t m v kT 2 2
t 按自由度均分
每个自由度 上 都 得到了相同 的 (1/2)k T 的平均平动动能
1 1 1 1 2 2 2 2 mv mv x mv y mv z 2 2 2 2 1 2 1 2 1 2 1 m v x m v y m v z kT 2 2 2 2
气体动理论公式总结
1.自由度i=t+r
单原子分子 i=t=3
刚性双原子 i=t+r=3+2 刚性三原子i=t+r=3+3
2.分子平均平动动能
t
t 2
kT
3 2
kT
3.分子平均转动动能
r
r 2
kT
4.分子平均动能
k
i kT 2
5.气体内能
E
i RT
2
i pV 2
2
四、麦克斯韦速率分布律
1.速率分布函数: f (v) dN Ndv
3、均匀带电无限长直导线
E 2 0 r
4.半径为R的均匀带电球面
E外
q
4 0r 2
E内 0
q
q
U外 4 0r U内 40R
5.无限大均匀带电平面
E
2 0
15
七、静态平衡时的导体 1. 导体内部场强为0。导体表面附近场强方向与导
体表面垂直。 2.导体为等势体(电势处处相等)。
3. 导体内无电荷,所有电荷分布于表面。
(1)
D dS q0 电场的高斯定律
(2)
E dl
L
S
B
d
S
电 场 的
环路定理
t
(变化的磁场激发电场)
(3) B d S 0
磁场的高斯定律
(4)
S
H dl
L
Ic
d D
dt
Ic
D dS t
磁 场 的 环 路 定 理 (变化的电场激发磁场)
27
第13 章量子物理
一、黑体辐射
v2 b v2 f (v)dv / b f (v)dv
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想气体状态方程与分子动理论理想气体状态方程与分子动理论是研究气体行为和性质的重要理论
基础。
通过这两个理论,我们可以深入认识气体分子的运动方式、气
体的性质以及气体体积、压强、温度之间的相互关系。
一、理想气体状态方程
理想气体状态方程是描述理想气体状态的方程,通常记作PV=nRT。
其中,P为气体的压强,V为气体的体积,n为气体的物质量,R为气
体常数,T为气体的绝对温度。
这个方程的推导基于分子动理论,将气体看作是由大量微观粒子
(分子或原子)组成的。
具体来说,气体分子在容器中自由运动,与
容器壁碰撞时会产生压力,而气体的体积则取决于容器的大小。
理想气体状态方程在实际应用中非常重要。
它可以被用来计算气体
的性质,例如气体的摩尔质量、密度以及其他涉及压强、体积、温度
关系的物理量。
通过理想气体状态方程,我们可以更好地理解气体的
宏观特性。
二、分子动理论
分子动理论是描述气体微观粒子行为的理论。
它假设气体分子是微
小的、质量可以忽略不计的,它们之间没有相互作用力。
根据这个理论,气体分子在运动过程中具有以下特点:
1. 分子自由运动:气体分子在容器内自由运动,并且具有各向同性,即没有固定的方向。
2. 分子碰撞:气体分子之间以及与容器壁之间不断发生碰撞,这些
碰撞是弹性碰撞,即能量和动量守恒。
3. 分子速度分布:气体分子的速度符合麦克斯韦-波尔兹曼分布,即速度的分布不均匀,符合高斯曲线。
通过分子动理论,我们可以解释气体的几个重要性质。
首先,气体
的压强取决于气体分子与容器壁的碰撞频率和碰撞力量。
其次,气体
的温度与气体分子的平均动能有关,即温度越高,分子的平均动能越大。
总结
理想气体状态方程与分子动理论为我们理解气体的行为和性质提供
了基础。
理想气体状态方程通过关联气体的压强、体积、物质量和温
度之间的关系,帮助我们计算气体的性质。
而分子动理论则从微观角
度解释了气体的行为,揭示了气体分子的运动状态和碰撞特点。
通过深入理解理想气体状态方程与分子动理论,我们可以更好地理
解气体的宏观特性,从而应用于实际问题的解决。
这两个理论为我们
提供了强大的工具,帮助我们研究和理解气体在自然界和工业生产中
的重要作用。
