焦作一中强基班招生数学试卷

合集下载

河南省焦作市2024年数学(高考)统编版摸底(提分卷)模拟试卷

河南省焦作市2024年数学（高考）统编版摸底(提分卷)模拟试卷一、单项选择题（本题包含8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题执行如图所示的程序框图，输出的（）A．18B．22C．25D．第(2)题某高校计划在今年暑假安排编号为A，B，C，D，E，F的6名教师，到4个不同的学校进行宣讲，每个学校至少安排1人，其中B，D必须安排在同一个学校.则不同的安排方法共有（）A．96种B．144种C．240种D．384种第(3)题实数x，y满足条件则的取值范围是（）A．B．C．D．第(4)题如果一个复数的实部和虚部相等，则称这个复数为“等部复数”，若复数（其中）为“等部复数”，则复数在复平面内对应的点在（）A．第一象限B．第二象限C．第三象限D．第四象限第(5)题为迎接第24届冬季奥林匹克运动会，某校安排甲､乙､丙､丁､戊共五名学生担任冰球､冰壶和短道速滑三个项目的志愿者，每个比赛项目至少安排1人.则学生甲不会被安排到冰球比赛项目做志愿者的概率为（）A．B．C．D．第(6)题将函数的图像向右平移个单位长度后得到曲线，若关于轴对称，则的最小值是（）A．B．C．D．第(7)题对于无穷数列，给出如下三个性质：①；②对于任意正整数，都有；③对于任意正整数，存在正整数，使得定义：同时满足性质①和②的数列为“s数列”，同时满足性质①和③的数列为“t数列”，则下列说法正确的是（）A．若为“s数列”，则为“t数列”B．若，则为“t数列”C．若，则为“s数列”D．若等比数列为“t数列”则为“s数列”第(8)题在中，，，，则（）A．1B．C．D．2二、多项选择题（本题包含3小题，每小题6分，共18分。

在每小题给出的四个选项中，至少有两个选项正确。

全部选对的得6分，选对但不全的得3分，有选错或不答的得0分） (共3题)第(1)题定义复数的大小关系：已知复数，，，，，．若或（且）,称．若且,称．共余情形均为．复数u，v，w分别满足：，，，则（）A．B．C．D．第(2)题在长方体中，，E，F，P，Q分别为棱AB，AD，，的中点，则（）A．AC⊥BPB．⊥平面EFPQC．平面平面EFPQD．直线CE和所成角的余弦值为第(3)题抛物线的焦点为，准线为直线，过点的直线交抛物线于，两点，分别过，作抛物线的切线交于点，于点，于点，则（）A．点在直线上B．点在直线上的投影是定点C．以为直径的圆与直线相切D．的最小值为三、填空（本题包含3个小题，每小题5分，共15分。

河南省焦作市第一中学2024届高三上学期11月月考数学试题

河南省焦作市第一中学2024届高三上学期11月月考数学试题一、单选题1．已知集合{}{}223,log 1M x x N x x =-≤≤=≤，则M N =I （）A ．[2,3]-B ．[2,2]-C ．(0,2]D ．(0,3] 2．若0,0a b >>，则“1ab <”是“1a b +<”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．若3tan 4α=，则21sin 212sin αα+=-（） A ．17- B ．7- C ．17 D ．74．已知ABC V 是边长为1的等边三角形，点D ，E 分别是边,AB BC 的中点，连结DE 并延长到点F ，使得2DE EF =，则AF BC ⋅u u u r u u u r 的值为（）A ．18-B ．18C ．1D ．8-5．定义方程()()f x f x '=的实数根0x 叫做函数()f x 的“躺平点”.若函数()ln g x x =，3()1h x x =-的“躺平点”分别为α，β，则α，β的大小关系为（）A ．αβ≥B ．αβ>C ．αβ≤D ．αβ<6．已知x ，y 为非零实数，向量a r ，b r 为非零向量，则“a b a b +=+r r r r ”是“存在非零实数x ，y ，使得0xa yb +=r r r ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7．在ABC V 中，AB AC ⊥u u u r u u u r ，且AB AC ==u u u r u u u r ，M 是BC 的中点，O 是线段AM 的中点，则()OA OB OC ⋅+u u u r u u u r u u u r 的值为（）A ．0B ．C ．12-D ．28．如图，圆M 为ABC V 的外接圆，4AB =，6AC =，N 为边BC 的中点，则AN AM ⋅=u u u r u u u u r （）A ．5B ．10C ．13D ．26二、多选题9．已知实数a 满足，3i 2i 1i a +=+-（i 为虚数单位），复数(1)(1)i z a a =++-，则（） A ．z 为纯虚数 B ．2z 为虚数 C ．0z z += D ．4z z ⋅= 10．已知不等式2210x ax b ++->的解集是{}x x d ≠，则b 的值可能是（）A ．1-B ．3C ．2D ．011．关于函数()sin |||cos |f x x x =+有下述四个结论，则（）A ．()f x 是偶函数B ．()f x 的最小值为1-C ．()f x 在[2,2]ππ-上有4个零点D ．()f x 在区间,2ππ⎛⎫ ⎪⎝⎭单调递增 12．如图，正方形ABCD 与正方形DEFC 边长均为1，平面ABCD 与平面DEFC 互相垂直，P 是AE 上的一个动点，则（）A ．CPB ．当P 在直线AE 上运动时，三棱锥D BPF-的体积不变C ．PD PF +D ．三棱锥A DCE -的外接球表面积为3π三、填空题13．已知曲线e ln x y m x x =+在1x =处的切线方程为3y x n =+，则n =.14．已知数列{}n a 是等差数列，1370,30a a a >+=，则使0n S >的最大整数n 的值为. 15．某区域规划建设扇形观景水池，同时紧贴水池周边建设一圈人行步道.要求总预算费用24万元，水池造价为每平方米400元，步道造价为每米1000元（不考虑宽度厚度等因素），则水池面积最大值为平方米.16．已知()f x 是定义在R 上的奇函数，且(1)()f x f x -=，则()f x 的最小正周期为；若对任意的121,0,2x x ⎡⎤∈⎢⎥⎣⎦，当时12x x ≠，都有()()1212f x f x x x π->-，则关于x 的不等式()sin f x x π≤在区间33,22⎡⎤-⎢⎥⎣⎦上的解集为.四、解答题17．已知向量2sin ,2sin 4a x x π⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭r，向量cos sin )b x x x ⎛⎫=- ⎪⎝⎭r ，记()()f x a b x =⋅∈R r r .(1)求()f x 表达式；(2)解关于x 的不等式()1f x ≥.18．记n S 为数列{}n a 的前n 项和，已知11,n n S a a ⎧⎫=⎨⎬⎩⎭是公差为13的等差数列． (1)求{}n a 的通项公式；(2)证明：121112na a a +++<L ． 19．ABC V 中，sin 2A －sin 2B －sin 2C =sin B sin C ．(1)求A ；(2)若BC =3，求ABC V 面积的最大值．20．已知数列{}n a 满足111,22n n na a a a +==-． (1)若11n nb a =-，证明数列{}n b 为等比数列，并求通项公式n b ； (2)数列{}nc 的前n 项和为(1)1,2(*)2n n n n S c b n N -+=+∈，求2n S ． 21．有人收集了春节期间平均气温x 与某取暖商品销售额y 的有关数据，如下表所示．(1)根据以上数据，用最小二乘法求出回归方程$$y bxa =+$； (2)预测平均气温为9C ︒-时，该商品的销售额为多少万元． ()()()$1122211,n ni i i ii i n n ii i i x x y y x y nx y b a y bx x x x nx ====---===---∑∑∑∑$$ 22．设函数()()ln f x a x =-，已知0x =是函数()y xf x =的极值点．（1）求a ；（2）设函数()()()x f x g x xf x +=．证明:()1g x <．。

河南省焦作市第一中学2022-2023学年高一下学期4月月考数学试题

（其中 2 = 1.414 ××× ， 3 = 1.732××× ，精确到 0.1 ）
A． 60.6m
B． 78.7m
C． 70.7m
D． 80.8m
5．设非零向量
ar,
r b,
cr
，满足
ar
=
r b
=
cr
，
ar
+
r b
=
cr
，则向量
ar,
r b
的夹角等于（
）
A．150°
B．120°
C． 60°
D． 30°
A．
1 2
B． 2 2
C．1
D． 3
三、填空题 13．台风中心从 A 地以每小时 20 千米的速度向东北方向移动，离台风中心 30 千米内的地区为危险区，城市 B 在 A 的正东 40 千米处，则 B 城市处于危险区的时间为小
时．
14．设函数
f
(x)
=
sin(2
x
+
p 6
),
x
Î[-
p 6
,
a]
共线且模长相等，则
r a
=
r b
或
r a
=
r -b
，B
错；
对于 C 选项，任何两个向量不能比大小，C 错；
( ) ( ) ( ) r r r r
rr
对于 D 选项， la ×b = l a ×b = lb × a 恒成立，D 对.
答案第41 页，共22 页
故选：ABC. 10．ABD
【分析】根据向量运算求出
2i
)
4i
(1-
2i)
-1
=

河南省焦作市(新版)2024高考数学人教版质量检测(培优卷)完整试卷

河南省焦作市（新版）2024高考数学人教版质量检测(培优卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题设，则（）A．3B．C．1D．第(2)题复数在复平面内对应的点为，则（）A．B．C．D．第(3)题已知为虚数单位，复数满足，则下列判断正确的是（）A．的虚部为B．C．的实部为D．在复平面内所对应的点在第一象限第(4)题已知集合，，则（）A．B．C．D．第(5)题在棱长为的正方体中，、分别为棱、的中点，则平面与正方体外接球的交点轨迹长度为（）A．B．C．D．第(6)题设x，y满足约束条件，则z＝2x＋y的最小值是（）A．－15B．－9C．1D．9第(7)题已知，，是双曲线上的三个点，直线经过原点，经过右焦，若，且，则该双曲线的离心率为A．B．C．D．第(8)题若关于x的方程有三个不等的实数解，，，且，其中，为自然对数的底数，则的值为 A．B．e C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知平面向量，，，若，是夹角为的两个单位向量，，，则下列结论正确的有（）A．B．C．D．第(2)题已知数列是公差为的等差数列，若它的前项的和，则下列结论正确的是（）A．若，使的最大的值为B．是的最小值C．D．第(3)题某学校高三年级学生有500人，其中男生320人，女生180人.为了获得该校全体高三学生的身高信息，现采用分层抽样的方法抽取样本，并观测样本的指标值（单位：cm），计算得男生样本的均值为174，方差为16，女生样本的均值为164，方差为30.则下列说法正确的是（）A．如果抽取25人作为样本，则抽取的样本中男生有16人B．该校全体高三学生的身高均值为171C．抽取的样本的方差为44.08D．如果已知男､女的样本量都是25，则总样本的均值和方差可以作为总体均值和方差的估计值三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题若曲线上的点P与曲线上的点Q关于坐标原点对称，则称P，Q是，上的一组奇点.若曲线（且）与曲线有且仅有一组奇点，则的取值范围是___________.第(2)题已知双曲线的离心率为为双曲线的右焦点，点在双曲线的右支上，为关于坐标原点的对称点，且．若，则______．第(3)题设椭圆的左右焦点分别为，，焦距为，点在椭圆的内部，椭圆上存在点使得成立，则椭圆的离心率的取值范围为______.四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知函数．(1)当时，函数有三个零点，求m取值范围；(2)若，求a的取值范围．第(2)题已知曲线的方程为，曲线的参数方程为(为参数).（1）求的参数方程和的普通方程；（2）设点在上，点在上，求的最小值.第(3)题某校组织学生进行跳绳比赛，以每分钟跳绳个数作为比赛成绩（单位：个）.为了解参赛学生的比赛成绩，从参赛学生中随机抽取50名学生的比赛成绩作为样本，整理数据并按比赛成绩分成，，，，，这6组，得到的频率分布直方图如图所示.(1)估计该校学生跳绳比赛成绩的中位数；(2)若跳绳比赛成绩不低于140分的为优秀，以这50名学生跳绳比赛成绩的频率作为概率，现从该校学生中随机抽取3人，记被抽取的比赛成绩优秀的学生人数为，求的分布列与期望.第(4)题如图，在几何体中，，，，四边形为矩形，平面平面，．（1）求证：平面平面；（2）点在线段上运动，设平面与平面所成二面角的平面角为，试求的取值范围．第(5)题为普及学生安全逃生知识与安全防护能力，某学校高一年级举办了安全知识与安全逃生能力竞赛，该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛，现将所有参赛选手参加笔试的成绩（得分均为整数，满分为分）进行统计，制成如下频率分布表.分数（分数段）频数（人数）频率合计（1）求表中，，，，的值；（2）按规定，预赛成绩不低于分的选手参加决赛.已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为，求的分布列和数学期望.。

2024年河南省普通高中招生考试《数学》试卷(附答案)

2024年河南省普通高中招生考试试卷数学注意事项：1. 本试卷共6页，三个大题，满分 120分，考试时间100分钟。

2.本试卷上不要答题，请按答题卡上注意事项的要求，直接把答案填写在答题卡上。

答在试卷上的答案无效。

一、选择题(每小题3分，共30分.下列各小题均有四个选项，其中只有一个是正确的)1.如图，数轴上点 P 表示的数是A. -1B.0C.1D.22. 据统计，2023年我国人工智能核心产业规模达5784亿元.数据“5784亿”用科学记数法表示为 A.5784×10⁸ B.5.784×10¹⁰ C.5.784×10′′ D.0.5784×10¹² 3.如图，乙地在甲地的北偏东50°方向上，则∠1的度数为 A.60° B.50° C.40° D.30°4.信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒，它的主视图为(第4题)A. x>2B. x<0C. x<-2D. x>-36. 如图,在▱ABCD 中,对角线AC,BD 相交于点O,点E 为OC 的中点,EF∥AB 交BC 于点 F.若AB = 4,则EF 的长为 A. 12 B.1 C. 43 D.2 7. 计算 (a ⋅a ,⋯⋅a )3的结果是a 个A. a ⁵B. a ⁶C. a ⁴⁺³D. a³a数学试卷第1页(共6页)8.豫剧是国家级非物质文化遗产，因其雅俗共赏，深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示，它们除正面外完全相同.把这三张卡片背面朝上洗匀，从中随机抽取一张，放回洗匀后，再从中随机抽取一张，两次抽取的卡片正面相同的概率为A. 19B. 16C. 15D. 139. 如图,⊙O 是边长为4 √3的等边三角形ABC 的外接圆，点D 是BC 的中点,连接BD,CD.以点 D为圆心，BD 的长为半径在⊙O 内画弧，则阴影部分的面积为 A.8π3 B.4π C.16π3 D.16π10.把多个用电器连接在同一个插线板上，同时使用一段时间后，插线板的电源线会明显发热，存在安全隐患.数学兴趣小组对这种现象进行研究，得到时长一定时，插线板电源线中的电流I 与使用电器的总功率P 的函数图象(如图1)，插线板电源线产生的热量Q 与I 的函数图象(如图2).下列结论中错误．．的是A. 当P =440 W 时, I =2 AB. Q 随I 的增大而增大C. I 每增加 1 A,Q 的增加量相同D.P 越大，插线板电源线产生的热量Q 越多二、填空题(每小题3分，共15分)11. 请写出2m 的一个同类项: .12.2024年3月是第8个全国近视防控宣传教育月，其主题是“有效减少近视发生，共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动，并对各班的宣传板报进行评分，得分情况如图，则得分的众数为分.数学试卷第 2页(共6页)13. 若关于x的方程12x2−x+c=0有两个相等的实数根，则c的值为 .14. 如图，在平面直角坐标系中，正方形ABCD的边AB在x轴上，点A的坐标为(-2，0)，点 E在边 CD 上. 将△BCE沿BE折叠,点C落在点F 处. 若点 F的坐标为(0,6),则点 E 的坐标为 .15. 如图,在Rt△ABC 中,∠ACB =90°,CA = CB =3,线段 CD 绕点 C 在平面内旋转,过点B作AD的垂线，交射线AD于点E.若CD=1，则AE的最大值为，最小值为 .三、解答题(本大题共8个小题，共75分)16. (10分)(1) 计算:√2×√50−(1−√3)0; (2) 化简:(3a−2+1)÷a+1a2−4.17.(9分)为提升学生体质健康水平，促进学生全面发展，学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中，甲、乙两名队员表现优异，他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.比赛得分统计图队员平均每场得分平均每场篮板平均每场失误甲26.582乙26103根据以上信息，回答下列问题.(1)这六场比赛中，得分更稳定的队员是 (填“甲”或“乙”)；甲队员得分的中位数为27.5分，乙队员得分的中位数为分.(2)请从得分方面分析：这六场比赛中，甲、乙两名队员谁的表现更好.(3)规定“综合得分”为：平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1)，且综合得分越高表现越好.请利用这种评价方法，比较这六场比赛中甲、乙两名队员谁的表现更好.数学试卷第 3 页(共6页)18.(9分)如图，矩形ABCD的四个顶点都在格点(网格线的交点)上，对角线AC，BD相交(x⟩0)的图象经过点 A.于点 E，反比例函数y=kx(1)求这个反比例函数的表达式.(2)请先描出这个反比例函数图象上不同于点A的三个格点，再画出反比例函数的图象.(3)将矩形ABCD向左平移，当点E落在这个反比例函数的图象上时，平移的距离为 .19.(9分)如图,在Rt△ABC中,CD是斜边AB上的中线,BE‖DC交AC的延长线于点 E.(1)请用无刻度的直尺和圆规作∠ECM，使∠ECM=∠A,且射线 CM交 BE 于点 F(保留作图痕迹，不写作法).(2) 证明(1) 中得到的四边形 CDBF是菱形.20.(9分)如图1，塑像AB在底座BC上，点D 是人眼所在的位置.当点 B 高于人的水平视线DE时，由远及近看塑像，会在某处感觉看到的塑像最大，此时视角最大.数学家研究发现：当经过A，B两点的圆与水平视线DE相切时(如图2)，在切点P处感觉看到的塑像最大，此时∠APB为最大视角.(1)请仅就图2的情形证明∠APB>∠ADB.(2) 经测量,最大视角∠APB为30°,在点P处看塑像顶部点A 的仰角∠APE为60°,点P到塑像的水平距离PH为6m . 求塑像AB的高(结果精确到0.1m.参考数据：√3≈1.73).数学试卷第4页(共6页)21.(9分)为响应“全民植树增绿，共建美丽中国”的号召，学校组织学生到郊外参加义务植树活动，并准备了A，B两种食品作为午餐.这两种食品每包质量均为50g，营养成分表如下.(1) 若要从这两种食品中摄入4600 kJ热量和70g蛋白质，应选用A，B 两种食品各多少包?(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包，要使每份午餐中的蛋白质含量不低于90g，且热量最低，应如何选用这两种食品?22.(10分)从地面竖直向上发射的物体离地面的高度h(m)满足关系式ℎ=−5t²+v₀t,其中t(s)是物体运动的时间，v₀(m/s)是物体被发射时的速度.社团活动时，科学小组在实验楼前从地面竖直向上发射小球.(1)小球被发射后 s时离地面的高度最大(用含v₀的式子表示).(2)若小球离地面的最大高度为20m，求小球被发射时的速度.(3)按(2)中的速度发射小球，小球离地面的高度有两次与实验楼的高度相同.小明说：“这两次间隔的时间为3s.”已知实验楼高15 m，请判断他的说法是否正确，并说明理由.数学试卷第5页(共6页)23. (10分) 综合与实践在学习特殊四边形的过程中，我们积累了一定的研究经验.请运用已有经验，对“邻等对补四边形”进行研究.定义：至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30°和45°角的直角三角形纸板拼出如图1所示的4个四边形，其中是邻等对补四边形的有 (填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.如图2，四边形ABCD是邻等对补四边形，AB=AD,，AC 是它的一条对角线.①写出图中相等的角，并说明理由；②若.BC=m,DC=n,∠BCD=2θ,,求AC 的长(用含m,n,θ的式子表示).(3)拓展应用如图3，在Rt△ABC中,∠B=90°,AB=3,BC=4,,分别在边BC,AC上取点M,N,使四边形ABMN是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时，请直接写出 BN的长.数学试卷第6页(共6页)2024年河南省普通高中招生考试数学试题参考答案(注：第15题只填对1空得2分)三、解答题(本大题共8个小题，共75分)16.(1)原式=10-1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分=9.……………………………………………………………………5分(2) 原式=a+1a−2⋅(a+2)(a−2)a+1…4分=a+2.………………………………………………………………………5分17.(1)甲29⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分(2)因为甲的平均每场得分大于乙的平均每场得分，且甲的得分更稳定，所以甲队员表现更好.(注：答案不唯一，合理即可)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分(3) 甲的综合得分为:26.5×1+8×1.5+2×(-1)=36.5.乙的综合得分为:26×1+10×1.5+3×(-1)= 38.因为38>36.5,所以乙队员表现更好.…………………………………………9分18.(1)∵ 反比例函数y=kx(x⟩0)的图象经过点A(3,2),∴2=k3.∴ k = 6.∴ 这个反比例函数的表达式为y=6x.………………3分数学试题参考答案第1页(共4页)(2) 如图.7分(3)92………………………………………………………9分19.(1) 如图.……………………… ……… 4分(2) 由(1),得∠ECF =∠A.∴ CF∥AB.∵ BE∥DC,∴四边形CDBF是平行四边形.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7分∵ CD 是Rt△ABC斜边AB上的中线,∴ CD =BD.∴□CDBF是菱形.…………………………………………………………9分20.(1) 如图,连接BM.则∠AMB=∠APB.∵ ∠AMB>∠ADB,∴∠APB>∠ADB.…………………………3分(2) 在Rt△AHP 中,∠APH = 60°,PH = 6.,∵tan∠APH=AHPH∴ AH = PH·tan 60°=6×√₃ =6√₃. …… 6分∵ ∠APB = 30°,∴ ∠BPH =∠APH--∠APB =60°-30°=30°.数学试题参考答案第2页(共4页)在Rt△BHP 中, tan∠BPH =BHPH ,∴BH =PH ⋅tan30∘=6×√33=2√3. … …8分∴AB =AH −BH =6√3−2√3=4√3≈4×1.73≈6.9(m).答:塑像AB 的高约为6.9m.……………………………………………………9分21.(1) 设选用A 种食品x 包，B 种食品y 包，根据题意，得{700x +900y =4600,10x +15y =70.…3分解方程组，得 {x =4,y =2.答：选用A 种食品4包，B 种食品2包.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分(2)设选用A 种食品a 包，则选用B 种食品(7-a)包，根据题意，得10a+15(7-a)≥90.∴a≤3.…………………………………………………………………………7分设总热量为wkJ ，则w=700a+900(7-a)=-200a+6300.∵ -200<0,∴ w 随a 的增大而减小. ∴ 当a=3时,w 最小.∴ 7-a=7-3 =4.答：选用A 种食品3包，B 种食品4包.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9分22.(1)ⁿ₀…………………………………3分(2)根据题意,得当 t =v10时,h=20.∴−5×(v 010)2+v 0×v 010=20.∴v₀=20(m s ⁄). …………………………………………………6分 (3)小明的说法不正确.(注：若没写出结果，但后续说理正确，不扣分)⋯7分理由如下：由(2),得 ℎ=−5t²+20t.当h = 15时, 15=−5t²+20t.解方程，得 l₁=1,t₂=3.……………………………………………9分 ∵ 3-1=2(s),∴小明的说法不正确.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10分数学试题参考答案第3 页(共4页)23.(1)②④(注：全部填对的得2分，对但不全的得1分，有错的得0分)⋯⋯⋯2分(2)①∠ACD=∠ACB.(注:若没写出结果,但后续说理正确,不扣分)………4分理由如下：延长CB至点 E,使 BE = DC. 连接AE.∵ 四边形ABCD 是邻等对补四边形，∴∠ABC+∠D=180°.∵∠ABC+∠ABE=180°,∴ ∠ABE =∠D.∵AB=AD,∴△ABE≅△ADC.∴∠E=∠ACD,AE=AC.∴ ∠E =∠ACB.∴∠ACD=∠ACB.………………………………………………………6分②过点A作AF⊥EC,垂足为点 F.∵ AE=AC,∴CF=12CE=12(BC+BE)=12(BC+DC)=m+n2.∵ ∠BCD =2θ,∴ ∠ACB =∠ACD=θ.在Rt△AFC中,cosθ=CFAC,∴AC=CFcosθ=m+n2cosθ.…8分(3)12√25或12√27.…10分数学试题参考答案第4页(共4页)。

河南省焦作市第一中学2022-2023学年高一下学期3月月考数学试题

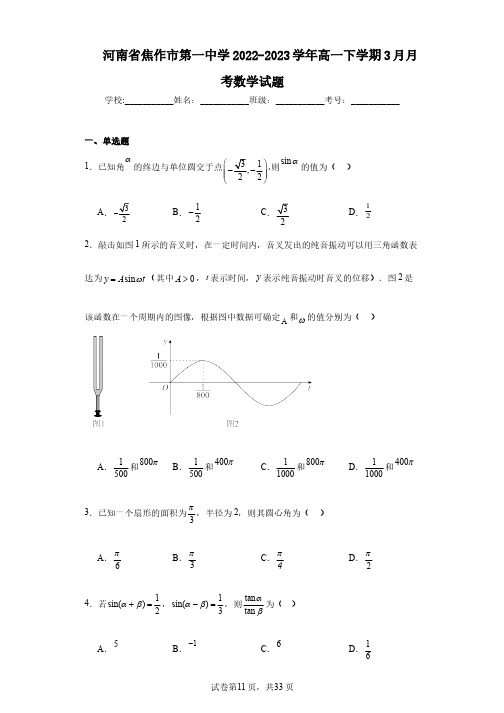
r a
=
ur 3e1
+
uur 3e2
，
r b
=
ur e1
+
uur e2
C．
r a
=
ur e1
-
ur 2e2
，
r b
=
ur e1
+
uur e2
D．
r a
=
ur e1
-
ur 2e2
，
r b
=
ur 2e1
-
uur 4e2
7．在
DABC
中，
G
为
DABC
的重心，
M
为
AC
上一点，且满足
uuuuv MC
=
uuuuv 3AM
cr
，求
cr
×
(ar
+
r b)
的值.
21．已知向量
av
与向量
v b
的夹角为
45°，其中
av
=
2
，
v b
=1.
（1）求
av
+
v 2b
的值；
（2）若向量
2av
-
v lb
与
lav
-
v 3b
的夹角是锐角，求实数
l
的取值范围.
22．设函数
f
(x)
=
cos
x
×
cos
æ çè
x
-
p 6
ö ÷ø
+
3
sin2
x
-
33 4
试卷第11 页，共33 页
D． 1 6
5．设非零向量

2023年河南省焦作市中考一模数学试题(含答案解析)

2023年河南省焦作市中考一模数学试题学校:___________姓名：___________班级：___________考号：___________A．．C．．【答案】D【分析】根据从上往下看看到的视图是俯视图即可解答．．故选D．【点睛】本题考查简单组合体的三视图，解题的关键是注意：能看到的线用实线，看不A ．65︒B 【答案】A∵1115a b ∠=︒∥，，∴31115∠=∠=︒，A ．8B ．16【答案】B【分析】根据三角形的中位线的性质可以得到根据菱形的性质和勾股定理，即可得到【详解】解：取CD 的中点G ，连接点E 为AD 的中点，点F 为OC 12EG AC ∴=，EG AC ∥，FG 四边形ABCD 是菱形，BAD ∠AC BD ∴⊥，60ADC ∠=︒，ODC ∠A．918(,)55B．【答案】A【分析】连接OB，根据勾股定理得到矩形ABCO的顶点B的坐标为∴==，3 AB OC4==，OA BC22∴=+=，345OBA．8B．6C．【答案】C【分析】分点P在AD上，DB上两种情况结合图像进行分析求解即可．∥，【详解】解：∵矩形ABCD中，AD BC∴当点P在边AD上运动时，y的值不变，由图像可知，当x a=时，点P与点D重合，∴2==，即矩形的长是2a，AD BC a二、填空题【答案】225/0.08【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与抽到∵共有25种等可能的结果，其中小航经过两次“玩转盘抽奖活动”，抽到有2种，∴小航抽到“可乐”的概率是225．【答案】π112+【分析】连接OD 、BD 332CD OD ==，然后根据【详解】解：连接OD 过OB 的中点C 作CD OD BD ∴=，OB OD = ，2OB OD BD ∴===，60BOD ∴∠=︒，在ABC 为等边三角形，∴23AC BC AB ===，点D 为AB 的中点，132AD CD AC ∴===，∴90ADB ∠=︒，∴(22BD AB AD =-=312DQ BD BQ =-=-=，在Rt ADQ △中，AQ AD =②Q 点在DB 的延长线上，如图所示：314QD BD BQ =+=+=，()222234AQ AD DQ ∴=+=+综上可知，当90ADQ ∠=︒时，AQ 故答案为：7或19．【点睛】本题考查了旋转的性质，勾股定理，等边三角形的性质，运用分类讨论的思想解决问题是解题关键．三、解答题16．（1）计算：0131832-⎛⎫---+ ⎪⎝⎭（2）化简：2111x x x x ⎛⎫÷- ⎪--⎝⎭．【答案】（1）103；（2）1x x -+(1)求I与R的函数表达式，并说明比例系数的实际意义；(2)求m的值，并说明m的实际意义；(3)如果以蓄电池为电源的用电器限制电流不得超过10A，那么用电器的可变电阻应控制在什么范围内？【答案】(1)48IR=，见解析(2)3，m的实际意义为：当电阻R为3Ω，电流大小为16A(3)该电路的可变电阻控制在不低于4.8Ω【分析】（1）根据题意设UIR=，然后将()8,6A代入求解记录；【答案】戏台的高度是6米【分析】设BC x =米，根据锐角三角函数的定义求出AC 的长度，然后根据等腰三角形的性质可知CD BC =，从而利用ED DC CE =-即可求出答案．【详解】解：设BC x =米，在Rt ACE 中，tan CE EAC AC∠=，【点睛】本题考查解直角三角形的应用，熟练运用锐角三角函数的定义是解题的关键．20．为落实《健康中国行动（2019排球促进校园体育活动．据了解，某体育用品超市每个足球的价格比排球的价格多元，用500元购买的足球数量和(1)求每个足球和排球的价格；(2)学校决定购买足球和排球共50买最少花费多少钱？(3)在（2）方案下，体育用品超市为支持学校体育活动，对足球提供供7.5折优惠．学校决定将节约下的资金全部用于再次购买足球和排球（此时按原价购∴201002080x -=-=，答：每个足球的价格为100元，每个排球的价格为80元；（2）解：设学校决定购买足球a 个，本次购买花费y 元，则购买排球(50)a -个，则05050a a a<<⎧⎨>-⎩，解得：2550a ≤<，由题意得：10080(50)204000y a a a =+-=+，∵200>，∴y 随a 的增大而增大，∴当25a =时，y 有最小值202540004500=⨯+=，答：本次购买最少花费4500元钱；（3）解：在（2）方案下，学校购买足球和排球各25个，花费4500元，∵体育用品超市为支持学校体育活动，对足球提供8折优惠，排球提供7.5折优惠，∴学校节约资金：100(10.8)2580(10.75)251000⨯-⨯+⨯-⨯=（元），设学校再次购买足球m 个，排球n 个，由题意得：100801000m n +=，整理得：5450m n +=，∵m 、n 都是非负整数，∴100m n =⎧⎨=⎩或65m n =⎧⎨=⎩或210m n =⎧⎨=⎩，∴学校再次购买足球和排球的方案有3个：①只购买10个足球；②购买6个足球，5个排球；③购买2个足球，10个排球．【点睛】本题考查了分式方程的应用、一次函数的应用、一元一次不等式的应用以及二元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）正确求出一次函数关系式；（3）找准等量关系，正确列出二元一次方程．21．“沙包掷准”是同学们非常喜爱的一项趣味运动．沙包行进的路线呈抛物线形状，经研究，小航在掷沙包时，掷出起点处高度为1m ，当水平距离为2m 时，沙包行进至最高点2m ；建立如图所示直角坐标系，并设抛物线的表达式为2()y a x h k =-+，其中(m)x 是水平距离，(m)y 是行进高度．(1)求抛物线的表达式；(2)若地靶的中心到起掷线的距离为5m，设沙包落点与地靶中心的距离为与得分对应如表，请问小航成绩怎样？并说明理由．(1)请用无刻度的直尺和圆规过点(2)连接AB ，若（1）中所作垂线分别与①求证：CBD DCB ∠∠＝；②若O 的半径为4，cos （2）①证明：∵直线l 与∴OB l ⊥，∴90OBD ∠=︒，即90OBA DBC ∠+∠=︒，∵OD OA ⊥，(1)操作判断操作一：将一副等腰直角三角板两斜边重合，按图1放置；操作二：将三角板ACD沿CA方向平移（两三角板始终接触）至图2位置．∵将三角板ACD 沿CA 方向平移，∴AA CC CD C D CD C D ''''''==，，∥，∴C D AB C D AB ''''=，∥，∴四边形ABC D ''是平行四边形，故答案为：AA CC ''=，平行四边形；（2）四边形ABC D ''的形状可以是菱形，如图3，连接AD BC ''，，∵6cm 3090AB ACB ABC =∠=︒∠=︒，，，∴12cm 606cm AC BAC BC =∠=︒=，，，∵将三角板ACD 沿CA 方向平移，∴CD C D AB CD C D AB ''''==，∥∥，∴四边形ABC D ''是平行四边形，∴当6cm BC AB '==时，四边形ABC D ''是菱形，∵6cm 60BC AB BAC '==∠=︒，，∴ABC '△是等边三角形，∴6cm AB AC BC ''===，∴6cm CC '=；（3）①当BC CC ''=时，BCC ' 为等腰三角形，如图，∵BC CC ''=，∴30BCC CBC ''∠=∠=︒，∴60AC B '∠=︒，∵30ACB BH AC ∠=︒⊥，，∴33cm,39cm BH CH BH ===，∵BC BC BH AC '=⊥，，∴218cm CC CH '==，∵四边形ABC D ''是平行四边形，∴AD BC ''=，∴BC BD AD BD ''''+=+，∵将三角板ACD 沿CA 方向平移，∴DD AC ¢∥，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

焦作一中强基班招生数学试卷
焦作一中强基班招生数学试卷

1. 背景与介绍
焦作一中强基班是焦作市最为优秀的中学重点班级之一，以高质量的
教学和严格的选拔制度著称。每年，数百名学生参加强基班的选拔考
试，而不到100名的入选者则有幸加入这个优秀的团队，接受高水平、
高难度的课程教育。

在强基班的选拔考试中，数学试卷一直以来都是众多参考者最为头疼
的一道难题。因此，对于焦作一中强基班的考生来说，数学试卷是一
个必须要认真准备的难关。

2. 数学试卷概述
焦作一中强基班数学试卷的总分为150分，一共有30道试题。其中，
15道是选择题，每一道选择题4个选项，只有1个正确答案，每道题3
分，总分45分。另外，还有15道非选择题，每一道题9分，总分105
分。在非选择题部分，有两道应用题，要求考生进行详细的解释和说
明。

3. 数学试卷难度分析
焦作一中强基班的数学试卷难度较高，主要是考察考生的思维能力和
分析能力。选择题虽然只有3分，但考察点十分齐全，主要包括代数、
几何、概率、统计和计算等方面，不太可能出现简单的计算题。而非
选择题则更加考验考生的能力，主要以证明题和应用题为主，需要学
生进行反复推理和分析，才能得到正确答案。

4. 应试策略
对于焦作一中强基班数学试卷的应试策略，可以从以下方面着手：
1) 认真阅读题目，了解题目要求及其所包含的信息，不可快速浏览或
潦草读题；
2) 充分利用手中的草稿纸，尽可能多的记录中间过程，以防丢失；
3) 针对难题采用“面对”不“逃避”的策略，敢于尝试、勇于推理、善于
总结；
4) 时间分配上要合理，可以适当多给难题一些时间；
5) 经常检查自己的答案是否准确，以防疏漏。

5. 总结
焦作一中强基班数学试卷的难度较高，但这正是选拔考试需要的，对
于准备参加强基班考试的学生而言，应该抓住每一次练习机会，尽自
己最大的努力，准备好每一个环节。同时，在考试过程中，要清晰明
确自己的应试计划，严格按照规定时间完成，并时时检查自己的答案
是否准确，这样才能更好地应对本次考试，才能有望成为焦作一中强
基班的一员。