物 理 - 福建省永春第一中学
泉州高中排名前十名

泉州高中排名前十名
2023泉州高中排名前十名:1.福建省泉州第五中学;2.泉州第七中学;3.泉州第一中学;4.福建省南安第一中学;5.福建省惠安第一中学;6.养正中学;7.培元中学;8.福建省永春第一中学。
2023泉州高中排名前十名
泉州第七中学
福建省泉州市第七中学,是福建省首批省级示范性普通高中,福建省一级达标中学。
学校现有天后、金山、江南三个校区,是一所由鲤城区人民政府领导管理的全日制完全中学。
江南校区占地面积达77000余平方米,规划办学规模为76个教学班。
泉州第一中学
泉州第一中学,简称泉州一中,位于泉州市区梅石路学府街,北枕清源山,西伴梅石路。
其前身可追溯至明朝嘉靖八年创办的“一峰书院”,已有400多年历史。
泉州一中为福建省首批办好的重点中学一级达标高中。
特训01高一下学期物理选择30题必刷题(尖子生专用)
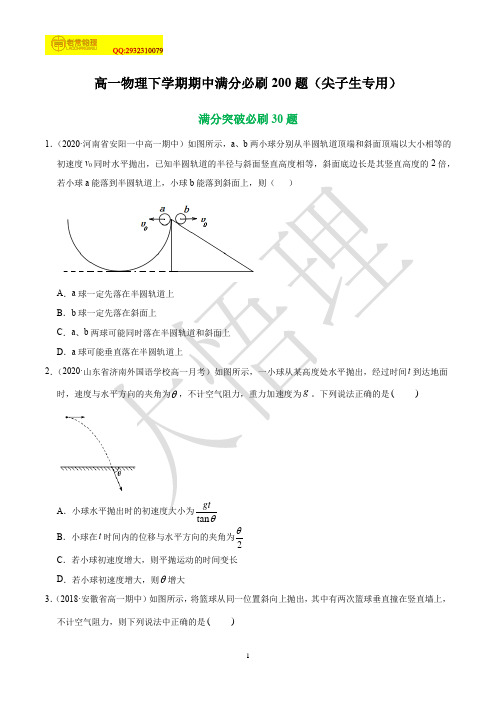
高一物理下学期期中满分必刷200题(尖子生专用)满分突破必刷30题1.(2020·河南省安阳一中高一期中)如图所示,a、b两小球分别从半圆轨道顶端和斜面顶端以大小相等的初速度v0同时水平拋出,已知半圆轨道的半径与斜面竖直高度相等,斜面底边长是其竖直高度的2倍,若小球aA.aB.bC.a、bD.a2.(2020·)gtAθB.小球在t时间内的位移与水平方向的夹角为2C.若小球初速度增大,则平抛运动的时间变长D.若小球初速度增大,则θ增大3.(2018·安徽省高一期中)如图所示,将篮球从同一位置斜向上抛出,其中有两次篮球垂直撞在竖直墙上,不计空气阻力,则下列说法中正确的是()A.从抛出到撞墙,第二次球在空中运动的时间较短BCD4.(()A.vC.v5.(A.vC.v D6.(2018·河北省定州一中高一期中)静止的城市绿化洒水车,由横截面积为S的水龙头喷嘴水平喷出水流,水流从射出喷嘴到落地经历的时间为t,水流落地点与喷嘴连线与水平地面间的夹角为θ,忽略空气阻力,以下说法正确的是()A.水流射出喷嘴的速度为2gttanθB.空中水柱的水的体积为2 2tan SgtθC.水流落地时位移大小为22singtθD.水流落地时的速度为2gtcotθ7.(2019·甘南藏族自治州合作第一中学高三期中)如图所示,AB是半圆弧的直径,处于水平,O是圆弧的圆心,C是圆弧上一点,∠OAC=37°,在A、O两点分别以一定的初速度同时水平抛出两个小球,结果都落在C点,则两个球抛出的初速度v1、v2的大小之比为(sin 37°=0.6,cos 37°=0.8,取g=10 m/s2,不计空气阻力)()A.v1∶v2=32∶7B.v1∶v2=16∶7C.v1∶v2=16∶3D.v1∶v2=16∶98.(2018·河北省开滦第二中学高一期中)如图所示,在M点分别以不同的速度将两小球水平抛出。
福建省永春第一中学2022-2023学年高二下学期6月月考数学试题

福建省永春第一中学2022-2023学年高二下学期6月月考数学试题学校:___________姓名:___________班级:___________考号:___________四、双空题16.无穷数列{}n a 满足:只要()*,p qa a p q =ÎN ,必有11p q a a ++=,则称{}n a 为“和谐递进数列”.若{}na 为“和谐递进数列”,且124681,2,1,6a a a a a ===+=,则7a =__________,n S 为数列{}na 的前n 项和,则2022S =__________.(1)求证:FM P 平面ADE ;(2)若1,BC =已知直线AF 与平面ABCD 所成角为30°,求二面角A FB C --的余弦值.20.某校从高二年级随机抽取了20名学生的数学总评成绩和物理总评成绩,记第i 名学生的成绩为()(),1,2,3,20iix yi =×××,其中i x ,i y 分别为第i 名学生的数学总评成绩和物理总评成绩.抽取的数据列表如下(按数学成绩降序整理):11.AC【分析】A 选项,作出辅助线,得到AC ⊥BD ,1AC DD ^,得到线面垂直,证明出AC ⊥BP ;B 选项,假设1B D ⊥平面EFPQ ,推出矛盾,B 错误;C 选项,作出辅助线,得到//EF BD ,1//FP BC ,证明出面面平行;D 选项,作出辅助线,找到异面直线CE 和1FD 所成角,求出各边长,利用余弦定理求出答案.【详解】对于A ,如图1所示,因为AB =BC ,所以四边形ABCD 是正方形,所以AC ⊥BD ,又因为几何体为长方体,所以1DD ⊥平面ABCD ,因为AC Ì平面ABCD ,所以1AC DD ^,又因为1BD DD D =I ,1,BD DD Ì平面1BDD ,所以AC ⊥平面1BDD ,又因为BP Ì平面1BDD ,所以AC ⊥BP ,故结论正确;对于B ,如图2所示,假设1B D ⊥平面EFPQ .因为PQ Ì平面EFPQ ,所以1B D ⊥PQ .因为P ,Q 分别为棱1DD ,1BB 的中点,所以四边形PQDB 为平行四边形,故//PQ BD ,所以1B D BD ^,显然1B D BD ^不成立,故假设错误,所以结论错误;对于C ,如图3所示,连接BD ,1AD ,1C B ,1C D ,由条件可知//EF BD ,因为EF Ì平面EFPQ ,BD Ë平面EFPQ ,所以//BD 平面EFPQ ,又1//FP AD ,11//BC AD ,所以1//FP BC ,因为PF Ì平面EFPQ ,1BC Ë平面EFPQ ,所以1//BC 平面EFPQ ,又因为1BC BD B =I ,1,BC BD Ì平面1BC D ,所以平面1//BC D 平面EFPQ ,故结论正确;对于D ,如图4所示,在CD 上取靠近D 的一个四等分点G ,连接FG ,1D G ,取CD 中点H ,连接AH ,则G 是DH 的中点,所以//FG AH ,又四边形AECH 为平行四边形,所以//CE AH ,故//FG EC ,所以CE 和1FD 所成角即为1D FG Ð或其补角,设13DD =,则AD =CD =2,。
2017—2018学年度福建省永春第一中学高一年上学期期中考试

高一年化学期中考命题人:陈增平 审题人:陈跃生考生须知:1. 本试卷分试题卷和答题卡两部分。
满分100分,考试时间90分钟。
2. 所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
3. 考试结束后,只需上交答题卷。
第Ⅰ卷(选择题44分)一、选择题(共22小题,每小题只有一个正确选项,每小题2分,共44分)1、下列关于物质分类的说法正确的是( )A .根据原子最外层电子数的多少可将元素分为金属元素和非金属元素B .根据酸分子中含有的氢原子个数可将酸分为一元酸、二元酸、三元酸等C .汽油、漂白粉、水玻璃、王水均为混合物D .纯碱、熟石灰、醋酸、食盐水均为电解质2、“纳米材料”是粒子直径为1~100 nm 的材料,纳米碳就是其中一种,若将纳米碳均匀地分散到蒸馏水中,所形成的物质具有的性质有( )①是溶液 ②是胶体 ③能产生丁达尔效应 ④能透过滤纸 ⑤不能透过滤纸 ⑥静置后会析出黑色沉淀A .①④⑤B .②③⑤C .②③④D .①③④⑥3、关于胶体的性质与应用,相关说法错误的是( )A .静电除尘器除去空气或工厂废气中的飘尘是利用胶体粒子的带电性而加以除去B .明矾净水是利用胶体的吸附性C .从颜色上无法区别FeCl 3溶液和Fe(OH)3胶体D .由于胶粒之间的排斥作用胶粒不易聚集成大的颗粒,所以胶体的性质相对比较稳定4、前几年,部分巨能钙被检出含有双氧水,而双氧水有致癌性,可加速人体衰老,因此卫生部已开始加紧调查巨能钙。
下列有关说法错误的是( )A .H 2O 2、Na 2O 2都属于过氧化物B .双氧水是绿色氧化剂,可作医疗消毒剂C .H 2O 2既有氧化性,又有还原性,与Cl 2、KMnO 4反应时表现H 2O 2的氧化性D .H 2O 2作漂白剂是利用其氧化性,漂白原理与HClO 类似、与SO 2不同5、将标准状况下的a L 氯化氢气体溶于100 g 水中,得到的盐酸的密度为b g·mL -1,则该盐酸的物质的量浓度(mol·L -1)是( )A.a 22.4B.ab 22 400C. 1 000ab 2 240+36.5aD.ab 22 400+36.5a6、下图是某同学用500 mL 容量瓶配制0.10 mol·L -1 NaOH 溶液的过程:该同学的错误步骤有( )A .1处B .2处C .3处D .4处7、已知Co 2O 3在酸性溶液中易被还原成Co 2+,Co 2O 3、Cl 2、FeCl 3、I 2的氧化性依次减弱。
福建省泉州市永春第一中学2025届高三上学期11月一模语文试卷(含答案)

福建省永春第一中学2025届高三上学期11月一模语文试卷学校:___________姓名:___________班级:___________考号:___________一、现代文阅读阅读下面的文字,完成下列小题。
在我看来,无聊作为人类行为的一个要素,在整个历史时期,都是一个巨大的推动力量,今天更是如此。
无聊似乎是人类独有的情绪。
囚笼中的动物确实会无精打采,但自然状态下它们是不会有这种类似无聊的反应的,因为它们大部分时间里都在搜寻食物或逃避敌人。
无聊的本质之一,是人的机能没有“全力以赴”。
逃离试图夺你性命的敌人肯定不是件愉快的事,但一定不会让你觉得无聊。
无聊的另一本质,是现实环境与向往的环境之间存在反差而令人不满。
无聊的人总是期望有事情发生——就算并非好事也行——从而感受到这一天总算有所不同。
总而言之,与无聊相对的不是愉快,而是兴奋。
逃避无聊确实是自然本性,人类从心底里渴望兴奋,特别是男性。
农耕时代的生活容易单调乏味,一家人晚饭后围坐在一起,度过所谓的“幸福的时光”:男人在打瞌睡,妻子在编织,女儿则在想这种日子何时是尽头。
机器时代到来之后,人们可以精神抖擞地寻找各种刺激。
过去恋人们在整部小说里一直期待的激动人心的约会,今天的年轻人每星期都可以经历一次。
而且社会阶层越提升,对刺激的追求也越迫切,他们不停地寻欢、跳舞、饮酒,乐此不疲。
然而,昨夜越是刺激,今晨就越是无聊,越感到无聊难以忍受。
如今人们比祖先少了一些沉闷乏味,反而更加害怕无聊。
也许像挥霍经济资本那样挥霍生命资本是极不明智的。
正如酒精之类麻醉品或许能让痛苦的神经得到舒缓,但人们决不可放纵本能,对其上瘾。
嗜酒成癖的人对酒精的依赖越来越高,一旦停止喝酒便无法忍受,在此过程中,身体的健康和感受的机能逐渐被摧毁,反而导致生活更加痛苦。
同样道理,一定量的兴奋可以消除无聊,但过度的兴奋不仅有害健康,而且会使人们对各种快乐的欣赏能力变得脆弱,使得广泛的机体满足为兴奋所代替,智慧被机灵所代替,美感被惊诧所代替。
专题26 线段中的常见思想方法的应用(师)

专题26线段中的常见思想方法的应用【题型1 线段中的整体思想】 【题型2 线段中的方程思想】 【题型3 线段中的分类讨论思想】 【题型4 线段中的数形结合思想】【题型1 线段中的整体思想】【例1】(2022·全国·七年级专题练习)线段AB =16,C ,D 是线段AB 上的两个动点(点C 在点D 的左侧),且CD =2,E 为BC 的中点.(1)如图1,当AC =4时,求DE 的长.(2)如图2,F 为AD 的中点.点C ,D 在线段AB 上移动的过程中,线段EF 的长度是否会发生变化,若会,请说明理由;若不会,请求出EF 的长. 【答案】(1)DE =4 (2)EF =7【分析】(1)首先根据题意求出BC 的长度,然后由E 为BC 的中点求出BE 的长度,最后即可求出DE 的长;(2)由题意可得AD +BC =AB +CD ,由F 为AD 的中点和E 为BC 的中点表示出FD +CE =12(AD +BC ),代入EF =FD +CE −CD ,即可求出EF 长.【详解】(1)∵AB =16,CD =2,AC =4,∵BC =AB −AC =16−4=12,AD =AC +CD =6,∵E 为BC 的中点,∵BE =12BC =6,∵DE =AB −AD −BE =16−6−6=4; (2)线段EF 的长度不会发生变化,EF =7, ∵AB =16,CD =2,∵AD +BC =AB +CD =16+2=18,∵F 为AD 的中点,E 为BC 的中点, ∵FD +CE =12(AD +BC )=12×18=9,∵EF =FD +CE −CD =9−2=7.【点睛】此题考查了线段的和差计算以及有关线段中点的计算问题,解题的关键是正确分析题目中线段之间的数量关系.【变式1-1】(2022·黑龙江大庆·期末)如图1,已知点C 在线段AB 上,且AM =13AC ,BN =13BC .(1)若AC =12,CB =6,求线段MN 的长. (2)若C 为线段AB 上任意一点,且满足AC +BC =a ,其他条件不变,求线段MN 的长.【答案】(1)12;(2)23a【分析】(1)若AC =12,CB =6,求线段MN 的长; (2)若点C 为线段AB 上任意一点,且满足AC +BC =a ,请直接写出线段MN 的长;(1)解:因为AM =13AC ,BN =13BC ,AC =12,CB =6,所以AM =13×12=4,BN =13×6=2.AB =AC +BC =12+6=18.所以MN =AB −AM −NB =18−4−2=12. (2)解:因为AM =13AC ,BN =13BC ,AC +BC =a , 所以:AM +BN =13(AC +BC )=13a , 所以MN =AB −(AM +BN )=AC +BC −(AM +BN )=a −13a =23a .【点睛】本题考查了两点间的距离,利用AM =13AC .BN =13BC ,得出AM 的长,BN 的长是解题关键.点C 是线段AB 上的一点,点M 、N 、P 分别是线段AC ,BC ,AB 的中点.(1)若AB =10cm ,求线段MN 的长; (2)若AC =3cm ,CP =1cm ,求线段PN 的长. 【答案】(1)MN =5cm ;(2)PN =32cm【分析】(1)根据线段中点的性质可得MC =12AC ,CN =12BC .再根据MN =MC +CN =12AC +12BC =12(AC +BC )代入计算即可得出答案;(2)先根据题意可计算出AP 的长度,由线段中点的性质可得AB =2AP ,CB =AB ﹣AC ,CN =12CB ,再根据PN =CN ﹣CP 代入计算即可得出答案. (1)解:∵M 、N 分别是AC 、BC 的中点, ∵MC =12AC ,CN =12BC ,∵MN =MC +CN =12AC +12BC =12(AC +BC )=12AB =12×10=5(cm ).(2)解:∵AC =3,CP =1,∵AP =AC +CP =4, ∵点P 是线段AB 的中点, ∵AB =2AP =8,CB =AB -AC =5,∵点N 是线段CB 的中点,∵C N =12CB =52(cm ),∵PN =CN -CP =52-1=32(cm ).【点睛】本题主要考查了两点间距离的计算,熟练掌握两点间的距离计算方法进行求解是解决本题的关键.已知B 、C 在线段AD 上,M 是AB 的中点,N 是CD 的中点,且AB =CD .(1)如图线段AD 上有6个点,则共有______条线段;(2)比较线段的大小:AC ______BD (填“>”、“=”或“<”);(3)若AD=12,BC =8,求MN 的长度. 【答案】(1)15;(2)=;(3)10【分析】(1)根据线段有两个端点,得出所有线段的条数;(2)依据AB =CD ,即可得到AB +BC =CD +BC ,进而得出AC =BD ;(3)依据线段的和差关系以及中点的定义,即可得到MN 的长度.(1)∵线段AD 上有6个点,∵图中共有线段条数为6×(6−1)÷2=15; 故答案为:15;(2)∵AB =CD ,∵AB +BC =CD +BC , 即AC =BD ;故答案为:=; (3)∵AD =12,BC =8, ∵AB +CD =AD −BC =4, ∵M 是AB 的中点,N 是CD 的中点, ∵BM =12AB ,CN =12CD ,∵BM +CN =12(AB +CD )=12×4=2,∵MN =BM +CN +BC =2+8=10.【点睛】本题主要考查了两点间的距离以及线段的和差关系,利用中点性质转化线段之间的倍分关系,在不同情况下灵活选用它的不同表示方法,有利于解题的简洁性.【题型2 线段中的方程思想】【例2】(2022·河南信阳·七年级期末)如图,A ,B ,C ,D 四点在同一条直线上.(1)若AB =CD ,①比较线段的大小:AC ______BD ;(填“>”“=”或“<”)②若BC =34AC ,且AC =24cm ,则AD 的长为______cm ;(2)若线段AD被点B,C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是20cm,求AD的长.【答案】(1)①=;②30;(2)30cm【分析】(1)①根据等式的性质,得出答案;②求出BC的值,再求出AB、CD的长,进而求出AD 的长即可;(2)根据线段的比,线段中点的意义,设未知数,列方程求解即可.(1)①∵AB= CD,∵AB+ BC= CD+ BC,即,AC= BD,故答案为:=;②∵BC=34AC,且AC = 24cm,∵BC=34×24= 18(cm),∵AB=CD=AC-BC=24-18=6 (cm)∵AD= AC+CD= 24+6= 30 (cm);故答案为:30;(2)解:如图1所示,∵线段AD被点B,C分成了3:4:5三部分,设AB=3x,则BC=4x,CD=5x,因为M是AB的中点,N是CD的中点,所以BM=12AB=32x,CN=12CD=5x2,所以32x+4x+52x=20;得x=52;所以AD=3x+4x+5x=12x=12×52=30cm.【点睛】本题考查线段的和差及其中点的有关计算,理解线段中点的意义是正确计算的前提,以及根据已知,用方程思想解决问题是解题关键.阶段练习)如图,点A、B在线段EF上,点M、N分别是线段EA、BF的中点,EA:AB:BF=1:2:3,若MN=6cm,求线段EF的长.【答案】EF的长为9cm.【分析】由于EA:AB:BF=1:2:3,可以设EA=x,AB=2x,BF=3x,而M、N分别为EA、BF的中点,那么线段MN可以用x表示,而MN=6cm,由此即可得到关于x的方程,解方程即可求出线段EF的长度.【详解】解:设EA=xcm,∵EA:AB:BF=1:2:3,∵AB=2xcm,BF=3xcm,而M、N分别为EA、BF的中点,∵MA=12EA,NB=12BF,∵MN=MA+AB+BN=12x+2x+32x=4xcm,∵MN=6cm,∵4x=6,∵x=32,∵EF=EA+AB+BF=6x=9cm.∵EF的长为9cm.【点睛】本题考查了两点间的距离.利用线段中点的性质转化线段之间的倍分关系是解题的关键,同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.【变式2-2】(2022·山东泰安·期中)如图,已知数轴上有两点A,B,它们的对应数分别是a,b,其中a=12.(1)在B左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求尺规作图,不写作法,保留作图痕迹)(2)若点C对应的数是c,点D对应的数是d,且AB=40,求c,d的值.(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=4DN,请直接写出MN的长.【答案】(1)见解析;(2)c=-68,d=92;(3)MN=28或3403【分析】(1)利用圆规量得AB的长度,以点B为圆心,AB为半径画弧,交点B左边的坐标轴于一点,即为点C;再点A为圆心,AB为半径画弧,交点A右边的坐标轴于一点,再以此点为圆心,AB为半径画弧,交圆心右边的坐标轴于另一点,则此交点为点D ;(2)根据线段之间的等量关系求得AC 、AD 的长度,从而得出点所表示的数;(3)分两种情况分析:①点N 在线段CD 上;②点N 在线段CD 的延长线上.【详解】(1)解:线段BC 、BD 为所求线段,如图所示:(2)解:∵AB =40,BC =AB ,∵AC =2AB =80, ∵a =12,∵c =12-80=-68, ∵BD =3AB ,∵BD =120,∵AD =80,设d 为x 则,x -12=80,解得:x =92,∵d =92. (3)解:①当点N 在线段CD 上时,由(2)得CD =92﹣(﹣68)=160,点B 对应的数为12﹣40=﹣28,∵BD =92﹣(﹣28)=120, ∵点M 是BD 的中点,∵点M 对应的数为92﹣60=32, ∵CN =4DN ,∵DN =15CD =32, ∵点N 对应的数为92−32=60, ∵MN =60−32=28;②当点N 在线段CD 的延长线上时,∵CN =4DN ,∵CD =3DN =160, ∵DN =1603,∵点N 对应的数为92+1603=4363,∵MN =4363−32=3403; 故MN 的长为28或3403.【点睛】本题主要考查了数轴与有理数的关系和线段中点的有关计算,解题关键是抓住线段之间的关系,体现了数形结合思想.【变式2-3】(2022·山西晋城·七年级期末)如图,数轴上点A 、B 对应着数10、15.C 、D 两点同时从点A 、原点O 出发分别以1cm/s 和2cm/s 的速度沿数轴向右运动.设运动时间为ts .(1)当t =2时,请说明BC =12AD ; (2)当t >5,且CD =AB 时,求t 的值;(3)取线段CD 的中点M ,当BM =14OA 时,求t 的值. 【答案】(1)BC =12AD ;(2)t =15;(3)t =5或t =253【分析】(1)分别计算出BC 和AD 即可等到BC =12AD ;(2)先计算得到CD 的关于t 的表达式,再根据CD =AB 求出t 即可;(3)根据M 在点B 前面和后面两种情况分别计算出BM 关于t 的表达式,再根据BM =14OA 即可计算出t .(1)当t =2时,AC =1×t =2,BC =OB −(OA +AC)=15−10−2=3 ,OD =2×t =4,AD =OA −OD =10−4=6,∵BC =12AD ; (2)当D 在C 后面时,如下图所示,OD =2t ,OC =OA +AC =10+t ,CD =OC −OD =10−t ,AB =15−10=5∵CD =AB ,∵10−t =5,∵t =5(舍去), 点D 在点C 的前面时,如下图所示,CD =OD −OC =2t −(10+t )=t −10, ∵CD =AB ,∵t −10=5,即t =15.(3)当点M 在点B 左边时,BM =OB −OM =OB −OD −DM =15−2t −12(10+t −2t)=10−32t又∵BM =14OA ,∵10−32t =14×10即t =5; 当点M 在点B 右边时,BM =OM −OB =OD +DM −OB=2t +12(10+t −2t)−15=32t −10又∵BM =14OA ,32t −10=14×10 即t =253,∵t =5或t =253.【点睛】本题考查数轴上的点及线段的长度,解题的关键是根据题意建立等式. 【例3】(2022·全国·七年级专题练习)已知线段AB 上有两点C 、D ,使得AC ∶CD ∶DB =1∶2∶3,M 是线段AC 的中点,点N 是线段AB 上的点,且满足DN =14DB ,AB =24,求MN 的长.【答案】7或13【分析】设AC =x ,则CD =2x ,DB =3x ,根据题意得x +2x +3x =24,计算得x =4,即可得AC =4,CD =8,DB =12,CB =20,根据点M 是线段AC 的中点得MC =12AC =2,根据DB =12,DN =14DB 得DN =3,分以下两种情况:①当点N 在线段CD 上时, ②当点N 在线段DB 上时,进行计算即可得.【详解】解:设AC =x ,则CD =2x ,DB =3x , ∵AB =24,∵x +2x +3x =24,6x =24解得x =4,∵AC =4,CD =8,DB =12,CB =20, ∵点M 是线段AC 的中点,∵MC =12AC =2, ∵DB =12,DN =14DB ,∵DN =14×12=3, 分以下两种情况:①当点N 在线段CD 上时,MN =MC +CD −DN =2+8−3=7,②当点N 在线段DB 上时,MN =MC +CD +DN =2+8+3=13,综上所述,线段MN 的长度为7或13.【点睛】本题考查了一元一次方程的应用,两点间的距离的计算,线段的中点的性质,解题的关键是掌握线段中点的性质,分类讨论.【变式3-1】(2022·福建省永春第一中学七年级阶段练习)如图,在数轴上A 点表示数a ,B 点表示数b ,AB 表示A 点和B 点之间的距离,且a 、b 满足(a +1)2+|b −3|=0.(1)填空:a = ,b = ,AB = ;(2)若数轴上存在一点C ,且AC =2BC ,求C 点表示的数;(3)若在原点O 处放一挡板,一小球甲从点A 处以1个单位/秒的速度向左运动,同时另一小球乙从点B 处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t (秒). ①分别表示甲、乙两小球到原点的距离(用t 表示); ②求甲、乙两小球到原点的距离相等时经历的时间.【答案】(1)-1,3,4;(2)53或7(3)①甲:t +1;乙:3−2t 或2t −3;②t =23秒或t =4秒【分析】(1)先根据非负数的性质求出a 、b 的值,再根据两点间的距离公式求得A 、B 两点之间的距离;(2)分C 点在线段AB 上和线段AB 的延长线上两种情况讨论即可求解;(3)①甲球到原点的距离=甲球运动的路程+OA 的长,乙球到原点的距离分两种情况:(∵)当0<t ≤32时,乙球从点B 处开始向左运动,一直到原点O ,此时OB 的长度-乙球运动的路程即为乙球到原点的距离;(∵)当t >32时,乙球从原点O 处开始向右运动,此时乙球运动的路程-OB 的长度即为乙球到原点的距离;②分两种情况:(∵)0<t ≤32,(∵)t >32,根据甲、乙两小球到原点的距离相等列出关于t 的方程,解方程即可.(1)因为(a+1)2+|b−3|=0,所以a+1=0,b−3=0,所以a=−1,b=3;所以AB的距离=|b−a|=4,故答案为:-1,3,4;(2)设数轴上点C表示的数为c.因为AC=2BC,所以|c−a|=2|c−b|,即|c+1|=2|c−3|.因为AC=2BC>BC,所以点C不可能在BA的延长线上,则C点可能在线段AB上和线段AB的延长线上.①当C点在线段AB上时,则有−1<c<3,得c+1=2(3−c),解得c=53;②当C点在线段AB的延长线上时,则有c>3,得c+1=2(c−3),解得c=7.故当AC=2BC时,c=53或c=7;(3)①因为甲球运动的路程为:1×t=t,OA=1,所以甲球与原点的距离为:t+1;乙球到原点的距离分两种情况:(I)当0<t≤32时,乙球从点B处开始向左运动,一直到原点O,因为OB=3,乙球运动的路程为:2×t=2t,所以乙球到原点的距离为:3−2t;(I I)当t>32时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2t−3;②当0<t≤32时,得t+1=3−2t,解得t=23;当t>32时,得t+1=2t−3,解得t=4.故当t=23秒或t=4秒时,甲乙两小球到原点的距离相等.【点睛】本题考查了一元一次方程的应用,非负数的性质,方程的解法,数轴,两点间的距离,有一定难度,运用分类讨论思想、方程思想及数形结合思想是解题的关键.【变式3-2】(2022·全国·七年级专题练习)如图,点C是线段AB上的一点,线段AC=8m,AB=32BC.机器狗P从点A出发,以6m/s的速度向右运动,到达点B后立即以原来的速度返回;机械猫Q从点C出发,以2m/s的速度向右运动,设它们同时出发,运动时间为xs.当机器狗P与机械猫Q 第二次相遇时,机器狗和机械猫同时停止运动.(1)BC=______m,AB=______m;(2)试通过计算说明:当x为何值时,机器狗P在点A与机械猫Q的中点处?(3)当x为何值时,机器狗和机械猫之间的距离PQ =2m?请直接写出x的值.【答案】(1)16,24.(2)当x=45,即运动45秒时,机器狗P在点A与机械猫Q的中点处.(3)当x=32或x=52或x=194,即运动x=32或x=52或x=194秒时,机器狗和机械猫之间的距离PQ=2m.【分析】(1)由AB=32BC且AC=8cm得8+BC=32BC,先求出BC的长,然后再求出AB的长即可;(2)先确定机器狗P在点A与机械猫Q的中点处只存在一种情况,即机器狗P与机械猫Q第一次相遇之前,再根据线段AP=12AQ列方程求出x的值即可;(3)分三种情况,一是点P在线段AQ上,可根据AP+2=AQ列方程求出x的值;二是点P在线段BQ 上且点P到达点B之前,可根据AP-2=AQ列方程求出x的值;三是点P在线段BQ上且点P从点B 返回时,可根据2AB减去点P运动的距离等于AQ+2列方程求出x的值即可.【详解】(1)解:∵AB =32BC ,AB =AC +BC ,AC =8m , ∵8+BC =32BC ,解得:BC =16m ,∵AB =32×16=24m .故答案为:16,24.(2)解:由题意可得::机器狗P 在点A 与机械猫Q 的中点处只存在一种情况,即机器狗P 与机械猫Q 第一次相遇之前,∵6x =12{8+2x ),解得x =45. 答:当x =45,即运动45秒时,机器狗P 在点A 与机械猫Q 的中点处.(3)解:当点P 在线段AQ 上且PQ =2m 时,则6x +2=8+2x ,解得x =32;当点P 在线段BQ 上且PQ =2m 时,则6x -2=8+2x 或24×2-6x =8+2x +2,解得x =52或x=194.答:当x =32或x =52或x =194,即运动x =32或x =52或x =194秒时,机器狗和机械猫之间的距离PQ =2m . 【点睛】本题主要考查了解一元一次方程、一元一次方程的应用、线段上的动点问题的求解等知识点,正确地用含x 的代数式表示线段A P 和AQ 的长是解答本题的关键.江西省丰城中学七年级期中)已知数轴上A 点表示的数是a ,B 点表示的数是b ,且a ,b 满足式子(a +3)2+|b −6|=0. (1)写出a =______,b =______.(2)将数轴上线段AB 剪下来,并把AB 这条线段沿着某点折叠,然后在重叠部分某处剪一刀得到三条线段,若这三条线段的长度之比为1:2:2,求折痕处对应的点所表示的数. 【答案】(1)−3;6;(2)35或32或125【分析】(1)根据绝对值的非负性与偶次方的非负性,非负数的性质得出a +3=0,b −6=0,再解方程即可求解.(2)设折痕处点表示数为x ,被剪处为点C 、D ,分三种情况:①当AC:CD:DB =1:2:2时,②当AC:CD:DB =2:1:2时,③当AC:CD:DB =2:2:1时,分别求解好戏可.(1)解:∵(a +3)2+|b −6|=0, 又∵(a +3)2≥0,|b −6|≥0,∵a +3=0,b −6=0,∵a =−3,b =6. 故答案为:−3;6.(2)解:设折痕处点表示数为x , ①当AC:CD:DB =1:2:2时,AB =5AC =9,∵AC =95, ∵x =−3+2×95=35.②当AC:CD:DB =2:1:2时,则AB =5CD =9,∵CD =95, ∵AC +12CD =52CD =52×95=92,∵x =−3+92=32.③当AC:CD:DB =2:2:1时,则AB =5DB =9,∵DB =95,∵AC +12CD =3DB =3×95=275.∵x =−3+275=125.∵综上,折痕处表示的数为:35或32或125.【点睛】本题考查用数轴上的点表示有理数,非负数的性质,线段和差倍分,熟练掌握偶次方与绝对值的非负性,分类讨论思想的应用是解题的关键. 【例4】(2022·广东东莞·七年级期末)如图,C 是线段AB 上一点,AB =12cm ,AC =4cm ,P 、Q 两点分别从A 、C 出发以1cm/s 、2cm/s 的速度沿直线AB向右运动,运动的时间为ts.(1)当t=1s时,CP=cm,QB=cm;(2)当运动时间为多少时,PQ为AB的一半?(3)当运动时间为多少时,BQ=AP?【答案】(1)3,6;(2)运动时间为2s时,PQ为AB的一半;(3)运动时间为83s或8s时,BQ=AP【分析】(1)根据CP=AC−AP,QB=AB−AQ 的关系,由P、Q两点分别从A、C出发以1cm/s、2cm/s的速度沿直线AB向右运动,求解当t=1s对应的长度即可;(2)通过建立一元一次方程进行求解即可;(3)通过分类讨论的思想,当点Q到点B的左边或右边时,通过建立一元一次方程进行求解.(1)解:∵CP=AC−AP,当t=1s,AP=1cm,∴CP=4−1=3cm,∵QB=AB−AQ,当t=1s,CQ=2cm,∴QB=12−4−2=6cm,故答案为:3,6;(2)解:设运动t秒时,PQ是AB的一半,当点P到点C的左边时,∴PQ=PC+CQ=4−t+ 2t=6,解得:t=2,当点P到点C的右边时,PQ的距离大于AB的一半,不满足题意,故运动时间为2s时,PQ是AB的一半;(3)解:当点Q到点B的左边时,设运动t秒时,BQ=AP,则8−2t=t,解得:t=83,当点Q到点B的右边时,设运动t秒时,BQ=AP,则2t−8=t,解得:t=8,故运动时间为83s或8s时,BQ=AP.【点睛】本题考查了数轴上的动点问题,一元一次方程,两点间的距离,解题的关键是通过数形结合及分类讨论的思想进行求解.【变式4-1】(2022·山东德州·七年级期末)已知,线段AB=20,M是线段AB的中点,P是线段AB上任意一点,N是线段PB 的中点.(1)当P是线段AM的中点时,求线段NB的长;(2)当线段MP=1时,求线段NB的长;(3)若点P在线段BA的延长线上,猜想线段PA与线段MN的数量关系,并画图加以证明.【答案】(1)7.5;(2)4.5或5.5;(3)PA=2MN,画图证明见解析.【分析】(1)画出符合题意的图形,先求解AM= 10,再求解AP=5,可得PB=15,再利用中点的含义可得答案;(2)分两种情况讨论:当P在M左边时,当P在M右边时,先求解PB,再利用中点的含义可得答案;(3)当P在线段BA延长线上时,如图,设PA=t,求解NB=10+12t,再求解MN=NB−MB=12t,从而可得结论.【详解】解:(1)如图,∵M是线段AB的中点,AB= 20∵MA=12AB=10∵P是线段AM的中点,∵AP=12AM=5∵PB=AB−AP=20−5=15∵N是线段PB的中点,∵NB=12PB=7.5(2)∵MP=1,∵当P在M左边时,如图,BP=MB+MP=11,∵N是线段PB的中点,∵NB=12PB=5.5,如图,当P在M右边时,BP=MB−MP=9,∵N是线段PB的中点,∵NB=12PB=4.5.(3)线段PA和线段MN的数量关系是:PA=2MN,理由如下:当P在线段BA延长线上时,如图,设PA= t,则PB=20+t∵N是线段PB的中点,∵NB=12PB=10+12t∵M是线段AB的中点,AB=20,∵MB=12AB=10∵MN=NB−MB=12t又∵PA=t,∵PA=2MN【点睛】本题考查的是线段的和差关系,线段的中点的含义,整式的加减运算,分类思想的运用,掌握以上知识是解题的关键.【变式4-2】(2022·全国·七年级专题练习)如图,已知直线l上有两条可以左右移动的线段:AB=m,CD=n,且m,n满足|m−4|+(n−8)2=0,点M,N分别为AB,CD中点.(1)求线段AB,CD的长;(2)线段AB以每秒4个单位长度向右运动,线段CD 以每秒1个单位长度也向右运动.若运动6秒后,MN=4,求此时线段BC的长;(3)若BC=24,将线段CD固定不动,线段AB以每秒4个单位速度向右运动,在线段AB向右运动的某一个时间段t内,始终有MN+AD为定值.求出这个定值,并直接写出t在哪一个时间段内.【答案】(1)线段AB的长是4,线段CD的长是8(2)16或8(3)当7.5≤t≤9时,MN+AD为定值,定值为6【分析】(1)利用绝对值和平方的非负性求出m 和n的值即可;(2)分M′在N′的左侧和M′在N′的右侧两种情况,根据线段的和差关系列出方程,即可求解;(3)由题意,运动t秒后,MN=|30−4t|,AD= |36−4t|,分段讨论即可求解.(1)解:∵|m−4|+(n−8)2=0,∵|m−4|=0,(n−8)2=0,∵m=4,n=8,∵AB=4,CD=8,即线段AB的长是4,线段CD的长是8;(2)解:∵AB=4,CD=8,∵MB=12AB=2,CN=12CD=4,设运动后点M对应点为M′,点N对应点为N′,分两种情况,若6秒后,M′在N′的左侧时:MN+ NN′=MM′+M′N′,∵MB+BC+CN+NN′=MM′+M′N′,即2+BC+4+6×1=6×4+4,解得BC=16.若6秒后,M′在N′的右侧时:MM′=MN+NN′+ M′N′,∵MM′=MB+BC+CN+NN′+M′N′,即6×4=2+BC+4+6×1+4,解得BC=8.即线段BC的长为16或8;(3)解:∵BC=24,AB=4,CD=8,∵MN=BC+12AB+12CD=24+2+4=30,AD=BC+AB+CD=24+4+8=36,∵线段CD固定不动,线段AB以每秒4个单位速度向右运动,∵运动t秒后,MN=|30−4t|,AD=|36−4t|,当0≤t<7.5时,MN+AD=30−4t+36−4t= 66−8t;当7.5≤t≤9时,MN+AD=4t−30+36−4t= 6;当t>9时,MN+AD=4t−30+4t−36=8t−66;故当7.5≤t≤9时,MN+AD为定值,定值为6.【点睛】本题考查非负数的性质,一元一次方程的应用,线段的和差关系,以及数轴上的动点问题,解题的关键是掌握分类讨论思想.【变式4-3】(2022·河南周口·七年级期末)学习了线段的中点之后,小明利用数学软件GeoGebra做了n次取线段中点实验:如图,设线段OP0=1.第1次,取OP0的中点P1;第2次,取P0P1的中点P2;第3次,取P1P2的中点P3,第4次,取P2P3的中点P4;…(1)请完成下列表格数据.(2)小明对线段OP4的表达式进行了如下化简:因为OP4=1−12+122−123+124,所以2OP4=2(1−12+122−123+124)=2−1+12−1 22+123.两式相加,得3OP4=2+124.所以OP4=23+13×24.请你参考小明的化简方法,化简OP5的表达式.(3)类比猜想:P n−1P n=__________,OP n=_________________,随着取中点次数n的不断增大,OP n的长最终接近的值是__________.【答案】(1)P4P5=125,OP5=OP4−P4P5=1−12+1 22−123+124−125(2)OP5=23−13×25(3)12n,23+(−1)n3×2n,23【分析】(1)根据表中的规律可求出P4P5,根据OP5=OP4−P4P5可得出答案;(2)参照小明对线段OP4的表达式的化简可得OP5的表达式;(3)根据类比猜想可得答案.(1)解:P4P5=125,OP5=OP4−P4P5=1−12+122−123+124−125;故答案为:P4P5=125,OP5=OP4−P4P5=1−12+122−123+124−125;(2)解:因为OP5=1−12+122−123+124−125,所以2OP5=2(1−12+122−123+124−125)=2−1+12−122+123−124.两式相加,得3OP5=2−125.所以OP5=23−13×25;(3)解:P n−1P n=12n,OP n=23+(−1)n3×2n,随着取中点次数n的不断增大OP n的长最终接近的值是23.故答案为:12n,23+(−1)n3×2n,23.【点睛】本题考查规律型:图形的变化类,找到规律并会表现出来是解题关键.次数Pi-1Pi线段OPi的长第1次P0P1=12OP1=OP0−P0P1=1−12第2次P1P2=122OP2=OP1+P1P2=1−12+122第3次P2P3=123OP3=OP2−P2P3=1−12+122−123第4次P3P4=124OP4=OP3+P3P4=1−12+122−123+124第5次………。
第二章+机械振动+单元练习-2022-2023学年高二上学期物理人教版(2019)选择性必修第一册
选择性必修一第二章机械振动【知识网络】考向一:简谐运动的规律1.如图9甲所示,一弹簧振子在A、B之间做简谐运动,O点为振子静止的位置,其振动图像如图乙所示,规定向右的方向为正方向,试根据图像分析以下问题:图9(1)在t=0时刻,振子所处的位置为________,正在向________(选填“左”或“右”)运动.(2)A、B两点间的距离为________ cm.(3)在图乙中,振子在t=1 s、t=2 s和t=3 s时所处的位置依次是________、________和________.(4)在t=2 s时,振子速度的方向与t=0时速度的方向________.(5)振子在前4 s 内的位移等于________ cm ,其路程为________ cm.2.一个做简谐运动的质点,先后以同样的速度通过相距10 cm 的A 、B 两点,历时0.5 s(如图所示).过B 点后再经过t =0.5 s ,质点以大小相等、方向相反的速度再次通过B 点,则质点振动的周期是( ) A .0.5 s B .1.0 s C .2.0 s D .4.0 s3.弹簧振子以O 点为平衡位置做简谐运动,从振子通过O 点时开始计时,振子第一次到达M 点用了0.3 s ,又经过0.2 s 第二次通过M 点,求振子第三次通过M 点还要经过的时间.●如图所示为水平的弹簧振子示意图,振子运动过程中各物理量的变化情况如下表.振子的运动 A →O O →A ′ A ′→O O →A 位移 方向 向右 向左 向左 向右 大小 减小 增大 减小 增大 回复力 方向 向左 向右 向右 向左 大小 减小 增大 减小 增大 加速度 方向 向左 向右 向右 向左 大小 减小 增大 减小 增大 速度方向 向左 向左 向右 向右 大小增大 减小 增大 减小 振子的动能 增大 减小 增大 减小 弹簧的势能 减小 增大 减小 增大 系统总能量不变不变不变不变考向二:简谐运动的表达式及图像1.(2020·福建省永春第一中学月考)有一个弹簧振子,振幅为0.8 cm ,周期为0.5 s ,初始时具有负方向的最大加速度,则它的振动方程是( )A .x =8×10-3sin(4πt +π2) mB .x =8×10-3sin(4πt -π2) mC .x =8×10-3sin(4πt +3π2) mD .x =8×10-3sin(π4t +π2) m2.如图甲所示,弹簧振子以O 点为平衡位置,在M 、N 两点之间做简谐运动,以向右为正方向.振动物体的位移x 随时间t 变化的图像如图乙所示.下列判断正确的是( )A .t =0.8 s 时,振动物体的速度方向向右B .振动物体做简谐运动的表达式为x =12sin (1.25πt ) cmC .t =0.4 s 和t =1.2 s 时,振动物体的加速度相同D .从t =0.4 s 到t =0.8 s 时间内,振动物体的速度逐渐减小考向三:简谐运动的回复力1.如图1所示,物体A 与滑块B 一起在光滑水平面上做简谐运动,A 、B 之间无相对滑动,已知水平轻质弹簧的劲度系数为k ,A 、B 的质量分别为m 和M ,最大静摩擦力等于滑动摩擦力,重力加速度为g ,则下列说法不正确的是( )A .物体A 的回复力是由滑块B 对物体A 的摩擦力提供的 B .滑块B 的回复力是由弹簧的弹力提供的C .物体A 与滑块B (整体看成一个振子)的回复力大小跟位移大小之比为kD .若A 、B 之间的动摩擦因数为μ,则A 、B 间无相对滑动的最大振幅为μ(m +M )gk2.如图10所示,轻弹簧的下端系着A 、B 两球,m A =100 g ,m B =500 g ,系统静止时弹簧伸长x =15 cm ,未超出弹性限度.若剪断A 、B 间细绳,则A 在竖直方向做简谐运动.问: (1)A 球的振幅为多大?(2)A 球的最大加速度为多大?(g 取10 m/s 2)考向四:单摆1.如图所示,在两根等长的细线下悬挂一个小球(体积可忽略),组成了双线摆,若细线长均为l ,两线与天花板的夹角均为α,重力加速度为g ,当小球垂直纸面做简谐运动时,周期为( ) A .2πl g B .2π2l g C .2π2l cos αgD .2πl sin αg2.(2020·太原市现代双语学校期中)将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动.用频闪照相机拍到如图所示的单摆运动过程的频闪照片,以下说法不正确的是( )A .这个实验说明了动能和势能可以相互转化,转化过程中机械能守恒B .摆线碰到障碍物前后的摆长之比为9∶4C .摆球经过最低点时,线速度不变,做圆周运动的半径减小,摆线张力变大D .摆球经过最低点时,角速度变大,做圆周运动的半径减小,摆线张力不变3.(2020·烟台市高二上期中)如图7所示,一个光滑弧形凹槽半径为R ,弧长为L (已知R ≫L ).现将一质量为m 的小球从凹槽边缘由静止释放,小球以最低点为平衡位置做简谐运动.已知重力加速度大小为g ,下列说法正确的是( ) A .小球做简谐运动的回复力为重力和支持力的合力B .小球做简谐运动的回复力为重力沿凹槽圆弧切线方向的分力C .小球做简谐运动的周期为2πLgD .小球运动到凹槽最低点时所受合力为零4.如图所示,一单摆悬于O 点,摆长为L ,若在O 点正下方的O ′点钉一个光滑钉子,使OO ′=L2.将摆球拉至A 处由静止释放,小球将在A 、C 之间来回振动,若振动过程中摆线与竖直方向的夹角小于5°,重力加速度大小为g ,则以下说法正确的是( ) A .由于机械能守恒,可得摆角大小不变B.A点高于C点C.周期T=2π(Lg+L2g)D.周期T=π(Lg+L2g)考向五:实验:用单摆测量重力加速度1.注意事项(1)选择细而不易伸长的线,长度一般不应短于1 m;摆球应选用密度较大、直径较小的金属球.(2)摆动时摆线偏离竖直方向的角度应很小.(3)摆球摆动时,要使之保持在同一竖直平面内,不要形成圆锥摆.(4)计算单摆的全振动次数时,应从摆球通过最低位置时开始计时,要测n次全振动的时间t. 1.某同学利用单摆测当地重力加速度。
福建省永春第一中学2022-2023学年高一上学期数学竞赛试题
2.25班级:___________座位号:___________姓名:___________成绩:___________一、填空题(每题7分,共84分)1.【2021年吉林预赛】已知四个整数a,b,c,d都是偶数,且0<a<b<c<d,d−a=90,若a,b,c成等差数列,b,c,d 成等比数列,则a+b+c+d=.2.【2021年福建预赛】若正实数x,y满足x(x+2y)=9,则x5y的最大值为.3.【2021年浙江预赛】设直角坐标平面上两个区域为M={(x,y)∈ℝ2∣0≤y≤min(2x,3−x)},N={(x,y)∈ℝ2∣t≤x≤t+2},记M与N的公共部分面积为f(t)。
当0≤t≤1时,则f(t)的表达式为. 4.【2021年广西预赛】已知xy+yz+zx=1,其中x,y,z均为正数,则√3xy+1+√3yz+1+√3zx+1的整数部分为.5.【2020年福建预赛】已知a、b、c、d为正数,且a+20b=c+20d=2.则1a +1bcd的最小值为.6.【2021年全国高中数学联赛A卷一试】设函数f(x)满足:对任意非零实数x,均有f(x)=f(1)⋅x+f(2)x−1,则f(x)在(0,+∞)上的最小值为.7.【2021年全国高中数学联赛B卷一试】设函数f(x)的定义域为D=(−∞,0)∪(0,+∞),且对任意x∈D,均有f(x)=f(1)⋅x2+f(2)⋅x−1x,则f(x)的所有零点之和为.8.【2021年全国高中数学联赛B卷一试】设a,b,c>1,满足(a2b)log a c=a⋅(ac)log a b,则log c(ab)的值为.9.【2020高中数学联赛A卷(第01试)】设a,b>0,满足:关于x的方程√|x|+√|x+a|=b恰有三个不同的实数解x1,x2,x3,且x1<x2<x3=b,则a+b的值为.10.【2020高中数学联赛B卷(第01试)】若实数x满足log2x=log4(2x)+log8(4x),则x=. 11.【2020高中数学联赛B卷(第01试)】已知首项系数为1的五次多项式f(x)满足: f(n)=8n,n=1,2,⋯,5,则f(x)的一次项系数为.12.【2020年福建预赛】已知函数f(x)是定义在R上的偶函数,且对任意实数x,均有f(x+1)=f(1−x)成立,当1⩽x⩽2时,f(x)=lnx.若关于x的方程f(x)+ax−1=0在x∈[3,5]上有两个不相等的实数根,则a的取值范围是.二、解答题(16分)13.【2020年福建预赛】如图所示,在△ABC中,AB<AC,△ABC的内切圆⊙I与边BC、CA分别切于点D、E,联结AI并延长,与△ABC的外接圆⊙O交于点N,联结ND、NO并延长,分别与⊙O交于点G、M,联结GE并延长,与⊙O交于点F.证明(1)△NIG∼△NDI;(2)MF//AC.。
人教版九年级下册物理光学作图专题例题+习题 九年级物理第四章
光学作图考向一:光的反射例题引领(2019·福建初二期中)请在图中画出反射光线OB的入射光线AO,并标出入射角及其大小。
【参考答案】【详细解析】因为反射光线与镜面的夹角为60°,所以反射角为30°,可得入射角也为30°,在法线右侧画出入射光线AO,角度为30°,如图所示:变式拓展1.(2019·贵州中考模拟)下图是表示某一段光导纤维,一束激光从一端射入光导纤维,试在图中画出激光在光导纤维中传播时的情形。
【答案】【解析】激光在光导纤维中传播时的情形,遵循光的反射定律,满足反射角等于入射角,光路图如下:2.(2019·山东中考模拟)潜水艇下潜后,艇内的人员可以用潜望镜来观察水面上的情况。
我们利用两块平面镜就可以制作一个潜望镜。
如果一束光水平射入潜望镜镜口,它将经过怎样的路径射出?画出光路图来。
【答案】【解析】过入射点画出法线,根据反射角等于入射角画出反射光线,再过二次入射点画出法线,根据反射角等于入射角画出反射光线,如图所示:考向二:平面镜成像例题引领(2019·福建初二期中)根据平面镜成像的特点,在图中画出物体AB在平面镜MN中所成的像A'B'。
【参考答案】【详细解析】分别作出物体AB的端点A. B关于平面镜的对称点A′、B′,用虚线连接A′、B′即为AB在平面镜中的像。
如图所示:变式拓展1.(2019·高邮市朝阳中学初二期中)如图所示,AB、CD是平面镜前一点光源S发出的光经平面镜M 反射后的两条反射光线,请在图中标出光源S和像点S 的位置,并完成光路图。
【答案】【解析】先将两条反射光线反向延长交于一点,该点即像点S',再作出S'关于平面镜的对称点,该点即光源S的位置,连接S与两个入射点画出两条入射光线,如图所示:2.(2019·山东中考模拟)平静水面的上方有一只小鸟,水中有条小鱼,水面一侧C点的人眼恰好看到它们在水中的像重合。
如何用导数解决含参函数的单调性问题
49
如何用导数解决含参函数的单调性问题余铭战(福建省永春第一中学 362601)1 提出问题我们在解决单调性问题中,常常遇到一类含有参数的函数(简称含参函数)在某区间单调问题:
问题1 已知函数f(x)=
13x3-1
2ax2+(a-
1)x+1在(1,4)内是减函数,在(6,+
∞)内是增函
数,求a的取值范围.
问题2 如果函数f(x)=
1
2(a-1)x2+ax
在
(1,3)上为增函数,求实数a的取值范围.
问题3 (2005年湖南,理21(Ⅰ))已知函数
f(x)=lnx,g(x)=12ax2+bx,a≠0.若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
问题4 (2005年湖南,文19)设t≠0,点P(t,
0)是函数f(x)=x3+ax与g(x)=bx2+c
的图象
的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用t表示a,b,c;
(Ⅱ)若函数y=f(x)-g(x)在(-1,3)上单调递减,求t的取值范围.
上述问题是逆向单调性问题.
2 探究问题在逆向解决单调性时,至少应考虑题设成立的必要条件.而在教材[1]中对函数的单调性是这样描述的:“一般地,设函数y=f(x)在某个区间内可导,如果f′(x)>0,则f(x)为增函数;如果f′(x)
<0,则f(x)为减函数.”它给复杂函数单调性的判断带来了极大方便,但它给出的只是单调性的充分
条件.如函数f(x)=x3的单调性,由单调性的定义,易证f(x)在(-∞,+∞)上为增函数,而由导数得f′(x)=3x2≥0.这说明如果要使函数严格单调的话,导函数在某些点可以取零,但取零的点必须是离散的才行,否则只能说它是不严格单调.在教材[1]中还有:“如果函数在某个区间内恒有f′(x)=0,则f(x)为常数”,又由于“常数的导数为0”,因而它给出了函数在某个区间为常数函数的充要条件.这说明f′(x)=0在某区间上有连续解时,
f(x)不具有单调性,而f′(x)=0只是离散解时,不影响f(x)的单调性.于是我们可得出如下结论:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二年(理科班)各学科寒假学习指导
2013年2月1日
语文
为了让同学们过一个愉快、充实而有意义的寒假,根据语文科特点,提出以下学习要求,希望予以重视
和落实。
一、总体要求
1、读书是语文的第一要务。
2、提高作文成绩是提高语文成绩的关键。
二、具体任务
1、根据《文学名著、文化经典阅读计划》,认真阅读《子夜》和《孟子》(《万章上》《万章下》《告
子上》《告子下》);也可巩固此前要求阅读的内容。
2、主动融入生活,注意观察生活、体验生活,把自己的所见所闻所感在“周记”中记录下来;把自己
的读书心得在“周记”中记录下来。这样的作文每周不少于2篇。
3、“周记”和“寒假作业”下学期开学时交给科代表。
英语
数学(理
科)
2月1日 寒假开始,学生回家休整
2月2日一4日 看至少一本英语名著简写本或阅读英文报纸
2月5日一6日 复习Module5单词及课文知识点,补缺补漏,做寒假练习卷(一)
2月7日一8日 复习Module5单词及课文知识点,补缺补漏,做寒假练习卷(二)
2月9日一12日 欢度春节,并可利用网上资源浏览有关春节的英语报道
2月13日一14日 复习Module6单词及课文知识点,补缺补漏,做寒假练习卷(三)
2月15日一16日 复习Module6单词及课文知识点,补缺补漏,做寒假练习卷(四)
2月17日 预习Module7Unit19单词及课文,做好开学准备
时间 温习知识:重做配套练习册的章末练习,有缺漏自己及时补。
2月1日 正弦定理、余弦定理
2月2日 等差数列及前n项和
2月3日 等比数列及前n项和
2月4日 不等式性质、一元二次不等式及其解法
2月5日 线性规划
2月6日 基本不等式
2月7日 必修5综合测试卷2份
2月8日 简易逻辑
2月9-12日 欢度春节
2月13日 椭圆
2月14日 双曲线
物 理
1、对本学期教学内容进行复习整合,注重理解场的概念、场的表征及其力和能的属性、电与磁的统一。
2、完成物理寒假作业共有电场、电路、磁场、综合四部分,每部份限时90分钟,要联想反思融会贯
通。
3、预习新课《电磁感应》,理解磁通量、磁通变化量、磁通变化率的异同。
化学
1、本学期学习的模块《化学反应原理》是高考的重要内容,高考中所占的分值较多,同学应给予充分
重视。部分学生练习册《顶尖课课练》单元练习没有完成,希利用假期复习、完成。
2、完成年段统一的寒假作业。
3、预习选修3《物质结构》
4、参加竞赛辅导的同学完成的竞赛辅导材料练习主要《有机化学》、《无机化学》、《物理化学》和《分
析化学》。
2月15日 抛物线
2月16日 选修2-1综合测试卷2分
时间 复习完成内容
2.1.一2.3 第一章 化学反应与能量 完成寒假作业
2.4一2.6 第二章 反应速率与化学平衡专题 完成寒假作业
2.7一2.8 第三章 电离平衡 溶液的酸碱性 完成寒假作业
2.9一2.12 庆祝春节
2.13一2.14 第三章 盐类水解 沉淀溶解平衡 完成寒假作业
2.15一2.17 预习选修3《物质结构》
生物
一、复习高中生物必修3课本、《阳光课堂》练习册中做错的题再看看,再研究。
二、学习高中生物选修3课本专题一和专题二。
三、认真、按时按质完成生物寒假作业。
四、学习计划:
五、参加生物辅优的同学还必须完成:
1.期末竞赛试卷的更正;
2.复习已辅导的知识内容和相关练习;
3.学习《新编高中生物奥赛指导》之动物生理和生态学与动物行为学等部分。
时间 学习内容 完成相关练习
2.1——2.4 第一章 至第二章(必修Ⅲ) 高二年生物寒假作业(一)
2.5——2.7 第三章 至第四章(必修Ⅲ) 高二年生物寒假作业(二)
2.8——2.12 庆祝春节
2.13——2.15 第五章 至第六章(必修Ⅲ) 高二年生物寒假作业(三)
2.16——2.17 专题一(选修Ⅲ) 高二年生物寒假作业(四)
