高分子物理-聚合物的非晶态
高分子物理第五章聚合物分子运动与转变

P131 图5-2
15
5.2.1 非晶态聚合物
形变
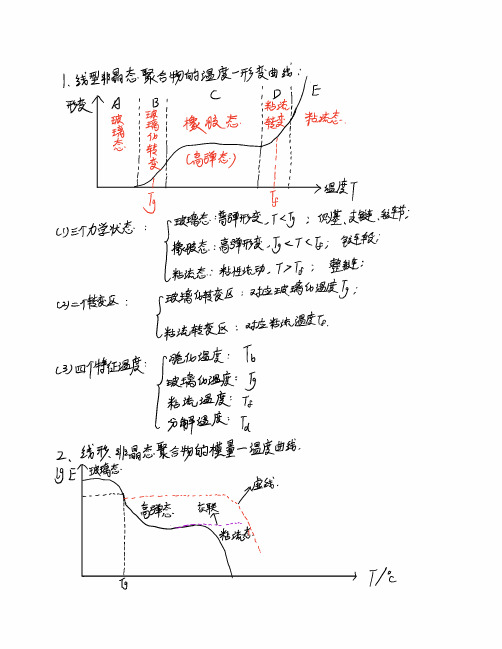
三种力学状态: 玻璃态(Tg 以下) 高弹态(Tg ~ Tf) 粘流态(Tf 以上)
高弹态 粘流态 玻璃态
三态两区
Tg
Tf
温度
温度-形变曲线(热-机曲线)
三种状态之间的两个转变: 玻璃态转变为高弹态,转变温度称为玻璃化温度Tg 高弹态转变为粘流态,转变温度称为粘流温度Tf
22
5.2.2 晶态聚合物的力学状态
晶态高聚物中总有非晶区存在,非晶部分高聚物 在不同温度下也要发生上述二种转变,但它的宏 观表现与结晶度大小有关 1,轻度结晶聚合物 2,结晶度高于40%的聚合物
23
1,轻度结晶聚合物
试样存在明显的玻璃化温度转变。温度上升时,非晶部分由玻 璃态转变为高弹态。但由于微晶的存在起着交联点的作用,所 以非晶区不会发生很大的形变,形成皮革状。
高弹态
Tg ~ T f
粘流态
Tf
以上
18
两个转变时的分子运动与宏观表现
玻璃化转变 Glass transition: 整个大分子链还 无法运动,但链段开始发生运动,模量下降3~4 个数量级。 粘流转变 Viscosity flow transition: 分子链重 心开始出现相对位移。模量再次急速下降。聚合 物既呈现橡胶弹性,又呈现流动性。对应的转温 度Tf称为粘流温度。
高分子物理作业解答

高分子物理作业-2-答案聚合物的力学状态及转变1. 解释名词:(1)聚合物的力学状态及转变由于高分子链之间的作用力大于主链的价键力,所以聚合物只具有固态和液态力学状态。
随着温度的升高,分子热运动能量逐渐增加,当达到某一温度时,即可发生两相间的转变。
(2)松弛过程与松弛时间松弛过程:在一定温度和外场(力场、电场、磁场等)作用下,聚合物由一种平衡态通过分子运动过渡到另一种与外界条件相适应的、新的平衡态,这个过程是一个速度过程。
松弛时间τ是用来描述松弛快慢的物理理。
在高聚物的松弛曲线上,∆x t ()变到等于∆x o 的1/e 倍时所需要的时间,即松弛时间。
(3)自由体积与等自由体积状态 分子中未被占据的体积为自由体积;在玻璃态下,由于链段运动被冻结晶,自由体积也被冻结,并保持一恒定值,自由体积“孔穴”的大小及其分布也将基本上维持固定。
因此,对任何高聚物,玻璃温度就是自由体积达到某一临界值的温度,在这临界值以下,已经没有足够的窨进行分子链的构象调整了。
因而高聚物的玻璃态可视为等自由体积状态。
(4)玻璃态与皮革态当非晶态高聚物在较低的温度下受到外力时,由于链段运动被冻结,只能使主链的键长和键角有微小的改变,因此从宏观上来说,高聚物受力变形是很小的,形变与受力和大小成正比,当外力除去后形变能立刻回复。
这种力学性质称为普弹性,非晶态高聚物处于具有普弹性的状态,称为玻璃态;部分结晶聚合物,存在玻璃化转变与高弹态,但由于晶区链段不能运动,此时玻璃化转变不再具有很大弹性的高弹态,而表现为具有一定高弹性、韧而硬的皮革态,即皮革态。
2. 试定性地绘出下列聚合物的形变—温度曲线(画在一张图上)1) 低分子玻璃态物质 2) 线性非晶态聚合物(1M )3) 线性非晶态聚合物(212,M M M 〉212,M M M 〉>1M ) 4) 晶态聚合物(1M )5) 晶态聚合物(212,M M M 〉212,M M M 〉>1M ) 6) 交联聚合物(交联度较小) 7) 交联聚合物(交联度较大)3. 判断下列聚合物(写出分子式)的Tg 的高低,阐述其理由:1) 聚乙烯、聚对苯二甲酸乙二酯、聚苯、聚二甲基硅氧烷 2) 聚氯乙烯、聚氯丁二烯、聚偏二氯乙烯、顺式1,4聚丁二烯 3) 聚乙烯、聚异丁烯、聚苯乙烯、聚乙烯基咔锉 4) 聚乙烯、聚丙烯、聚氯乙烯、聚丙烯腈5) 聚甲基乙烯基醚、聚乙基乙烯基醚、聚正丙基乙烯基醚、聚正丁基乙烯基醚1) 聚乙烯、聚对苯二甲酸乙二酯、聚苯、聚二甲基硅氧烷CH 2CH 2n聚乙烯CO C OO CH 2CH 2On聚对苯二甲酸乙二酯n聚苯Si CH 33On聚二甲基硅氧烷聚二甲基硅氧烷<聚乙烯<聚对苯二甲酸乙二酯<聚苯理由:当主链中引入苯基、联苯基、萘基和均苯甲酸二酰胺基等芳杂环以一,链上可以内旋转的单键比例相对减少,分子链的刚性增大,因此有利于玻璃化温度的提高。
高分子物理常用图形整理
以四个特征温度脆化温度后玻璃化温度可粘流温度不不分解温度uT c3.分⼦子量量对温度形变曲线形状的影响T粘流态原⾼高弹态TN玻璃态可m4分⼦子量量越⼤大缠结越严重克服缠结所需的温度越⾼高平台越⻓长⼋八g E M cuz MKM4M5panhrgflthpnperatumy Mz M4M55低结晶度⾼高聚物的印曲线E⼋八Me My11-ii iI i i班y h f结晶⾼高聚物的晶区熔融后是否进⼊入粘流态由分⼦子是决定分⼦子量量不不⼤大⾮非晶区的不不低于熔点不不那么熔融后进⼊入粘流态相反分⼦子量量⼤大使粘流温度⾼高于熔点晶区熔融后将出现⾼高弹态6轻度结晶〇和⾮非晶态聚合物的温度形变区线⼋八形变i微晶体起iiimz li ⽂文联的作⽤用i i_ˊˊm m____ˊg东丽温度轻度结晶聚合物8交联聚合物橡胶平台⽆无限⻓长i y E i 橡胶11-1patithe sili 11iy3试分别画出低密度阷轻度交联橡胶的下列列曲线并说明理理由以温度形变曲线a a1_fiiih4画出模拟⾼高聚物应⼒力力松弛过程的⼒力力学模型给出应⼒力力松弛⽅方程并说明该模型适合于描述何种⾼高聚物的应⼒力力松弛过程为什什么我古聚合物M 的流动温度下⼀一晶态⾼高聚物熔点温度不不Mz粘流态温度6已知某类⾼高聚物在拉伸过程中的应加应变曲线如下图所示回答下列列问题以指明⾼高聚物可能的类型以试⽤用微观分⼦子运动观点解释曲线01312发展过程0A 1017i -答处于玻璃态单轴⾮非晶态⾼高聚物A 脆性断裂B 屈服应⼒力力c D断裂应⼒力力绑性断裂0-13段⾼高模量量⼩小变形⻁虎克弹性体的弹性由⾼高分⼦子键⻆角键⻓长变化13-12段⼤大形变阶段⾼高分⼦子链运动贡献在⼤大外⼒力力作⽤用下分⼦子链伸展⼈人。
高分子物理

高分子物理第五章概念:1三大转变①玻璃化转变:非晶聚合物通过降温从高弹态进入玻璃态,或者通过升温从玻璃态进入高弹态的过程称为玻璃化转变,从分子运动的角度,聚合物的玻璃化转变对应于链段运动从“运动状态”到“冻结状态”的转变。
②粘流转变:高聚物从高弹态向粘流态的转变③次级转变:在玻璃化温度下与小尺寸运动单元的运动所对应的松驰转变2玻璃化转变温度Tg :发生玻璃化转变的温度称为玻璃化转变温度。
流动温度Tf :3时温等效原理:升高温度或者延长观察时间对于观察同一个松弛过程是等效的,对于研究聚合物的分子运动也是等效的。
4 Avram 指数:与成核机理和晶体生长方式有关的常数,等于晶体生长的空间维数和成核过程的时间维数之和 5半结晶时间:结晶程度达到1/2时的时间 问答1三大力学状态的特点①玻璃态:(1)大应力下的小形变,模量高(2)形变量与应力成正比,普弹形变(3)形变 瞬时可逆。
常温下玻璃态聚合物常用作塑料②高弹态:(1)小应力下的大形变,模量低(2)形变滞后可逆,松弛时间长(滞后高弹形 变)常温下用作橡胶③粘流态1)不可逆的黏性形变(2)模量极低且随温度升高急剧下降(3)黏流转变温度与 分子量有关2从分子运动的角度说明非晶态聚合物随温度升高呈现出三种不同的力学状态的特点。
答: 1)玻璃态: T<Tg 运动单元:键长、键角的改变或链节、支链、侧基等小尺寸单元的运动2)高弹态: T g ~T f 运动单元:链段运动3)粘流态: Tf ~Td 运动单元:整链分子产生相对位移→流动3测Tg 的方法及原理(1) 膨胀计方法——热膨胀系数发生突变(2)示差扫描量热法(DSC )——比热发生突变(3)热机械分析法——模量发生突变(4)动态力学分析法——模量突变及力学损耗增大(5)NMR 核磁共振松弛法:在较低温度下,NMR 谱线很宽,在较高 温度下谱线变狭,在玻璃化转变时,谱线的宽度有很大的改变。
(6).介电松弛法:介电性质在玻璃化转变区发生明显的变化,可以用 来测定Tg 。
华理--高分子物理课后习题答案--高分子科学教程(第二版)--韩哲文

高分子科学教程(第二版)—高分子物理部分第7章 聚合物的结构 P2371.试述聚合物的结构特点2.简述聚合物的结构层次答:高分子结构的内容可分为链结构与聚集态结构两个组成部分。
链结构又分为近程结构和远程结构。
近程结构包括构造与构型,构造是指链中原子的种类和排列、取代基和端基的种类、单体单元的排列顺序、支链的类型和长度等。
构型是指某一原子的取代基在空间的排列。
近程结构属于化学结构,又称一级结构。
远程结构包括分子的大小与形态、链的柔顺性及分子在各种环境中所采取的构象。
远程结构又称二级结构。
聚集态结构是指高分子材料整体的内部结构,包括晶态结构、非晶态结构、取向态结构、液晶态结构以及织态结构。
前四者是描述高分子聚集体中的分子之间是如何堆砌的,又称三级结构。
织态结构则属于更高级的结构。
3.写出聚异戊二稀的各种可能的构型和名称(只考虑头-尾键接方式)。
解:(1)1,2-聚合:全同立构1,2-聚异戊二稀;间同立构1,2-聚异戊二稀;无规立构1,2-聚异戊二稀。
(2)3,4-聚合:全同(间同,无规)立构-聚3,4-聚异戊二稀。
(3)1,4聚合:顺式(反式)1,4-聚异戊二稀。
注意:一般来说,顺式、反式聚合都是在特定的催化剂下进行的,当催化剂一定时,产物结构就一定,所以不存在无规的几何异构体。
4.已知聚乙烯试样的聚合度为4105⨯,C-C 键长为0.154nm ,键角为109.5︒,试求:(1)若把聚乙烯看作自由旋转链时的聚乙烯试样的均方末端距;(2)若聚乙烯的末端距符合高斯分布时聚乙烯试样的平均末端距和最可几末端距。
解:54101052=⨯⨯=n ;nm l 154.0=; 5.109=θ(1)22522222.4743)154.0(10225.109cos 15.109cos 1cos 1cos 1nm nl nl nl r =⨯⨯==+-⋅=+-⋅=θθ (2)由于聚乙烯的末端距符合高斯分布,因此它应该是自由结合链)(87.44154.014159.33108385nm l n r =⨯⨯⨯=⋅=π)(76.39154.03102325nm l n r =⨯⨯=⋅=*注意:末端距复合高斯分布的链为高斯链,自由结合链和等效自由结合链都是高斯链。
玻璃化转变温度(Tg值)

在材料学中,Tg指的就是玻璃化转变温度,其英文名字为glass transition temperature。
学过高分子物理的人都知道,非晶态聚合物在一定应力下,由于温度的改变,可呈现三种物理状态:玻璃态、高弹态(橡胶态)、粘流态。
(感兴趣的朋友可找《高分子物理》书详细研究下)非晶态聚合物的温度形变曲线玻璃化转变温度指的就是非晶态聚合物(也包括晶态聚合物中的非晶态部分)在玻璃态向高弹态之间转变时的温度,是无定型聚合物大分子链段自由运动的最低温度。
从分子结构上讲,玻璃化转变温度是高聚物无定形部分从冻结状态到解冻状态的一种松弛现象,而不像相转变那样有相变热,所以它不是一级相变。
在玻璃化转变温度以下,高聚物处于玻璃态,分子链和链段都不能运动,只是构成分子的原子(或基团)在其平衡位置作振动;而在玻璃化转变温度时分子链虽不能移动,但是链段开始运动,表现出高弹性质,温度再升高,就使整个分子链运动而表现出粘流性质。
目前Tg的测试方法主要有:热机械分析法(TMA)、差热分析法(DTA)和示差扫描量热法(DSC)三种。
其中最方便的方法是用DSC测量比热容随温度的变化。
此外,还可以用核磁共振谱仪(NMR)来测定。
其原理主要是聚合物的许多物理性能如热容、密度、热膨胀系数、电导率等都在该温度范围发生急剧变化,从而可以通过检测这些变化来测定其Tg。
由于它们的测试方法原理不同,因而测试结果相差较大,不能相比。
玻璃化转变温度(Tg)是非晶态聚合物的一个非常重要的物理参数,那在实际应用中有什么指导作用呢?由于热固性树脂的固化物都属于非晶态聚合物,而产品都是在玻璃态使用,因此Tg越高,也就意味着产品的耐温性能越好。
因此,Tg是衡量树脂耐温性能一个非常重要的指标。
既然聊起了温度,除了玻璃化转变温度,长弓侠还想跟大家再聊一个,那就是热变形温度。
热变形温度(全称负荷热变形温度,英文缩写:HDT)指的是对高分子材料或聚合物施加一定的负荷,以一定的速度升温,当达到规定形变时所对应的温度。
高分子物理和高分子化学复习要点
⾼分⼦物理和⾼分⼦化学复习要点构型(Configuration):分⼦中由化学键所固定的原⼦在空间的⼏何排列。
⾼分⼦的构型:旋光异构⼏何异构键接异构全同⽴构间同⽴构⽆规⽴构反式构型顺式构型头-头结构头-尾结构键接异构体:因结构单元在⾼分⼦链中的连接⽅式不同引起的异构体。
1)在缩聚和开环聚合中,结构单元的键接⽅式是确定的。
2)在加聚过程中,会出现键接异构现象。
共聚物的序列、平均序列长度与嵌段数序列:由同类单体直接相连的嵌段。
平均序列长度:n= (单元A的数⽬)/(A的序列数)= 9/5嵌段数R:指在100个单体单元中出现的各种嵌段的总和。
R=200 /(n+ n)R=100时,为交替共聚;R=0时,为嵌段共聚;R愈⼤愈有交替性,R愈⼩愈有嵌段性。
SBS树脂:⽤阴离⼦聚合法制得的苯⼄烯和丁⼆烯的三嵌段共聚物。
其分⼦链的中段是聚丁⼆烯(70%),两端是聚苯⼄烯(30%),SBS具有两相结构,橡胶相PB连续相,PS形成微区分散在橡胶相中,起物理交联作⽤。
SBS是⼀种热塑性弹性体,连续相PB具有柔性链段的软区,分散相PS具有刚性链段的硬区,起物理交联作⽤。
构象:由于单键内旋转⽽产⽣的分⼦在空间的不同形态。
⾼分⼦链的构象有微构象与宏构象之分:1)微构象:指⾼分⼦主链键构象(⾼分⼦主链中⼀个键的构象)。
2)宏构象:指整个⾼分⼦链的形状。
构象的改变并不需要化学键的断裂,只要化学键的旋转就可实现。
链段:可以把由若⼲个键组成的⼀段链作为⼀个独⽴运动的单元,称为“链段”。
⾼分⼦的链段之间可以⾃由旋转,⽆规取向。
链段是⾼分⼦链中能够独⽴运动的最⼩单元。
实际的⾼分⼦链为受阻旋转链。
⾼分⼦链的柔顺性取决于分⼦内旋转的受阻程度。
⾼分⼦链能够改变其构象的性能称为⾼分⼦链的柔顺性。
⾼分⼦链是通过单键的内旋转改变其构象的,因此单键的内旋转是⾼分⼦链具有柔顺性的原因。
影响⾼分⼦链的柔顺性的因素内在因素(结构因素)主链结构:主链全由单键组成的,⼀般柔性较好;不同的单键,柔顺不同(考虑⾮近邻原⼦距离、键长和键⾓):-Si-O-> -C-O-> -C-C-;含有芳杂环,由于芳杂环不能内旋转,所以主链中含有芳杂环结构的⾼分⼦链柔顺性较差;主链含有孤⽴双键,柔顺性较好;带有共轭双键的⾼分⼦链不能内旋转,柔性差;侧基(或取代基):极性取代基:极性取代基将增加分⼦内的相互作⽤,使内旋转困难, 柔性下降; 极性越⼤, 柔性越差;⾮极性取代基(主要考虑其体积),取代基的体积越⼤, 内旋转越困难, 柔性越差;取代基的对称性,聚偏氯⼄烯>PVC,前者对称,分⼦偶极矩⼩,内旋转容易.聚异丁烯(PIB)的每个链节上,有对称的甲基,使主链间距离增⼤,键间作⽤⼒减少,内旋转容易其它结构因素:⽀化与交联:⽀链很长时,阻碍链的内旋转起主导作⽤,柔性下降;低交联(如含硫2%~3%橡胶),柔顺性影响不⼤,但含硫30%以上影响链柔顺性;⾼分⼦链的长度:分⼦链越长,分⼦构象数⽬越多,链的柔顺性越好;分⼦间作⽤⼒:分⼦间作⽤⼒⼤,柔顺性差。
高分子物理讲义-第三章 高聚物的力学性能
ε
8
晶态聚合物应力晶态聚合物应力-应变曲线
21
银纹(crazing) 银纹(crazing)
环境银纹——聚合物载环境介质与应力的共同作用形成 聚合物载环境介质与应力的共同作用形成 银纹化的临界应变——随环境介质对聚合物的溶解度的增 随环境介质对聚合物的溶解度的增 加而降低,随溶剂化聚合物的T 的降低而降低。 加而降低,随溶剂化聚合物的 g的降低而降低。
σ真
0
0
λ
0
15
材料的屈服判据
屈服判据( 组合应力状态下, 屈服判据(yield criterion)——组合应力状态下,材料的屈 ) 组合应力状态下 服条件。 服条件。 3个正应力(σxxσyy σ zz ), 个切应力(σ xy σ yz σ zx ) 个正应力( ),3个切应力 个切应力( 个正应力
在某平面出现屈服行为的临界应力σs与垂直于该平面的正 在某平面出现屈服行为的临界应力 压力σ 成正比: 压力 N成正比: σs =K +µσN µ——内摩擦系数 内摩擦系数
σs随着 N增加而增加 随着σ
17
剪切带的结构形态
剪切滑移变形带(Shear band)——450角,剪切应力 剪切滑移变形带( ) 起重要作用。 起重要作用。
HBS
HRS
HS
27
聚合物的破坏
聚合物的破坏——高分子主链的化学键断裂,高分子链 高分子主链的化学键断裂, 高分子主链的化学键断裂
高分子物理知识点
1 / 8构象:具有一定组成和构型的高分子链通过单键的内旋转而形成的分子中的原子在空间的排列 柔性: 高分子链中单键内旋的能力; 高分子链改变构象的能力; 高分子链中链段的运动能力; 高分子链自由状态下的卷曲程度。
链段:两个可旋转单键之间的一段链,称为链段 影响柔性因素: 1支链长,柔性降低;交联度增加,柔顺性减低。
2一般分子链越长,构象数越多,链的柔顺性越好。
3分子间作用力越大,聚合物分子链所表现出的柔顺性越小。
分子链的规整性好,结晶,从而分子链表现不出柔性。
控制球晶大小的方法: 1控制形成速度; 2采用共聚方法,破坏链的均一性和规整性,生成较小的球晶; 3外加成核剂,可获得小甚至微小的球晶。
聚合物的结晶形态: 1单晶:稀溶液,慢降温,螺旋生长 2球晶:浓溶液或熔体冷却3树枝状晶:溶液中析出,低温或浓度大,分子量大时析出;4纤维状晶:存在流动场,分子量伸展,并沿流动方向平行排列;5串晶:溶液低温,边结晶边搅拌;6柱晶:熔体在应力作用下冷却结晶;7伸直链晶:高压下融融结晶,或熔体结晶加压热处理。
结晶的必要条件:1内因: 化学结构及几何结构的规整性;2外因:一定的温度、时间。
结晶速度的影响因素:1温度——最大结晶温度:低温有利于晶核形成和稳定,高温有利于晶体生长;2压力、溶剂、杂质:压力、应力加速结晶,小分子溶剂诱导结晶; 3分子量:M 小结晶速度块,M 大结晶速度慢;熔融热焓∆H m :与分子间作用力强弱有关。
作用力强,∆H m 高熔融熵∆S m :与分子间链柔顺性有关。
分子链越刚,∆S m 小聚合物的熔点和熔限和结晶形成的温度T c 有一定的关系:结晶温度Tc 低(< Tm ),分子链活动能力低,结晶所得晶体不完善,从而熔限宽,熔点低;结晶温度Tc 高(~ Tm ),分子链活动力强,结晶所得晶体更加完善,从而熔限窄,熔点高。
取向:在外力作用下,分子链沿外力方向平行排列。
聚合物的取向现象包括分子链、链段的取向以及结晶聚合物的晶片等沿特定方向的择优排列。
《高分子物理》课后习题—— 聚合物的转变与松弛
《高分子物理》课后习题——聚合物的转变与松弛1.以分子运动观点和分子间物理缠结概念说明非晶态聚合物随着温度升高粘弹行为的4个区域,并讨论分子量对应力松弛模量-温度曲线的影响规律。
答:(1)a.玻璃态区,玻璃化温度以下,分子运动主要限于振动和短程的旋转运动;b.玻璃-橡胶转变区,可解析为远程、协同分子运动的开始;c.橡胶-弹性平台区,由于分子间存在几个链段平行排列的物理缠结,聚合物呈现远程橡胶弹性;d.末端流动区,物理缠结来不及松弛,材料仍然表现为橡胶行为,温度升高,发生解缠作用,导致整个分子产生滑移运动,即产生流动,这种流动是作为链段运动结果的整链运动。
(2)聚合物分子量越高,橡胶-弹性平台就越长。
2.讨论结晶、交联聚合物的模量-温度曲线和结晶度、交联度对曲线的影响规律。
解:略。
3.写出四种测定聚合物玻璃化温度的方法,简述其基本原理。
不同实验方法所得结果是否相同?为什么?答:(1)a.膨胀计法,热膨胀的主要机理是克服原子间的主价力和次价力,膨胀系数较小;b.量热法,聚合物在玻璃化时的热学性质的变化;c.温度-形变法,利用聚合物玻璃化转变时形变量的变化来测定其玻璃化温度;d.核磁共振法,利用电磁性质的变化研究聚合物玻璃化转变的方法。
(2)不同,略。
4.聚合物的玻璃化转变是否是热力学相变?为什么?聚合物的玻璃化转变并不是一个真正的热力学相变。
因为非晶态聚合物发生玻璃化转变时,其体积,焓或熵是连续变化的,而K,α和出现不连续的变化,要使体系达到热力学平衡,需要无限缓慢的变温速率和无限长的测试时间,实验上不可能做到,因此,玻璃化温度的测定过程体系不能满足热力学平衡条件,转变过程是一个松弛过程,所测得的玻璃化温度不是一个真正的热力学相变。
5.试用玻璃化转变的自由体积理论解释:(1)非晶态聚合物冷却时体积收缩速率发生变化;(2)冷却速度愈快,测得的Tg值愈高。
答:(1)在以上,非晶态聚合物体积收缩时,包括聚合物分子占有体积的收缩以及自由体积的收缩,而在以下,自由体积处于冻结状态,所以,聚合物体积收缩只有聚合物占有体积的收缩,因此,体积收缩速率会有变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2 非晶态聚合物的力学状态和热转变
• 1.力学状态:根据试样的力学性质随温度变
化的特征,可以把非晶态高聚物按温度区 域不同划为三种力学状态。
• 玻璃态( Tg 以下) • 高弹态( Tg ~Tf ) • 粘流态( Tf以上)
• 2. 热转变:三种力学状态是内部分子处于不同运
动状态的宏观表现。
• 玻璃态:链段处于被冻结的状态,只有那些较小
的运动单元,如侧基、支链和小链节能运动,因 此高分子链不能实现从一种构象到另一种构象的 转变。受力时主链的键长和键角有微小改变,形 变是很小的,形变与受力的大小成正比,当外力 除去后形变能立刻回复。这种力学性质称虎克型 弹性,又称普弹性。 松弛时间几乎为无穷大
A exp( BVห้องสมุดไป่ตู้ /V f )
ln (T ) ln A BV0 (T ) /V f (T )
ln (Tg ) ln A BV0 (Tg ) /V f (Tg )
由上两式得
ln
(T ) (Tg )
B
V0 (T ) /V f
(T )
V0 (Tg
)
/Vf
(Tg
)
因为 所以
fT
V f (T ) V0 (T ) V f (T )
V f (T ) V0 (T )
ln (T ) (Tg )
B
1 fT
1 fg
B
fg fT fT fg
B f (T Tg ) B
• 2.两相球粒模型:
• 非晶态高聚物存在着一定程度的局部有序。
其中包含粒子相和粒间相两个部分,而粒子又 可分为有序区和粒界区两个部分。
• 在有序区中,分子链是互相平行排列的,其有
序程度与链结构、分子间力和热历史等因素有 关。它的尺寸约2—4纳米。有序区周围有1— 2纳米大小的粒界区,由折叠链的弯曲部分、 链端、缠结点和连结链组成。粒间相则由无规 线团、低分子物、分子链末端和连结链组成, 尺寸约1—5纳米。
• WLF方程 :Williams, Landel和Ferry认
为不管什么聚合物,发生玻璃化转变时, 自由体积分数都等于0.025,并且提出一个 半经验的著名WLF方程
lg (T ) 17.44(T Tg ) (Tg ) 51.6 (T Tg )
f g 0.025
•Doolittle方程把液体的粘度与自由体积联系起来
玻璃态
高弹态的转变
• 在高聚物发生玻璃化转变时,许多物理性
能发生急剧的变化,特别是力学性能 。
• 高于Tg 则不能作塑料用,因为已经软化;
低于Tg就不能当橡胶用,因为已成为玻璃 态。
5.3.1 玻璃化温度Tg的测量
• 所有在玻璃化转变过程中发生显著变化或突
变的物理性质,都可以利用来测量玻璃化温 度。
(1)当温度降低时,自由体积逐步减少, 到某一温度时,自由体积将达到某一 值,即无法提供足够空间供链段运动, 这时高聚物进入玻璃态,链段运动被 冻结,这一临界温度叫玻璃化温度, 在此临界值以下,已经没有足够的空 间进行分子链构象的调整了,因此高 聚物的玻璃态可称为等自由体积状态。
(2)在玻璃态下,高聚物随温度升高发生的膨 胀,只是由于正常的分子膨胀过程造成的, 包括分子振动幅度的增加和键长的变化。到 玻璃化转变点,分子热运动已具有足够的能 量,而且自由体积也开始解冻而参加到整个 膨胀过程中去,因而链段获得了足够的运动 能量和必要自由空间,从冻结进入运动。在 玻璃化温度以上,除了这种正常的膨胀过程 之外,还有自由体积本身的膨胀,因此高弹
自由体积理论
• 液体或固体物质,其体积由两部分组成:一
部分是被分子占据的体积,称为已占体积; 另一部分是未被占据的自由体积。
• 当高聚物冷却时,起先自由体积逐渐减小,
到某一温度时,自由体积将达到一最低值, 这时高聚物进入玻璃态。
• 对任何高聚物,玻璃化温度就是自由体积达
到某一临界值的温度,在这临界值以下,已 经没有足够的空间进行分子链构象的调整了。 因而高聚物的玻璃态可视为等自由体积状态。
第五章 聚合物的非晶态
• 高分子的凝聚态结构:
高分子链之间的排列和堆砌结构,也称为 超分子结构。
• 高分子聚集态结构形式: • 非晶态结构, • 晶态结构, • 取向态结构, • 液晶态结构, • 织态结构。
5.1 高聚物的非晶态结构模型
1.无规线团模型
• Flory认为:非晶态高聚物的本体
中,分子链的构象与在溶液中一样, 呈无规线团状,线团分子之间是无 规缠结的,因而非晶态高聚物在聚 集态结构上是均相的。
• 例如:比容、线膨胀系数、折光率、溶剂在
聚合物中的扩散系数、比热容、动态力学损 耗等。
• 最方便的方法是用示差扫描量热计(DSC)
测量比热容随温度的变化。
6.2.2 玻璃化转变理论
• 对于玻璃化转变,目前常有的三种
理论解释:
• 热力学理论(定性) • 动力学理论(定性) • 自由体积(半定量)
• 高弹态:分子链可以通过单键的内旋转和链段的
改变构象以适应外力的作用,变形量却大得多。 松弛时间减少到与实验测量时间同一个数量
级。
• 粘流态:高聚物在外力作用下发生粘性流动,是
不可逆的变形,外力除去后,变形不再能自发回 复。分子链移动的松弛时间也缩短到与我们实验
5.3非晶态高聚物的玻璃化转变
• 高聚物的玻璃化转变是指非晶态高聚物从
态的膨胀系数 r 远远大于玻璃态的膨胀系
数 g 。
•T=Tg 时,聚合物总体积:
V0:绝对零度时的占有体积。
Vg
Vf
V0
dV dT
g
Tg
•T>Tg 时, 聚合物总体积:
V
Vg
(dV dT
)r (T
Tg )
•T>Tg
时,
自由体积:
(V f
)T
Vf
[ dV dT
r
dV dT
](T g
Tg )
•令
r
1 Vg
dV dT
r
g
1 Vg
dV dT
g
•则自由体积的膨胀系数: f r g
•自由体积的分数: fT f g f (T Tg )
(T Tg )
