2019年中考数学二轮复习专题练【几何图形的证明及计算问题】附答案解析
2019中考数学二轮复习题型突破五【几何图形探究题】精练及解析

2019中考数学二轮复习题型突破五【几何图形探究题】精练及解析1中考数学二轮复习题型突破五【几何图形探究题】精练类型一几何图形静态探究1.(2017·成都)问题背景:如图①,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=12∠BAC=60°,于是BCAB=2BDAB=3;
迁移应用:如图②,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;②请直接写出线段AD,BD,CD之间的等量关系式;拓展延伸:如图③,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;②若AE=5,CE=2,求BF的长.
2.(2017·许昌模拟)在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE=12∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;(2)通过观察、测量、猜想:BFPE=__________,并结合图②证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求BFPE的值.(用含α的式子表示)
3.(2014·河南)(1)问题发现如图①,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.2019中考数学二轮复习题型突破五【几何图形探究题】精练及解析2填空:①∠AEB的度数为__________;②线段AD,BE之间的数量关系为__________.(2)拓展探究如图②,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
【中考二轮】2019年 中考数学 二轮专题复习 图形与变换(含答案)
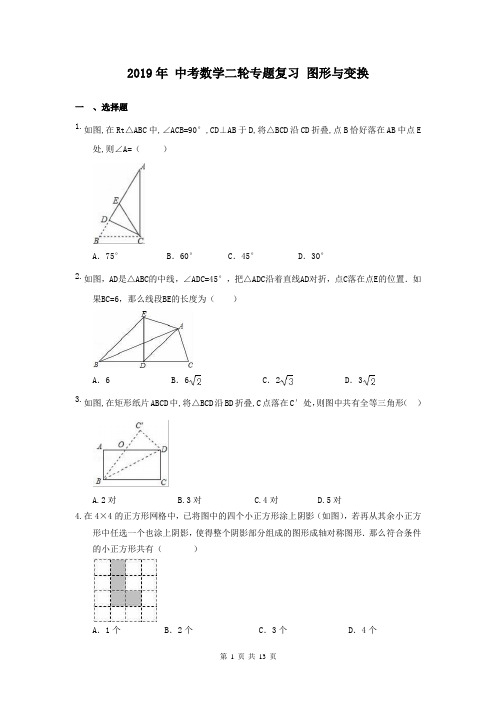
2019年中考数学二轮专题复习图形与变换一、选择题1.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,将△BCD沿CD折叠,点B恰好落在AB中点E处,则∠A=()A.75° B.60° C.45° D.30°2.如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为()A.6 B.6 C.2 D.33.如图,在矩形纸片ABCD中,将△BCD沿BD折叠,C点落在C′处,则图中共有全等三角形()A.2对B.3对C.4对D.5对4.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有()A.1个 B.2个C.3个 D.4个5.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°6.如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为()A.2B.3C.2D.37.如图是一块矩形ABCD的场地,AB=102m,AD=51m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪的面积为()A.5050m2B.4900m2C.5000m2D.4998m28.如图,A(,1),B(1,).将△AOB绕点O旋转150°得到△A′OB′,则此时点A 的对应点A′的坐标为()A.(-,-1)B.(-2,0)C.(-1,-)或(﹣2,0)D.(-,-1)或(-2,0)9.如图①是一个直角三角形纸片,∠A=30°,将其折叠,使点C落在斜边上的点C处,折痕为BD,如图②,再将②沿DE折叠,使点A落在DC′的延长线上的点A′处,如图③,若折痕DE的长是cm,则BC的长是()A.3cmB.4cmC.5cmD.6cm10.小明是我校手工社团的一员,他在做折纸手工,如图所示在矩形ABCD中,AB=6,BC=8,点E是BC的中点,点F是边CD上的任意一点,△AEF的周长最小时,则DF的长为()A.1B.2C.3D.411.如图,对折矩形纸片ABCD,使BC与AD重合,折痕为EF,把纸片展平;再一次折叠纸片,使BC与EF重合,折痕为GH,把纸片展平;再一次折叠纸片,使点A落在GH上的点N 处,并使折痕经过点B,折痕BM交GH于点I.若AB=4cm,则GI的长为()12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,点P是AB的中点,点D,E是AC,BC边上的动点,且AD=CE,连接DE. 有下列结论:①∠DPE=90°;②四边形PDCE面积为1;③点C到DE距离的最大值为.其中正确的个数是().A.0B.1C.2D.3二、填空题13.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= .14.如图,矩形ABCD对角线AC=10,BC=6,则图中四个小矩形的周长和为15.如图(1)是四边形纸片ABCD,其中∠B=120°,∠D=50度.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(2)所示,则∠C= 度.16.把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是.17.如图,矩形ABCD中,AD=4,∠CAB=30o,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是18.如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,点A的坐标为(1,0),反比例函数y=图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是.三、作图题19.已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.(1)画出△ABC向上平移6个单位得到的△A1B1C1;(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.20.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).四、解答题21.如图,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.(1)写出点Q的坐标是;(2)若把点Q向右平移m个单位长度,向下平移2m个单位长度后,得到的点Q′恰好落在第三象限,求m的取值范围.22.如图,四边形ABCD表示一张矩形纸片,AB=10,AD=8.E是BC上一点,将△ABE沿折痕AE向上翻折,点B恰好落在CD边上的点F处,⊙O内切于四边形ABEF.求:(1)折痕AE的长;(2)⊙O的半径.23.如图①,将矩形ABCD沿DE折叠使点A落在点A′处,然后将矩形展平,如图②沿EF折叠使点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE 上的点H处.(1)求证:EG=CH;(2)已知AF=错误!未找到引用源。
2019年中考数学二轮复习专题二解答重难点题型突破题型五几何图形探究题课件

在正方形 CDEF 中,∠FEC=12∠FED=45°,
在 Rt△CEF 中,sin∠FEC=CCEF= 22,∴CCFE=CCBA, ∵∠FCE=∠ACB=45°,∴∠FCB+∠ACB=∠FCB+∠FCE,∴∠FCA =∠ECB,
2AF,
∴S△PMN 最大=12PM2=12×12MN2=14×(7 2)2=429.
19
【对应训练】 1.(2017·濮阳模拟)(1)【问题发现】
如图①,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中 点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF 的数量关系为________; (2)【拓展研究】 在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线 段BE与AF的数量关系有无变化?请仅就图②的情形给出证明; (3)【问题发现】 当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.
同(1)的方法得,PN∥BD,∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC
=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,
17
(2) 由旋转知,∠BAD=∠CAE, ∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD=CE,
同(1)的方法,利用三角形的中位线得,PN=12BD,PM=12CE,∴PM=PN,
∴△PMN 是等腰三角形,
同(1)的方法得,PM∥CE,∴∠DPM=∠DCE,
安徽省2019年中考数学二轮复习题型二:选择压轴题之几何图形最值问题(含答案)

题型二选择压轴题之几何图形最值问题类型一线段最值问题1.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM 的最小值为()A.1.2B. 1.3C.1.4D. 2.4第1题图第2题图2.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是()A.125 B. 4 C.245D. 53.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有▱ADCE中,DE的最小值是()A.3B. 2C.4D. 5第3题图第4题图4.如图,菱形ABCD中,∠ABC=60°,边长为3,P是对角线BD上的一个动点,则12PB+PC的最小值是()A.3B. 332 C.3D. 32+ 35.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4B. 5C.6D. 7第5题图第6题图6.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点,且BE=CF,连接BF、DE,则BF+DE的最小值为()A.2 5B. 45C.23D. 4 37.如图,在四边形ABCD中,∠BAD=120°,∠B=∠D=90°,AB=2,AD=4,点M,点N分别在边BC,CD上,则△AMN周长的最小值为()A.37B. 47C.27+6D. 11第7题图第8题图8.如图,在直角坐标系中,点A、B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是()A.(0,1)B. (0,2)C.(0,3)D. (0,4)9.如图,矩形ABCD中,AB=8,BC=6,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为()A.43B. 10C.87D. 20第9题图第10题图10.如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP,BP,则AP+12BP的最小值为()A.37B. 6C.217D. 411.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,动点F在边BC上运动,连接AF,过点C作CD⊥AF于点D,交AB 于点E,则B、D两点之间距离的最小值为()A.2B. 4C.213-3D. 213-4第11题图第12题图12.如图,在等边△ABC中,BF是AC边上中线,点D在BF 上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是()A.30°B. 45°C.60°D. 90°13.在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(3,0)、B(33,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是()A.23-2B. 25-2C.27-2D. 210-214.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F 在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是()A.3B. 65 C.35D. 2第14题图第15题图第16题图15.如图,正方形ABCD的边长为2,点E、F分别是边BC、CD的延长线上的动点,且CE=DF,连接AE、BF,交于点G,连接DG,则DG的最小值为()A.3-1B. 5-1C. 3D. 516.在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心,4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为()A.8B. 7C.6D. 5类型二面积最值问题(拓展)1.如图,点E为边长为4的等边△ABC的BC边上一动点(点E 不与B、C重合),以AE为边作等边△AEF,则△AEF面积的最小值是()A.2B. 4C.3D. 3 3第1题图第2题图2.(2017合肥蜀山区模拟)如图,⊙O的半径是2,直线l与⊙O 相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是()A.2B. 4C.2 2D. 4 23.如图,在矩形ABCD中,AD>AB,点E、F分别是BC、DC上的点,且CE+CF=8,若sin∠ABD=45,BD=20,则△AEF的面积的最小值为()A.24B. 46C.64D. 96第3题图第4题图4.如图,在菱形ABCD中,∠BAD=135°,AB=42,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为()A.4 2B. 8-52 3 C.4-2 2D. 82-8类型一线段最值问题1. A2. C3. A4. B5. B6. B7. B8. D9. D10. A 11. D12. D13. C14. B15. B16. B类型二面积最值问题(拓展)1. D2. D3. B4. D参考答案。
2019届中考数学复习-专项二 解答题专项 五、简单的几何证明课件

例1(2018·陕西中考)如图,AB∥CD,E,F分别为AB,CD上的点,且EC∥BF, 接AD,分别与EC,BF相交于点G,H,若AB=CD,求证:AG=DH。
【证明】∵AB∥CD,∴∠A=∠D。 ∵CE∥BF,∴∠AHB=∠DGC。
A D, 在△ABH和△DCG中, AH B D G C ,
新一代精独品家PP教T育教资学源参为考你模提版供,,感t谢ha你nk的y浏ou览与使 用
专项二 解答题专项
五、 简单的几何证明 (针对陕西中考第18题或第19
题)
新一代精独品家PP教T育教资学源参为考你模提版供,,感t谢ha你nk的y浏ou览与使 用
解答题专项
中考解读:简单的几何证明为陕西近8年中考解答题的必考题,分值为5分或7 分。图形背景为三角形、四边形(一般为特殊平行四边形),设问类型有(1) 证明线段相等;(2)证明线段平行;(3)证明三角形全等。
AB DC ,
∴△ABH≌△DCG(AAS),∴AH=DG。 ∵AH=AG+GH,DG=DH+GH, ∴AG=DH。
一、证明三角形全等的思路
新一代精独品家PP教T育教资学源参为考你模提版供,,感t谢ha你nk的y浏ou览与使 用
解答题专项二、常见的Fra bibliotek等三角形的模型
1.平移模型:
2.对称模型:
3.旋转模型:
4.三垂直模型:
新一代精独品家PP教T育教资学源参为考你模提版供,,感t谢ha你nk的y浏ou览与使 用
解答题专项
(广西专用)2019中考数学二轮新优化复习 第二部分 专题综合强化 专题6 圆的相关证明与计算针对训

第二部分 专题六类型1 与全等三角形相关证明与计算1.(xx·梧州)如图,过⊙O 上的两点A ,B 分别作切线,并交BO 、AO 的延长线于点C ,D ,连接CD ,交⊙O 于点E ,F ,过圆心O 作OM ⊥CD ,垂足为M 点.求证:(1)△ACO ≌△BDO ; (2)CE =DF .证明:(1)∵AC ,BD 为⊙O 的切线, ∴∠CAO =∠DBO =90°, 在△ACO 和△BDO 中, ⎩⎪⎨⎪⎧∠CAO =∠DBO ,AO =BO ,∠AOC =∠BOD ,∴△ACO ≌△BDO (A S A ). (2)∵△ACO ≌△BDO ,∴CO =DO .∵OM ⊥CD ,∴MC =DM ,EM =MF ,∴CE =DF .2.(xx·北京)如图,AB 是⊙O 的直径,过⊙O 外一点P 作⊙O 的两条切线PC ,PD ,切点分别为C ,D ,连接OP ,CD .(1)求证:OP ⊥CD ;(2)连接AD ,BC ,若∠DAB =50°,∠CBA =70°,OA =2,求OP 的长.(1)证明:如答图,连接OC ,OD .∴OC =OD .∵PD ,PC 是⊙O 的切线, ∴∠ODP =∠OCP =90°.在Rt △ODP 和Rt △OCP 中,⎩⎪⎨⎪⎧OD =OC ,OP =OP ,∴Rt △ODP ≌Rt △OCP (HL), ∴∠DOP =∠COP , ∵OD =OC ,∴OP ⊥CD .(2)解:∵OA =OD =OC =OB =2,∴∠ADO =∠DAO =50°,∠BCO =∠CBO =70°, ∴∠AOD =80°,∠BOC =40°, ∴∠COD =60°.∵OD =OC , ∴△COD 是等边三角形, 由(1)知,∠DOP =∠COP =30°, 在Rt △ODP 中,OP =ODcos30°=433.3.(xx·贺州)如图,⊙O 是△ABC 的外接圆,AB 为直径,∠BAC 的平分线交⊙O 于点D ,过点D 的切线分别交AB ,AC 的延长线于E ,F ,连接BD .(1)求证:AF ⊥EF ;(2)若AC =6,CF =2,求⊙O 的半径. (1)证明:如答图1,连接OD .∵EF 是⊙O 的切线,且点D 在⊙O 上, ∴OD ⊥EF .∵OA =OD ,∴∠DAB =∠ADO . ∵AD 平分∠BAC ,∴∠DAB =∠DAC , ∴∠ADO =∠DAC ,∴AF ∥OD ,∴AF ⊥EF .(2)解:如答图2,过D 作DG ⊥AE 于点G ,连接CD .∵∠BAD =∠DAF ,AF ⊥EF ,∴BD =CD ,DG =DF ,在Rt △ADF 和Rt △ADG 中,⎩⎪⎨⎪⎧AD =AD ,DF =DG ,∴Rt △ADF ≌Rt △ADG (HL), 同理可得Rt △CDF ≌Rt △BDG ,∴BG =CF =2,AG =AF =AC +CF =6+2=8, ∴AB =AG +BG =8+2=10, ∴⊙O 的半径为12AB =5.4.(xx·苏州)如图,AB 是⊙O 的直径,点C 在⊙O 上,AD 垂直于过点C 的切线,垂足为D ,CE 垂直AB ,垂足为E .延长DA 交⊙O 于点F ,连接FC ,FC 与AB 相交于点G ,连接OC .(1)求证:CD =CE ;(2)若AE =GE ,求证:△CEO 是等腰直角三角形. 证明:(1)连接AC .∵CD 是⊙O 的切线, ∴OC ⊥CD .∵AD ⊥CD ,∴∠DCO =∠D =90°, ∴AD ∥OC ,∴∠DAC =∠ACO .∵OC =OA , ∴∠CAO =∠ACO ,∴∠DAC =∠CAO . ∵CE ⊥AB ,∴∠CEA =90°,在△CDA 和△CEA 中,∵⎩⎪⎨⎪⎧∠D =∠CEA ,∠DAC =∠EAC ,AC =AC ,∴△CDA ≌△CEA (AA S),∴CD =CE . (2)连接BC .∵△CDA ≌△CEA , ∴∠DCA =∠EC A.∵CE ⊥AG ,AE =EG , ∴CA =CG ,∴∠ECA =∠ECG .∵AB是⊙O的直径,∴∠ACB=90°,∵CE⊥AB,∴∠ACE=∠B.∵∠B=∠F,∴∠F=∠ACE=∠DCA=∠ECG.∵∠D=90°,∴∠DCF+∠F=90°,∴∠F=∠DCA=∠ACE=∠ECG=22.5°,∴∠AOC=2∠F=45°,∴△CEO是等腰直角三角形.类型2 与相似三角形相关证明与计算1.(xx·玉林适应考试)如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,点C在OP上,且BC=PC.(1)求证:直线BC是⊙O的切线;(2)若OA=3,AB=2,求BP的长.(1)证明:如答图,连接OB.∵OA=OB,∴∠A=∠OB A.又∵BC=PC,∴∠P=∠CBP.∵OP⊥AD,∴∠A+∠P=90°,∴∠OBA+∠CBP=90°,∴∠OBC=180°-(∠OBA+∠CBP)=90°.∵点B在⊙O上,直线BC是⊙O的切线.(2)解:如答图,连接DB.∵AD是⊙O的直径,∴∠ABD=90°,∴Rt △ABD ∽Rt △AOP ,∴AB AO =AD AP ,即23=6AP,解得AP =9, ∴BP =AP -BA =9-2=7.2.(xx·贺州)如图,AB 是⊙O 的弦,过AB 的中点E 作EC ⊥OA ,垂足为C ,过点B 作直线BD 交CE 的延长线于点D ,使得DB =DE .(1)求证:BD 是⊙O 的切线;(2)若AB =12,DB =5,求△AOB 的面积. (1)证明:∵OA =OB ,DB =DE ,∴∠A =∠OBA ,∠DEB =∠DBE .∵EC ⊥OA ,∠DEB =∠AEC , ∴∠A +∠DEB =90°,∴∠OBA +∠DBE =90°,∴∠OBD =90°. ∵OB 是⊙O 的半径,∴BD 是⊙O 的切线.(2)解:过点D 作DF ⊥AB 于点F ,连接OE ,如答图.∵点E 是AB 的中点,AB =12, ∴AE =EB =6,OE ⊥AB . 又∵DE =DB ,DF ⊥BE , ∴DE =DB =5,∴EF =BF =3,∴DF =DE 2-EF 2=4. ∵∠AEC =∠DEF ,∴∠A =∠EDF .∵OE ⊥AB ,DF ⊥AB ,∴∠AEO =∠DFE =90°, ∴△AEO ∽△DFE ,∴EO FE =AEDF,即EO 3=64,得EO =92, ∴S △AOB =12AB ·OE =12×12×92=27.3.(xx·随州)如图,AB 是⊙O 的直径,点C 为⊙O 上一点,CN 为⊙O 的切线,OM ⊥AB 于点O ,分别交AC ,CN 于D ,M 两点.(1)求证:MD =MC ;(2)若⊙O 的半径为5,AC =45,求MC 的长. (1)证明:如答图,连接OC .∵CN 为⊙O 的切线,∴OC ⊥CM ,∠OCA +∠ACM =90°. ∵OM ⊥AB ,∴∠OAC +∠ODA =90°. ∵OA =OC ,∴∠OAC =∠OCA , ∴∠ACM =∠ODA =∠CDM ,∴MD =MC .(2)解:由题意可知AB =5×2=10,AC =4 5. ∵AB 是⊙O 的直径, ∴∠ACB =90°, ∴BC =102-452=2 5.∵∠AOD =∠ACB ,∠OAD =∠CAB ,∴△AOD ∽△ACB, ∴OD BC =AO AC ,即OD 25=545,可得OD =52.设MC =MD =x ,在Rt △OCM 中,由勾股定理得(x +52)2=x 2+52,解得x =154,即MC =154.4.(xx·来宾)如图,在△ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,DE ⊥AD ,交AB 于点E ,AE 为⊙O 的直径.(1)判断BC 与⊙O 的位置关系,并证明你的结论;(2)求证:△ABD ∽△DBE ; (3)若cos B =223,AE =4,求CD .(1)解:结论:BC 与⊙O 相切. 证明:如答图,连接OD .∵OA =OD , ∴∠OAD =∠OD A. ∵AD 平分∠CAB ,∴∠CAD =∠DAB ,∴∠CAD =∠ADO , ∴AC ∥OD .∵AC ⊥BC ,∴OD ⊥BC ,∴BC 是⊙O 的切线. (2)证明:∵BC 是⊙O 的切线,∴∠ODB =90°, ∴∠BDE +∠ODE =90°.∵AE 是⊙O 的直径, ∴∠ADE =90°,∴∠DAE +∠AED =90°. ∵OD =OE ,∴∠ODE =∠OED , ∴∠DAB =∠BDE .∵∠ABD =∠DBE , ∴△ABD ∽△DBE .(3)解:在Rt △ODB 中,∵cos B =BD OB =223,∴设BD =22k ,OB =3k .∵OD 2+BD 2=OB 2, ∴4+8k 2=9k 2,∴k =2,∴BO =6,BD =4 2. ∵DO ∥AC, ∴BD CD =BO AO ,∴42CD =62,∴CD =423.类型3 与锐角三角函数相关证明与计算1.(xx·毕节)如图,在△ABC 中,以BC 为直径的⊙O 交AC 于点E ,过点E 作AB 的垂线交AB 于点F ,交CB 的延长线于点G ,且∠ABG =2∠C .(1)求证:EG 是⊙O 的切线;(2)若tan C =12,AC =8,求⊙O 的半径.(1)证明:如答图,连接OE ,BE .∵∠ABG =2∠C ,∠ABG =∠C +∠A ,∴∠C =∠A ,∴BC =AB .∵BC 是⊙O 的直径, ∴∠CEB =90°,∴CE =AE . ∵CO =OB ,∴OE ∥AB . ∵GE ⊥AB ,∴EG ⊥OE .又∵OE 是⊙O 半径,∴EG 是⊙O 的切线.(2)解:∵AC =8,∴CE =AE =4.∵tan C =BE CE =12,∴BE =2,∴BC =CE 2+BE 2=25,∴CO =5,即⊙O 的半径为 5.2.(xx·贵港二模)如图,已知在Rt △ABC 中,∠ABC =90° ,以AB 为直径的⊙O 与AC 交于点D ,点E 是BC 的中点,连接BD, DE .(1)求证: DE 是⊙O 的切线; (2)若AB =3AD ,求si nC .(1)证明:连接OD .∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠BDC =90°.∵E 为BC 的中点, ∴DE =BE =CE ,∴∠EDB =∠EBD .∵OD =OB , ∴∠ODB =∠OBD .∵∠ABC =90°,∴∠EDO =∠EDB +∠ODB =∠EBD +∠OBD =∠ABC =90°,∴OD ⊥DE ,∵OD 是⊙O 的半径, ∴DE 是⊙O 的切线.(2)解:∵AB 为⊙O 的直径, ∴∠ADB =90°, ∴∠ABD +∠BAD =90°.∵∠ABC =90°,∴∠C +∠BAC =90°,∴∠C =∠ABD .∵AB =3AD ,∴si n ∠ABD =AD AB =13,∴si nC =13.3.(xx·柳州三模)如图,AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K .(1)求证: KE =GE ;(2)若KC 2=KD ·CE ,试判断AC 与EF 的位置关系,并说明理由; (3)在(2)的条件下,若si nE =35,AK =2 5 ,求FG 的长.第3题答图(1) 解:如答图1,连接OG .∵EG 是⊙O 的为切线,∴∠KGE +∠OGA =90. ∵CD ⊥AB, ∴∠AKH +∠OAG =90°. 又∵OA =OG, ∴∠OGA =∠OAG, ∴∠KGE =∠AKH =∠GKE, ∴KE =GE .(2)解:AC ∥EF .理由:连接GD ,如答图2所示. ∵KG 2=KD ·GE ,即KG KD =GE KG , ∴KG GE =KD KG, 又∵∠KGE =∠GKE ,∴△GKD ∽△EGK , ∴∠E =∠AGD .又∵∠C =∠AGD, ∴∠E =∠C, ∴AC ∥EF .(3) 解:连接OG ,OC ,如答图3所示.∵si nE =si n ∠ACH =35,设AH =3t ,则AC =5t ,CH =4t .∵KE =GE ,AC ∥EF, ∴CK =AC =5t,∴HK =CK -CH =t .在Rt △AHK 中,根据勾股定理得AH 2+HK 2=AK 2,即(3t )2+t 2=(25)2, 解得t = 2.设⊙O 的半径为r ,在Rt △OCH 中,OC =r ,OH =r -3t ,CH =4t ,由勾股定理得OH 2+CH 2=OC 2,即(r -3t )2+(4t )2=r 2,解得r =2526. ∵EF 为⊙O 的切线,∴△OGF 为直角三角形,在Rt △OGF 中,OG =r ,tan ∠OFG =tan ∠CAH =CH AH =43,∴FG =OG t an ∠OFG =252643=2528.4.(xx·北海)在△ABC 中,AB =AC .以AB 为直径的⊙O 交AC 于点E ,交BC 于点D, ⊙O 的切线BP 与AC 的延长线交于点P ,连接DE ,BE .(1)求证:BD ︵ =DE ︵; (2)求证:∠AED =∠BCP ;(3)已知:si n ∠BAD =55,AB =10,求BP 的长. (1)证明:∵AB 是⊙O 的直径,∴∠ADB =90°,即AD ⊥BC .又∵AB =AC , ∴AD 平分∠BAC ,∴∠BAD =∠DAC ,∴BD ︵ =DE ︵. (2)证明: ∵AB 是⊙O 的直径,AD ⊥BC , ∴BD =DC .∵BD ︵ =DE ︵,∴BD =DE , ∴DC =DE ,∴∠DEC =∠DCE .∵∠AED +∠DEC =180°,∠DCE +∠BCP =180°, ∴∠AED =∠BCP . (3)解:∵si n ∠BAD =BD AB =55,AB =10, ∴AC =AB =10,BD =25,∴DC =DE =2 5. 设EC =x ,则AE =10-x ,∵在Rt △ABE 中,BE 2=AB 2-AE 2,在Rt △BEC 中,BE 2=BC 2-EC 2,∴AB 2-AE 2=BC 2-EC 2, 即102-(10-x )2=(25+25)2-x 2,解得x =4,∴ EC =4,AE =6,∴BE =AB 2-AE 2=102-62=8. ∵∠ABE +∠EBP =90°,∠EBP +∠P =90°, ∴∠ABE =∠P .又∵∠AEB =∠ABP =90°,∴△ABE ∽△APB ,∴AE AB =BE BP ,即610=8BP ,∴BP =403.类型4 与特殊三角形相关证明与计算1.(xx·钦州)如图,在△ABC 中,AB =AC ,AD 是角平分线,BE 平分∠ABC 交AD 于点E ,点O 在AB 上,以OB 为半径的⊙O 经过点E ,交AB 于点F .(1)求证:AD 是⊙O 的切线;(2)若AC =4,∠C =30°,求EF ︵的长.(1)证明:如答图,连接OE .∵OB =OE , ∴∠OBE =∠OEB . ∵BE 平分∠ABC , ∴∠OBE =∠EBD ,∴∠OEB =∠EBD ,∴OE ∥BD .∵AB =AC ,AD 平分∠BAC ,∴AD ⊥BC ,∴∠OEA =∠BDA =90°.∵点F 有⊙O 上,∴AD 是⊙O 的切线. (2)解:∵AB =AC =4,∠C =∠B =30°,∴BD =2 3.设⊙O 的半径为r ,则BO =OE =r ,AO =AB -OB =4-r .∵OE ∥BD ,∴AO AB =OEBD, 即4-r 4=r 23,解得r =83-12,∴l EF ︵ =30π83-12180=(433-2)π.2.(xx·巴中)如图,在△ABC 中,AB =BC ,以AB 为直径的⊙O 交BC 于点D ,交AC 于点F ,过点C 作CE ∥AB ,与过点A 的切线相交于点E ,连接AD .(1)求证:AD =AE ;(2)若AB =6,AC =4,求AE 的长. (1)证明:∵AE 与⊙O 相切,AB 是⊙O 的直径,∴∠BAE =90°,∠ADB =90°.∵CE ∥AB ,∴∠E =90°, ∴∠E =∠ADB .∵在△ABC 中,AB =BC , ∴∠BAC =∠BC A. ∵CE ∥AB , ∴∠BAC =∠ACE ,∴∠BCA =∠ACE .又∵AC =AC , ∴△ADC ≌△AEC (AA S),∴AD =AE . (2)解:设AE =AD =x ,CE =CD =y , 则BD =6-y .∵△AEC 和△ADB 为直角三角形,∴AE 2+CE 2=AC 2,AD 2+BD 2=AB 2,将AB =6,AC =4,AE =AD =x ,CE =CD =y ,BD =6-y 代入,解得x =823,y =43,即AE 的长为823. 3.(xx·南宁)如图,在Rt △ABC 中,∠C =90°,BD 是角平分线,点O 在AB 上,以点O 为圆心,OB 为半径的圆经过点D ,交BC 于点E .(1)求证:AC 是⊙O 的切线; (2)若OB =10,CD =8,求BE 的长. (1)证明:如答图,连接OD . ∵BD 为∠ABC 的平分线, ∴∠1=∠2.∵OB =OD , ∴∠1=∠3,∴∠2=∠3, ∴OD ∥BC .∵∠C =90°, ∴∠ODA =90°. ∵点D 在⊙O 上, ∴AC 为⊙O 的切线;(2)解:过O 作OG ⊥BC ,连接OE ,如答图.∴四边形ODCG 为矩形, ∴GC =OD =OB =10,OG =CD =8,在Rt △OBG 中,利用勾股定理得 BG =6.∵OG ⊥BE ,OB =OE ,∴BE =2BG =12.类型5 与特殊四边形相关证明与计算1.(xx·毕节)如图,已知⊙O 的直径CD =6,A ,B 为圆周上两点,且四边形OABC 是平行四边形,过A 点作直线EF ∥BD ,分别交CD ,CB 的延长线于点E ,F ,AO 与BD 交于G 点.(1)求证:EF 是⊙O 的切线;(2)求AE 的长.(1)证明:∵CD 为⊙O 的直径,∴∠DBC =90°, ∴BD ⊥BC .∵四边形OABC 是平行四边形, ∴AO ∥BC ,∴BD ⊥OA .∵EF ∥BD ,∴OA ⊥EF .∵点A 在⊙O 上,∴EF 是⊙O 的切线. (2)解:连接OB ,如答图.∵四边形OABC 是平行四边形,∴OA =BC ,而OB =OC =OA , ∴OB =OC =BC ,∴△OBC 为等边三角形,∴∠C =60°. ∴∠AOE =∠C =60°. 在Rt △OAE 中, ∵tan ∠AOE =AE OA, ∴AE =3tan60°=3 3.2.(xx·贵港二模)如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 的长为半径的⊙O 与AD ,AC 分别交于点E ,F ,且∠ACB =∠DCE .第2题图(1)求证:直线CE 与⊙O 相切;(2)若tan ∠BAC =2,BC =2,求⊙O 的半径. (1)证明:∵四边形ABCD 是矩形,∴BC ∥AD , ∴∠BCA =∠DAC .又∵∠ACB =∠DCE , ∴∠DAC =∠DCE .连接OE , 则∠DAC =∠AEO =∠DCE . ∵∠DCE +∠DEC =90°, ∴∠AEO +∠DEC =90°, ∴∠OEC =90°,即OE ⊥CE .又∵OE 是⊙O 的半径, ∴直线CE 与⊙O 相切.(2)解:∵tan ∠BAC =2,BC =2,∴AB = 2 , ∴AC = 6.∵∠DCE =∠ACB , ∴tan ∠DCE =tan ∠ACB =22, ∴DE =DC ·tan∠DCE =1.在Rt △CDE 中,CE =CD 2+DE 2= 3. 设⊙O 的半径为r ,则在Rt △COE 中,CO 2=OE 2+CE 2,即(6-r )2=r 2+3,解得r =64. 3.(xx·贵港)如图,在菱形ABCD 中,点P 在对角线AC 上,且PA =PD ,⊙O 是△PAD 的外接圆.(1)求证:AB 是⊙O 的切线; (2)若AC =8,tan ∠BAC =22,求⊙O 的半径. (1)证明:连接OP ,OA ,OP 交AD 于点E ,如答图.第3题答图∵PA =PD ,∴AP ︵ =DP ︵,∴OP ⊥AD ,AE =DE , ∴∠1+∠OPA =90°. ∵OP =OA ,∴∠OAP =∠OPA , ∴∠1+∠OAP =90°. ∵四边形ABCD 为菱形,∴∠1=∠2,∴∠2+∠OAP =90°, ∴OA ⊥AB ,∴AB 是⊙O 的切线. (2)解:连接BD ,交AC 于点F ,如答图. ∵四边形ABCD 为菱形, ∴DB 与AC 互相垂直平分. ∵AC =8,tan ∠BAC =22, ∴AF =4,tan ∠DAC =DF AF=22,∴DF =22,∴AD =AF 2+DF 2=26, ∴AE = 6.在Rt △PAE 中,tan ∠1=PEAE =22, ∴PE = 3.设⊙O 的半径为R ,则OE =R -3,OA =R ,在Rt △OAE 中, ∵OA 2=OE 2+AE 2, ∴R 2=(R -3)2+(6)2, ∴R =332,即⊙O 的半径为332.4.如图,正方形ABCD 顶点A ,D 在⊙O 上,边BC 经过⊙O 上一定点P ,且PF 平分∠AFC ,边 AB ,CD 分别与⊙O 相交于点E ,F ,连接EF .(1)求证:BC 是⊙O 的切线; (2)若FC =2,求PC 的长. (1)证明:如答图,连接OP .∵四边形ABCD 是正方形, ∴∠B =∠C =∠D =90°,AB =BC . ∵PF 平分∠AFC ,∴∠AFP =∠PFC .∵OP =OF , ∴∠AFP =∠OPF ,∴∠PFC =∠OPF , ∴OP ∥CD ,∴∠BPO =∠C =90°,∴OP ⊥BC . 又∵OP 是⊙O 的半径, ∴BC 是⊙O 的切线.(2)解:如答图,连接AP .∵∠D =90°, ∴AF 是⊙O 的直径,∴∠AEF =∠APF =90°, ∴∠BEF =∠B =∠C =90°. ∵OP ∥CD ,∴OP ∥CD ∥BA , ∴AO AF =BP BC =12,∴BP =12BC =12B A.∵∠APB +∠FPC =90°,∠PFC +∠FPC =90°, ∴∠APB =∠PFC .∵∠B =∠C =90°, ∴△APB ∽△PFC,∴FC PB =CP BA =12,∴FC CP =PB BA =12,∴PC =2FC =4.(本资料素材和资料部分来自网络,供参考。
2019中考数学二轮专项练习测试题(11)及解析.doc

2019中考数学二轮专项练习测试题(11)及解析【一】教材内容八年级第二学期第二十二章四边形22.1-22.6〔21课时〕【二】“课标”要求1、理解多边形及其有关概念,通过实验活动探索多边形的内角和及外角和,掌握多边形内角和定理,理解多边形外角和定理。
2、理解平行四边形的概念;由平行四边形是中心对称图形探索它的性质,掌握平行四边形的性质定理。
3、掌握平行四边形的判定定理,会用平行四边形的判定定理和性质定理解决简单的几何证明或计算问题。
深入体会演绎推理方法。
4、经历从一般到特殊的研究过程,掌握矩形、菱形、正方形的特殊性质和判定方法;懂得它们之间的内在联系,体会集合思想。
5、理解梯形的有关概念,掌握等腰梯形的性质与判定;掌握三角形中位线定理和梯形中位线定理;建立梯形与三角形之间的联系,领悟对立统一的思想观点。
图形与几何〔5〕〔四边形〕一、选择题.〔6×4’=24’〕1.以下图形中,既是轴对称,又是中心对称的图形是〔〕〔A〕平行四边形; (B) 等腰梯形; (C) 菱形; (D) 直角梯形、〔A〕两条对角线相等的四边形是矩形;〔B〕两条对角线互相垂直的四边形是菱形;〔C〕两条对角线互相平分的四边形是平行四边形;〔D〕两条对角线互相垂直且相等的四边形是正方形、3.用两个全等的直角三角形一定能拼成的四边形是、、、、、、、、、、、-〔〕〔A〕等腰梯形;〔B〕正方形;〔C〕菱形;〔D〕平行四边形、4.顺次连接等腰梯形四边中点,所组成的四边形是、、、、、、、、、、、、、、、、、〔〕(A)矩形;(B)菱形;(C)正方形;(D)梯形、5.边长为a的等边三角形,顺次联结各边的中点,得到的三角形的周长是〔〕〔A〕3a;〔B〕2a;〔C〕a;〔D〕3a.26.多边形的边数增加2,这个多边形的内角增加〔〕〔A 〕90°;〔B 〕180°;〔C 〕360°;〔D 〕540°.【二】填空题.〔12×4’=48’〕7.平行四边形ABCD 中,︒=∠50C ,那么=∠A .8.在平行四边形ABCD 中,cm BC cm AB 3,2==,那么它的周长是cm .9.平行四边形ABCD 的面积为212cm ,AB 边上的高为cm 3,那么=AB cm 、10.菱形的周长为m ,那么这个菱形的边长为〔用m 的代数式表示〕、11.梯形的中位线长为6cm ,高为5cm ,那么它的面积等于cm 2、12.菱形的周长为40c m ,一条对角线长为12c m ,那么另一条对角线长为 cm 、13.直角梯形的一个底角为600,上、下底的长分别是2和3,那么这个梯形的周长、14.在梯形ABCD 中,AD ∥BC ,对角线AC 与BD 相交于点O ,如果AD=2,BC=3,那么△AOD 与△BOC 的面积之比为.15.假设梯形的两底之比为2:5,中位线的长为14cm ,那么较大底的长为cm.16.要使平行四边形ABCD 是矩形,需添加一个条件,这个条件可以是〔只要填写一种情况〕.17.矩形ABCD 中,8,6==BC AB ,将矩形翻折,使点C 与点A 重合,那么折痕EF 的长为.18.在梯形ABCD 中,AD ∥BC ,,54,36︒=∠︒=∠B C M 、N 分别是AD 、BC 的中点,假设的长为则MN AD BC ,6,10==、【三】简答题〔19-22每题10分,23、24每题12分,25题14分,共78分〕19.:如图平行四边形ABCD 中,E 、F 分别是边BC 和AD 上的点,且BE=DF , 求证:四边形AECF 是平行四边形.20.:如图,在等腰梯形ABCD 中,AB//CD ,点E 、F 分别在AD 、BC 上,且DE=CF.求证:AF =BE. 21.如图,在直角梯形ABCD 中,AD ∥BC ,DC ⊥BC ,将直角梯形ABCD 沿对角线BD 折叠,点A 刚好落在BC 上的点E 处..假设∠A=120°,AB=4,求EC 的长. 22.如图,在正方形ABCD 中,E 为CB 延长线上一点,F 在AD 边上,且BE=DF ,EF 与AC 交于点O 、求证:△OEC 为等腰直角三角形、 23.如图,在梯形ABCD 中,AD ∥BC ,∠BCD =90°,5==BC AB ,,2=AD (1)求CD 的长;(2)假设∠ABC 的平分线交CD 于点E ,连结AE ,求∠AEB 的正切值、 24.抛物线x c bx ax y 与++=2轴交于点A 〔2,0〕,B 〔4,0〕,与y 轴交于点C ,直线第20题图F E D C B A F E D C B A 第19题图E D C B A第21题图O FE D C B A第22题图ED CA8+-=x y 经过点C 、〔1〕求这个二次函数的解析式;〔2〕过点A 作轴x AD ⊥,与直线8+-=x y 交于点D ,如以AD 为一条边作平行四边形,使平行四边形的另两个顶点E 在抛物线c bx ax y ++=2上,顶点F 在直线8+-=x y 上,求点E 、F 的坐标、25.在平行四边形ABCD 中,AB=5,AD=3,sinA=32,点P 是AB 上一动点,〔点P 不与点A 、点B 重合〕,过点P 作PQ ∥AD 交BD 于Q ,连结CQ ,设AP 的长为x ,四边形QPBC 的面积为y 、〔1〕计算平行四边形ABCD 的面积;〔2〕写出y 关于x 的函数解析式,并指出自变量x 的取值范围;〔3〕是否存在实数x ,使得BCQ BPQ S S ∆∆=?如果存在,求出x 的值;如果不存在,请说明理由、参考答案 1.C ;2.C ;3.D ;4B ;5.D;6.C7.︒50;8.10;9.4;10.4m ;11.30;12.16cm ;13.37+;14.4:9;15.20cm ;16.︒=∠90A 或AC=BD 等;17.7.5;18.2;19.证:∵四边形ABCD 是平行四边形∴BC ∥AD,BC=AD.…………………………………(4分)∵BE=DF∴AF ∥EC,AF=EC.………………………………(4分)∴四边形AECF 是平行四边形.……………………(2分)20.证明:∵四边形ABCD 是等腰梯形∴∠DAB =∠CBA ,AD =BC ………………………………(2分)又∵DE =CF ∴AE =BF …………………………………(2分)在△AFB 与△BEA 中,AE BF EAB FBAAB BA =⎧⎪∠=∠⎨⎪=⎩……………………………………………(3分) ∴△AFB ≌△BEA …………………………………………………(2分)∴AF =BE …………………………………………………………(1分)21.解∵△ABD 与△EBD 关于对角线BD 对称∴∠BED=∠A=120°…………………………………………………(1分)∵点E 在BC 边上∴∠DEC=60°……………………………(1分)∵AD ∥BC ∴∠ABC==∠-︒A 18060°……………………(1分)Q P D CBA∴∠ABC=∠DEC …………………………………………………〔1分〕 ∴AB ∥DE …………………………………………………(1分)∴四边形ABED 为平行四边形………………………(1分)∴DE=AB=4……………………………………………(1分)在Rt △DEC 中,DE EC =60cos …………………(1分) ∴EC=21×4=2………………………………………(1分)其它方法:求出∠EDC=30°给2分,求出DE=4给5分.22.证明:连BD ………………………………………………………〔1分〕∵四边形ABCD 是正方形∴AC=BD ,∠DBC=∠ACB=45°…〔2分〕∵四边形ABCD 是正方形∴AD ∥BC ,∴DF ∥BE ……………〔1分〕∵BE=DF∴四边形EFDB 为平行四边形…………………………………〔1分〕 ∴EF//BD …………………………………………………………〔1分〕∴∠FEC=∠DBC …………………………………〔1分〕∴∠FEC=45°…………………………………〔1分〕∵∠ACB=45°,∴∠FEC=∠ACB ,∴∠EOC=90°∴△OEC 为等腰直角三角形……………〔2分〕23.〔1〕过点A 作AF ⊥BC 垂足为F,由题意得FC=AD=2,AF=CD ,、、、、、、2分 ∵BC=5,∴BF=3,、、、、、、、、、、、、、、、、、、、、、、、2分 在Rt △AFB 中解得AF=4,∴CD=4…………………2分〔2〕设EC=x ,由AB=BC ,∠ABE=∠CBE ,BE=BE ,得△ABE ≌△CBE ,AE=EC=x ,∠AEB=∠CEB …………………….2分DE=x -4,在Rt △ADE 中,222DE AD AE +=2222)4(+-=x x ,得25=x …………………..2分 5tan tan 252BC AEB CEB CE ∠=∠===…………..2分24.解:由题意得:点C 〔0,8〕……………………………〔1分〕⎪⎩⎪⎨⎧==++=++80416024c c b a c b a 解得:⎪⎩⎪⎨⎧=-==861c b a ………………〔2分〕∴二次函数的解析式为:862+-=x x y ;……………〔1分〕〔2〕∵轴x AD ⊥,点D 在直线8+-=x y ,∴D 〔2,6〕……………〔1分〕 A B D E第20题图 F∴AD ∥EF,AD=EF=6.……………〔1分〕∵顶点E 在抛物线862+-=x x y 上,顶点F 在直线8+-=x y 上, 设点E 〔,x 862+-x x 〕,点F 〔8,+-x x 〕……………………〔1分〕 68862=-++-∴x x x ……………………………………〔2分〕解得:263,1===-=x x x x 或或或〔舍去〕…………………〔1分+1分〕 ∴E 〔-1,15〕、F 〔-1,9〕或E 〔3,-1〕、F 〔3,5〕或E 〔6,8〕、F 〔6,2〕、……………………………〔1分〕25⑴作DH ⊥AB 垂足为H 〔1分〕∵在Rt △ADH 中, ∴DH =AD ·sinA =2〔1分〕 ∴S □ABCD =AB ·DH =5·2=10〔1分〕 ⑵解法1∵PQ ∥AD ∴∴〔1分〕 过Q 作直线KR ∥DH 交AB 于R ,交CD 于K ,在平行四边形ABCD ∵DH ⊥AB ∴KR ⊥AB ,KR ⊥CD∵∠QPB =∠A ∴sin ∠QPB = ∴〔2分〕 ∴〔1分〕 〔1分〕 〔1分〕 ∴ ∴〔0<x <5〕〔2分〕 〔解法2:AB BP BD BQ S S AB BP S S S S S S BCD BAD BCQ BPQ ==⎪⎭⎫ ⎝⎛===∆∆∆∆22121,,,由设会更简洁〕⑶当〔1分〕解得x 1=0或x 2=5〔1分〕∵0<x <5∴不存在实数x ,使S △BPQ =S △BCQ 〔1分〕 32sin ==AD DH A AB BP AD PQ =355⋅-=x PQ PQ RQ =32)5(5232x PQ QR -=⋅=2)5(51)5(52)5(21x x x S PBQ -=-⋅-=∆x x RQ KR KQ 52)5(522=--=-=x x S S S CDQ BCD BQC -=⋅⋅-=-=∆∆∆5525215)5()5(512x x y -+-=103512+-=x x y x x -=-5)5(512K R Q PH D CB A。
安徽省2019年中考数学二轮复习题型二:选择压轴题之几何图形最值问题(含答案)

题型二 选择压轴题之几何图形最值问题类型一 线段最值问题1. 如图,在△ABC 中,∠BAC =90°,AB =3,AC =4,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 的中点,则PM 的最小值为( )A.1.2B. 1.3C.1.4D. 2.4第1题图 第2题图 2. 如图,在Rt △ABC 中,∠ACB =90°,AC =6,BC =8,AD 是∠BAC 的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC +PQ 的最小值是( )A. B. 4 C. D. 51252453. 如图,在Rt △ABC 中,∠B =90°,AB =3,BC =4,点D 在BC 上,以AC 为对角线的所有▱ADCE 中,DE 的最小值是( )A.3B. 2C.4D. 5第3题图 第4题图 4. 如图,菱形ABCD 中,∠ABC =60°,边长为3,P 是对角线BD 上的一个动点,则PB +PC 的最小值是( )12 A. B. C.3 D. +33323235. 如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( )A.4B. 5C.6D. 7 第5题图 第6题图 6. 如图,在边长为4的正方形ABCD 中,点E 、F 分别是边BC 、CD 上的动点,且BE =CF ,连接BF 、DE ,则BF +DE 的最小值为( )A.2 B. 4 C.2 D. 455337. 如图,在四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,AB =2,AD =4,点M ,点N 分别在边BC ,CD 上,则△AMN 周长的最小值为( )A.3B. 4C.2+6D. 11777第7题图 第8题图8. 如图,在直角坐标系中,点A 、B 的坐标分别为(1,5)和(4,0),点C 是y 轴上的一个动点,且A 、B 、C 三点不在同一条直线上,当△ABC 的周长最小时,点C 的坐标是( )A.(0,1)B. (0,2)C.(0,3)D. (0,4)9. 如图,矩形ABCD 中,AB =8,BC =6,点E ,F ,G ,H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )A.4B. 10C.8D. 2037第9题图 第10题图10. 如图,在Rt △ABC 中,∠ACB =90°,CB =4,CA =6,⊙C 半径为2,P 为圆上一动点,连接AP ,BP ,则AP +BP 的最小值为( )12A. B. 6 C.2 D. 4371711. 如图,在Rt △ABC 中,∠ACB =90°,AC =8,BC =6,动点F 在边BC 上运动,连接AF ,过点C 作CD ⊥AF 于点D ,交AB 于点E ,则B 、D 两点之间距离的最小值为( )A.2B. 4C.2-3D. 2-41313第11题图 第12题图12. 如图,在等边△ABC 中,BF 是AC 边上中线,点D 在BF 上,连接AD ,在AD 的右侧作等边△ADE ,连接EF ,当△AEF 周长最小时,∠CFE 的大小是( )A.30°B. 45°C.60°D. 90°13. 在平面直角坐标系中,点O 为坐标原点,点A 、B 、C 的坐标分别为A (,0)、3B (3,0)、C (0,5),点D 在第一象限内,且∠ADB =60°,则线段CD 的长的最小值是( )3A.2-2B. 2-2C.2-2D. 2-23571014. 如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,点F 在边AC 上,并且CF =2,点E 为边BC 上的动点,将△CEF 沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是( )A.3B.C.D. 26535 第14题图 第15题图 第16题图15. 如图,正方形ABCD 的边长为2,点E 、F 分别是边BC 、CD 的延长线上的动点,且CE =DF ,连接AE 、BF ,交于点G ,连接DG ,则DG 的最小值为( )A.-1B. -1C.D. 353516. 在Rt △ABC 中,∠ACB =90°,AC =8,BC =6,点D 是以点A 为圆心,4为半径的圆上一点,连接BD ,点M 为BD 中点,线段CM 长度的最大值为( )A.8B. 7C.6D. 5类型二 面积最值问题(拓展)1. 如图,点E 为边长为4的等边△ABC 的BC 边上一动点(点E 不与B 、C 重合),以AE 为边作等边△AEF ,则△AEF 面积的最小值是( )A.2B. 4C.D. 333第1题图 第2题图 2. (2017合肥蜀山区模拟)如图,⊙O 的半径是2,直线l 与⊙O 相交于A 、B 两点,M 、N 是⊙O 上的两个动点,且在直线l 的异侧,若∠AMB =45°,则四边形MANB 面积的最大值是( )A.2B. 4C.2D. 4223. 如图,在矩形ABCD 中,AD >AB ,点E 、F 分别是BC 、DC 上的点,且CE +CF =8,若sin ∠ABD =,BD =20,则△AEF 的面积的最小值为( )45A.24 B. 46 C.64 D. 96第3题图 第4题图 4. 如图,在菱形ABCD 中,∠BAD =135°,AB =4,点P 是菱形ABCD 内或边上的2一点,且∠DAP +∠CBP =90°,连接DP ,CP ,则△DCP 面积的最小值为( )A.4 B. 8- C.4-2 D. 8-8252322参考答案类型一 线段最值问题1. A2. C3. A4. B5. B6. B7. B8. D9. D 10. A 11. D 12. D 13. C 14. B 15. B 16. B类型二 面积最值问题(拓展)1. D2. D3. B4. D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年中考数学二轮复习专题练【几何图形的证明及计算问题】附答案解析类型一与全等三角形有关的证明及计算1.如图,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM 上的点,且MB=MN.(1)求证:BN平分∠ABE;(2)若BD=1,连接DN,当四边形DNBC为平行四边形时,求线段BC的长;第1题图2.如图①,在等腰三角形ABC中,AB=AC,在底边BC上取一点D,在边AC上取一点E,使AE=AD,连接DE,在∠ABD的内部作∠ABF=2∠EDC,交AD于点F.(1)求证:△ABF是等腰三角形;(2)如图②,BF的延长线交AC于点G.若∠DAC=∠CBG,延长AC至点M,使GM=AB,连接BM,点N是BG的中点,连接AN,试判断线段AN、BM之间的数量关系,并证明你的结论.第2题图3.如图①,在△ABC中,∠ACB=90°,AC=BC,E为AC边上的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G.(1)求证:CF=BG;(2)如图②,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB =CP+CF;(3)在(2)问的条件下,当∠GAC=2∠FCH时,若S△AEG=33,BG=6,求AC的长.图①图②第3题图4.如图①,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.(1)求证:∠CAE=∠CBD;(2)如图②,F是BD的中点,连接CF交AE于点M,求证:AE⊥CF;(3)如图③,F,G分别是BD,AE的中点,连接GF,若AC=2 2 ,CE=1,求△CGF的面积.第4题图5.如图①,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE=OB,OE交CD于点F.(1)求证:△OBC≌△ODC;(2)求证:∠DOE=∠ABC;(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=52°,求∠DOE的度数.第5题图6.已知:如图①,等腰直角△ABC和△ECD中,∠ACB=∠ECD=90°,AC=BC,EC=DC.(1)求证:BE=AD;(2)如图②,若将△ECD绕点C按逆时针方向旋转一个锐角,①延长BE交AD于点F,交AC于点O.求证:BF⊥AD;②如图③,取BE的中点M,AD的中点N,连接MN,NC,求∠MNC的度数.第6题图类型二与相似三角形有关的证明及计算1.如图①,已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的点,过点Q作AC的垂线交线段AB(如图①)或线段AB的延长线(如图②)于点P.(1)当点P在线段AB上时,求证:△AQP∽△ABC;(2)当△PQB为等腰三角形时,求AP的长.第1题图2. 如图,在四边形ABCD 中,AC 平分∠DAB ,∠ADC =∠ACB =90°,E 为AB 的中点,连接DE 、CE .(1)求证:AC 2=AB ·AD ; (2)求证:CE ∥AD ;(3)若AD =5,AB =7,求ACAF 的值.第2题图3. 如图①,在△ABC 中,AB =AC ,点D 、E 、F 分别在BC 、AB 、AC 上,∠EDF =∠B. (1)求证:DE ·CD =DF ·BE ;(2)如图②,若D 为BC 中点,连接EF ,A D. ①求证:DE 平分∠BEF ;②若四边形AEDF 为菱形,求∠BAC 的度数及AEAB 的值.第3题图4. 如图①,△ABC 中,点D 在线段AB 上,点E 在线段CB 延长线上,且BE =CD ,EP ∥AC 交直线CD 的延长线于点P ,交直线AB 的延长线于点F ,∠ADP =∠AC B.(1)图①中是否存在与AC 相等的线段?若存在,请找出,并加以证明,若不存在,说明理由; (2)若将“点D 在线段AB 上,点E 在线段CB 延长线上”改为“点D 在线段BA 延长线上,点E 在线段BC 延长线上”,其他条件不变(如图②).当∠ABC =90°,∠BAC =60°,AB =2时,求线段PE 的长.第4题图5. 如图①,△ABC 中,BC >AC ,CD 平分∠ACB 交AB 于D ,E ,F 分别是AC ,BC 边上的两点,EF 交CD 于H .(1)若∠EFC =∠A ,求证:CE ·CD =CH ·BC ;(2)如图②,若BH 平分∠ABC ,CE =CF ,BF =3,AE =2,求EF 的长;(3)如图③,若CE ≠CF ,∠CEF =∠B ,∠ACB =60°,CH =5,CE =4 3 ,求 AC BC 的值.第5题图类型三与全等和相似三角形有关的证明及计算1.如图,等边△ABC边长是8,过点C的直线l∥AB,点D为BC上一点(不与点B,C重合),将一个60°角的顶点放在D处,它的边始终过点A,另一边与直线l交于点E,DE交AC于点F.(1)若BD=6,求CF的长;(2)若点D是BC的中点,判定△ADE的形状,并给出证明;(3)若点D不是BC的中点,则(2)中的结论成立吗?如果成立,请给予证明,如果不成立,请说明理由.第1题图2.如图①,在△ABC中,AC=BC,∠ACB=90°,点D、P分别为AC、AB的中点,连接BD、CP,CP交BD于点E,点F在AB上且∠ACF=∠CB D.(1)求证:CF=BE;(2)如图②,过点A 作AG ⊥AB 交BD 的延长线于点G . ①若CF =6,求DG 的长; ②设CF 交BD 于点H ,求HECH 的值.第2题图3. 如图①,已知D 是△ABC 的边BC 上的中点,DE ⊥AB 于点E ,DF ⊥AC 于点F ,且BE =CF ,点M 、N 分别是AE 、DE 上的点,AN ⊥FM 于点G .(1)若∠BAC =90°,求证:△ABC 为等腰直角三角形; (2)如图②,若∠BAC ≠90°,AF =2DF . ①求证:FM AN =EM DN ; ②求AN ∶FM 的值.图① 图②第3题图4. (2018六安市模拟)我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点I 为△ABC 的内心.(1)如图①,连接AI 并延长交BC 于点D ,若AB =AC =3,BC =2,求ID 的长; (2)如图②,过点I 作直线交AB 于点M ,交AC 于点N . ①若MN ⊥AI ,求证:MI 2=BM ·CN ;②如图③,AI 的延长线交BC 于点D ,若∠BAC =60°,AI =4,求1AM +AN1的值.第4题图5. 如图①,在△ABC 中,∠ACB =90°,AC =BC ,顶点C 恰好在直线l 上,过A 、B 分别作AD ⊥l ,BE ⊥l ,垂足分别为D 、E .(1)求证:DE=AD+BE;(2)如图②,在△ABC中,当AC=kBC,其他条件不变,猜想DE与AD、BE的关系,并证明你的结论;(3)如图③,在Rt△ABC中,AC=4,BC=12,∠ACB=90°,点D是AC的中点,点E在BC上,过点E作EF⊥DE交AB于点F,若恰好EF=2DE,求CE的长.图①图②图③第5题图6.如图①,在等腰Rt△ABC中,∠ACB=90°,AC=BC, D为AB的中点,连接CD,将一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF 与AC交于点M,DE与BC交于点N.(1)若CE=CF,求证:△DCE≌△DCF;(2)如图②,在∠EDF绕点D旋转的过程中:①探究线段AB与CE、CF之间的数量关系,并证明;②若AB=42,CE=2CF,求DN的长.第6题图类型一 与全等三角形有关的证明及计算1. (1)证明:∵AB =AC ,点M 是BC 的中点,∴AM ⊥BC ,∠BAM =∠CAM , ∴∠CAM +∠ACM =90°, ∵AC ⊥BD ,∴∠MBE +∠ACM =90°, ∴∠BAN =∠CAM =∠MBE , ∵MB =MN , ∴∠MNB =∠MBN ,∵∠MNB =∠ABN +∠BAN ,∠MBN =∠MBE +∠NBE , ∴∠ABN +∠BAN =∠MBE +∠NBE , ∴∠ABN =∠NBE , 即BN 平分∠ABE ;(2)解:连接DN ,∵点M 为BC 中点,MB =MN , ∴MB =MN =12BC ,∵四边形DNBC 为平行四边形, ∴BN =CD ,BN ∥CD , ∴∠DBN =∠BDC , 由(1)知∠ABN =∠DBN , ∴∠ABN =∠BDC , ∵AB =BD =1, ∴△ABN ≌△BDC , ∴AN =BC ,∴AM =AN +MN =32BC ,参考答案由(1)中条件可知AM ⊥BC ,即∠AMB =90°, ∴AM 2+MB 2=AB 2,即(32BC )2+(12BC )2=1,解得BC =105.第1题解图2. (1)证明:∵等腰三角形ABC 中,AB =AC ,∴∠ABD =∠ACD , ∵AE =AD , ∴∠ADE =∠AED ,∵∠BAD +∠ABD =∠ADE +∠EDC ,∠EDC +∠ACD =∠AED , ∴∠BAD =2∠EDC , ∵∠ABF =2∠EDC , ∴∠BAD =∠ABF , ∴△ABF 是等腰三角形; (2)解:AN =12BM .证明:如解图,延长CA 至点H ,使AG =AH ,连接BH , ∵点N 是BG 的中点,点A 是HG 的中点, ∴AN =12BH ,∵(1)中已证明∠BAD =∠ABF ,且∠DAC =∠CBG , ∴∠CAB =∠CBA , ∴CA =CB 又∵AB =AC ,∴△ABC 是等边三角形,∠BAC =∠BCA =60°, ∴∠BAH =∠BCM , ∵GM =AB ,AB =AC , ∴AC =GM , ∴CM =AG , ∴AH =CM ,在△BAH 和△BCM 中,⎩⎨⎧AB =BC∠BAH =∠BCM AH =CM, ∴△BAH ≌△BCM (SAS), ∴BH =BM , ∴AN =12BM .第2题解图3. (1)证明:∵∠ACB =90°,AC =BC ,∴∠A =45°, ∵CG 平分∠ACB , ∴∠ACG =∠BCG =45°, ∴∠A =∠BCG , 在△BCG 和△CAF 中,⎩⎨⎧∠A =∠BCGAC =BC∠ACF =∠CBE,∴△BCG ≌△CAF (ASA), ∴CF =BG ;(2)证明:∵PC ∥AG , ∴∠PCA =∠CAG ,∵AC =BC ,∠ACG =∠BCG ,CG =CG , ∴△ACG ≌△BCG (SAS ), ∴∠CAG =∠CBE ,∵∠PCG =∠PCA +∠ACG =∠CAG +45°=∠CBE +45°,∠PGC =∠GCB +∠CBE =∠CBE +45°, ∴∠PCG =∠PGC , ∴PC =PG ,∵PB =BG +PG ,BG =CF , ∴PB =CP +CF ;(3)解:如解图,过E 作EM ⊥AG ,交AG 于M , ∵S △AEG =12AG ·EM =33, 由(2)得:△ACG ≌△BCG , ∴BG =AG =6, ∴ 12×6×EM =33, 解得EM =3,设∠FCH =x °,则∠GAC =2x °, ∴∠ACF =∠EBC =∠GAC =2x °, ∵∠ACH =45°, ∴2x +x =45, 解得x =15,∴∠ACF =∠GAC =30°,在Rt △AEM 中,AE =2EM =23, AM =(23)2-(3)2=3, ∴M 是AG 的中点,第3题解图∴AE =EG =23, ∴BE =BG +EG =6+23, 在Rt △ECB 中,∠EBC =30°, ∴CE =12BE =3+3,∴AC =AE +EC =23+3+3=33+3. 4. (1)证明:在△ACE 和△BCD 中,⎩⎨⎧AC =BC∠ACE =∠BCD CE =CD, ∴△ACE ≌△BCD , ∴∠CAE =∠CBD ;(2)证明:在Rt △BCD 中,点F 是BD 的中点, ∴CF =BF , ∴∠BCF =∠CBF , 由(1)知,∠CAE =∠CBD , ∴∠BCF =∠CAE ,∴∠CAE +∠ACF =∠BCF +∠ACF =∠BCA =90°, ∴∠AMC =90°, ∴AE ⊥CF ;(3)解:∵AC =2 2 , ∴BC =AC =2 2 , ∵CE =1, ∴CD =CE =1,在Rt △BCD 中,根据勾股定理得,BD =CD 2+BC 2=3 , ∵点F 是BD 中点, ∴CF =DF =12BD =32 ,同理:EG =12AE =32 ,如解图,连接EF ,过点F 作FH ⊥BC 于点H , ∵∠ACB =90°,点F 是BD 的中点, ∴FH =12CD =12,∴S △CEF =12CE ·FH =12×1×12=14, 由(2)知,AE ⊥CF ,∴S △CEF =12CF ·ME =12×32ME =34ME , ∴ 34ME =14,∴ME =13 ,∴GM =EG -ME =32-13=76 ,∴S △CFG =12CF ·GM =12×32×76=78. 5. (1)证明:∵AC 是正方形ABCD 的对角线,∴BC =DC ,∠BCA =∠DCA , 在△OBC 和△ODC 中,⎩⎨⎧BC =DC∠BCO =∠DCO CO =CO, ∴△OBC ≌△ODC (SAS);(2)证明:由(1)知,△OBC ≌△ODC , ∴∠CBO =∠CDO , ∵OE =OB , ∴∠CBO =∠E , ∴∠CDO =∠E , ∵∠DFO =∠EFC ,∴180°-∠DFO -∠CDO =180°-∠EFC -∠E ,即∠DOE =∠DCE ,第4题解图∵AB ∥CD , ∴∠DCE =∠ABC , ∴∠DOE =∠ABC ;(3)解:∵AC 是菱形ABCD 的对角线, ∴BC =DC ,∠BCA =∠DCA , 在△BCO 和△DCO 中,⎩⎨⎧BC =DC∠BCO =∠DCO CO =CO, ∴△BCO ≌△DCO (SAS), ∴∠CBO =∠CDO , ∵OE =OB , ∴∠CBO =∠E , ∴∠CDO =∠E , ∵∠DFO =∠EFC ,∴180°-∠DFO -∠CDO =180°-∠EFC -∠E , 即∠DOE =∠DCE , ∵AB ∥CD , ∴∠DCE =∠ABC , ∴∠DOE =∠ABC =52°. 6. (1)证明:在△BEC 和△ACD 中,⎩⎨⎧BC =AC∠ACB =∠ECD EC =DC, ∴△BEC ≌△ADC (SAS), ∴BE =AD ;(2)①证明:∵∠ACB =∠ECD =90°, ∴∠ACB -∠ACE =∠ECD -∠ACE , 即∠BCE =∠ACD ,在△BEC 和△ADC 中,⎩⎨⎧BC =AC∠BCE =∠ACD EC =DC, ∴△BEC ≌△ADC (SAS), ∴∠CBE =∠CAD ,在△BCO 和△AFO 中,∠CBE =∠CAD ,∠BOC =∠AOF , ∴∠AFB =∠ACB =90°, ∴BF ⊥AD ;②解:如解图,连接MC , ∵∠ACB =∠ECD =90°, ∴∠BCE =∠ACD , 又∵AC =BC ,EC =DC , ∴△BEC ≌△ADC ,∴∠CBE =∠CAD ,AD =BE , ∵M 是BE 的中点,N 是AD 的中点, ∴BM =AN ,在△BMC 和△ANC 中,⎩⎨⎧BM =AN∠CBE =∠CAD BC =AC, ∴△BMC ≌△ANC (SAS), ∴CM =CN ,∠BCM =∠ACN , ∴∠ACN +∠MCA =∠BCM +∠MCA , ∴∠MCN =∠ACB =90°, ∴△MCN 是等腰直角三角形, ∴∠MNC =45°.第6题解图类型二 与相似三角形有关的证明及计算1. (1)证明:∵PQ ⊥AQ ,∴∠AQP =90°=∠ABC . 在△AQP 与△ABC 中, ∵∠AQP =∠ABC , ∠QAP =∠BAC , ∴△AQP ∽△ABC ;(2)解:在Rt △ABC 中,AB =3,BC =4,由勾股定理得AC =5. ①当点P 在线段AB 上时,如题图①所示. ∵∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =PQ , 由(1)可知,△AQP ∽△ABC , ∴P A AC =PQBC ,即3-PB 5=BP 4, 解得PB =43,∴AP =AB -PB =3-43=53;②当点P 在线段AB 的延长线上时,如题图②所示. ∵∠QBP 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =BQ . ∴∠BQP =∠P ,∵∠BQP +∠AQB =90°,∠A +∠P =90°, ∴∠AQB =∠A ,∴BQ =AB , ∴AB =BP ,∴AP =2AB =2×3=6.综上所述,当△PQB 为等腰三角形时,AP 的长为53或6. 2. (1)证明:∵AC 平分∠DAB ,∴∠DAC =∠CAB .又∵∠ADC =∠ACB =90°, ∴△ADC ∽△ACB , ∴AD AC =AC AB , ∴AC 2=AB ·AD ;(2)证明:∵E 为AB 的中点, ∠ACB =90°, ∴CE =12AB =AE , ∴∠EAC =∠ECA , ∵∠DAC =∠CAB , ∴∠DAC =∠ECA . ∴AD ∥CE ; (3)解:∵CE ∥AD , ∴∠DAF =∠ECF , 又∵∠DF A =∠EFC , ∴△AFD ∽△CFE , ∴AD CE =AF CF , ∵CE =12AB , ∴CE =12×7=72, ∵AD =5,∴572=AFCF,∴CFAF=710,∴AF+CFAF=1+CFAF=1710,即ACAF=1710.3. (1)证明:∵△ABC中,AB=AC,∴∠B=∠C,∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,∴∠FDC=∠DEB,∴△CFD∽△BDE,∴DEDF=BECD,即DE·CD=DF·BE;(2)①证明:由(1)证得△BDE∽△CFD,∴BECD=DEDF,∵D为BC中点,∴BD=CD,∴BEBD=DEDF,∵∠B=∠EDF,∴△BDE∽△DFE,∴∠BED=∠DEF,∴ED平分∠BEF;②解:∵四边形AEDF为菱形,∴∠AEF=∠DEF,由(2)知,∠BED=∠DEF,∵∠AEF+∠DEF+∠BED=180°,∴∠AEF =60°,∵AE =AF ,∴∠BAC =60°.∵AB =AC ,∴△ABC 是等边三角形,∴∠B =60°,又∵∠BED =∠AEF =60°,∴△BED 是等边三角形,∴BE =DE ,∵AE =DE ,∴AE =BE =12AB ,∴AE AB =12.4. 解:(1)AC =BF .证明如下:∵∠ADP =∠ACD +∠A ,∠ACB =∠ACD +∠BCD ,∠ADP =∠ACB ,∴∠BCD =∠A ,又∵∠CBD =∠ABC ,∴△CBD ∽△ABC ,∴ CD AC =BC BA ,①∵FE ∥AC ,∴∠CAB =∠EFB ,又∵∠ABC =∠FBE ,∴△ABC ∽△FBE ,∴ BC BA =BE BF ,②由①②可得CD AC =BE BF ,∵BE =CD ,∴BF =AC ;(2)∵∠ABC =90°,∠BAC =60°,∴∠ACB =30°=∠ADP ,∴∠BCD =60°,∠ACD =60°-30°=30°,∵PE ∥AC ,∴∠E =∠ACB =30°,∠CPE =∠ACD =30°,∴CP =CE ,∵BE =CD ,∴BE -CE =CD -CP ,∴BC =DP ,∵∠ABC =90°,∠D =30°,∴BC =12CD ,∴DP =12CD ,即P 为CD 的中点,又∵PF ∥AC ,∴F 是AD 的中点,∴FP 是△ADC 的中位线,∴FP =12 AC ,∵∠ABC =90°,∠ACB =30°,∴AB =12AC ,∴FP =AB =2,∵DP =CP =BC ,CP =CE ,∴BC =CE ,即C 为BE 的中点,又∵EF ∥AC ,∴A 为FB 的中点,∴AC 是△BEF 的中位线,∴EF =2AC =4AB =8,∴PE =EF -FP =8-2=6.5. (1)证明:∵∠EFC +∠FEC +∠ECF =180°,∠A +∠B +∠ACB =180°,又∵∠EFC =∠A ,∠ECF =∠ACB ,∴∠CEF =∠B ,∵∠ECH =∠DCB ,∴△ECH ∽△BCD ,∴EC BC =CH CD ,∴CE ·CD =CH ·BC ;(2)解:如解图①,连接AH .∵BH 、CH 分别是∠ABC 和∠ACB 的平分线,∴AH 是∠BAC 的平分线,∴∠BHC =180°-12(∠ABC +∠ACB )=180°-12(180°-∠BAC )=90°+12∠BAC =90°+∠HAE ,∵CE =CF ,∠HCE =∠HCF ,∴CH ⊥EF ,HF =HE ,∴∠CHF =90°,∵∠BHC =∠BHF +∠CHF =∠BHF +90°,∴∠HAE =∠BHF ,∵CE =CF ,∴∠CFE =∠CEF ,∴∠AEH =∠BFH ,∴△AEH ∽△HFB ,∴ AE HF =EH FB ,∴FH ·EH =6,∴HE =HF =6,∴EF =26;第5题解图①(3)解:如解图②,作HM ⊥AC 于M ,HN ⊥BC 于N .设HF =x ,FN =y .∵∠HCM =∠HCN =30°,HC =5,∴HM =HN =52 ,CM =CN =532,∵CE =4 3 ,∴EM =332, ∴EH =EM 2+HM 2=13 ,∵S △HCF ∶S △HCE =FH ∶EH =FC ∶EC ,∴x ∶13=(y + 532)∶43,又∵x 2=y 2+(52)2 ,解得y =5314或332,∵当y =332时,CF =CN +NF =43,又∵CE ≠CF ,∴y ≠332,即FN =5314,∴CF =2037 ,∵∠CEF =∠B ,∠ECF =∠ACB ,∴△ECF ∽△BCA ,∴ EC BC =CFAC ,∴ AC BC =CF EC =203743=57.第5题解图②类型三 与全等和相似三角形有关的证明及计算1. 解:(1)∵△ABC 是等边三角形,∴∠B =∠FCD =60°,∵∠BAD =180°-60°-∠ADB ,∠FDC =180°-∠ADE -∠ADB =180°-60°-∠ADB , ∴∠BAD =∠FDC ,∴△ABD ∽△DCF ,∴AB DC =BD CF ,∴CF =DC ·BD AB =(8-6)×68=32;(2)△ADE 是等边三角形.证明:若D 点是BC 边中点,则AD ⊥BC ,∴∠CDE =∠ADC -∠ADE =90°-60°=30°,又∵l ∥AB ,∴∠DCE =180°-∠ABC =180°-60°=120°,∴∠CED =180°-∠DCE -∠CDE =180°-120°-30°=30°,即∠CDE =∠CED ,∴CE =CD .在△ACD 和△ACE 中,⎩⎨⎧AC =AC∠ACD =∠ACE =60°DC =EC,∴△ACD ≌△ACE (SAS),∴AD =AE ,又∵∠ADE =60°,∴△ADE 是等边三角形;(3)(2)中结论仍然成立.证明:如解图,过点D 作DG ∥l 交AC 于点G ,则△GDC ∽△ABC , ∴△GDC 是等边三角形,∴DG =DC ,∠GDC =∠DGC =60°,∵∠ADE =60°,∴∠ADE =∠GDC ,∴∠ADG =∠EDC ,又∵∠AGD =180°-60°=120°,∠DCE =180°-∠ABC =120°,∴∠AGD =∠DCE ,在△ADG 和△EDC 中,⎩⎨⎧∠ADG =∠EDCDG =DC ∠AGD =∠DCE ,∴△ADG ≌△EDC (ASA),∴AD =DE ,又∵∠ADE =60°,∴△ADE 是等边三角形.2. (1)证明:∵P 为AB 的中点,AC =BC ,∠ACB =90°, ∴∠BCE =12∠ACB =12×90°=45°,∠A =45°,∴∠A =∠BCE ,在△ACF 和△CBE 中第1题解图⎩⎨⎧∠A =∠BCEAC =BC ∠ACF =∠CBD,∴△ACF ≌△CBE (ASA),∴CF =BE ;(2)解:①由(1)得CF =BE ,∴BE =CF =6,∵AC =BC ,CE 平分∠ACB ,P 为AB 的中点,∴CP ⊥AB ,∵AG ⊥AB ,∴CE ∥AG ,∴∠GAD =∠ECD ,又∵∠ADG =∠CDE ,∴△ADG ∽△CDE ,∵点D 是AC 的中点,∴AD =CD ,即相似比k =1,∴△ADG ≌△CDE ,∴DG =DE =12GE ,∵CE ∥AG 且P 为AB 中点,∴GE =BE =6,∴DG =3;②设EP =a ,由(2)① 得EP ∥AG ,∴AG =2a ,又由上题得△ADG ≌△CDE ,∴CE =AG =2a ,∴CP =CE +EP =3a ,∵等腰直角△ABC 中 CP ⊥AB ,∴BP =CP =3a ,由题得∠ACP =∠CBP =45°,∵∠ACF =∠CBD ,∴∠ACP -∠ACF =∠CBP -∠CBD ,即∠HCE =∠PBE , ∵∠CEH =∠PEB ,∴∠CHE =180°-∠CEH -∠HCE ,∠BPE =180°-∠PBE -∠PEB , ∴∠CHE =∠BPE =90°,∴△CHE 是直角三角形,∴△CHE ∽△BPE ,∴HE CH =PE BP =a 3a =13.3. (1)证明:∵DE ⊥AB ,DF ⊥AC ,∴∠BED =∠CFD =90°,∵D 是BC 的中点,∴BD =CD ,在Rt △BED 和Rt △CFD 中,⎩⎨⎧BD =CDBE =CF ,∴Rt △BED ≌Rt △CFD (HL),∴∠B =∠C ,∵∠BAC =90°,∴△ABC 为等腰直角三角形;(2)①证明:如解图,连接AD 、EF ,相交于点O ,∵由(1)可得Rt △BED ≌Rt △CFD ,∴∠B =∠C ,DE =DF ,∴AB =AC ,∵BE =CF ,∴AE =AF ,∴AD ⊥EF ,又∵∠NEM =∠MGN =90°,∴∠GME +∠ENG =∠DNG +∠ENG =180°, ∴∠EMF =∠DNA ,又∵∠AEO +∠EAO =90°,∠EAO +∠NDA =90°, ∴∠AEO =∠NDA ,∴△FME ∽△AND ,∴FM AN =EM DN ;第3题解图②解:设AF =2k ,DF =k ,在Rt △ADF 中,AD =(2k )2+k 2=5k , 由①可得∠B =∠C ,DE =DF ,∴AD 垂直平分EF ,则OF =12EF ,∵DF ⊥AC ,∴S △ADF =12×5k ·OF =12×2k ×k ,∴OF =255k ,EF =455k ,∴ADEF =54,又∵△FME ∽△AND ,∴AN FM =AD EF =54,即AN ∶FM =5∶4.4. (1)解:如解图①中,作IE ⊥AB 于E .设ID =x , ∵AB =AC =3,AI 平分∠BAC ,∴AD ⊥BC ,BD =CD =1,在Rt △ABD 中,AD =AB 2-BD 2=32-12=2 2 ,在△BEI 和△BDI 中,⎩⎨⎧∠EBI =∠DBI ,∠BEI =∠BDI =90°,BI =BI ,∴△BEI ≌△BDI ,∴ID =IE =x ,BD =BE =1,AE =2,在Rt △AEI 中,∵AE 2+EI 2=AI 2,∴22+x 2=(22-x )2 ,∴x =22,∴ID =22;第4题解图(2)①证明:如解图②,连接BI 、CI .∵I 是内心,∴∠MAI =∠NAI ,∵AI ⊥MN ,∴∠AIM =∠AIN =90°,又∵AI =AI ,∴△AMI ≌△ANI (ASA),∴∠AMN =∠ANM ,∴∠BMI =∠CNI ,设∠BAI =∠CAI =α,∠ACI =∠BCI =β,∴∠NIC =90°-α-β,∵∠ABC =180°-2α-2β,∴∠MBI=90°-α-β,∴∠MBI=∠NIC,∴△BMI∽△INC,∴BMNI=MINC,∴NI·MI=BM·CN,∵NI=MI,∴MI2=BM·CN;②解:如解图③,过点N作NG∥AD交MA的延长线于G. ∵NG∥AD,∴∠ANG=∠DAN,∠AGN=∠BAD,∵∠BAC=60°,∴∠BAD=∠DAN=30°,∴∠ANG=∠AGN=30°,∴AN=AG,NG=3AN,∵AI∥NG,∴∠MIA=∠MNG,∠MAI=∠MGN,∴△AMI∽△GMN,∴AMMG=AING,∴AMAM+AN=43AN,∴AM+ANAM=3AN4,∴1AM+1AN=34.第4题解图③5.(1)证明:∵∠ACB =90°,∴∠ACD +∠BCE =90°,∵AD ⊥DE ,BE ⊥DE ,∴∠DAC +∠DCA =90°,∠ADC =∠BEC ,∴∠DAC =∠ECB ,在△ADC 和△CEB 中,⎩⎨⎧∠ADC =∠CEB∠DAC =∠ECBAC =CB,∴△ADC ≌△CEB (AAS),∴AD =CE ,CD =BE ,∴DE =CE +DC =AD +BE ;(2)解:DE =kBE +1k AD .证明:∵∠ACB =90°,∴∠ACD +∠BCE =90°,∵AD ⊥DE ,∴∠DAC +∠DCA =90°,∴∠DAC =∠ECB ,∵AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∴△ADC ∽△CEB ,∴AD CE =DC BE =AC BC =k ,∴DC =kBE ,CE =1k AD ,∴DE =DC +CE =kBE +1k AD ;(3)解:如解图,过点F 作FG ⊥BC 于点G ,∵AC =4,D 是AC 的中点,∴CD =2,∵EF =2DE ,易证△DCE ∽△EGF ,FG =2CE ,EG =2DC =4, 设CE =x ,则BG =BC -CG =12-4-x =8-x ,∵FG ⊥BC ,AC ⊥BC ,∴∠ACB =∠FGB =90°,∵∠B =∠B ,∴△FGB ∽△ACB ,∴FG AC =BG BC ,即2x 4=8-x 12,解得x =87,即CE 的长为87.第5题解图6. (1)证明:∵∠ACB =90°,AC =BC ,D 为AB 的中点,∴∠BCD =∠ACD =45°,∠BCE =∠ACF =90°,∴∠DCE =∠DCF =135°,在△DCE 与△DCF 中,⎩⎨⎧CE =CF∠DCE =∠DCFCD =CD,∴△DCE ≌△DCF (SAS);(2) ①解:AB 2=4CE ·CF .证明:∵∠DCF =∠DCE =135°,∴∠CDF +∠F =180°-135°=45°,∵∠CDF +∠CDE =45°,∴∠F =∠CDE ,∴△CDF ∽△CED , ∴CD CE =CF CD ,即CD 2=CE ·CF ,∵∠ACB =90°,AC =BC ,CD 平分∠ACB ,∴CD =AD =BD =12AB ,∴(12AB )2=CE ·CF ,∴AB 2=4CE ·CF ;②解:如解图,过D 作DG ⊥BC 于G ,由①得AB 2=4CE ·CF , ∵AB =42,CE =2CF ,∴CE =4,CF =2,∵DG ⊥BC 于G ,由题得∠B =45°,BD =12AB =2 2∴△DGB 是等腰直角三角形,∴BG =DG =22·sin 45°=2,∵DG ⊥BC ,AC ⊥BC ,∴DG ∥AC 即DG ∥CE ,∴∠ECN =∠DGN 又∵∠ENC =∠DNG ∴△CEN ∽△GDN ,∴CE DG =CN NG =42=2,又∵D 点为AB 中点,DG ∥AC ,∴CG =BG =2, ∴NG =13CG =23,在Rt △DGN 中,DN =DG 2+NG 2=22+(23)2=2103.第6题解图。
