专题五七:三角形、四边形、圆证明(含答案)
初中数学几何证明经典试题(含答案)【范本模板】
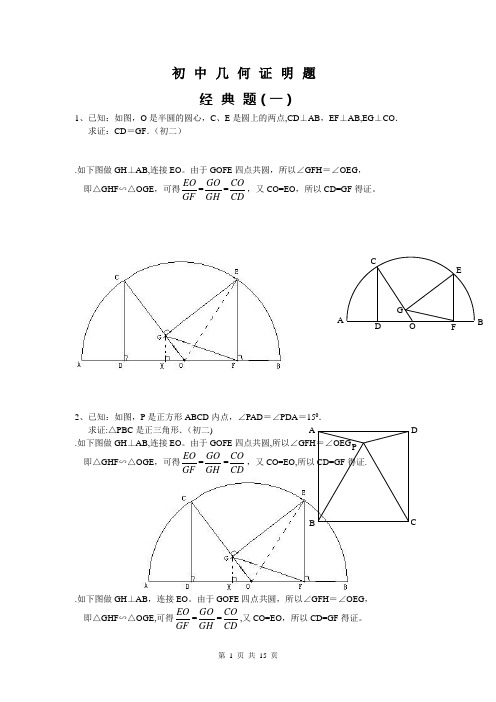
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
中考数学专题测试-四边形的证明与计算(答案解析)

【考点分析】一、证明两线段相等1.两全等三角形中对应边相等。
2.同一三角形中等角对等边。
3.等腰三角形顶角的平分线或底边的高平分底边。
4.平行四边形的对边或对角线被交点分成的两段相等。
5.直角三角形斜边的中点到三顶点距离相等。
6.线段垂直平分线上任意一点到线段两段距离相等。
7.角平分线上任一点到角的两边距离相等。
8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。
9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。
10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。
11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。
12.两圆的内(外)公切线的长相等。
二、证明两角相等1.两全等三角形的对应角相等。
2.同一三角形中等边对等角。
3.等腰三角形中,底边上的中线(或高)平分顶角。
4.两条平行线的同位角、内错角或平行四边形的对角相等。
5.同角(或等角)的余角(或补角)相等。
6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。
7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。
8.相似三角形的对应角相等。
9.圆的内接四边形的外角等于内对角。
10.等于同一角的两个角相等三、证明两直线平行1.垂直于同一直线的各直线平行。
2.同位角相等,内错角相等或同旁内角互补的两直线平行。
3.平行四边形的对边平行。
4.三角形的中位线平行于第三边。
5.梯形的中位线平行于两底。
6.平行于同一直线的两直线平行。
7.一条直线截三角形的两边(或延长线)所得的线段对应成比例,则这条直线平行于第三边。
四、证明两直线互相垂直1.等腰三角形的顶角平分线或底边的中线垂直于底边。
2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。
3.在一个三角形中,若有两个角互余,则第三个角是直角。
4.邻补角的平分线互相垂直。
(完整版)初中数学几何证明经典试题(含答案),推荐文档
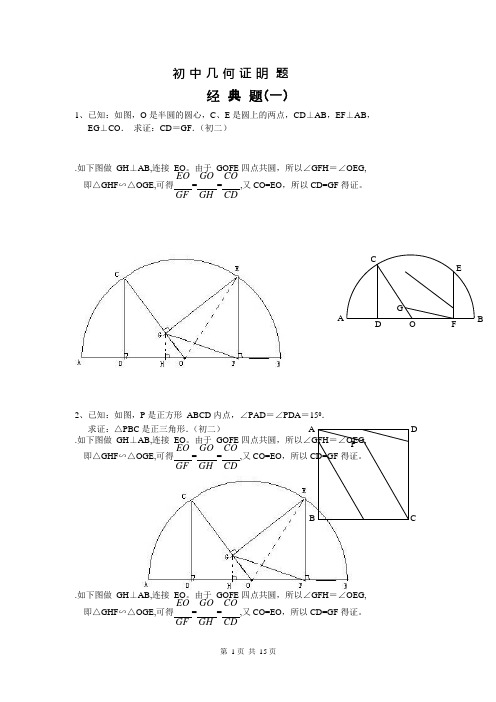
CEG P 初 中 几 何 证 明 题经 典 题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做 GH ⊥AB,连接 EO 。
由于 GOFE 四点共圆,所以∠GFH =∠OEG, EO GO CO即△GHF ∽△OGE,可得==,又 CO=EO ,所以 CD=GF 得证。
GF GH CDADOFB2、已知:如图,P 是正方形 ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) AD.如下图做 GH ⊥AB,连接 EO 。
由于 GOFE 四点共圆,所以∠GFH =∠OEG, EO GO CO即△GHF ∽△OGE,可得==,又 CO=EO ,所以 CD=GF 得证。
GF GH CDBC.如下图做 GH ⊥AB,连接 EO 。
由于 GOFE 四点共圆,所以∠GFH =∠OEG, EO GO CO即△GHF ∽△OGE,可得==,又 CO=EO ,所以 CD=GF 得证。
GF GH CDA 2D 2 A 1D 1B 1C 1B 2C 2F E NCDA D3、如图,已知四边形 ABCD 、A 1B 1C 1D 1 都是正方形,A 2、B 2、C 2、D 2 分别是AA 1、BB 1、CC 1、DD 1 的中点.求证:四边形 A 2B 2C 2D 2 是正方形.(初二)BC4、已知:如图,在四边形 ABCD 中,AD =BC ,M 、N 分别是 AB 、CD 的中点,AD 、BC的延长线交 MN 于 E 、F . 求证:∠DEN =∠F .经 典 题(二)ABM1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且 OM ⊥BC 于 M .(1)求证:AH =2OM ;A(2) 若∠BAC =600,求证:AH =AO .(初二)O· H EGECO ·B DF2、设 MN 是圆 O 外一直线,过 O 作 OA ⊥MN 于 A ,自 A 引圆的两条直线,交圆于B 、C 及 D 、E ,直线 EB 及 CD 分别交 MN 于 P 、Q . 求证:AP =AQ .(初二)MP AQ N3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设 MN 是圆 O 的弦,过 MN 的中点 A 任作两弦 BC 、DE ,设 CD 、EB 分别交 MN于 P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的 AC 和 BC 为一边,在△ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点 P 是 EF 的中点.求证:点 P 到边 AB 的距离等于 AB 的一半.(初二)DEFAQB经 典 题(三)1、如图,四边形 ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与 CD 相交于 F . 求证:CE =CF .(初二)ADEGCPB2、如图,四边形ABCD 为正方形,DE∥AC,且CE=CA,直线EC 交DA 延长线于F.求证:AE=AF.(初二)3、设P 是正方形ABCD 一边BC E 求证:PA=PF.(初二) A DFB PC E4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE、AF 与直线PO 相交于B、D.求证:AB=DC,BC=AD.(初三)AP B O DEF经典题(四)CA1、已知:△ABC 是正三角形,P 是三角形内一点,PA=3,PB=4,PC=5.求:∠APB 的度数.(初二)PB C2、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)A DPB C3、设ABCD 为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)PPP4、平行四边形 ABCD 中,设 E 、F 分别是 BC 、AB 上的一点,AE 与 CF 相交于 P ,且AE =CF .求证:∠DPA =∠DPC .(初二)A DF经 典 难 题(五)PBE CA1、 设 P 是边长为 1 的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.BC2、已知:P 是边长为 1 的正方形 ABCD 内的一点,求 PA +PB +PC 的最小值.A DB C3、P 为正方形 ABCD 内的一点,并且 PA =a ,PB =2a ,PC =3a ,求正方形的边长.ADB CADBCED4、如图,△ABC 中,∠ABC=∠ACB=800,D、E 分别是AB、AC 上的点,∠DCA=300,∠EBA=200,求∠BED 的度数.AB C经典题(一)1.如下图做GH⊥AB,连接EO。
2020中考数学 几何基础:三角形和四边形(含答案)

2020中考数学 几何基础:三角形和四边形(含答案)1. 已知:直线l 1∥l 2,一块含30︒角的直角三角板如图1-2所示放置,125∠=︒,则2∠等于( )A .30︒B .35︒C .40︒D .45︒2. 如图1-1,在ABC △中,D ,E 分别是边AC 、BC 的中点,若4DE =,则AB =______.3. 若三角形的三边长分别为8、19、a ,则最长的边a 的取值范围是__________.CDE211l 2l图1-1 图1-24. 如图1-3,在ABC △中,B ∠与C ∠的平分线交于点O .过O 点作DE//BC ,分别交AB 、AC 于D 、E .若5AB =,4AC =,则ADE △的周长是__________.5. 如图1-4,15AOE BOE ∠=∠=︒,EF//OB ,EC OB ⊥,若1EC =,则EF =________.6. 如图1-5,在ABC △中,47B ∠=︒,三角形的外角DAC ∠和ACF ∠的平分线交于点E ,则AEC ∠=__________.BAD EOCO B CEABC F EAD图1-3 图1-4 图1-5(1)B ;(2)8;(3 )1927a ≤<;(4)9;(5)2;(6)66.5︒.7. 如图3-1,在ABC △中,AB =6,AC =8,BC =10,P 为边BC 上一动点(且点P 不与点B 、C 重合),PE AB ⊥于E ,PF AC ⊥于F .则EF 的最小值为__________.8. 如图3-2,在ABC △中,90ABC ∠=︒,BD 为AC 边的中线,过点C 作CE BD ⊥于点E ,过点A 作BD 的平行线,交CE 的延长线于点F ,在AF 的延长线上截取FG BD =,连接BG 、DF .若12AB =,5BC =,则四边形BDFG 的周长为__________. 9. 已知如图3-3,正方形ABCD 的边长为3,E 在BC 边上,且1EC =,P 是BD 上一动点,则PE PC +的最小值为__________.A BC P E FC DABEG F图3-1 图3-2 图3-3(7)245;(8)26;(910. 如图,在ABC △中,AD 是ABC △的中线,1tan 2B =,cos C =,AC =,则sin ADC ∠的值___________.11. 在ABC △中,3tan 4B =,10AB =,AC =,则线段BC 的长为__________.(10;(11)5或11.PE D C B A B A12. 如图5-1,五边形ABCDE 中,120A ∠=︒,90B E ∠=∠=︒,1AB BC ==,2AE DE ==,在BC 、DE 上分别找一点M 、N ,使AMN △的周长最小,则AMN △的周长最小值为________.13. 如图5-2,在锐角ABC △中,AB =45BAC =︒∠,BAC ∠的平分线交BC 于点D 、M 、N 分别是AD 和AB 上的动点,则BM MN +的最小值是________.ABMCD NECAN B MD图5-1 图5-2(12)(13)4.14. 如图6-1,在ABC △中,90C ∠=︒,4AC =,2BC =,点A 、C 分别在x 轴、y 轴正半轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最大距离是( ) A.2B.C.D .615. 如图6-2,在ABC △中,90C ∠=︒,4AC =,3BC =,点A 、C 分别在x 轴、y 轴上,当点A 在x 轴上运动时,点C 随之在y 轴上运动,在运动过程中,点B 到原点的最小距离是__________.16. 如图6-3,E 、F 是正方形ABCD 的边AD 上两个动点,满足AE DF =,连接CF 交BD于点G ,连接BE 交AG 于点H ,若正方形的边长为2,则线段DH 长度的最小值是_______.图6-1 图6-2 图6-3(14)A ;(152;(161.图1 图2 图3(1)∵点(0,2)C -,(3,2)D --,∴3CD =,且CD//x 轴,∴BCD △的面积13232=⨯⨯=;(2)∵BQ 平分CBA ∠,∴ABQ CBQ ∠=∠,∵AC BC ⊥,∴90CBQ CQP ∠+∠=︒, 又∵90ABQ CPQ ∠+∠=︒,∴CQP CPQ ∠=∠; (3)在ACE △中,E DAC ACE αβ∠=∠-∠=-; (4)在AOE △和BOC △中,180E EAO AOE ∠+∠+∠=︒,180ABC BCO BOC ∠+∠+∠=︒, ∵CD//x 轴,∴EAO ADC α∠=∠=, 又∵AOE BOC ∠=∠(对顶角相等),∴E EAO ABC BCO ∠+∠=∠+∠,即ABC αβαβ-+=∠+,∴2()ABC αβ∠=-,∴12E ABC ∠=∠,(是定值,不变). HGFE D C BA。
初中数学几何证明经典试题(含答案)

初中数学⼏何证明经典试题(含答案)初中⼏何证明题经典题(⼀)1、已知:如图,O 是半圆的圆⼼,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .2、已知:如图,P 是正⽅形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三⾓形.3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正⽅形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正⽅形.4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(⼆)1、已知:△ABC 中,H 为垂⼼(各边⾼线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .2、设MN 是圆O 外⼀直线,过O 作OA ⊥MN 于A ,⾃A 及D 、E ,直线EB及CD 分别交MN 于P 、Q .求证:AP =AQ .3、如果上题把直线MN 由圆外平移⾄圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .4、如图,分别以△ABC 的AC 和BC 为⼀边,在△ABC 的外侧作正⽅形ACDE 和正⽅形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的⼀半.经典题(三)1、如图,四边形ABCD 为正⽅形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .2、如图,四边形ABCD 为正⽅形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .3、设P 是正⽅形ABCD ⼀边求证:PA =PF .4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF B、D .求证:AB =DC ,BC =AD .经典题(四)1、已知:△ABC 是正三⾓形,P 是三⾓形内⼀点,PA =3,PB =4,求:∠APB 的度数.2、设P是平⾏四边形ABCD 内部的⼀点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC·4、平⾏四边形ABCD 中,设E 、F 分别是BC 、AB 上的⼀点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .经典难题(五)1、设P 是边长为1的正△ABC 内任⼀点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正⽅形ABCD 内的⼀点,求PA +PB +PC 的最⼩值.3、P 为正⽅形ABCD 内的⼀点,并且PA =a ,PB =2a ,PC =3a ,求正⽅形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典题(⼀)1.如下图做GH⊥AB,连接EO。
四边形几何证明题精选含解析
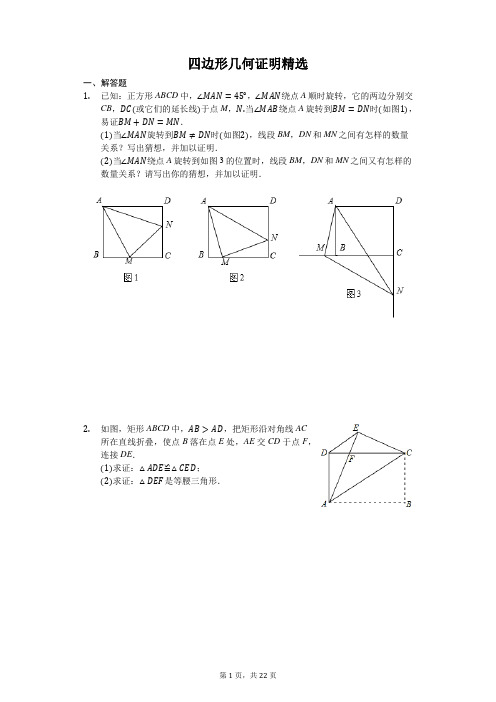
四边形几何证明精选一、解答题1.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAB绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.(1)当∠MAN旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请写出你的猜想,并加以证明.2.如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△ADE≌△CED;(2)求证:△DEF是等腰三角形.3.【问题情境】如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.【探究展示】(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.(2)如图2,若点E是BC边上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.【拓展延伸】(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.4.如图1,在正方形ABCD中,P为对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F,连接CE.(1)求证:△PCE是等腰直角三角形;(2)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.5.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.6.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;(2)将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并证明你的判断.7.如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.8.如图所示,E、F分别为平行四边形ABCD边AB、CD的中点,AG//DB交CB的延长线于点G.(1)求证:DE//BF;(2)若∠G=90°,判断四边形DEBF的形状,并说明理由.9.如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.求证:(1)△ADA′≌△CDE;(2)直线CE是线段AA′的垂直平分线.10.如图,在▱ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.11.如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.12.已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF//BC交CD于点O.(1)求证:OE=OF;(2)若点O为CD的中点,求证:四边形DECF是矩形.13.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.14.如图1,四边形ABCD是正方形,点G是BC边上任意一点.DE⊥AG于点E,BF//DE且交AG于点F.(1)求证:AE=BF;(2)如图2,如果点G是BC延长线上一点,其余条件不变,则线段AF、BF、EF有什么数量关系?请证明出你的结论.15.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.16.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB延长线于点F,其它条件不变,OE=OF还成立吗?17.如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.(1)求证:四边形BEDF是平行四边形;(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.18.如图,EF是平行四边ABCD的对角线BD的垂直平分线,EF与边AD,BC分别交于点E,F.(1)求证:四边形BFDE是菱形;(2)若ED=5,BD=8,求菱形BFDE的面积.19.如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于F,连接AF、CE.(1)求证:四边形AECF为平行四边形;(2)当四边形AECF为菱形,M点为BC的中点时,求∠CBD的度数.20.如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH//BC分别交AF,CD于G,H两点.(1)求证:DE=DC;(2)求证:AF⊥BF;答案和解析1.【答案】解:(1)BM +DN =MN 成立.证明:如图,把△ADN 绕点A 顺时针旋转90°,得到△ABE ,则可证得E 、B 、M 三点共线(图形画正确).∴∠EAM =90°−∠NAM =90°−45°=45°,又∵∠NAM =45°,∴在△AEM 与△ANM 中,{AE =AN ∠EAM =∠NAM AM =AM,∴△AEM≌△ANM(SAS),∴ME =MN ,∵ME =BE +BM =DN +BM ,∴DN +BM =MN ;(2)DN −BM =MN .在线段DN 上截取DQ =BM ,在△ADQ 与△ABM 中,∵{AD =AB∠ADQ =∠ABM DQ =MB,∴△ADQ≌△ABM(SAS),∴∠DAQ =∠BAM ,∴∠QAN =∠MAN .在△AMN 和△AQN 中,{AQ =AM ∠QAN =∠MAN AN =AN,∴△AMN≌△AQN(SAS),∴MN =QN ,∴DN −BM =MN .【解析】(1)结论:BM +DN =MN 成立,证得B 、E 、M 三点共线即可得到△AEM≌△ANM ,从而证得ME =MN .(2)结论:DN −BM =MN.首先证明△ADQ≌△ABM ,得DQ =BM ,再证明△AMN≌△AQN(SAS),得MN =QN ,本题考查正方形的性质、旋转变换等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.2.【答案】证明:(1)∵四边形ABCD 是矩形,∴AD =BC ,AB =CD .由折叠的性质可得:BC =CE ,AB =AE ,∴AD =CE ,AE =CD .在△ADE 和△CED 中,{AD =CEAE =CD DE =ED,∴△ADE≌△CED(SSS).(2)由(1)得△ADE≌△CED,∴∠DEA=∠EDC,即∠DEF=∠EDF,∴EF=DF,∴△DEF是等腰三角形.【解析】(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD= CE、AE=CD,进而即可证出△ADE≌△CED(SSS);(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质,解题的关键是:(1)根据矩形的性质结合折叠的性质找出AD=CE、AE=CD;(2)利用全等三角形的性质找出∠DEF=∠EDF.3.【答案】(1)证明:取AB的中点M,连结EM,如图1:∵M是AB的中点,E是BC的中点,∴在正方形ABCD中,AM=EC,∵CF是∠DCG的平分线,∴∠ECF=90°+45°=135°,∵BM=BE,∴∠BME=45°,∴∠AME=∠ECF=135°,∵∠BEA+∠CEF=90°,∠MAE+∠BEA=90°,∴∠MAE=∠CEF,在△AME与△ECF中,{∠MAE=∠CEF AM=EC∠AME=∠ECF,∴△AME≌△ECF(ASA),∴∠BAE+∠EFC=∠FCG=∠DCF;(2)证明:取AB上的任意一点M,使得AM=EC,连结EM,如图2:∵AE⊥EF,AB⊥BC,∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,∴∠MAE=∠CEF,∵AM=EC,∴在正方形ABCD中,BM=BE,∴∠AME=∠ECF=135°,在△AME与△ECF中,{∠MAE=∠CEF AM=EC∠AME=∠ECF,∴△AME≌△ECF(ASA),∴∠BAE+∠EFC=∠FCG=∠DCF;(3)证明:取BA延长线上的一点N使得AN=CE,如图3:∵AN=CE,AB⊥BC,∴∠ANE=45°,∴∠ECF=∠ANE=45°,∵AD//BE,∴∠DAE=∠BEA,∵NA⊥AD,AE⊥EF,∴∠NAE=∠CEF,在△ANE与△ECF中,{∠NAE=∠CEFAN=CE∠ANE=∠ECF,∴△ANE≌△ECF(ASA),∴AE=EF.【解析】(1)取AB的中点M,连结EM,根据正方形的性质和全等三角形的判定证明即可;(2)在AB上取一点M,使AM=EC,连接EM,根据已知条件利用ASA判定△AME≌△ECF,利用全等三角形的性质证明即可.(3)在BA的延长线上取一点N,使AN=CE,连接NE,根据已知利用ASA判定△ANE≌△ECF,利用全等三角形的性质证明即可.此题主要考查全等三角形的判定和性质,关键是熟练掌握正方形的性质,角平分线的性质及全等三角形的判定方法.4.【答案】(1)证明:如图1中,∵四边形ABCD是正方形,∴AD=DC,∠ADB=∠CDB=45°,∠ADC=90°,在△PDA和△PDC中,{PD=PD∠PDA=∠PDC DA=DC,∴△PDA≌△PDC,∴PA=PC,∠3=∠1,∵PA=PE,∴∠2=∠3,∴∠1=∠2,∵∠EDF=90°,∠DFE=∠PFC,∴∠FPC=∠EDF=90°,∴△PEC是等腰直角三角形.(2)解:如图2中,结论:△PCE是等边三角形.理由:∵四边形ABCD是菱形,∴AD=DC,∠ADB=∠CDB,∠ADC=∠ABC=120°,在△PDA和△PDC中,{PD=PD∠PDA=∠PDC DA=DC,∴△PDA≌△PDC,∴PA=PC,∠3=∠1,∵PA=PE,∴∠2=∠3,PA=PE=PC,∴∠1=∠2,∵∠DFE=∠PFC,∴∠EPC=∠EDC,∵∠ADC=120°,∴∠EDC=60°,∴∠EPC=60°,∵PE=PC,∴△PEC是等边三角形.【解析】本题考查正方形的性质、菱形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.(1)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,推出∠1=∠2,由∠EDF=90°,∠DFE=∠PFC,推出∠FPC=∠EDF=90°,推出△PEC是等腰直角三角形;(2)由△PDA≌△PDC,推出PA=PC,∠3=∠1,由PA=PE,推出∠2=∠3,PA=PE= PC,推出∠1=∠2,由∠DFE=∠PFC,推出∠EPC=∠EDC,由∠ADC=120°,推出∠EDC=60°,推出∠EPC=60°,由PE=PC,即可证明△PEC是等边三角形.5.【答案】(1)证明:∵四边形ABCD是正方形,∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC−∠CBF=∠EBF−∠CBF,∴∠ABF=∠CBE.在△ABF和△CBE中,有{AB=CB∠ABF=∠CBE BF=BE,∴△ABF≌△CBE(SAS).(2)解:△CEF是直角三角形.理由如下:∵△EBF是等腰直角三角形,∴∠BFE=∠FEB=45°,∴∠AFB=180°−∠BFE=135°,又∵△ABF≌△CBE,∴∠CEB=∠AFB=135°,∴∠CEF=∠CEB−∠FEB=135°−45°=90°,∴△CEF是直角三角形.【解析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB= 135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.6.【答案】解:(1)延长BG交DE于点H,在△BCG与△DCE中,{BC=DC∠BCG=∠DCECG=CE,∴△BCG≌△DCE(SAS),∴∠GBC=∠EDC,BG=DE,∵∠BGC=∠DGH,∴∠DHB=∠BCG=90°,∴BG⊥DE;(2)BG=DE,BG⊥DE仍然成立如图2,∠BCD+∠DCG=∠ECG+∠DCG,即∠BCG=∠DCE,在△BCG与△DCE中,{BC=DC∠BCG=∠DCE CG=CE,∴△BCG≌△DCE(SAS),∵∠BHC=∠DHG,∴∠BCD=∠DOB=90°,即BG⊥DE【解析】(1)延长BG交DE于点H,易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠DHB=90°;(2)易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠BCD=90°.本题主要考查正方形,涉及正方形的性质,旋转的性质,全等三角形的判定与性质,综合程度较高,需要学生根据所学知识灵活解答.7.【答案】证明:如图所示:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,在△BAF和△DAF中,{AB=AD ∠BAF=∠DAF AF=AF ,∴△BAF≌△DAF(SAS),∴BF=DF;(2)∵BE的垂直平分线FG交对角AC于点F,∴BF=EF,∵BF=DF,∴EF=DF,∴∠FDE=∠FED,∵△BAF≌△DAF,∴∠ABF=∠FDE,∴∠ABF=∠FED,∵∠FED+∠FEA=180°,∴∠ABF+∠FEA=180°,∴∠BAE+∠BFE=180°,∴∠BFE=90°,∴BF⊥FE.【解析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF≌△DAF,得出对应边相等即可;(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE= 90°即可.本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.8.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AB//CD,AB=CD.∵点E、F分别是AB、CD的中点,∴BE=12AB,DF=12CD.∴BE=DF,BE//DF,∴四边形DFBE是平行四边形,(2)解:四边形DEBF 是菱形;理由如下:∵∠G =90°,AG//BD ,AD//BG ,∴四边形AGBD 是矩形,∴∠ADB =90°,在Rt △ADB 中∵E 为AB 的中点,∴AE =BE =DE ,∵四边形DFBE 是平行四边形,∴四边形DEBF 是菱形.【解析】(1)根据已知条件证明BE =DF ,BE//DF ,从而得出四边形DFBE 是平行四边形,即可证明DE//BF ,(2)先证明DE =BE ,再根据邻边相等的平行四边形是菱形,从而得出结论.本题主要考查了平行四边形的性质、菱形的判定,直角三角形的性质:在直角三角形中斜边中线等于斜边一半,比较综合,难度适中.9.【答案】证明:(1)∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =90°,∴∠A′DE =90°,根据旋转的方法可得:∠EA′D =45°,∴∠A′ED =45°,∴A′D =ED ,在△AA′D 和△CED 中{AD =CD∠ADA′=∠CDE A′D =ED,∴△ADA′≌△CDE(SAS);(2)由正方形的性质及旋转,得CD =CB′,∠CB′E =∠CDE =90°,又CE =CE ,∴Rt △CEB′≌Rt △CED∴∠B′CE =∠DCE ,∵AC =A′C∴直线CE 是线段AA′的垂直平分线.【解析】(1)根据正方形的性质可得AD =CD ,∠ADC =90°,∠EA′D =45°,则∠A′DE =90°,再计算出∠A′ED =45°,根据等角对等边可得A′D =ED ,即可利用SAS 证明△ADA′≌△CDE ;(2)首先由AC =A′C ,可得点C 在AA′的垂直平分线上;再证明△AEB′≌△A′ED ,可得AE =A′E ,进而得到点E 也在AA′的垂直平分线上,再根据两点确定一条直线可得直线CE 是线段AA′的垂直平分线.此题主要考查了正方形的性质,以及旋转的性质,关键是熟练掌握正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;找准旋转后相等的线段.10.【答案】(1)证明:∵四边形ABCD 是平行四边形,∴AB//DF ,∴∠BAF =∠CFA .∵E 为BC 的中点,在△AEB和△FEC中,{∠BAE=∠CFA ∠AEB=∠FEC BE=EC,∴△AEB≌△FEC(AAS)∴AB=CF;(2)解:当BC=AF时,四边形ABFC是矩形,理由:∵AB=CF,AB‖CF,∴四边形ABFC是平行四边形,∵BC=AF,∴四边形ABFC是矩形.【解析】此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,正确得出△AEB≌△FEC(AAS)是解题关键.(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;(2)首先得出四边形ABFC是平行四边形,进而得出答案.11.【答案】(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,∴四边形AEBD是平行四边形,∵AB=AC,AD是∠BAC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是∠BAC的角平分线,∴AD=BD=CD,∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.【解析】(1)利用平行四边形的判定首先得出四边形AEBD是平行四边形,进而由等腰三角形的性质得出∠ADB=90°,即可得出答案;(2)利用等腰直角三角形的性质得出AD=BD=CD,进而利用正方形的判定得出即可.此题主要考查了正方形的判定以及矩形的判定和等腰直角三角形的性质等知识,熟练掌握正方形和矩形的判定是解题关键.12.【答案】证明:(1)∵CE平分∠BCD、CF平分∠GCD,∴∠BCE=∠DCE,∠DCF=∠GCF,∵EF//BC,∴∠BCE=∠FEC,∠EFC=∠GCF,∴∠DCE=∠FEC,∠EFC=∠DCF,∴OE=OC,OF=OC,∴OE=OF;(2)∵点O为CD的中点,∴OD=OC,又OE=OF,∵CE平分∠BCD、CF平分∠GCD,∴∠DCE=12∠BCD,∠DCF=12∠DCG,,即∠ECF=90°,∴四边形DECF是矩形.【解析】本题利用了角平分线的定义、平行线的性质、等角对等边、等量代换、平行四边形的判定、矩形的判定.(1)由于CE平分∠BCD,那么∠DCE=∠BCE,而EF//BC,于是∠FEC=∠BCE,等量代换∠FEC=∠DCE,那么OE=OC,同理OC=OF,等量代换有OE=OF;(2)由于O是CD中点,故OD=OC,而OE=OF,那么易证四边形DECF是平行四边形,又CE、CF是∠BCD、∠DCG的角平分线,∠BCD+∠DCG=180°那么易得∠ECF=90°,从而可证四边形DECF是矩形.13.【答案】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE//AC,AC=2DE,∵EF=2DE,∴EF//AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE;(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC=12AB=AE,∴△AEC是等边三角形,∴AC=CE,又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.【解析】(1)由三角形中位线定理得出DE//AC,AC=2DE,求出EF//AC,EF=AC,得出四边形ACEF是平行四边形,即可得出AF=CE;(2)由直角三角形的性质得出∠BAC=60°,AC=12AB=AE,证出△AEC是等边三角形,得出AC=CE,即可得出结论.本题考查了平行四边形的判定与性质、菱形的判定、三角形中位线定理、直角三角形斜边上的中线性质、等边三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形是等边三角形是解决问题的关键.14.【答案】(1)证明:∵四边形ABCD是正方形,BF⊥AG,DE⊥AG,∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,{∠BAF=∠ADE∠AFB=∠DEA=90°DA=AB,∴△ABF≌△DAE(AAS),∴BF=AE,(2)AF+EF=BF;∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,{∠BAF=∠ADE∠AFB=∠DEA=90°DA=AB,∴△ABF≌△DAE(AAS),∴BF=AE,AF=DE,∴AF+EF=BF.【解析】(1)根据正方形的四条边都相等可得DA=AB,再根据同角的余角相等求出∠BAF=∠ADE,然后利用“角角边”证明△ABF和△DAE全等,再根据全等三角形对应边相等可得BF=AE,AF=DE,然后根据图形列式整理即可得证;(2)根据题意作出图形,然后根据(1)的结论可得BF=AE,AF=DE,然后结合图形写出结论即可.本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,熟记正方形的四条边都相等,每一个角都是直角,然后求出三角形全等是解题的关键.15.【答案】(1)证明:∵AG//BD,BD=FG,∴四边形BGFD是平行四边形,∵CE⊥BD∴CE⊥AG,又∵BD为AC的中线,∴BD=DF=12AC,∴四边形BDFG是菱形;(2)解:∵四边形BDFG是菱形,∠ABC=90°,点D为AC的中点,∴GF=DF=12AC=5,∵CF⊥AG,∴AF=√AC2−CF2=√102−62=8,∴AG=AF+GF=8+5=13.【解析】(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;(2)由菱形的性质求得GF=DF=12AC=5,由勾股定理得AF的长,继而求得AG的长.本题主要考查了菱形的判定与性质、直角三角形斜边的中线的性质以及勾股定理,注意掌握数形结合思想是解答此题的关键.16.【答案】①证明:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,{∠BOE=∠AOF OB=OA ∠OBE=∠OAF ,∴△BOE≌△AOF(ASA),∴OE=OF;②解:OE=OF还成立;理由如下:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,{∠BOE=∠AOF OB=OA ∠OBE=∠OAF ,∴△BOE≌△AOF(ASA),∴OE=OF.【解析】本题考查了正方形的性质、全等三角形的判定与性质有关知识.①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.17.【答案】证明:(1)∵四边形ABCD是矩形,∴AB//DC、AD//BC,∴∠ABD=∠CDB,∵BE平分∠ABD、DF平分∠BDC,∴∠EBD=12∠ABD,∠FDB=12∠BDC,∴∠EBD=∠FDB,∴BE//DF,又∵AD//BC,∴四边形BEDF是平行四边形;(2)当∠ABE=30°时,四边形BEDF是菱形,∵BE平分∠ABD,∴∠ABD=2∠ABE=60°,∠EBD=∠ABE=30°,∵四边形ABCD是矩形,∴∠A=90°,∴∠EDB=90°−∠ABD=30°,∴∠EDB=∠EBD=30°,∴EB=ED,∴四边形BEDF是菱形.【解析】(1)由矩形可得∠ABD=∠CDB,结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB,即可知BE//DF,根据AD//BC即可得证;(2)当∠ABE=30°时,四边形BEDF是菱形,由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°,结合∠A=90°可得∠EDB=∠EBD=30°,即EB=ED,即可得证.本题主要考查矩形的性质、平行四边形、菱形,熟练掌握矩形的性质、平行四边形的判定与菱形的判定是解题的关键.18.【答案】(1)证明:∵EF垂直平分BD,∴OB=OD,∵四边形ABCD为平行四边形,∴AD//BC,∴∠EDO=∠FBO,∠DOE=∠BOF,∴△DOE≌△BOF(ASA),∴OE=OF,∴四边形AFCE为菱形;(2)解:∵BD=8,∴OD=4且ED=5,∴EO=3,∴S菱形BFDE =12BD×EF=EO·BD=3×8=24.【解析】本题主要考查平行四边形的性质、垂直平分线的性质,全等三角形的判定与性质以及菱形的判定与性质.(1)先证明△DOE≌△BOF,得出OE=OF,再根据EF垂直平分BD,可得出四边形BFDE 为菱形;(2)根据勾股定理可得出OE的长,根据菱形的面积求解即可.19.【答案】(1)证明∵四边形ABCD是平行四边形(已知),∴BC//AD(平行四边形的对边相互平行),∴∠ADE=∠CBD,AD=BC又∵AM丄BC(已知),∴AM⊥AD;∵CN丄AD(已知),∴AM//CN,∴AE//CF;在△ADE和△CBF中,{∠DAE=∠BCF AD=CB∠ADF=∠CBE∴△ADE≌△CBF(ASA),∴AE=CF(全等三角形的对应边相等),∴四边形AECF为平行四边形(对边平行且相等的四边形是平行四边形);(2)如图,连接AC交BF于点0,当四边形AECF为菱形时,则AC与EF互相垂直平分,∵BO=OD(平行四边形的对角线相互平分),∴AC与BD互相垂直平分,∴▱ABCD是菱形(对角线相互垂直平分的平行四边形是菱形),∴AB=BC(菱形的邻边相等);∵M是BC的中点,AM丄BC(已知),∴AB=AC(等腰三角形的性质),∴△ABC为等边三角形,∴∠ABC=60°,∠CBD=30°.【解析】(1)根据平行四边形的性质、垂直的定义、平行线的判定定理可以推知AE//CF;然后由全等三角形的判定定理ASA推知△ADE≌△CBF;最后根据全等三角形的对应边相等知AE=CF,所以一组对边平行且相等的四边形是平行四边形;(2)根据M是BC的中点,AM丄BC(已知),可证明△ABC为等边三角形,然后根据三线合一定理即可求解.本题综合考查了全等三角形的判定与性质、菱形的判定与性质以及等边三角形的判定与性质等知识点.20.【答案】解:(1)∵四边形ABCD是矩形,∴AB//CD,∴∠DCE=∠CEB,∵EC平分∠DEB,∴∠DEC=∠CEB,∴∠DCE=∠DEC,∴DE=DC;(2)如图,连接DF,∵DE=DC,F为CE的中点,∴DF⊥EC,∴∠DFC=90°,在矩形ABCD中,AB=DC,∠ABC=90°,∴BF=CF=EF=12EC,∴∠ABF=∠CEB,∵∠DCE=∠CEB,∴∠ABF=∠DCF,在△ABF和△DCF中,{BF=CF∠ABF=∠DCF AB=DC,∴△ABF≌△DCF(SAS),∴∠AFB=∠DFC=90°,∴AF⊥BF;(3)CE=4√7.理由如下:∵AF⊥BF,∴∠BAF+∠ABF=90°,∵EH//BC,∠ABC=90°,∴∠BEH=90°,∴∠FEH+∠CEB=90°,∵∠ABF=∠CEB,∴∠BAF=∠FEH,∵∠EFG=∠AFE,∴△EFG∽△AFE,∴GFEF =EFAF,即EF2=AF⋅GF,∵AF⋅GF=28,∴EF=2√7,∴CE=2EF=4√7.【解析】(1)根据平行线的性质以及角平分线的定义,即可得到∠DCE=∠DEC,进而得出DE=DC;(2)连接DF,根据等腰三角形的性质得出∠DFC=90°,再根据直角三角形斜边上中线的性质得出BF=CF=EF=12EC,再根据SAS判定△ABF≌△DCF,即可得出∠AFB=∠DFC=90°,据此可得AF⊥BF;(3)根据等角的余角相等可得∠BAF=∠FEH,再根据公共角∠EFG=∠AFE,即可判定△EFG∽△AFE,进而得出EF2=AF⋅GF=28,求得EF=2√7,即可得到CE=2EF= 4√7.本题属于四边形综合题,主要考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质以及直角三角形的性质的综合应用,解决问题的关键是作辅助线,构造全等三角形.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.。
届云南中考数学题型专项(五)四边形的有关证明与计算(含答案)

题型专项(五) 四边形的有关证明与计算四边形的有关计算与证明是历年中考的必考内容之一,通常结合三角形等知识综合考查,以计算题、证明题的形式出现,解答此类问题除熟练掌握四边形的性质和判定定理外,还须综合三角形等知识解题.1.(2015·黄冈)已知,如图,在四边形ABCD 中,AB ∥CD ,E ,F 为对角线AC 上两点,且AE =CF ,DF ∥BE.求证:四边形ABCD 为平行四边形.证明:∵AB ∥CD ,∴∠BAE =∠DCF.∵BE ∥DF ,∴∠BEF =∠DFE.∴∠AEB =∠CFD.在△AEB 和△CFD 中,⎩⎪⎨⎪⎧∠BAE =∠DCF ,AE =CF ,∠AEB =∠CFD ,∴△AEB ≌△CFD(ASA).∴AB =CD.∵AB ==∥CD , ∴四边形ABCD 是平行四边形.2.(2016·吉林)如图,菱形ABCD 的对角线AC ,BD 相交于点O ,且DE ∥AC ,AE ∥BD.求证:四边形AODE 是矩形.证明:∵四边形ABCD 为菱形,∴AC ⊥BD.∴∠AOD =90°.∵DE ∥AC ,AE ∥BD ,∴四边形AODE 为平行四边形.∴四边形AODE 是矩形.3.(2015·昆明盘龙区二模)如图,在▱ABCD 中,O 是CD 的中点,连接AO 并延长,交BC 的延长线于点E.(1)求证:△AOD ≌△EOC ;(2)连接AC ,DE ,当∠B =∠AEB =45°时,四边形ACE D 是正方形,请说明理由.解:(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC.∴∠ADC =∠DCE.∵O 是CD 的中点, ∴OD =OC.在△AOD 和△EOC 中,⎩⎪⎨⎪⎧∠ADC =∠DCE ,OD =OC ,∠AOD =∠EOC ,∴△AOD ≌△EOC(ASA).(2)理由:由△AOD ≌△EOC ,得OA =OE ,OD =OC.∴四边形ADEC 是平行四边形.∵∠B =∠AEB =45°,∴AB =AE.又∵在▱ABCD 中,AB ==∥CD , ∴CD =AE.∴四边形ADEC 是矩形.∴∠ACE =90°.∴∠CAE =90°-∠AEC =90°-45°=45°. ∴∠CAE =∠AEC.∴AC =CE.∴四边形ADEC 是正方形.4.(2016·曲靖模拟)已知:如图,▱ABCD 中,∠ABC 的平分线交AD 于E ,∠CDA 的平分线交BC 于F.(1)求证:△ABE ≌△C DF ;(2)连接EF 、BD ,求证:EF 与BD 互相平分.证明:(1)∵四边形ABCD 是平行四边形,∴AB =CD ,∠A =∠C ,∠ABC =∠CDA.∵BE 平分∠ABC ,DF 平分∠CDA ,∴∠ABE =12∠ABC ,∠CDF =12∠CDA. ∴∠ABE =∠CDF.在△ABE 和△CDF 中,⎩⎪⎨⎪⎧∠ABE =∠CDF ,AB =CD ,∠A =∠C ,∴△ABE ≌△CDF(ASA).(2)连接EF 、BD.∵△ABE ≌△CDF ,∴AE =CF.∵四边形ABCD 是平行四边形,∴AD =CB ,AD ∥BC.∴DE =BF 且DE ∥BF.∴四边形BFDE 是平行四边形.∴EF 与BD 互相平分.5.(2016·云南考试说明)如图,已知点D 在△ABC 的边BC 上,DE ∥AC 交AB 于点E ,DF ∥AB 交AC 于点F.(1)求证:AE =DF ;(2)若AD 平分∠BAC ,试判断四边形AEDF 的形状,并说明理由.解:(1)证明:∵DE ∥AC ,DF ∥AB ,∴四边形AEDF 是平行四边形.∴AE =DF.(2)若AD 平分∠BAC ,则四边形AEDF 是菱形.理由:∵DE ∥AC ,DF ∥AB ,∴四边形AEDF 是平行四边形.∵∠DAF =∠EAD ,∠FDA =∠EAD ,∴∠DAF =∠FDA.∴AF =DF.∴四边形AEDF 是菱形.6.(2016·云南模拟)如图,矩形ABCD 中,AB =8,AD =6,点E 、F 分别在边CD 、AB 上.(1)若DE =BF ,求证:四边形AFCE 是平行四边形;(2)若四边形AFCE 是菱形,求菱形AFCE 的周长.解:(1)证明:∵四边形ABCD 为矩形,∴AB =CD ,AB ∥CD.∵DE =BF ,∴AF =CE ,AF ∥CE.∴四边形AFCE 是平行四边形.(2)∵四边形AFCE 是菱形,∴AE =CE.设DE =x ,则AE =62+x 2,CE =8-x. 则62+x 2=8-x ,解得x =74. 则菱形的边长为:8-74=254. 周长为:4×254=25. 故菱形AFCE 的周长为25.7.(2016·遵义)如图,矩形ABCD 中,延长AB 至E ,延长CD 至F ,BE =DF ,连接EF ,与BC ,AD 分别相交于P ,Q 两点.(1)求证:CP =AQ ;(2)若BP =1,PQ =22,∠AEF =45°,求矩形ABCD 的面积.解:(1)证明:∵四边形ABCD 是矩形,∴∠A =∠ABC =∠C =∠ADC =90°,AB =CD ,AD =BC ,AB ∥CD ,AD ∥BC.∴∠E =∠F. ∵BE =DF ,∴AE =CF.在△CFP 和△AEQ 中,⎩⎪⎨⎪⎧∠C =∠A ,CF =AE ,∠F =∠E ,∴△CFP ≌△AEQ(ASA).∴CP =AQ.(2)∵AD ∥BC ,∴∠PBE =∠A =90°.∵∠AEF =45°,∴△BEP 、△AEQ 是等腰直角三角形.∴BE =BP =1,AQ =AE.∴PE =2BP = 2.∴EQ =PE +PQ =2+22=3 2.∴AQ =AE =3.∴AB =AE -BE =2.∵CP =AQ ,AD =BC ,∴DQ =BP =1.∴AD =AQ +DQ =3+1=4.∴S 矩形ABCD =AB ·AD =2×4=8.8.(2016·云南考试说明)如图,在▱ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,BD 与AE ,AF 分别相交于G ,H 两点.(1)求证:△ABE ∽△ADF ;(2)若AG =AH ,求证:四边形ABCD 是菱形.证明:(1)∵AE ⊥BC ,AF ⊥CD ,∴∠AEB =∠AFD =90°.∵四边形ABCD 是平行四边形,∴∠ABE =∠ADF.∴△ABE ∽△ADF.(2)∵△ABE ∽△ADF ,∴∠BAG =∠DAH.∵AG =AH ,∴∠AGH =∠AHG.从而∠AG B =∠AHD.在△AGB 和△AHD 中,⎩⎪⎨⎪⎧∠BAG =∠DAH ,AG =AH ,∠AGB =∠AHD ,∴△ABG ≌△ADH(ASA).∴AB =AD.又∵四边形ABCD 是平行四边形,∴四边形ABCD 是菱形.9.(2016·株洲)已知正方形ABCD 中,BC =3,点E 、F 分别是CB 、CD 延长线上的点,DF =BE ,连接AE 、AF.(1)求证:△ADF ≌△ABE ;(2)若BE =1,求tan ∠AED 的值.解:(1)证明:∵四边形ABCD 为正方形, ∴AD =AB ,∠ADC =∠ABC =90°. ∴∠ADF =∠ABE =90°.在△ADF 与△ABE 中,⎩⎪⎨⎪⎧AD =AB ,∠ADF =∠ABE ,DF =BE ,∴△ADF ≌△ABE(SAS).(2)过点A 作AH ⊥DE 于点H.在Rt △ABE 中,∵AB =BC =3,BE =1, ∴AE =10,ED =CD 2+CE 2=5.∵S △AED =12AD ·BA =92, S △ADE =12DE ·AH =92, 解得AH =1.8.在Rt △AHE 中,EH =2.6,∴tan ∠AED =AH EH =1.82.6=913.。
初中数学-几何证明经典试题(含答案)
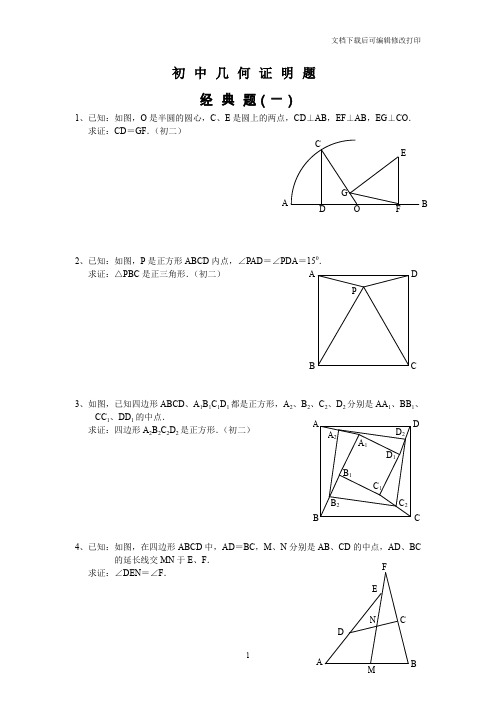
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 N FE CDPCGFB QA D E 经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DE C N M · A经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)A P CB P A D CB C B D A F PDE C B A经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题五七:三角形、四边形、圆证明(含答案)1、如图1,OP 是MON ∠的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:(1)如图2,在ABC △中,ACB ∠是直角,60B ∠=,AD ,CE 分别是BAC ∠,BCA ∠的平分线,AD ,CE 相交于点F .请你判断并写出FE 与FD 之间的数量关系;(2)如图3,在ABC △中,如果ACB ∠不是直角,而(1)中的其他条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.2、如图,O 为ABCD 的对角线AC 的中点,过点O 作一条直线分别与AB CD ,交于点M N ,,点E F ,在直线MN 上,且OE OF =.(1)图中共有几对全等三角形,请把它们都写出来;(2)求证:MAE NCF =∠∠.3、(1)已知:如图①,在AOB △和COD △中,OA OB =,OC OD =,60AOB COD ==∠∠,求证:①AC BD =;②60APB =∠.(2)如图②,在AOB △和COD △中,若OA OB =,OC OD =,AOB COD α==∠∠,则AC 与BD 间的等量关系式为________________;APB ∠的大小为__________________.(3)如图③,在AOB △和COD △中,若OA k OB =,()1OC k OD k =>,AOB COD α==∠∠,则AC 与BD 间的等量关系式为___________;APB ∠的大小为O NPM 图3 图1 图2AE M D FCB O 12NA OD B C P 图① α αOA P C D 图② α α D OB A P C图③专题六:与四边形有关的证明题1、如图,在Rt ABC △中,90BAC =∠,E F ,分别是BC AC ,的中点,延长BA 到点D ,使12AD AB =.连结DE DF ,. (1)求证:AF 与DE 互相平分; (2)若4BC =,求DF 的长.2、如图,在Rt ABC △中,60A =∠,点E F ,分别在AB AC ,上,沿EF 对折,使点A 落在BC 上的点D 处,且FD BC ⊥.(1) 确定点E 在AB 上和点F 在AC 上的位置; (2) 求证:四边形AEDF 是菱形.3、如图,已知长方形ABCD ,过点C 引A ∠的平分线AM 的垂线,垂足为M ,AM 交BC 于E ,连结MB ,MD . (1)求证:BE DC =;(2)求证:MBE MDC ∠=∠.AD F EBFDE60专题七:与圆有关的证明题1、已知:如图,O 与A 相交于C D ,两点,AO ,分别是两圆的圆心,ABC △内接于O ,弦CD 交AB 于点G ,交O 的直径AE 于点F ,连结BD .(1)求证:ACG DBG △∽△;(2)求证:2AC AG AB =;(3)若A ,O的直径分别为15,且:1:4CG CD =,求AB 和BD 的长.2、如图,PA 为O 的切线,A 为切点,PBC 为割线,APC ∠的平分线交AB 于点E ,交AC 于点F ,点M 为BC 的中点.求证:AM PF ⊥.3、如图,AB D E ,,,四点在O 上,AE BD ,的延长线相交于点C ,直径AE 为8,12OC =,EDC BAO ∠=∠. (1)求证:CD CEAC CB=;(2)计算CD CB 的值,并指出CB 的取值范围.EOCE DBA4、已知:如图,在Rt ABC △中,90ACB ∠=,4AC =,43BC =,以AC 为直径的O 交AB 于点D ,点E 是BC 的中点,连结OD OB DE ,,.(1)求证:OD DE ⊥;(2)求sin ABO ∠的值.5、如图,BD 为O 的直径,AB AC =,AD 交BC 于E ,2AE =,4ED =. (1)求证:ABE ADB △∽△,并求AB 的长;(2)延长DB 到F ,使BF BO =,连接FA ,那么直线FA 与O 相切吗?为什么?6、如图,已知AB 是1O 的直径,点C 是1O 上不同于A B ,的一点,以线段AC 为直径作2O 交AB 于点D ,过点D 作DE BC ∥,交2O 于点E ,交AC 于点F .求证:(1)EC 是1O 的切线;(2)2CE EF BC =. A BC ODEF ACEBDACD F1O2O1、(1)FE 与FD 之间的数量关系为FE FD =.(2)答:(1)中的结论FE FD =仍然成立.证法一:如图4,在AC 上截取AG AE =,连结FG .因为12∠=∠,AF 为公共边, 可证AEF AGF △≌△. 所以AFE AFG ∠=∠,FE FG =. 由60B ∠=,AD CE ,分别是BAC BCA ∠∠,的平分线, 可得2360∠+∠=.所以60AFE CFD AFG ∠=∠=∠=.所以60CFG ∠=.由34∠=∠及FC 为公共边,可得CFG CFD △≌△. 所以FG FD =.所以FE FD =.2、(1)有4对全等三角形.分别为AMO CNO OCF OAE ,△≌△△≌△, AME CNF ABC CDA ,△≌△△≌△.(2)证明:12OA OC OE OF ===,,∠∠,OAE OCF ∴△≌△,EAO FCO ∴=∠∠.在ABCD 中,AB CD ∥,BAO DCO EAM NCF ∴=∴=.∠∠∠∠.3、(1)证明:①60AOB COD ==∠∠,AOB BOC COD BOC ∴+=+∠∠∠∠, 即:AOC BOD =∠∠.又OA OB =,OC OD =,AOC BOD ∴△≌△.AC BD ∴=. ②由①得:OAC OBD =∠∠,又AEO PEB =∠∠,()180APB BEP OBD =-+∠∠∠,()180AOB OAC AEO =-+∠∠∠, 60APB AOB ∴==∠∠.(2)AC BD =,α.(3)AC k BD =,180α-.图4 图5AODB CPE AD1、(1)连结EF AE ,.点E F ,分别为BC AC ,的中点,12EF AB EF AB ∴=,∥. 又12AD AB =,EF AD ∴=. 又EF AD ∥,∴四边形AEFD 是平行四边形. ∴AF 与DE 互相平分.(2)在Rt ABC △中,E 为BC 的中点,4BC =,122AE BC ∴==.又四边形AEFD 是平行四边形,2DF AE ∴==.2、(1)解:ABC △为Rt △,60A =∠, 30C ∴=∠.12AF DF FC ∴==,即13AF AC =.FD BC ⊥, BDE ∴∠与EDF ∠互余.而60EDF A ==∠∠,30BDE ∴=∠.1122BE ED AE ∴==,即13BE AB =.(2)证明:3090BDE B ==,∠∠,60BED A ∴==∠∠,ED AF ∴∥.AB BC FD BC ⊥⊥,, FD AE ∴∥.∴四边形AEDF 为平行四边形.又AE ED =, ∴四边形AEDF 为菱形.3、证明:(1)AM 平分90BAD BAD =,∠∠,45BAE ∴=∠.BAE ∴△为等腰直角三角形,又AB DC =, BE DC ∴=.(2)由CM AM ⊥易得,MEC △为等腰直角三角形,ME CM ∴=且45MEC MCE ==∠∠.135BEM DCM ∴==∠∠.又BE DC =,BEM DCM ∴△≌△. MBE MDC ∴=∠∠.专题七:与圆有关的证明题答案 FDE60ACG DBG ∴△∽△.(2)证明:连结AD ,则AC AD =.在ACG △和ABC △中, AC AD ACG ABC =∴=,∠∠.又CAG BAC ACG ABC =∴∠∠,△∽△.AC AG AB AC∴=,即2AC AG AB =.(3)解:连结CE ,则90ACE =∠.O 与A 相交于C D ,两点,∴圆心O A ,在弦CD 的垂直平分线上,即AO 垂直平分弦CD . CF DF CF AE ∴=⊥,且AC AD =.A O ,的直径分别为15,15AC AE ∴==.在Rt CFA △和Rt ECA △中,ACF ADC AEC ==∠∠∠,Rt Rt CFA ECA ∴△∽△.AC AF AE AC ∴=,即(22315AC AF AE ===.在Rt AFC △中,222AC AF CF =+,即(2223CF =+.解得6CF =(舍去负值). :1:439CG CD CG FG DG =∴===,,.在Rt AFG △中,222223318AG AF FG =+=+=,AG ∴=. 由(2),有2AC AG AB =,即(22AB =.解得2AB =. 由(1),有ACG DBG △∽△,得AC AG DB DG =.353AC DG BD AG ∴=== 2、证明:方法一:PF 平分APC ∠,12∴=∠∠.又PA 是O 的切线,C PAB ∴=∠∠.12AEF PAB AFE C =+=+∠∠∠,∠∠∠, AEF AFE ∴=∠∠,即AE AF =. M 是BC 的中点,BAM CAM ∴=∠∠. AM PF ∴⊥.方法二:M 是BC 的中点,BAM CAM ∴=∠∠.又PA 是O 的切线,C PAB ∴=∠∠.PDA C DAC PAD PAB BAM =+=+∠∠∠,∠∠∠, PDA PAD ∴=∠∠,即PA PD =.E3、(1)证明:EDC BAO C C ∠=∠∠=∠,CDE CAB ∴△∽△CD CEAC CB∴= (2)直径812AE OC ==,124161248AC CE ∴=+==-=,又CD CEAC CB=,168128CDCB AC CE ∴==⨯=·· 连接OB ,在OBC △中,142OB AE ==,12OC =,816BC ∴<<4、(1)证明:连结CD ,则90ADC BDC ∠=∠=.E 是BC 的中点,DE BE EC ∴==.OA OD DE BE ==,,ADO A ∴∠=∠,DBE BDE ∠=∠.90DBE A ∠+∠=,90BDE ADO ∴∠+∠=.90EDO ∴∠=.∴直线DE 是O 的切线.(2)解:作OF AD ⊥.AOD △是边长为2的等边三角形, 3OF ∴=.在Rt BOC △中,448213BO =+=.339sin 26213OF ABO OB ∴∠===. 5、(1)证明:AB AC =,ABC C ∴=∠∠,C D =∠∠,ABC D ∴=∠∠.又BAE DAB =∠∠,ABE ADB ∴△∽△.AB AEAD AB∴=. ()()224212AB AD AE AE ED AE ∴==+=+⨯=. 23AB ∴=.(2)直线FA 与O 相切. 连接OA .BD 为O 的直径,90BAD ∴=∠.()22212244843BD AB AD ∴=+=++==.11432322BF BO BD ∴===⨯=. OCE DB AEA OBDCF6、答案:证明:(1)连结1O C ,如图,则1O CB B =∠∠DE BC ∥EDA B ∴=∠∠EDA ECA =∠∠1ECA O CB ∴=∠∠ AB 是1O 的直径1190ACO OCB ∴+=∠∠ 1ECA O CB =∠∠190ACO ECA ∴+=∠∠EC ∴是1O 的切线.(2)连结CD ,如图3,则90CDA CDB ==∠∠90DE BC ACB =∥,∠90CFD ACB ∴==∠∠AC 是2O 的直径AC ∴垂直平分ED EF FD CE CD ∴==,90FDC DCB CFD BDC ===∠∠,∠∠CFD BDC ∴△∽△ 2CD FD CD FD BC BC CD∴=∴=,EF FD CE CD ==,2CE EF BC ∴=。
