(整理)灰色预测法
第7章灰色预测方法课件-新版.doc

第7 章灰色预测方法预测就是借助于对过去的探讨去推测、了解未来。
灰色预测通过原始数据的处理和灰色模型的建立,发现、掌握系统发展规律,对系统的未来状态做出科学的定量预测。
对于一个具体的问题,究竟选择什么样的预测模型应以充分的定性分析结论为依据。
模型的选择不是一成不变的。
一个模型要经过多种检验才能判定其是否合适,是否合格。
只有通过检验的模型才能用来进行预测。
本章将简要介绍灰数、灰色预测的概念,灰色预测模型的构造、检验、应用,最后对灾变预测的原理作了介绍。
7.1 灰数简介7.1.1 灰数灰色系统理论中的一个重要概念是灰数。
灰数是指未明确指定的数,即处在某一范围内的数,灰数是区间数的一种推广。
灰色系统用灰数、灰色方程、灰色矩阵等来描述,其中灰数是灰色系统的基本“单元”或“细胞”。
我们把只知道大概范围而不知其确切值的数称为灰数。
在应用中,灰数实际上指在某一个区间或某个一般的数集内取值的不确定数,通常用记号“”表示灰数。
灰数有以下几类:1.仅有下界的灰数有下界而无上界的灰数记为a, 或 a ,其中a为灰数的下确界,它是一个确定的数,我们称a, 为的取数域,简称的灰域。
一棵生长着的大树,其重量便是有下界的灰数,因为大树的重量必大于零,但不可能用一般手段知道其准确的重量,若用表示大树的重量,便有0, 。
2.仅有上界的灰数有上界而无下界的灰数记为( ,a ] 或(a),其中a为灰数的上确界,是一个确定的数。
一项投资工程,要有个最高投资限额,一件电器设备要有个承受电压或通过电流的最高临界值。
工程投资、电器设备的电压、电流容许值都是有上界的灰数。
3.区间灰数既有下界a又有上界a的灰数称为区间灰数,记为a, a 。
海豹的重量在20~25 公斤之间,某人的身高在 1.8~1.9 米之间,可分别记为21 20,25 , 1. 8,1.94.连续灰数与离散灰数在某一区间内取有限个值或可数个值的灰数称为离散灰数,取值连续地充满某一区间的灰数称为连续灰数。
灰色预测

用最小二乘法估计为
Uˆ
aˆ uˆ
(BT
B)1 BT
y
将a与u的估计值代入微分方程可得
xˆ(1) (k 1) [x(1) (1) uˆ ]eaˆk uˆ
aˆ
aˆ
GM(1,1)模型
求模拟值 x(1) 并累减还原出 x(0) 的模拟值。 对其做累减还原即可得到原始数列的灰色预测 模型为:
Xˆ (0) (k) Xˆ (1) (k 1) Xˆ (1) (k)
灰色生成
将原始数据列中的数据,按某种要求作数据处 理称为生成.对原始数据的生成就是企图从杂 乱无章的现象中去发现内在规律.
常用的灰色生成方式有: 累加生成,累减生 成,均值生成,级比生成等
灰色生成
累加生成
累加前的数列称原始数列,累加后的数列称为生成数 列.累加生成是使灰色过程由灰变白的一种方法,它在 灰色系统理论中占有极其重要地位,通过累加生成可 以看出灰量积累过程的发展态势,使离乱的原始数据 中蕴含的积分特性或规律加以显化.累加生成是对原 始数据列中各时刻的数据依次累加,从而生成新的序 列的一种手段.
常用到的灰色预测模型
• GM(1,1)模型——是1阶方程,包含有1个变量 的灰色模型
• GM(1,N)模型——是1 阶方程,包含有N 个 变量的灰色模型。
• GM(0,1)模型——是0 阶方程,包含有N 个变 量的灰色模型。表达式上相当于统计回归
• GM(2,1)模型——是2阶方程,包含有1 个变 量的灰色模型。
模型精度检验
+ 相对误差大小检验法(最常用) + 后验差检验法 + 关联度检验法
模型精度检验
相对误差大小检验法
相对误差大小检验法,它是一种直观的逐点进 行比较的算术检验方法,它是把预测数据与实 际数据相比较,观测其相对误差是否满足实际 要求。 设按该模型以求出Xˆ (1) ,并将 Xˆ (1) 做一次累 减转化为Xˆ (0) ,即
灰色预测法1讲解

据上,其和作为生成列的第三个数据,
按此规则进行下去,便可得到生成列。
回总目录 回本章目录
记原始时间序列为:
X 0 X 0 1, X 0 2, X 0 3,... X 0 n
生成列为:
X 1 X 1 1, X 1 2, X 1 3,... X 1 n
确定的关系。
回总目录 回本章目录
(2)灰色预测法 • 灰色预测法是一种对含有不确定因素的系 统进行预测的方法。
• 灰色预测是对既含有已知信息又含有不确定
信息的系统进行预则,就是对在一定范围内
变化的、与时间有关的灰色过程进行预测。
回总目录 回本章目录
• 灰色预测通过鉴别系统因素之间发展趋
势的相异程度,即进行关联分析,并对
上标1表示一次累加,同理,可作m次累加:
X m k X m 1 i
i 1 k
回总目录 回本章目录
• 对非负数据,累加次数越多则随机性弱化
越多,累加次数足够大后,可认为数据序
列已由随机序列变为非随机序列。
• 一般随机序列的多次累加序列,大多可用
指数曲线逼近。
回总目录 回本章目录
原始数据进行生成处理来寻找系统变动
的规律,生成有较强规律性的数据序列,
然后建立相应的微分方程模型,从而预
测事物未来发展趋势的状况。
回总目录 回本章目录
• 灰色预测法用等时距观测到的反映预测对 象特征的一系列数量值构造灰色预测模型, 预测未来某一时刻的特征量,或达到某一
特征量的时间。
回总目录 回本章目录
回总目录 回本章目录
二、生成列 设已知数据变量组成序列X(0),则我们可得 到数据序列
统计预测之灰色预测法

主要内容
What
How
Why
概念引入 灰色系统的定义
客观世界
白色系统
内部信息 完全确知
黑色系统
内部信息 一无所知
灰色系统
部分已知 部分未知
灰色系统理论是我
控制论专家邓聚龙 教授于1982 年创立 的。
研究对象
灰色系统理论
特点
核心
“部分信息已知,部分未知”的小 样本和“贫信息”不确定性系统
有限的离散的参数里寻找发展规 律,预测复杂系统
灰色动态模型,生成函数和灰色微 分方程
灰色预测法
➢ 灰色预测是对既含有已知信息又含有不确 定信息的系统进行预测。
➢
灰色预测通过鉴别系统因素之间发展趋势
的相异程度,即进行关联分析,并对原始数据
进行生成处理来寻找系统变动的规律,生成有
较强规律性的数据序列 , 然后建立相应的微分
X 0 k X 0 1 , X 0 2 ,X . 0 . n .
则关联系数定义为:
(k)mm X ˆi0 X n ˆ ki0 n k X 0 X k0 k m m m am X ˆ x a a 0 X ˆ x k x a 0 k X x 0 X k0 k
X 2 1 ,1 .0,1 6 .13 2 ,1 .1 24 783
X 3 1 ,0 . ,9 1 .072 ,1 .0 92 4 94 X 4 1 ,1 .01 ,0 .8 4 ,0 0 .7 9 5
第二步:求序列差 2 0 ,0 .11 ,0 .1 59 ,0 5 .2 93 235
3 0 ,0 .02 ,0 .1 20 ,5 0 .1 51 946
k
Xmk Xm1 i i1
➢累减的定义
数学建模算法:灰色预测模型GM(1,1)及Python代码
数学建模算法:灰⾊预测模型GM(1,1)及Python代码灰⾊预测模型GM(1,1)灰⾊预测模型\(GM(1,1)\)是在数学建模⽐赛中常⽤的预测值⽅法,常⽤于中短期符合指数规律的预测。
其数学表达与原理分析参考⽂章尾部⽹页与⽂献资料。
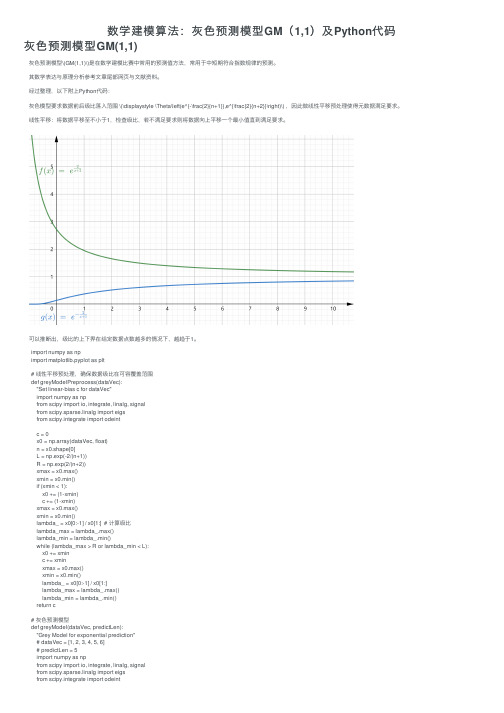
经过整理,以下附上Python代码:灰⾊模型要求数据前后级⽐落⼊范围 \(\displaystyle \Theta\left(e^{-\frac{2}{n+1}},e^{\frac{2}{n+2}}\right)\) ,因此做线性平移预处理使得元数据满⾜要求。
线性平移:将数据平移⾄不⼩于1,检查级⽐,若不满⾜要求则将数据向上平移⼀个最⼩值直到满⾜要求。
可以推断出,级⽐的上下界在给定数据点数越多的情况下,越趋于1。
import numpy as npimport matplotlib.pyplot as plt# 线性平移预处理,确保数据级⽐在可容覆盖范围def greyModelPreprocess(dataVec):"Set linear-bias c for dataVec"import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintc = 0x0 = np.array(dataVec, float)n = x0.shape[0]L = np.exp(-2/(n+1))R = np.exp(2/(n+2))xmax = x0.max()xmin = x0.min()if (xmin < 1):x0 += (1-xmin)c += (1-xmin)xmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:] # 计算级⽐lambda_max = lambda_.max()lambda_min = lambda_.min()while (lambda_max > R or lambda_min < L):x0 += xminc += xminxmax = x0.max()xmin = x0.min()lambda_ = x0[0:-1] / x0[1:]lambda_max = lambda_.max()lambda_min = lambda_.min()return c# 灰⾊预测模型def greyModel(dataVec, predictLen):"Grey Model for exponential prediction"# dataVec = [1, 2, 3, 4, 5, 6]# predictLen = 5import numpy as npfrom scipy import io, integrate, linalg, signalfrom scipy.sparse.linalg import eigsfrom scipy.integrate import odeintx0 = np.array(dataVec, float)n = x0.shape[0]x1 = np.cumsum(x0)B = np.array([-0.5 * (x1[0:-1] + x1[1:]), np.ones(n-1)]).TY = x0[1:]u = linalg.lstsq(B, Y)[0]def diffEqu(y, t, a, b):return np.array(-a * y + b)t = np.arange(n + predictLen)sol = odeint(diffEqu, x0[0], t, args=(u[0], u[1]))sol = sol.squeeze()res = np.hstack((x0[0], np.diff(sol)))return res# 输⼊数据x = np.array([-18, 0.34, 4.68, 8.49, 29.84, 50.21, 77.65, 109.36])c = greyModelPreprocess(x)x_hat = greyModel(x+c, 5)-c# 画图t1 = range(x.size)t2 = range(x_hat.size)plt.plot(t1, x, color='r', linestyle="-", marker='*', label='True')plt.plot(t2, x_hat, color='b', linestyle="--", marker='.', label="Predict")plt.legend(loc='upper right')plt.xlabel('xlabel')plt.ylabel('ylabel')plt.title('Prediction by Grey Model (GM(1,1))')plt.show()误差分析部分:可就绝对误差、相对误差、级⽐、残差做数据分析,以下⽰例为最⼩⼆乘法线性回归分析。
什么是灰色预测法

什么是灰色预测法?灰色预测是就灰色系统所做的预测。
所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部分信息已知,部分信息未知,那么这一系统就是灰色系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
编辑本段灰色预测的类型1、数列预测。
对某现象随时间的顺延而发生的变化所做的预测定义为数列预测。
例如对消费物价指数的预测,需要确定两个变量,一个是消费物价指数的水平。
另一个是这一水平所发生的时间。
2、灾变预测。
对发生灾害或异常突变时间可能发生的时间预测称为灾变预测。
例如对地震时间的预测。
3、系统预测。
对系统中众多变量间相互协调关系的发展变化所进行的预测称为系统预测。
例如市场中替代商品、相互关联商品销售量互相制约的预测。
4、拓扑预测。
将原始数据作曲线,在曲线上按定值寻找该定值发生的所有时点,并以该定值为框架构成时点数列,然后建立模型预测未来该定值所发生的时点。
编辑本段为了弱化原始时间序列的随机性在建立灰色预测模型之前,需先对原始时间序列进行数据处理,经过数据处理后的时间序列即称为生成列。
灰色预测模型
dx
(t)
(1)
ax
(t)b,
dt
解为
b
a
(
t
1
) b
x(
t)
(
x(
1
))
e
.
a
a
(
1
)
(
0
)
(3)
于是得到预测值
b
b
(
1
)
(
0
)
ak
ˆ
x(
k
1
)
(
x(
1
)
)
e
,
k
1
,
2
,
,
n
1
,
a
a
从而相应地得到预测值:
(
0
)
(
1
)
(
1
)
ˆ
ˆ
ˆ
x
(
k
1
)
x
(
k
1
)
x
(
k
lim
dt
t
t 0
而 ( 1)( x ( k )) x ( k ) x ( k 1 ), 相当于
t 1
(3)加权邻值生成
(
0
)
(
0
)
(
0
)
(
0
)
x
(
x
(
1
),
x
(
2
),
,
x
(
n
))
设原始数列为
灰色预测
作m次累加:
X
X (1) (1) X (0) (1)
m
k X
i 1
k
m 1
i
X (1) (2) X (0) (1) X (0) (2) X (1) (1) X (0) (2) ...... X
(1)
( n) X (()) (i ) X (1) ( n 1) X (0) ( n)
度,根据经验,当ρ=0.5时,关联度大于0.6便 满意了。
(3)后验差检验
a.计算原始序列标准差:
S1
X i X
0
0 2
n
b. 计算绝对误差序列的标准差:
S2
i
0
0 2
n
c. 计算方差比:
S2 C S1
注:(1)原始数据不一定全部用来建模,数 据不同,模型不同。 (2)数据的取舍应保证建模序列等时矩、 相连,不得有跳跃出现。 (3)一般建模数据应当有最新的数据及其相 邻数据构成。
三、模型检验 灰色预测检验一般有残差检验、关联度检 验和后验差检验。
(1)残差检验
ˆ 1 i , 按预测模型计算X
1 0 X 1 X 1 (3)取
b ak b 0 1 ˆ X k 1 X 1 e a a
k 1, 2..., n
(4)还原值
ˆ 0 k 1 X ˆ 1 k 1 X ˆ 1 k X
灰色预测法
王卉
灰色预测
一、灰色预测的概念
(1)灰色系统、白色系统和黑色系统
• 白色系统是指一个系统的内部特征是完全已知的,
预测方法——灰色预测模型
预测⽅法——灰⾊预测模型灰⾊预测模型主要特点是模型使⽤的不是原始数据序列,⽽是⽣成的数据序列,核⼼体系为灰⾊模型(GM),即对原始数据作做累加⽣成(累减⽣成,加权邻值⽣成)得到近似指数规律再进⾏建模。
优点:不需要很多数据;将⽆规律原始数据进⾏⽣成得到规律性较强的⽣成序列。
缺点:只适⽤于中短期预测,只适合指数增长的预测。
GM(1,1)预测模型GM(1,1)模型是⼀阶微分⽅程,且只含⼀个变量。
1. 模型预测⽅法2. 模型预测步骤1. 数据检验与处理为保证建模⽅法可⾏,需要对已知数据做必要的检验处理。
设原始数据列为x(0)=(x0(1),x0(2),….x0(n)),计算数列的级⽐λ(k)=x(0)(k−1)x(0)(k),k=2,3,...,n如果所有的级⽐都落在可容覆盖区间X=(e−2n+1,e2n+1)内,则数列可以建⽴GM(1,1)模型且可以进⾏灰⾊预测。
否则,对数据做适当的变换处理,如平移变换:y(0)(k)=x(0)(k)+c,k=1,2,...,n取c使得数据列的级⽐都落在可容覆盖内。
2. 建⽴模型根据1中⽅程的解,进⼀步推断出预测值ˆx(1)(k+1)=(x(0)(1)−ba)e−ak+ba,k=1,2,...,n−13. 检验预测值1. 残差检验ε(k)=x(0)(k)−ˆx(0)(k)x(0)(k),k=1,2,...,n如果对所有的|ε(k)|<0.1|ε(k)|<0.1,则认为到达较⾼的要求;否则,若对所有的|ε(k)|<0.2|ε(k)|<0.2,则认为达到⼀般要求。
2. 级⽐偏差值检验ρ(k)=1−1−0.5a1+0.5aλ(k)如果对所有的|ρ(k)|<0.1,则认为达到较⾼的要求;否则,若对于所有的|ρ(k)|<0.2,则认为达到⼀般要求。
4. 预测预报根据问题需要给出预测预报。
3. py实现import numpy as npimport pandas as pddata=[71.1,72.4,72.4,72.1,71.4,72.0,71.6] # 数据来源len=len(data) # 数据量# 数据检验lambdas=[]for i in range(1,len):lambdas.append(data[i-1]/data[i])X_Min=np.e**(-2/(len+1))X_Max=np.e**(2/(len+1))l_min,l_max=min(lambdas),max(lambdas)if l_min<X_Min or l_max> X_Max:print("该组数据为通过数据检验,不能建⽴GM模型!")else:print("改组数据通过检验")# 建⽴GM(1,1)模型data_1=[] # 累加数列z_1=[]data_1.append(data[0])for i in range(1,len):data_1.append(data[i]+data_1[i-1])z_1.append(-0.5*(data_1[i]+data_1[i-1]))B=np.array(z_1).reshape(len-1,1)one=np.ones(len-1)B=np.c_[B,one]Y=np.array(data[1:]).reshape(len-1,1)a,b=np.dot(np.dot(np.linalg.inv(np.dot(B.T,B)),B.T),Y)print('a='+str(a))print('b='+str(b))## 数据预测data_1_prd=[]data_1_prd.append(data[0])data_prd=[] # 预测datadata_prd.append(data[0])for i in range(1,len):data_1_prd.append((data[0]-b/a)*np.e**(-a*i)+b/a)data_prd.append(data_1_prd[i]-data_1_prd[i-1])# 模型检验## 残差检验e=[]for i in range(len):e.append((data[i]-data_prd[i])/data[i])e_max=max(e)if e_max<0.1:print("数据预测达到较⾼要求!")elif e_max<0.2:print("数据预测达到⼀般要求!")# 输出预测数据for i in range(len):print(data_prd[i])灰⾊Verhulst预测模型主要⽤于描述具有饱和状体的过程,即S型过程,常⽤于⼈⼝预测,⽣物⽣长,繁殖预测及产品经济寿命预测等。
灰色预测方法
= ( x (1) (1), x (1) (2),
(1) 对 x 建立单变量的一阶微分方程 GM (1,1) 模型
dx( )
1
dt
相应的灰微分方程模型为:
+ ax( ) = b
1
(1)
x (0) (k ) + az (1) (k ) = b, k = 2,3,
使用最小二乘法可确定 a, b 。
dx (1) (t) (3) GM (1,1)的白化型 : + ax (1) (t) = b, 求解 dt b b 白化型方程的解 : x (1) (t)=( x (0) (1) − )e − a ( t −1) + a a b − ak b ˆ 离散解 : x (1) (k+1)=( x (0) (1) − )e + a a
Y = ( y (1), y (2),
, y (n) ) 为 X (0) 的初值生成序列。
初值生成一般用于数据的无量纲化。
灰色预测方法
E-mail:luqian@
3
4、灰色生成数
定义 3 (一次累加生成) 对原始序列
X (0) = ( x (0) (1), x (0) (2),
使用最小二乘法可确定 a , b 。
n ⎧ C = ∑ z (1) (k ) ⎧ ⎪ k =2 ⎪ ⎪a = n ⎪ ⎪ (0) 由 ⎪ D = ∑ x (k ) 可得 ⎨ ⎪ k =2 ⎪b = ⎨ n ⎪E = ⎪ z (1) (k ) x (0) (k ) ⎩ ∑ ⎪ k =2 ⎪ n ⎪F = z (1) (k ) 2 ∑ ⎪ k =2 ⎩
,n 。
CD − ( n − 1) E , 2 ( n − 1) F − C (2) DF − CE ( n − 1) F − C 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色预测理论在数学建模中的应用
作者:胡金杭
摘要:灰色系统理论在自动控制领域中已取得了广泛的应用,本文针对灰色预测理论的特点,分析了它在数学建模中的具体应用。
首先,本文对如何将实际问题转化为灰色GM(1,1)预测模型给了具体的步骤,同时针对模型的特点,可以对其的预测精度进行后验差检验,随后,针对基本灰色GM(1,1)预测模型单调性的特点,我们可以采用改进的等维灰数递补模型,这样可以大大的提高模型对实际问题的预测精度。
关键字:GM(1,1)预测模型后验差检验等维灰数递补模型
引言
现实中的很多实际问题,都需要通过分析现有的数据,对该问题未来的发展趋势进行预测,随后决策者参考预测得到的结果,就可以制定合理的解决方案。
在预测分析中,最基本的预测模型为线性回归方程,针对一些规律性较强的数据,该模型能作出精确的预测,但在实际中,我们得到的常是一些离散的,规律性不强的数据,为解决此类问题,线性的方法就不适用了,此时,就需要采用灰色预测的方法。
灰色预测理论是将看似离散的数据序列经数据变换后形成有规律的生成数列( 如累加生成、累减生成) ,然后对生成数列建立微分方程,得到模型的计算值后,再与实测值比较获得残差,用残差再对模型作修正,然后便可用建立的灰色模型对该问题进行预测。
一、具体的灰色GM(1,1)预测模型的建立:
我们设已知数据变量组成序列,则我们可得到数据序列
,用1-AGO生成一阶累加生成序列为:
其中 (1-1) 由于序列具有指数增长规律,而一阶微分方程的解恰是指数增长形式的解,因此我们可以认为序列满足下述一阶线性微分方程模型
(1-2)
我们利用离散差分方程的形式对上微分方程可以得到下矩阵形式:
(1-3)
简记为: (1-4)
式中;;
上述方程组中,和B 为已知量,A 为待定参数。
可用最小二乘法得到最小二乘近似值。
因此,式(1-4)可改写为
式中,E —误差项。
利用矩阵求导公式,可得
(1-5)
解得结果代入(2-2)中,我们可以得到
(1-6)
写成离散形式(令),得到GM(1,1)模型的时间响应函数
(K =1,2,…)(1-7) 我们对其做累减还原,即可得到原始数列的灰色预测模型为:
(K =1,2,…) (1-8) 将相关数据代入公式中进行运算,我们得到系数的具体值,即得到了具体的预测公式。
二、灰色模型精度的后验差检验:
对所建立的灰色预测模型,我们可以采用相应的后验差检验的方式进行预测数据的精度分析。
首先算得知残差平均值为
历史数据方差为
其中历史数据平均值为
残差方差为
后验差比值为
小误差概率为
最后,我们根据相关评判标准进行综合评定预测模型的小误差概率(P) 和后验差比值(C) .根据文献记载,我们一般可按下表五划分精度等级[5]。
我们从灰色预测模型公式中可以看出,它是一个典型的指数增长的模型,在进行预测时,最近一年的预测结果应该是很精确的,但对后续几年的预测误差会逐渐增大,为了提高预测模型的广泛适用性,我们做出了如下的改进。
三、基于灰色预测的等维灰数递补模型
为了进一步提高模型的精度,在GM(1,1)灰色预测模型的基础上还可以做进一步的改进,使得预测结果更加的精确。
GM(1,1)模型中具有预测意义的数据仅仅是数据x(n)以后的前几个数据,随着时间的推移,老的数据越来越不适应新的情况,也就是说,老数据的信息意义将随时间的推移而降低。
所以,要在原数据的基础上每次增加一个新信息时,就去掉一个老信息。
这种新数据补充、老数据除掉的数据列,由于其维数不变,因而叫等维信息数据列,或称为新陈代谢数据列,相应的模型叫等维灰数递补模型,或叫新陈代谢模型。
设原始数列为:
置入新信息, 去掉老信息, 可构成
新数列:
利用这一新数列建立的GM(1,1)模型,即为等维新息GM(1,1)模型。
由于在实际中,信息处于不断的变化之中,具有很大的随机性, 虽然历史信息对预测时刻的具体值有一定的相关性和影响,但与预测时刻更接近的信息对于该时刻的预测结果更有价值。
鉴于这种情况,可先用已知数列建立的GM(1,1)模型预测一个值, 然后补充一个新信息数据到已知数列中, 同时去掉最老的一个数据, 使序列等维, 接着再建立GM(1,1)模型,这样逐个滚动预测,依次递补,直到完成预测目标为止,通过此等维新息模型,我们再对具体问题进行预测,就可以得到更为精确的结果。
结束语
灰色预测模型能够根据现有的少量信息进行计算和预测,因而在人口、生态、农业、医学、工程技术、气象、水文及减灾等许多部门得到了广泛的应用,本文只是对灰色预测理论在数学建模中的应用做了基本的介绍,在实际应用中,它还有许多改进的理论,以及一些与其他理论结合使用的模型,如与人工神经网络组合的最优组合灰色神经网络预测模型,与模糊数学结合的灰色预测模糊控制理论,在实际应用中它们已取得了较好的效果。
总之,灰色预测理论在数学建模及其它领域将会发挥很好的作用。
参考文献
[1] 熊和金,徐华中,《灰色控制》,北京:国防工业出版社,2005.9。
[2] 刘思峰,郭天榜.灰色系统理论及其应用.开封:河南大学出版社1991.
灰色数学模型预测
灰色预测法: 统计学上是不是有一种预测方法叫灰色预测法比如预测地震等
灰色预测是就灰色系统所做的预测。
所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部分信息已知,部分信息未知,那么这一系统就是灰箱系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色预测一般有四种类型:1、数列预测;2、灾变预测;3、系统预测;4、拓扑预测。
例:
我手上有2001-2007年的实际数值:57.55 、63.32 、76.4、71.31、85.55、98.04、115.59,想通过灰色数学模型预测2008-2020年的预测值。
1.令序列X0(k)={57.55 、63.32 、76.4、71.31、85.55、98.04、115.59}
2.通过一次累加得到X1(k)={57.55,57.55+6
3.32,57.55+63.32+76.4,……,
57.55+63.32+……+115.59}
3.然后有矩阵B=[-Z1(2),1; -Z1(3),1;-Z1(4),1;-Z1(5),1;],
Y=[X0(2);X0(3);X0(4);X0(5);]
其中Z1(k)= 0.5*(X1(k)+X1(k-1));
4.待定系数矩阵[a;b]=inv(B'*B)*B'*Y,其中inv表示求逆,B'表示转置
5.得到X0(k+1)=(1-exp(a))*(X0(1)-b/a)*exp(-a*k)
取k=7,8,……,19可得预测值
以上只是计算过程,具体原理可以查阅相关论文。
另外,可以考虑将X0(k)先做差分,对差分序列进行灰色预测后再还原。
125.73657 141.55648 159.36681 179.41801 201.99201
227.40621 256.01799 288.22963 324.49407 365.32123
411.28518 463.03222 521.28995。
