《机械设计基础》第五版摆动导杆机构设计
机械设计基础(高教版第五版)精品教案:绪论部分
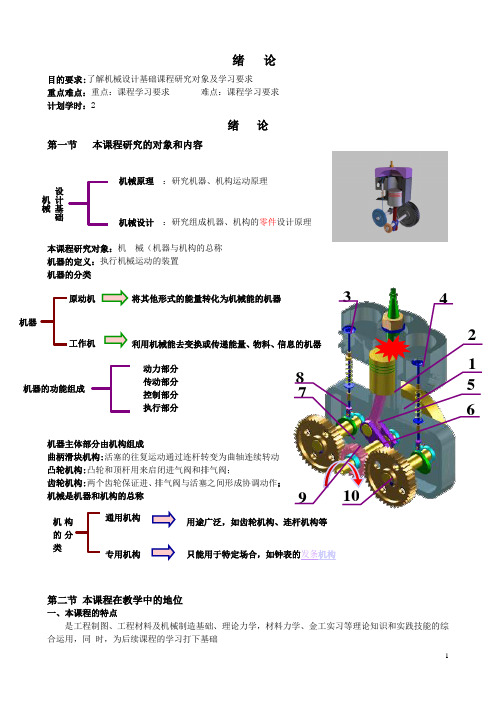
绪 论目的要求:了解机械设计基础课程研究对象及学习要求重点难点:重点:课程学习要求 难点:课程学习要求计划学时:2绪 论第一节 本课程研究的对象和内容本课程研究对象:机 械(机器与机构的总称 机器的定义:执行机械运动的装置 机器的分类 机器主体部分由机构组成 曲柄滑块机构:活塞的往复运动通过连杆转变为曲轴连续转动 凸轮机构:凸轮和顶杆用来启闭进气阀和排气阀; 齿轮机构:两个齿轮保证进、排气阀与活塞之间形成协调动作; 机械是机器和机构的总称第二节 本课程在教学中的地位 一、本课程的特点 是工程制图、工程材料及机械制造基础、理论力学,材料力学、金工实习等理论知识和实践技能的综合运用,同 时,为后续课程的学习打下基础 机构的分类 通用机构 专用机构 用途广泛,如齿轮机构、连杆机构等 只能用于特定场合,如钟表的发条机构 机械原理 机械设计 :研究机器、机构运动原理:研究组成机器、机构的零件设计原理 设计基础 机械机器 工作机 原动机 将其他形式的能量转化为机械能的机器 利用机械能去变换或传递能量、物料、信息的机器 机器的功能组成 动力部分 传动部分 控制部分 执行部分 6 5 4 3 8 7 1 2 9 10通过本课程的学习,可以培养大家初步具备运用手册设计简单机械设备的能力,为今后操作、维护、管理、革新工程机械设备创造条件三、怎样学好本课程1.重思考,常想几个问题:A.什么样子B.怎么运动C.工作原理、方式D.现实生活中的实际例子2.会查表、会用工具书3.不注重公式的记忆——哪些公式要记忆,会在课堂上和考试前提醒4.多看一些设计方面的书,如工业设计、机械优化设计等5.一定要会几个设计软件二维的:AUTOCAD 三维的:Pro/E、UG等。
机械设计基础(第五版)_杨可桢主编_课后习题答案

时间:二 O 二一年七月二十九日机械设计基础(第五版)课后习题谜底(完整版)之阿 布丰王创作时间:二 O 二一年七月二十九日杨可竺、程光蕴、李仲生主编 1-1 至 1-4 解 机构运动简图如下图所示.图 1.11 题 1-1 解 图 图 1.12 题 1-2 解图图 1.13 题 1-3 解 图 图 1.14 题 1-4 解图 1-5 解 1-6 解 1-7 解 1-8 解 1-9 解 1-10 解 1-11 解 1-12 解 1-13 解 该导杆机构的全部瞬心如图所示,构件 1、3 的角速比为: 1-14 解 该正切机构的全部瞬心如图所示,构件 3 的速度为:,方 向垂直向上. 1-15 解 要求轮 1 与轮 2 的角速度之比,首先确定轮 1、轮 2 和机 架 4 三个构件的三个瞬心,即 , 和 ,如图所示.则:,轮 2 与轮 1 的转向相反. 1-16 解 ( 1)图 a 中的构件组合的自由度为:构件之间不能发生相对运 动.自由度为零,为一刚性桁架,所以时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日( 2)图 b 中的 CD 杆是虚约束,去失落与否不影响机构的运动. 故图 b 中机构的自由度为:所以构件之间能发生相对运动.题 2-1 答 : a ),且最短杆为机架,因此是双曲柄机构.b),且最短杆的邻边为机架,因此是曲柄摇杆机构.c),不满足杆长条件,因此是双摇杆机构.d),且最短杆的对边为机架,因此是双摇杆机构.题 2-2 解 : 要想成为转动导杆机构,则要求 与 均为周转副.( 1 )当 为周转副时,要求 能通过两次与机架共线的位置.见图 2-15 中位置和.在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号).综合这二者,要求即可.( 2 )当 为周转副时,要求 能通过两次与机架共线的位置.见图 2-15 中位置和.在位置时,从线段 来看,要能绕过 点要求:(极限情况取等号);在位置时,因为导杆 是无限长的,故没有过多条件限制.( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 .图 2.16题 2-4 解 : ( 1 )由公式方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时 ,转过的角度为,,并带入已知数据列时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日因此其转速为:转 / 分钟题 2-5解 : ( 1 )由题意踏板 在水平位置上下摆动 ,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置.取适当比例 图 尺,作出两次极限位置和(见图2.17 ).由图量得:,.解得 :由已知和上步求解可知:,,,( 2 ) 因最小传动角位于曲柄与机架两次共线位置,因此取和代入公式( 2-3 )计算可得:或:代入公式( 2-3 )′,可知 题 2-6 解: 因为本题属于设计题,只要步伐正确,谜底不惟一.这 里给出基本的作图步伐,不 给出具体数值谜底.作图步伐如下(见图 2.18 ):( 1 )求 ,;并确定比例尺 .( 2 )作,.(即摇杆的两极限位置)( 3 )以 为底作直角三角形,,.( 4 )作的外接圆,在圆上取点 即可.在图上量取, 和机架长度.则曲柄长度,摇杆长度.在获得具体各杆数据之后,代入公式 ( 2 — 3 ) 和 ( 2-3 )′求最小传动角 ,能满足即可.图 2.18 题 2-7 图 2.19解 : 作图步伐如下 (见图 2.19 ) :( 1 )求 ,;并确定比例尺 .( 2 )作,顶角,.时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日( 3 )作的外接圆,则圆周上任一点都可能成为曲柄中心.( 4 )作一水平线,于 相距,交圆周于 点.( 5 )由图量得,.解得 :曲柄长度:连杆长度: 题 2-8 解 : 见图 2.20 ,作图步伐如下:(1).( 2 )取 ,选定 ,作 和 ,. ( 3 )定另一机架位置:角平分线,.(4),.杆即是曲柄,由图量得 曲柄长度: 题 2-9 解: 见图 2.21 ,作图步伐如下:( 1 )求 , 性.( 2 )选定比例尺 ,作 两极限位置)( 3 )做,与( 4 )在图上量取.,由此可知该机构没有急回特,.(即摇杆的交于 点. ,和机架长度曲柄长度:连杆长度:题 2-10 解 : 见图 2.22 .这是已知两个活动铰链两对位置设计四杆机构,可以用圆心法.连接 , ,作图 2.22 的中垂线与 交于 点.然后连接 ,,作 的中垂线与 交于 点.图中画出了一个位置.从图中量取各杆的长度,获得:,时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日, 题 2-11 解 : ( 1 )以 为中心,设连架杆长度为,根据作出 ,,.( 2 )取连杆长度,以 , , 为圆心,作弧.( 3 )另作以 点为中心,、,架杆的几个位置,并作出分歧半径的许多同心圆弧.( 4 )进行试凑,最后获得结果如下:的另一连,,,.机构运动简图如图 2.23 .题 2-12 解 : 将已知条件代入公式( 2-10 )可获得方程组:联立求解获得:,,.将该解代入公式( 2-8 )求解获得:,,,.又因为实际,因此每个杆件应放年夜的比例尺为:,故每个杆件的实际长度是:,,,.题 2-13 证明 : 见图 2.25 .在 上任取一点 ,下面求证点的运动轨迹为一椭圆.见图可知 点将 分为两部份,其中,.又由图可知,,二式平方相加得可见 点的运动轨迹为一椭圆.3-1 解图 3.10 题 3-1 解图如图 3.10 所示,以 O 为圆心作圆并与导路相切,此即为偏距圆.过B 点作偏距圆的下切线,此线为凸轮与从动件在 B 点接触时,导路的方向线.推程运动角 如图所示.3-2 解图 3.12 题 3-2 解图时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日如图 3.12 所示,以 O 为圆心作圆并与导路相切,此即为偏距圆.过 D 点作偏距圆的下切线,此线为 凸轮与从动件在 D 点接触时,导路的方向线.凸轮与从动件在 D 点 接触时的压力角 如图所示. 3-3 解 :从动件在推程及回程段运动规律的位移、速度以及加速 度方程分别为: ( 1)推程:0°≤ ≤ 150°( 2)回程:等加速段 ≤60 °等减速段0°≤60°≤ ≤120 °为了计算从动件速度和加速度,设移、速度以及加速度值如下:总转角 0°位移 (mm) 0速度(mm/s) 0加速度( mm/s 65.7972)总转角 120°15° 0.734 19.41662.577 135°30° 2.865 36.93153.231 150°45° 60° 6.183 10.365 50.832 59.75738.675 20.333 165° 180°. 计算各分点的位75° 1562.83290° 19.63559.757105° 23.81750.8320 195°-20.333 -38.675 210° 225°时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日位移 (mm) 27.135 29.266 3030速度(mm/s) 36.932 19.416 00加速度( mm/s -53.231 -62.577 -65.797 02)3029.066 26.250 21.5630-25-50-75-83.333 -83.333 -83.333 -83.333总转角 240° 255° 270° 285° 300° 315° 330° 345°位移 (mm) 158.438 3.750.938 0000速度(mm/s) -100-75-50-250000加速度( mm/s -83.333 -83.333 83.333 83.333 83.333 0002)根据上表 作图如下(注:为了图形年夜小协调,将位移曲线沿纵轴放年夜了 5 倍.):图 3-13 题 3-3 解图3-4 解 :图 3-14 题 3-4 图根据 3-3 题解作图如图 3-15 所示.根据(3.1)式可知,取最年夜,同时 s 2 取最小时,凸轮机构的压力角最年夜.从图 3-15 可知,这点可能在推程段的开始处或在推程的中点处.由图量得在推程的开始处凸轮机构的压力角最年夜,此时<[ ]=30° .图 3-15 题 3-4 解图3-5 解 :( 1)计算从动件的位移并对凸轮转角求导当凸轮转角 在 0≤ ≤ 过程中,从动件按简谐运动规 律上升 h=30mm.根据教材(3-7)式 可 得:0≤ ≤当凸轮转角 在 S 2 =500≤ ≤≤ ≤ 过程中,从动件远休. ≤≤≤≤当凸轮转角 在 ≤ ≤ 运动规律下降到升程的一半.根据 教材(3-5)式 可得:过程中,从动件按等加速度时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日≤≤≤≤当凸轮转角 在 ≤ ≤ 速度运动规律下降到起始位置.根 据教材(3-6)式 可得:过程中,从动件按等减≤≤当凸轮转角 S 2 =50≤≤ 在 ≤≤过程中,从动件近休. ≤≤≤≤ ( 2)计算凸轮的理论轮廓和实际轮廓本题的计算简图及坐标系如图 3-16 所示,由图可知,凸轮理 论轮廓上 B 点(即滚子中心)的直角坐标 为 图 3-16式中.由图 3-16 可知,凸轮实际轮廓的方程即 B ′ 点的坐标方程式为因为所以故由上述公式可得 理论轮廓曲线和实际轮廓的直角坐标,计算结果如下表,凸轮廓线如图 3-17 所示.x′y′x′y′0°49.301 8.333 180° -79.223 -8.88510°47.421 16.843 190° -76.070 -22.42120°44.668 25.185 200° -69.858 -34.84030°40.943 33.381 210° -60.965 -45.36940°36.089 41.370 220° -49.964 -53.35650°29.934 48.985 230° -37.588 -58.312时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日60°22.34770°13.28480°2.82990°-8.778100° -21.139110° -33.714120° -45.862130° -56.895140° -66.151150° -73.052160° -77.484170° -79.562180° -79.223图 3-17 题 3-5 解图55.943 61.868 66.326 68.871 69.110 66.760 61.695 53.985 43.904 31.917 18.746 5.007 -8.885240° 250° 260° 270° 280° 290° 300° 310° 320° 330° 340° 350° 360°-24.684 -12.409 -1.394 8.392 17.074 24.833 31.867 38.074 43.123 46.862 49.178 49.999 49.301-59.949 -59.002 -56.566 -53.041 -48.740 -43.870 -38.529 -32.410 -25.306 -17.433 -9.031 -0.354 8.3333-6 解:图 3-18 题 3-6 图从动件在推程及回程段运动规律的角位移方程为:1. 推 程 :≤ 150°2.回程:≤120 °计算各分点的位移值如下:总转角( °)015 30 45 60 75 90 105角位移( °)00.367 1.432 3.092 5.182 7.5 9.818 11.908总转角( °)120 135 150 165 180 195 210 225角位移( °)13.568 14.633 15 15 15 14.429 12.803 0.370总转角( °)240 255 270 285 300 315 330 345角位移( °)7.5 4.630 2.197 0.571 0 000根据上表 作图如下:图 3-19 题 3-6 解图3-7 解:从动件在推程及回程段运动规律的位移方程为:1.推程:0°≤ ≤ 120°2.回程:0°≤ ≤120 °计算各分点的位移值如下:总转角( °)0位移( mm) 015 30 45 60 0.761 2.929 6.173 1075 90 105 13.827 17.071 19.2390°≤ 0°≤时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日总转角( °)120 135 150位移( mm) 20 20 20总转角( °)240 255 270位移( mm) 2.929 0.761 0图 3-20 题 3-7 解图4.5 课后习题详解4-1 解 分度圆直径齿顶高165 180 195 210 19.239 17.071 13.827 10 285 300 315 330 000 0齿根高 顶隙225 6.173 345 0中心距 齿顶圆直径 齿根圆直径 基圆直径 齿距 齿厚、齿槽宽4-2 解由 分度圆直径可得模数4-3 解 由得4-4 解 分度圆半径分度圆上渐开线齿廓的曲率半径分度圆上渐开线齿廓的压力角基圆半径 基圆上渐开线齿廓的曲率半径为 0; 压力角为 .齿顶圆半径 齿顶圆上渐开线齿廓的曲率半径 齿顶圆上渐开线齿廓的压力角 4-5 解 正常齿制渐开线标准直齿圆柱齿轮的齿根圆直径:时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日基圆直径假定则解得故当齿数时,正常齿制渐开线标准直齿圆柱齿轮的基圆年夜于齿根圆;齿数,基圆小于齿根圆.4-6 解 中心距内齿轮分度圆直径内齿轮齿顶圆直径内齿轮齿根圆直径 4-7 证明 用齿条刀具加工标准渐开线直齿圆柱齿轮,不发生根切 的临界位置是极限点 正好在刀具 的顶线上.此时有关系:正常齿制标准齿轮、,代入上式短齿制标准齿轮、,代入上式图 4.7 题 4-7 解图 图 4.8 题 4-8 图图 4.9 题 4-8 解图4-8 证明 如图所示, 、 两点为卡脚与渐开线齿廓的切点,则线段 即为渐开线的法线.根据渐开线的特性:渐开线的法线必与基圆相切,切点为 .再根据渐开线的特性:发生线沿基圆滚过的长度,即是基圆上被滚过的弧长,可知:AC对任一渐开线齿轮,基圆齿厚与基圆齿距均为定值,卡尺的位置不影响丈量结果.4-9 解 模数相等、压力角相等的两个齿轮,分度圆齿厚相等.可是齿数多的齿轮分度圆直径年夜,所以基圆直径就年夜.根据渐开线的性质,渐开线的形状取决于基圆的年夜小,基圆小,则渐开线曲率年夜,基圆年夜,则渐开线越趋于平直.因此,齿数多的齿轮与齿数少的齿轮相比,齿顶圆齿厚和齿根圆齿厚均为年夜值.4-10 解 切制变位齿轮与切制标准齿轮用同一把刀具,只是刀具的位置分歧.因此,它们的模数、压力角、齿距均分别与刀具相同,从而变位齿轮与标准齿轮的分度圆直径和基圆直径也相同.故参数 、、 、 不变.变位齿轮分度圆不变,但正变位齿轮的齿顶圆和齿根圆增年夜,时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日且齿厚增年夜、齿槽宽变窄.因此 、 、 变年夜, 变小. 啮合角 与节圆直径 是一对齿轮啮合传动的范畴.4-11 解 因螺旋角 端面模数端面压力角当量齿数分度圆直径 齿顶圆直径 齿根圆直径 4-12 解 (1)若采纳标准直齿圆柱齿轮,则标准中心距应说明采纳标准直齿圆柱齿轮传动时,实际中心距年夜于标准 中心距,齿轮传动有齿侧间隙,传动不 连续、传动精度低,发生振动和噪声.( 2)采纳标准斜齿圆柱齿轮传动时,因螺旋角分度圆直径节圆与分度圆重合,4-13 解4-14 解 分度圆锥角分度圆直径 齿顶圆直径 齿根圆直径外锥距时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日齿顶角、齿根角 顶锥角 根锥角当量齿数4-15 答: 一对直齿圆柱齿轮正确啮合的条件是:两齿轮的模数和压力角必需分别相等,即、.一对斜齿圆柱齿轮正确啮合的条件是:两齿轮的模数和压力角分别相等,螺旋角年夜小相等、方向相反(外啮合),即、、.一对直齿圆锥齿轮正确啮合的条件是:两齿轮的年夜端模数和压力角分别相等,即、.5-1 解: 蜗轮 2 和蜗轮 3 的转向如图粗箭头所示,即 和.图 5.5图5.65-2 解: 这是一个定轴轮系,依题意有:齿条 6 的线速度和齿轮 5 ′分度圆上的线速度相等;而齿轮 5 ′的转速和齿轮 5 的转速相等,因此有: 通过箭头法判断获得齿轮 5 ′的转向顺时针,齿条 6 方向水 平向右. 5-3 解:秒针到分针的传递路线为: 6→5→4→3,齿轮 3 上带 着分针,齿轮 6 上带着秒针,因此有:. 分针到时针的传递路线为: 9→10→11→12,齿轮 9 上带着分 针,齿轮 12 上带着时针,因此有:图 5.7. 图 5.8时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日5-4 解: 从图上分析这是一个周转轮系,其中齿轮 1、3 为中 心轮,齿轮 2 为行星轮,构件 为行星架.则有:∵∴∴当手柄转过 ,即时,转盘转过的角度,方向与手柄方向相同.5-5 解: 这是一个周转轮系,其中齿轮 1、3 为中心轮,齿轮2、2′为行星轮,构件 为行星架.则有:∵,∴∴传动比 为 10,构件 与 的转向相同.图 5.9图 5.105-6 解: 这是一个周转轮系,其中齿轮 1 为中心轮,齿轮 2 为行星轮,构件 为行星架.则有: ∵,,∵∴∴5-7 解: 这是由四组完全一样的周转轮系组成的轮系,因此只需要计算一组即可.取其中一组作分析,齿轮 4、3 为中心轮,齿轮 2 为行星轮,构件 1 为行星架.这里行星轮 2 是惰轮,因此它的齿数与传动比年夜小无关,可以自由选取.(1)由图知(2)又挖叉固定在齿轮上,要使其始终坚持一定的方向应有:(3)联立( 1)、(2)、(3)式得:时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日图 5.11图 5.125-8 解: 这是一个周转轮系,其中齿轮 1、3 为中心轮,齿轮2、2′为行星轮, 为行星架.∵,∴∴与 方向相同5-9 解: 这是一个周转轮系,其中齿轮 1、3 为中心轮,齿轮2、2′为行星轮, 为行星架.∵设齿轮 1 方向为正,则,∴∴与 方向相同图 5.13图 5.145-10 解: 这是一个混合轮系.其中齿轮 1、2、2′3、 组成周转轮系,其中齿轮 1、3 为中心轮,齿轮 2、2′为行星轮, 为行星架.而齿轮 4 和行星架 组成定轴轮系.在周转轮系中:(1)在定轴轮系中:(2)又因为:(3)联立( 1)、(2)、(3)式可得: 5-11 解: 这是一个混合轮系.其中齿轮 4、5、6、7 和由齿轮 3 引出的杆件组成周转轮系,其中齿 轮 4、7 为中心轮,齿轮 5、6 为行星轮,齿轮 3 引出的杆件为行 星架 .而齿轮 1、2、3 组成定轴轮系.在周转轮系中:在定轴轮系中:又因为:,(2)(1)时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日联立( 1)、(2)、(3)式可得:( 1)当,时,, 的转向与齿轮 1 和 4 的转向相同.( 2)当时,( 3)当,时,, 的转向与齿轮 1和 4 的转向相反.图 5.15图 5.165-12 解: 这是一个混合轮系.其中齿轮 4、5、6 和构件 组成周转轮系,其中齿轮 4、6 为中心轮,齿轮 5 为行星轮, 是行星架.齿轮 1、2、3 组成定轴轮系.在周转轮系中:(1)在定轴轮系中:(2)又因为:,(3)联立( 1)、(2)、(3)式可得: 即齿轮 1 和构件 的转向相反. 5-13 解: 这是一个混合轮系.齿轮 1、2、3、4 组成周转轮系, 其中齿轮 1、3 为中心轮,齿轮 2 为 行星轮,齿轮 4 是行星架.齿轮 4、5 组成定轴轮系.在周转轮系中:,∴(1)在图 5.17 中,当车身绕瞬时回转中心 转动时,左右两轮走过的弧长与它们至 点的距离成正比,即: 联立( 1)、(2)两式获得:(2) ,(3)在定轴轮系中:则当:时,代入( 3)式,可知汽车左右轮子的速度分别为,时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日5-14 解: 这是一个混合轮系.齿轮 3、4、4′、5 和行星架 组成周转轮系,其中齿轮 3、5 为中心轮,齿轮 4、4′为行星轮.齿轮 1、2 组成定轴轮系. 在周转轮系中:(1)在定轴轮系中:又因为:,,依题意,指针 转一圈即(2) (3) (4)此时轮子走了一公里,即(5)联立( 1)、(2)、(3)、(4)、(5)可求得图 5.18图 5.195-15 解: 这个起重机系统可以分解为 3 个轮系:由齿轮3′、4 组成的定轴轮系;由蜗轮蜗杆 1′和 5组成的定轴轮系;以及由齿轮 1、2、2′、3 和构件 组成的周转轮系,其中齿轮 1、3 是中心轮,齿轮 4、2′为行星轮,构件 是行星架.一般工作情况时由于蜗杆 5 不动,因此蜗轮也不动,即 (1)在周转轮系中:(2)在定轴齿轮轮系中:(3)又因为:,, (4)联立式( 1)、(2)、(3)、(4)可解得:.当慢速吊重时,机电刹住,即 有:,此时是平面定轴轮系,故5-16 解: 由几何关系有: 又因为相啮合的齿轮模数要相等,因此有上式可以获得:故行星轮的齿数: 图 5.20图 5.21时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日5-17 解: 欲采纳图示的年夜传动比行星齿轮,则应有下面关 系成立:( 1) (2) (3)又因为齿轮 1 与齿轮 3 共轴线,设齿轮 1、2 的模数为 ,齿 轮 2′、3 的模数为 ,则有:(4) 联立( 1)、(2)、(3)、(4)式可得(5)当时,(5)式可取得最年夜值 1.0606;当时,(5)式接近 1,但不成能取到 1.因此的取值范围是(1,1.06).而标准直齿圆柱齿轮的模数比是年夜于 1.07 的,因此,图示的年夜传动比行星齿轮不成能两对都采纳直齿标准齿轮传动,至少有一对是采纳变位齿轮.5-18 解: 这个轮系由几个部份组成,蜗轮蜗杆 1、2 组成一个定轴轮系;蜗轮蜗杆 5、4′组成一个定轴轮系;齿轮 1′、5′组成一个定轴轮系,齿轮 4、3、3′、2′组成周转轮系,其中齿轮 2′、4 是中心轮,齿轮 3、3′为行星轮,构件 是行星架.在周转轮系中: 在蜗轮蜗杆 1、2 中: 在蜗轮蜗杆 5、4′中:(1) (2)(3)在齿轮 1′、5′中:(4)又因为:,,,(5)联立式( 1)、(2)、(3)、(4)、(5)式可解得:,即.时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日5-19 解: 这个轮系由几个部份组成,齿轮 1、2、5′、 组 成一个周转轮系,齿轮 1、2、2′、3、 组成周转轮系,齿轮 3′、4、5 组成定轴轮系. 在齿轮 1、2、5′、 组成的周转轮系中:由几何条件分析获得:,则(1) 在齿轮 1、2、2′、3、 组成的周转轮系中:由几何条件分析获得:,则(2) 在齿轮 3′、4、5 组成的定轴轮系中:(3)又因为:,(4)联立式( 1)、(2)、(3)、(4)式可解得:6-1 解顶圆直径齿高齿顶厚齿槽夹角棘爪长度图 6.1 题 6-1 解图6-2 解 拔盘转每转时间0槽轮机构的运动特性系数槽轮的运动时间槽轮的静止时间 6-3 解 槽轮机构的运动特性系数因: 6-4 解 要保证所以 则槽轮机构的运动特性系数应为时间:二 O 二一年七月二十九日时间:二 O 二一年七月二十九日因得,则槽数 和拔盘的圆销数 之间的关系应为:由此适当取槽数~8 时,满足运动时间即是停歇时间的组合只有一种: , .6-5 解:机构类型工作特点结构、运动及动力 性能适用场所棘轮机构摇杆的往复摆动酿成棘轮的单 向间歇转动结构简单、加工方 便,运动可靠,但冲击、噪 音年夜,运动精度低适用于低速、转角 不年夜场所,如转位、分 度以及超越等.槽轮机构拨盘的连续转动酿成槽轮的间结构简单,效率高,传用于转速不高的轻歇转动动较平稳,但有柔性冲击 工机械中不完全齿从动轮的运动时间和静止时间需专用设备加工,有用于具有特殊要求轮机构的比例可在较年夜范围内变动较年夜冲击的专用机械中凸轮式间只要适当设计出凸轮的轮廓,歇运念头构 就能获得预期的运动规律.运转平稳、定位精 度高,动荷小,但结构较复 杂可用于载荷较年夜 的场所7-1 解 :( 1)先求解该图功的比例尺.( 2 ) 求最年夜盈亏功 .根据 图 7.5 做能量指示图.将和曲线的交点标注 ,, , , , , , , .将各区间所围的面积分为盈功和亏功,并标注“+”号或“-”号,然后根据各自区间盈亏功的数值年夜小按比例作出能量指示图(图 7.6)如下:首先自 向上做,暗示 区间的盈功;其次作 向下暗示 区间的亏 功;依次类推,直到画完最后一个封闭矢量 .由图知该机械系统在 绝对值为:( 3 )求飞轮的转动惯量曲轴的平均角速度:区间呈现最年夜盈亏功,其 ;系统的运转不均匀系数:则飞轮的转动惯量: 图 7.57-2; 图 7.6时间:二 O 二一年七月二十九日时间:二O二一年七月二十九日图 7.7 图时间:二O二一年七月二十九日。
《机械设计基础》答案
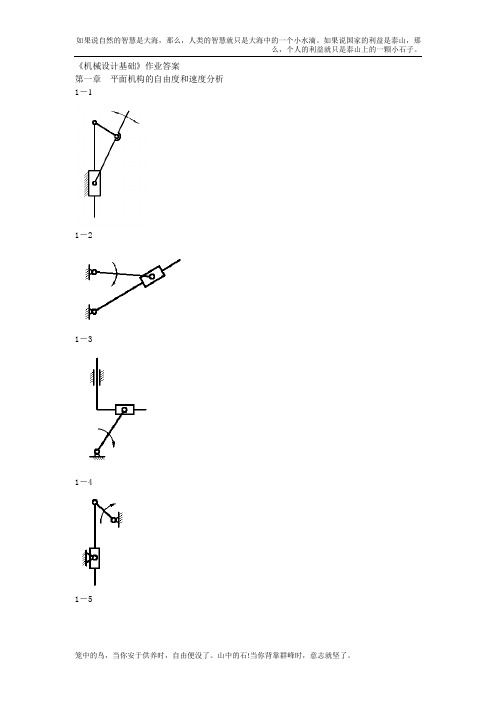
《机械设计基础》作业答案第一章平面机构的自由度和速度分析1-11-21-31-41-5自由度为:11 19211)0192(73')'2(3=--=--+⨯-⨯=--+-=FPPPnFHL或:1182632 3=-⨯-⨯=--=HLPPnF1-6自由度为11)01122(93')'2(3=--+⨯-⨯=--+-=FPPPnFHL或:11 22241112832 3=--=-⨯-⨯=--=HLPPnF1-10自由度为:1128301)221142(103')'2(3=--=--⨯+⨯-⨯=--+-=F P P P n F H L或:122427211229323=--=⨯-⨯-⨯=--=H L P P n F1-1122424323=-⨯-⨯=--=H L P P n F 1-13:求出题1-13图导杆机构的全部瞬心和构件1、3的角速度比。
1334313141P P P P ⨯=⨯ωω11314133431==P P ω1-14:求出题1-14图正切机构的全部瞬心。
设s rad /101=ω,求构件3的速度3v 。
s mm P P v v P /20002001013141133=⨯===ω1-15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试用瞬心法求轮1与轮2的角速度比21/ωω。
构件1、2的瞬心为P 12P 24、P 14分别为构件2与构件1相对于机架的绝对瞬心1224212141P P P P ⨯=⨯ωω121214122421r P P ==ω 1-16:题1-16图所示曲柄滑块机构,已知:s mm l AB /100=,s mm l BC /250=,s rad /101=ω,求机构全部瞬心、滑块速度3v 和连杆角速度2ω。
在三角形ABC 中,BCAAB BC ∠=sin 45sin 0,52sin =∠BCA ,523cos =∠BCA ,45sin sin BC ABCAC =∠,mm AC 7.310≈s mm BCA AC P P v v P /565.916tan 1013141133≈∠⨯===ω1224212141P P P P ωω=s rad AC P P P P /9.21002101001122412142≈-⨯==ωω1-17:题1-17图所示平底摆动从动件凸轮1为半径20=r 的圆盘,圆盘中心C 与凸轮回转中心的距离mm l AC 15=,mm l AB 90=,s rad /101=ω,求00=θ和0180=θ时,从动件角速度2ω的数值和方向。
机械设计基础.平面连杆机构习题及解答

平面连杆机构习题及解答一、复习思考题1、什么是连杆机构?连杆机构有什么优缺点?2、什么是曲柄?什么是摇杆?铰链四杆机构曲柄存在条件是什么?3、铰链四杆机构有哪几种基本形式?4、什么叫铰链四杆机构的传动角和压力角?压力角的大小对连杆机构的工作有何影响?5、什么叫行程速比系数?如何判断机构有否急回运动?6、平面连杆机构和铰链四杆机构有什么不同?7、双曲柄机构是怎样形成的?8、双摇杆机构是怎样形成的?9、述说曲柄滑块机构的演化与由来。
10、导杆机构是怎样演化来的?11、曲柄滑块机构中,滑块的移动距离根据什么计算?12、写出曲柄摇杆机构中,摇杆急回特性系数的计算式?13、曲柄摇杆机构中,摇杆为什么会产生急回运动?14、已知急回特性系数,如何求得曲柄的极位夹角?15、平面连杆机构中,哪些机构在什么情况下才能出现急回运动?16、平面连杆机构中,哪些机构在什么情况下出现“死点”位置?17、曲柄摇杆机构有什么运动特点?18、试述克服平面连杆机构“死点”位置的方法。
19、在什么情况下曲柄滑块机构才会有急回运动?20、曲柄滑块机构都有什么特点?21、试述摆动导杆机构的运动特点?22、试述转动导杆机构的运动特点。
23、曲柄滑块机构与导杆机构,在构成上有何异同?二、填空题1、平面连杆机构是由一些刚性构件用副和副相互联接而组成的机构。
2、平面连杆机构能实现一些较复杂的运动。
3、当平面四杆机构中的运动副都是副时,就称之为铰链四杆机构;它是其他多杆机构的。
4、在铰链四杆机构中,能绕机架上的铰链作整周的叫曲柄。
5、在铰链四杆机构中,能绕机架上的铰链作的叫摇杆。
6、平面四杆机构的两个连架杆,可以有一个是,另一个是,也可以两个都是或都是。
7、平面四杆机构有三种基本形式,即机构,机构和机构。
8、组成曲柄摇杆机构的条件是:最短杆与最长杆的长度之和或其他两杆的长度之和;最短杆的相邻构件为,则最短杆为。
9、在曲柄摇杆机构中,如果将杆作为机架,则与机架相连的两杆都可以作____ 运动,即得到双曲柄机构。
机械设计基础课后习题答案(第五版)(完整版)之欧阳语创编

机械设计基础(第五版)课后习题答案(完整版)时间:2021.03.01 创作:欧阳语高等教育出版社杨可桢、程光蕴、李仲生主编1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图 1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图b中的 CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
题2-1答: a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题 2-2解 : 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题2-4解: (1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解: (1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
机械设计基础课后习题答案(第五版)(完整版)之欧阳道创编

机械设计基础(第五版)课后习题答案(完整版)时间:2021.03.06 创作:欧阳道高等教育出版社杨可桢、程光蕴、李仲生主编1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图 1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮 1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
(2)图b中的CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
题 2-1答 : a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题2-2解: 要想成为转动导杆机构,则要求与均为周转副。
(1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
(2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题2-4解: (1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解 : ( 1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
《机械设计基础》答案
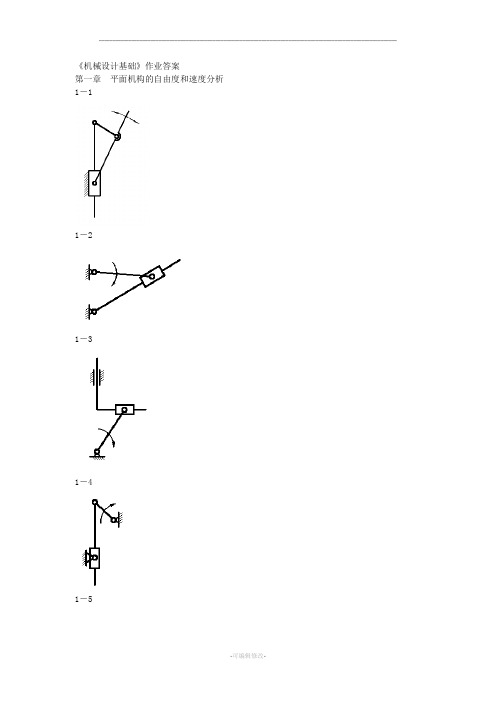
《机械设计基础》作业答案第一章平面机构的自由度和速度分析1-11-21-31-41-5自由度为:11 19211)0192(73')'2(3=--=--+⨯-⨯=--+-=FPPPnFHL或:1182632 3=-⨯-⨯=--=HLPPnF1-6自由度为11)01122(93')'2(3=--+⨯-⨯=--+-=FPPPnFHL或:11 22241112832 3=--=-⨯-⨯=--=HLPPnF1-10自由度为:11 28301)221142(103')'2(3=--=--⨯+⨯-⨯=--+-=FPPPnFHL或:12 242721122932 3=--=⨯-⨯-⨯=--=HLPPnF1-1122424323=-⨯-⨯=--=HL P P n F1-13:求出题1-13图导杆机构的全部瞬心和构件1、3的角速度比。
1334313141P P P P ⨯=⨯ωω141314133431==P P P P ωω1-14:求出题1-14图正切机构的全部瞬心。
设s rad /101=ω,求构件3的速度3v 。
s mm P P v v P /20002001013141133=⨯===ω1-15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试用瞬心法求轮1与轮2的角速度比21/ωω。
构件1、2的瞬心为P 12P 24、P 14分别为构件2与构件1相对于机架的绝对瞬心1224212141P P P P ⨯=⨯ωω1212141224212r r P P P P ==ωω 1-16:题1-16图所示曲柄滑块机构,已知:s mm l AB /100=,s mm l BC /250=,s rad /101=ω,求机构全部瞬心、滑块速度3v 和连杆角速度2ω。
在三角形ABC 中,BCA AB BC∠=sin 45sin 0,52sin =∠BCA ,523cos =∠BCA , 045sin sin BCABC AC=∠,mm AC 7.310≈s mm BCA AC P P v v P /565.916tan 1013141133≈∠⨯===ω1224212141P P P P ωω=s rad AC P P P P /9.21002101001122412142≈-⨯==ωω1-17:题1-17图所示平底摆动从动件凸轮1为半径20=r 的圆盘,圆盘中心C 与凸轮回转中心的距离mm l AC 15=,mm l AB 90=,s rad /101=ω,求00=θ和0180=θ时,从动件角速度2ω的数值和方向。
《机械设计基础》答案

《机械设计基础》作业答案第一章平面机构的自由度和速度分析1-11-21-31-41-5自由度为:11 19211)0192(73')'2(3=--=--+⨯-⨯=--+-=FPPPnFHL或:1182632 3=-⨯-⨯=--=HLPPnF1-6自由度为11)01122(93')'2(3=--+⨯-⨯=--+-=FPPPnFHL或:11 22241112832 3=--=-⨯-⨯=--=HLPPnF1-10自由度为:1128301)221142(103')'2(3=--=--⨯+⨯-⨯=--+-=F P P P n F H L或:122427211229323=--=⨯-⨯-⨯=--=H L P P n F1-1122424323=-⨯-⨯=--=H L P P n F 1-13:求出题1-13图导杆机构的全部瞬心和构件1、3的角速度比。
1334313141P P P P ⨯=⨯ωω11314133431==P P ω1-14:求出题1-14图正切机构的全部瞬心。
设s rad /101=ω,求构件3的速度3v 。
s mm P P v v P /20002001013141133=⨯===ω1-15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试用瞬心法求轮1与轮2的角速度比21/ωω。
构件1、2的瞬心为P 12P 24、P 14分别为构件2与构件1相对于机架的绝对瞬心1224212141P P P P ⨯=⨯ωω121214122421r P P ==ω 1-16:题1-16图所示曲柄滑块机构,已知:s mm l AB /100=,s mm l BC /250=,s rad /101=ω,求机构全部瞬心、滑块速度3v 和连杆角速度2ω。
在三角形ABC 中,BCAAB BC ∠=sin 45sin 0,52sin =∠BCA ,523cos =∠BCA ,45sin sin BC ABCAC =∠,mm AC 7.310≈s mm BCA AC P P v v P /565.916tan 1013141133≈∠⨯===ω1224212141P P P P ωω=s rad AC P P P P /9.21002101001122412142≈-⨯==ωω1-17:题1-17图所示平底摆动从动件凸轮1为半径20=r 的圆盘,圆盘中心C 与凸轮回转中心的距离mm l AC 15=,mm l AB 90=,s rad /101=ω,求00=θ和0180=θ时,从动件角速度2ω的数值和方向。
