流动的分类拉格朗日法和欧拉法质点导数迹线和流线、流
流体力学概念精简版

1.拉格朗日法:以研究个别流体质点的运动为基础,通过对每个流体质点运动规律的研究来获得整个流体运动的规律性2.欧拉法:以考察不同流体质点通过固定的空间点的运动情况来了解整个流体空间内的流动情况3.过流断面:在流束上作出的与流线正交的横断面4.流场:运动流体占据的空间5.恒定流:流体的各点运动要素不随时间变化非恒定流:流体上点的运动要素随时间改变6.当地加速度:由于时间过程而使空间上的质点速度发生变化的加速度迁移加速度:流动过程中质点由于位移占据不同的空间点而发生速度变化的加速度全加速度:流体质点速度随时间的变化率7.迹线:流体质点在某一时段的运动轨迹流线:某一时刻不同流体质点的速度方向8.流管:一非流线且不自交的封闭曲线,从封闭曲线上各个点绘出流线,组成封闭管状曲面流束:流管内的流体元流:过流断面面积无限小的流束总流:过流断面面积具有一定大小的有限尺寸的流束9.流量:单位时间内通过某一过流断面的流体数量(体积流量,重量流量,质量流量)10.均匀流:某一时刻,各点速度不随位置而变化的流体运动相应点速度相等的流体运动非均匀流:在某一时刻,各点速度随位置而变化相应点速度不相等的流体运动渐变流:所有流线是一组几乎平行的直线急变流:各流线之间夹角很大,或各流线的曲率半径很小11.有压流:边界全部为固体的流体运动无压流(明渠流):边界部分为固体,部分为大气射流:运动的流体脱离原来限制它的固体边界在充满流体的空间继续流动的流体运动12.三维流:流体的运动要素是空间三个坐标和时间t的函数的流体运动二维流:流体的运动要素是空间两个坐标和时间t的函数的流体运动一维流:流体的运动要素是空间一个坐标和时间t的函数的流体运动13.流体微元:由大量流体质点组成的具有线性尺度效应的微小流体团流体运动的形式:平移,变形(线变形,角变形),转动14.无涡流:每一流体微元的角转速为零,又称有势流速度势有涡流:每一流体微元的角转速不为零,流场中有角转速存在15.皮托管:测量流体点速度16.驻点:速度为零的点,驻点处流体的动能全部转化为压能17.平面势流18.水力坡度(能线坡度):单位长度上的水头损失19.总流伯努利方程的物理意义:总流各过流断面上单位重量流体所具有的势能平均值与动能平均值之和,即总机械能的平均值沿流程减少20.能量损失:沿程阻力和沿程损失,局部阻力和局部损失21.文丘里管:测量恒定有压管流的流量22.水泵扬程:单位重量的水流通过水泵后增加的能量水泵扬程=上下游水面高差+全部管路中的水头损失提水高度(扬水高度:上下游水面高差)23.断面平均流速:假设总流同一过流断面上各点的速度都相等,大小均为断面平均流速,以断面平均流速通过的流量等与该过流断面上各点实际速度不相等情况下所通过的流量。
流体力学欧拉法和拉格朗日法

流体力学欧拉法和拉格朗日法流体力学是研究流体运动规律的学科,它是物理学、数学和工程学的交叉学科。
在流体力学中,欧拉法和拉格朗日法是两种常用的描述流体运动的方法。
欧拉法是以欧拉方程为基础的一种描述流体运动的方法。
欧拉方程是描述流体运动的基本方程,它是由质量守恒、动量守恒和能量守恒三个基本方程组成的。
欧拉法的基本思想是将流体看作是一个连续的介质,通过对流体的宏观性质进行描述,如流体的密度、速度、压力等。
欧拉法适用于研究流体的宏观性质,如流体的流量、压力、速度等。
拉格朗日法是以拉格朗日方程为基础的一种描述流体运动的方法。
拉格朗日方程是描述流体运动的另一种基本方程,它是由质点的运动方程和流体的连续性方程组成的。
拉格朗日法的基本思想是将流体看作是由无数个质点组成的,通过对每个质点的运动进行描述,如质点的位置、速度、加速度等。
拉格朗日法适用于研究流体的微观性质,如流体的粘性、湍流等。
欧拉法和拉格朗日法各有优缺点,应用范围也不同。
欧拉法适用于研究流体的宏观性质,如流量、压力、速度等,但对于流体的微观性质,如粘性、湍流等,欧拉法的描述能力较弱。
而拉格朗日法适用于研究流体的微观性质,如粘性、湍流等,但对于流体的宏观性质,如流量、压力、速度等,拉格朗日法的描述能力较弱。
在实际应用中,欧拉法和拉格朗日法常常结合使用,以充分发挥它们各自的优势。
例如,在研究飞机的气动力学问题时,可以使用欧拉法来研究飞机的气动力学特性,如升力、阻力等;而在研究飞机的流场问题时,可以使用拉格朗日法来研究流体的微观性质,如湍流、涡旋等。
欧拉法和拉格朗日法是描述流体运动的两种基本方法,它们各有优缺点,应用范围也不同。
在实际应用中,需要根据具体问题选择合适的方法,以充分发挥它们的优势。
工程流体力学 第4章 流体运动学

qV
vdA
A
断面平均流速:过流断面各点速度的断面平均值,以V标记,有
V
vdA
A
qV
AA
对任一点有
v V v
§4-2 描述流体运动的基本概念
四、一、二、三元流动
一、二、三元流动又称为一、二、三维流动。 一元流动(One-dimensional Flow):流体的运动
v v (x, y, z) p p(x, y, z)
§4-2 描述流体运动的基本概念
三、流管、流束、流量与平均速度 流管:流场中过封闭曲线上各点作流线所围成的管状
曲面,见图。
流束:流管内所有流线的集合为流束。 微小流束:断面积无限小的流束。 总流:无数流束的总和。 注:(1)流束表面没有流体穿越;
间曲线,该瞬时位于曲线上各点的流体质点的速度与曲线在 该点相切,(如图示)。
§4-2 描述流体运动的基本概念
(2)流线的作法:欲作流场中某瞬时过A点的流线,可
在该瞬时作A点速度 v1 ;在 v1 上靠近A点找点 2,并在同 一时刻作 2点速度 v2;再在 v2上靠近2点找点3,也在同一 时刻作速度 v3 ;依次作到 N点,得到折线A-2-3-…-N,当
工程流体力学 第四章 流体运动学
§4-1 描述流体运动的两种方法
流体运动学研究流体运动的规律,不追究导致运动的力 学因素。
研究流体运动的方法
一、拉格朗日法(Lagrange Method) 拉格朗日法又称随体法。它追踪研究每一个流体质点的
运动规律,综合所有的流体质点,从而得到整个流场的运动 规律,参见图。
a y
《高等流体力学》第1章 流体运动学

§1-2 迹线与流线
一、迹线:流体质点运动形成的轨迹。 拉格朗日法中质点运动方程就是迹线参数方程:
xα = xα ( b1 , b2 , b3 , t )
对于给定的 b1 , b2 , b3 消去t可得迹线方程。 欧拉法:由速度场来建立迹线方程: 迹线的微元长度向量:d r = v ( x1 , x2 , x3 , t ) dt 二、流线:其上任一点的切线方向为速度方向。
任意坐标平面内:
1 ∂vβ ∂vα )= ε βα ε αβ = ( + 2 ∂xα ∂xβ
当α=β时,εαβ退化为线变 ∂v3 ∂v1 ∂v2 ε 33 = ε 22 = 形速率,因此可以把角变 ε11 = ∂x1 ∂x2 ∂x3 形、线变形速率统一起来
流体微元的旋转角速度 对比:
2
1 ∂v2 ∂v1 1 ∂v2 ∂v1 )+ ( ) ωπ 4 = ( − − 2 ∂x1 ∂x2 2 ∂x2 ∂x1
A1 A2
因A1与A2是任取的,故在同一时刻,沿同一涡管各 界面的涡通量不变—涡管通量守恒。 结论: (1)对于同一微元涡管,面积越小,流体旋转角速度 越大; (2)涡管截面不可能收缩到零。
1 ∂vβ ∂vα aαβ = ( )= ωγ = − −aβα 2 ∂xα ∂xβ
二、变形率张量和涡量张量 前面得到了变形率张量和涡量张量:
1 ∂vβ ∂vα )= ε βα ε αβ = ( + 2 ∂xα ∂xβ Байду номын сангаасαβ 1 ∂vβ ∂vα ( )= = − − aαβ 2 ∂xα ∂xβ
在任意坐标平面中:
2
∂v2 ∂v1 ∂vn ∂v2 ∂v1 2 2 = cos θ + sin θ cos θ − − sin θ ∂l ∂x1 ∂x2 ∂x2 ∂x1
水力学第三章
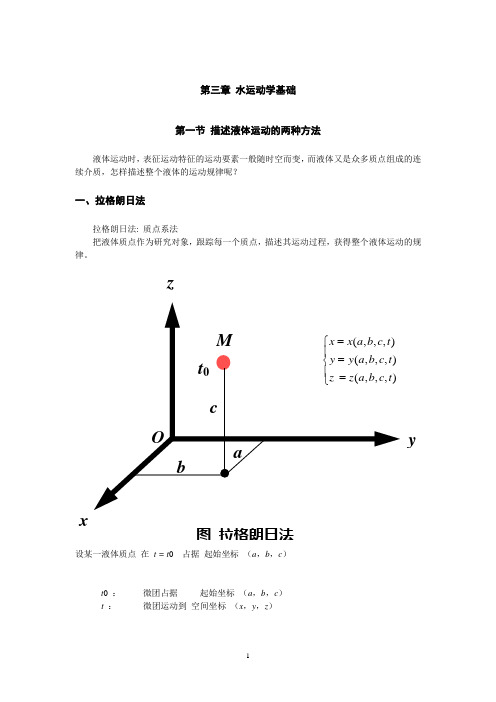
拉格朗日法
(a, b, c)
:
质点起始坐标
t
:
任意时刻
(x, y, z)
:
质点运动的位置坐标
(a, b, c , t ) :
拉格朗日变数
欧拉法
(x, y, z)
: 空间固定点(不动)
t
: 任意时刻
(x, y, z , t ) : 欧拉变数
t = t0 = 给定时刻,(x,y,z)= 变数
同一时刻,不同空间点上液体质点的流速分布,即流场。
dx dy
dz
ux (a,b, c,t)dt uy (a,b, c,t)dt uz (a,b, c,t)dt
dx ux
=
dy ux
= dz ux
=f
(x,
y,
z,t)
7
2.2 流线 某瞬时在流场中的一条空间曲线,曲线上所有液体质点的速度向量都与该曲线相切。
流线画法
z
u1
A3
u2
A2
A4
A1
Δs2 Δs3 Δs1
uz
dz(a,b, c,t) dt
d dt
ux u y
dx(a,b, c,t) dt
dy(a,b, c,t) dt
ax a y
d 2x(a,b, c,t) dt 2
d 2 y(a,b, c,t) dt 2
uz
dz(a,b, c,t) dt
az
d 2z(a,b, c,t) dt 2
第三章 水运动学基础
第一节 描述液体运动的两种方法
液体运动时,表征运动特征的运动要素一般随时空而变,而液体又是众多质点组成的连 续介质,怎样描述整个液体的运动规律呢?
3-流体运动学ppt课件

不可压缩流体 分流时 合流时
c
QQi Qi Q
Q1 Q2
v1A1v2A2
ቤተ መጻሕፍቲ ባይዱ
应用连续性方程注意事项:
①流体必须是稳定流动; ②流体必须是连续的; ③分清是可压缩流体还是不可压缩流体,以便采用相应的公式; ④对中途有流体输入或输出的分支管道,连续性方程有不同的表达式。
例1 水泵汲入管外径为88.5mm,壁厚4mm,压出管外径为75.5mm,壁厚 3.75mm,汲入管的流速为1.2m/s,试求压出管中水的流速。
6.流量
体积流量 质量流量 不可压缩流体
7.断面平均流速
Q udA
A
Qm udA
A
Qm Q
m3 / s kg/ s
v Q A
Q vA
三、连续性方程
v1 A1
1
A2 v2 2
在dt时间内,流入断面1的流体质量必等于流出断面2的 流体质量,则
1Q1d t 2Q2d t 1Q 12Q2
1v1A1 2v2A2 ——连续性方程的积分形式
z(a,b,c,t) uz t
ax
ux(a,b,c,t) t
ay
uy(a,b,c,t) t
az
uz(a,b,c,t) t
2.欧拉法(设立空间观察点) 某瞬时,整个流场各空间点处的状态
uxux(x,y,z,t)
uyuy(x,y,z,t) uzuz(x,y,z,t) pp(x,y,z,t)
(x,y,z,t)
流体运动学
一、研究流体运动的两种方法 二、欧拉法的基本概念 三、连续性方程
(完整版)第二章液体运动的流束理论
pdA p dpdA dG cos dm a
其中, dm dAds
cos dz
ds
a du du ds du u dt ds dt ds
z p u2 C
2g
28
z p u2 C
2g
或
z1
p1
u12 2g
z2
p2 u22
2g
理想液体恒定元流的能量方程
29
二、实际液体恒定元流的能量方程
恒定流的运动要素仅随空间位置变化,不随时间 变化。 例子:库水位不变时,引水隧洞中的水流。
5
2、非恒定流 流场中空间点的运动要素随时间变化的水流。 非恒定流的运动要素是时间和空间的函数。 实际水流严格上讲均为非恒定流。
6
二、流线、迹线 1、迹线 单个液体质点在空间的运动轨迹。 2、流线 某时刻在流场中绘制的一条光滑曲线。曲线上各 点切线的方向代表了同一时刻处于该点处的液体 质点的运动方向。
1、均匀流
流速的大小、方向沿流动方向(空间)都不变 的流动。
明渠均匀流
管道均匀流
31
均匀流特性 ①所有流线为相互平行的直线。
推论:过水断面为平面。 ②同一流线上各点流速相同。
推论:过水断面平均流速沿程不变。 注:不同流线上流速不一定相同。
7
3、流线的基本特性 对恒定流,流线形状不随时间变化,流线与 迹线重合;对非恒定流,流线只具有瞬时性, 流线与迹线不重合。 同一时刻,流场中的各条流线不相交。 流线为光滑的曲线。
8
流线分布的疏密程度反映流速的大小。流线 密的地方则流速大,流线疏的地方流速小。
1
2
9
溢流坝流线
10
三、 微小流束、总流 1、流管 在流场中,通过一个封闭线的周边上所有流线 围成的一个管状曲面。
第三章 流体运动学讲解
1 v1
2
3 3
v3
4 v4
v2 1
2
解:由题意 v4 A4 4 v4 4
v1
4
取过水断面1-1到3-3和4-4间 为对象
有: Q1 Q3 Q4 所以:
Q3 Q1 Q4
取过水断面1-1到2-2 为对象
4
有: v1 A1 v2 A2
试检查流动是否满足连续条件。
解:代入连续性方程,看是否满足连续性条件:
(2 x) (2 y ) (1) 22 0 x y
满足连续性条件
(0) (3xy) (2) 0 3x 0 x y
不满足连续性条件,说明该流动不存在。
见“流体力学课内练习”
例:不可压缩二维流动的流速分量为 ux x 4 y, u y y 4x 求 (1)流动是否存在,若存在,写出流函数表达式;(2)流 动是否有势,若有势,写出速度势表达式。 解:(1) (2) u y 4, u x 4 x y u x u y 1 u y u x 1 (1) 0 z ( )0 x y 2 x y
3-2 描述流体运动的基本概念 一、流管、元流和总流 1、流管
在流场中任取一封闭曲线,通过此封闭曲线上的每 一点作某一瞬时的流线,由这些流线所构成的管状曲 面称为流管。(P44图3-5)
2、元流 当封闭曲线所包围的面积无限小时,充满微小流管内 的液流称为元流。 3、总流 当封闭曲线取在运动液体的边界上时,则充满流管内 的整股液流称为总流。
5、掌握流函数、速度势函数与速度的关系。
3-1 1、拉格朗日法
流动描述
一、描述流体运动的两种方法
拉格朗日法又称质点系法,它是跟踪并研究每一个 液体质点的运动情况,把它们综合起来掌握整个液体 运动的规律。 在固体力学中应用较多。 2、欧拉法
流体力学第三章 (2)
1 v1 A1 2 v2 A2
v2
对于不可压流体:
qv1 qv 2
v1 A1 v2 A2
v1
2020/1/23
14
当不可压缩流体(液体)在圆形管道中流动时:
v1 A1 v2 A2
v1 v2
d
2 2
d
2 1
1
2
综合:
1
2
1qv1 2qv2 ——恒定流的连续性方程 1v1 A1 2v2 A2
对于不可压缩流体:
q qv1 qv2 qv3 qv4
qv4
qv1
qv2
qv3
风道送风
2020/1/23
16
§3-3 一元恒定流能量方程
一、恒定元流能量方程
在不可压流体中,任取一个元流段1—2,分析其在dt时间
内外力对其作的功和其能量的变化:
1、外力做功
摩擦力做功
p1dA1u1dt - p2dA2u2dt - dW ( p1 - p2 )dqvdt - dW 2、位能的变化
第三章 一元流体动力学基础
第一节 流体运动的基本概念 第二节 一元恒定流连续性方程 第三节 一元恒定流能量方程 第四节 能量方程的应用 第五节 一元恒定气流能量方程 第六节 一元恒定流动量方程
2020/1/23
1
§3-1 流体运动的基本概念
一、描述流体运动的两种方法
拉格朗日法:通过对流场中每一个流体质点运动的 描述,得到整个流体的运动情况。(以流体质点为研 究对象,又称质点系法)
二元流 (平面流): 运动参数随两个位置坐标 x、 y变化。如: 水在桌面上的流动近似平面流。
一元流 (管道流):
1流线-脉线-基线
2021/4/9
流场分布 4
拉格朗日与欧拉的联系 求导时a, b,c 作为参数不变 ,意即跟定流 体质点
❖ 在拉格朗日描述方法中,通常利用初始时刻流体质点的直角 坐标或曲线坐标 a、b、c作为区分不同流体质点的标志。流 体质点(a,b,c)在t时刻的物理量f可表为f=f(a,b,c, t)。在空间点(x,y,,z)在t时刻,正由拉格朗日描述方法欧 拉描述方法中,在流体占领的空间点(x,y,z)上,在时刻 t的流体物理量f是:f=F(x,y,z,t)
着眼于流体质点
跟踪个别 流体质点
2021/4/9
研究其位 移、速度、 加速度等随
时间的变
化情况
综合流场中 所有流体质 点的运动
流场分布
3
欧拉法
通过描述物理 量在空间的分 布来研究流体 运动的方法。
选定某一空 间固定点
记录其位 移、速度、 加速度等随
时间的变
化情况
着眼于研究空间 固定点的情况
综合流场中 许多空间点 随时间的变 化情况
2021/4/9
9
2021/4/9
流线
性质: ❖ 流线不能相交。因为流场中任一流
点只有一个速度方向。流线的疏密 程度反映了流速的大小。流线集密 处流速相对较大,反之,流线疏处 流速相对较小。 ❖ 流向不能突然折转。因为流点有速 度,就有惯性,因此流线只能是连 续光滑曲线。 ❖ 定常流动中,流线是稳定不变的曲 线。而在非定常流动中,同一点在 不同时刻的流线是不同的曲线。 ❖ 靠近固体壁面的流线通常与壁面平 行;若流线不平行而脱离壁面时, 两者间会出现能量损失。
2021/4/9
7
DV Dt
=
V t
+ (V )V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)按空间变化特性可分一、二、三维流动 一维流动:通常流体速度只沿一个空间坐
标变化的流动称为一维流动。
二维流动:通常流体速度只沿二个空间坐 标变化的流动称为二维流动。录像1 录像2
三维流动:通常流体速度只沿三个空间坐 标变化的流动称为三维流动。
5
说明一点:流动的维数与流体速度的分量数不是一
回事。如图(a) 、(b)所示。
y
(a)二维流动
Vx=0 x Vy=0 VzVz= Vz(x,y) Z
Vr=0 r Vθ=0 θ
Vz= Vz(r) z
(b)一维流动
思考题:如果对于图(a)中有
Vx=0, Vy=0, Vz= Vz(x,y,z)
则应该属于几维流动?其流动有何特点?
6
(3)按流动状态可分为层流和湍流(1.2.3.)
1883年,著名的雷诺实验揭示出粘性流动有两种 性质不同的型态,层流和湍流。
流态的判断:雷诺准数Re=ρud /μ 对于管内流动,Re<2300为层流, Re>4000为湍流。
7
2.2 描述流体运动的两种方法
2.2.1拉格朗日法(又称质点法) 通过研究流场中单个质点的运动规律,进
而研究流体的整体运动规律。具体地说:是沿 流体质点运动的轨迹进行跟踪研究。
基本思想:将流体质点表示为空间坐标、 时间的函数。在描述流体时,跟踪流体质点, 指出各流体质点在不同时刻的位置和有关的物 理参数(比如速度,压强、密度、温度)。
式中:a,b,c被称为拉格朗日变数。不同的一组(a,b,c)
表示不同的流体质点。
10
对于任一流体质点,其速度可表示为:
v
r t
x t
i
y t
j
z t
k vx
i vy
j vz
k
其加速度可表示为:
a
v t
vx t
i
vy t
j
vz t
k
axiayj Nhomakorabeaaz
k
式中:
v x = vx(a,b,c,t) ax = ax(a,b,c,t)
13
2.2.2 欧拉法(也叫场法)
基本思想:在确定的空间点上来考察流体的流动, 将流体的运动和物理参量直接表示为空间坐标和时间的 函数,而不是沿运动的轨迹去追踪流体质点。
例:在直角坐标系的任意点(x,y,z)来考察流体流 动,该点处流体的速度、密度和压力表示为:
v=v(x,y,z,t)=vx(x,y,z,t)i+ vy(x,y,z,t)j+ vz(x,y,z,t)k
对于任一流体质点的任一物理参数B的变化率都可 以表示为:
12
B B(a, b, c, t)
t
t
用拉格朗日法描述流体运动看起来比较简 单,实际上函数B(a,b,c,t)一般是不容易找到的, 往往不能用统一的函数形式描述所有质点的物 理参数的变化。所以这种方法只在少数情况下 使用,在本书中主要使用欧拉法。
9
要跟踪流体,首先要区别流体质点,最简单的方法是: 以某一初始时刻t0质点的位置作为质点的标志。
流体质点在不同时刻的位置用直角坐标系可表示为:
(a,b,c,t0) r0
r
(x,y,z,t)
x=x(a,b,c,t) y=y(a,b,c,t) z=z(a,b,c,t)
或用矢量表示为
r→=x→i+y→j+z→k =→r(a,b,c,t)
vy = vy(a,b,c,t) ay = ay(a,b,c,t)
vz = vz(a,b,c,t)
az = az(a,b,c,t)
11
同样流体密度、压力和温度可表示为:
ρ=ρ(a,b,c,t) p= p (a,b,c,t) T= T(a,b,c,t)
对于流体任一物理参数B均可类似地表示为 B=B(a,b,c,t).
2.2.3 质点导数
定义:流体质点的物理量对于时间的变化率。
拉格朗日法中,由于直接给出了质点的物理量的表达 式,所以很容易求得物理量的质点导数表达式。
B B(a,b,c,t)
t
t
如速度的质点导数(即加速度)为:
v(a,b, c,t)
a (a, b,
c, t )
t
16
对于欧拉法描述的流场,质点导数以速度为例 分析:
z
假设在直角坐标系中存在速度
p vΔt ṕ 场 v(x,y,z,t)。
x
y 设在时刻t和空间点p(x,y,z)处, 流体质点的速度为:
vp=v(x,y,z,t)
经过时间间隔Δt后,该流体质点运动到
p′(x+vxΔt,y+vyΔt,z+vzΔt)点,质点移动的距离为vΔt 。
在p′点处流体质点的速度为:
考虑流体变形的因素。
2
在数学上,流体的运动参数被表示为空间 和时间的函数。
vx = vx (x, y, z, t) vy = vy (x, y, z, t) vz = vz (x, y, z, t) 场:由于流体团所占据的空间每一点都是 研究对象,因此就将其看成一个“场”。
流场:充满流体的空间被称为“流场”。 相应地有“速度场”、“加速度场”、 “应力场”、“密度场”等。
17
vp′=v(x+vxΔt,y+vyΔt,z+vzΔt,t+Δt)
显然,经过时间间隔Δt后,流体质点的速度增量为:
Δv= vp′- vp= v(x+vxΔt,y+vyΔt,z+vzΔt,t+Δt)-v(x,y,z,t)
对上式右边第一项作泰勒展开并略去二阶以上高阶无穷 小量得:
3
2.1.2 流动的分类
(1)按随时间变化特性:稳态流动和非稳态流动
稳态流动:流体运动参数与时间无关,也叫 定常流动、恒定流动。
vx= vx(x,y,z) vy= vy(x,y,z) vz= vz(x,y,z)
非稳态流动:流体运动参数与时间有关,也 叫非定常流动、非恒定流。(例1.2.3.)
说明一点:流体流动稳态或非稳态流动与所选 定的参考系有关。
2 流体运动学基本概念
• 流动的分类* • 拉格朗日法和欧拉法* • 质点导数* • 迹线和流线*、流管 • 有旋流动、无旋流动*
1
2.1概述
2.1.1 流体运动的特点
流体运动的复杂性: (1)流体由无穷多个质点构成,很难采用质点曲线
运动理论来研究; (2)流体运动过程中,除了平动和转动外,还必须
ρ=ρ (x,y,z,t)
p=p (x,y,z,t)
14
按欧拉法,流动问题有关的任意物理量φ(可以 是矢量,也可以是标量)均可表示为:
φ = φ(x,y,z,t)
若流场中任何一物理量φ都不随时间变化,这 个流场就称之为稳态流场。相应的流动称为稳态 流动或定常流动,或者说对于稳态流动有:
0
t 15
