浅谈固体物理学中的近似方法
高中物理解题技巧之14.近似法

十四、近似法方法简介近似法是在观察物理现象、进行物理实验、建立物理模型、推导物理规律和求解物理问题时,为了分析认识所研究问题的本质属性,往往突出实际问题的主要方面,忽略某些次要因素,进行近似处理.在求解物理问题时,采用近似处理的手段简化求解过程的方法叫近似法.近似法是研究物理问题的基本思想方法之一,具有广泛的应用.善于对实际问题进行合理的近似处理,是从事创造性研究的重要能力之一.纵观近几年的物理竞赛试题和高考试题,越来越多地注重这种能力的考查.赛题精讲例1:一只狐狸以不变的速度1υ沿着直线AB 逃跑,一只猎犬以不变的速率2υ追击,其运动方向始终对准狐狸.某时刻狐狸在F 处,猎犬在D 处,FD ⊥AB ,且FD=L ,如图14—1所示,求猎犬的加速度的大小.解析:猎犬的运动方向始终对准狐狸且速度大小不变,故猎犬做匀速率曲线运动,根据向心加速度r r a ,22υ=为猎犬所在处的曲率半径,因为r 不断变化,故猎犬的加速度的大小、方向都在不断变化,题目要求猎犬在D 处的加速度大小,由于2υ大小不变,如果求出D 点的曲率半径,此时猎犬的加速度大小也就求得了.猎犬做匀速率曲线运动,其加速度的大小和方向都在不断改变.在所求时刻开始的一段很短的时间t ∆内,猎犬运动的轨迹可近似看做是一段圆弧,设其半径为R ,则加速度=a R 22υ 其方向与速度方向垂直,如图14—1—甲所示.在t ∆时间内,设狐狸与猎犬分别 到达D F ''与,猎犬的速度方向转过的角度为=α2υt ∆/R而狐狸跑过的距离是:1υt ∆≈L α 因而2υt ∆/R ≈1υt ∆/L ,R=L 2υ/1υ图14—1图14—2—甲所以猎犬的加速度大小为=a R22υ=1υ2υ/L 例2 如图14—2所示,岸高为h ,人用绳经滑轮拉船靠岸,若当绳与水平方向为θ时,收绳速率为υ,则该位置船的速率为多大?解析 要求船在该位置的速率即为瞬时速率,需从该时刻起取一小段时间求它的平均速率,当这一小段时间趋于零时,该平均速率就为所求速率.设船在θ角位置经t ∆时间向左行驶x ∆距离,滑轮右侧的绳长缩短L ∆,如图14—2—甲所示,当绳与水平方向的角度变化很小时,△ABC 可近似看做是一直角三角形,因而有L ∆=θcos x ∆两边同除以t ∆得:θcos tx t L ∆∆=∆∆,即收绳速率θυυcos 船= 因此船的速率为θυυcos =船例3 如图14—3所示,半径为R ,质量为m 的圆形绳圈,以角速率ω绕中心轴O 在光滑水平面上匀速转动时,绳中的张力为多大?解析 取绳上一小段来研究,当此段弧长对应的圆心角θ∆很小时,有近似关系式.sin θθ∆≈∆若取绳圈上很短的一小段绳AB=L ∆为研究对象,设这段绳所对应的圆心角为θ∆,这段绳两端所受的张力分别为A T 和B T (方向见图14—3—甲),因为绳圈匀速转动,无切向加速度,所以A T 和B T 的大小相等,均等于T . A T 和B T 在半径方向上的合力提供这一段绳做匀速圆周运动的向心力,设这段绳子的质量为m ∆,根据牛顿第二定律有:R m T 22sin 2ωθ∆=∆; 因为L ∆段很短,它所对应的圆心角θ∆很小所以22sin θθ∆=∆ 将此近似关系和πθπθ22∆=⋅∆⋅=∆m R m R m 代入上式得绳中的张力为πω22R m T = 例4 在某铅垂面上有一固定的光滑直角三角形细管轨道ABC ,光滑小球从顶点A 处沿图14—2 图14—2—甲图14—3 图—14—3—甲斜边轨道自静止出发自由地滑到端点C 处所需时间,恰好等于小球从顶点A 处自静止出发自由地经两直角边轨道滑到端点C 处所需的时间.这里假设铅垂轨道AB 与水平轨道BC 的交接处B 有极小的圆弧,可确保小球无碰撞的拐弯,且拐弯时间可忽略不计.在此直角三角形范围内可构建一系列如图14—4中虚线所示的光滑轨道,每一轨道是由若干铅垂线轨道与水平轨道交接而成,交接处都有极小圆弧(作用同上),轨道均从A 点出发到C 点终止,且不越出该直角三角形的边界,试求小球在各条轨道中,由静止出发自由地从A 点滑行到C 点所经时间的上限与下限之比值.解析 直角三角形AB 、BC 、CA 三边的长分别记为1l 、2l 、3l ,如图14—4—甲所示,小球从A 到B 的时间记为1T ,再从B到C 的时间为2T ,而从A 直接沿斜边到C 所经历的时间记为3T ,由题意知321T T T =+,可得1l :2l :3l =3:4:5,由此能得1T 与2T 的关系. 因为21121121T gT l gT l ==所以21212T T l l = 因为1l :2l =3:4,所以 1232T T =小球在图14—4—乙中每一虚线所示的轨道中,经各垂直线段所需时间之和为11T t =,经各水平段所需时间之和记为2t ,则从A 到C 所经时间总和为21t T t +=,最短的2t 对应t 的下限min t ,最长的2t 对应t 的上限.max t小球在各水平段内的运动分别为匀速运动,同一水平段路程放在低处运动速度大,所需时间短,因此,所有水平段均处在最低位置(即与BC 重合)时2t 最短,其值即为2T ,故min t =.35121T T T =+ 2t 的上限显然对应各水平段处在各自可达到的最高位置,实现它的方案是垂直段每下降小量1l ∆,便接一段水平小量2l ∆,这两个小量之间恒有αcot 12l l ∆=∆,角α即为∠ACB ,水平段到达斜边边界后,再下降一小量并接一相应的水平量,如此继续下去,构成如图所示的微齿形轨道,由于1l ∆、2l ∆均为小量,小球在其中的运动可处理为匀速率运动,分别所经的时间小量)(1i t ∆与)(2i t ∆之间有如下关联:αcot )()(1212=∆∆=∆∆l l i t i t 于是作为)(2i t ∆之和的2t 上限与作为)(1i t ∆之和的1T 之比也为.cot α故2t 的上限必为1T αcot ,即得:.37cot 111max T T T t =+=α 这样:max t min t =7:5例5 在光滑的水平面上有两个质量可忽略的相同弹簧,它们的一对端点共同连接着一个光滑的小物体,另外一对端点A 、B 固定在水平面上,并恰使两弹簧均处于自由长度状态且在同一直线上,如图14—5所示.如果小物体在此平面上沿着垂直于A 、B 连线的方向稍稍偏离初始位置,试分析判断它是否将做简谐运动?解析 因为一个物体是否做简谐运动就是要看它所受的回复力是否是一个线性力,即回复力的大小与位移大小成正经,方向相反.因此分析判断该题中的小物体是否做简谐运动,关键是求出所受的回复力的表达式(即此题中所受合外力的表达式).以AB 中点为原点,过中点且垂直于AB 的直线为x 轴,如图14—5—甲所示,取x 轴正方向为正方向,小物体所受回复力为:θsin )(20l l k F x --= ①其中k 为弹簧的劲度系数,0l 为弹簧的自由长度,l 为弹簧伸长后的长度,θ为弹簧伸长后与AB 直线的夹角.由几何知识可得lx =θsin ② 220x l l += ③将②、③代入①式得:203202212200)]211(1[2])(1[2l kx x l x k x x l l k F x -=---=+--== 由此可见,小物体受的合外力是一个非线性回复力,因此小物体将不做简谐运动.同时本题表明,平衡位置附近的小振动未必都是简谐运动.例6 三根长度均为m 2,质量均匀的直杆,构成一正三角形框架ABC ,C 点悬挂在一光滑水平转轴上,整个框架可绕转轴转动.杆AB 是一导轨,一电动玩具松鼠可在导轨上运动,如图14—6所示,现观察到松鼠正在导轨上运动,而框架却静止不动,试论证松鼠的运动是一种什么样的运动.解析 松鼠在AB 轨道运动,当框架不动时,松鼠受到轨道给它的水平力F ′作用,框架也受到松鼠给它的水平力F 作用,设在某一时刻,松鼠离杆AB 的中点O 的距离为x ,如图14—6所示,松鼠在竖直方向对导轨的作用力等于松鼠受到的重力mg ,m 为松鼠的质量.以C 点为轴,要使框架平衡,必须满足条件FL FL mgx 2360sin =︒=,松鼠对AB 杆的水平力为 )3/(2L mgx F =,式中L 为杆的长度.所以对松鼠而言,在其运动过程中,沿竖直方向受到的合力为零,在水平方向受到杆AB 的作用力为F ′,由牛顿第三定律可知F ′=F ,即kx L mgx F =-=')3/(2 其中L mk 32-=即松鼠在水平方向受到的作用力F ′作用下的运动应是以O 点为平衡位置的简谐运动,其振动的周期为.64.22/322s g L k m T ===ππ当松鼠运动到杆AB 的两端时,它应反向运动,按简谐运动规律,速度必须为零,所以松鼠做简谐运动的振幅小于或等于L/2=1m.由以上论证可知,当框架保持静止时,松鼠在导轨AB 上的运动是以AB 的中点O 为平衡位置,振幅不大于1m 、周期为2.64s 的简谐运动.例7 在一个横截面面积为S 的密闭容器中,有一个质量为m 的活塞把容器中的气体分成两部分.活塞可在容器中无摩擦地滑动,活塞两边气体的温度相同,压强都是p ,体积分别是V 1和V 2,如图14—7所示.现用某种方法使活塞稍微偏离平衡位置,然后放开,活塞将在两边气体压力的作用下来回运动.容器保持静止,整个系统可看做是恒温的.(1)求活塞运动的周期,将结果用p 、V 1、V 2、m 和S 表示;(2)求气体温度0=t ℃时的周期τ与气体温度τ'=30℃时的周期τ'之比值.解析 (1)活塞处于平衡时的位置O 为坐标原点.0=x 当活塞运动到右边距O 点x 处时,左边气体的体积由V 1变为V 1+Sx ,右边气体的体积由V 2变为V 2Sx -,设此时两边气体的压强分别为1p 和2p ,因系统的温度恒定不变,根据玻意耳定律有:222111)()(pV Sx V p pV Sx V p =-=+ 而以上两式解出:)1(2,)1(22221111V Sx V pV p V Sx V pV p +=+= ① 按题意,活塞只稍许离开平衡位置,故上式可近似为:),1(11x V S p p -≈ )1(22x V S p p +≈,于是活塞受的合力为.)11()(21221x V V pS S p p +-=-所以活塞的运动方程是x V V V V pS x V V pS ma 21212212)11(+-=+-= 其中a 是加速度,由此说明活塞做简谐运动,周期为)(221221V V pS V mV +=πτ (2)设温度为t 时,周期为τ,温度为t '时,周期为τ'.由于T p T p ''=,得出 T T T TV V pS V m V V V S p V m V '='⋅+=+'='τππτ)(2)(22122121221 所以TT '='ττ,将数值代入得95.0:='ττ 例8 如图14—8所示,在边长为a 的正三角形三个顶点A 、B 、C 处分别固定电量为Q 的正点电荷,在其中三条中线的交点O 上放置一个质量为m ,电量为q 的带正电质点,O点显然为带电质点的平衡位置,设该质点沿某一中线稍稍偏离平衡位置,试证明它将做简谐运动,并求其振动周期.解析 要想证明带电质点是否做简谐运动,则需证明该带电质点沿某一中线稍稍偏离平衡位置时,所受的回复力是否与它的位移大小成正比,方向相反.因此该题的关键是求出它所受回复力的表达式,在此题也就是合外力的表达式.以O 为坐标原点,以AOD 中线为坐标x 轴,如图14—8—甲所示,设带电质点在该轴上偏移x ,A 处Q 对其作用力为1F ,B 、C 处两个Q 对其作用的合力为2F ,取x 轴方向为正方向. 有2221)1()(---=--=r x r kQq x r kQqF 因为a OC OB OA r 33====++=--r xr x21)1(2当x 很小时可忽略高次项所以)361(321a x a Qqk F +-=232222222])()2)[((2))()2()()2((2-+++=+++⋅++=x h a x h kQq x h a xh x h a kQq F2322)24)((2-+++=hx h a x h kQq (略去2x 项)232)333)((2-++=ax a x h kQq23232)31()3)((2--++=x a a x h kQq)3231(363x a a x h kQq -+=)233(363x hx a h a Qqk +-= (略去2x 项))2331(363h xx a h a Qqk +-=)231(33x a aQq k += 因此带电质点所受合力为qx a Q k x aa x q a Q k F F F x 3221239)2336(3-=--=+= 由此可知,合外力x F 与x 大小成正比,方向相反. 即该带电质点将做简谐运动,其振动周期为kQqam a k m T 32322ππ== 例9 欲测电阻R 的阻值,现有几个标准电阻、一个电池和一个未经标定的电流计,连成如图14—9所示的电路.第一次与电流计并联的电阻r 为50.00Ω,电流计的示度为3.9格;第二次r 为100.00Ω,电流计的示度为5.2格;第三次r 为10.00Ω,同时将待测电阻R 换成一个20.00k Ω的标准电阻,结果电流计的示度为7.8格.已知电流计的示度与所通过的电流成正比,求电阻R 的阻值.解析 在测试中,除待求量R 外,电源电动势E ,电源内阻r ,电流计内阻g R 以及电流计每偏转一格的电流0I ,均属未知.本题数据不足,且电流计读数只有两位有效数字,故本题需要用近似方法求解. 设电源电动势为E ,电流计内阻为g R ,电流计每偏转一格的电流为0I ,用欧姆定律对三次测量的结果列式如下:09.3150505050I R R R r R R R Eg g g gg=⋅+⋅+++ 02.51100100100100I R R R r R R R E g g g gg=⋅+⋅+++ 08.711010200001010I R R R r R R E gg g g g=⋅+⋅+++ 从第三次测量数据可知,当用20k Ω电阻取代R ,而且r 阻值减小时电流计偏转格数明显增大,可推知R 的阻值明显大于20k Ω,因此电源内阻完全可以忽略不计,与R相比,电图14—9流计内阻g R 与r 的并联值对干路电流的影响同样也可以忽略不计,故以上三式可近似为:09.35050I R R E g=+⋅① 02.5100100I R R E g=+⋅② 08.7101020000I R E g=+⋅ ③ 待测电阻R=120k Ω解①、②、③三式,可得g R =50Ω例10 如图14—10所示,两个带正电的点电荷A 、B 带电量均为Q ,固定放在x 轴上的两处,离原点都等于r .若在原点O放另一正点电荷P ,其带电量为q ,质量为m ,限制P 在哪些方向上运动时,它在原点O 才是稳定的?解析 设y 轴与x 轴的夹角为θ,正电点电荷P 在原点沿y 轴方向有微小的位移s 时,A 、B 两处的点电荷对P 的库仑力分别为A F 、B F ,方向如图14—10所示,P 所受的库仑力在y 轴上的分量为βαcos cos B A y F F F -= ① 根据库仑定律和余弦定理得θcos 222rs s r kqQ F A ++= ② θcos 222rs s r kqQ F B +-= ③ θθαcos 2cos cos 22rs s r sr +++= ④ θθβcos 2cos cos 22rs s r sr ++-= ⑤将②、③、④、⑤式代入①得:23222322)cos 2()cos ()cos 2()cos (θθθθrs s r s r kqQ rs s r s r kqQ F y -+--+++=图14—10因为s 很小,忽略2s 得: ])cos 21(cos )cos 21(cos [23233θθθθr s s r rs sr r kqQ F y ---++= 又因为1cos 2,<≤θr s r s 所以利用近似计算x x 231)1(23≈±-得 )]cos 31)(cos ()cos 31)(cos [(3θθθθr s s r r s s r rkqQ F y +--++≈忽略2s 得)1cos 3(23--=θrkqQs F y 当(0)1cos 32>-θ时y F 具有恢复线性形式,所以在31cos 2>θ范围内,P 可围绕原点做微小振动,所以P 在原点处是稳定的.例11 某水池的实际深度为h ,垂直于水面往下看,水池底的视深为多少?(设水的折射率为n )解析 如图14—11所示,设S 为水池底的点光源,在由S 点发出的光线中选取一条垂直于面MN 的光线,由O 点垂直射出,由于观察者在S 正方,所以另一条光线与光线SO 成极小的角度从点S 射向水面点A ,由点A 远离法线折射到空气中,因入射角极小,故折射角也很小,进入人眼的两条折射光线的反向延长线交于点S ′,该点即为我们看到水池底光源S 的像,像点S ′到水面的距离h ',即为视深. 由几何关系有,/tan ,/tan h AO i h AB r ='=所以h h i r '=/tan /tan ,因为r 、i 均很小,则有i i r r sin tan ,sin tan ≈≈,所以h h i r '≈/sin /sin 又因i r n sin sin =所以视深n h h /='针对训练1.活塞把密闭气缸分成左、右两个气室,每室各与U 形管压强计的一臂相连,压强计的两臂截面处处相同.U 形管内盛有密度为5.7=ρ×102kg/m 3的液体.开始时左、右两气室的体积都为V 0=1.2×10-2m 3,气压都为0.40=ρ×103Pa ,且液体的液面处在同一高度,如图14—12所示.现缓缓向左推动活塞,直到液体在U 形管中的高度差h =40cm.求此时左、右气室的体积V 1、V 2.假定两气室的温度保持不变.计算时可以不计U 形管和连接管道中气体的体积.取g =10m/s 2.2.一汽缸的初始体积为V 0,其中盛有2mol 的空气和少量的水(水的体积可忽略),其平衡时气体的总压强是3.0大气压.经过等温膨胀使其体积加倍,在膨胀过程结束时,其中的水刚好全部消失,此时的总压强为2.0大气压.若让其继续作等温膨胀,使其体积再次加倍,试计算此时:(1)汽缸中气体的温度;(2)汽缸中水蒸气的摩尔数;(3)汽缸中气体的总压强. (假定空气和水蒸气均可当做理想气体处理)3.1964年制成了世界上第一盏用海浪发电的航标灯,它的气室示意图如图14—13所示.利用海浪上下起伏力量,空气能被吸进来,压缩后再推入工作室,推动涡轮机带动发电机发电.当海水下降时,阀门S 1关闭,S 2打开,设每次吸入压强为1.0×106Pa 、温度为7℃的空气0.233m 3(空气可视为理想气体),当海上升时,S 2关闭,海水推动活塞绝热压缩空气,空气压强达到32×105Pa 时,阀门S 1才打开.S 1打开后,活塞继续推动空气,直到气体全部推入工作室为止,同时工作室的空气推动涡轮机工作.设打开S 1后,活塞附近的压强近似保持不变,活塞的质量及活塞筒壁间的摩擦忽略不计.问海水每次上升时所做的功是多少?已知空气从压强为1ρ、体积为V 1的状态绝热的改变到压强为2ρ、体积为V 2的状态过程中,近似遵循关系式1ρ/2ρ=(V 2/V 1)5/3,1mol 理想气体温度升高1K 时,内能改变为3R/2.[R=8.31J/(mol·K)]4.如图14—14所示,在O x 轴的坐标原点O 处,有一固定的电量为)0(>Q Q 的点电荷,在L x -=处,有一固定图14—13图14—14的、电量为Q 2-的点电荷,今有一正试探电荷q 放在x 轴上0>x 的位置,并设斥力为正,引力为负.(1)当q 的位置限制在O x 轴上变化时,求q 的受力平衡的位置,并讨论平衡的稳定性;(2)试定性地画出试探电荷q 所受的合力F 与q 在O x 轴上的位置x 的关系图线.5.如图14—15所示,一人站在水面平静的湖岸边,观察到离岸边有一段距离的水下的一条鱼,此人看到鱼的位置与鱼在水下的真实位置相比较,应处于什么方位.6.如图14—16所示,天空中有一小鸟B ,距水面高m h 31=,其正下方距水面深m h 42=处的水中有一条小鱼A.已知水的折射率为4/3,则小鸟看水中的鱼距离自己是多远?小鱼看到鸟距离自己又是多远?参考答案1.V 1=0.8×10-2m 3 ,V 2=1.6×10-2m 3 2.(1)373K (2)2mol (3)1.0大气压3.8.15×104J 4.(1)平衡是稳定的 (2)5.应在鱼的右上方6.6m ,8m。
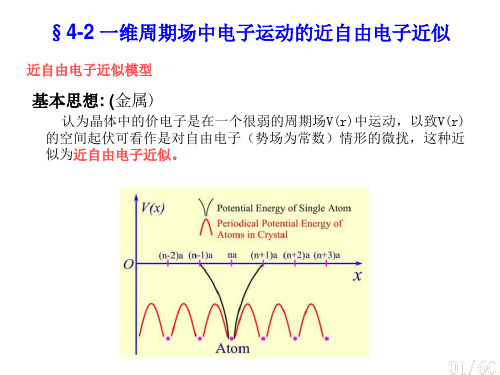
固体物理学:4-2 一维周期场中电子运动的近自由电子近似
—— 主要影响的态 —— 只考虑影响最大的状态,忽略其它状态的影响
状态
,状态
的影响
6:简并微扰 简并波函数 薛定谔方程
考虑到
分别以
或
利用
线性代数方程
从左边乘方程,对 x 积分
a, b有非零解
能量本征值 (1) 波矢k离 较远,k状态的能量和状态k’差别较大
将
按
展开
结论:k和k’能级相互作用的结果 是原来能级较高的k’提高,原来能级较低的k下压
(4)利用以上特点,可以画出在波矢空间近自由电子的能 带。
—— 量子力学中微扰作用下,两个相互影响的能级 总是原来较高的能量提高了,原来较低的能量降低了
—— 能级间“排斥作用”
原来能级较高的k’提高,原来能级较低的k下降
(2) 波矢k非常接近
,k状态的能量和k’能量差别很小
将
按
展开
(3)结果分析 : 1) 两个状态k和k’微扰后,能量变为E+和E原能量高的态 ,能量提高;原能量低的态
1)对于k距 较远的范围,已可用于非简并微扰,电子的能量与自 由电子的能量相差类似。
能量本征值
电子波矢取值
当N很大时,能级视为准连续
—— 一个l,有一个量子态k
能级的准连续分布形成了一系列的能带
2) 能量本征值在
处断开 带隙(禁带)形成
—— 晶体弱周期性势场的微扰,电子能谱在布里渊边界 发生能量跃变
• 三维情况下沿某一方向 变化所出现的 能隙不一定就是禁带。
• 出现能隙的物理原因是晶格周期场, • 在近自由电子近似中自由电子作为零级近
似,波函数为平面波,它在晶体中传播时 就如同 X射线一样,当波失 不满足布拉格 条件时,晶格的影响很弱,电子几乎不受 阻碍地通过晶体,这时电子基本上是自由 的,其能量与自由电子的能量差别不大, • 但当波失 满足布拉格条件时,电子波被 晶格的某一族晶面所反射,电子就不能自 由地通过晶体了,相应的能级也发生劈裂。
固体物理:3.4 长波近似

EL
b21
0 b22
WL
由黄昆方程得:
W
b11W
b12 E
(1)
P b21W b22E (2)
将上式中的有旋场与无旋场分开得到:
WT
b11WT
b12ET
由麦克斯韦电磁波理论可知,ET EL ,则上式变为
上面两方框中式子均为简谐方程,由此得振动频率
2 T0
b11,
2 L0
b11
e E' e E'
由上式 (a) m (b) M
u 2u e*
得 : E
mMuu
22uu
uueeEE'
'
(a)
(b)
mM
mM
将 E E
1
P
代入,得: 3 0
P
1
Ω 1
1
e
u
E
3 0 Ω
2
e 2
3 0 Ω 1
3 0 Ω
u
1
e
3 0
Ω
E
,
u
2
e 2
3 0 Ω 1
3 0 Ω
u
1
e
3 0 Ω
E,
P
1
Ω 1
1
e
u
E
3 0 Ω
引进位移参量
W u
Ω
mM
mM
则有
W
b11W
b12E
P b21W b22E
(1) ---黄昆方程
( 2)
W
b11W
b12E
P b21W b22E
(1)
( 2)
e 2
1 Ω
E
浅析中学物理中一种常见的科学方法-近似处理法

浅析中学物理中常见的科学方法—近似处理法江苏省如皋市丁堰中学张毕生近似处理法作为一种解决个别问题的算法,在中学物理教学中应用较为广泛。
由于它不是物理学科所特有的科学方法,常被不少人所忽视,现就此法在中学物理应用中的广泛发兵和重要性谈一些粗浅认识,敬请各位同仁指教。
一、模型建立和应用中含近似实际物理现象和过程一般都是十分复杂的,物理模型的建立排除了非本质因素的干扰,穿出反映事物的本质特征,从而使物理现象或过程得到简化和理想化。
中学物理涉及的模型常有:质点、单摆、理想气体、点电荷、理想变压器、原子模型等等,这些化模型的建立和应用中无不包含了近似处理的观点。
在建立质点模型时,忽略了研究对象的形状、线度,而抓住了其质量这一本质特征。
这样的近似处理研究问题大大简化。
当然,能否作这样的近似处理是有一定的条件的,即物体本身的形状、线度研究问题无影响或影响不大。
如研究地球的公转,地球可看成质点,但在研究地球自转时则不能作这样的近似处理;足球运动员踢出去的足球的运动轨迹,在旋转程度不大时常可看成质点,而常见的“香蕉球”则不能作这样的近似处理。
另外,实际气体在温度不太低、压强不太大的情况下可近似地看成理想气体;实际变压器在忽略了其铜损、铁损、磁损时可以看成理想变压器等,这些都合理地运用了近似处理的方法。
在理想模型的应用中能否作近似处理一定要根据其条件把握好其“度”,才能不失其科学性。
二、规律和应用中显近似 物理规律是在实验或假说及数学演绎的基础上建议起来的,与自然规律相比它总是显得不够精细。
物理规律的近似来源于两个方面,首选来源于物理实验仪器的精度限制和实验环境的影响一方面来源于物理实验仪器的精度限制和实验环境蝗影响另一方面来源于对实际物理过程的理想化。
天空自由落体运动时,我们认为物体自由下落时,作初速度为零,加速度为g的匀加速直线运动。
但试想一下,我们如果不断提升物体下落的高度,若我们有足够精密的仪器测量其加速度,它还能作匀加速运动吗?对其受力分析不难得到:mf-+h)(=m-fa=R M G F (其中:G —重力常数;M —地球质量;R —地球半径;h—物体高度;f —空气阻力;m —物体质量)。
固体物理 04-02一维周期场中电子运动的近自由电子近似

2 2 k 0 Ek V 2m
固 体 物 理
Solid State Physics
波函数和能量本征值
2 2 k 0 Ek V 2m
k E 2m
0 k
2
2
西 南 科 技 大 学
固 体 物 理
Solid State Physics
周期边界条件
1 ikx 1 ik ( x Na ) ( x) e e L L
0 k (1) k
k0 ( x ) (1/ L )eikx
波函数的一级修正
(1) k
k '| H '| k 0 k' 0 0 Ek Ek ' k'
西 南 科 技 大 学
k k n(2 / a)
k | H | k V (n)
k k n(2 / a)
Ek Ek0 Ek(1) Ek( 2 ) .
Ek(1) k | H ' | k
k | V ( x) V | k
E
西 南 科 技 大 学
(1) k
0 L
L
1 ikx 1 ikx e [V ( x ) V ] e dx L L
E
(1) k
1 ikx 1 ikx [ e V ( x ) e dx ] V 0 L 0 L
k | H | k 0
固 体 物 理
Solid State Physics
(1) k
k '| H '| k 0 k' 0 0 Ek Ek ' k'
k0 ( x ) (1/ L )eikx
物理学中的固体物理学方法

物理学中的固体物理学方法物理学是一门研究自然界中各种物质和能量相互作用的学科。
在物理学的众多分支中,固体物理学是一门非常重要的领域。
固体物理学研究的是固体物质的性质和行为,涉及到电子结构、晶体结构、磁性、声学等多个方面。
本文将探讨固体物理学中的一些常用方法和技术。
一、X射线衍射X射线衍射是固体物理学中最常用的实验技术之一。
通过将X射线照射到固体样品上,观察样品中的晶体衍射图样,可以得到关于晶体结构的重要信息。
X射线衍射技术广泛应用于研究晶体的晶格结构、晶体缺陷以及晶体的相变等问题。
通过分析衍射图样,可以确定晶体的晶胞参数、晶体的点群对称性以及晶体中原子的排列方式等。
二、扫描隧道显微镜扫描隧道显微镜(Scanning Tunneling Microscope,STM)是一种能够观察到原子尺度的表面形貌和电子结构的仪器。
STM的工作原理是利用隧道效应,通过控制探针与样品之间的距离,测量电子的隧道电流来获得样品表面的拓扑结构和电子分布。
STM的分辨率可以达到亚埃的尺度,因此在研究固体材料的表面形貌、表面缺陷以及表面电子结构等方面具有重要的应用价值。
三、拉曼光谱拉曼光谱是一种通过测量物质散射光的频率变化来研究物质的结构和振动特性的技术。
在固体物理学中,拉曼光谱常用于研究晶格振动、晶格畸变以及材料的电子结构等问题。
通过测量样品散射光的频率偏移,可以得到关于样品中原子振动的信息。
拉曼光谱技术在研究固体材料的结构和性质方面具有广泛的应用。
四、核磁共振核磁共振(Nuclear Magnetic Resonance,NMR)是一种通过测量物质中核自旋的共振现象来研究物质的结构和性质的技术。
在固体物理学中,NMR常用于研究材料的晶体结构、晶体缺陷以及材料中的自旋相互作用等问题。
通过测量样品中核自旋的共振频率和强度,可以得到关于样品中原子的排列方式和相互作用的信息。
NMR技术在研究固体材料的结构和性质方面具有重要的应用价值。
探析物理学中的近似法
1222013年第28卷第6期南昌教育学院学报高职教育收稿日期:2013-05-20作者简介:房成敏(1963-),女,辽宁营口人,高级讲师,从事物理学向研究。
近似法是指在分析、处理和研究某些物理现象和问题时,忽略研究对象和问题的次要因素,突出其主要矛盾和本质特征,科学、合理地对所研究的问题进行近似处理的方法。
近似法是物理学的重要研究方法之一,善于对实际问题进行合理的近似处理,是从事科学研究和学习的重要能力,是科学素质和综合能力的体现。
一、近似法在物理模型构建中的应用客观世界错综复杂,但在一定的条件和目的下,可以忽略事物的次要因素,抓住事物的主要方面,把研究对象抽象为一个简单但足以表征其主要特征的理想化模型,用理想的条件下的物理模型代替实际研究对象,进而使得研究的过程和方法得以简化。
(一)研究的对象模型化对物理模型的近似,是从实际情况中把物体抽象出来,是对研究对象本身的近似。
如忽略物体的体积和形状但有质量的质点、忽略线圈电阻和能量损失的理想变压器、在任意外力作用下都不发生形变的刚体等。
(二)研究条件的模型化对研究对象所处外界环境的近似,即把研究对象所处的外部条件合理化,忽略对物理过程没有决定性作用的因素而得到的一种理想模型。
如绝对光滑、轻杆、匀强电场、空气阻力忽略不计等,(三)运动的过程模型化很多物理过程均比较复杂,所以要对相关的过程加以分解简化,利用熟悉的物理情景和掌握的数学方法加以处理。
如等温气压公式推导过程中近似地把大气温度视为恒量等。
另外,匀速直线运动、匀速圆周运动、准静态过程、绝热过程、弹性碰撞等都是属于物理过程的近似。
二、近似法的应用实例例题1:求均匀带电圆盘轴线上P 点的场强。
已知圆盘半径为R ,电荷面密度为(>0)。
解:设P 点距圆心O 点的距离为Z ,取图示小面元,其所带电量为。
当和足够小时,可近似认为为点电荷,由点电荷场强公式可求得它在轴线处P 点的场强大小为:(1)方向如图所示。
固体物理(第16课)紧束缚近似资料
V为晶体的体积
2. 微扰计算结果
k
(
r
)
1 N
N
e ikRn i
(r
Rn
)
n1
Ek Ei J ss
e J ik( Rn Rs ) sn
J SS
J SN
V V
* i
* i
(r (r
与sR近s邻)的Hˆn Rs )Hˆ
i i
(r (r
Rs )d Rn )d
E
k
Ei
J ss
ห้องสมุดไป่ตู้
e J ik( Rn Rs ) sn
与s近邻的n
E
k
Gh
Ei
J ss
e J i (k Gh )( Rn Rs ) sn
与s近邻的n
Ei J ss
e e J ik( Rn Rs )
iGh ( Rn Rs ) sn
与s近邻的n
Ek (3) Ek随k变化,它们构成了与Ei相联系的能带
能带的宽度取决于J sn
示意图
零级近似:
Hˆ 0
k
0
(r
)
Ek 0
k
0
(r
)
Ekk00(r)Ei
i
(r
Rn )
孤立原子
k
l1 N1
b1
l2 N2
b2
l3 N3
b3
其中
Ni 2
li
Ni 2
N为晶体中的原 子数或布喇菲晶 格的原胞数
在第一布里渊区有N个值不同的 值,对应这些准连续函数取值的 波矢k, E(k)构成一个准连续的能 带.
积分值才不为0,当Rs 0时,波函数重叠最大,
固体物理第16、7讲、一维周期场中电子运动的近自由电子近似
'
Vn 2
E
0 k
)
2
按
4 Vn 2
(
E
0 k
'
E
0 k
)
2
泰勒级数展开
22
1(Ek40' VnE2k0)2 1(Ek20' VnE2k0)2
E 1 2{E k 0E k 0' (E k 0' E k 0)[1(E k 2 0' V n E 2 k 0)2]}
E
E
0 k'
E
0 k
Vn 2
E
0 k'
,能量提高;原来能量低的状态
0 k
能量降低
27
两个相互影响的状态k和k'微扰后,能量变为E+和E-
E V Tn Vn
2Tn
(
2Tn Vn
1)
E V Tn Vn
2Tn
(
2Tn Vn
1)
28
ii) 当 0 时
EVTnVn
—— > 0, < 0 两种情形下完全对称 的能级图
—— A和C、B和D代 表同一状态 —— 它们从>0, <0 两个方向当0的共 同极限
线性代数方程 ( E k 0 E ) a V n * b 0 & V n a ( E k 0 ' E ) b 0
a, b有非零解
Ek0 E Vn
Vn* 0 Vn k ' V k
Ek0' E
Vn* k V k '
能量本征值 E 1 2 { E k 0 E k 0 '(E k 0 E k 0 ')2 4 V n2} 21
浅谈近似法在高中物理中的应用
浅谈近似法在高中物理中的应用李建立浙江省象山县石浦中学高中阶段,由于受到学生认知结构和数学水平的限制,很多的物理问题均要做近似处理后方可被学生接受。
因而常常用到近似法,所谓近似法是指在研究物理问题时,忽略问题的次要因素,抓住问题的主要因素,采用近似处理的手段简化求解的过程。
在高中阶段,近似法是学生学习和处理物理问题时最常用的一种方法。
一近似法在物理模型构建中的应用解决物理问题,无不联系着一定的物理模型,对这些模型的数字描述,不可能也没必要追求“精确”,可以运用近似处理的方法,通过简化的运算和描述来反映基本的物理特征,即要用理想条件下的模型代替实际研究对象,从而使得研究的过程和方法得以简化,在高中阶段学生常见的模型有:1.研究对象的模型化研究某一具体的物理过程时,首先要选择研究对象,而现实世界中物体的形状千奇百怪,当我们研究它们时,必须排除它们的次要因素,从实际情况中把物体抽象出来,如单摆、光线、质点、点电荷、光滑平面、轻质弹簧、理想变压器、点光源、电场线、磁感线等。
2.研究条件的模型化将研究对象抽象后,接下来要分析物体的运动过程,而影响物体运动的因素有很多,所以仍要将一些次要因素予以排除,如:绝对光滑、匀强电场、空气阻力不计等。
当然很多的条件模型要分清适应的场所,如带电粒子在电场运动中重力是否可忽略不计,要看具体情况。
3.运动过程的模型化做好以上两点后,接下来应具体分析物体的运动过程。
很多的物理过程均比较复杂,因此要对相关的过程加以分解,利用熟悉的物理情景和掌握的数学方法加以处理。
如匀速直线运动、匀变速直线运动、匀速圆周运动等。
例1,光滑水平面AB长l=0.134m,与光滑的圆弧轨道BC相连,图1所示BC所对圆心角为,圆弧半径R=1m,在C处有一质量为m1的小球甲由静止下滑,滑至B点与质量为m2的静止小球乙正碰,碰撞后甲球以原来速率的反向弹回,乙球滑至A点与挡板弹性碰撞(动能不变),要使甲乙两球再次相遇于B点,则两球的质量之比应为多少?解析:要使甲乙两球经碰撞以后再次在B点相遇,应求得碰撞后甲球往返所需时间,而甲球在圆弧上运动的时间是很难用运动学知识得到的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学 年 论 文
题 目:浅谈固体物理学中近似方法
系 别:
专 业:
年 级:
学 号:
学 生:
指导老师:
2012年12月
浅谈固体物理学中的近似方法
学生姓名 指导教师:
系别: 专业: 班级: 学号:
摘要:本文从物理学的角度对近似法进行了介绍,并通过固体物理学中近似法的引
用,让大家对近似法有了一个初步的认识,并解释了近似法在物理教学中的重要性
与实用性。
关键词:近似法 固体物理 晶格
0引言
固体物理学是研究固体的性质、它的微观结构及其各种内部运动,以及这种微观
结构和内部运动同固体的宏观性质的关系的学科。固体的内部结构和运动形式很复
杂,固体物理学中近似方法是一种重要的计算方法.指以近似数为计算对象的数学
计算方法。近似地表示某一个量的真正值的数(准确数),称为近似数。在实际问题
中所遇到的数,多半是近似数,因此,近似计算方法是极其重要的。
1 近似法
“近似法”是指在分析、处理和研究某些物理现象和问题时,根据所研究问题的
需要,忽略研究对象和问题的次要因素,突出其主要矛盾和本质特征,科学、合理
地对所研究的问题进行近似处理的方法。近似法不仅是一种常用的解题方法和思维
方法,而且也是物理学的重要研究方法之一。善于对实际问题进行合理的近似处理,
是从事创造性研究的重要能力之一。因此在中学物理教学中注重近似方法的理解和
应用,主要应使学生理解学习近似计算的实际意义,正确地建立起近似数的概念;
同时使学生学会计算法则,进行合理的近似计算。固体物理中《周期场中的电子态》
的内容当中单电子近似,布洛赫波,近自由电子近似和紧束缚近似,能带,这些都
是在用“近似法”。比如近自由电子近似和紧束缚近似两种极端情形下的讨论中得出
了共同的结论,即晶体中电子的能极形成允带和禁带,但为了能和实际晶体的实验
结果相比较,使用尽可能符合晶体实际情况的周期势,求解具体Schredinger 方程
的尝试从没有停止过,最早的一个模型是1931年kronig 一penncy 一维方形势场
模型,它可以用简单的解析函数严格求解,也得出了周期场中运动的粒子允许能级
形成带,能带之间是禁带的结论,但这是一维周期势场,还不能算是真正的尝试。
不过近来却常使用keonig 一peuncy 势讨论超晶格的能带。
“近似法”是在观察物理现象、进行物理实验、建立物理模型、推导物理规律和
求解物理问题时,为了分析认识所研究问题的本质属性,往往突出实际问题的主要
方面,忽略某些次要因素,进行近似处理。在求解物理问题时,采用近似处理的手
段简化求解过程的方法。近似法是研究物理问题的基本思想方法之一,具有广泛的
应用。英国的约翰·牛顿1916 年提出广义相对论中一种被广泛应用求解爱因斯坦场
方程的近似方法。中国,智利,1966 年,用形式近似法研究初步阶稀释示踪剂对穿
过微血管的交换作用。牛顿近似试图模仿牛顿力学的形式来解决较弱引力场的相对
论问题。具体做法是对微小的牛顿力学量加以展开,可以选择展开的项有速度或者
牛顿引力势,这实则是对相对论一种弱场低速的近似。后来牛顿力学近似方法在引
力波天文学中得到了广泛的应用,最重要的用途是从理论上计算双星系统所辐射的
引力波的波形。
2 固体物理学中的近似方法
关于晶体结构问题中,一维晶格是晶体结构中最简单的形式,但对一维晶格的描
述却包含晶体结构的全部性质。从一维晶格的描述可用近似法得出三维晶格的结构
和性质。一维晶格原胞基矢1aa,其倒格子基矢可由以下公式求出
321
32
1
2aaaaab•
;
321
13
2
2aaaaab•
;
321
21
3
2aaaaab•
;
对于一维晶格,只有一个基矢1aa,在计算倒格矢时可以假想有2a,3a两单
位矢量与1a相互垂直,从而求出其倒格矢aaabb21,对于三维晶格计算方法
相同。
一维晶格和三维晶格一样,也存在简单格子和复式格子。简单格子中每个原子的
位置可表示为11al,复式格子中每个原子的位置可表示为11alr(r表示原胞内
各种等价原子之间的相对位移,i,,3,2,1。设有i种不等价原子)推广到三维
晶格,可以将三维简单格子中各原子的位置表示为332211alalal,复式格子中每
个原子的位置可表示为332211alalalr。
一维晶格具有最简单的晶体结构,具有最低的配位数(配位数2,链状结构),
依此类推配位数为3的为层状结构晶体,配位数4 、6 、8 、12 的为三维晶格。
关于晶格的振动,一维原子链是学习格波的典型例子,它的振动既简单又可解,
又能较全面地表现格波的基木特点。在固体物理中我们常常通过求解一维单原子链
和双原子链的动力学方程,得到其色散关系。对于一维单原子链,第n个原子的运
动方程为nnntnuuududm21122,其通解是一简谐振动wtqnainAeu,从
而得色散关系qamwcos122;对于一维双原子链,色散关系为
21222sin411aqmm
mMmMMm
w
一维单原子链和双原子链的色散关系采用同样的周期性边界条件lqNa2(
l
为整数),q的取值范围(aqa),l只能取(22NlN),一共有
N
个不同的取值。所以,由N个原胞组成的一维双原子链,q可以取N个不同的值,
每个q对应两个解(两支格波),共有N2个不同的格波,正好等于链的自由度,也
即链的全部振动模。
三维晶格振动是极其复杂的问题,难以得到晶格振动的近似解。但我们仍可以用
近似法从一维复式格子,得到三维晶格振动的形式解,进而得到晶格振动的普遍规
律。由一维再推广到三维的情况,可得出结论:对一定的波矢q,有n3个格波(n为
原胞内原子数,其中3个声学波,33n个光学波),格波总数=n3=原胞内自由
度数原胞数=晶体自由度总数。边界条件允许的波矢q在单位波矢空间内均匀分布
的波矢密度为32V,而在一维和二维情况下的波矢分布密度2L和22S。
3 结论
上述对“近似法”及固体物理学中近似法的应用进行了简要的说明与举例,从而
让作为师范生专业的我们对近似法有了一个初步的认识,并了解到物理教学中近似
法的实际应用。我们应在物理教学中解释好近似法的应用,让学生准确理解近似法
的基本概念、基本理论,这样教学过程形象生动,教学效果良好,同时为进一步的
研究打下了基础。近似法不仅是一种常用的解题方法和思维方法,而且也是物理学
的重要研究方法之一。因此在物理教学中注重近似方法的理解和应用,主要应使学
生理解学习近似计算的实际意义,正确地建立起近似数的概念;同时使学生学会计
算法则,进行合理的近似计算。在物理教学中有意识地加强科学方法教育,是培养
学生思维敏捷性和解决实际问题的能力,提高素质的一个有效途径。
参考文献:
[1]黄昆.固体物理学.北京:高等教育出版社,1988.
[2]王矜奉.固体物理教程.济南:山东大学出版杜,2001 .
[3]文尚胜.固体物理简明教程.广州:华南理工出版社,2007.
[4]高钦翔,田强.一维非线性双原子链晶格振动的色散关系[J].西南师范大学学
报,2001,26 ( 6 ) .
TALK ABOUT THE APPROXIMATE METHOD OF SOLID PHYSICS
Abstract:
This article from the point of view of the physics of approximate method are
introduced, and through the solid physics approximations of the reference, let everyone to
the approximate method have a preliminary understanding of, and explained the approximate
method in high school physics teaching in importance and practical.
Keywords:
approximation; Solid physics;lattice
(注:可编辑下载,若有不当之处,请指正,谢谢!)
