沪教版 九年级数学 暑假同步讲义 第14讲 锐角的三角比章节复习(解析版)
沪教版初中数学九年级第一学期 特殊锐角的三角比义 课件优秀课件资料
9. 因为我不能,所以一定要;因为一定要,所以一定能。 六、不忘初心,能得始终,永远不要放弃属于自己的梦想,但也不能纠结着坚持着错误的,失去淡然。
。只是现在遭遇青春时我们有些激动罢了。期待着想象中的花季盛开,经历青春的时候,我们哭着、笑着、灿烂着、张扬着、美丽着,也哀愁 着、体验着、感动着、慢慢长大着。
8、新路开始常是狭窄的,但它却是自己延伸拓宽的序曲。 6、昂着头出征,夹着尾巴回家,是庸驽而又好战的人的常态。 4、无才无以立足,不苦不能成才。 10. 太阳每天都是新的,你是否每天都在努力。 9、我们不要把眼睛生在头顶上,致使用了自己的脚踏坏了我们想得之于天上的东西。 3、对微小事物的仔细观察,就是事业、艺术、科学及生命各方面的成功秘诀。 9、如果不想做点事情,就甭想到达这个世界上的任何地方。 8、别想一下造出大海,必须先由小河川开始。
老师提示: Sin2300表示(sin300)2, cos2300表示(cos300)2,其余 类推.
11、生活呆以是甜的,也可以是苦的,但不能是没味的。你可以胜利,也可以失败,但你不能屈服。 5. 拼一载春秋,搏一生无悔。 15、出淤泥而不染,濯清涟而不妖。 3.如果你想成功,你必须每天都努力,虽然努力不一定成功,但放弃一定失败,离开舒适区,做那些常人难以想象的事情。 六、不忘初心,能得始终,永远不要放弃属于自己的梦想,但也不能纠结着坚持着错误的,失去淡然。
2
60° —√——3
2
cosα
—√——3
2
—√——2
2
—12
tanα
沪教版 九年级数学 锐角三角比的模考汇编复习

锐角三角比的模考汇编复习知识定位考情分析:锐角的三角比相关内容作为模拟考以及中考常见知识点之一,常出现在选择题、填空题以及解答题中,其本身知识点难度不高,因而考题较为简单。
本讲主要讲解锐角的三角比的意义、特殊锐角的三角比的值、各锐角的三角比的关系以及解直角三角形的三种应用,即分别是关于坡度坡角、仰角俯角和方向角问题。
相关重点是会根据直角三角形中两边的长求相应的锐角的三角比的值,熟练运用特殊的锐角的三角比的值进行相关计算,而难点是在几何图形和直角坐标系中灵活运用锐角的三角比进行解题,以及各锐角的三角比的关系在代数中的灵活运用。
考试占比:一般单纯考察锐角三角比的试题分值至少在14分左右,此外函数压轴题以及几何压轴题中还会涉及部分的解直角三角形的应用,因而这部分的内容显得格外重要,由于锐角三角比本身难度较小,因此同学们只要平时加强练习,都可以完全攻克这部分内容!!!童鞋,你做好学习本节课的准备了么?Are you ready?题型梳理例题精讲题型梳理1:锐角三角比的概念辨析 【题目】【2018徐汇区一模】在Rt △ABC 中,∠C=90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,下列等式中,正确的是( ) A .cb A =sin B .ac B =cos C .ba A =tan D .ab B =cot 【题目分析】本题考察了锐角三角函数的定义,在Rt △ABC 中,∠C=90°:(1)正弦:我们把锐角A 的对边a 与斜边c 的比叫做∠A 的正弦,记作sinA ; (2)余弦:锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦,记作cosA ; (3)正切:锐角A 的对边a 与邻边b 的比叫做∠A 的正切,记作tanA ; (4)三角函数:锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数; 因此先根据题意画出图形,再根据三角函数的定义解答即可,属于基础概念题。
【答案】C 【解析】解:根据三角函数的定义:A 、c a A =sin ,错误;B 、c aB =cos ,错误;C 、b a A =tan ,正确;D 、baB =cot ,错误故选:C 。
沪教版九年级上册数学25.1-25.2 锐角的三角比

25.1-25.2锐角三角比的意义及求值【学习目标】1、通过实验、观察、探究、交流、猜测等数学活动,探索锐角三角比的意义。
2、理解锐角三角比的意义,记住三角比的符号,会进行三角比的文字语言与符号语言的转化。
3、会求直角三角形中指定锐角的三角比。
4、应用锐角三角比的意义及运用特殊锐角三角比值进行计算。
【主要概念】【一】锐角的三角函数的意义【1】正切的概念在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比,叫做∠A的正切,记作tanA.【2】正弦和余弦的概念如图,在Rt△ABC中,∠C=90°,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即【3】三角函数的概念:在直角三角形中,锐角A 的正切(tanA)、正弦(sinA)、余弦(cosA),都叫做∠A 的三角函数.【二】同角的三角函数之间的关系 【1】平方关系:sin 2α+cos 2α=1【2】商数关系:【三】互余的两角的关系任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值,任意锐角的正切值与它的余角的正切值的积等于1.即若A+B=90°,则sinA=cosB ,cosA=sinB ,tanA·tanB=1.【四】特殊锐角的三角函数值0° 30°45°60°90° sinA1cosA 1tanA1—典型例题:例1、在Rt ⊿ABC 中,∠C=900,AC=3,BC=2,求tanA 和tanB 的值. 解:在Rt ⊿ABC 中,∵AC=3,BC=2∴tanA=32=AC BCtanB=23=BC AC .分析:(1)要求sinα与cosα的关系的值,而已知tanα的值,故可通过来求值.A B C(2)已知tanα的值,也可通过,把要求的式子的分子,分母同时除以cos 2α转化成关于tanα的关系,这样便可求出结论.点评:在进行三角函数有关计算时,常利用有关公式进行变换.例3、在Rt ⊿ABC 中,∠C=900,BC=4,AB=5,求cotA 和cotB 的值. 解:在Rt ⊿ABC 中,由勾股定理得 AB 2=AC 2+BC 2 ∵BC=4,AB=5, ∴AC=3452222=-=-BC AB .∴cotA=43=BC AC cotB=34=AC BC . 例4、在Rt △ABC 中,∠C=90°,若,求cosB ,tanB 的值.分析:本题主要考查锐角三角函数的定义,结合图形求解可化繁为简,迅速得解. 解:如图,设BC=3m ,则AB=5m ,AB C例5、如图所示,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是()分析:因为AB是⊙O的直径,所以∠ACB=90°.因为BC=6,AC=8,所以AB=10.因为∠ABD=∠ACD=∠ABC,所以在Rt△ACB中,故正确答案为D.答案:D例6、计算分析:这是一组有关特殊角三角函数值的计算题,计算中最关键是将它们先化成具体的数值,同时还要应用其它一些知识帮助求值,如(1)注意分母有理化,(2)应掌握整数指数幂的意义.解:点评:学过锐角三角函数后,特殊角的三角函数的计算是常考不衰的内容,做这类题主要分两步:(一)代入;(二)计算.因此,特殊角的三角函数值必须牢记.例7、若α为锐角且sinα>sinβ,那么()A.tanα>tanβB.tanα<tanβC.tanα=tanβ D.tanα、tanβ大小关系不确定例8、求适合下列各式的锐角α.点拨:所有锐角三角函数值都是正数,而且正弦和余弦值都不大于1,不符合条件的三角函数值应舍去.例9、如图,在△ABC中,∠A=30°,∠B=45°,AC=4,求BC的长.分析:题中有30°,45°特殊角,想把它们放到直角三角形中,利用三角函数来解题.点评:(1)在作高线构造直角三角形时,一般不过特殊角的顶点作垂线,这样便于利用特殊角解题.(2)有些简单的几何图形可分解为几个直角三角形的组合,从而利用三角函数的定义求解.例10、如图所示.在四边形ABCD中,AB=2,CD=1,∠A=60°,∠D=∠B=90°,求此四边形ABCD的面积.分析:由已知∠B=90°,∠A=60°这两个条件想到延长BC,AD,使它们相交,构成直角三角形.例11、在矩形ABCD中DE⊥AC于E,设∠ADE=α,且,AB=4,求AD.分析:在矩形中AB=DC=4,可证∠α=∠1,于是条件转移到△DCE中来了,求出DE.解:在矩形中AB=DC=4,∠2+∠α=90°又DE⊥AC,∠1+∠2=90°∴∠1=∠α点评:注意把条件集中到一起.例12 、如图Rt △ABC 中,∠C =90°,AC =3,BC =4.求:sin A ,cos A ,tanB ,cotB 的值。
第25章 锐角的三角比 九年级数学上册单元复习(沪教版)解析版

第25章锐角的三角比【真题训练】考试时间90分钟满分150分考生注意:1.本试卷含三个大题,共25题.一、选择题(每小题4分,共24分)1.(2020杨浦区一模)在Rt△ABC中,∠C=90°,若BC=3,AC=4,则sin B的值为()A. 45B. 35C. 34D. 43【答案】A【分析】根据三角函数的定义解决问题即可.【详解】解:如图,在Rt△ABC中,∵∠C=90°,BC=3,AC=4,∴AB5==,∴sinB=ACAB=45故选:A.【点睛】本题考查解直角三角形的应用,解题的关键是熟练掌握基本知识,属于中考常考题型.2.(2020崇明区一模)在Rt ABC ∆中,90C ∠=︒,如果 8AC =, 6BC =,那么B 的余切值为( )A.34B.43C.35D.45【答案】A【分析】根据余切函数的定义解答即可.【详解】如图,在Rt △ABC 中,∵∠C =90°,AC =8,BC =6,∴cotB =6384BC AC ==, 故选:A .【点睛】本题考查解直角三角形,解题的关键是熟练掌握基本知识,属于中考常考题型. 3.(虹口区)若cos α=,则锐角α的度数是( )A .30°B .45°C .60°D .90°【分析】根据cos α=,求出锐角α的度数即可.【解答】解:∵cos α=,∴α=60°. 故选:C .4.(松江区)在以O 为坐标原点的直角坐标平面内,有一点A (3,4),射线OA 与x 轴正半轴的夹角为α,那么cosα的值为A. 35B.43C.45D.34【答案】A【分析】利用锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解.【详解】解:∵在以O为坐标原点的直角坐标平面内有一点A(3,4)∴5OA==,∴35 cosα=故选:A.【点睛】本题考查了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理的知识.5.(松江区)如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角α,它们重叠部分(阴影部分)的面积是1.5,那么sinα的值为()A.34B.12C.23D.32【答案】C【分析】重叠部分为菱形,运用三角函数定义先求边长AE ,再根据面积求出sin α. 【详解】解:如图示:作BC CD ⊥交CD 于C 点,AD CD ⊥交CD 于D 点,由阴影部分是两条宽度都为1的纸条,交叉重叠放在一起可知,阴影部分是一个菱形, 则有AB AE =,1AD =, ∴1sin AB AE α==∴1=1 1.5sin S AB AD α=⨯=阴影 解之得:2sin 3α=, 故选:C【点睛】本题考查了菱形的判定与性质,三角函数的应用,判断出阴影部分是一个菱形是解题的关键.6.(徐汇区)跳伞运动员小李在200米的空中测得地面上的着落点A 的俯角为60°,那么此时小李离着落点A的距离是()A. 200米B. 400米C. 米D.【答案】D【分析】已知直角三角形的一个锐角和直角边求斜边,运用三角函数定义解答.【详解】根据题意,此时小李离着落点A的距离是200=sin30︒故选:D.【点睛】本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助俯角构造直角三角形并解直角三角形.二、填空题(每小题4分,共48分)7.(黄浦区)在△ABC中,AB=AC=5,BC=8,如果点G为重心,那么∠GCB的余切值为_____.【答案】4;【分析】根据等腰三角形的中线、角平分线和垂线三线合一,利用勾股定理求出AD的长,再利用重心的性质即可求出GA的长,进而得出DG的长,利用勾股定理和三角函数解答即可.【详解】设AG交BC于D∵AB=AC=5,BC=8,点G为重心,∴AD⊥BC,BD=CD=12BC=12×8=4,∴AD2=AC2−CD2,AD=3,∴GA=2,∴DG=1,∴BG∴∠CBG的余切值=BDDG=4,故答案为4.【点睛】本题考查的是三角形的重心,熟练掌握三角形的重心是解题的关键.8.(黄浦区)如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=45,那么GE=_______.【分析】过点E作EF⊥BC交BC于点F,分别求得AD=3,BD=CD=4,EF=32,DF=2,BF=6,再结合△BGD∽△BEF即可.【详解】过点E作EF⊥BC交BC于点F.∵AB=AC,AD为BC的中线∴AD⊥BC ∴EF为△ADC的中位线.又∵cos∠C=45,AB=AC=5,∴AD=3,BD=CD=4,EF=32,DF=2 ∴BF=6∴在Rt △BEF 中2, 又∵△BGD ∽△BEF∴BG BD=BE BF,即GE=BE-BG=2. 【点睛】本题考查的知识点是三角形的相似,解题的关键是熟练的掌握三角形的相似. 9.(杨浦区)如图,在菱形ABCD 中,O 、E 分别是AC 、AD 的中点,联结OE .如果AB =3,AC =4,那么cot ∠AOE =______.; 【分析】根据O 、E 分别是AC 、AD 的中点,知OE 是中位线得AOE ACD ∠=∠,连接BD ,根据菱形的性质知AC 与BD 垂直平分,在Rt OCD △中,根据勾股定理可求得OD ,继而求得答案.【详解】如图,连接BD ,在菱形ABCD 中,O 是AC 的中点,∴O 也是对角线的交点,且AC 与BD 垂直平分, ∵O 、E 分别是AC 、AD 的中点, ∴OE CD , ∴AOE ACD ∠=∠ 在Rt OCD ∆中,114222OC AC ==⨯=,3CD AB ==,∴OD =∴cot ∠AOE = cot5OC ACD OD ∠===【点睛】本题考查了求角的正切余切函数,涉及的知识有:菱形的性质,中位线的性质以及勾股定理,利用中位线的性质证得AOE ACD ∠=∠是解题的关键.10.(杨浦区)如图,在四边形ABCD 中,∠B=∠D=90°,AB =3, BC =2,tanA =43,则CD =_____.【答案】6 5【分析】延长AD和BC交于点E,在直角△ABE中利用三角函数求得BE的长,则EC的长即可求得,然后在直角△CDE中利用三角函数的定义求解.【详解】如图,延长AD、BC相交于点E,∵∠B=90°,∴4 tan3BEAAB==,∴BE=44 3AB⋅=,∴CE=BE-BC=2,5=,∴3 sin5ABEAE==,又∵∠CDE=∠CDA=90°,∴在Rt△CDE中,sinCDECE =,∴CD=36sin255 CE E⋅=⨯=.11.(宝山区)如图,△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE .若BE =9,BC =12,则cosC = .【分析】根据线段垂直平分线的性质,可得出CE =BE ,再根据等腰三角形的性质可得出CD =BD ,从而得出CD :CE ,即为cosC . 【解答】解:∵DE 是BC 的垂直平分线, ∴CE =BE , ∴CD =BD , ∵BE =9,BC =12, ∴CD =6,CE =9, ∴cosC ===,故答案为.12.(奉贤区)已知ABC ∆中,90C =∠,3cos 4A =,6AC =,那么AB 的长是________. 【答案】8【分析】根据锐角三角函数的定义,即可求解. 【详解】∵ABC ∆中,90C =∠,3cos 4A =,6AC =,∴AB=683cos4ACA==,故答案是:8.【点睛】本题主要考查三角函数的定义,牢记余弦三角函数的定义,是解题的关键. 13.(虹口区)如图,点A(2,m)在第一象限,OA与x轴所夹的锐角为α,如果tanα=.那么m=.【分析】如图,作AE⊥x轴于E.根据正切函数的定义构建关系式即可解决问题.【解答】解:如图,作AE⊥x轴于E.∵A(2,m),∴OE=2,AE=m,∵tanα==,∴=,∴m=3,故答案为3.14.(虹口区)如图,在Rt△ABC中,∠C=90°,AC=1,BC=2,点D为边AB上一动点,正方形DEFG的顶点E、F都在边BC上,联结BG,tan∠DGB=.【分析】设DE与BG交于点O,根据题意可得△BDE∽△ABC,可得,由正方形的性质可得GF=DE=EF,进而得出,再证明△DOG∽△EOB∽△FGB,可得.【解答】解:如图,DE与BG交于点O,∵正方形DEFG,∴∠DEB=∠EDG=∠GFB=90°,GF=DE=EF,∴△BDE∽△ABC,∴,∴,∵∠DOG=∠EOB,∴△DOG∽△EOB∽△FGB,∴,∴tan∠DGB=.故答案为:15.(嘉定区)如图,有一个斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1:2.5,那么该斜坡的水平距离AC的长____m【答案】75【分析】根据坡度的定义解题即可.【详解】坡度tanA=i=BCAC =301:2.5AC,解得AC=75故答案为75【点睛】本题主要考查坡度的概念,掌握坡度的概念是解题的关键.16(静安区)如图,在大楼AB的楼顶B处测得另一栋楼CD底部C的俯角为60度,已知A、C两点间的距离为15米,那么大楼AB的高度为_____米.(结果保留根号)【答案】【分析】由解直角三角形,得tan ABACBAC∠=,即可求出AB的值.【详解】解:根据题意,△ABC是直角三角形,∠A=90°,∴tanAB ACBAC∠=,∴tan15tan60AB AC ACB=•∠=⨯︒=∴大楼AB的高度为米.故答案为:【点睛】此题考查了解直角三角形的应用——仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.17(静安区)矩形的一条对角线长为26,这条对角线与矩形一边夹角的正弦值为513,那么该矩形的面积为___.【分析】由矩形的性质和三角函数求出AB,由勾股定理求出AD,即可得出矩形的面积.【详解】解:如图所示:∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD=26,∵5 sin13ABADBBD∠==,∴5261013AB=⨯=,∴24AD==,∴该矩形的面积为:2410240⨯=;故答案为:240.【点睛】本题考查了矩形的性质、勾股定理、三角函数;熟练掌握矩形的性质,由勾股定理求出AB和AD是解决问题的关键.18.(闵行区)已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在BC的延长线上的点E处,那么tan BAE∠=______.【分析】根据旋转不变性,BD=BE .根据三角函数的定义可得tan ∠BAE 的值.【详解】由题意,得BD=BE=tan 2BE BAE BA ===∠.【点睛】本题主要突破两点:一是三角函数的定义;二是旋转图形的性质. 三、解答题:(本大题共7题,满分78分)19.(杨浦区)计算:13tan 3045cos60︒︒︒-【答案】1. 【分析】将特殊角的三角函数值代入,根据实数的运算法则求值即可. 【详解】原式=131322⨯-1=1.【点睛】本题考查了特殊角的三角函数值以及实数的混合运算,熟记特殊角的三角函数值、熟练掌握实数的运算法则是解题的关键.20.(静安区)先化简,再求值:2222244x y x yx y x xy y--÷+++,其中x=sin45°,y=cos60°.【分析】利用分式乘法和除法进行化简,再把x、y的值代入计算,即可得到答案. 【详解】解:原式=2(2)2()()x y x yx y x y x y-+⋅++-=2x yx y++.当x=sin45°=2,y=cos60°=12时,12+⨯=【点睛】本题考查了特殊角的三角函数值,分式的化简求值,以及分式的混合运算,解题的关键是正确的进行化简,掌握特殊角的三角函数值. 的21.(静安区)如图,在Rt△ABC中,∠ACB=90°,AC=20,3sin5A=,CD⊥AB,垂足为D.(1)求BD的长;(2)设AC a=,BC b=,用a、b表示AD.【答案】(1)9;(2)1616 2525a b-【分析】(1)根据解直角三角形,先求出CD的长度,然后求出AD,由等角的三角函数值相等,有tan∠DCB=tan∠A,即可求出BD的长度;(2)由(1)可求AB的长度,根据三角形法则,求出AB,然后求出AD.【详解】解:(1)∵CD⊥AB,∴∠ADC=∠BDC=90°,在Rt△ACD中,sin CDAAC=,∴3sin20125CD AC A=⋅=⨯=.∴16 AD==,∴3 tan4CDAAD==.∵∠ACB=90°,∴∠DCB+∠B =∠A+∠B=90°,∴∠DCB=∠A.∴3tan tan1294BD CD DCB CD A=⋅∠=⋅=⨯=;(2)∵16925AB AD DB=+=+=,∴1625 ADAB=,又∵AB AC BC a b=+=-,∴161616252525AD AB a b==-.【点睛】本题考查了解直角三角形,向量的运算,勾股定理,解题的关键是熟练掌握解直角三角形求三角形的各边长度.22.(黄浦区)如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°(1)求道路AB段的长(结果精确到1米)(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002【整体分析】(1)根据锐角三角函数的定义即可求出答案.(2)求出汽车的实际车速即可判断.【满分解答】解:(1)在Rt△ACD中,AC=CD•tan∠ADC=400×2=800,在Rt△ABC中,AB=ACsin ABC=8000.5736≈1395(米);(2)车速为:139590≈15.5m/s=55.8km/h<60km/h,∴该汽车没有超速.【点睛】本题考查解直角三角形的应用,解题的关键是熟练运用锐角三角函数的定义,本题属于中等题型.23.(杨浦区、崇明)如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm 的连杆BC、CD与AB始终在同一平面上.(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?【整体分析】(1)作BO⊥DE于O,根据矩形的判定,可得四边形ABOE是矩形,先求出∠DBO,然后根据锐角三角函数即可求出OD,从而求出DE;(2)过C作CG⊥BH,CK⊥DE,根据锐角三角函数,即可求出CG,从而求出KH,再求出∠DCK,利用锐角三角函数即可求出DK,从而求出此时连杆端点D离桌面l的高度,即可求出结论.【满分解答】解:(1)如图2中,作BO⊥DE于O.∵∠OEA=∠BOE=∠BAE=90°,∴四边形ABOE 是矩形,∴∠OBA =90°,∴∠DBO =150°﹣90°=60°,∴OD =BD •sin60°=cm ),∴DE =OD +OE =OD +AB =(+5)cm ;(2)过C 作CG ⊥BH ,CK ⊥DE ,由题意得,BC =CD =20m ,CG =KH ,∴在Rt △CGB 中,sin ∠CBH =202CG CG BC ==,∴CG =,∴KH =,∵∠BCG =90°﹣60°=30°,∴∠DCK =150°﹣90°﹣30°=30°,在Rt △DCK 中,sin ∠DCK =DK DC =DK 20=12, ∴DK =10cm ,∴此时连杆端点D 离桌面l 的高度为10++5=(cm∴比原来降低了(+5)﹣()=10,答:比原来降低了(10)厘米.【点睛】此题考查的是解直角三角形的应用,掌握构造直角三角形的方法和用锐角三角函数解直角三角形是解决此题的关键.24.(杨浦,青浦)水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)【整体分析】根据正切的概念表示出BD、BC,根据题意列出方程,解方程即可.【满分解答】由题意,得∠ABD =90°,∠D =20°,∠ACB =31°,CD =13.在Rt △ABD 中, ∵tan ∠=AB D BD, ∴tan 200.36==︒AB AB BD . 在Rt △ABC 中, ∵tan ∠=AB ACB BC, ∴tan 310.6==︒AB AB BC . ∵CD =BD -BC , ∴130.360.6=-AB AB . 解得11.7≈AB 米.答:水城门AB 的高约为11.7米.【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的概念是解题的关键.25.(长宁、金山区)图1是一台实物投影仪,图2是它的示意图,折线O ﹣A ﹣B ﹣C 表示支架,支架的一部分O ﹣A ﹣B 是固定的,另一部分BC 是可旋转的,线段CD 表示投影探头,OM 表示水平桌面,AO ⊥OM ,垂足为点O ,且AO =7cm ,∠BAO =160°,BC ∥OM ,CD =8cm .将图2中的BC 绕点B 向下旋转45°,使得BCD 落在BC ′D ′的位置(如图3所示),此时C ′D ′⊥OM ,AD ′∥OM ,AD ′=16cm ,求点B 到水平桌面OM 的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm )【整体分析】过B 作BG ⊥OM 于G ,过C ′作C ′H ⊥BG 于H ,延长D ′A 交BG 于E ,则C ′H =D ′E ,HE =C ′D ′=8,设AE =x ,解直角三角形即可得到结论.满分解答】解:过B 作BG ⊥OM 于G , 过C ′作C ′H ⊥BG 于H ,延长D ′A 交BG 于E ,则C ′H =D ′E ,HE =C ′D ′=8,设AE =x ,∴C ′H =D ′E =16+x ,∵∠BC ′H =45°,∴BH =C ′H =16+x ,∴BE =16+x +8=24+x ,∵∠BAO =160°,∴∠BAE =70°,【∴tan70°=2410.36 BE xAE x+==,解得:x=13.5,∴BE=37.5,∴BG=BE+EG=BE+AO=37.5+7=44.5cm,答:B到水平桌面OM的距离为44.5cm.【点睛】此题主要考查了解直角三角形的应用,充分体现了数学与实际生活的密切联系,解题的关键是构造直角三角形.。
沪教版(上海)九年级上册数学 25.1 锐角三角比的意义 课件
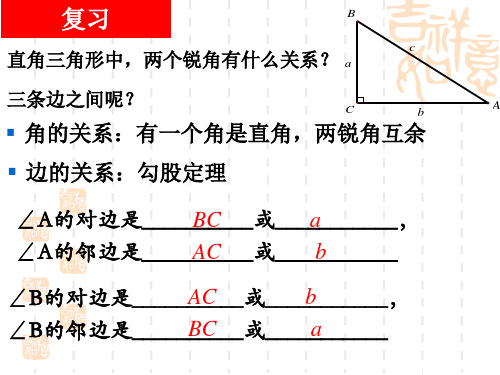
在直角三角形中,一个锐角的正切、余切的值(D
(A)与这个三角形的面积 大小有关 (B)与这个角的对边、邻 边的大小有关 (C)只与这个三角形的斜 边大小有关 (D)只与这个角的大小有 关
一个确定的值
探索与思考
问题2:当直角三角形中一个锐角的大小变化时, 这个锐角的对边与邻边的长度的比值随着变化吗?
结论2:直角三角形中,一个锐角的对边与邻 边的长度的比值随着这个锐角的大小的变化而 变化。
可角以结的论得对1边:到与如:邻果在边给的定R长直t△度角A的三B比角C值形中就的(是一一∠个个锐C确角=定,90的那°数么)。这,个锐当锐 角A的大小确定后,不论Rt△ABC的边长怎样变 化,度结∠的论比A2值:的随直对着角边这三个角BC锐形与角中的,邻大一边小个A的锐C变角的化的比而对变边值化与总。邻是边的确长定的。
C
A
tan B
AC BC
3 4
在RtABC中, C 90,如果将这个三角形的
各边扩大2倍后得到ABC,那么tan A与tan A的
关系是( C )
(A)tan A 2 tan A
(B)tan A 2 tan A
(C)tan A tan A
(D)大小不能确定
当直角三角形的一个锐角的大小确定时,这个 锐角的对边与邻边的比值也是确定的。
我们把直角三角形中一个锐角的对边与邻边的比 叫做这个锐角的正切。(tangent)
如图,锐角A的正锐角A的邻边
BC AC
a b
例题解析
例题1 : 在ABC中,C 90,AC 3, BC 2,求(1)tan A和 tan B的值。
解:在RtABC中,
AC 3,BC 2,
AC AB 2 BC 2 cot A AC 3
沪教版九年级上册数学-25.1-25.2-锐角的三角比的意义-求锐角的三角比的值-教学案

沪教版(上海)九年级上册数学-25.1-25.2-锐角的三角比的意义-求锐角的三角比的值-教学案(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--锐角的三角比的意义 求锐角的三角比的值 教案【学习目标】1.结合图形理解记忆锐角三角函数的定义;2.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值; 3.理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C =90°,∠A 所对的边BC 记为a ,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b ,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c ,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cos A bA c ∠==的邻边斜边;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tan A aA A b∠==∠的对边的邻边;锐角A 的邻边与对边的比叫做∠A 的余切,记作cotA ,即cot A bA A a∠==∠的邻边的对边.同理sin B b B c ∠==的对边斜边;cos B aB c∠==的邻边斜边;tan B b B B a ∠==∠的对边的邻边; cot B a B B b∠==∠的邻边的对边要点诠释:(1)正弦、余弦、正切、余切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA ,cosA ,tanA ,cotA 分别是一个完整的数学符号,是一个整体,不能写成,,,cot A •不能理解成sin 与∠A ,cos 与∠A ,tan 与∠A ,cot 与∠A 的乘积.书写时习惯B Ca b c上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、、2cot A()常写成、、、2cot A.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°间变化时,,,tanA>0 cotA>0.要点二、特殊角的三角函数值利用三角函数的定义,可求出30°、45°、60°角的各三角函数值,归纳如下:锐角cotα30°45°1160°要点诠释:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦、余切值随锐角度数的增大(或减小)而减小(或增大).要点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;tanA=cot(90°-∠A)=cotB , tanB=cot(90°-∠B)=cotA.(2)平方关系:;(3)倒数关系:或;(4)商的关系:sin cos tan,cotcos sinA AA AA A==要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【典型例题】类型一、锐角三角函数值的求解策略例题1.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2 B .C .D .【答案】D.【解析】解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.举一反三:【变式】在Rt△ABC中,∠C=90°,若a=3,b=4,则c=,sinA=,cosA=,sinB=,cosB=.【答案】c= 5 ,sinA=35,cosA=45,sinB=45,cosB=35.Cabc类型二、特殊角的三角函数值的计算例题2.求下列各式的值:(1)6tan230°﹣sin60°﹣2sin45°;(2)sin60°﹣4cos230°+sin45°?tan60°;(3)+cot30°﹣.【答案与解析】解:(1)原式==﹣.(2) 原式=×﹣4×()2+×=﹣3+=;(3) 原式=+﹣=2+﹣=3﹣2+2=+2.举一反三:【变式】在Rt△ABC中,∠C=90°,若∠A=45°,则∠B=,sinA=,cosA=,sinB=,cosB=.【答案】∠B=45°,sinA=2,cosA=2,sinB=2,cosB=2.类型三、锐角三角函数之间的关系例题3.已知△ABC 中的∠A 与∠B 满足(1﹣tanA )2+|sinB ﹣|=0(1)试判断△ABC 的形状. (2)求(1+sinA )2﹣2﹣(3+tanC )0的值.【答案与解析】解:(1)∵|1﹣tanA )2+|sinB ﹣|=0,∴tanA=1,sinB=,∴∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°, ∴△ABC 是锐角三角形;(2)∵∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°,∴原式=(1+)2﹣2﹣1=.类型四、锐角三角函数的拓展探究与应用例题4.如图所示,AB 是⊙O 的直径,且AB =10,CD 是⊙O 的弦,AD 与BC 相交于点P ,若弦CD =6,试求cos ∠APC 的值.【答案与解析】连结AC ,∵ AB 是⊙O 的直径, ∴ ∠ACP =90°,又∵ ∠B =∠D ,∠PAB =∠PCD , ∴ △PCD ∽△PAB ,∴ PC CDPA AB=. 又∵ CD =6,AB =10, ∴在Rt △PAC 中,63cos 105PC CD APC PA AB ∠====.例题5.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图1①,在△ABC 中,AB =AC ,顶角A 的正对记作sadA ,这时sadA BCAB==底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=________.(2)对于0<A <180°,∠A 的正对值sadA 的取值范围是_______.(3)如图1②,已知sinA =35,其中∠A 为锐角,试求sadA 的值.【答案与解析】(1)1;(2)0<sadA <2;(3)如图2所示,延长AC 到D ,使AD =AB ,连接BD .设AD =AB =5a ,由3sin 5BC A AB ==得BC =3a , ∴ 22(5)(3)4AC a a a =-=,∴ CD =5a-4a =a ,22(3)10BD a a a =+=, ∴ 10sadA BD AD ==. 【总结】(1)将60°角放在等腰三角形中,底边和腰相等,故sadA =1;(2)在图①中设想AB =AC 的长固定,并固定AB 让AC 绕点A 旋转,当∠A 接近0°时,BC 接近0,则sadA 接近0但永远不会等于0,故sadA >0,当∠A 接近180°时,BC 接近2AB ,则sadA 接近2但小于2,故sadA <2;(3)将∠A 放到等腰三角形中,如图2所示,根据定义可求解.。
初三第一轮复习-锐角三角比(沪教版)
30
10、已知传送带与水平面所成斜坡的坡度i=1:2,它把物体
5 5 送到离地面5米高的地方,物体所经过的路程为______米.
2013年中考
某地下车库出口处“两段式栏杆”如图1所示,点A是栏杆转动的支点, 点E是栏杆两段的连接点.当车辆经过时,栏杆 AEF升起后的位置 如图2,其中AB⊥BC,EF∥BC,∠EAB=143°,AB=AE=1.2米, 求当车辆经过时栏杆EF段距离地面的高度(即直线EF上任意一点到直线BC的距离).
13 25
6.在Rt△ABC中, ∠C=90°,BC=2AC,那么∠ A的正弦值是____
5
仰角与俯角
从下向上看,视线与水平线的 夹角叫做仰角 从上往下看,视线与水平线的 夹角叫做俯角
视线
铅Hale Waihona Puke 垂仰角线俯角
水平线
视线
7、水平地面上,由点A测得旗杆BC顶点C的仰角为60°,
点A到旗杆的距离AB=12米,则旗杆的高度为( )
②两锐角之间的关系: ∠ A+ ∠ B= 90º
③边角之间的关系:
tanA=
a b
sinA= a
c
cotA=
b a
cosA=
b c
2.解直角三角形所需条件
①一个锐角和一条边
②两条边
4.在Rt△ABC中, ∠C=90°,BC=3,COSB= ,
1
18 那么AB=_____
6 5
5.等腰△ABC中,AB=AC=13,BC=10,那么COS ∠ B=____
结果精确到0.1米,栏杆宽度忽略不计, 参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角的三角比是九年级数学上学期第二章的内容.本章的基本要求是理解锐角三角比的概念,会求特殊锐角的三角比的值,会解直角三角形,需理解仰角、俯角、方向角、坡度和坡角等概念,并能解决有关的实际问题.重点是应用锐角三角比的意义及运用解直角三角形的方法进行有关的几何计算.难点是解直角三角形的应用.已知锐角,求三角比已知锐角的三角比,求锐角锐角的三角比的概念已知一边和一个锐角已知两边直角三角形中 的边角关系解 直 角 三 角 形解直角三角形 的应用单元练习:锐角的三角比内容分析知识结构步同级年九2 / 17【练习1】 已知Rt ABC ∆中,90C ∠=︒,那么ba是A ∠的( ) A .正弦B .余弦C .正切D .余切【答案】D 【解析】=邻边余切对边. 【总结】考查锐角三角比的定义.【练习2】 将锐角α所在的三角的三边同时扩大三倍,这时角α的正弦值( )A .变大B .变小C .不变D .不确定【答案】B【解析】考查锐角三角比的定义.【练习3】 已知Rt ABC ∆中,90C ∠=︒,AC = 2,BC = 3,那么下列各式中正确的是( ) A .2sin 3B = B .2cos 3B =C .2tan 3B = D .2cot 3B =【答案】C【解析】考查锐角三角比的定义.【练习4】 已知Rt ABC ∆中,90C ∠=︒,AB = c ,AC = b ,BC = a ,则下列关系不成立的是( ) A .cos b c A = B .tan a b B = C .cos ac B =D .tan tan 1A B =【答案】B【解析】考查锐角三角比的定义及相关变形.【练习5】 计算2sin 60° + 3tan30°的值为( )A .3B .23C .33D .43【答案】B选择题【解析】2sin 60° + 3tan30°3233333232=+=⨯+⨯=. 【总结】考查特殊角的锐角三角比值及代数式求值.【练习6】 下列不等式成立的是( )A .sin60sin45sin30︒<︒<︒B .cos60cos45cos30︒>︒>︒C .tan60tan45tan30︒<︒<︒D .cot60cot 45cot30︒<︒<︒【答案】D【解析】通过计算特殊角的锐角三角比的值,可以判断D 正确.【总结】当锐角的度数逐渐增大时,正切值和正弦值也逐渐增大,而余切值和余弦值反而逐渐减小.【练习7】 在Rt ABC ∆中,90C ∠=︒,下列条件中不能解直角三角形的是( )A .已知c 和aB .已知b 和A ∠C .已知a 和bD .已知A ∠和B ∠ 【答案】D【解析】考查解直角三角形的条件.【总结】要解直角三角形,必须至少知道一条边.【练习8】 已知AD 是Rt ABC ∆的斜边BC 边上的高,BC = a ,B β∠=,那么AD 等于( ) A .2sin a βB .2cos a βC .sin cos a ββD .sin tan a ββ【答案】C【解析】解:在ABC Rt △中,BCAB=βcos ,∴βcos a AB =.在ABDRt△中,ABAD=βsin∴βββsincossin aABAD==.【总结】本题主要考查利用锐角三角比解直角三角形.【练习9】如果等腰三角形的底角为30°,腰长为6厘米,则这个三角形的面积为()A.4.5平方厘米B.C.平方厘米D.36平方厘米【答案】B【解析】解:根据题意解直角三角形可得:等腰三角形的高为3,底边长为36,则三角形的面积为3933621=⨯⨯.【总结】本题主要考查30°角的锐角三角比的值.【练习10】如图,设点A(m,n)是锐角α的一条边上的任意一点,则mn的值()A.只与角α的大小有关B.只与点A在角α的边上的位置有关C.与角α的大小及点A在角α的边上的位置有关D.与角α的大小及点A在角α的边上的位置无关【答案】A【解析】=cotmnα,所以只与角α的大小有关.【总结】本题主要考查锐角三角比的概念及相关性质.【练习11】等腰三角形的两条边分别为5和6,关于底角A下列等式中成立的是()A.3sin5A=B.3cos5A=C.3sin5A=或512D.3cos5A=或512【答案】D【解析】①等腰三角形的两腰为5,底为6时,3cos5A=;②等腰三角形的两腰为6,底为5时,5cos12A=.【总结】本题主要考查锐角三角比的概念,注意要分类讨论.【练习12】 如图,CD 是平面镜,光线从点A 出发经CD 上点E 反射后照射到点B ,若入射角为α,AC ⊥CD ,BD ⊥CD ,垂足分别为C 、D ,且AC = 3,BD = 6,CD = 11,则tan α的值为( )A .113B .311C .911D .11【答案】D【解析】解:由光线反射定律可知:BED AEC ∠=∠.则BED AEC ∠=∠tan tan . ∴DE BDCE AC =. ∴CE CE -=1163,解得:311=CE . ∴9113311tan tan ====AC CE A α.【总结】本题主要是跟物理知识相结合,注意反射角等于入射角的运用.【练习13】 菱形的边长为4,有一个内角为40°,则较短的对角线是( )A .4sin40︒B .4sin20︒C .8sin20︒D .8cos20︒【答案】C【解析】考查菱形对角线平分一组内角和解直角三角形基础知识.【练习14】 如图,在ABC ∆中,30A ∠=︒,E 为AC 上一点,且AE : EC = 3 : 1,EF ⊥AB步同级年九6 / 17于点F ,连接FC ,则cot CFB ∠的值为( )A 136B 132C 433D 134【答案】D【解析】过C 作CG ⊥AB .∵EF ⊥AB ,CG ⊥AB ,∴EF ∥CG ∴43===AG AF GC EF AC AE . 设a FE 3=,则a CG 4=. 在AEF Rt △中,AF EF A =tan ,∴AFa333=,∴a AF 33=. ∵43=AG AF ,∴a GF 3= ∴在GFC Rt △中,4343cot ===∠a a CG FG CFB . 【总结】本题主要考查通过添加辅助线将所要求的锐角放到直角三角形中求解.【练习15】 在ABC ∆中,AD 是BC 边上的高,且3AD BD ==CD = 1,那么BAC ∠的大小可能是( ) A .15° B .75° C .15°,75° D .105°【答案】C【解析】解:在ABD Rt △中,133tan ===∠AD BD BAD ,∴︒=∠45BAD . 在ACD Rt △中,3331tan ===∠AD CD CAD ,∴︒=∠30CAD . ∴①︒=︒+︒=∠+∠=∠753045DAC BAD BAC ; ②︒=︒-︒=∠-∠=∠153045DAC BAD BAC .ABCDE【总结】本题主要考查解直角三角形,注意分类讨论.【练习16】 如图,沿AC 方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC 上一点B ,取145ABD ∠=︒,BD = 500米,55D ∠=︒,要使A 、C 、E 成一直线,那么开挖点E 离点D 的距离是( )米 A .500sin55︒ B .500cos55︒C .500tan55︒D .500cot55︒【答案】B【解析】解:∵145ABD ∠=︒,∴︒=∠35CBD .∵55D ∠=︒,∴︒=∠90E .在BED Rt △中,BD EDD =cos ,∴︒=55cos 500ED .【总结】本题主要考查解直角三角形的运用,注意分析题目中的条件.【练习17】 如图,四边形ABCD 中,=135A ∠︒,90B D ∠=∠=︒,23BC =,AD = 2,则四边形ABCD 的面积是( ) A .42B .3C .4D .6【答案】C【解析】延长CD 和BA 交于点E .∵=135A ∠︒,90B D ∠=∠=︒,∴45C EAD ∠=∠=.∴()4221322121212222=⨯-⨯=-=AD BC S ABCD 四边形.【总结】本题主要考查通过解直角三角形求几何图形的面积.步同级年九8 / 17ABCD A BC【练习18】 如图,在梯形ABCD 中,AD // BC ,AC ⊥AB ,AD = CD ,4cos 5DCA ∠=, BC = 10,则AB 的值是( ) A .3B .6C .8D .9【答案】B【解析】解:∵AD = CD ,∴DCA DAC ∠=∠.∵AD // BC ,∴ACB DAC ∠=∠, ∴ACB DCA ∠=∠. ∴BCA DCA ∠=∠cos cos 在ABC Rt △中,BCACACB =∠cos , ∴1054AC =,解得:8=AC . ∴68102222=-=-=AC BC AB .【总结】当两个锐角相等时,它们的相应的锐角三角比的值也相等.【练习19】 如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB = 1.8米,要在窗子外面上方安装水平当光板AC ,使午间光线不能直接射入室内,则挡光板的宽度AC 为( ) A .1.8sin80︒B .1.8cos80︒C . 1.8sin80︒D .以上都不对【答案】D【解析】正确答案为︒80cot 8.1.【总结】本题主要考查锐角三角比的准确运用.填空题【练习20】 在Rt ABC ∆中,90C ∠=︒,a =c = 3,则sin A = ______.【答案】32.【解析】sin a A c ==. 【总结】考查锐角三角比的定义.【练习21】 ABC ∆三边长分别为7,24,25,那么这个三角形最小角的余切值为______. 【答案】724.【解析】根据勾股定理逆定理可知,ABC ∆是直角三角形,则最小角为7所对的角,则 此角的余切值为724.【总结】考查锐角余切的概念及勾股定理逆定理的运用.【练习22】 ABC ∆中,90C ∠=︒,817a c =,那么tan A = ______. 【答案】158. 【解析】设k a 8=,k c 17=. 由勾股定理可知:k a c b 1522=-=∴158158tan ===k k b a A . 【总结】本题主要考查锐角的正切的概念.【练习23】 ABC ∆中,90C ∠=︒,1cos 2A =,则22tan +cotB B = ______. 【答案】310. 【解析】∵1cos 2A =,∴︒=∠60A ,∴︒=︒-︒=∠306090B .∴()310333cot tan 2222=+⎪⎪⎭⎫⎝⎛=+B B . 【总结】本题主要考查特殊角的锐角三角比的值.【练习24】 ABC ∆中,90C ∠=︒,AC = 6,如果ABC S ∆=那么A ∠的度数是______. 【答案】60°. 【解析】解:∵31821=⋅⋅=BC AC S ABC △,6=AC ,∴36=BC .∴3636tan ===AC BC A , ∴︒=∠60A .【总结】本题主要考查特殊角的锐角三角比的值.【练习25】 在Rt ABC ∆中,A ∠是锐角,则sin A -= ______.【答案】1.【解析】解:原式=1sin 1sin =-+A A . 【总结】本题主要考查锐角的正弦的取值范围.【练习26】 若()tan 20x +︒=,则x = ______. 【答案】10°.【解析】︒=︒+3020x ,∴︒=10x .【总结】本题主要考查特殊角的锐角三角比的值.【练习27】菱形的两条对角线长为和6,则菱形较小的内角为______. 【答案】60°.【解析】∵菱形的对角线互相垂直且每条对角线平分一组内角, ∴最小内角一半的正切值是33, ∴最小内角一半为30°,∴最小内角为60°.【总结】本题主要考查特殊角的锐角三角比的值以及菱形的性质.【练习28】 如果24cos 8cos 30αα-+=,那么锐角α= ______. 【答案】60°.【解析】解方程可得:23cos =α或21cos =α,∵1cos 0<<α,∴21cos =α,∴︒=60α.【总结】本题主要考查特殊角的锐角三角比的值.【练习29】 校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞______米.【答案】13.【解析】如图,AB =8,CD =13,BD =12.过A 作AE ⊥DC , 则四边形ABDE 为矩形. ∴AB =DE =8,BD =AE =12,∴135122222=+=+=CE AE AC .【总结】本题主要考查根据题目中的已知条件求直角三角形的斜边.【练习30】 等腰三角形ABC 中,AB = AC , BC = 10,253ABC S ∆=,那么A ∠=______. 【答案】120°. 【解析】∵12532ABC S BC h ∆=⋅⋅=, BC = 10, ∴335=h .∴33533521tan ===BC h B ,∴︒=∠30B . ∴︒=∠-︒=∠1202180B A .【总结】本题主要考查特殊角的锐角三角比的值以及等腰三角形的性质.ABC D 【练习31】 ABC ∆中,90C ∠=︒,斜边上的中线CD = 6,sin A =13,则ABC S ∆= _____.【答案】【解析】∵90C ∠=︒,斜边上的中线CD = 6, ∴AB = 2CD = 12.∵sin A =13, ∴31=AB BC . ∴4=BC .∴284122222=-=-=CB AB AC .∴11422ABCSAC BC ==⨯⨯= 【总结】本题主要考查解直角三角形以及直角三角形的性质.【练习32】 如图,在C 处测得铁塔AB 的塔顶A 的仰角为30°,向塔前进10米到达D 处,在D 处测得A 的仰角为45°,则铁塔的高为______.【答案】535+.【解析】由题意,可设x BD AB ==.在ABC Rt △中,33tan ==BC AB C ,∴x CB 3=. ∴x x 310=+,解得:535+=x .【总结】本题主要考查解直角三角形与仰角结合的应用.【练习33】 某拦水坝的横截面为梯形ABCD ,其中斜面AB 的坡比为1 : 3,如果自A 向B走了米,那么升高的高度为______米.【答案】10.【解析】设斜面AB 的垂直高度为x ,则水平高度为x 3, ∴()101010322==+x x x ,解:10=x∴升高的高度为10米.【总结】本题主要考查解直角三角形在坡比问题中的应用.【练习34】 如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4米.如果在坡度为1:34的山坡上种树,也要求株距为4米,则相邻两树间的坡面距离是______.【答案】5.【解析】考查坡度的定义.【练习35】 用高为h 的测角仪测得铁塔AB 的顶点A 的仰角为α,测角仪到铁塔距离为m ,那么铁塔高度为____________.【答案】αtan m h +. 【解析】考查仰角的定义. . .,【练习36】 计算:cos 45sin 301cos60tan 452︒-︒︒+︒.【答案】212-. 解答题步同级年九14 / 17【解析】解:原式=212121212122-=⨯+-. 【总结】本题主要考查特殊角的锐角三角比的值及代数式求值.【练习37】 已知α为锐角,且11tan α-无意义,求()()2cos 15615sin ααα+︒-︒的值.【答案】21-. 【解析】∵α为锐角,且11tan α-无意义.∴1tan =α,∴︒=45α.∴原式=212223621245sin 30cos 660cos 2-=⨯⨯-⨯=︒︒-︒. 【总结】本题主要考查特殊角的锐角三角比的值以及分式无意义的条件.【练习38】 如图,在ABC ∆中,90C ∠=︒,AC = BC ,BD 为AC 边上的中线.求sin ABD ∠和tan ABD ∠的值.【答案】1010,31. 【解析】过D 作DE ⊥AB ,垂足为E . 设AE =DE =x ,则x AD 2=.∵BD 为AC 边上的中线, ∴x AC 22=.∴x AC AB 42==. ∴x BE 3=. ∴x BE DE BD 1022=+=.∴101010sin ===∠x x DB DE ABD ,313tan ===∠x x EB DE ABD . 【总结】本题主要考查解直角三角形以及锐角三角比的概念.【练习39】 如图,等腰梯形ABCD ,AD // BC ,45DBC ∠=︒,翻折梯形ABCD ,使点B重合于点D ,折痕分别交AB 、BC 于点F 、E ,若AD = 2,BC = 8.求:(1)BE 的长;(2)CDE ∠的正切值.【答案】(1)5;(2)53.【解析】∵EF 垂直平分BD , ∴DE BE =. ∴︒=∠=∠45BDE DBC , ∴︒=∠90DEB . 过A 作AG ⊥BC ,由等腰梯形的性质可得:3==EC BG . ∴538=-=-=EC BC BE . ∴5==BE DE .∴在DEC Rt △中,53tan ==∠DE CE CDE . 【总结】本题综合性较强,主要考查翻折的性质以及等腰梯形的性质和特殊角的锐角三角 比的值.【练习40】 如图,已知梯形ABCD 中,AD // BC ,90ABC ∠=︒,45C ∠=︒,BE ⊥CD 于点E ,AD = 1,CD =.求BE 的长.【答案】223.【解析】过D 作DF ⊥BC ,垂足为F ,则可得四边形ABFD 为矩形. ∵在DCF Rt △中,DC DFC =sin ,∴2222DF =,∴2=FD . ∴2=CF . ∴2=AB ,1==AD BF . ∴3=BC .∵在BCE Rt △中,BCBEC =sin ,A B CDE FG AB CDEF∴322BE =,∴223=BE . 【总结】本题主要考查解直角三角形,注意通过添加垂线,将特殊角放到直角三角形中.【练习41】 如图,在电线杆上的C 处引拉线CE 、CF 固定电线杆,拉线CE 和地面成60°.在 离电线杆6米的B 处安置测角仪,在A 处测得C 处的仰角为30°,已知测角仪高AB 为1.5米,求拉线CE 的长.【答案】34+.【解析】过A 作AG ⊥CD ,垂足为G . 由题意可得:︒=∠30CAG ,︒=∠60CED ,6==BD AG .∵在ACG Rt △中,AG CGCAG =∠tan ,∴633CG =,∴32=CG , ∴2332+=CD .∵在CED Rt △中,CECDCED =∠sin , ∴CE233223+=,∴34+=CE .【总结】本题主要考查解直角三角形在仰角问题中的应用.【练习42】 如图,有一朝向为正南方向的居民楼CD ,该居民楼的一楼是高6米的超市, 超市以上是居民住房,在该楼的前面15米处要盖一栋高20米的新楼AB ,当冬季正午阳光与水平线的夹角为30°时.(1)问超市以上的居民住房采光是否有影响?为什么? (2)若要超市采光不受影响,两楼应相距多少米? 【答案】(1)不受影响,理由见解析;(2)320. 【解析】(1)由题意可知:︒=∠30AEF ,15=EF .在CED Rt △中,∵FE AF AEF =∠tan ,∴1533AF=,∴=AF∵636.113520>≈-==BF EC ,∴超市以上的居民住房采光不受影响.E AB CDEFG(2)当︒=∠30ACB 时,超市采光不受影响,在ACB Rt △中,BCABACB =∠tan , ∴BC2033=,∴320=BC . ∴两楼至少相距320米. 【总结】本题主要考查解直角三角形在实际生活中的应用.。
