中考数学总复习考点突破(第32讲)图形的相似(含答案)
2025年中考数学一轮复习课件:第三十二讲++投影与视图

【跟踪训练】
1.(2021·绍兴中考)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=
5 m,树影AC=3 m,树AB与路灯O的水平距离AP=4.5 m,则树的高度AB长是( A )
A.2 m
B.3 m
C.32 m
D.130 m
2.(2022·北部湾中考)古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的 顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是 4米,同一时刻测得OA是268米,则金字塔的高度BO是____1_3_4___米.
3.(2022·黔东南州中考)一个物体的三视图如图所示,则该物体的形状是( B ) A.圆锥 B.圆柱投影与视图
必备知识·夯根基
【知识要点】 1.投影 (1)平行投影:由____平__行__光__线____形成的投影. (2)中心投影:由____同__一__点____(点光源)发出的光线形成的投影. (3)正投影:在平行投影中,投影线____垂__直__于____投影面产生的投影.
【对点练习】 1.(1)夜晚路灯下同样高的旗杆,离路灯越近,它的影子越____短____(填“长”或“短”). (2)下列投影:①中午林荫道旁树的影子;②海滩上撑起的伞的影子;③跑道上同学 们的影子;④晚上路灯下亮亮的手在墙上的投影.其中是平行投影的是___①__②__③____ (填序号).
【名师点金】 无论是平行投影还是中心投影,往往构造出相似三角形,借助相似三角形对应
边成比例计算.
考点2 几何体的三视图 【例2】(2024·广元中考)一个几何体如图水平放置,它的俯视图是( C )
【跟踪训练】 1.(2024·安徽中考)某几何体的三视图如图所示,则该几何体为( D )
中考数学第一轮总复习课件32

(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点另一侧画出△A2B2C2,使
.
全效学习中考学练测
宝剑锋从磨砺出, 梅花香自苦寒来!
十年寒窗无人问, 一举成名天下知!
全效学习中考学练测
知识梳理 考点例析 当堂训练 能力提升
考点例析 考点一 比例性质
例1已知 ,则
的值是( D )
A.
B.
C.
D.
考点二 相似三角形的判定
例2如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个 条件,不正确的是 ( C )
A.∠ABD=∠C
B.∠ADB=∠ABC
C.
D.h2= h1
全效学习中考学练测
知识梳理 考点例析 当堂训练 能力提升
考点例析
例7如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF= 90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转 ,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q .
A.1: 6
B.1: 3
C.1: 2
D.2: 3
全效学习中考学练测
知识梳理 考点例析 当堂训练 能力提升
当堂训练
5.已知△ABC与△A1B1C1相似,且面积比为4:25,则△ABC与△A1B1C1的相 似比为___2_:5____.
6.如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE; (2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当 BP=a,CQ= a时,P、Q两点间的距离(用含a的代数式表示).
人教版中考数学考点聚焦《第31讲:图形的相似》课件

6.相似三角形的性质 相似三角形的对应角相等,对应边成比例,对应高、对应中线、对应角平 分线的比都等于相似比,周长比等于相似比,面积比等于相似比的平方.
7.射影定理:如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高, 则有下列结论.
(1)AC 2=AD·AB; (2)BC 2=BD·AB; (3)CD 2=AD·BD; (4)AC 2∶BC 2=AD∶BD; (5)AB·CD=AC·BC.
命题点5:相似三角形的应用 5.(2017·天水)如图,路灯距离地面8米,身高1.6米的小明站在距离灯 的底部(点O)20米的A处,则小明的影子AM长为__5__米.
相似三角形的性质及判定
【例 1】 (1)(2017·连云港)如图,已知△ABC∽△DEF,AB∶DE=1∶2,
则下列等式一定成立的是( D )
【探索研究】 (2)若点 O 是 AC 上任意一点(不与 A,C 重合),求证:AMMB·BNNC·OCOA=1; 【拓展应用】 (3)如图②,点 P 是△ABC 内任意一点,射线 AP,BP,CP 分别交 BC, AC,AB 于点 D,E,F,若ABFF=13,BCDD=12,求ACEE的值.
解:(1)过点 A 作 AG∥MN 交 BN 延长线于点 G,∴∠G=∠BNM,又∠B =∠B,∴△ABG∽△MBN,∴BBGN=MABB,∴BBGN-1=MABB-1,∴BGB-NBN =ABM-BMB,即NBNG=AMMB,同理,在△ACG 和△OCN 中,NCNG=ACOO,∴ACOO =NCNG,∵O 为 AC 中点,∴AO=CO,∴NG=CN,∴CBNN=NBNG=ABMM=31
命题点 1:比例的性质 1.(2017·兰州)已知 2x=3y(y≠0),则下面结论成立的是( A ) A.xy=32 B.3x=y2 C.xy=23 D.x2=y3
全效学习中考数学 第十单元 相似形 第32课时 相似形练

相似形第32课时相似形(60分)一、选择题(每题5分,共30分)1.丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥,比例尺为1∶500的图纸上的大桥的长度约为1.04 m,则大桥的实际长度约是 (D)A.104 m B.1 040 mC.5 200 m D.520 m【解析】设大桥的实际长度为x,依题意,得1∶500=1.04∶x;得x=1.04×500=520(m).2.[2015·南京]如图32-1,在△ABC中,DE∥BC,ADDB=12,则下列结论中正确的是 (C)A.AEAC=12B.DEBC=12C.△ADE的周长△ABC的周长=13D.△ADE的面积△ABC的面积=133.[2015·永州]如图32-2,下列条件不能判定△ADB∽△ABC的是(D)A.∠ABD=∠ACB B.∠ADB=∠ABCC.AB2=AD·AC D.ADAB=ABBC【解析】在△ADB和△ABC中,∠A是它们的公共角,那么当ADAB=ABAC时,才能使△ADB∽△ABC,不是ADAB=ABBC.故答案选D.4.[2014·河北]在研究相似问题时,甲乙同学的观点如下:甲:将边长为3,4,5的三角形按图32-3①的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.①②图32-3乙:将邻边为3和5的矩形按图32-3②的方式向外扩张,得到新矩形,它们的对应边间距图32-1图32-2为1,则新矩形与原矩形相似.对于两人的观点,下列说法正确的是 (C)A .两人都对B .两人都不对C .甲对,乙不对D .甲不对,乙对 5.如图32-4,在平行四边形ABCD 中,E是AB 的中点,CE 和BD 交于点O ,设△OCD 的面积为m ,△OEB 的面积为5,则下列结论中正确的是 (B) A .m =5 B .m =4 5 C .m =3 5 D .m =10【解析】 ∵AB ∥CD ,∴△OCD ∽△OEB , 又∵E 是AB 的中点,∴2EB =AB =CD ,∴S △OEB S △OCD =⎝ ⎛⎭⎪⎫BE CD 2,即5m =⎝ ⎛⎭⎪⎫122, 解得m =4 5. ∴m 的值为4 5.6.[2015·武威]如图32-5,D ,E 分别是△ABC 的边AB ,BC 上的点,DE ∥AC ,若S △BDE ∶S △CDE =1∶3,则S △DOE ∶S △AOC 的值为 (D) A.13 B.14 C.19D.116【解析】 ∵S △BDE ∶S △CDE =1∶3, ∴BE ∶EC =1∶3, ∴BE ∶BC =1∶4,∵DE ∥AC ,∴△DOE ∽△COA ,△BED ∽△BCA ,∴DE AC =BE BC =14, ∴S △DOE ∶S △AOC =⎝ ⎛⎭⎪⎫DE AC 2=116.二、填空题(每题5分,共20分)7.[2015·东莞]若两个相似三角形的周长比为2∶3,则它们的面积比是__4∶9__.8.[2015·金华]如图32-6,直线l 1,l 2,…,l 6是一组等距的平行线,过直线l 1上的点A 作两条射线,分别与直线l 3,l 6相交于B ,E ,C ,F ,若BC =2,则EF 的长是__5__.图32-69.[2015·梅州]如图32-7,△ABC 中,点E 是AB 边的中点,点F 在AC 边上,若以A ,E ,F 为顶点的三角形与△ABC 相似,则需要增图32-4图32-5加的一个条件是__AF =12AC或∠AFE =∠ABC __.(写出一个即可) 【解析】 分两种情况: ①∵△AEF ∽△ABC , ∴AE ∶AB =AF ∶AC , 即1∶2=AF ∶AC , ∴AF =12AC ;②∵△AEF ∽△ACB , ∴∠AFE =∠ABC .∴要使以A ,E ,F 为顶点的三角形与△ABC 相似,则AF =12AC 或∠AFE =∠ABC .10.[2015·泰州]如图32-8,△ABC 中,D 为BC 上一点, ∠BAD =∠C ,AB =6,BD =4,则CD 的长为__5__.【解析】 ∵∠BAD =∠C ,∠B =∠B ,∴△BAD ∽△BCA , ∴BA BC =BD BA. ∵AB =6,BD =4, ∴6BC =46, ∴BC =9,∴CD =BC -BD =9-4=5. 三、解答题(共20分)11.(10分)[2015·泰安]如图32-9,在△ABC 中,AB =AC ,点P ,D 分别是BC ,AC 边上的点,且∠APD =∠B .(1)求证:AC ·CD =CP ·BP ;(2)若AB =10,BC =12,当PD ∥AB 时,求BP 的长.图32-9解:(1)证明:∵AB =AC , ∴∠B =∠C . ∵∠APD =∠B , ∴∠APD =∠B =∠C . ∵∠APC =∠BAP +∠B , ∠APC =∠APD +∠DPC , ∴∠BAP =∠DPC , ∴△ABP ∽△PCD , ∴BP CD =AB PC, ∴AB ·CD =PC ·BP .图32-7图32-8∵AB =AC ,∴AC ·CD =CP ·BP ;(2)∵PD ∥AB ,∴∠APD =∠BAP . ∵∠APD =∠C ,∴∠BAP =∠C . ∵∠B =∠B , ∴△BAP ∽△BCA , ∴BA BC =BP BA.∵AB =10,BC =12, ∴1012=BP 10, ∴BP =253.12.(10分)[2015·滨州]如图32-10,已知B ,C ,E 三点在同一条直线上,△ABC 与△DCE 都是等边三角形,其中线段BD 交AC 于点G ,线段AE 交CD 于点F ,求证: (1)△ACE ≌△BCD ; (2)AG GC =AF FE.证明:(1)∵△ABC 与△DCE 都为等边三角形, ∴AC =BC ,CE =CD ,∠ACB =∠DCE =60°,∴∠ACB +∠ACD =∠DCE +∠ACD ,即∠ACE =∠BCD , 在△ACE 和△BCD 中,⎩⎪⎨⎪⎧AC =BC ,∠ACE =∠BCD ,CE =CD ,∴△ACE ≌△BCD (SAS ); (2)∵△ACE ≌△BCD , ∴∠BDC =∠AEC , 在△GCD 和△FCE 中, ⎩⎪⎨⎪⎧∠GCD =∠FCE =60°,CD =CE ,∠BDC =∠AEC , ∴△GCD ≌△FCE (ASA ), ∴CG =CF ,∴△CFG 为等边三角形, ∴∠CGF =∠ACB =60°, ∴GF ∥CE , ∴AG GC =AF FE.(20分)13.(10分)如图32-11,在△ABC 和△ADE 中,∠BAD =∠CAE ,图32-10∠ABC =∠ADE .(1)写出图中两对相似三角形(不得添加辅助线); (2)请分别说明两对三角形相似的理由.【解析】 由两个角对应相等得两三角形相似,关键是得到∠BAC =∠DAE . 解:(1)△ABC ∽△ADE ,△ABD ∽△ACE ; (2)∵∠BAD =∠CAE ,∴∠BAD +∠DAC =∠CAE +∠DAC , 即∠BAC =∠DAE . 又∵∠ABC =∠ADE , ∴△ABC ∽△ADE . ∴AB AD =AC AE.又∵∠BAD =∠CAE ,∴△ABD ∽△ACE .14.(10分)[2014·资阳]如图32-12,AB 是⊙O 的直径,过点A 作⊙O 的切线并在其上取一点C ,连结OC 交⊙O 于点D ,BD 的延长线交AC 于E ,连结AD . (1)求证:△CDE ∽△CAD ;(2)若AB =2,AC =22,求AE 的长.解:(1)∵AB 是⊙O 的直径,∴∠ADB =90°, ∴∠ABD +∠BAD =90°.又∵AC 是⊙O 的切线,∴AB ⊥AC ,∴∠BAC =90°, ∴∠CAD +∠BAD =90°,∴∠ABD =∠CAD . ∵∠ABD =∠BDO =∠CDE , ∴∠CAD =∠CDE ,又∵∠C =∠C ,∴△CDE ∽△CAD ; (2)在Rt △OAC 中,∠OAC =90°, ∴OA 2+AC 2=OC 2,即12+(22)2=OC 2, ∴OC =3,则CD =2.又∵△CDE ∽△CAD ,得CD CE =CA CD ,即2CE =222, ∴CE =2,∴AE =AC -CE =22-2= 2.(10分)15.(10分)[2015·巴中]如图32-13,AB 是⊙O 的直径,OD ⊥弦BC 于点F ,交⊙O 于点E ,连结CE ,AE ,CD ,若∠AEC =∠ODC . (1)求证:直线CD 为⊙O 的切线;(2)若AB =5,BC =4,求线段CD 的长. 解:(1)证明:如答图,连结CO ,∵圆周角∠AEC 与∠ABC 所对弧相同,∴∠ABC =∠AEC .又∠AEC =∠ODC ,∴∠ABC =∠ODC . ∵OC =OB ,OD ⊥BC ,∴∠OCB =∠OBC ,且∠OCB +∠COD =90°.∴∠ODC +∠COD =90°.∴∠OCD =180°-∠ODC -∠COD =90°,即OC ⊥CD .图32-12图32-13第15题答图又OC 为半径,∴直线CD 为⊙O 的切线; (2)在⊙O 中,OD ⊥弦BC 于点F , ∴BF =CF =12BC =2.又OB =12AB =52,∴OF =OB 2-BF 2=32.由(1)知∠OBF =∠CDF ,且∠OFB =∠CFD ,∴△OFB ∽△CFD .∴OF OB =CF CD ,∴CD =OB ·CF OF =52×232=103. ∴线段CD 的长为103.。
2018届中考数学《第32课时:相似图形》同步练习(有答案)

第十单元 相似图形第32课时 相似图形(70分)一、选择题(每题5分,共30分)1.[2017·重庆A 卷]若△ABC ∽△DEF ,相似比为3∶2,则对应高的比为( A ) A .3∶2 B .3∶5 C .9∶4D .4∶9【解析】 因为△ABC ∽△DEF ,根据相似三角形的性质“相似三角形对应高之比等于相似比”,故选A.2.[2018·中考预测]如图32-1,下列条件不能判定△ADB ∽△ABC 的是( D ) A .∠ABD =∠ACB B .∠ADB =∠ABC C .AB 2=AD ·AC D.AD AB =AB BC那么当ADAB =【解析】 在△ADB 和△ABC 中,∠A 是它们的公共角,AB AC 时,才能使△ADB ∽△ABC ,不是AD AB =AB BC .故选D. 3.[2017·枣庄]如图32-2,在△ABC 中,∠A =78°,AB =4,AC =6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( C)图32-1图32-2【解析】A.阴影部分的三角形与原三角形有两个角相等,故两三角形相似;B.阴影部分的三角形与原三角形有两个角相等,故两三角形相似;C.两三角形的对应边不成比例,故两三角形不相似;D.两三角形对应边成比例且夹角相等,故两三角形相似.故选C.4.[2017·哈尔滨]如图32-3,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连结AF交DE于点G,则下列结论中一定正确的是(C)A.ADAB=AEEC B.AGGF=AEBDC.BDAD=CEAE D.AGAF=ACEC图32-3 图32-45.[2017·恩施]如图32-4,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为(C)A.6 B.8C.10 D.12【解析】∵DE∥BC,∴∠ADE=∠B.∵∠ADE=∠EFC,∴∠B=∠EFC,∴BD∥EF.∵DE∥BF,∴四边形BDEF为平行四边形,∴DE=BF.∵DE∥BC,∴△ADE∽△ABC,∴DE BC=AD AB=ADAD+BD =58,∴BC=85DE,∴CF=BC-BF=35DE=6,∴DE=10.6.[2017·绥化]如图32-5,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连结BE并延长交AD于点F,已知S△AEF=4,则下列结论:①AF FD =12;②S △BCE =36;③S △ABE =12;④△AEF ∽△ACD ,其中一定正确的是( D ) A .①②③④ B.①④ C .②③④D.①②③【解析】 在▱ABCD 中,AO =12AC ,∵点E 是OA 的中点,∴AE =13CE .∵AD ∥BC ,∴△AFE ∽△CBE ,∴AF BC =AE CE =13.∵AD =BC ,∴AF =13AD ,∴AF FD =12,故①正确;∵S △AEF =4,S △AEF S △BCE =⎝ ⎛⎭⎪⎫AF BC 2=19,∴S △BCE=36,故②正确;∵EF BE =AE CE =13,∴S △AEF S △ABE =13,∴S △ABE =12,故③正确;∵BF 不平行于CD ,∴△AEF 与△ADC 只有一个角相等,∴△AEF 与△ACD 不一定相似,故④错误.综上,正确的有①②③.二、填空题(每题5分,共20分)7.如图32-6,直线l 1,l 2,…,l 6是一组等距的平行线,过直线l 1上的点A 作两条射线,分别与直线l 3,l 6相交于点B ,E ,C ,F ,若BC =2,则EF 的长是__5__.8.[2017·自贡]如图32-7,在△ABC 中,MN ∥BC ,分别交AB ,AC 于点M ,N ,若AM =1,MB =2,BC =3,则MN 的长为__1__.【解析】 ∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MN BC .∵AM =1,MB =2,BC =3,∴11+2=MN3,解得MN =1.图32-7图32-89.[2017·潍坊]如图32-8,在△ABC 中,AB ≠AC ,D ,E 分别为边AB ,AC 上的点,AC =3AD ,AB =3AE ,点F 为BC 边上一点,添加一个条件:__∠A =∠BDF (答案不唯一,合理即可)__,可以使△FDB 与△ADE 相似.(只需写出一个)图32-6【解析】 ∵AC =3AD ,AB =3AE ,∴AD AC =AE AB =13,又∵∠A =∠A ,∴△ADE ∽△ACB ,∴∠AED =∠B .故要使△FDB 与△ADE 相似,只需再添加一组对应角相等,或夹角的两边成比例即可.10.[2016·舟山]如图32-9,已知△ABC 和△DEC 的面积相等,点E 在BC 边上,DE ∥AB 交AC 于点F ,AB =12,EF =9,则DF 的长是__7__. 【解析】 ∵△ABC 与△DEC 的面积相等,∴△CDF 与四边形AFEB 的面积相等,∵AB ∥DE ,∴△CEF ∽△CBA ,∵EF =9,AB =12,∴EF ∶AB =9∶12=3∶4,∴S △CEF ∶S △CBA =9∶16,设△CEF 的面积为9k ,则四边形AFEB 的面积为7k .∵△CDF 与四边形AFEB 的面积相等,∴S △CDF =7k ,∵△CDF 与△CEF 是同高不同底的三角形,∴面积比等于底之比,∴DF ∶EF =7k ∶9k ,∴DF =7. 三、解答题(共20分)11.(10分)如图32-10,在△ABC 和△ADE 中,∠BAD =∠CAE ,∠ABC=∠ADE .(1)写出图中两对相似三角形(不得添加辅助线); (2)请分别说明两对三角形相似的理由.【解析】 由两个角对应相等得两三角形相似,关键是得到∠BAC =∠DAE . 解:(1)△ABC ∽△ADE ,△ABD ∽△ACE ; (2)∵∠BAD =∠CAE ,∴∠BAD +∠DAC =∠CAE +∠DAC ,即∠BAC =∠DAE . 又∵∠ABC =∠ADE , ∴△ABC ∽△ADE ,∴AB AD =AC AE . 又∵∠BAD =∠CAE ,∴△ABD ∽△ACE .12.(10分)[2017·宿迁]如图32-11,在△ABC 中,AB =AC ,点E 在边BC 上移动(点E 不与点B ,C 重合),满足∠DEF =∠B ,且点D ,F 分别在边AB ,AC 上. (1)求证:△BDE ∽△CEF ;(2)当点E 移动到BC 的中点时,求证:FE 平分∠DFC . 证明:(1)∵AB =AC ,∴∠B =∠C , ∵∠BDE =180°-∠B -∠DEB , ∠CEF =180°-∠DEF -∠DEB ,图32-9图32-10图32-11∵∠DEF =∠B ,∴∠BDE =∠CEF , ∴△BDE ∽△CEF ;(2)∵△BDE ∽△CEF ,∴BE CF =DEEF ,∵点E 是BC 的中点,∴BE =CE ,∴CE CF =DEEF , ∵∠DEF =∠B =∠C ,∴△DEF ∽△ECF , ∴∠DFE =∠CFE ,∴FE 平分∠DFC .(15分)13.(15分)[2017·株洲]如图32-12,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF 上,EF 与BC 相交于点G ,连结CF .求证: (1)△DAE ≌△DCF ; (2)△ABG ∽△CFG .图32-12 第13题答图证明:(1)∵四边形ABCD 是正方形,△EDF 是等腰直角三角形, ∴∠ADC =∠EDF =90°,AD =CD ,DE =DF , ∴∠ADE +∠ADF =∠ADF +∠CDF , ∴∠ADE =∠CDF ,在△DAE 和△DCF 中,⎩⎨⎧DE =DF ,∠ADE =∠CDF ,DA =DC ,∴△DAE ≌△DCF (SAS ); (2)如答图,延长BA ,交ED 于点M , ∵△ADE ≌△CDF ,∴∠EAD =∠FCD , 即∠EAM +∠MAD =∠BCD +∠BCF , ∵∠MAD =∠BCD =90°, ∴∠EAM =∠BCF ,∵∠EAM =∠BAG ,∴∠BAG =∠BCF , ∵∠AGB =∠CGF ,∴△ABG ∽△CFG .(15分)14.(15分)[2018·中考预测]如图32-13,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC 的外接圆于点F,连结FB,FC.(1)求证:∠FBC=∠FCB;(2)已知F A·FD=12,若AB是△ABC外接圆的直径,F A=2,求CD的长.解:(1)证明:∵四边形AFBC内接于圆,∴∠FBC+∠F AC=180°,∵∠CAD+∠F AC=180°,∴∠FBC=∠CAD,∵AD是△ABC的外角∠EAC的平分线,∴∠EAD=∠CAD,∵∠EAD=∠F AB,∴∠F AB=∠CAD,又∵∠F AB=∠FCB,∴∠FBC=∠FCB;(2)由(1),得∠FBC=∠FCB,又∵∠FCB=∠F AB,∴∠F AB=∠FBC,∵∠BF A=∠BFD,∴△AFB∽△BFD,∴FBFD=F AFB,∴FB2=F A·FD=12,∴FB=23,∵F A=2,∴FD=6,AD=4,∵AB为圆的直径,∴∠BF A=∠BCA=90°,∴tan∠FBA=AFFB=223=33,∴∠FBA=30°,又∵∠FDB=∠FBA=30°,∴CD=AD·cos30°=4×32=2 3.图32-13。
新初中数学图形的相似知识点总复习附答案解析(2)
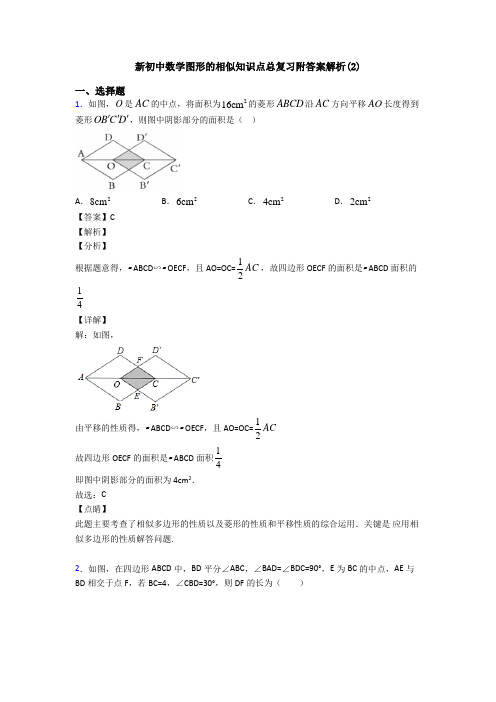
新初中数学图形的相似知识点总复习附答案解析(2)一、选择题1.如图,O 是AC 的中点,将面积为216cm 的菱形ABCD 沿AC 方向平移AO 长度得到菱形OB C D ''',则图中阴影部分的面积是( )A .28cmB .26cmC .24cmD .22cm【答案】C【解析】【分析】 根据题意得,▱ABCD ∽▱OECF ,且AO=OC=12AC ,故四边形OECF 的面积是▱ABCD 面积的14【详解】解:如图,由平移的性质得,▱ABCD ∽▱OECF ,且AO=OC=12AC 故四边形OECF 的面积是▱ABCD 面积14即图中阴影部分的面积为4cm 2.故选:C【点睛】 此题主要考查了相似多边形的性质以及菱形的性质和平移性质的综合运用.关键是 应用相似多边形的性质解答问题.2.如图,在四边形ABCD 中,BD 平分∠ABC ,∠BAD=∠BDC=90°,E 为BC 的中点,AE 与BD 相交于点F ,若BC=4,∠CBD=30°,则DF 的长为( )A.235B.233C.334D.435【答案】D【解析】【分析】先利用含30度角的直角三角形的性质求出BD,再利用直角三角形的性质求出DE=BE=2,即:∠BDE=∠ABD,进而判断出DE∥AB,再求出AB=3,即可得出结论.【详解】如图,在Rt△BDC中,BC=4,∠DBC=30°,∴3连接DE,∵∠BDC=90°,点D是BC中点,∴DE=BE=CE=12BC=2,∵∠DCB=30°,∴∠BDE=∠DBC=30°,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠BDE,∴DE∥AB,∴△DEF∽△BAF,∴DF DE BF AB=,在Rt△ABD中,∠ABD=30°,3,∴AB=3,∴23 DFBF=,∴25 DFBD=,∴DF=224323555BD =⨯=, 故选D .【点睛】此题主要考查了含30度角的直角三角形的性质,相似三角形的判定和性质,角平分线的定义,判断出DE ∥是解本题的关键.3.如图,四边形ABCD 内接于O e ,AB 为直径,AD CD =,过点D 作DE AB ⊥于点E ,连接AC 交DE 于点F .若3sin 5CAB ∠=,5DF =,则AB 的长为( )A .10B .12C .16D .20【答案】D【解析】【分析】 连接BD ,如图,先利用圆周角定理证明ADE DAC ∠=∠得到5FD FA ==,再根据正弦的定义计算出3EF =,则4AE =,8DE =,接着证明ADE DBE ∆∆∽,利用相似比得到16BE =,所以20AB =.【详解】解:连接BD ,如图,AB Q 为直径,90ADB ACB ∴∠=∠=︒,AD CD =Q ,DAC DCA ∴∠=∠,而DCA ABD ∠=∠,DAC ABD ∴∠=∠,DE AB ∵⊥,90ABD BDE ∴∠+∠=︒,而90ADE BDE ∠+∠=︒,ABD ADE ∴∠=∠,ADE DAC ∴∠=∠,5FD FA ∴==,在Rt AEF ∆中,3sin 5EF CAB AF ∠==Q , 3EF ∴=, 22534AE ∴=-=,538DE =+=,ADE DBE ∠=∠Q ,AED BED ∠=∠,ADE DBE ∴∆∆∽,::DE BE AE DE ∴=,即8:4:8BE =,16BE ∴=,41620AB ∴=+=.故选:D .【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90︒的圆周角所对的弦是直径.也考查了解直角三角形.4.如图,在ABC V 中,点D ,E 分别为AB ,AC 边上的点,且//DE BC ,CD 、BE 相较于点O ,连接AO 并延长交DE 于点G ,交BC 边于点F ,则下列结论中一定正确的是( )A .AD AE AB EC= B .AG AE GF BD = C .OD AE OC AC = D .AG AC AF EC = 【答案】C【解析】【分析】 由//DE BC 可得到DEO V ∽CBO V ,依据平行线分线段成比例定理和相似三角形的性质进行判断即可.【详解】解:A.∵//DE BC ,∴AD AE AB AC= ,故不正确; B. ∵//DE BC ,∴AG AE GF EC = ,故不正确; C. ∵//DE BC ,∴ADE V ∽ABC V ,DEO V ∽CBO V ,DE AE BC AC ∴=,DE OD BC OC = . OD AE OC AC∴= ,故正确; D. ∵//DE BC ,∴AG AE AF AC= ,故不正确; 故选C .【点睛】 本题主要考查的是相似三角形的判定和性质,熟练掌握相似三角形的性质和判定定理是解题的关键.5.如图,点E 是ABCD Y 的边AD 上一点,2DE AE =,连接BE ,交AC 边于点F ,下列结论中错误的是( )A .3BC AE =B .4AC AF = C .3BF EF =D .2BC DE =【答案】D【解析】【分析】 由平行四边形的性质和相似三角形的性质分别判断即可.【详解】解:∵在ABCD Y 中,//AD BC ,AD BC =,∴AEF CBF V :V ,∴AE AF EF CB CF BF==, ∵2DE AE = ∴332BC DE AE ==,选项A 正确,选项D 错误, ∴133AF AE AE CF CB AE ===,即:3CF AF =, ∴4AC AF =,∴选项B 正确,∴133EF AE AE BF CB AE ===,即:3BF EF =, ∴选项C 正确,故选:D .【点睛】此题主要考查了平行四边形的性质以及相似三角形的判定与性质,能熟练利用相似三角形对应边成比例是解题关键.6.如图,正方形OABC 的边长为6,D 为AB 中点,OB 交CD 于点Q ,Q 是y =k x上一点,k 的值是( )A .4B .8C .16D .24【答案】C【解析】【分析】 延长根据相似三角形得到:1:2BQ OQ =,再过点Q 作垂线,利用相似三角形的性质求出QF 、OF ,进而确定点Q 的坐标,确定k 的值.【详解】解:过点Q 作QF OA ⊥,垂足为F ,OABC Q 是正方形,6OA AB BC OC ∴====,90ABC OAB DAE ∠=∠=︒=∠,D Q 是AB 的中点,12BD AB ∴=, //BD OC Q ,OCQ BDQ ∴∆∆∽,∴12 BQ BD OQ OC==,又//QF ABQ,OFQ OAB∴∆∆∽,∴22213QF OF OQAB OA OB====+,6AB=Q,2643QF∴=⨯=,2643OF=⨯=,(4,4)Q∴,Q点Q在反比例函数的图象上,4416k∴=⨯=,故选:C.【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定,利用相似三角形性质求出点Q的坐标是解决问题的关键.7.如图,将ABC∆沿BC边上的中线AD平移到A B C'''∆的位置.已知ABC∆的面积为16,阴影部分三角形的面积9.若1AA'=,则A D'等于()A.2 B.3 C.4 D.32【答案】B【解析】【分析】由S△ABC=16、S△A′EF=9且AD为BC边的中线知1922A DE A EFS S'∆'∆==,182ABD ABCS S∆∆==,根据△DA′E∽△DAB知2A DEABDSA DAD S∆∆'⎛⎫='⎪⎝⎭,据此求解可得.【详解】16ABCS∆=Q、9A EFS∆'=,且AD为BC边的中线,1922A DE A EF S S ∆∆''∴==,182ABD ABC S S ∆∆==, Q 将ABC ∆沿BC 边上的中线AD 平移得到A B C '''∆,//A E AB ∴', DA E DAB '∴∆~∆, 则2A DE ABD S A D AD S ∆∆'⎛⎫=' ⎪⎝⎭,即22991816A D A D ⎛⎫== '⎪+⎝⎭', 解得3A D '=或37A D '=-(舍), 故选:B .【点睛】本题主要平移的性质,解题的关键是熟练掌握平移变换的性质与三角形中线的 性质、相似三角形的判定与性质等知识点.8.在Rt △ABC 中,∠BAC =90°,AD 是△ABC 的中线,∠ADC =45°,把△ADC 沿AD 对折,使点C 落在C ′的位置,C ′D 交AB 于点Q ,则BQ AQ的值为( ) ABCD【答案】A【解析】【分析】根据折叠得到对应线段相等,对应角相等,根据直角三角形的斜边中线等于斜边一半,可得出AD =DC =BD ,AC =AC′,∠ADC =∠ADC ′=45°,CD =C′D ,进而求出∠C 、∠B 的度数,求出其他角的度数,可得AQ =AC ,将BQ AQ 转化为BQ AC ,再由相似三角形和等腰直角三角形的边角关系得出答案.【详解】解:如图,过点A 作AE ⊥BC ,垂足为E ,∵∠ADC =45°,∴△ADE 是等腰直角三角形,即AE =DE=2AD , 在Rt △ABC 中,∵∠BAC =90°,AD 是△ABC 的中线,∴AD =CD =BD ,由折叠得:AC =AC ′,∠ADC =∠ADC ′=45°,CD =C ′D ,∴∠CDC ′=45°+45°=90°,∴∠DAC =∠DCA =(180°﹣45°)÷2=67.5°=∠C ′AD ,∴∠B=90°﹣∠C=∠CAE=22.5°,∠BQD=90°﹣∠B=∠C′QA=67.5°,∴AC′=AQ=AC,由△AEC∽△BDQ得:BQAC=BDAE,∴BQAQ=BQAC=ADAE=2AEAE=2.故选:A.【点睛】考查直角三角形的性质,折叠轴对称的性质,以及等腰三角形与相似三角形的性质和判定等知识,合理的转化是解决问题的关键.9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为()A.32B.92C33D.3【答案】A【解析】【分析】【详解】解:∵Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∴△ACD∽△ABC,∴AC:AB=AD:AC,∵AC=3,AB=6,∴AD=32.故选A.考点:相似三角形的判定与性质.10.如图,已知在平面直角坐标系中,点O 是坐标原点,AOB V 是直角三角形,90AOB ∠=︒,2OB OA =,点B 在反比例函数2y x =上,若点A 在反比例函数k y x=上,则k 的值为( )A .12B .12-C .14D .14- 【答案】B【解析】【分析】通过添加辅助线构造出相似三角形,再根据相似三角形的性质可求得1,2x A x ⎛⎫- ⎪⎝⎭,然后由点的坐标即可求得答案.【详解】解:过点B 作BE x ⊥于点E ,过点A 作AF x ⊥于点F ,如图:∵点B 在反比例函数2y x=上 ∴设2,B x x ⎛⎫ ⎪⎝⎭∴OE x =,2BE x =∵90AOB ∠=︒∴90AOD BOD ∠+∠=︒∴90BOE AOF ∠+∠=︒∵BE x ⊥,AF x ⊥∴90BEO OFA ∠=∠=︒∴90OAF AOF ∠+∠=︒∴BOE OAF ∠=∠∴BOE OAF V V ∽∵2OB OA = ∴12OF AF OA BE OE BO ===∴121122OF BE x x =⋅=⋅=,11222x AF OE x =⋅=⋅= ∴1,2x A x ⎛⎫- ⎪⎝⎭∵点A 在反比例函数k y x=上 ∴12x k x=- ∴12k =-. 故选:B【点睛】本题考查了反比例函数与相似三角形的综合应用,点在函数图象上则点的坐标就满足函数解析式,结合已知条件能根据相似三角形的性质求得点A 的坐标是解决问题的关键.11.如图,Rt ABC V 中,90,60ABC C ∠=∠=o o ,边AB 在x 轴上,以O 为位似中心,作111A B C △与ABC V 位似,若()3,6C 的对应点()11,2C ,则1B 的坐标为( )A .()1,0B .3,02⎛⎫ ⎪⎝⎭C .()2,0D .()2,1【答案】A【解析】如图,根据位似图形的性质可得B 1C 1//BC ,点B 在x 轴上,由∠ABC=90°,可得B 1C 1⊥x 轴,根据C 1坐标即可得B 1坐标.【详解】如图,∵111A B C △与ABC V 位似,位似中心为点O ,边AB 在x 轴上,∴B 1C 1//BC ,点B 在x 轴上,∵∠ABC=90°,∴B 1C 1⊥x 轴,∵C 1坐标为(1,2),∴B 1坐标为(1,0)故选:A .【点睛】本题考查位似图形的性质,位似图形的对应边互相平行,对应点的连线相交于一点,这一点叫做位似中心.12.在平面直角坐标系中,已知点E (﹣4,2),F (﹣2,﹣2),以原点O 为位似中心,相似比为,把△EFO 缩小,则点E 的对应点E′的坐标是A .(﹣2,1)B .(﹣8,4)C .(﹣8,4)或(8,﹣4)D .(﹣2,1)或(2,﹣1)【答案】D【解析】试题分析:根据位似的性质,缩小后的点在原点的同侧,为(-2,1),然后求在另一侧为(2,-1).故选D考点:位似变换13.在相同时刻,物高与影长成正比,如果高为1米的标杆影长为2米,那么影长为30米的旗杆的高为( )A .20米B .18米C .16米D .15米【答案】D【解析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似,利用标杆的高:标杆影长=旗杆的高:旗杆的影长,列出方程,求解即可得出旗杆的高度.【详解】解:根据题意解:标杆的高:标杆影长=旗杆的高:旗杆的影长,即1:2=旗杆高:30,∴旗杆的高=130=152⨯米.故选:D.【点睛】本题主要考察的是相似三角形的应用,正确列出方程是解决本题的关键.14.如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点,作BM⊥AE于点M,作KN⊥AE于点N,连结MO、NO,以下四个结论:①△OMN是等腰三角形;②tan∠OMN=3;③BP=4PK;④PM•PA=3PD2,其中正确的是()A.①②③B.①②④C.①③④D.②③④【答案】B【解析】【分析】根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理△ADP≌△ECP,由相似三角形的性质得到AD=CE,作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质得到1=4KP PIKB BE=,得到BP=3PK,故③错误;作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,故①正确;根据直角三角形的性质和锐角三角函数求出∠OMN=33,故②正确;然后根据射影定理和三角函数即可得到PM•PA=3PD2,故④正确.【详解】解:作PI∥CE交DE于I,∵四边形ABCD为菱形,∴∠DAP=∠CEP ,∠ADP=∠ECP ,在△ADP 和△ECP 中,DAP CEP ADP ECP DP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADP ≌△ECP ,∴AD=CE , 则PI PD CE DC =,又点P 是CD 的中点, ∴1=2PI CE , ∵AD=CE , ∴1=4KP PI KB BE =, ∴BP=3PK ,故③错误;作OG ⊥AE 于G , ∵BM 丄AE 于M ,KN 丄AE 于N ,∴BM ∥OG ∥KN ,∵点O 是线段BK 的中点,∴MG=NG ,又OG ⊥MN ,∴OM=ON ,即△MON 是等腰三角形,故①正确;由题意得,△BPC ,△AMB ,△ABP 为直角三角形,设BC=2,则CP=1,由勾股定理得,则根据三角形面积公式,BM=7, ∵点O 是线段BK 的中点,∴PB=3PO ,∴OG=13BM=21, MG=23MP=27, tan ∠OMN=OG MG ,故②正确; ∵∠ABP=90°,BM ⊥AP ,∴PB 2=PM•PA ,∵∠BCD=60°,∴∠ABC=120°,∴∠PBC=30°,∴∠BPC=90°,∴PB=3PC ,∵PD=PC ,∴PB 2=3PD ,∴PM •PA=3PD 2,故④正确.故选B .【点睛】本题考查相似形综合题.15.已知线段MN =4cm ,P 是线段MN 的黄金分割点,MP >NP ,那么线段MP 的长度等于( )A .(5)cmB .(5﹣2)cmC 5)cmD 51)cm 【答案】B【解析】【分析】 根据黄金分割的定义进行作答.【详解】由黄金分割的定义知,51MP MN -=MN=4,所以,5- 2. 所以答案选B. 【点睛】本题考查了黄金分割的定义,熟练掌握黄金分割的定义是本题解题关键.16.如图,矩形AEHC 是由三个全等矩形拼成的,AH 与BE 、BF 、DF 、DG 、CG 分别交于点P 、Q 、K 、M 、N ,设BPQ ∆,DKM ∆,CNH ∆的面积依次为1S 、2S 、3S ,若1320S S +=,则2S 的值为( )A .6B .8C .10D .1【答案】B【解析】【分析】 由已知条件可以得到△BPQ ∽△DKM ∽△CNH ,然后得到△BPQ 与△DKM 的相似比为12,△BPQ 与△CNH 的相似比为13,由相似三角形的性质求出1S ,从而求出2S . 【详解】解:∵矩形AEHC 是由三个全等矩形拼成的,∴AB=BD=CD ,AE ∥BF ∥DG ∥CH ,∴四边形BEFD 、四边形DFGC 是平行四边形,∠BQP=∠DMK=∠CHN ,∴BE ∥DF ∥CG ,∴∠BPQ=∠DKM=∠CNH ,∴△ABQ ∽△ADM ,△ABQ ∽△ACH , ∴12AB BQ AD DM ==,13BQ AB CH AC ==, ∴△BPQ ∽△DKM ∽△CNH , ∵12BQ MD =,13BQ CH =, ∴1214S S =,1319S S =, ∴214S S =,319S S =,∵1320S S +=,∴12S =,∴2148S S ==;故选:B.【点睛】本题考查了相似三角形的判定和性质,矩形的性质以及平行四边形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质,正确得到214S S =,319S S =,从而求出答案.17.若△ABC 的每条边长增加各自的50%得△A 'B 'C ',若△ABC 的面积为4,则△A 'B 'C '的面积A .9B .6C .5D .2 【答案】A【解析】【分析】根据两个三角形三边对应成比例,这两个三角形相似判断出两个三角形相似,根据相似三角形的性质即可得到结论.【详解】解:∵△ABC 的每条边长增加各自的50%得△A ′B ′C ′,∴△ABC 与△A ′B ′C ′的三边对应成比例,∴△ABC ∽△A ′B ′C ′, ∴214()150%9ABC A B C S S '''==+V V , ∵△ABC 的面积为4,则△A'B'C'的面积是9.故选:A .【点睛】本题考查了相似三角形的性质和判定,熟练掌握相似三角形的判定是解题的关键.18.两个相似三角形的对应边分别是15cm 和23cm ,它们的周长相差40cm ,则这两个三角形的周长分别是( )A .45cm ,85cmB .60cm ,100cmC .75cm ,115cmD .85cm ,125cm 【答案】C【解析】【分析】根据相似三角形的周长的比等于相似比列出方程,解方程即可.【详解】设小三角形的周长为xcm ,则大三角形的周长为(x+40)cm ,由题意得,154023x x =+, 解得,x=75,则x+40=115,故选C .19.如图,点D 是ABC V 的边BC 上一点,,2BAD C AC AD ∠=∠= ,如果ACD V 的面积为15,那么ABC V 的面积为( )A .20B .22.5C .25D .30【解析】【分析】先证明C ABD BA ∽△△,再根据相似比求出ABC V 的面积即可.【详解】∵,BAD C B B ∠=∠=∠∠∴C ABD BA ∽△△∵2AC AD =∴4S ABD S CBA =V V ∴43S ACD S CBA =V V ∵ACD V 的面积为15∴44152033S CBA S ACD ==⨯=VV 故答案为:A .【点睛】 本题考查了相似三角形的问题,掌握相似三角形的性质以及判定定理是解题的关键.20.如图,在Rt ABC △中,90ACB ∠=︒,CD AB ⊥于点D ,2CD =,1BD =,则AD 的长是( )A .1.B 2C .2D .4【答案】D【解析】【分析】 由在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,根据同角的余角相等,可得∠ACD=∠B ,又由∠CDB=∠ACB=90°,可证得△ACD ∽△CBD ,然后利用相似三角形的对应边成比例,即可求得答案.【详解】∵在Rt △ABC 中,∠ACB=90°,CD ⊥AB ,∴∠CDB=∠ACB=90°,∴∠ACD+∠BCD=90°,∠BCD+∠B=90°,∴∠ACD=∠B ,∴△ACD ∽△CBD ,∴=AD CD CD BD, ∵CD=2,BD=1, ∴2=21AD , ∴AD=4.故选D.【点睛】此题考查相似三角形的判定与性质,解题关键在于证得△ACD ∽△CBD.。
初中数学综合课件第32课时 相似图形
第1页 第十单元 相似图形 第32课时 相似图形
(70分) 一、选择题(每题5分,共30分) 1.丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥,在比例尺为1∶500的图纸上的大桥的长度约为1.04 m,则大桥的实际长度约是 ( D ) A.104 m B.1 040 m C.5 200 m D.520 m 【解析】 设大桥的实际长度为x,依题意得1∶500=1.04∶x, 解得x=1.04×500=520(m). 2.[2016·巴中]如图32-1,D,E分别为△ABC的边AB,AC上的中点,则△ADE的面积与四边形BCED的面积的比为 ( B )
图32-1 A.1∶2 B.1∶3 C.1∶4 D.1∶1 3.[2015·永州]如图32-2,下列条件不能判定△ADB∽△ABC的是 ( D )
图32-2 第2页
A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD·AC D.ADAB=ABBC 【解析】 在△ADB和△ABC中,∠A是它们的公共角,那么当ADAB=ABAC时,才能使△ADB∽△ABC,不是ADAB=ABBC.故选D.
4.[2016·山西]宽与长的比是5-12(约为0.618)的矩形叫做黄金矩形.黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图32-3,作正方形ABCD,分别取AD,BC的中点E,F,连结EF;以F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H.则图中下列矩形是黄金矩形的是 ( D ) A.矩形ABFE B.矩形EFCD C.矩形EFGH D.矩形DCGH
图32-3 【解析】 设正方形的边长为2,则CD=2,CF=1, 在Rt△DCF中,DF=12+22=5, ∴FG=5,∴CG=5-1,
∴CGCD=5-12, ∴矩形DCGH为黄金矩形.故选D. 5.如图32-4,在▱ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积
2020年中考数学一轮复习练习题 第32课时 相似(含答案)
1 第十章 相似形 第32课时 相似 (70分) 一、选择题(每题5分,共30分) 1.[2019·重庆A卷]如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5 2.[2019·雅安]如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是 ( )
3.[2019·杭州]如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B,C重合)连接AM交DE于点N,则( )
A.ADAN=ANAE B.BDMN=MNCE C.DNBM=NEMC D.DNMC=NEBM 4.[2019·淄博]如图,在△ABC中,AC=2,BC=4,D为BC边上的一点,且∠CAD=∠B.若△ADC的面积为a,则△ABD的面积为( )
A.2a B.52a 2
C.3a D.72a 5.[2019·安徽]如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12.点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
A.3.6 B.4 C.4.8 D.5 6.[2019·巴中]如图,在▱ABCD中,F为BC的中点,延长AD至点E,使DE∶AD=1∶3,连接EF交DC于点G,则S△DEG∶S△CFG=( )
A.2∶3 B.3∶2 C.9∶4 D.4∶9 二、填空题(每题4分,共20分)
7.[2018·成都]已知a6=b5=c4,且a+b-2c=6,则a的值为________. 8.[2018·北京]如图,在矩形ABCD中,E是边AB的中点,连接DE,交对角线AC于点F.若AB=4,AD=3,则CF=____________.
9.[2017·潍坊]如图,在△ABC中,AB≠AC,D,E分别为边AB,AC上的点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件:________________________,可以使得△FDB与△ADE相似(只需写出一个即可).
2018届中考数学《第32课时:相似图形》同步练习(有答案)
第十单元 相似图形第32课时 相似图形(70分)一、选择题(每题5分,共30分)1.[2017·重庆A 卷]若△ABC ∽△DEF ,相似比为3∶2,则对应高的比为( A ) A .3∶2 B .3∶5 C .9∶4D .4∶9【解析】 因为△ABC ∽△DEF ,根据相似三角形的性质“相似三角形对应高之比等于相似比”,故选A.2.[2018·中考预测]如图32-1,下列条件不能判定△ADB ∽△ABC 的是( D ) A .∠ABD =∠ACB B .∠ADB =∠ABC C .AB 2=AD ·AC D.AD AB =AB BC那么当AD AB =ABAC 时,【解析】 在△ADB 和△ABC 中,∠A 是它们的公共角,才能使△ADB ∽△ABC ,不是AD AB =ABBC .故选D. 3.[2017·枣庄]如图32-2,在△ABC 中,∠A =78°,AB =4,AC =6.将△ABC 沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( C)图32-1图32-2【解析】 A .阴影部分的三角形与原三角形有两个角相等,故两三角形相似;B.阴影部分的三角形与原三角形有两个角相等,故两三角形相似;C.两三角形的对应边不成比例,故两三角形不相似;D.两三角形对应边成比例且夹角相等,故两三角形相似.故选C.4.[2017·哈尔滨]如图32-3,在△ABC 中,D ,E 分别为AB ,AC 边上的点,DE ∥BC ,点F 为BC 边上一点,连结AF 交DE 于点G ,则下列结论中一定正确的是( C )A.AD AB =AE ECB.AG GF =AE BDC.BD AD =CE AED.AG AF =AC EC图32-3图32-45.[2017·恩施]如图32-4,在△ABC 中,DE ∥BC ,∠ADE =∠EFC ,AD ∶BD =5∶3,CF =6,则DE的长为( C )A .6B .8C .10D .12【解析】 ∵DE ∥BC ,∴∠ADE =∠B .∵∠ADE =∠EFC ,∴∠B =∠EFC ,∴BD ∥EF .∵DE ∥BF ,∴四边形BDEF 为平行四边形,∴DE =BF .∵DE ∥BC ,∴△ADE ∽△ABC ,∴DE BC =AD AB =AD AD +BD =58,∴BC =85DE ,∴CF =BC -BF =35DE =6,∴DE =10. 6.[2017·绥化]如图32-5,在▱ABCD 中,AC ,BD 相交于点O ,点E 是OA 的中点,连结BE 并延长交AD 于点F ,已知S △AEF =4,则下列结论:①AF FD =12; ②S △BCE =36;③S △ABE =12;④△AEF ∽△ACD ,其中一定正确的是( D )A .①②③④ B.①④ C .②③④D.①②③【解析】 在▱ABCD 中,AO =12AC ,∵点E 是OA 的中点,∴AE =13CE .∵AD ∥BC ,∴△AFE ∽△CBE ,∴AF BC =AE CE =13.∵AD =BC ,∴AF =13AD ,∴AF FD =12,故①正确;∵S △AEF =4,S △AEF S △BCE =⎝ ⎛⎭⎪⎫AF BC 2=19,∴S △BCE =36,故②正确;∵EF BE =AE CE =13,∴S △AEF S △ABE =13,∴S △ABE =12,故③正确;∵BF 不平行于CD ,∴△AEF 与△ADC 只有一个角相等,∴△AEF 与△ACD 不一定相似,故④错误.综上,正确的有①②③.二、填空题(每题5分,共20分)7.如图32-6,直线l 1,l 2,…,l 6是一组等距的平行线,过直线l 1上的点A 作两条射线,分别与直线l 3,l 6相交于点B ,E ,C ,F ,若BC =2,则EF 的长是__5__. 8.[2017·自贡]如图32-7,在△ABC 中,MN ∥BC ,分别交AB ,AC 于点M ,N ,若AM =1,MB =2,BC =3,则MN 的长为__1__. 【解析】 ∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MN BC .∵AM =1,MB =2,BC =3,∴11+2=MN3,解得MN =1.图32-7图32-89.[2017·潍坊]如图32-8,在△ABC 中,AB ≠AC ,D ,E 分别为边AB ,AC 上的点,AC =3AD ,AB =3AE ,点F 为BC 边上一点,添加一个条件:__∠A =∠BDF (答案不唯一,合理即可)__,可以使△FDB 与△ADE 相似.(只需写出一个)【解析】 ∵AC =3AD ,AB =3AE ,∴AD AC =AE AB =13,又∵∠A =∠A ,∴△ADE ∽△ACB ,∴∠AED =∠B .故要使△FDB 与△ADE 相似,只需再添加一组对应角相等,或夹角的两边成比例即可. 10.[2016·舟山]如图32-9,已知△ABC 和△DEC 的面积相等,点E 在BC边上,图32-6DE∥AB交AC于点F,AB=12,EF=9,则DF的长是__7__.【解析】∵△ABC与△DEC的面积相等,∴△CDF与四边形AFEB的面积相等,∵AB∥DE,∴△CEF∽△CBA,∵EF=9,AB=12,∴EF∶AB=9∶12=3∶4,∴S△CEF∶S△CBA=9∶16,设△CEF 的面积为9k,则四边形AFEB的面积为7k.∵△CDF与四边形AFEB的面积相等,∴S△CDF=7k,∵△CDF与△CEF是同高不同底的三角形,∴面积比等于底之比,∴DF∶EF=7k∶9k,∴DF=7. 三、解答题(共20分)11.(10分)如图32-10,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)写出图中两对相似三角形(不得添加辅助线);(2)请分别说明两对三角形相似的理由.【解析】由两个角对应相等得两三角形相似,关键是得到∠BAC=∠DAE.解:(1)△ABC∽△ADE,△ABD∽△ACE;(2)∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.又∵∠ABC=∠ADE,∴△ABC∽△ADE,∴ABAD=ACAE.又∵∠BAD=∠CAE,∴△ABD∽△ACE.12.(10分)[2017·宿迁]如图32-11,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.证明:(1)∵AB=AC,∴∠B=∠C,∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,∵∠DEF=∠B,∴∠BDE=∠CEF,∴△BDE∽△CEF;(2)∵△BDE∽△CEF,∴BECF=DEEF,∵点E是BC的中点,∴BE=CE,∴CECF=DEEF,∵∠DEF=∠B=∠C,∴△DEF∽△ECF,图32-10图32-11∴∠DFE =∠CFE ,∴FE 平分∠DFC .(15分)13.(15分)[2017·株洲]如图32-12,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF 上,EF与BC 相交于点G ,连结CF .求证: (1)△DAE ≌△DCF ; (2)△ABG ∽△CFG .图32-12 第13题答图证明:(1)∵四边形ABCD 是正方形,△EDF 是等腰直角三角形, ∴∠ADC =∠EDF =90°,AD =CD ,DE =DF , ∴∠ADE +∠ADF =∠ADF +∠CDF , ∴∠ADE =∠CDF ,在△DAE 和△DCF 中,⎩⎨⎧DE =DF ,∠ADE =∠CDF ,DA =DC ,∴△DAE ≌△DCF (SAS ); (2)如答图,延长BA ,交ED 于点M , ∵△ADE ≌△CDF ,∴∠EAD =∠FCD , 即∠EAM +∠MAD =∠BCD +∠BCF , ∵∠MAD =∠BCD =90°, ∴∠EAM =∠BCF ,∵∠EAM =∠BAG ,∴∠BAG =∠BCF , ∵∠AGB =∠CGF ,∴△ABG ∽△CFG .(15分)14.(15分)[2018·中考预测]如图32-13,已知AD 是△ABC 的外角∠EAC 的平分线,交BC 的延长线于点D ,延长DA 交△ABC 的外接圆于点F ,连结FB ,FC . (1)求证:∠FBC =∠FCB ;(2)已知F A ·FD =12,若AB 是△ABC 外接圆的直径,F A =2,求CD图32-13的长.解:(1)证明:∵四边形AFBC内接于圆,∴∠FBC+∠F AC=180°,∵∠CAD+∠F AC=180°,∴∠FBC=∠CAD,∵AD是△ABC的外角∠EAC的平分线,∴∠EAD=∠CAD,∵∠EAD=∠F AB,∴∠F AB=∠CAD,又∵∠F AB=∠FCB,∴∠FBC=∠FCB;(2)由(1),得∠FBC=∠FCB,又∵∠FCB=∠F AB,∴∠F AB=∠FBC,∵∠BF A=∠BFD,∴△AFB∽△BFD,∴FBFD=F AFB,∴FB2=F A·FD=12,∴FB=23,∵F A=2,∴FD=6,AD=4,∵AB为圆的直径,∴∠BF A=∠BCA=90°,∴tan∠FBA=AFFB=223=33,∴∠FBA=30°,又∵∠FDB=∠FBA=30°,∴CD=AD·cos30°=4×32=2 3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形的相似
一、选择题(每小题6分,共24分)
1.(2014·重庆)如图,△ABC∽△DEF,相似比为1∶2,若BC=1,则EF的长是( B )
A.1 B.2 C.3 D
.4
2.(2014·泰安)在△ABC和△A1B1C1中,下列四个命题:
①若AB=A1B1,AC=A1C1,∠A=∠A1,则△ABC≌△A1B1C1;②若AB=A1B1,AC=A1C1,∠
B=∠B1,则△ABC≌△A1B1C1;③若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;④若AC:A1C
1
=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1.其中真命题的个数为( B )
A.4个 B.3个 C.2个 D
.1个
3.(2014·宁波)如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则
△ABC与△DCA的面积比为( C )
A.2∶3 B
.2∶5
C.4∶9 D
.2∶3
解析:∵AD∥BC,∴∠ACB=∠DAC,又∵∠B=∠ACD=90°,∴△CBA∽△ACD,BCAC=
AC
AD
=ABDC,AB=2,DC=3,∴BCAC=ACAD=ABDC=23,∴BCAC=23,∴cos∠ACB=BCAC=23,cos∠DAC=ACDA=23,
∴BCAC·ACDA=23×23=49,∴BCDA=49,∵△ABC与△DCA的面积比=BCDA,∴△ABC与△DCA的面积比
=49,故选:C
4.(2013·孝感)在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为
位似中心,相似比为12,把△EFO缩小,则点E的对应点E′的坐标是( D )
A.(-2,1) B
.(-8,4)
C.(-8,4)或(8,-4) D
.(-2,1)或(2,-1)
解析:如图
二、填空题(每小题6分,共24分)
5.(2014·邵阳)如图,在▱ABCD中,F是BC上的一点,直线DF与AB的延长线相交于
点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形:__△ABP∽△AED(答
案不唯一)__.
,第5题图) ,第6题图)
6.(2014·滨州)如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则ADAB=
__22__.
7.(2013·安徽)如图,P为平行四边形ABCD边AD上一点,E,F分别为PB,PC的中点,
△PEF,△PDC,△PAB的面积分别为S,S1,S2,若S=2,则S1+S2=__8__.
解析:过点P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,∴四边形PQCD与四边
形APQB都为平行四边形,∴△PDC≌△CQP,△ABP≌△QPB,∴S△PDC=S△CQP,S△ABP=S△QPB,∵
EF为△PCB的中位线,∴EF∥BC,EF=12BC,∴△PEF∽△PBC,且相似比为1∶2,∴S△PEF∶
S△PBC=1∶4,S△PEF=2,∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=8
,第7题图) ,第8题图)
8.(2014·娄底)如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高
度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为__9__m.
三、解答题(共52分)
9.(10分)(2013·巴中)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=63,AF=43,求AE的长.
(1)证明:∵▱ABCD,∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD
+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C.在△ADF与△DEC中,∠AFD=∠C,∠ADF=∠DEC,∴△
ADF∽△DEC
(2)解:∵▱ABCD,∴CD=AB=8.由(1)知△ADF∽△DEC,∴ADDE=AFCD,∴DE=AD·CDAF=
63×8
43
=12.在Rt△ADE中,由勾股定理得AE=DE2-AD2=122-(63)2=6
10.(10分)(2014·巴中)如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为
A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请
画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即S△A1B1C1:S△A2B2C2=____(不写解答过程,直接
写出结果).
解:(1)如图所示:△A1B1C1即为所求
(2)如图所示:△A2B2C2即为所求
(3)∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,
∴△A1B1C1与△A2B2C2的相似比为1∶2,∴S△A1B1C1∶S△A2B2C2=1∶4
11.(10分)(2013·德宏州)如图,是一个照相机成像的示意图.
(1)如果像高MN是35 mm,焦距是50 mm,拍摄的景物高度AB是4.9 m,拍摄点离景物
有多远?
(2)如果要完整的拍摄高度是2 m的景物,拍摄点离景物有4 m,像高不变,则相机的
焦距应调整为多少毫米?
解:根据物体成像原理知:△LMN∽△LBA,∴MNAB=LCLD.(1)∵像高MN是35 mm,焦距是
50 mm,拍摄的景物高度AB是4.9 m,∴3550=4.9LD,解得LD=7,∴拍摄点距离景物7米
(2)拍摄高度是2 m的景物,拍摄点离景物有4 m,像高不变,∴35LC=24,解得LC=70,
∴相机的焦距应调整为70 mm
12.(10分)(2014·遵义)如图,▱ABCD中,BD⊥AD,∠A=45°,E,F分别是AB,CD
上的点,且BE=DF,连接EF交BD于点O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于点G,当FG=1时,求AD的长.
(1)证明:∵四边形ABCD是平行四边形,∴DC=AB,DC∥AB,∴∠ODF=∠OBE,在△ODF
与△OBE中,∠ODF=∠OBE,∠DOF=∠BOE,DF=BE,∴△ODF≌△OBE(AAS),∴BO=DO
(2)解:∵BD⊥AD,∴∠ADB=90°,∵∠A=45°,∴∠DBA=∠A=45°,∵EF⊥AB,
∴∠G=∠A=45°,∴△ODG是等腰直角三角形,∵AB∥CD,EF⊥AB,∴DF⊥OG,∴OF=FG,
△DFG是等腰直角三角形,∵△ODF≌△OBE(AAS),∴OE=OF,∴GF=OF=OE,即2FG=EF,
∵△DFG是等腰直角三角形,∴DF=FG=1,∴DG=DF2+FG2=2,∵AB∥CD,∴ADDG=EFFG,
即AD2=21,∴AD=22
13.(12分)(2013·衢州)
(1)提出问题
如图①,在等边△ABC中,点M是BC上的任意一点(不含端点B,C),连接AM,以AM
为边作等边△AMN,连接CN.求证:∠ABC=∠ACN.
(2)类比探究
如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其他条件不变,
(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)拓展延伸
如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B,C),连接AM,
以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连接CN.试探究∠ABC与∠ACN的数量关系,
并说明理由.
(1)证明:∵△ABC,△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,∵在△BAM和△CAN中,AB=AC,∠BAM=∠CAN,AM=AN,∴△BAM≌△CAN(SAS),∴∠ABC
=∠ACN
(2)解:结论∠ABC=∠ACN仍成立.理由如下:∵△ABC,△AMN是等边三角形,∴AB
=AC,AM=AN,∠BAC=∠MAN=60°,∴∠BAM=∠CAN,∵在△BAM和△CAN中,
AB=AC,
∠BAM=∠CAN,
AM=AN,
∴△BAM≌△CAN(SAS),∴∠ABC=∠ACN (3)解:∠ABC=∠ACN.理由如
下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN,∴△ABC∽△AMN,∴
AB
AM
=ACAN,又∵∠BAM=∠BAC-∠MAC,∠CAN=∠MAN-∠MAC,∴∠BAM=∠CAN,∴△BAM∽△
CAN,∴∠ABC=∠ACN
2015年名师预测
1.如图,M是Rt△ABC的斜边BC上异于B,C的一定点,过M点作直线截△ABC,使截
得的三角形与△ABC相似,这样的直线共有( C )
A.1条 B.2条 C.3条 D
.4条
,第1题图) ,第2题图)
2.如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在
x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则
点P的坐标为__(2,4-22)__.
