刚体自测题
第03章---刚体力学习题汇总

(A)匀角速转动; (B)匀角加速转动;
(D)
(C)角加速度越来越大的变加速运动;
(D)角加速度越来越小的变加速运动。
分析:当棒转到θ角位置时,棒所受 到的外力矩为:
θ
M 1 mgLcos 根据转动定律 M I ,有:
2
mg
1 mgL cos
可见角5
5. (a)(b)两图中的细棒和小球均相同,系统可绕o 轴在竖直面内自由转动系统从水平位置静止释放,转
(D)只有动量守恒
(C)
分析:
(A)错。非弹性碰撞,机械能不守恒。 (B)错。轴上有外力,动量不守恒。
(C)对。外力矩为零,角动量守恒。
2
2.一绕固定水平轴0匀速转动的转盘,沿图示的同一 水平直线从相反方向射入两颗质量相同、速率相等的 子弹并留在盘中,则子弹射入转盘后的角速度
(A)增大 (B)不变 分析:
边缘并粘在上面,则系统的角速度是
3v
。
分析:取如图的细长条面积:
4b
b
I r 2ds r 2adr
1 ab3 1 mb2
0
3
3
合外力矩为零,系统角动量守恒。
mvb (1 mb2 mb2 )
3
3v
4b
9
二、填空题
1.如图,半径为R,质量为M的飞轮,
可绕水平轴o在竖直面内自由转动(飞
R2
2 3
mgR
11
3.一飞轮的转动惯量为I,在t=0时角速度为 0 , 此后
飞轮经历制动过程。阻力矩M的大小与角速度的平方
成正比,比例系数K>0。当 0 / 3 时,飞轮的角加
速度 = k02 9I ,从开始制动到 0 / 3所经过
4刚体-例题
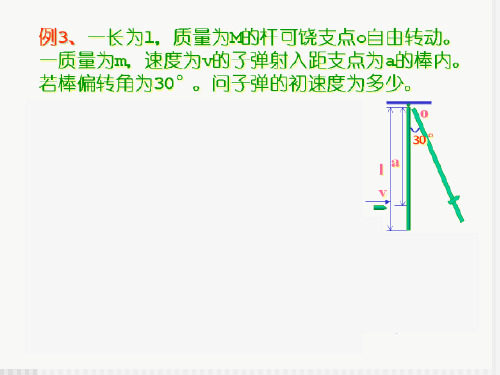
2vc d dt l sin
3(sin 3 sin 2 cos 2 cos ) g ac (1 3 sin 2 ) 2 4 6 cos 3 cos N m( g ac ) m g (1 3 sin 2 ) 2
动平衡
练习14.18(p533):
半径为a的匀质球以速度v沿水平表面作纯滚动的过程中与高度为 h<a的台阶发生非弹性碰撞。求球能翻越台阶的最小速度(假定在 碰撞点没有发生滑动)
解:碰撞前后关于A点角动量守恒:
m v0 (a h) I c0 I A
w0 a
v0
A
0 v0 / a
练习13.7(p528):
镜框紧帖着墙站在粗糙的钉上,稍受扰动就向下倾倒。求镜框跳离钉 子时与墙所作的角。
解:
m glsin I =? m g N m ay
m glsin / I 1 2 I m gl(1 cos ) 2
2
14.10(p413) 半径为r的匀质球体在半径为R的球形碗 内作无滑动的滚动。求球在碗底附近小幅度摆动的周期。
解法二:用能量守恒求解
即
上式求导可得
解法三:关于瞬心角动量定理
14.16(p413)将半径为r的小球轻轻搁在半径为R的静止大 球的顶端,小球就向下滚动。问小球滚到何处将飞离大球。
A点竖直速度为零:
C mg vc N A
l vc sin 2 1 I c ml 2 12
vc
2 l
3gl(1 cos ) sin vc 2 1 3 sin
2 2
dvc d 3gl(1 cos ) sin 2 d 2vc 2 dt d 1 3 sin dt
刚体习题

2
3
例2 求一质量为m,半径为R的均匀实心球对其一条直 径为轴的转动惯量。 解法一:实心球可被看作由 许多个小薄圆盘构成,如图 所示选取其中一小薄圆盘, 球体绕Z轴转动,离球心Z高 处切一厚为dz的薄圆盘。 其半径为: r
R2 Z 2
其体密度:
其体积: dV
m
r dZ ( R Z )dZ
2 2 2
4 3 R 3
其质量:dm
dV ( R Z )dZ
2 2
4
1 2 1 其转动惯量: dI r dm ( R 2 Z 2 ) 2 dZ 2 2
整个实心球体的转动惯量:
1 8 2 2 2 2 5 I dI ( R Z ) dZ R mR2 R 2 15 5
4 3 4 3 0 0
2 R sin2 d cos
4 0
2 R 1 cos2 d cos
4 0源自 cos 2 R cos 3 0
3 4
m 1 2 4 1 2 2 R 1 1 mR 3 3 3 4 R 2
R
5
6
7
2
该小圆环的质量:
dm dS 2 R sin d
2
1
该小圆环关于其转轴的转动惯量:
dI r dm R sin 2 R2 sin d 2 R4 sin3 d
2 2
则整个球壳关于转轴的转动惯量为:
I dI 2 R sin d 2 R sin d
例1求一质量为m,半径为R的空心薄球壳对其一条直径 为轴的转动惯量。 m r R sin 解法一:薄球壳的质量 面密度为:
刚体定轴转动习题

刚体定轴转动习题刚体定轴转动⼀、选择题(每题3分)1、个⼈站在有光滑固定转轴的转动平台上,双臂伸直⽔平地举起⼆哑铃,在该⼈把此⼆哑铃⽔平收缩到胸前的过程中,⼈、哑铃与转动平台组成的系统的( )(A)机械能守恒,⾓动量守恒; (B)机械能守恒,⾓动量不守恒,(C)机械能不守恒,⾓动量守恒; (D)机械能不守恒,⾓动量不守恒.2、⼀圆盘绕通过盘⼼且垂直于盘⾯的⽔平轴转动,轴间摩擦不计.如图射来两个质量相同,速度⼤⼩相同,⽅向相反并在⼀条直线上的⼦弹,它们同时射⼊圆盘并且留在盘内,则⼦弹射⼊后的瞬间,圆盘和⼦弹系统的⾓动量L以及圆盘的⾓速度ω的变化情况为( ) (A) L 不变,ω增⼤ (B) 两者均不变(C) L不变,ω减⼩ (D) 两者均不确定3、有两个⼒作⽤在⼀个有固定转轴的刚体上:(1)这两个⼒都平⾏于轴作⽤时,它们对轴的合⼒矩⼀定是零(2)这两个⼒都垂直于轴作⽤时,它们对轴的合⼒矩可能是零(3)当这两个⼒的合⼒为零时,它们对轴的合⼒矩也⼀定是零(4)当这两个⼒对轴的合⼒矩为零时,它们的合⼒也⼀定是零在上述说法中,正确的是()(A)只有(1)是正确的(B)只有(1)、(2)正确(C)只有(4)是错误的(D)全正确4、以下说法中正确的是()(A)作⽤在定轴转动刚体上的⼒越⼤,刚体转动的⾓加速度越⼤。
(B)作⽤在定轴转动刚体上的合⼒矩越⼤,刚体转动的⾓速度越⼤。
(C)作⽤在定轴转动刚体上的合⼒矩越⼤,刚体转动的⾓加速度越⼤。
(D)作⽤在定轴转动刚体上的合⼒矩为零,刚体转动的⾓速度为零。
5、⼀质量为m的均质杆长为l,绕铅直轴o o'成θ⾓转动,其转动惯量为()6、⼀物体正在绕固定光滑轴⾃由转动()(A) 它受热膨胀或遇冷收缩时,⾓速度不变.(B) 它受热时⾓速度变⼩,它遇冷时⾓速度变⼤.(C)它受热或遇冷时,⾓速度均变⼤.(D) 它受热时⾓速度变⼤,它遇冷时⾓速度变⼩.O7、关于刚体对轴的转动惯量,下列说法中正确的是( )(A) 只取决于刚体的质量,与质量的空间分布和轴的位置⽆关.(B) 取决于刚体的质量和质量的空间分布,与轴的位置⽆关.(C) 取决于刚体的质量,质量的空间分布和轴的位置.(D) 只取决于转轴的位置,与刚体的质量和质量的空间分布⽆关.8、两个均质圆盘A 和B 的密度分别为A ρ和B ρ,若A ρ﹥B ρ,但两圆盘的质量与厚度相同,如两盘对通过盘⼼垂直于盘⾯的转动惯量各为J A 和J B ,则()(A )J A >J B (B )J B >J A(C )J A = J B (D )J A 、 J B 哪个⼤,不能确定9、某转轮直径d =40cm ,以⾓量表⽰的运动⽅程为θ=3t -3.02t +4.0t ,式中θ的单位为rad,t 的单位为s,则t =2.0s 到t =4.0s 这段时间内,平均⾓加速度为( )(A)212-?srad (B)26-?s rad(C)218-?s rad (C)212-?s m10、轮圈半径为R ,其质量M 均匀分布在轮缘上,长为R 、质量为m 的均质辐条固定在轮⼼和轮缘间,辐条共有2N 根。
刚体习题和答案

作业5 刚体力学♫刚体:在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad s ω=,t =20s 时角速度为00.8ωω=,那么飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间飞轮所转过的角度θ= 250rad . 【解答】飞轮作匀变速转动,据0t ωωβ=+,可得出:200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律:定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如下图.绳与轮之间无相对滑动.假设某时刻滑轮沿逆时针方向转动,那么绳中的力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1<m 2),实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得:21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于. (B) 大于,小于2. (C) 大于2. (D) 等于2. 【解答】设飞轮的半径为R ,质量为m ,根据刚体定轴转动定律M J β=,当挂质量为m 的重物是:mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时,有: '2mgR J β=,2'mgRJβ=,比拟二者可得出结论。
刚体的转动习题

第四章刚体的转动习题(一)教材外习题一、选择题:1.关于刚体对轴的转动惯量,下列说法中正确的是(A)只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C)取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
()2.两个均质圆盘A和B的密度分别为ρA和ρB,若ρA>ρB,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面轴的转动惯量各为J A和J B,则(A)J A>J B(B)J B>J A(C)J A=J B(D)J A、J B哪个大,不能确定()3.花样滑冰运动员绕过自身的竖直轴转动,开始时两臂伸开,转动惯量为J0角速度为ω0,然后她将两臂收回,使转动惯量减少J0/3。
这时她转动的角速度变为(A)ω0/3 (B)(1/3)ω0(C)3ω0 (D)3ω0()4.如图所示,一水平刚性轻杆,质量不计,杆长l =20cm,其上穿有两个小球。
初始时,两小球相对杆中心O对称放置,与O的距离d=5cm,二者之间用细线拉紧。
现在让细杆绕通过中心O的竖直固定轴作匀角速的转动,转速为ω0,再烧断细线让两球向杆的两端滑动。
不考虑转轴的和空气的摩擦,当两球都滑至杆端时,杆的角速度为(A)ω0 (B)2ω0(C)ω0/2 (D)ω0/4()二、填空题:1.半径为r =1.5m的飞轮,初角速度ω0=10rad·s-1,角加速度β = -5rad·s-2,则在t=_______ _________时角位移为零,而此时边缘上点的线速度v= _______________________。
2.半径为30cm的飞轮,从静止开始以0.50rad·s-2的匀角加速度转动,则飞轮边缘上一点在飞轮转过240︒时的切向加速度a t =______________,法向加速度a n =_______________。
第三章 刚体习题
一计算题3-1-1 一汽车发动机曲轴的转速在s12内由13minr102.1-⋅⨯均匀地增加到13minr107.2-⋅⨯。
求:(1) 曲轴转动的角加速度;(2) 在此时间内,曲轴转了多少转?3-1-2 用落体观察法测定飞轮的转动惯量,如图所示。
将半径为R的飞轮支撑在O点上,然后再绕过飞轮的绳子的一端挂一质量为m的重物,令重物由静止开始下落,带动飞轮转动。
记录重物下落的距离和时间,便可计算出飞轮的转动惯量。
试写出它的计算式(轴承的摩擦忽略不计)。
3-1-3 质量为1m和2m的两物体A、B分别悬挂在如图所示的组合轮两边,设两轮的半径分别为R和r,两轮的转动惯量分别为J1和J2,轮与轴承间的摩擦力略去不计,绳的质量也略去不计。
试求两物体的加速度和两边绳的张力(假设21mm>)。
3-1-4 如图所示装置,定滑轮是半径为R,质量为m2匀质圆盘,滑轮两边分别悬挂质量均为m的物体A、B。
置于倾角为30=θ的光滑斜面上,若B向下作加速运动时,求:(1) B下落的加速度大小;(2) 滑轮两边绳子的张力。
(设绳的质量及伸长均不及,绳与滑轮间无滑动,滑轮与轴承近光滑)。
3-1-5 1970年4月24日,我国发射第一颗人造卫星,其近地点为m1039.45⨯,远地点高度为m1038.26⨯。
求卫星在近地点和远地点时的速率(已知地球半径为km6378=R)。
3-1-6 一根均匀米尺,在mc60刻度处被钉到墙上,且可以在竖直平面内自由转动。
先用手使米尺保持水平,然后释放。
求刚释放时米尺的角加速度和米尺到竖直位置时的角速度各是多少?3-1-7 长为l、质量为m的均匀细杆可绕端点O固定水平光滑轴转动。
把杆摆平后无初速地释放,杆摆到竖直位置习题3-1-2图习题3-1-3图习题3-1-4图习题3-1-7图时刚好和水平桌面上的小物块相碰。
小物块的质量为2/m 。
设碰撞是完全非弹性的,碰后物块沿摩擦系数为μ的水平面滑动,试求此物快滑过的距离。
刚体力学 习题库
第四章 刚体力学一、计算题 1。
如图所示,一个质量为m 的物体与绕在定滑轮上的绳子相联,绳子质量可以忽略,它与定滑轮之间无滑动.假设定滑轮质量为M 、半径为R ,其转动惯量为221MR ,滑轮轴光滑.试求该物体由静止开始下落的过程中,下落速度与时间的关系.解:根据牛顿运动定律和转动定律列方程 对物体: mg -T =ma ①2分对滑轮: TR = J β ② 2分 运动学关系: a =R β ③ 1分将①、②、③式联立得a =mg / (m +21M ) 1分 ∵ v 0=0,∴ v =at =mgt / (m +21M ) 2分2.如图所示,转轮A 、B 可分别独立地绕光滑的固定轴O 转动,它们的质量分别为m A =10 kg 和m B =20 kg,半径分别为r A 和r B .现用力f A 和f B 分别向下拉绕在轮上的细绳且使绳与轮之间无滑动.为使A 、B 轮边缘处的切向加速度相同,相应的拉力f A 、f B 之比应为多少?(其中A 、B 轮绕O 轴转动时的转动惯量分别为221A A A r m J =和221B B B r m J =)解:根据转动定律 f A r A = J A βA ① 1分其中221A A A r m J =,且 f B r B = J B βB ② 1分 其中221B B B r m J =.要使A 、B 轮边上的切向加速度相同,应有a = r A βA = r B βB ③ 1分由①、②式,有BB B AA AB A B A B A B A r m r m r J r J f f ββββ== ④ 由③式有 βA / βB = r B / r A将上式代入④式,得 f A / f B = m A / m B = 212分3。
一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示).解:设绳子对物体(或绳子对轮轴)的拉力为T ,则根据牛顿运动定律和转动定律得:mg 。
刚体习题
16. 质量为m 的矩形均匀薄板,长为a 宽为b ,求它 对通过板的几何中心并与板面垂直的z 轴的转动 惯量。
y
a
z b
x
y
解:薄板位于xOy面内。
x
a z b y
Jx Jy
a 2 a 2
m 1 2 y bdy ma ab 12
2
同理:
b 2 b 2
m 1 x adx mb2 ab 12
T2 m2 g
M T1 T
m1
1
a
m1 g
ห้องสมุดไป่ตู้对定滑轮
1 rT1 rT2 Mr 2 2 且有 a r
(m1 m2 ) g 可得 M (m1 m2 )r 2
M (2m1m2 m1 ) g 2 T1 M m1 m2 2
(m1 m2 ) g a M m1 m2 2
,则该时刻P点的 v =_________。
14.一个物体可否具有角动量而无动量(为0)? 可 ____________ (填可、否); 一个物体可否具有动量而无角动量(为0)? 可 ____________ (填可、否); 一个物体可否具有动量而无机械能(为0)? 可 ____________ (填可、否); 一个物体可否具有机械能而无动量(为0)? ____________ (填可、否)。 可
Ny
O
O
M i外z I z
Nx
i
1 2 Fl ml 3
lˊ
l
lˊ
C
Fi外 mac
i
mg
F F
l F N x macx mac m 2
N y mg macy macn m 2 l 0 2
《大学物理》刚体的转动练习题及答案
《大学物理》刚体的转动练习题及答案一、简答题:1、为什么刚体绕定轴转动的动能的改变只与外力矩有关,而与内力矩无关?答案:对刚体,由于刚体内各质点间相对位移始终为零,内力总是成对出现,每对内力大小相等,方向相反,在一直线上,故内力矩做功之和一定为零,故刚体绕定轴转动的动能的改变与内力矩无关。
2、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案:刚体定轴转动时,若所受合外力矩为零或不受外力矩,则刚体的角动量保持不变。
3、下列物理量中,哪些量与原点的选择有关:(1) 速度,(2) 位矢,(3) 位移,(4) 角动量,(5) 动量 答案:与原点有关的物理量为:位矢,角动量。
4、质量、半径相同的两个圆盘,第一个质量分布均匀,第二个大部分质量分布在盘边缘,当它们以相同的角速度绕通过盘中心的轴转动时,哪个盘的转动动能大?为什么?答案:第二个盘的动能大。
因为由刚体转动动能221ωJ E k =知,在角速度一样时,转动惯量大的动能大;又因为2121mR J =,22mR J ≈,第二个转动惯量较大,所以转动动能较大。
5、在某一瞬时,刚体在一外力矩作用下,其角速度可以为零吗? 其角加速度可以为零吗?答案:由刚体转动定律αJ M =,知,在某一瞬时,刚体在一外力矩作用下,其角加速度不可以为零;由dtd ωα=,有⎰+=t dt 00αωω,可知其角速度此时可以为零。
6、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案:刚体绕定轴转动的转动定律:刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比。
表达式为:αJ M =。
7、简述刚体定轴转动时的特点有哪些, 常用哪些物理量来描述刚体的转动?答案:刚体定轴转动的特点:转轴相对参照系固定,刚体内所有点都具有相同的角位移、角速度、角加速度;质点在垂直转轴的平面内运动,且作圆周运动。
刚体的转动通常用转动惯量J 、力矩M 、角加速度α、角动量L 等来描述。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
1(计算题 绕定轴转动的刚体的转动定律 动能定理
一、 选择、填空题
1. 一半径为R ,质量为m 的圆形平板在粗糙水平桌面上,绕垂直于平板器且过圆心的轴转
动,摩擦力对OO’轴之力矩为
【 A 】
m g R 32)
A (μ;m gR )
B (μ;mgR 2
1
)C (μ;0)D ( 2. 转动着的飞轮的转动惯量为J ,在t=0时角速度为ω0。
此后飞轮经历制动过程,阻力矩
M 的大小与角速度ω的平方成正比,比例系数为k (k 为大于0的常数),当03
1
ωω=时,飞
轮的角加速度J 9K 2
0ωβ-=,从开始制动到031ωω=所经过的时间K
J
2t 0ω=。
3. 一根均匀棒长l ,质量m ,可绕通过其一端且与其垂直的定轴在铅直面内自由转动,开始时棒静止水平位置,它当自由下摆时,它的角速度等于0,初角加速度等于l
2g
3。
已知均匀棒对于通过其一端垂直于棒的转动惯量为2
ml 3
1J =。
4. 在半径为R 的定滑轮上跨一细绳,绳的两端分别挂着质量为m 1和m 2的物体,且m 1>m 2。
若滑轮的角加速率为β,则两侧绳中的张力分别为βR m g m T 111-=,βR m g m T 222+=。
二、 计算题
1. 如图所示,一个质量为m 的物体与绕在定滑轮上的绳子相联,绳子质量可以忽略,它与定滑轮之间无滑动,假设定滑轮质量为M 、半径为R ,其转动惯量为2MR 2
1
J =
,滑轮轴光滑。
试求该物体由静止下落的过程中,下落速率与时间的关系。
研究系统:物体和滑轮,受力分析如图所示
当物体下降x 距离时,物体和滑轮的运动方程为
ma T mg =-
β2MR 21R 'T =
, R
a ,'T T ==β dt dv m T mg =-,dt
dv
M 21T =
两式相加得到:dt dv )M 21m (mg +=,dt )M m 2(mg 2dv +=
, t )M m 2(m g
2v +=
)
2(计算题θ
)
4(计算题2. 一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示。
轴水平且垂直于轮轴面,其半径为R ,整个装置架在光滑的固定轴承之上,当物体从静止释放后,在时间t 内下降了一段距离s ,试求整个轮轴的转动惯量(用m 、R 、t 和s 表示)。
✉ 研究系统,物体和轮轴,受力分析如图所示
当物体下降s 距离时,物体和滑轮的运动方程为
ma T mg =-
βJ R 'T =, R
a ,'T T =
=β dt dv m T mg =-,dt dv R J T =, 两式相加得到:dt
dv
)R J m (mg 2+=,
t )
R
J m (mg
v 2+=
根据:dt
ds
v =,tdt )R J m (mg ds 2+=
,2
2
t )R J m (mg 21s +=, 22mR )1s 2gt (
J -= 3. 以M=20N ⋅m 的恒力矩作用在有固定轴的转轮上,在10s 内该轮的转速由零增大到100 rev/min 。
此时移去该力矩,转轮因摩擦力矩的作用又经100 s 而停止。
试推算此转轮的转
动惯量。
✉ 设转轮受到的阻力矩:f M
根据题意:βJ M M f =-,根据:1t βω=,得到:1
f t J M M ω
=- 移去外力矩后:βJ M f =-,根据:2t 0βω+=,得到:2
f t J M ω
=
所以:2
1
t J
t J
M ω
ω
+=,)
t t (t Mt J 212
1+=
ω,2m kg 4.17J ⋅=
4. 一均质细杆,质量为0.5 kg ,长为0.40 m ,可绕杆一端的水平轴转动。
若将此杆放在水平位置,然后从静止释放,试求杆转动到铅直位置时的动能和角速度。
✉ 细棒绕通过A 点的定轴转动,取顺时针转过的角度为正,当
细棒由水平位置转过角度θ,重力矩做的功为:
θθθ
d cos mg 2
1
A 0
g ⎰
=,θsin mgR 21A g =
根据刚体绕定轴转动的动能定理:0J 21A 2g -=
ω,0J 2
1
sin mgl 212-=ωθ 转过任一角度时,角速度为:
J sin mgl θω=,将2ml 31J =代入,得到:l
sin g 3θω=
)
1(计算题杆转动到铅直位置时的动能:2
π
θ=
,细棒的动能:mgl 2
1
E k =
, J 98.0E k = 杆转动到铅直位置时的角速度:2
π
θ=,l
g
3=
ω,s /rad 57.8=ω
一、 选择、填空题
1. 花样滑冰运动员绕自身的竖直轴转动,开始时臂伸开,转动惯量为J 0角速度为ω0,然后她将两臂收回,使转动惯量减少为0J 3
1
J =。
这时她转动的角速度变为 【 C 】
00
003)
D (3)C ()3/1()B (3
1)
A (ωωωω
4. 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂,现有一个小球自左方水平打击细杆,设小球与细杆之间为非弹性碰撞,则在碰撞过
程中对细杆与小球这一系统。
【 C 】
(A) 只有机械能守恒; (B) 只有动量守恒;
(C) 只有对轴O 的角动量守恒; (D) 机械能、动量和角动量均守恒。
5. 匀质园盘水平放置,可绕过盘心的铅直轴自由转动,园盘对该轴的转动惯量为J 0,当转动角速度为ω0时,有一质量为m 的质点落到园盘上,并粘在距轴R/2处(R 为园盘半径),则它们的角速度02
00
m
R 4
J J ωω+=
二、 计算题
1. 长为l 质量为m 0的细杆可绕垂直于一端的水平轴自由转动。
杆原来处于平衡状态。
现有一质量为m 的
)4(选择题)
5(选择题
)
4(计算题小球沿光滑水平面飞来,正好与杆下端相碰(设碰撞为完全弹性碰撞)使杆向上摆到
60=θ处,如图所示,求小球的初速度。
✉ 研究系统为小球和直杆,系统所受外力对于转轴
的力矩为零。
系统角动量守恒:ω200l m 3
1
mvl l mv +=
弹性碰撞系统动能守恒:
22022
0)l m 3
1(21mv 21mv 21ω+= 碰撞后,直杆绕固定轴转过角度
60=θ,直杆重力矩做的功等于直杆动能的增量
22000)l m 31
(210)60cos 1(gl m 21ω-=-- 2l 3
1g 21ω= 由以上三式得到:gl 6m
12m
3m v 0
0+=
4. 有一圆板状水平转台,质量M=200 kg ,半径R=3 m ,台上有一人,质量m=50 kg ,当他站在离转轴r=1m 处时,转台和人一起以ω1=1.35 rad/s 的角速度转动。
若轴处摩擦可以忽略不计,问当人走到台边时,转台和人一起转动的角速度ω为多少?
✉ 研究系统为人和转台,系统所受外力对
转轴的力
矩为零,系统角动量守恒:
ωωωω221212mR MR 2
1
mr MR 21+=+ 当人走到台边时,转台和人一起转动的角速度:12
22
2mR
2MR mr 2MR ωω++=,s /rad 95.0=ω 刚体力学习题课 (二)
1. 一电机的电枢转速为1800 r/min ,当断电后,电枢经20s 停下,试求 (1) 在此时间内电枢转了多少圈?
(2) 电枢经过10 s 时的角速度以及电枢周边的线速度,切向加速度和法向加速度。
✉ 刚体绕定轴转动的角速度:t 0βωω+=,t
ωωβ-=
,t
ωβ-
=,2
s /rad 3πβ-=
转过的角度:20t 21t βωθ+
=, rad 600πθ=,转过的圈数:3002N ==π
θ 当s 10t =,t 0βωω+=,s /rad 30πω=
)
4(计算题线速度:s /m 3R v πω==,切向加速度:βτR dt
dv
a ==
,2s /m 3.0a πτ-= 法向加速度:22
n R R
v a ω==,22n s /m 90a π=
4. 长为L 的均匀细杆可绕端点O 固定水平光滑轴转动。
把杆摆平后无初速地释放,杆摆到竖直位置时刚好和光滑水平桌面上的小球相碰。
球的质量与杆相同。
设碰撞是弹性 ,求碰后小球获得的速度。
研究对象为直杆和小球
过程一为直杆在重力矩的作用下,绕通过O 的轴转 动,重力矩做的功等于直杆的转动动能 根据刚体动能定理:
0J 2
1
mgl 212O -=ω 碰撞前的角速度:l
g
3=
ω 过程二为直杆和小球发生弹性碰撞:系统的角动量和动能守恒
mvl 'J J O O +=ωω和2O 22O 'J 2
1
mv 21J 21ωω+=,
将l g 3=ω代入上述两式:得到gl 32
1
v =。
