第四章-曲线坐标系下张量分析
4.7张量方程的曲线坐标分量表示法
张量分析 及连续介质力学
4.7 张量方程的曲线坐标分量表示法
由笛卡儿坐标系中相对简单的张量分量方程得到任意曲 线坐标系中的张量分量方程的步骤: 线坐标系中的张量分量方程的步骤: 步 骤 示 1. 运动方程
4.
σ i ;j j + ρf i = ρwi
或
i ij → g ij
或 i ( ) → i (
( ),i → ( );i
ijk
上述做法的理由是张量方程在笛卡儿坐标系中成立, 上述做法的理由是张量方程在笛卡儿坐标系中成立,则 在任意其它坐标系中也成立。 在任意其它坐标系中也成立。
σ xx σ xy σ xz + + + ρf x = ρwx x y z σ yx x + σ yy y + σ yz z + ρf y = ρwy
例
1. 按照笛卡儿坐标系列出 方程。 方程。
σ zx σ zy σ zz + + + ρf z = ρwz x y z
2. 应用求和约定将上述方程 写程指标形式。 写程指标形式。
eijk →
e →
ijk
σ ij ; j + ρf i = ρwi
(i = 1,
2, 3)
)
2.
σ ij x
j
+ ρf i = ρwi
(i = 1,
2, 3)
3. 上升和降低指标,使哑指 上升和降低指标, 标一上一下, 标一上一下,自由指标在 相同位置。 相同位置。
3.
σ i j + ρf i = ρwi j x 或 σ ij + ρf i = ρwi x j
第四章变形梯度与应变(徐春晖、李明瑞)
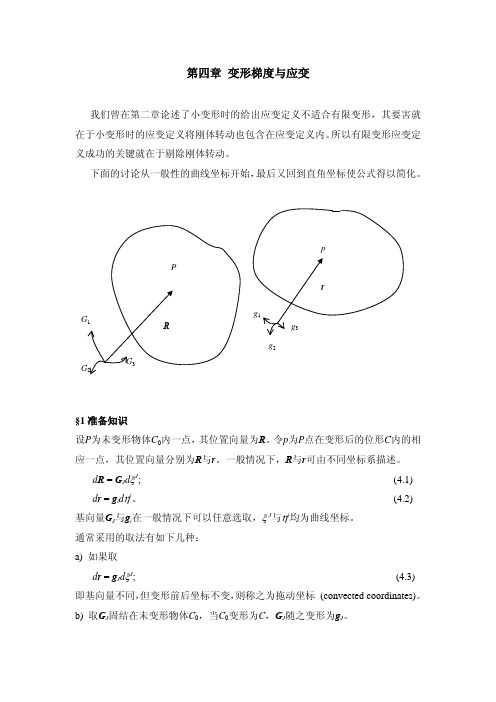
第四章 变形梯度与应变我们曾在第二章论述了小变形时的给出应变定义不适合有限变形,其要害就在于小变形时的应变定义将刚体转动也包含在应变定义内。
所以有限变形应变定义成功的关键就在于剔除刚体转动。
下面的讨论从一般性的曲线坐标开始,最后又回到直角坐标使公式得以简化。
§1准备知识设P为未变形物体C0内一点,其位置向量为R。
令p为P点在变形后的位形C内的相应一点,其位置向量分别为R与r。
一般情况下,R与r可由不同坐标系描述。
d R = G J dξJ;(4.1)d r = g i dηi。
(4.2) 基向量G J与g i在一般情况下可以任意选取,ξ J与ηi均为曲线坐标。
通常采用的取法有如下几种:a) 如果取d r = g J dξJ; (4.3) 即基向量不同,但变形前后坐标不变,则称之为拖动坐标 (convected coordinates)。
b) 取G J固结在未变形物体C0,当C0变形为C,G J随之变形为g J。
c) 取g J固结在已变形物体C,G J为相应的未变形前的,按照同一变形规律变过来的基向量。
d) G J与g i取为固定空间中的基向量,不随物体的变形而变,二者可以相同,也可不同,特别是二者均取之为同一的直角坐标系。
在变形前微线段的弧长向量平方为d R⋅d R = dξI dξJ G I⋅ G JG I⋅ G J = G IJ是基向量G I的度量张量。
变形后的弧长向量平方为d r⋅d r= dηi dηj g i⋅ g jg i⋅ g j = g ij是基向量g i的度量张量。
变形前后弧长平方的改变量为:d r⋅d r -d R⋅d R = dηi dηj g i⋅ g j- dξI dξJ G I⋅ G J。
如果将变形后的坐标看作是以变形前的坐标为自变量的函数,η = η(ξ),则有dηi dηj= ∂ηi/∂ξM∂ηj/∂ξK dξM dξK变换张量的求和指标(一般称为哑标,可以用任意字母表示),有d r⋅d r - d R⋅d R= ∂ηm/∂ξI∂ηk/∂ξJ dξI dξJ g m⋅ g k - dξI dξJ G I⋅ G J=( g mk∂ηm/∂ξI∂ηk/∂ξJ- G IJ) dξI dξJ = 2E IJ dξI dξJ (4.4) 张量E IJ为Green-Lagrange应变张量,也有称之为Green应变张量或Lagrange应变张量。
张量变换坐标系

张量变换坐标系引言:张量是一种广泛应用于数学、物理、计算机科学等领域的数学对象。
它是一个多维数组或矩阵,可以有效地表示和处理多维数据。
张量的坐标系变换在某些领域中非常重要,如物体运动模拟、图像处理、机器学习等。
本文将深入探讨张量的坐标系变换,并介绍其在实际应用中的重要性和应用示例。
二. 张量的基本概念在深入探讨张量的坐标系变换之前,我们先来了解一下张量的基本概念。
张量是一个多维数组,可以看做是一个具有多个维度的矩阵。
一维张量是一个向量,二维张量是一个矩阵,三维张量是一个立体数组,以此类推。
张量的维度可以是任意整数,因此可以表示各种复杂的数据结构。
张量的坐标系变换是指在不同坐标系中表示和操作张量的过程。
坐标系变换可以对张量进行平移、旋转、缩放等操作,从而改变张量在空间中的表示和性质。
三. 坐标系的表示和变换坐标系是描述空间中位置和方向的一种数学工具。
在二维空间中,我们通常使用笛卡尔坐标系,其由两个垂直的轴组成。
在三维空间中,我们使用三个互相垂直的轴来构成笛卡尔坐标系。
坐标系的变换可以通过矩阵运算来表示。
假设我们有一个三维向量[Vx, Vy, Vz],表示在原坐标系中的坐标。
若我们希望将该向量转换到新的坐标系中,可以使用一个变换矩阵T,通过T与原向量相乘,得到在新坐标系中的坐标。
变换后的向量的坐标表示为:[T * Vx, T * Vy, T * Vz]变换矩阵通常由坐标轴的方向向量构成,并且是一个正交矩阵。
在实际应用中,可以通过平移、旋转和缩放等操作来构造变换矩阵。
四. 张量的坐标系变换张量的坐标系变换是指将张量从一个坐标系变换到另一个坐标系中的过程。
在坐标系变换中,我们使用同样的变换矩阵来对张量的每一个元素进行变换。
假设我们有一个三维张量T,其坐标表示为[Tx, Ty, Tz]。
如果我们希望将该张量从原坐标系变换到新坐标系中,可以通过定义一个变换矩阵A,对T中的每一个元素应用A进行变换。
变换后的张量的坐标表示为:[A * Tx, A * Ty, A * Tz]需要注意的是,对张量的坐标系进行变换并不会改变张量的维度和形状。
张量分析及其应用

⎧1, i = j δ ij = ⎨ ⎩0, i ≠ j
δ 其中 i,j 为自由指标,取遍1,2,3;因此, i j 可确 定一单位矩阵:
⎡δ 11 δ 12 δ 13 ⎤ ⎡1 0 0⎤ ⎢δ δ 22 δ 23 ⎥ = ⎢0 1 0⎥ ⎢ 21 ⎥ ⎢ ⎥ ⎢δ 31 δ 32 δ 33 ⎥ ⎢0 0 1⎥ ⎣ ⎦ ⎣ ⎦
∂U i =0 ∂xi
或
∂U1 ∂U 2 ∂U 3 + + =0 ∂x1 ∂x2 ∂x3
∂U x ∂U y ∂U z + + =0 ∂x ∂y ∂z
1.4 指标记法的运算
1.4.5 例题 ——熟悉指标记法和普通记法的转换 不可压缩牛顿流体的Navier-Stokes方程:
∂U i ∂p ∂U i ∂U i ) = ρ bi − ρ( +U j +μ ∂x j∂x j ∂t ∂x j ∂xi
写出其普通记法
1.4 指标记法的运算
1.4.5 例题 ——熟悉指标记法和普通记法的转换 弹性力学平衡方程方程:
∂Txx ∂Txy ∂Txz + + + bx = 0 ∂x ∂z ∂y ∂Tyx ∂x + ∂Tyy ∂y + ∂Tyz ∂z + by = 0
∂Tzx ∂Tzy ∂Tzz + + + bz = 0 ∂x ∂z ∂y
是一个数值,即
δ ii = 3
δi j
的作用:1)换指标;2)选择求和。
例1:
Ai → Ak
δ k i Ai = δ k k Ak = Ak
思路:把要被替换的指标 i 变成哑标,哑标能 用任意字母,因此可用变换后的字母 k 表示
张量分析提纲及部分习题答案

y
对静止的连续介质,有
ζ n fd 0 , ζd fd 0 ,
A
ζ f 0。
(21) 证明应力是一个张量; 记 ij :表示在给定基 g i 下,在面 g j 上,单位面积受力 F j 在 g i 方向上的分量为
对斜圆锥面上任一点 (图中黑点处) , 不难由相似三角形得到,
z z R cos C i R sin j zk ,进而可得, H H r Rz sin zR cos r R cos C R g i j, gz i sin j k , H H z H H r
dx g dx I g dx II 1 4 x I 2 dx I 6 x I x II 2 dx II Pdx I Q dx II 11 12 1 1 I 。 2 4 dxII g 21dx I g 22 dx II 6 x I x II dx I 9 x II dx II P2 dx I Q2 dx II
Pi Qi 时,坐标 xI , xII 才可能存在。即向量场 P, Q 无旋时,其在两点间 x II x I Pi Qi 的路径积分与路径无关,积出的值就是坐标。本例中, II I ,故相应的“协 x x
当 变坐标”不存在。 (正因为如此,坐标也没有逆变、协变之说。 ) (9) 有点类似曲面第一基本型(1.3.12) 。 (10) Lame 常数定义(1.3.13)在非正交系中也成立,但此时(1.3.12a)不成立。
1.9-1.13:略; 1.14: 注意,所谓斜圆锥是指, O 点沿 z 方向在大圆平面上的投影 M 在大圆的直径上。
张量

一、概论1.标量:最简单的物理量,是常量,是一个实数,例如:距离、时间、温度等2.矢量:有方向的,需要用空间坐标系中的三个分量来表示的物理量,如位移、速度、力等;3.张量:最复杂的物理量,需要用空间坐标系中的三个矢量,也即九个分量才能完整地表示出来。
例如:应力状态、应变状态等。
张量是矢量的推广,与矢量相类似,可以定义由若干个当坐标系改变时满足转换关系的分量所组成的集合为张量。
这表明张量的分量之间存在一定的函数关系,这些函数值与坐标选取无关。
即张量的不变量性质。
张量所带的下角标的数目称为张量的阶数。
标量为零阶张量,矢量为一阶张量,用矩阵表示的(张量)为二阶张量,三阶张量用图形无法表示出来。
二、张量1:张量(tensor)的理论来源。
亚瑟·凯莱( Arthur Cayley)着力研究的不变量理论( invariant theory)导致了矩阵理论的建立, 引进了现代意义上的行列式的代数表达, 这成为射影几何的重要工具。
凯莱的不变量理论产生于19世纪前半叶的英国着重对代数及代数在几何方面的应用研究这样的背景下。
矩阵理论对线性变换的研究引进了向量的代数定义, 而这是张量概念的先导。
另一方面, 格奥尔格·弗雷德里希·波恩哈德·黎曼( Georg Friedrich Bernhard Riemann)提出的n维流形的概念, 这在客观上提出了深入研究代数形式的课题。
黎曼的几何思想在拓展几何学的同时,提高了代数在表达几何对象方面的抽象程度。
黎曼之后, 在克里斯托弗、里奇和列维-契维塔等人的努力下, 形成了张量分析这样的数学方法, 黎曼几何学也因此而建立起来了。
2:张量的定义、性质与应用价值从代数角度讲,它是向量的推广。
我们知道,向量可以看成一维的“表格”(即分量按照顺序排成一排),矩阵是二维的“表格”(分量按照纵横位置排列),那么n阶张量就是所谓的n维的“表格”。
张量的严格定义是利用线性映射来描述的。
张量分析及场论
u
w
v
图 1.1、矢量加法的平行四边形法则
W | F || u | cos
其中 F 、| u |分别表示矢量 F 、 u 的大小,θ表示矢量 F 与矢量 u 之间的夹角,这就 定义了一种称为点积的运算。
点积的定义: 设 u ,v 为两个任意不为零的矢量, 设| u |, | v |分别为其大小 (也称为模) 。 θ为这两个矢量之间的夹角,则 u 与 v 的点积为
张 量 分 析 及 场 论 Tensor Analysis and Field Theory
刘长根第一章 张量代数 ..................................................................................................................... 1 §1.1 点积、矢量分量及记号 ij .......................................................................................... 1 1.2 记号 ijk 、矢积(叉乘)、 关系 ........................................................................ 5 1.3、坐标变换 ...................................................................................................................... 9 1.4、并矢、张量 ................................................................................................................ 12 1.5 张量的代数运算 ........................................................................................................... 14 1.6 张量识别定理(商判则) ........................................................................................... 16 1.7、二阶张量 .................................................................................................................... 17 1.8、张量举例 .................................................................................................................... 21 习题一 ................................................................................................................................. 36 第二章 正交曲线坐标系中的张量分析与场论 ................................................................. 39 2.1、矢量函数、及其导数与微分 .................................................................................... 39 2.2 场 ................................................................................................................................... 43 2.3、曲线坐标 .................................................................................................................... 45 2.4、标量场的方向导数、梯度 ........................................................................................ 49 2.5、矢量场的通量、散度、奥高定理 ............................................................................ 53 2.6、矢量场的环量、旋度、斯托克斯公式 .................................................................... 56 2.7、哈密顿算子 ................................................................................................................ 58 2.8、基矢量对坐标的导数及其应用 ................................................................................ 62 2.9、几种重要的场 ............................................................................................................ 69 习题二 ................................................................................................................................. 75 第三章 一般曲线坐标系中的张量分析初步 ....................................................................... 77 3.1、曲线坐标,基矢量,度量张量 ................................................................................ 77 3.2、克里斯托弗尔符号及其性质 .................................................................................... 80 3.3、协变导数,逆变导数 ................................................................................................ 82
4.6Riemann-Christoffel张量(曲率张量)
s Γ ik r r r s r s r Sikj = ai,kj ar ,k Γ ij ai,r Γ kj ar , j Γ ik as j Γ rk Γ ij Γ ir Γ kj x
s s Γ ik Γ ij i j k s r r s i j k (Sijk Sikj )g g g = as j k + Γ rj Γik Γij Γ rk g g g x x Γ lik Γ lij i j k s l r r l = as g + Γ rj Γ ik Γ ij Γ rk gl g g g x j x k = as g s Rlijk gl g i g j g k
yi 的非线性微分方程组。这组方程的可积性条件是 x p 对 yi 的非线性微分方程组。 混合偏导数与求导次序无关,此时这 个方程彼此是协调的 个方程彼此是协调的。 混合偏导数与求导次序无关,此时这18个方程彼此是协调的。
即
2x p x r x q p 2 x p x r x q p i′ j ′ + i′ j′ Γ rq = j ′ i′ k ′ + i′ k ′ Γ rq k′ y y y y y y y y y y
使满足
( )
或
x i = x i y l′
( )
2x p x r x q p y l ′ Γ = i′ j ′ + i′ Γ rq p = 0 j′ y y x y y
l′ i ′j ′
空间的条件。 方程的可积性条件就是空间是否为 Euclidean 空间的条件。 若在上式中固定 i,j,考察 l =1,2,3 三个方程,令 , , , , 三个方程,
是与坐标无关的标量, 是一个正定二次型, 式中 ds2 是与坐标无关的标量,aαβ 是一个正定二次型,称为 曲面的第一基本型系数。对于这种距离的平方 ds2 的由一个正 面的第一基本型系数。 定二次型决定的空间, 空间。 定二次型决定的空间,定义为 Riemann 空间。Euclidean 空间 空间。 本身也是一中特殊的 Riemann 空间。
张量分析总结
一、知识总结1张量概念1.1指标记法哑标和自由指标的定义及性质自由指标:在每一项中只出现一次,一个公式中必须相同。
性质:在表达式或方程中自由指标可以出现多次,但不得在同项内重复出现两次。
哑标:一个单项式内,在上标(向量指标)和下标(余向量指标)中各出现且仅出现一次的指标性质:哑标可以把多项式缩写成一项;自由指标可以把多个方程缩写成一个方程。
例:A11x1A12X2A13X3B1A21A22 X2A23X3B(1.1)A31 X1A32X2A33X3B3式(1.1)可简单的表示为下式:A j X jB (1.2)其中:i为自由指标,j为哑标。
特别区分,自由指标在同一项中最多出现一次,表示许多方程写成一个方程;而哑标j则在同项中可出现两次,表示遍历求和。
在表达式或者方程中自由指标可以出现多次,但不得在同项中出现两次。
1.2 Kron ecker 符号定义ij为:ij 1, i j0, i j(1.3)的矩阵形式为:1 0 0j0 1 0 (1.4)0 0 1可知j j ii »3。
S 符号的两指标中有一个与同项中其它因子的指标相同时,可把该因子的重指标换成S 的另一个指标,而S 符号消失。
如:ij jk ik ij jk kl il的作用:更换指标、选择求和1.3 Ricci 符号为了运算的方便,定义Ricci 符号或称置换符号:1, i, j,k 为偶排列 l jk 1, i,j,k 为奇排列0,其余情况图1.1 i,j,k 排列图l jk 的值中,有3个为1,3个为-1,其余为0。
Ricci 符号(置换符号)是 与任何坐标系都无关的一个符号,它不是张量。
1.4坐标转换图1.2坐标转换(1.5)(1.6)如上图所示,设旧坐标系的基矢为e,新坐标系的基矢为e。
有ee j e'e j j e在e下进仃分解:e i'i e,「2曳i 3氏i' j e j, Illie j在e 下进行分解:e j i'j e ?jQ 3,j e3 ^e其中,i'j cos(e,q) e e j e j e为新旧坐标轴间的夹角余弦,称为坐标转换系数。
R 张量分析讲稿谢锡麟 - 复旦大学精品课程
g m (x) ∈ Rm×m ,
谢
锡 麟
hp
曲线坐标系
谢锡麟
式中 g i (x)
λ→0
lim
X (x + λii ) − X (x) ∈ Rm , λ
其几何意义为物理空间中 xi 曲线在 X (x) 点的切向量. 由于 DX (x) 非奇异, 因此 {g i (x)}m i=1 为线性无关向量组, 亦即成为 Rm 中的一个基, 且这种基随空间位置变化, 称为曲线坐标系的局 及微分同胚, 有 ∂x1 ∂X 1 · · · . Dx(X ) = . . ∂xm ··· ∂X 1 ( =: g 1 · · · g i 式中 g (X )
◦
f (x0 + h) − f (x0 ) = Df (x0 )(h) + o(|h|Rp ) ∈ Rq ,
讲
˜ h ˜ x+h
其在 x0 ∈ Dx 的可微性定义如下 .
◦
量
稿
yq f O
一般有限维 Euclid 空间之间的映照可以表示为 x1 f 1 (x) . . q . . f (x) : Rp ⊃ Dx ∋ x = . → f (x) = . ∈ R , xp f q (x)
谢锡麟
1. 首先有 ) ∂gij ∂ ( (x) = g i (x), g j (x) Rm = k k ∂x ∂x = Γki,j (x) + Γkj,i (x). 同理可得
(
∂ gi (x), g j (x) ∂xk
)
Rm
( ) ∂ gj + g i (x), k (x) ∂x Rm
∂gjk (x) = Γij,k (x) + Γik,j (x); ∂xi ∂gik (x) = Γjk,i (x) + Γji,k (x). ∂xj
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章:曲线坐标系张量分析张量场函数:()=T f r 在空间中每一点定义一个张量T 曲线坐标系回顾:笛卡尔坐标系下空间一点的矢径 123123x x x =++r e e ei x 坐标线:只变化一个坐标i x 时,矢径的轨迹。
直线坐标系下,坐标线都是直线。
当()i i 123x x ,,=ξξξ,1ξ,2ξ,3ξ坐标线中至少有一个是曲线时,称为曲线坐标系协变基:i i ∂=∂ξrg所以:ki k i x ∂=∂ξg e '''k i i i i i k i i x ∂ξ∂ξ==∂ξ∂∂∂ξξe g gjj mm x∂ξ=∂g e '''j j j j j m m j jx ∂ξ∂∂ξ∂ξ==∂ξ∂ξg e g 原因:k j m jj j m m i i ji ii k m x x x x ∂ξ∂∂ξ⋅=⋅=∂==δ∂∂ξ∂∂ξ∂ξξ∂e e g g 曲线坐标系中,基矢量是曲线坐标的函数 基矢量的导数基矢量对曲线坐标的导数还是矢量,因而可以用基矢量的线性组合表示:j k k ij k ij,k i∂=Γ=Γ∂ξg g g其中组合系数kijΓ 称为第二类Christoffel 符号 ij,k Γ称为第一类Christoffel 符号Christoffel 符号是协变基矢量对曲线坐标的导数在基底矢量下的分解系数。
事实上:j k k iji ∂Γ=⋅∂ξg g jij,k k i∂Γ=⋅∂ξg g① 指标对称性第二类Christoffel 符号的两个协变指标用于指示哪一个协变基矢量(第二个协变指标)对哪一个曲线坐标(第一个协变指标)求导数。
然而,根据协变基矢量的定义:j j ∂=∂ξrg 可得:2jk k k i i kk ij ji i j j ∂∂∂=⋅=⋅=⋅=∂ξ∂ξ∂ξΓ∂ξΓg r g g g g2ji k k k i i j ij,kji,j k ∂∂∂=⋅=⋅=⋅=∂ξ∂ξ∂ξΓΓ∂ξg r gg g g 说明Christoffel 符号相对它的前两个协变指标是对称的。
②不是张量在直线坐标系中,由于基矢量不随坐标而改变,所以第二类Christoffel 符号全部为零。
如果它是张量,它在任意坐标系中都应是零。
② 两类Christoffel 符号之间的联系由于Christoffel 符号的第三个指标是矢量的分量指标,所以可以通过度量张量进行升降。
k jjk k kmkm ijm ij,mi ij jm mij,kkm km ij i i gg g g ∂∂Γ=⋅=⋅=Γ∂ξ∂ξ∂∂Γ=⋅=⋅=Γ∂ξ∂ξg g g g g g g g④逆变基矢量的导数 由 i i j j ⋅=δg g 可知:ij i j k k 0∂∂⋅+⋅=∂ξ∂ξg g g g 从而i ij kj k ∂⋅=-Γ∂ξg gi i jkj k ∂=-Γ⋅∂ξg g (逆变基导数表达式符合张量指标规则,但要加负号)⑤与度量张量分量导数之间的关系ki kj,i ijj ij i k k k ,j g ∂∂∂=⋅+⋅=+∂ξ∂ξΓ∂ξΓg g g g (a)jk ij,k ik,j ig ∂=Γ+∂ξΓ(b) jk kiij,k j ,i g ∂+ΓΓ=∂ξ(c)(b)+(c)-(a)jk ij ki ij,k i j k g g 1g ()2∂∂∂Γ=+-∂ξ∂ξ∂ξ规则:① 分别求度量张量分量对曲线坐标i j k ,,ξξξ的导数,度量张量的分量指标按与曲线坐标指标构成顺时针排序确定;② 曲线坐标的指标为i,j 时为正,曲线坐标的指标为k 时为负; ③ 将所得结果相加的一半即为ij,k Γ。
例题123()=⋅⨯g g g 对曲线坐标的导数123i123231312i i i k k k i1k 23i21k 3i312k 123i1i2i3123k [()]()()()()()()()()∂⋅⨯=∂ξ∂ξ∂∂∂=⋅⨯+⋅⨯+⋅⨯∂ξ∂ξ∂ξ=Γ⋅⨯+Γ⋅⨯+Γ⋅⨯=Γ+Γ+Γ⋅⨯=Γg g g g g g g g g g g g g g g g g g g g g g g g 从中可得Christoffel 符号的一个重要性质:kikΓ==Hamilton 算子∇ 定义: ii ∂∇=⊗∂ξg 运算规则:作用于张量时,运算结果由对张量对曲线坐标求偏导数与相应的基矢量组成;基矢量指标与曲线坐标指标相同;基矢量与张量偏导数之间的运算与算子与张量之间的运算相同:ijkii ∂∇=⊗∂ξT T g i i ∂∇=⊗∂ξTT g (张量的左右梯度)i i ∂∇⋅=⋅∂ξT T g ii∂⋅∇=⋅∂ξT T g (张量的左右散度) i i ∂∇⨯=⨯∂ξT T g ii∂⨯∇=⨯∂ξT T g (张量的左右旋度) Hamilton 算子是一种不依赖坐标系的微分算子,计算结果与坐标系的选择无关:证明:i ii i i i i i i i i i ''''''⎛⎫∂∂ξ∂∂∂ξ∂⊗=⊗=⊗=⊗ ⎪∂ξ∂ξ∂ξ∂ξ∂ξ∂ξ⎝⎭g g g gHamilton 算子与张量之间的运算结果是张量例如:''''''i i k ki k k k i k i i ∂∂ξ∂ξ∂∇==⊗=⊗=∂ξ∂ξ∂ξ∂ξ∂∂⊗⊗∂ξ∂ξT T T g g T T g g''''''i i k k k i k k k i i i ∂∂ξ∂ξ∂∇⋅==⋅=⋅=∂ξ∂ξ∂∂∂⋅⋅∂∂ξξξ∂ξT T g g T T T g g ''''''i i k k k i k k k i i i ∂∂ξ∂ξ∂∇⨯==⨯=⨯=∂ξ∂ξ∂∂∂⨯⨯∂∂ξξξ∂ξT T g g T T T g g张量分量的协变导数张量 ijk l ..kl i j T =⊗⊗⊗T g g g g 对曲线坐标的导数ijk L..kL i j smj k L imk Lm m ..kL j ..kL i s s m m ij L ij k..mL i j ..km i j s s ij mj i im j ij m ij m k L ..kL ..kL s s ms ..kL ms ..mL ks ....k km Ls i j s T T T T T T (T T T T )T ∂⊗⊗⊗∂ξ∂∂+⊗⊗⊗+⊗⊗⊗∂ξ∂ξ∂∂+⊗⊗⊗+⊗⊗⊗∂ξ∂ξ∂=+Γ+Γ∂=∂-Γ-Γ⊗⊗⊗∂ξ=∇ξg g g g g g g g g g g g g g g g g g g T g g g g gij ij L ..kL;s k L k Li j i jT ⊗⊗⊗=⊗⊗⊗g g g g g g g g张量分量的协变导数ij ij ij mj i im j ij m ij mij ..kL s ..kL..kL;s..kL ms ..kL ms ..mL ks ..km Ls..kL;s sT TTT T T T T ∂∇=+Γ+Γ-Γ-Γ∂ξ由以下几个部分组成:① 普通偏导数:ij ..kLsT ∂∂ξ② 含逆变指标的分量与第二类Christoffel 符号相乘:mj i..kL ms T Γ其中i ms Γ的逆变指标为张量分量的逆变指标原张量分量的逆变指标与i ms Γ的第一个协变指标构成一对哑指标i ms Γ的第二个协变指标为曲线坐标的指标③ 含协变指标的分量与负第二类Christoffel 符号相乘:ij m ..mL ks T -Γ其中m ks Γ的第一个协变指标为张量分量的协变指标 原张量分量的协变指标与m ks Γ的逆变指标构成一对哑指标m ks Γ的第二个协变指标为曲线坐标的指标 由于''k i k i ∂∂∇=⊗=⊗∂ξ∂ξT T T g g按张量分量协变导数的定义:∇T =ij s k l i'j's'k 'l's ..kl i j s'..k 'l'i'j'T T ∇⊗⊗⊗⊗=∇⊗⊗⊗⊗g g g g g g g g g g 可见张量分量的协变导数ijs ..kl T ∇是张量梯度的分量,因而是张量分量。
1. 度量张量的协变导数为零.j.j .j .m j .j m j j is i s i i ms m is is is sg 00∂δ∇=∇δ=+δΓ-δΓ=+Γ-Γ=∂ξ2. 置换张量的协变导数为零 (作业)ijk i j k ()ε=⋅⨯g g g ijkj i kj k i k i j s s s sm m mis m j k js i m k ks i m is m ks ijmm js k m m im k j j ()()()()()()Γ∂ε∂∂∂=⋅⨯+⋅⨯+⋅⨯∂ξ∂ξ∂ξ∂ξ=Γ⋅⨯+Γ⋅⨯+Γ⋅⨯=+Γεε+Γεg g g g g g g g g g g g g g g g g g m mjk is mij ijk s ij m m imk js k s sk 0εε∂ε∇ε=---=∂ξεΓΓΓ3. ij ij ij s mn s mn s mn (A B )(A )B A (B )∇=∇+∇设 ij A =⊗A g g ; m n mn B =⊗B g g ;=⊗C A B 则有:s s s ∂∂∂=⊗+⊗∂ξ∂ξ∂ξC A B B A 以及ij s i j s A ∂=∇⊗∂ξA g g ; m ns mn sB ∂=∇⊗∂ξB g g 因此:ij m n s mn i j (A B )∇⊗⊗⊗g g g g()ij m n ij m n s mn i j s mn i j ijijmns mn s mn i j (A )B A (B )(A )B A (B )=∇⊗⊗⊗+∇⊗⊗⊗=∇+∇⊗⊗⊗g g g g g g g g g g g g所以 ij ij ij s mn s mn s mn (A B )(A )B A (B )∇=∇+∇即:张量分量乘积的协变导数符合标量函数乘积的求导法则 该结论对高阶张量同样成立:ijk ijk ijk s mn s mn s mn (A B )(A )B A (B )∇=∇+∇根据度量张量和置换张量协变导数为零的性质,可从上式中得到: 推论1:ijk ijk s mn s mn (A g )(A )g ∇=∇ 推论2:ijk ijk s mn s mn (B )(B )∇ε=ε∇4. 张量分量的缩并与求协变导数次序可交换:先求ij ..k T 的协变导数:ijij mj i im j ijm ..k s ..k..k ms ..k ms ..m ks s T T T T T ∂∇=+Γ+Γ-Γ∂ξ然后缩并 i,k 指标可得:j j mj m j j m..k s ..k..k ms ..k ms ..m kss kj km j ..k ..k ms s kj km j ..k k k k k kj m kj m ..m ks k ..k ..m ks mss T T T T T T T T T T T ∂∇=+Γ+Γ-Γ∂ξ∂=++Γ-∂ξ∂=+Γ∂ΓΓξ先缩并后求导(自由指标减少2个):kjkj km j..k s ..k..k ms s T T T ∂∇=+Γ∂ξ比较后可知两者是相等的。
