第二章 极限与连续
分析第二章第八节连续函数与极限计算

第二章 函数、函数的极限与函数的连续性第八节 连续函数与极限计算利用连续函数计算极限的原理: (1) 如果函数f 在点0x 处连续,那么)()(0lim 0x f x f x x =→ 。
此式表明:计算函数f 在其连续点极限,就相当于计算在那一点的函数值。
这就大大地简化了初等函数在其定义域上的每一点的极限计算。
函数f 在点0x 处连续这一事实也可以表示为)()(lim lim 0x f x f x x x x →→=,这个式子表明:对于连续函数而言,极限符号与函数符号可以交换。
(2)定理 如果)(lim 0u x g x x =→,(g 可以在0x 处不连续))()(0lim 0uf u f u u =→,(即f 在0u 处连续) 则)(lim 0x g f x x ο→ ))((lim 0x g f x x →=)()(0lim 0u f u f u u ==→))((lim 0x g f x x →= 。
(3)定理 如果l u f u u =→)(lim 0)(lim 0ux g x x =→,(0)(u x g ≠),则)(lim 0x g f x x ο→ ))((lim 0x g f x x →=lu f u u ==→)(lim 0。
再加上前面介绍过的已知的极限和已知的连续函数等,这些结论以后可以直接使用。
例1 计算:(1)xx x 1)1(lim +→;(2)x x x )1ln(lim 0+→; (3)x a xx 1lim 0-→; (4)x x x 1)1(lim 0-+→α。
解 (1) 令x y 1=,则当0→x 时∞→y ,反之亦然。
xx x 1)1(lim +→e y yy =+=∞→)11(lim ; (2)x x x )1ln(lim 0+→xx x 10)1ln(lim +=→ 1ln ))1(ln(10lim ==+=→e x xx ;(3)作变换1-=xa t 。
《高等数学一课件——第二章 一元函数的极限与连续》

四则运算法则
加减乘除法则让我们能够在计 算极限时更加灵活和高效。
复合函数法则
学习如何计算由多个函数构成 的复合函数的极限。
连续函数法则
利用连续函数的性质求解极限 问题。
极限存在定理
极限存在定理是我们研究极限时常用的工具,它能够帮助我们确定函数极限的存在与计算。
夹逼定理
掌握夹逼定理的原理和应用,用于计算复杂函数的极限。
极限的定义与性质
探索极限的定义,了解极限的性质及其应用。
左极限和右极限
学习左极限和右极限的概念和计算方法。
极限的存在准则
掌握判断极限是否存在的准则和方法。
无穷小和无穷大
理解无穷小与无穷大的概念及其在极限计算中的应用。
极限的运算法则
了解极限运算法则对于处理复杂的极限计算非常有帮助。运用这些法则,可以简化极限的求解过程。
连续函数的运算法则
探索连续函数的运算法则和 推论。
介值定理和零点定理
介值定理和零点定理是函数连续性的重要应用,它们能够帮助我们更好地理解函数曲线和解决实 际问题。
1
介值定理
了解介值定理的原理和应用,解决函数连续性相关问题。
2
零点定理
掌握零点定理的思想和技巧,寻找函数方程的解。
总结与回顾
本课件回顾了一元函数的极限与连续的重要概念和性质,希望能够为学习者 提供全面和深入的理解,并进一步激发对数学的兴趣和热爱。
Stolz定理
学习Stolz定理的使用方法,解决极限问题时提供新的思路。
L'Hopital法则
探索L'Hopital法则在计算极限时的作用和适用条件。
一元函数的连续性
连续性是函数理论中非常重要的概念,它揭示了函数曲线的稳定性与变化规律。
(完整版)赵树嫄微积分第四版第二章极限与连续

x从右侧无限趋近x0 , 记作x x0 (或x x0 0 ) .
左极限:
0, 0,使当x0 x x0时, 恒有 | f ( x) A | .
记作 lim f ( x) A 或 x x0
f ( x0 0) A .
x0
x0
x
左极限:
0, 0,使当x0 x x0时, 恒有 | f ( x) A | .
定义无限接近于无限增大时sinlimsinlim为中心线直线图形完全落在以函数lim不存在arctanlim不存在lim的一条水平渐近线就是那么的距离趋于零这时我们称直线lim的一条水平渐近线就是那么为常数二自变量趋于有限点处时函数的极限问题
第二章 极限与连续
本章介绍极限的概念、性质和运算法则,以及与极 限概念密切相关的,并且在微积分运算中起重要作 用的无穷小量的概念和性质。此外还给出了两个极 其有用的重要极限。随后,运用极限引入了函数的 连续性概念,它是客观世界中广泛存在的连续变化 这一现象的数学描述,微积分学中讨论的函数主要 是连续函数。
x
x
故 lim ex 不存在. x
o
x
一条伸展到无穷远的曲线 y f ( x) ,当点P( x, f ( x)) 沿 曲线无限远离原点时,点 P 到直线 y A 的距离趋于零, 这时我们称直线 y A 是曲线 y f ( x) 的水平渐近线.
如果 lim f ( x) A 或 lim f ( x) A ( A 为常数),
性质2 有界性
对于数列{an } ,如果存在常数 M 0 ,使对一切 n,有
| an | M , 则称数列{an } 是有界的。
定理2 收敛的数列必定有界。 注1 有界性是数列收敛的必要条件,不是充分条件。
第二章 极限与连续习题

习题二1.写出下列数列的前五项:(1)nn y 211-= (2)nn n y ⎪⎭⎫⎝⎛-=11(3)n n y n πsin 1= (4)4)12(32+++=n n n n y n(5)!n n m m m y n )1()1(+--=2、用数列极限的定义证明下列极限: (1)11lim=+∞→n n n (2)1211lim =⎪⎪⎭⎫⎝⎛-∞→n n (3)01lim=∞→n n3.用观察的方法判断下列数列是否收剑。
(1)y n :-31,53,-75,97 ,-119,… (2)y n :1,23,31,45,51 ,67,…(3)y n :0,21,041,0,61 ,0,81,…4、用极限的定义证明下列极限: (1)8)13(lim 3=-→x x (2)232lim=+∞→x x x (3)424lim 22-=+--→x x x (4)02lim =-∞→x x5.设⎩⎨⎧≥-<=3133)(x x x xx f 作f (x )的图形,并讨论当x →3时,f (x )的左右极限(利用第4题(1)的结果)。
6.证明x xx 0lim →不存在。
7.函数2)1(1-=x y 在什么变化过程中是无穷大量?又在什么变化过程中是无穷小量?8.以下数列在n →∞时是否为无穷小量?(1)nn n y 21)1(1+-= (2)ny nn)1(1-+=(3)21ny n =9.当x →0时,下列变量中哪些是无穷小量? 100x 2,3x ,x 2,01.0x ,2x x ,xx 2,x 2+0.1x 221x x - 10.求下列各极限:(1))253(lim 22+--→x x x (2)13lim 2423++-→x x x x(3)⎪⎭⎫ ⎝⎛--→321lim 0x x (4)23lim22--→x x x (5)121lim221---→x x x x (6)xx x x x x 2324lim2220+--→(7)221123limx x x x -+-→ (8)h x h x h 330)(lim -+→(9)11lim 1--→x x n x (n 为正整数)(10)1632lim-+∞→x x x (11)211000lim xxx +∞→(12)u u u ++∞→11lim 43 (13)1)1(lim 2+-∞→n n n(14)502030)12()23()12(lim+--+∞→x x x x(15)22011limx x x +-→ (16)3231lim xx x +---∞→(17)22312lim 4---+→x x x(18)⎪⎪⎭⎫⎝⎛---→x x x 1113lim 31 (19))11(lim 22+--+++∞→x x x x x(20))))(((lim x q x p x x -+++∞→(21)⎪⎪⎭⎫⎝⎛+-+++∞→2222111lim n n n n n n n (22))cos 3(1lim 32x x x x x +++∞→11.设f (x )=x ,求h x f h x f h )()(lim 0-+→12.设⎪⎩⎪⎨⎧<≤<+≤+=x x x x x x f x1101023)(22分别讨论x →0及x →1时f (x )的极限是否存在? 13.设⎪⎪⎩⎪⎪⎨⎧<-≤<-=<=x x x xx x x x f x 263202000)(212 讨论x →0及x →2时f (x )的极限是否存在,并且求)(lim x f x -∞→及)(lim x f x +∞→。
微积分第2版-朱文莉第2章极限与连续习题祥解

微积分第2版-朱文莉第2章极限与连续习题祥解第二章 极限与连续习题 2.1(A)1. 观察下列数列{}n x ,当n →∞时,极限是否存在,如存在,请写出其极限值.(1) {}(1)1n n x n ⎧⎫-=+⎨⎬⎩⎭; (2) {}1sin n x n ⎧⎫=⎨⎬⎩⎭;(3) {}1(1)2n n x ⎧⎫+-=⎨⎬⎩⎭; (4) {}11n n x n -⎧⎫=⎨⎬+⎩⎭;(5) {}{}(1)nn x n =-; (6) {}21n n x n ⎧⎫-=⎨⎬⎩⎭.解 (1) 当n →∞时,极限为1;(2) 当n →∞时,极限为0; (3) 当n →∞时,极限不存在; (4) 当n →∞时,极限为1; (5) 当n →∞时,极限不存在; (6) 当n →∞时,极限不存在. 2. 对于数列{}⎭⎬⎫⎩⎨⎧+=1n n x n ),2,1( =n ,给定 (1) 1.0=ε,(2) 01.0=ε, (3) 001.0=ε时,分别取怎样的N ,才能使当N n >时,不等式ε<-1n x 成立? 并利用极限的定义证明此数列的极限为1.解 (1) 要使1.011111=<+=-+=-εn n n x n ,只要101.011=>+n ,9n >,故取9=N 即可.(2) 要使01.011111=<+=-+=-εn n n x n ,只要10001.011=>+n ,99n >,故99=N 即可.(3) 要使001.011111=<+=-+=-εn n n x n ,只要1000001.011=>+n ,999n >,故取999=N 即可.对于任意给定的0>ε,要使ε<+=-+=-11111n n n x n ,即ε11>+n ,11->εn .取正整数⎥⎦⎤⎢⎣⎡-=11εN ,则当N n >时,恒有ε<-+=-111n nx n ,故lim 11n nn →∞=+. 习题 2.1 (B)1. 用数列极限的定义证明下列极限:(1) 1(1)lim 01nn n →∞+-=+; (2) 1lim313n n n →∞=+. 证明 (1) 对于任意给定的0ε>,要使不等式n x a -=1(1)22011n n n nε+--≤<<++成立,只需2n ε>成立. 取2N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,恒有ε.所以 1(1)lim 01nn n →∞+-=+.(2) 对于任意给定的0ε>,要使不等式n x a -=1113133(31)9n n n nε--=<<++ 成立,只需19n ε>成立. 取19N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,恒有 1313n n ε-<+. 所以 1lim313n n n →∞=+.2. 利用数列极限的定义证明:0n →∞=. 证明 对于任意给定的0ε>,要使不等式=-a xn 0ε-=<<成立,只需21n ε>成立. 取112+⎥⎦⎤⎢⎣⎡=εN ,则当n N >时,恒有0ε-<.所以 )0n →∞=.3. 若数列{}n x 有界,且lim 0n n y →∞=,证明lim 0n n n x y →∞=.证明 因为数列{}n x 有界,所以存在0M >,对所有的n x 都有n x M ≤,对于任意给定的0ε>,要使不等式0n n x y -=n n n x y M y ε≤<成立,只需n y M ε<,又因为lim 0n n y →∞=,所以对于给定的0Mεε'=>,存在N ,则当n N>时,恒有n y Mεε'<=. 取},max{N M K =,则当K n >时,恒有εε=<MMy x n n .所以lim 0n n n x y →∞=.4.对于数列}{n x ,若a x k →-12 )(∞→k ,a x k →2)(∞→k ,证明:a x n →)(∞→n .证明 因为a x k →-12 )(∞→k ,所以0>∀ε,1k ∃0>,当1k k >时,有ε<--a x k 12;又因为a x k →2)(∞→k ,所以对上述0>ε,2k ∃0>,当2k k >时,有ε<-a x k 2. 记},max{21k k K =,取K N 2=,则当N n >时,若12-=k n ,则121k K k >+>,得ε<-=--a x a x k n 12,若k n 2=,则2k K k ≥>,得ε<-=-a x a x k n 2. 从而只要N n >,就有ε<-a x n ,即lim n n x a →∞=.习题2.2(A)1. 对下图中所示函数)(x f ,求下列极限,如果极限不存在,说明理由.(1) 2lim ()x f x →-; (2) 1lim ()x f x →-; (3)0lim ()x f x →.解 (1) 2lim ()0x f x →-=;(2)1lim ()1x f x →-=-;(3)0lim ()x f x →不存在,因为)0()0(+-≠f f .2. 对下图中所示函数)(x f ,下列陈述中哪些是对的,哪些是错的?(1) 0lim ()x f x →不存在; (2) 0lim ()0x f x →=;(3) 0lim ()1x f x →=; (4)1lim ()0x f x →=;(5) 1lim ()x f x →不存在; (6) 对每个)1,1(0-∈x , 0lim ()x x f x →存在.解 (1) 错,因为0lim ()x f x →存在与否,与)0(f 的值无关.(2) 对,因为0)0()0(==+-f f .(3) 错,因为0lim ()x f x →的值与)0(f 的值无关.(4) 错,0)01(=+f ,1)01(-=-f ,故1lim ()x f x →不存在.(5) 对,因为)01()01(-≠+f f . (6) 对.3. 用极限定义证明:(1) 1lim(21)1x x →-=; (2) 224lim 42x x x →--=-+;(3) 23lim2x x x →∞+=; (4) lim 0x =.证明 (1)对于任意给定的0ε>,要使不等式()f x A -(21)121x x ε=--=-<成立,只需12x ε-<成立. 取2εδ=,则当01x δ<-<时,恒有(21)1x ε--<.所以 1lim(21)1x x →-=.(2)对于任意给定的0ε>,要使不等式()f x A -24(2)(2)(4)4222x x x x x x ε--+=--=+=+<++成立,只需取δε=即可. 则当0x δ<+<时,恒有24(2x x ε--+. 所以224lim 42x x x →--=-+.(3)对于任意给定的0ε>,要使不等式()f x A -2332x x xε+=-=< 成立,只需3x ε>成立. 取3M ε=,则当x M >时,恒有232x xε+-<. 所以 23lim2x x x →∞+=.(4)对于任意给定的0ε>,要使不等式()0f x A ε-=<< 成立,只需⎥⎦⎤⎢⎣⎡>21εx 成立. 取⎥⎦⎤⎢⎣⎡=21εM ,则当x M >时, 恒有0ε-<. 所以lim0x =.习题2.2 (B)1. 当2→x 时,4)(2→=x x f ,问δ等于多少,使当δ<-2x 时,001.04)(<-x f ?解 由于2→x ,02→-x ,不妨设12<-x ,即31<<x . 要使25)2)(2(42-<-+=-x x x x0002.02=-x , 取0002.0=δ,则当δ<-<20x 时,就有001.04)(<-x f .2. 当∞→x 时,2312)(22→++=x x x f ,问X 等于多少,使当X x >时,01.02)(<-x f ?解 因为222253523122)(x x x x x f <+=-++=-. 要使01.0231222<-++x x ,只要01.052<x,即510>x ,取510=X ,则当X x >时,就有01.02)(<-x f . 3. 讨论0x →时,下列函数的极限是否存在.(1) 1,0()0, 01,0x x f x x x x -<⎧⎪==⎨⎪+>⎩; (2) ⎩⎨⎧<<<<-=10 ,0,sin )(x x x x x f π. 解 (1)由于 0lim ()lim (1)1x x f x x --→→=-=-, 00lim ()lim (1)1x x f x x ++→→=+=,故 0lim ()lim ()x x f x f x -+→→≠. 所以 0lim ()x f x →不存在.(2)由于0lim ()lim sin 0x x f x x --→→==,0lim ()lim 0x x f x x ++→→==. 故0lim ()x f x -→0lim ()x f x +→=. 所以0lim ()0x f x →=. 4. 设函数3()53x x f x x x+=-,求:(1) lim ()x f x →+∞; (2) lim ()x f x →-∞;(3) 0lim ()x f x +→; (4) 0lim ()x f x -→.解 34(1)lim ()limlim2532x x x x x xf x x xx→+∞→+∞→+∞+===-.321(2)lim ()limlim5384x x x x x x f x x x x →-∞→-∞→-∞+===-.3(3)lim ()lim 253x x x x x f x x x ++→→→+==-. 0321(4)lim ()lim lim 5384x x x x x x f x x xx ---→→→+===-. 5. 设函数212()22x x f x x a x ⎧+≥=⎨+<⎩,问当a 取何值时,函数)(x f 在2→x 时的极限存在.解 因为 22lim ()lim (2)4x x f x x a a --→→=+=+, 222lim ()lim (1)5x x f x x ++→→=+=. 由极限存在的条件,有 2lim ()x f x -→2lim ()x f x +→=,得1a =.习题2.3(A)1. 下列变量在何种情况下为无穷小,又在何种情况下为无穷大? (1)11x -; (2) 211x x --; (3) ln(1)x -.解 (1)由于1lim 01x x →∞=-,故x →∞时,变量11x-为无穷小. 由于11lim 1x x →=∞-,故1x →时,变量11x-为无穷大. (2) 由于21lim01x x x →∞-=-,故x →∞时,变量211x x --为无穷小. 由于211lim 1x x x →--=∞-, 故1x →-时,变量211x x --为无穷大.(3) 由于2lim ln(1)0x x →-=,故2x →时,变量为ln(1)x -无穷小.由于lim ln(1)x x →+∞-=+∞,或 1lim ln(1)x x +→-=-∞,故x →+∞或1x +→时变量ln(1)x -为无穷大.2. 根据定义证明:(1) 1-=x y 为当1→x 时的无穷小; (2) xxy sin =为当∞→x 时的无穷小. 解 (1) 因为0)1(-=--x x ,所以0>∀ε,取εδ=,则当δ-<10x 时,就有ε<--0)1(x ,即1-=x y 为当1→x 时的无穷小.(2) 因为xx x 10cos ≤-,所以0>∀ε,取ε1=X ,则当X x >时,恒有ε<-0cos xx, xxy cos =为当∞→x 时的无穷小. 3. 求下列极限.(1) sin lim x x x→∞; (2) 221lim 56x x x x →+-+; (3) 224lim 2x x x →--.解 (1)因为sin x 是有界函数,x →∞时,1x为无穷小. 所以 sin lim0x xx→∞=.(2)当2x →时,1x +有界,256x x -+为无穷小. 所以221lim56x x x x →+=∞-+.(3) 22224(2)(2)lim lim lim(2)422x x x x x x x x x →→→-+-==+=--.习题2.3 (B)1. 举例说明,两个无穷小的商不一定是无穷小;无穷小与无穷大的积不一定是无穷小.解 (1) 例如 0)1(lim 1=-→x x ,0)1(lim 21=-→x x ,但2)1(lim 11lim 121=+=--→→x x x x x . 不是无穷小.(2) 例如 0)1(lim 1=-→x x ,∞=-→11lim21x x ,但是2111lim 11lim 11)1(lim 12121=+=--=--→→→x x x x x x x x 不是无穷小.2. 函数x x y cos =在),(+∞-∞内是否有界?这个函数是否为+∞→x 时的无穷大?解 因为0>∀M ,总有),(0+∞∈M x ,使得1cos 0=x ,从而M x x x y >==000cos ,所以,函数x x y cos =在),(+∞-∞内无界.又存在00>N ,0>∀X ,总有),(0+∞∈X x ,0cos 0=x ,从而0000cos N x x y <==, 所以,函数x x y cos =不是当+∞→x 时的无穷大.3. 根据定义证明:函数xxy 21+=为当0→x 时的无穷大. 问x 应满足什么条件,能使410>y ?证明 因为212121-≥+=+x x x x ,要使M x x >+21,只要M x>-21,即21+<M x . 所以0>∀M ,取21+=M δ,当δ<-<00x 时,就有M xx>+21,即函数xxy 21+=为当0→x 时的无穷大. 令410=M ,取21014+=δ,当2101004+<-<x 时,就能使41021>+xx. 习题2.4(A)1. 简要回答下列问题.(1) 若数列{}n x 收敛,而数列{}n y 发散,则数列{}n n x y ±及数列{}n n x y 是否收敛? (2) 若数列{}n x ,{}n y 均发散,则数列{}n n x y ±及数列{}n n x y 是否发散?解 (1) 数列{}n n x y ±发散. 如果{}n n x y ±收敛,那么()n n n n y x x y =--或()n n n n y x y x =+-也收敛.数列{}n n x y 不一定收敛. 例如:数列1n x n=收敛,(1)nn y =-发散, 1(1)n n n x y n =-收敛;又数列1n x n=收敛,2n y n =发散, n n x y n =发散. (2) {}n n x y ±及数列{}n n x y 不一定发散. 2. 求下列函数的极限.(1) 322042lim 32x x x x x x→-++; (2) 22132lim 43x x x x x →-+-+;(3) 4x →(4) )limx x →+∞;(5) 3131lim 11x x x →⎛⎫- ⎪--⎝⎭; (6) ()()()2030502332lim 21x x x x →∞-++;(7) 332lim 1x x x x →∞+-+ ; (8) 220()lim h x h x h→+-.解 (1) 322200424211limlim 32322x x x x x x x x x x →→-+-+==++. (2) 2211132(1)(2)(2)1lim lim lim 43(1)(3)(3)2x x x x x x x x x x x x x →→→-+---===-+---.(3) x x →→=4x x →→===322.(4) 1lim )limlim2x x x x →+∞===. (5) 3211312lim lim 1111x x x x x x x →→+⎛⎫-==⎪--++⎝⎭.(6) 203030203050503223(23)(32)3lim lim (21)212x x x x x x x x →∞→∞⎛⎫⎛⎫-+ ⎪ ⎪-+⎛⎫⎝⎭⎝⎭== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭. (7) 3333232322lim 112lim lim 1111111lim 1x x x x x x x x x x x xx →∞→∞→∞→∞⎛⎫++ ⎪+⎝⎭===-+⎛⎫-+-+ ⎪⎝⎭.(8) 22222000()2limlim lim(2)2h h h x h x x xh h x x h x h h→→→+-++-==+=. 3. 求下列极限.(1) 1123lim 23n nn n n ++→∞++;(2)2n n(3) n →∞; (4) 1111242lim1111393n n n →∞++++++++; (5) 11lim 1335(21)(2n n →∞⎛+++⋅⋅-⎝.解 (1) 11212313lim lim 2332323nn nn n n n n ++→∞→∞⎛⎫+⎪+⎝⎭==+⎛⎫+ ⎪⎝⎭.(2) 2214n n n⎫⎪===. (3) lim n →∞0n ==.(4) 111121111112422lim lim 1111113933113n n n n n n ++→∞→∞⎛⎫- ⎪⎝⎭++++-==⎛⎫++++- ⎪⎝⎭-43. (5) 由于1111(21)(21)22121n n n n ⎛⎫=- ⎪-+-+⎝⎭,有1111323(21)(21)n n +++⋅⋅-+111111111123352121221n n n ⎛⎫⎛⎫=-+-++-=- ⎪ ⎪-++⎝⎭⎝⎭. 于是111111lim lim 11323(21)(21)2212n n n n n →∞→∞⎛⎫⎛⎫+++=-= ⎪ ⎪⋅⋅-++⎝⎭⎝⎭.习题2.4 (B)1. 设222lim 22x x ax bx x →++=--,求常数a ,b 的值.解 因为222lim 22x x ax bx x →++=--,推得b ax x ++2含有因式2x -,否则与已知矛盾.设2x ax b ++(2)()x x c =--,得2,(2)b c a c ==-+.又因为 22222(2)()2lim lim lim 22(2)(1)13x x x x ax b x x c x c cx x x x x →→→++----====---++,得4-=c ,从而得到2a =,8b =-.2. 设511lim 2-=⎪⎪⎭⎫⎝⎛+---∞→b ax x x x ,求常数a ,b 的值. 解 因为511)()1(lim 11lim 22-=⎪⎪⎭⎫⎝⎛---++-=⎪⎪⎭⎫ ⎝⎛+---∞→∞→x b x b a x a b ax x x x x ,推得105a ab -=⎧⎨+=-⎩, 得1a =,6b =-.3. 设⎪⎪⎩⎪⎪⎨⎧>≤<+≤+=,1,2,10,1,0,23)(2x xx x x x x f 分别讨论0→x 及1→x 的极限是否存在.解 (1) 由于 0lim ()lim (32)2x x f x x --→→=+=,200lim ()lim(1)1x x f x x ++→→=+=. 由于 0lim ()lim ()x x f x f x -+→→≠,所以 0lim ()x f x →不存在. (2) 由于 211lim ()lim(1)2x x f x x --→→=+=, 112lim ()lim 2x x f x x++→→==, 111lim ()lim ()lim ()2x x x f x f x f x -+→→→===, 所以 1lim ()x f x →存在.4. 设1lim ()x f x →存在,且21()2lim ()x f x x x f x →=+,求1lim ()x f x →和()f x .解 设1lim ()x f x A →=,则2()2f x x Ax =+,于是211lim ()lim(2)12x x A f x x Ax A →→==+=+,得1A =-,2()2f x x x =-.习题2.5(A)1. 求下列极限: (1) 0tan 2limsin 5x x x →;(2) 0lim x +→; (3) 02arcsin lim3x x x →; (4) lim 2sin (0)2nnn x x →∞≠;(5) 202lim sin 3x x x→; (6) 0tan sin limx x xx→-.解 (1) 00tan 22tan 222lim lim sin 5sin 5555x x xxx x x x xx→→==.(2) 00022lim limlim 2x x x x x+++→→→===(3) 令t x =arcsin ,则002arcsin 22limlim 33sin 3x t x t x t →→==.(4) sin 22lim 2sin lim sin lim 222nn n n n n n n nx x x x xx x x →∞→∞→∞===. (5) 22002293lim lim 9sin sin 33x x x x x x →→⎛⎫ ⎪⎝⎭==.(6) 0tan sin lim x x x x x →→-= 00sin (1lim lim cos x x x x x→→-=⋅2. 求下列极限:(1) 51lim 1n n n +→∞⎛⎫+ ⎪⎝⎭; (2) lim 1xx x x →∞⎛⎫⎪+⎝⎭; (3) 21lim 23xx x x →∞-⎛⎫⎪+⎝⎭; (4) 22lim 2xx x →-⎛⎫ ⎪⎝⎭; (5) ()1lim 12sin xx x →+; (6) ()3sec 2lim 1cos xx x π→+.解 (1) 55111lim 1lim 11n nn n e n n n +→∞→∞⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (2) 11lim lim 111xx x x x x e x →∞→∞⎛⎫== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭. (3) 令423t x -=+,则214lim lim 12323x xx x x x x →∞→∞--⎛⎫⎛⎫=+ ⎪ ⎪++⎝⎭⎝⎭2231322220lim(1)lim (1)lim(1)1t tt t t t t t e e ------→→→⎡⎤=+=++=⋅=⎢⎥⎣⎦. (4) 1221002lim lim 122xxx x x x e ---→→⎡⎤--⎛⎫⎛⎫⎢⎥=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. (5) 012sin lim20lim(12sin )x xxx x ee →→+==.(6) 3cos 3sec 322lim(1cos )lim(1cos )x xx x x x e ππ→→+=+=.3. 设 21001lim 5xc x x e x →∞+⎛⎫= ⎪-⎝⎭,求c . 解 222012lim 2012510011006lim lim 155x xxxc x x x x e e e x x →∞-→∞→∞+⎛⎫⎛⎫=+=== ⎪ ⎪--⎝⎭⎝⎭,2012=c .习题2.5 (B)1. 利用极限存在准则,计算下列各题.(1) 222111lim (1)()n n n n n →∞⎡⎤+++⎢⎥++⎣⎦; (2) n →∞. 解 (1)由于222221111()(1)()n n n n n n n n n n<+++<=+++, 又因为 1lim0n n →∞=,2lim 0()n nn n →∞=+,由夹逼准则,有 222111lim 0(1)()n n n n n →∞⎡⎤+++=⎢⎥++⎣⎦. (2) 因为1sin 1n -<<,所以有223311n nn n -<<++,此时23lim 01nn n →∞-=+,23lim 01n n n →∞=+,由夹逼准则,有 0n →∞=. 2. 利用极限存在准则证明:数列2,22+,222++,…的极限存在,并求出该极限.解 归纳证明这个数列是严格单调增加的,并以2为上界.2<,假设1n n a a -<,那么1n n a a +=<=,可见数列是单调增加的. 2<,2n a <,可推出12n a +=<=,所以数列以2为上界. 由准则Ⅱ知,此数列是收敛数列,记极限为a .由在递推公式1n a +1lim n n a +→∞=即a =2a =.3. 某企业计划发行公司债券,规定以年利率6.5%的连续复利计算利息,10年后每份债券一次偿还本息1000元,问发行时每份债券的价格应定为多少元?解 设发行时每份债券的价格应定为0A 元,则65.0010%5.601000e A e A ==⨯,所以05.522100065.00≈⋅=-e A (元).4. 设本金为p 元,年利率为r . 若一年分n 期,存期t 年,若以复利方式结算,则本金与利息之和是多少?现某人将1000p =元存入某银行,年利率为0.06r =,2t =;请按单利、季度、月利及连续复利等结算方式计算本利和.解 按单利计算:本利和为=00.1120206.010001000=⨯⨯+(元). 由复利公式有ntn r p ⎪⎭⎫ ⎝⎛+1, 按季度结算方式计算:4n =,利和为49.1126406.011000124≈⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⨯nt n r p (元),按月结算方式计算:12n =,本利和为.1511271206.0110001212≈⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⨯nt n r p (元),连续复利结算方式计算:本利和为 1000rt rtpe e =1127.49≈(元).5. 根据函数极限的定义,证明极限存在的准则I '.证明 仅就0x x →的情形证明准则I ',∞→x 的情形类似证明.0>∀ε,因为A x g x x =→)(lim 0,01>∃δ,当100δ<-<x x ,有ε<-A x g )(,即εε+<<-A x g A )(, (3)又A x h x x =→)(lim 0,对于上面的0>ε,02>∃δ,当200δ<-<x x ,有ε<-A x h )(,即εε+<<-A x h A )(. (4)取},min{21δδδ=,则当δ<-<00x x ,假设(1)及式(3)、(4)同时成立,从而有εε+<≤≤<-A x h x f x g A )()()(,即ε<-A x f )(.因此,0lim ()x x f x →存在,且等于A .习题2.6(A)1. 当0→x 时,下列各函数都是无穷小,试确定哪些是x 的高阶无穷小?同阶无穷小?等价无穷小?(1) x x +2; (2) x x sin +;(3) x x sin -; (4) x 2cos 1-; (5) x arctan ; (6) x 2tan .解 (1) 因为200lim lim(1)1x x x xx x→→+=+=,所以x x +2是与x 等价的无穷小.(2) 因为00sin sin limlim 1112x x x x x x x →→+⎛⎫=+=+= ⎪⎝⎭,所以x x sin +是与x 同价的无穷小. (3) 因为00sin sin limlim 10x x x x x x x →→-⎛⎫=-= ⎪⎝⎭,所以x x sin -是比x 高价的无穷小. (4) 因为20001sin 1cos 2sin 2lim lim lim sin 02x x x xx x x x x x →→→-⎛⎫==⋅= ⎪⎝⎭,所以x 2cos 1-是比x 高价的无穷小.(5) 因为00arctan limlim 1x x x xx x →→==,所以x arctan 是与x 等价的无穷小.(6) 因为00tan 22limlim 2x x x xxx →→==,所以x 2tan 是与x 同价的无穷小. 2. 当1x →时,无穷小111xx-+是否为等价的无穷小?解1111x x x→→-=. 故11xx -+与1.3. 当1x →时,无穷小1x -与下列无穷小是否同阶,是否等价?(1) 1 (2)2(1.解 (1) 由于11113x x x →→→===故1x -与1.(2) 由于112(1lim11x x x →→==-,故1x -与2(1等价.4. 利用等价无穷小代换原理求下列极限.(1) 0arctan 3lim sin 2x x x →; (2) 0sin lim (,)(sin )mn x x m n x →正数;(3) 201lim 1cos x x e x→--; (4) 201lim 3x x e x x →-+;(5) 21arcsin(1)lim (1)ln(21)x x x x →---; (6) 30tan sin lim ln(1)x x xx →-+;(7) 0x →; (8) 2330235lim 42tan x x x x x x →+-+.解 (1) 00arctan 333limlim sin 222x x x x x x →→==.(2) 00sin lim lim (sin )mmn n x x x x x x→→==0,1,,m n m n m n >⎧⎪=⎨⎪∞<⎩. (3) 222001limlim 21cos 2x x x e x xx →→-==-. (4) 22000111lim lim lim 3333x x x x e x x x x x x →→→-===+++. (5) 2211arcsin(1)(1)1lim lim (1)ln(21)(1)(22)2x x x x x x x x →→--==----.(6) 2333000tan sin tan (1cos )12limlim lim ln(1)ln(1)2x x x x x x x x x x x x →→→⋅--===++.(7) 22lim42x x xx x →→==+.(8) 2330235lim 42tan x x x x x x →+-+2200220lim(235)2352lim 1tan tan 242lim 42x x x x x x x x x x x x x →→→+-+-====⎛⎫++ ⎪⎝⎭.习题2.6 (B)1. 证明当0→x 时,有如下结论:(1) x x ~arctan ; (2) 221~1sec x x -; (3)221~1sin 1x x x -+; (4) 222~11x x x --+. 证明 (1) 令x t arctan =,则t x tan =,当0→x 时,0→t . 于是000arctan cos limlim lim 1sin tan x t t x t tt x tt →→→===,故x x ~arctan .(2) 因为200002222111sec 11cos cos 2lim lim lim lim 11111cos cos 2222x x x x xx x x x x x x x x →→→→---====⋅⋅, 所以,221~1sec x x -.(3)因为0022sin lim 111)22x x x x x x x →→→===, 所以,221~1sin 1x x x -+. (4) 因为20001x x x →→→===,所以222~11x x x --+.2. 证明无穷小的等价关系具有下列性质:(1) αα~(自反性); (2) 若βα~,则αβ~(对称性); (3) 若βα~,γβ~,则γα~(传递性).证明 (1) 因为1lim=αα,所以αα~. (2) 因为βα~,即1lim=βα,所以1lim =αβ,即αβ~.(3) 因为βα~,γβ~,即1lim=βα,1lim =γβ,所以 1lim lim lim lim=⋅=⎪⎪⎭⎫ ⎝⎛⋅=γββαγββαγα,即γα~. 3. 当0x →时,变量122(1)1kx +-与变量cos 1x -为等价无穷小,求常数k 的值.解 2122200(1)12lim lim 1cos 12x x kx kx k x x →→+-==-=--. 即 1k =-.解其中x 习题2.7(A)1. 讨论下列函数的连续性.(1) ⎩⎨⎧>≤=0 ,0 ,sin )(2x x x x x f ; (2) ⎪⎩⎪⎨⎧>≤≤--<-=1 ,111 ,1,1)(2x x x x x f .解 (1) 因为,当0<x 时,x x f sin )(=是连续的;当0>x 时,2)(x x f =是连续的,由于lim sin 0x x -→=,20lim 0x x +→=,00sin )0(==f ,故()f x 在0x =处连续. 从而函数)(x f 在) ,(∞+-∞内连续.(2) 因为)(x f 为分函数,当1-<x ,11<<-x ,1>x 时,函数)(x f 均是连续的.在1-=x 处,由于1lim (1)1x -→--=-,21lim 1x x +→-=,所以1-=x 是跳跃间断点;在1=x 处,由于21lim 1x x -→=,1lim11x +→=,且1)1(=f ,所以,函数在1=x 处连续. 综上所述:函数)(x f 在区间) ,1()1 ,(∞+---∞ 内连续.2. 确定常数a ,b 使下列函数连续.(1) ⎩⎨⎧>+≤=0 ,0 ,)(x a x x e x f x ; (2) ⎪⎪⎩⎪⎪⎨⎧>=<-=0,sin 0 ,20 ,)31ln()(x x axx x bx x x f .解 (1) 当0<x 与0>x 时,函数)(x f 为初等函数,它是连续的. 要使函数)(x f 在) ,(∞+-∞内连续,只需要函数)(x f 在0=x 处连续即可.因为1)0(0==e f ,0lim 1x x e -→=,0lim ()x x a a +→+=,所以当1=a 时,即有 00lim ()lim ()(0)1x x f x f x f -+→→===, 即当1=a 时,函数)(x f 在0=x 处连续. 故当取1=a 时,函数)(x f 在) ,(∞+-∞内连续.(2) 当0<x 与0>x 时,函数)(x f 为初等函数,故它是连续的. 要使函数)(x f 在) ,(∞+-∞内连续,只需要函数)(x f 在0=x 处连续即可.因为00033lim ()lim lim x x x x f x bx b---→→→-==-,000sin lim ()x x x a axf x a x ax +→+→+→==.由函数)(x f 在0=x 处连续知,00lim ()lim ()(0)2x x f x f x f -+→→===,即得,23=-=ba . 故当2=a ,23-=b 时,函数)(x f 在0=x 处连续. 也即函数)(x f 在) ,(∞+-∞内连续.3. 考察下列函数在指定点的连续性. 如果是间断点,指出其属于哪一类;如果是可去间断点,则补充或改变函数的定义使其成为函数的连续点.(1) 23122+--=x x x y ,1=x ,2=x ;(2) xxy sin =, πk x =,),2 ,1 ,0( ±±=k ; (3) xy 1cos 2=,0=x ;(4) ⎩⎨⎧>-≤-=1,31,12x x x x y ,1=x .解 (1) 因为)2)(1()1)(1(23122--+-=+--=x x x x x x x y ,函数在1=x ,2=x 处无定义,所以都是间断点.又因为221lim )2)(1()1)(1(lim 231lim 11221-=-+=--+-=+--→→→x x x x x x x x x x x x , ∞=+--→231lim 222x x x x , 所以,1=x 为第一类间断点(可去间断点),重新定义,当1=x 时,令2-=y ,则函数在1=x 处连续.2=x 为第二类间断点(无穷间断点).(2) 函数xxy sin =在 πk x =,),2 ,1 ,0( ±±=k 处无定义,所以它们都是间断点. 因为1sin lim0=→xxx ,故0=x 是函数y 的第一类间断点(可去间断点).若令1)0(=y ,则函数在0=x 处连续;若0≠k ,则∞=→xxk x sin lim π,故 πk x =),2 ,1( ±±=k 为函数y 的第二类间断点(无穷间断点).(3) 对0=x ,因为21lim cos x x -→及201lim cos x x+→均不存在,所以0=x 为函数的第二类间断点.(4) 对1=x ,因为11lim ()lim(21)1x x f x x --→→=-=,11lim ()lim(3)2x x f x x ++→→=-=,所以 1=x 第一类间断点(跳跃间断点).4. 求函数32233()6x x x f x x x +--=+-的连续区间,并求0lim ()x f x →,3lim ()x f x →-,2lim ()x f x →.解 由于323223333()6(3)(2)x x x x x x f x x x x x +--+--==+-+-, 得()f x 的定义域为()()(),33,22,-∞--+∞. 由于初等函数在其定义区间内连续,故函数()f x 的连续区间为()()(),33,22,-∞--+∞.01lim ()(0)2x f x f →==,22333(3)(3)18lim ()lim lim (3)(2)25x x x x x x x f x x x x →-→-→-+-+-===-+--,由于0)3)(1()2)(3(lim )(1lim222=+--+=→→x x x x x f x x ,故 222(3)(3)lim ()lim (3)(2)x x x x x f x x x →→+-+==∞+-.5. 求下列极限(1) 52lim 20+-→x x x ; (2) 34)2(sin lim x x π→;(3) sin 0lim xx x e→;(4) 145lim1---→x xx x .解 (1) 5502052lim 220=+⨯-=+-→x x x .(2) 142sin )2(sin lim 334=⎪⎭⎫ ⎝⎛=→ππx x . (3) e e eex x xxx x ===→→1sin limsin 00lim .(4) )45)(1()1(4lim145lim11x x x x x x x x x +---=---→→21==→x .习题2.7 (B)1. 设2,01()2,1ln(1), 13ax b x f x x bx x ⎧+<<⎪==⎨⎪+<≤⎩, a ,b 为何值时,()f x 在1x =处连续?解 由于211lim ()lim()x x f x ax b a b --→→=+=+,11lim ()lim ln(1)ln(1)x x f x bx b ++→→=+=+. 要使()f x 在1x =处连续,须有ln(1)2,2b a b +=+=.解之得 23a e =-,21b e =-. 2. 讨论下列函数的连续性.(1) 1()lim(0)1n n f x x x →∞=≥+; (2) 221()lim 1nnn x f x x x →∞-=+.解 (1) 1, 0111()lim , 1120, 1nn x f x x x x →∞≤<⎧⎪⎪===⎨+⎪>⎪⎩, 由于 11lim ()lim11x x f x --→→==,11lim ()lim 00x x f x ++→→==,故1x =为间断点. (2) 22, ||11()lim 0, 11,||1n nn x x x f x x x x x x →∞<⎧-⎪===±⎨+⎪>⎩-, 由于 11lim ()lim 1x x f x x --→→==,11lim ()lim()1x x f x x ++→→=-=-. 故1x =为间断点. 同理1x =-也为间断点. 3. 求下列极限.(1) 21limcos ln 1x x x →∞⎡-⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦; (2) sin 0lim xxx e →;(3) 01limarctan x x e x →⎛⎫- ⎪⎝⎭; (4) ()110lim 2x x x x e -→+. 解 (1) 2121limcos ln(1)cos ln lim(1)cosln 3x x x x x x →∞→∞--⎡⎤⎡⎤+=+=⎢⎥⎢⎥⎣⎦⎣⎦.(2) 0sin sin limlim x x xxxx eee →→==.(3) 0011limarctan arctan lim arctan14x x x x e e x x π→→⎛⎫⎛⎫--=== ⎪ ⎪⎝⎭⎝⎭. (4) ()()11ln 2ln 2111lim 2lim 2x x e xx x x x x eee +---→→+===. 4. 下列陈述中,哪些是对的,哪些是错的?如果是对的,说明理由;如果是错的,试给出一个反例.(1) 如果函数)(x f 在点0x 连续,那么)(x f 也在点0x 连续; (2) 如果函数)(x f 在点0x 连续,那么函数)(x f 也在点0x 连续. 解 (1) 对. 因为0)()()()(00→-≤-x f x f x f x f )(0x x →,所以)(x f 也在点0x 连续. (2) 错. 例如⎩⎨⎧<-≥=0,10,1)(x x x f , 则)(x f 在点00=x 连续,但函数)(x f 在点00=x 不连续.习题2.8(A)1. 证明方程3310x x --=在区间(1,2)内至少有一个实根.证明 因为函数3()31f x x x =--在闭区间[1, 2]上连续,又(1)30f =-<,(2)10f =>,根据零点定理,在开区间(1, 2)内至少有一点ξ,使得()0f ξ=,即3310ξξ--=.故方程3310x x --=在区间(1,2)内至少有一个实根ξ.2. 设函数()f x 在闭区间[,]a b 上连续,且(),()f a a f b b <>,证明:至少有一个(,)a b ξ∈,使()f ξξ=.证明 构造辅助函数x x f x g -=)()(.因为函数()f x 在闭区间[, b]a 上连续,且(),()f a a f b b <>,所以x x f x g -=)()(在闭区间[, b]a 上也连续,且0)()(<-=a a f a g ,0)()(>-=b b f b g . 根据零点定理,x x f x g -=)()(在开区间(, b)a 内至少有一点ξ,使得()()0g f ξξξ=-=,即 ()f ξξ=.3. 设函数()f x 在闭区间[0,2]a 上连续,且(0)(2)f f a =,证明:在[0,]a 至少存在一点ξ,使()()f f a ξξ=+.证明 构造辅助函数:)()()(x f a x f x g -+=.因为函数()f x 在闭区间[0,2]a 上连续,且(0)(2)f f a =,所以)()()(x f a x f x g -+=在闭区间[0,]a 上也连续,且()()0)()2()2()()()0(≤--=a f a f a f a f a g g .根据零点定理,)()()(x f a x f x g -+=在开区间(0,)a 内至少有一点ξ,使得()()()0g f a f ξξξ=+-=,即()()f f a ξξ=+.4. 证明方程 sin x a x b =+(其中0,0a b >>)至少有一正根,并且不超过a b +. 证明 令()sin ,f x a x b x =+-[]0,x a b ∈+,()f x 在[]0,a b +上连续,又(0)0f b =>,()sin()()[sin()1]0f a b a a b b a b a a b +=++-+=+-≤。
数学分析第二章极限与连续知识网络思维导图及复习
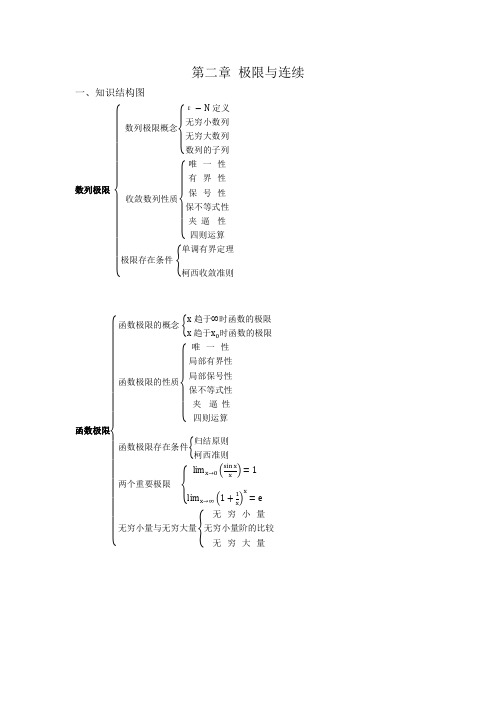
量求极限。 6、 理解函数连续的概念,会判断函数不连续点的类型。 7、 掌握用基本定理证明闭区间上连续函数的最大值、最小值、介值性定理的基本思路和方
法。 8、 理解一致连续的概念,并会应用其证明相关命题。 三、知识点梳理 1、数列极限的概念、性质与定理
不一致连续: 0
0,
xn
,xn
,
lim(
n
xn
x)
0 ,而 lim( n
f
(xn )
f
( xn)
c
0.
四、典型例题分析
基本题型 I 利用定义证明数列的极限
例
证明
lim
n
n 2n
0
证 明 : 0, 要 使 得
n 2n
0
成立,只要
n 2n
0
n 2n
2 n
(这是因为
2n (11)n 1 n n(n 1) ... n2
(ii) 同 阶 无 穷 小 : lim f (x) a 0 , 则 称 f (x) 是 g(x) 的 同 阶 无 穷 小 , 记 为 xx0 g(x)
f (x) Og(x) x x0 ,
0
特别地,如果 f (x) 在 O(x0 ) 有界,记作 f (x) O(1), (x x0 )
③ 函数的不连续点
(i)第一类不连续点: f (x0 0), f (x0 0) 存在,但不相等。
(ii)第二类不连续点: f (x0 0), f (x0 0) 中至少有一个不存在.
(iii)可移不连续点:
f (x0
0)
f
(x0
第2章 7-利用无穷小量代换求极限
简化计算步骤.
第二章 极限与连续
利用等价无穷小量代换求极限
等价无穷小量的性质
设1, 1, , 1, 为同一极限过程中的无穷小量, 且 ~ 1, ~ 1 , 则
lim f ( x) lim1 f ( x).
tan x ln(1 x ) lim x 0 sin x 2
例1.求极限
解:因为
sin x ~ x ( x 0) sin x 2 ~ x 2 ( x 2 0)
tan x ~ x ( x 0) ln(1 x ) ~ x ( x 0)
所以
tan x ln(1 x ) x x lim lim 2 lim1 1 2 x 0 x 0 x x 0 sin x
第二章 极限与连续
利用等价无穷小量代换求极限
等价无穷小量的性质
若在同一极限过程中, α, β, γ 均为无穷小量, 则
(1) α ~ α;
(2) 若α ~ β; 则 β ~ α; (3) 若α ~ β, β ~ γ ; 则 α ~ γ ;
(反身性)
(对称性) (传递性)
(4) 若α ~ β; 则 αγ ~ γ β .
例3 求极限
sin x ~ x ( x 0) sin x 2 ~ x 2 ( x 2 0) 解:因为 x2 tan x ~ x ( x 0) 1 cos x ~ ( x 0) 2 sin x 1 sin x 1 tan x sin x 所以 lim lim cos x 3 lim cos x x 0 x 0 x 0 sin 2 x sin3 x sin x x2 1 cos x 1 1 1 2 lim lim lim x 0 cos x sin 2 x x 0 cos x x 2 x 0 cos x 2 2
《高职应用数学(机电类)》教学课件 第2章 极限与连续
例 7 如图 2-5 所示,观察当 x 1时,函数 y x2 1的变化趋势. x 1
图2-5
1.2 当x→x0时,函数y=f(x)的极限
解 由图可知,当 x 无限接近于 1,即 x 1时,函数 y x2 1 无限接近于一个确定的常数 2,即 x 1
则有 lim 1 (或 0). f (x)
例如,因为 lim 2x ,所以 lim 1 0 .
x
2 x x
注意:(1)极限 lim f (x) 没有写出自变量 x 的变化过程,意味着此结论对自变量 x 的任意变化
过程都成立,但在做题时,一定要写出自变量 x 的变化过程. (2)无穷小与无穷大反映了自变量在某一变化过程中函数的两种特殊变化趋势——绝对值越
?高职应用数学?
第2章 极限与连续
目录
contents
函数的极限 无穷小与无穷大 极限的运算 函数的连续性
01
函数的极限
当x→∞时,函数f(x)的极限 当x→x0时,函数y=f(x)的极限
1.1 当x→∞时,函数f(x)的极限
“x ”是指 x 的取值可正可负,但其绝对值无限增大,它包含两层意思: (1) x 取正但其绝对值无限增大,记为 x ; (2) x 取负但其绝对值无限增大,记为 x . 首先研究 x 的情况.
性质 1 有限个无穷小的和差仍为无穷小.
性质 2 有限个无穷小的乘积仍为无穷小.
性质 3 有界函数与无穷小之积仍为无穷小.
2.1 无穷小
例 1 求 lim 1 cos x . x x
解 因 lim 1 0 ,所以 1 是 x 时的无穷小.
x x
x
又因 | cos x | 1,所以 cos x 是有界函数,再由性质 3 知, lim 1 cos x 0 . x x
极限与连续ppt
. . .. . . . .
...
分成若干充分小(长度无限接近零)曲线段, 这些曲线段也就无限接近(趋于)直线段. 据此,数学家找到一种用直线近似 代替曲线(以直代曲) 的处理曲线的方法,从而创立了微积分方法。
即: 先对曲线段无限细分; 再用直线来近似代替 曲线段(即以直代曲); 然后取极限(看无穷趋势)的数学方法, 我们称此为
同样可以看出,随着 n 的无限增大时, 上述其它数列的
无限变化趋势。
数列(2.3),即
{1} n
无限地接近常数0;
数列(2.4),即
{n} n 1
无限地接近常数1;
数列(2.5),即{2n} 无限增大;
数列(2.6),即{( 1) n } 不停地在1与-1之间摆动.
前四个数列(2.1)-(2.4)反映了一类数列的一
因为 12 +22 +
n2 =
1 (2n +1)n(n +1) 6
,所以
原式 limn1来自n(n(n
1)(2n
6n2
1)
)
lim
n
(n
1)(2n 6n2
1)
1
11
lim(1 )(2 )
6 n n
n
1 lim(1 1) lim(2 1) 1 .
6 n
bn )
lim
n
an
lim
n
bn
;
(2) (3)
lnim(an
bn
)
lim
n
an
lim
n
bn ;
若还满足 bn 0 ,且
第二章极限与连续的总结
第二章极限与连续的总结《第二章极限与连续的总结:探索数学未知世界的奇妙之旅》嘿,朋友们!今天咱来唠唠第二章极限与连续这一块儿。
说实在的,刚接触到这一章的时候,我感觉自己就像走进了一个充满迷雾的森林,有点晕头转向的。
那些个极限的定义、计算方法,还有连续的条件啥的,就跟一群小精灵在我脑子里蹦跶,一会儿这个跳跳,一会儿那个闹闹。
我记得最开始学极限的计算时,那可真是让我头大。
什么无穷小替换啦、洛必达法则啦,感觉每个都有自己的脾气。
有时候好不容易觉得自己掌握了一个方法,结果一做题,哎呀妈呀,又不对了!就像是好不容易抓住了一只小精灵,结果它嗖地一下又跑掉了。
不过呢,随着不断地学习和摸索,我慢慢也找到了一些门道。
就像是在森林里找到了指南针一样,虽然路还不是那么好走,但至少方向感有了。
我开始理解了极限的那种趋近却又永远达不到的微妙感觉,仿佛是在追逐一个永远在前方的目标,虽然追不上,但却能越来越近。
而连续呢,就像是给这些极限小精灵们搭建了一个安稳的家。
当一个函数在某个点连续时,就像是小精灵们在那个点安安稳稳地待着,不折腾了。
这种稳定的感觉还挺让人安心的。
整个第二章学下来,我觉得自己就像是一个勇敢的探险家,在数学的未知世界里闯荡。
有时候会遇到困难,会被荆棘划破皮肤,但每一次突破难关,都让我兴奋不已。
我也深刻体会到了学习就像爬山一样,过程可能很艰难,但当你爬到山顶,看到那美丽的风景时,一切付出都变得值得了。
现在再回头看看刚开始学的自己,真的觉得挺有意思的。
那时候的迷茫和困惑,现在都变成了有趣的回忆。
当然啦,我知道自己还有很多不足,还有很多需要继续探索和进步的地方。
但我一点也不害怕,因为我已经准备好了迎接更多的挑战,去探索数学世界里那些还未被我发现的精彩。
总之,第二章极限与连续让我收获满满,也让我对数学的热爱又增添了几分。
我相信,只要我坚持不懈地学习,一定能在数学的海洋里畅游,发现更多的奇妙和美好!。
