相似三角形单元测试卷
《相似三角形》单元测试卷 (2)

九年级数学(上)《图形的相似》单元测试题(2)姓名: 得分:一、选择题(每小题3分,共30分) 1、下列各组数中,成比例的是( )A 、-6,-8,3,4B 、-7,-5,14,5C 、3,5,9,12D 、2,3,6,12 2、 在比例尺为1:5000的地图上,量得甲,乙两地的距离25cm,则甲,乙的实际距离是( ) A 、1250km B 、125km C 、12.5km D 、1.25km3、D 、E 分别是△ABC 边 AB 、AC 上的一点,且△ADE ∽△ABC ,若AD=2,BD=4,则△ADE 与△ABC 的相似比是( )A 、1∶2B 、1∶3C 、2∶3D 、3∶2 4、如图所示,点E 是ABCD 的边BC 延长线上的一点,AE 与CD 相交于点F ,则图中相似三角形共有( ) A 、2对 B 、3对 C 、4对 D 、5对5、如图,P 是Rt ΔABC 的斜边BC 上异于B 、C 的一点,过点P 做直线截ΔABC ,使截得的三角形与ΔABC相似,满足这样条件的直线共有( ) A 、1条 B 、2条 C 、3条 D 、4条6、△ABC ∽△A 1B 1C 1,相似比为2︰3;△A 1B 1C 1∽△A 2B 2C 2,相似比为5︰4 则 △ABC ∽△A 2B 2C 2相似比为( ) A 、B 、C 、D 、7、如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点, 为使△PQR ∽△ABC , 则点R 应是甲、乙、丙、丁四点中的( ) A 、甲 B 、乙 C 、丙 D 、丁8、将一个矩形纸片ABCD 沿AD 和BC 的中点的连线对折,要使矩形AEFB 与原矩形相似,则原矩形的长和宽的比应为( )A 、2:1B 、1:3C 、1:2D 、1:19、下列结论中,不正确的是( )A 、有一个锐角相等的两个直角三角形相似B 、 有一个锐角相等的两个等腰三角形相似C 、有一个为600的两个等腰三角形相似 D 、 有一个角为1200的两个等腰三角形相似 10、在矩形ABCD 中,E 、F 分别是CD 、BC 上的点,若∠AEF=90°,则一定有 ( )A ΔADE ∽ΔAEFB ΔECF ∽ΔAEFC ΔADE ∽ΔECFD ΔAEF ∽ΔABF二、填空题(每小题3分,共30分) 1、已知43=y x ,则._____=-yy x 2、在△ABC 中,AB=6,AC=8,在△DEF 中,DE=4,DF=3,要使△ABC 与△DEF相似, 需添加的一个条件是 ,。
相似三角形单元测试卷(含答案)

相似三角形单元测试卷(含答案)第四章相似三角形单元测试卷一、选择题: 1.下列各组数中,成比例的是A.-6,-8,3,4 B.-7,-5,14,5 C.3,5,9,12 D.2,3,6,12 2.如图,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为A.23 B.33 C.43 D.63 3.如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC= A. AFBECD1121 B. C. D. 2334 ADFBEGC 4.如图,△ABC中,DE ∥FG∥BC,且DE、FG将△ABC的面积三等分,若BC=12cm,则FG的长为A、8cm B、6cm C、46cm D、62cm 5.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于A. 2:5:25:25 D. 4:216.如图, 小正方形的边长均为1, 则下列图中的三角形(阴影部分)与△ABC相似的是()7.如图,在□ABCD 中,E、F分别是AD、CD 边上的点,连接BE、AF,他们相交于点G,延长BE交CD的延长线于点H,则图中的相似三角形共有A.2对B.3对C.4对D.5对AD45°B 1 PC8.如图,在直角三角形ABC中,放置边长分别3,4,x的三个正方形,则x 的值为() A. 5 B. 6 C. 7 D. 129. 如果三条线段的长a、b、c满足5?1bc==,那么(a,b,c)叫做“黄金线段组\.黄2ab金线段组中的三条线段().A.必构成锐角三角形B.必构成直角三角形C.必构成钝角三角形D.不能构成三角形10. 如图,等腰直角△ABC的直角边长为3,P为斜边BC上一点,且BP=1,D为AC上一点,若∠APD=45°,则CD的长为A. 5 3 ?1 3C.32?1 3D. 35 二、填空题: C11.已知a=4,b=9,c是a、b的比例中项,则c =.BOD12. 如图,△ABC中,已知AB=4,AC=3。
初中数学相似三角形单元测试卷

相似三角形单元测试卷(满分120分,考试时间90分钟)一.选择题【本题共6题,每小题3分,共18分】1.在△ABC 中,点D 、E 分别在边AB 、AC 上,AD :BD =1:2,那么下列条件中能够判断DE//BC 的是……………………………………………………………………( ) (A) 21=BCDE ; (B) 31=BC DE ; (C) 21=AC AE ; (D) 31=AC AE2.如图,123//// ,下列比例式中正确的是…………………………………( ) (A )AD CE BC DF =; (B )AD DF BC CE =; (C )AB CD CD EF =; (D )AD BCBE AF =. 3.已知a ,b ,c 是非零向量,不能判定a ∥b的是……………………………( )(A )a ∥c ,b ∥c ;(B ) a =3b ;(C )a =b ;(D )a =12c ,b =-2c. 4.如图,△ABC 中,DE //BC 交AB 于点D ,交AC 于点E ,如果ADE BCED S S ∆=四边形,那么下列等式成立的是 ……………………………………………………………( ) (A ):1:2DE BC =;(B ):1:3DE BC =;(C ):1:4DE BC =;(D ):DE BC = 5.在Rt △ABC 和Rt △DEF 中,90C F ∠=∠=°,下列条件中不能判定这两个三角形相似的是…………………………………………………………………………………( )(A )55,35A D ∠=°∠=°; (B )9,12,6,8AC BC DF EF ====; (C )3,4,6,8AC BC DF DE ====;(D )10,8,15,9AB AC DE EF ====. 6.如图,在三角形纸片ABC 中,AB=AC ,∠A=36°。
《相似三角形》单元测试题含答案

《相像三角形》单元测试题一、精心选一选(每题4分,共32分)1. 以下各组图形有可能不相像的是( ).各有一个角是50°的两个等腰三角形各有一个角是100°的两个等腰三角形各有一个角是50°的两个直角三角形两个等腰直角三角形22.如图,D是⊿ABC的边AB上一点,在条件(1)△ACD=∠B,(2)AC=AD·AB,(3)AB边上与点C距离相等的点D有两个,(4)∠B=△ACB中,必定使⊿ABC∽⊿ACD的个数是()A)1(B)2(C)3(D)43.如图,∠ABD=∠ACD,图中相像三角形的对数是()(A)2(B)3(C)4(D)54.如图,在矩形 ABCD中,点E是AD上随意一点,则有()A)△ABE的周长+△CDE的周长=△BCE的周长B)△ABE的面积+△CDE的面积=△BCE的面积C)△ABE∽△DECD)△ABE∽△EBC5.假如两个相像多边形的面积比为9:4,那么这两个相像多边形的相像比为()A.9:4B.2:3C.3:2D.81:166.以下两个三角形不必定相像的是()。
A.两个等边三角形 B.两个全等三角形C.两个直角三角形 D.两个等腰直角三角形7.若⊿ABC∽⊿ABC,∠A=40°°,∠B=110,则∠C=()A.40°B110°C70°D30°8.如图,在ABC中,AB=30,BC=24,CA=27,AE=EF=FB,EG∥FD∥BC,FM∥EN∥AC,则图中暗影部分的三个三角形的周长之和为()A、70B、75C、81D、80二、仔细填一填(每题3分,共24分)如图,在△ABC中,△BAC=90°,D是BC中点,AE∥AD交CB延伸线于点E,则⊿BAE相像于______.110、在一张比率尺为1:10000的地图上,我校的周长为18cm,则我校的实质周长为。
11、假如两个相像三角形对应高的比为4:5,则这两个三角形的相像比是,它们的面积的比是。
相似三角形单元测试卷
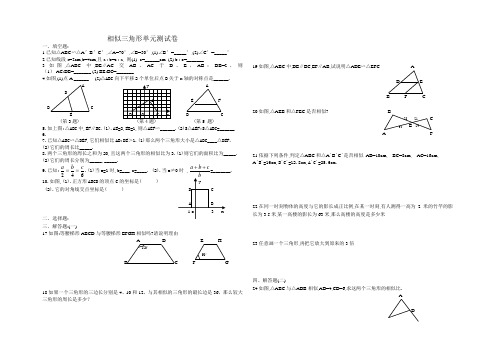
相似三角形单元测试卷一、填空题:1.已知△ABC ∽△A 'B 'C ',∠A=70°,∠B=50°,(1)∠B '=_____°,(2)∠C '=_____°.2.已知线段a=2cm,b=4cm,且a : b=c : a, 则(1). c=______cm. (2).b : c=_______.3.如图,△ABC 中,DE ∥AC 交AB 、AC 于D 、E ,AB :DB=2,则(1).AC:DE=_______.(2).BE:BC=_______.4.如图,(1)点A ______. (2)△ABC 向下平移2个单位后点B 关于x 轴的对称点是______. A y A DA E F B(第3题第5 题)5.如上图:△ABC 中,EF ∥BC.(1).AE=2,EB=1,则△AEF ∽______.(2)S △AEF:S △ABC=______6.7.已知△ABC ∽△DEF,它们相似比AB:DE >1.(1)那么两个三角形大小是△ABC____△DEF. (2)它们的周长比_____.8.两个三角形的周长之和为20,且这两个三角形的相似比为3.(1)则它们的面积比为_____. (2)它们的周长分别为_____,_____. 9.已知:642c b a ==.(1)当a=1时,b=___,c=____. (2).当a ≠0时 ,cb a ++=_______. 10.如图,(1).正方形ABCD 的顶点C 的坐标是 (2).它的对角线交点坐标是二、选择题: 三、解答题:(一)17.如图:等腰梯形ABCD 与等腰梯形EFGH 相似吗?请说明理由.A D E H 120° 60°B C F G18.如果一个三角形的三边长分别是4、10和12,与其相似的三角形的最长边是36,那么较大三角形的周长是多少?19.如图,△ABC 中,DE ∥BC,EF ∥AB,试说明△ADE ∽△EFC. AD EB F C20.如图,△AEB 和△FEC 是否相似? B 28 21 C 32 E 24 A F21.依据下列条件,判定△ABC 和△A ´B ´C ´是否相似. AB=10cm, BC=8cm, AC=16cm, A ´B ´=16cm,B ´C ´=12.8cm,A ´C ´=25.6cm.22.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为2米的竹竿的影长为3.5米,某一高楼的影长为63米,那么高楼的高度是多少米.23.任意画一个三角形,再把它放大到原来的3倍.四、解答题(二)24.如图,△ABC 与△ADB 相似,AD=4,CD=6,求这两个三角形的相似比. ADBC25.已知如图,△ABC 中,说明△ABC ∽△DAC.A40° 60° 20° B D C26.已知△ABC 和△DEF 的相似比为43,若△ABC 和△DEF 的面积之差为70,求△ABC 的面积.27.如图,平行四边形ABCD,CE ⊥AD 交AD 于E,CF ⊥AB 交AB 于F,(1)△DEC 与△BFC 相似吗?请说明.(2)若AD=4,平行四边形ABCD 面积为6,求CE.A E DFB C 28.已知E 是菱形ABCD 边上的一点,O 是对角线的交点,OE ∥BC 交AB 于E,证明OE=21BC. A DE OB C29.赵华和小东、张艺是某校初二年同学,一次数学兴趣小组活动中测量自家与学校的位置关系.已知他们三人测得的结果是:赵华在学校北偏东15 °约1500米处,小东在学校的西南方向约2000米处,张艺在学校的正东约1200米处.请你帮他们画出他们三人的位置并求出赵华与小东的大约直线距离. (比例尺为1:100000 ) 北30.如图,A 、B 是一座小山脚下的两点,想知道这两点间的直线距离,你能用你学到的知识设计一种可求出AB 之间的距离方法吗?(说出理由即可)。
第24章 专题15 相似三角形单元测试卷(学生版)

2021-2022学年九年级上册相似三角形单元测试卷第I 卷(选择题)一、单选题 1.若△ABC ∽∽DEF ,且对应中线比为2:3,则△ABC 与△DEF 的面积比为( ) A .3:2 B .2:3 C .4:9 D .9:162.如图,以点O 为位似中心,将ABC 缩小后得到'''A B C ,已知3'OB OB ,则'''A B C 与ABC 的面积的比为( )A .1:3B .1:4C .1:5D .1:93.如图,在4×4正方形网格中画出的三角形中,与图中的三角形相似的是( )A .B .C .D . 4.已知::2:4:5a b c =,则32a b c b--的值为( ) A .74 B .74- C .47 D .47-5.下列命题正确的是( )A .相似三角形的面积比等于相似比B .等边三角形是中心对称图形C .若直线(2)3y m x =-+经过一、二、四象限,则2m >D .二次函数222y x x =+-的最小值是3-6.若△ABC ∽△DEF ,相似比为4:3,则△ABC 与△DEF 对应的中线之比为( ) A .4:3 B .3:4 C .16:9 D .9:167.如图,将△ABC 绕点A 旋转任意角度得到△AB'C',连接BB'、CC',则BB':CC'等于( )A .AB :ACB .BC :AC C .AB :BCD .AC :AB 8.如图,AB 是O 的直径,BP 是O 的切线,AP 与O 交于点,C D 为BC 上一点,若36,P ∠=︒则ADC ∠等于( )A .18B .27C .36D .549.如图,正方形ABCD 的对角线上的两个动点E 、F ,满足AB EF ,点P 是BC 的中点,连接AF 、PE ,若AB =8,则当AF +PE 最小值时,线段AF 的长度为( )A .6BC .D .10.如图,D 、E 分别是△ABC 的边AB 、BC 上的点,DE ∥AC ,若S △BDE :S △CDE =1:4,则S △DOE :S △AOC 的值为( )A .14B .19C .116D .12511.△ABC 是等腰三角形,AB=AC△△A=30°△△ABC△△A′B′C ′,则∠C′=△ △A .30°B .60°C .50°D .75°12.如图,点D △E 分别在△ABC 的AB △AC 边上,增加下列条件中的一个:①△AED △△B △②△ADE △△C △③AE DE AB BC=△④AD AE AC AB =△⑤AC 2△AD •AE ,使△ADE 与△ACB 一定相似的有( )A .①②④B .②④⑤C .①②③④D .①②③⑤第II 卷(非选择题)二、填空题 13.已知线段a 、b 、c 、d 是成比例线段,且a=2cm ,b=0.6cm ,c=4cm ,那么d=______㎝. 14.如图,点M 是△ABC 内一点,过点M 分别作直线平行于△ABC 的各边,所形成的三个小三角形(图中阴影部分)的面积分别是S 1=1,S 2=4,S 3=9,则△ABC 的面积是___________15.如图,点1234A A A A ,,,在射线OA 上,点123B B B ,,在射线OB 上,且112233////A B A B A B ,213243////A B A B A B .若212A B B △,323A B B △的面积分别为1,4,则图中三个阴影三角形面积之和为___________.16.如图,l1//l2//l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为_____.17.大唐芙蓉园位于古都西安大雁塔东侧,是中国第一个全方位展示盛唐风貌的大型皇家园林式文化主题公园.该园占地面积约为800000m2,小明按比例尺1∶2000缩小后画出该园示意图,其面积大约为____________m2.18.如图所示,△ABC与△A′B′C′是位似图形,且顶点都在格点上,则位似中心的坐标是______,△ABC与△A′B′C′的相似比为______.19.如图,△ABC中,D在AC上,且AD△DC=1△n△E为BD的中点,AE的延长线交BC于F,那么BFFC的值为_____(用n表示).20.如图,AB∥CD∥EF,AF 与BE 相交于点G ,且AG =2,GD =1,DF =5,那么BC CE的值等于________.21.正方形CEDF 的顶点D 、E 、F 分别在△ABC 的边AB 、BC 、AC 上.(1)如图,若tan 2B =,则BE BC的值为___________;(2)将△ABC 绕点D 旋转得到△'''A B C ,连接'BB 、'CC .若''CC BB =,则tan B 的值为___________.22.G 是△DEF 的重心,若EF 过点G 且EF//BC ,交AB 、AC 于E 、F ,若BC=2,则EF=______.三、解答题 23.如图,在平面直角坐标系中,直线y kx b =+交x 轴于点B ,交y 轴于点A ,3OA OB ==.(1)求直线AB 的解析式;(2)如图,点C 在OA 的延长线上,点D 在x 轴的负半轴上,连接CD 交直线AB 于点E ,点E 为线段CD 的中点,设点D 的横坐标为t ,点C 的纵坐标为d ,求d 与t 的函数解析式; (3)如图,在(2)的条件下,过点E 作EF x ⊥轴于点F ,点G 在OB 的延长线上,点M 为EB 的中点,连接MG 并延长交线段EF 于点H ,点N 在AB 的延长线上,连接NG 、DN 、CM ,MNG ∠为钝角,若,,2FG d ACM GDN MG NG =∠=∠=,求点G 的坐标. 24.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O .(1)平移△AOB ,使得点A 移动到点D ,画出平移后的三角形(不写画法,保留画图痕迹); (2)在第(1)题画好的图形中,除了菱形ABCD 外,还有哪种特殊的平行四边形?请给予证明.25.数学活动 实验、猜想与证明问题情境(1)数学活动课上,小颖向同学们提出了这样一个问题:如图(1),在矩形ABCD 中,AB=2BC ,M、N分别是AB,CD的中点,作射线MN,连接MD,MC,请直接写出线段MD与MC之间的数量关系.解决问题(2)小彬受此问题启发,将矩形ABCD变为平行四边形,其中∠A为锐角,如图(2),AB=2BC,M,N分别是AB,CD的中点,过点C作CE⊥AD交射线AD于点E,交射线MN于点F,连接ME,MC,则ME=MC,请你证明小彬的结论;(3)小丽在小彬结论的基础上提出了一个新问题:∠BME与∠AEM有怎样的数量关系?请你回答小丽提出的这个问题,并证明你的结论.26.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:四边形AECF是平行四边形.。
浙教版数学九年级上册第四章相似三角形 单元测试(含答案)
浙教版数学九年级上册第四章相似三角形一、选择题1.已知c 是a 和b 的比例中项,a =2,b =18,则c =( )A .±6B .6C .4D .±32.如图,DE ∥BC ,在下列比例式中,不能成立的是()A .AD DB =AEECB .DE BC =AEEC C .AB AD =AC AED .DB EC =ABAC3.如果两个相似三角形的周长之比为5:7,那么这两个三角形的面积之比为( )A .5:7B .7:5C .25:49D .49:254.如图,已知AB ∥CD ∥EF ,AE =9,AC =6,BD =4,则BF 的长是( )A .5B .6C .7D .85.小明在测量楼高时,先测出楼房落在地面上的影长BA 为15米(如图),然后在A 处树立一根高2米的标杆,测得标杆的影长AC 为3米,则楼高为( )A .10米B .12米C .15米D .22.5米6.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是( )A .B .C.D.7.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).A.1:2B.1:3C.1:4D.1:58.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为5,则下列结论中正确的是( )A.m=5B.m=45C.m=35D.m=109.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,BDCD =73,则ADAC的值为( )A.12B.33C.13D.3210.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图像为( )A .B .C .D .二、填空题11.如图,线段AC 、BD 交于点O ,请你添加一个条件: ,使△AOB ∽△COD .12.如图,点G 为△ABC 的重心,GE ∥AC ,若DE =2,则DC = .13.在某市建设规划图上,城区南北长为120cm ,该市城区南北实际长为36km ,则该规划图的比例尺是 .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图, EB 为驾驶员的盲区,驾驶员的眼睛点 P 处与地面 BE 的距离为1.6米,车头 FACD 近似看成一个矩形,且满足 3FD =2FA ,若盲区 EB 的长度是6米,则车宽 FA 的长度为 米.16.如图,在△ABC中,点D是AC边上一点,将△ABD沿BD翻折得到△EBD,BE与AC交于点F,设AF=x,EF=y.(1)当BE⊥AC,x=9,y=3时,AD的长是 ;(2)当BD=BF,2x=7y时,△DEF与△ABD的面积之比是 .三、解答题17.如图,已知D、E分别是△ABC的边AB、AC上的点,DE∥BC,ADBD =32,求DEBC的值.18.如图,在△ABC中,D为BC上一点,∠BAD=∠C.(1)求证:△ABD∽△CBA;(2)若AB=6,BD=3,求CD的长.19.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部的(全身)的高度比,可以增加视觉美感,按比例,如果雕像的高为2m,那么它的下部设计为多高?(结果保留小数点后两位)参考数据:2=1.414,3=1.732,5=2.23620.如图,在矩形ABCD中,AB=6,BC=4,E是边BC上的一点(不与B、C重合),DF⊥AE,垂足为F.(1)求证:△ABE∽△DFA;S△ABE,求BE的长.(2)若S△DFA=1321.如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.22.如图,矩形ABCD中,点M在对角线BD上,过点A、B、M的圆与BC交于点E.(1)若AM=4,EB=EM=3,求BM.(2)若AB=6,BC=8,①求AM:ME.②若BM=7,求BE.23.如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长交BC于点E,过点Q作QF//AC,交BD于点F,设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形;(2)设五边形OECQF的面积为S(c m2),试确定S与t的函数关系式;(3)在运动过程中,当S五边形OECQF:S△ACD=9:16时.直接写出t的值.答案解析部分1.【答案】A2.【答案】B3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】C8.【答案】B9.【答案】A10.【答案】C11.【答案】AB∥CD(答案不唯一)12.【答案】6.13.【答案】1:3000014.【答案】9415.【答案】12716.【答案】5;1417.【答案】3518.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,∴△ABD∽△CBA(2)解:设DC=x,∵△ABD∽△CBA,∴ABBD=BCAB,∴63=2+x6,解得,x=9;即CD=719.【答案】1.24米.20.【答案】(1)证明:∵四边形ABCD是矩形,AB=6,BC=4,∴∠B=90°,AD∥BC,AD=BC=4,∴∠AEB=∠DAF,∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA;(2)解:∵△ABE∽△DFA,S△DFA=13S△ABE,∴(AEAD )2=S△ABES△DFA=3,∴AEAD=3或AEAD=−3(负数不符合题意,舍去),∴AE=3AD=43,∴BE=AE2−AB2=(43)2−62=12=23,∴BE的长为23.21.【答案】(1)解:设AD,EH交于点M,∵矩形EFGH,∴EH∥BC,AM⊥EH,∴△ABC∼△AEH,∴EHBC=AMAD∵EF=DM=x,AD=2∴AM=2−x∴EH3=2−x2∴EH=32(2−x)∴y=2(EH+EF)=2(3−32x+x)=−x+6(0<x<2)∴y关于x的函数解析式为∴y=−x+6(0<x<2)(2)解:当EFGH为正方形时,∴EF=EH,由(1)得:EF =x ,EH =32(2−x),∵EF =EH ,∴x =3(2−x)2,∴x =65,即EF =65.正方形EFGH 的面积=65×65=3625.22.【答案】(1)245(2)①43,②17423.【答案】(1)解:在矩形ABCD 中,AB =6cm ,BC =8cm ,∴AC =10,①当AP =PO =t ,如图1,过P 作PM ⊥AO 于点M ,∴AM =12AO =52,∵∠PMA =∠ADC =90°,∠PAM =∠CAD ,∴△APM∽△ACD ,∴AP AC =AM AD,∴AP =t =258,②当AP =AO =t =5,∴当t 为258或5时,△AOP 是等腰三角形;(2)解:如图2,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3cm ,由矩形的性质可知∠PDO =∠EBO ,DO =BO ,又得∠DOP =∠BOE ,∴△DOP≌BOE(ASA),∴BE =PD =8−t ,则S △BOE =12BE ⋅OH =12×3(8−t)=12−32t.∵FQ//AC ,∴△DFQ∽△DOC ,相似比为DQ DC =t6,∴S △DFQ S △DOC =t 236,∵S △DOC =14S 矩形ABCD =14×6×8=12c m 2,∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC −S △BOE −S △DFQ =12×6×8−(12−32t)−t 23=−13t 2+32t +12;∴S 与t 的函数关系式为S =−13t 2+32t +12;(3)t =3或32。
《相似三角形》单元过关测试(A卷)
《相似三角形》单元过关测试(A卷)注意事项:1.本卷共三大题,计 21小题,满分100分,考试时间为45分钟.2.卷中除要求近似计算的结果取近似值外,其余各题均应给出精确结果.一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的4个选项中,只有一项是符合题目要求的)1.已知d cb c ,则下列式子中正确的是( )A.a ∶b =c 2∶d 2B.a ∶d =c ∶bC.a ∶b =(a +c )∶(b +d )D.a ∶b =(a -d )∶(b -d )2.△ABC∽△A′B′C′,如果∠A=55°,∠B=100°,则∠C′的度数等于( )A.55°B.100°C.25°D.30°3.下列图形中一定相似的是( )A.有一个角相等的两个平行四边形B.有一个角相等的两个等腰梯形C.有一个角相等的两个菱形D.有一组邻边对应成比例的两平行四边形4.如图,等腰梯形ABCD的周长是104 cm,AD∥BC,且AD∶AB∶BC=2∶3∶5,则这个梯形的中位线的长是()A.72.8 cmB.51C.36.4D.28DC B A ED C B AE DC B A(第4题) (第5题) (第7题)5.如图,△ADE ∽△ACB ,∠AED =∠B ,那么下列比例式成立的是( ) A.BC DE AB AE AC AD == B.BCDE AC AE AB AD ==C.BC DE AB AC AE AD ==D.BCDE EC AE AB AD == 6.△ABC 和△A′B′C′符合下列条件,其中使△ABC 和△A′B′C′不相似的是( )A.∠A =∠A ′=45° ,∠B =26° ,∠B ′=109°B.AB=1,AC=1.5, BC=2 ,A′B′=4 ,A′C′=2,B′C′=3C.∠A=∠B′ ,AB=2 ,AC=2.4,A′B′=3.6,B′C′=3D.AB=3,AC=5,BC=7,A′B′=3,A′C′=5,B′C′=77.如图,在△ABC中,D、E分别是边AB、AC的中点,△ADE和四边形BCED的面积分别记为S 1、S 2,那么21S S 的值为( ) A.21B.41C.31D.328.下列说法中正确的是( )A.位似图形可以通过平移而相互得到B.位似图形的对应边平行且相等C.位似图形的位似中心不只有一个D.位似中心到对应点的距离之比都相等9.如图,△ABC中,∠B=900,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的C′处,并且C′D∥BC,则CD的长是( )(A)409 (B)509 (C)154 (D)254EDC BAC 'D C BAED CBA234(第9题) (第10题) (第14题)10.如图,在Rt△ABC 中,AD 为斜边BC 上的高,若S △CAD =3S △ABD ,则AB ∶AC 等于( )A.1∶3B.1∶4C.1∶3D.1∶2二、填空题(本大题共5小题,每小题4分,共20分)11.如果53=-b b a ,那么ba=________.12.已知△ABC∽△A 1B 1C 1,AB:A 1B 1=2:3,则S △ABC 与S △A 1B1C1之比为___________.13.两个相似多边形的相似比是81,则这两个多边形的对应对角线的比是________. 14.如图,∠C =∠E =90°,AC =3,BC =4,AE =2,则AD =____.15.点P 是△ABC 中AB 边上的一点,过点P 作直线(不与直线AB 重合)截△ABC,使截得的三角形与△ABC相似.满足这样条件的直线最多有____条.三、解答题(本大题共6小题,共50分.解答应写出文字说明,证明过程或演算步骤)16.(本题6分)判断下列两组三角形是否相似,并说明理由.(1)△ABC和△A′B′C′都是等边三角形.(2)△ABC中,∠C=90°,AC=BC;△A′B′C′中,∠C′=90°,A′C′=B′C′.17.(本题8分)某块地的平面图如图所示,∠A=90°,其比例尺为1∶2000,根据图中标注的尺寸(单位:cm),求该块地的实际周长和面积.DCBA12133418.(本题8分)如图,AB D E ,,,四点在O 上,AE BD ,的延长线相交于点C ,直径AE 为8,12OC =,EDC BAO ∠=∠.(1)求证:CD CEAC CB=;(2)计算O CED BACD·CB的值,并指出CB的取值范围.19.(本题8分)如图,图中的小方格都是边长为1的正方形,△ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点0; (2)求出△ABC与△A′B′C′的位似比;(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.20.(本题10分)在梯形ABCD中,AB∥CD,AB=8cm,CD=2cm,AD=BC=6cm,M、N 为同时从A点出发的两个动点,点M沿A→D→C→B的方向运动,速度为2cm/秒;点N 沿A→B的方向运动,速度为1cm/秒.当M、N其中一点到达B点时,点M、N运动停止.设点M、N的运动时间为x秒,以点A、M、N为顶点的三角形的面积为y cm2. (1)试求出当0 < x < 3时,y与x之间的函数关系式;(2)试求出当4 < x < 7时,y与x之间的函数关系式;(3)当3 < x < 4时,以A、M、N为顶点的三角形与以B、M、N为顶点的三角形是否有可能相似?若相似,试求出x的值. 若不相似,试说明理由.21.(本题10分)如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB 方向前进,小明一直站在点P的位置等候小亮.(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);(2)已知:MN=20 m,MD=8 m,PN=24 m,求(1)中的点C到胜利街口的距离CM.P参考答案1.C 2.C 3.C 4.D 5.A 6.D 7.C 8.D 9.A 10.C11.58 12.4:9 13.81 14.31015.4 16.(1)相似 (2)相似17.640 m,14400 m 218. (1)证明:EDC BAO C C ∠=∠∠=∠,,CDE CAB ∴△∽△,CD CEAC CB∴=. (2)直径812AE OC ==,,124161248AC CE ∴=+==-=,. 又CD CEAC CB=,168128CD CB AC CE ∴==⨯=··.连接OB ,在OBC △中,142OB AE ==,12OC =, 816BC ∴<<.19.(1)略;(2)位似比为 1:2.(3)略20.(1)223x y =.(2)223237x x y -=.(3)不可能相似21.(1)图略.(2)CM为16m.。
相似三角形 单元综合测试卷
1 相似三角形 单元综合测试卷 一、选择题 1.已知2x=5y(y≠0),则下列比例式成立的是( )
A.xy25 B.xy52 C.x2y5 D.x52y
2.若abc234,则a2b3ca等于( ) A.8 B.9 C.10 D.11 3.下列各组条件中,一定能推得△ABC与△DEF相似的是( ) A.∠A=∠E且∠D=∠F B.∠A=∠B且∠D=∠F
C.∠A=∠E且ABEFACED D.∠A=∠E且ABDFBCED 4.如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A.55 B.255 C.55或255 D.255或355 5.如图所示,△ABC中若DE∥BC,EF∥AB,则下列比例式正确的是( )
A.ADDEDBBC B.BFEFBCAD CAEBFECFC. D.EFDEABBC
6.如图,在△ABC中,DE∥BC,AD1DB2,DE=4,则BC的长是( ) A.8 B.10 C.11 D.12 7.如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
A.10 B.12 C.454 D.365
8.已知△ABC∽△A′B′C′且AB1AB2,则S△ABC:S△A'B'C′为( ) A.1:2 B.2:1 C.1:4 D.4:1
9.如图,铁路道口的栏杆短臂长1m,长臂长16m.当短臂端点下降0.5m时,长臂端点升高(杆的宽度忽略不计)( )
A.4m B.6m C.8m D.12m 10.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=3,AB=6,那么AD的值为( )
A.32 B.92 C.332 D.33
NM
E
D
CBA
FEDCBAED
CB
A
D1
C1B
1
A1
相似三角形》单元测试题(含答案)
《相似三角形》单元测试题 一、精心选一选(每小题4分,共32分) 1. 下列各组图形有可能不相似的是( ). (A)各有一个角是50°的两个等腰三角形 (B)各有一个角是100°的两个等腰三角形 (C)各有一个角是50°的两个直角三角形 (D)两个等腰直角三角形 2. 如图,D是⊿ABC的边AB上一点,在条件(1)△ACD=∠B,(2)AC2=AD·AB,(3)AB边上与点C距离相等的点D有两个,(4)∠B=△ACB中,一定使⊿ABC∽⊿ACD的个数是( ) (A)1 (B)2 (C)3 (D)4
3.如图,∠ABD=∠ACD,图中相似三角形的对数是( ) (A)2 (B)3 (C)4 (D)5
4.如图,在矩形ABCD中,点E是AD上任意一点,则有( ) (A)△ABE的周长+△CDE的周长=△BCE的周长 (B)△ABE的面积+△CDE的面积=△BCE的面积 (C)△ABE∽△DEC (D)△ABE∽△EBC
5.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为( ) :4 :3 :2 :16 6. 下列两个三角形不一定相似的是( )。 A. 两个等边三角形 B. 两个全等三角形 C. 两个直角三角形 D. 两个等腰直角三角形
7. 若⊿ABC∽⊿CBA,∠A=40°, ∠B=110°,则∠C=( ) A. 40° B110° C70° D30° 8.如图,在ΔABC中,AB=30,BC=24,CA=27, AE=EF=FB,
EG∥FD∥BC,FM∥EN∥AC,则图中阴影部分的三个三角形的周长之和为( ) A、70 B、75 C、81 D、80 二、细心填一填 (每小题3分,共24分) 9.如图,在△ABC中,△BAC=90°,D是BC中点,AE∥AD交CB延长线于点E,则⊿BAE相似于______. 10、在一张比例尺为1:10000的地图上,我校的周长为18cm,则我校的实际周长为 。 11、如果两个相似三角形对应高的比为4:5,则这两个三角形的相似比是 ,它们的面积的比是 。 12、已知⊿ABC∽⊿DEF,AB=21cm,DE=28cm,则⊿ABC和⊿DEF的相似比为 13、 某同学利用影子长度测量操场上旗杆的高度,在同一时刻,他测得自己影子长为0.8m,旗杆的影子长为7m,已知他的身高为1.6m,则旗杆的高度为 m. 14. 在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是_______cm2 15.如图,由边长为1的25个小正方形网格上有一个与⊿ABC相似且面积最大的⊿A1B1C1,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形单元测试卷
一、选择题(本题有8小题,每题3分,共24分) 1、已知3x=4y ,则
y x = ( ) A 、34 B 、43 C 、43- D 、-3
4 2.、下列各组中的四条线段成比列的是( ) A 、1cm 、2cm 、20cm 、30cm B 、1cm 、2cm 、3cm 、4cm C 、4cm 、2cm 、1cm 、3cm D 、5cm 、10cm 、10cm 、20cm 3、下列条件中不能判定△ABC 与△A ’B ’C ’相似的是( )
A.、∠B=250 ∠C=500 ∠B /=1050 ∠C /=250
B 、AB=
21A /B / AC=21A /C / BC=2
1B /C /
C 、AB=9 AC=6 A /B /
=4.5 A /C /
=3 ∠A=500
∠B /
=600
∠C /
=700
D 、AB=5 BC=3 A /B /=15 B /C /=9 ∠A=∠B /=300
4、若P 是线段AB 的黄金分割点(PA >PB ),设AB=1,则PA 的长约为 ( ) A 、0.191 B 、0.382 C 、0.5 D 、0.618
5、下面两个三角形一定相似的是( )
A 、两个等腰三角形
B 、两个直角三角形
C 、两个钝角三角形
D 、两个等边三角形 6、如图:点P 是△ABC 边AB 上一点(AB >AC ),下列条件不一定能使△ACP ∽△ABC 的是( )
A 、∠ACP =∠
B B 、∠AP
C =∠ACB C 、
AC AP AB AC = D 、AB
AC
BC PC =
7、如图,E 是平行四边形ABCD 的边BC 的延长线上的一点,连结AE 交CD 于F ,则图中共有相似三角形( )A 、1对 B 、2对
C 、3对
D 、4对
8、已知如图DE ∥BC ,12AD DB = 求DE BC =( ) A 、12 B 、1
3
C 、2
D 、3
二、填充题:(本题有8小题,每题3分,共24分)
9、已知:若
23
x y
=,则
2x y x y +=- 。
10、两个相似三角形的面积之比为1∶9,小三角形的周长为4,则另一个三角形的周长为
P
C B A 第6题 第7题 C B E
D
A 第8题
_____ .
11、在比例尺为1∶40000的平面图上,5.2平方厘米所表示的实际面积为_______平方米。
12、已知, AB 和DE 是直立在地面上的两根立柱.AB =5m ,某一时刻AB 在阳光下的投影为
3m ,同时测量出DE 在阳光下的投影长为6m ,则DE =. m 。
13、已知△ABC ∽△A ′B ′C ′,
1
2
AB A B ='',
求△A ′B ′C ′与△ABC 的相似比是 。
14、、如图,点O 是等边三角形PQR 的中心,P ′、Q ′、R ′分别是OP 、OQ 、OR 的中点,则△P ′Q ′R ′与△PQR 是位似三角形.此时,△P ′Q ′R ′与△PQR 的位似比为 . 15、如图,E 是平行四边形ABCD 边CD 的中点,连接AE 、BD 交于点O 。
如果△ADE 的面积是6,则△ABD 的面积是 。
16、如图,AB 是斜靠在墙上的长梯,梯脚B 距墙1.6米,梯上点D 距墙1.4米,BD 长为0.55米,梯子的长为
⒂ ⒃ 三、解答题(本题有8小题,共72分) 17、如图,已知AE 与CD 交于点B ,AC ∥DE ,
求证:⑴△ABC ∽△EDB
⑵若AC=2,BC=3,BD=6,求DE 的长。
(本题8分)
18、已知线段DE 分别交⊿ABC 的边AB 、AC 于D 、E , 且
2
3===DE BC AE AC AD AB ,⊿ABC 的周长是cm 6,面积是22cm , 求⊿ADE 的周长和面积。
(本题8分)
P Q
R
O P'Q'R'
E
D
B
C
A
A
B
C
D E A
D
B
E
D C
A
B
19、如图,∆ABC 中,DE ∥BC ,DE=2,且S 四边形DBCE =3S ∆ADE ,求BC 的长. (本题8分)
20、如图,在∆ABC 中,D 是AC 上的一点,已知AB 2=AD ·AC ,∠ABD=40°,求∠C 的度
数。
(本题8分)
21、如图,在平行四边形ABCD 中,E 是DC 上的一点,AE 的延长线交BC 于F , 求证:ED AF AE AB •=•(本题8分)
22、如图,把矩形ABCD 对折,折痕为MN ,矩形DMNC 与矩形ABCD 相似,已知4AB =. ⑴ 求AD 的长.
⑵ 求矩形DMNC 与矩形ABCD 的相似比.(本题10分)
A
C
D
B
E A B C
D E F
P
D
C
B
A
23、如图,在梯形ABCD 中,AB ∥CD ,∠D =900,AB =3,DC =7,AD =15,请你在AD 上找一点P ,使得以P 、A 、B 和以P 、D 、C 为顶点的两个三角形相似吗?若能,这样的P 点有几个?并求出AP 的长;若不能,请说明理由。
(本题10分)
24、如图,在△ABC 中,AB=BC=50㎝,AC=80㎝,点P 从A 点出发沿AB 以每秒4㎝的速度向B 点运动,同时点Q 从C 点出发,沿CA 以每秒3㎝的速度向A 点运动 ⑴经过多少秒后PQ ∥BC ?
⑵经过多少秒后,△APQ 的面积为△ABC 面积的一半? (本题12分)
C
Q
P
B
A。
