天津市2013届高三高考压轴卷文科综合试题

合集下载

2013年天津高考文科数学试题及答案解析word版

作出可行域如图，平移直线，由图象可知当直线经过点D时，直线的截距最小，此时最小，由2030x yy--=-=⎧⎨⎩，得，即代入得，选A.(3) 阅读右边的程序框图, 运行相应的程序, 则输出n的值为(A) 7 (B) 6(C) 5 (D) 4【答案】D【解析】第一次循环，；第二次循环，；第三次循环，；第四次循环，，满足条件输出，选D.(4) 设, 则“”是“”的(A) 充分而不必要条件(B) 必要而不充分条件(C) 充要条件(D) 既不充分也不必要条件【答案】A【解析】若，则，即。

2013年天津市高考数学试卷(文科)及答案(word版)

2013年普通高等学校招生全国统一考试(天津卷)文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟. 第Ⅰ卷1至2页, 第Ⅱ卷3至5页.答卷前, 考生务必将自己的姓名、准考证号填写在答题卡上, 并在规定位置粘贴考试用条形码. 答卷时, 考生务必将答案凃写在答题卡上, 答在试卷上的无效. 考试结束后, 将本试卷和答题卡一并交回.祝各位考生考试顺利! 第Ⅰ卷注意事项：1.每小题选出答案后, 用铅笔将答题卡上对应题目的答案标号涂黑. 如需改动, 用橡皮擦干净后, 再选凃其他答案标号. 2.本卷共8小题, 每小题5分, 共40分.参考公式:·如果事件A, B 互斥, 那么)()()(B P A P A P B ·棱柱的体积公式V = Sh ，其中S 表示棱柱的底面面积, h 表示棱柱的高. ·如果事件A, B 相互独立, 那么)()(()B P A A P P B ·球的体积公式34.3V R 其中R 表示球的半径. 一．选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的. (1) 已知集合 A = {x ∈R | |x|≤2}, B = {x ∈R | x ≤1}, 则A B (A) (,2](B) [1,2](C) [－2,2] (D) [－2,1] (2) 设变量x, y 满足约束条件360,20,30,xy yxy 则目标函数z = y －2x 的最小值为(A) －7(B) －4 (C) 1(D) 2 (3) 阅读右边的程序框图, 运行相应的程序, 则输出n 的值为(A) 7(B) 6 (C) 5(D) 4 (4) 设,a b R , 则“2()0a b a ”是“a b ”的(A) 充分而不必要条件(B) 必要而不充分条件(C) 充要条件(D) 既不充分也不必要条件(5) 已知过点P (2,2) 的直线与圆225(1)x y 相切, 且与直线10ax y 垂直, 则a(A) 12(B) 1(C) 2 (D) 12(6) 函数()sin 24f x x 在区间0,2上的最小值是(A) 1(B) 22(C) 22(D) 0(7) 已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)上单调递增. 若实数a 满足212(log )(log )2(1)f a f f a , 则a 的取值范围是(A) [1,2](B) 10,2(C) 1,22(D) (0,2](8) 设函数22,()ln )3(x x g x x x x f e . 若实数a, b 满足()0,()0f a g b , 则(A) ()0()g a f b (B) ()0()f bg a (C) 0()()g a f b (D) ()()0f b g a。

数学_2013年天津市高考数学试卷(文科)(含答案)

2013年天津市高考数学试卷（文科）一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.共8小题,每小题5分,共40分.1. 已知集合A ＝{x ∈R||x|≤2}，B ＝{x ∈R|x ≤1}，则A ∩B ＝（） A (−∞, 2] B [1, 2] C [−2, 2] D [−2, 1]2. 设变量x ，y 满足约束条件{3x +y −6≥0x −y −2≤0y −3≤0 ，则目标函数z ＝y −2x 的最小值为（）A −7B −4C 1D 23. 阅读如图所示的程序框图，运行相应的程序，则输出n 的值为（）A 7B 6C 5D 44. 设a ，b ∈R ，则“(a −b)a 2<0”是“a <b”的（）A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件 5. 已知过点P(2, 2)的直线与圆(x −1)2+y 2=5相切，且与直线ax −y +1=0垂直，则a =( )A −12B 1C 2D 126. 函数f(x)=sin(2x −π4)在区间[0, π2]上的最小值是( ) A −1 B −√22 C √22D 0 7. 已知函数f(x)是定义在R 上的偶函数，且在区间[0, +∞)单调递增．若实数a 满足f(log 2a)+f(log 12a)≤2f(1)，则a 的取值范围是（）A [1, 2]B (0,12] C [12，2] D (0, 2]8. 设函数f(x)＝e x +x −2，g(x)＝lnx +x 2−3．若实数a ，b 满足f(a)＝0，g(b)＝0，则（）A g(a)<0<f(b)B f(b)<0<g(a)C 0<g(a)<f(b)D f(b)<g(a)<0二．填空题：本大题共6小题，每小题5分，共30分. 9. i 是虚数单位．复数(3+i)(1−2i)=________．10. 已知一个正方体的所有顶点都在一个球面上．若球的体积为9π2，则正方体的棱长为________．11. 已知抛物线y 2＝8x 的准线过双曲线x 2a 2−y 2b 2=1(a >0,b >0)的一个焦点，且双曲线的离心率为2，则该双曲线的方程为________x 2−y 23=1 ．12. 在平行四边形ABCD 中，AD =1，∠BAD =60∘，E 为CD 的中点．若AC →⋅BE →=1，则AB 的长为________．13. 如图，在圆内接梯形ABCD 中，AB // DC ，过点A 作圆的切线与CB 的延长线交于点E ．若AB =AD =5，BE =4，则弦BD 的长为________． 14. 设a +b ＝2，b >0，则12|a|+|a|b的最小值为________．三．解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤. 15. 某产品的三个质量指标分别为x ，y ，z ，用综合指标S =x +y +z 评价该产品的等级．若S ≤4，则该产品为一等品．现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：(1)利用上表提供的样本数据估计该批产品的一等品率；（2）在该样品的一等品中，随机抽取2件产品， (I)用产品编号列出所有可能的结果；(II)设事件B 为“在取出的2件产品中，每件产品的综合指标S 都等于4”，求事件B 发生的概率． 16. 在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ．已知bsinA ＝3csinB ，a ＝3，cosB =23．（1）求b 的值；（2）求sin(2B −π3)的值．17. 如图，三棱柱ABC −A 1B 1C 1中，侧棱A 1A ⊥底面ABC ，且各棱长均相等，D ，E ，F 分别为棱AB ，BC ，A 1C 1的中点 (Ⅰ)证明EF // 平面A 1CD ；(Ⅱ)证明平面A 1CD ⊥平面A 1ABB 1；(Ⅲ)求直线B 1C 1与平面A 1CD 所成角的正弦值．18. 设椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ，离心率为√33，过点F 且与x 轴垂直的直线被椭圆截得的线段长为4√33． (Ⅰ)求椭圆的方程；(Ⅱ)设A ，B 分别为椭圆的左，右顶点，过点F 且斜率为k 的直线与椭圆交于C ，D 两点．若AC →⋅DB →+AD →⋅CB →=8，求k 的值．19. 已知首项为32的等比数列{a n }的前n 项和为S n (n ∈N ∗)，且−2S 2，S 3，4S 4成等差数列．(Ⅰ)求数列{a n }的通项公式； (Ⅱ)证明S n +1S n≤136(n ∈N ∗)．20. 设a ∈[−2, 0]，已知函数f(x)={x 3−(a +5)x,x ≤0x 3−a+32x 2+ax,x >0(Ⅰ) 证明f(x)在区间(−1, 1)内单调递减，在区间(1, +∞)内单调递增；(Ⅱ) 设曲线y ＝f(x)在点P i （x i , f(x i )）(i ＝1, 2, 3)处的切线相互平行，且x 1x 2x 3≠0，证明x 1+x 2+x 3>−13．2013年天津市高考数学试卷（文科）答案1. D2. A3. D4. A5. C6. B7. C8. A9. 5−5i 10. √3 11. x 2−y 23=112. 1213. 15214. 3415.解：(1)计算10件产品的综合指标S，如下表：其中S≤4的有A1，A2，A4，A5，A7，A9共6件，故样本的一等品率为610=0.6．从而可估计该批产品的一等品率为0.6；(2)(I)在该样本的一等品种，随机抽取2件产品的所有可能结果为{A1, A2}，{A1, A4}，{A1, A5}，{A1, A7}，{A1, A9}，{A2, A4}，{A2, A5}，{A2, A7}，{A2, A9}，{A4, A5}，{A4, A7}，{A4, A9}，{A5, A7}，{A5, A9}，{A7, A9}共15种．(II)在该样本的一等品种，综合指标S等于4的产品编号分别为A1，A2，A5，A7．则事件B发生的所有可能结果为{A1, A2}，{A1, A5}，{A1, A7}，{A2, A5}，{A2, A7}，{A5, A7}，共6种．所以P(B)=615=25．16. 在△ABC中，有正弦定理asinA =bsinB，可得bsinA＝asinB，又bsinA＝3csinB，可得a＝3c，又a＝3，所以c＝1．由余弦定理可知：b2＝a2+c2−2accosB，cosB=23，即b2＝32+12−2×3×cosB，可得b=√6．由cosB=23，可得sinB=√53，所以cos2B＝2cos2B−1=−19，sin2B＝2sinBcosB=4√59，所以sin(2B−π3)=sin2Bcosπ3−sinπ3cos2B=4√59×12−(−19)×√32=4√5+√318．17. 证明：(I)三棱柱ABC−A1B1C1中，AC // A1C1，AC＝A1C1，连接ED，可得DE // AC，DE=12AC，又F为棱A1C1的中点．∴ A1F＝DE，A1F // DE，所以A1DEF是平行四边形，所以EF // DA1，DA1⊂平面A1CD，EF⊄平面A1CD，∴ EF // 平面A1CD(II)∵ D是AB的中点，∴ CD⊥AB，又AA1⊥平面ABC，CD⊂平面ABC，∴ AA 1⊥CD ，又AA 1∩AB ＝A ，∴ CD ⊥面A 1ABB 1，又CD ⊂面A 1CD ， ∴ 平面A 1CD ⊥平面A 1ABB 1； (III)过B 作BG ⊥A 1D 交A 1D 于G ，∵ 平面A 1CD ⊥平面A 1ABB 1，且平面A 1CD ∩平面A 1ABB 1＝A 1D ， BG ⊥A 1D ，∴ BG ⊥面A 1CD ，则∠BCG 为所求的角，设棱长为a ，可得A 1D =√52a ，由△A 1AD ∽△BGD ，得BG =√55a ，在直角△BGC 中，sin∠BCG =BG BC=√55， ∴ 直线BC 与平面A 1CD 所成角的正弦值√55．18. （1）根据椭圆方程为x 2a 2+y 2b 2=1(a >b >0)． ∵ 过焦点且垂直于x 轴的直线被椭圆截得的线段长为4√33， ∴ 当x ＝−c 时，a 2−b 2a 2+y 2b 2=1，得y ＝±b 2a ，∴2b 2a=4√33， ∵ 离心率为√33，∴ ca=√33，解得b =√2，c ＝1，a =√3． ∴ 椭圆的方程为x 23+y 22=1；（2）直线CD:y ＝k(x +1)，设C(x 1, y 1)，D(x 2, y 2)，由{y =k(x +1)x 23+y 22=1消去y 得，(2+3k 2)x 2+6k 2x +3k 2−6＝0，△＝36k 4−4(2+3k 2)(3k 2−6)>0，∴ x 1+x 2=−6k 22+3k 2，x 1x 2=3k 2−62+3k 2，又A(−√3, 0)，B(√3, 0)， ∴ AC →⋅DB →+AD →⋅CB →＝(x 1+√3, y 1)⋅(√3−x 2．−y 2)+(x 2+√3, y 2)⋅(√3−x 1．−y 1)，＝6−(2+2k 2)x 1x 2−2k 2(x 1+x 2)−2k 2，＝6+2k 2+122+3k 2=8，解得k =±√2，满足△>0，则k ＝±√2．19. （1）设等比数列{a n }的公比为q ， ∵ −2S 2，S 3，4S 4等差数列，∴ 2S 3＝−2S 2+4S 4，即S 4−S 3＝S 2−S 4，得2a 4＝−a 3，∴ q =−12，∵ a 1=32，∴ a n =32⋅(−12)n−1=(−1)n−1⋅32n ；（2）证明：由(Ⅰ)得，S n =32[1−(−12)n ]1+12=1−(−12)n ，∴ S n +1S n=1−(−12)n +11−(−12)n，当n 为奇数时，S n +1S n=1+(12)n+11+(12)n=1+12n +2n1+2n =2+12n (2n +1)，当n 为偶数时，S n +1S n=1−(12)n +11−(12)n=2+12n (2n −1)，∴ 当n 为奇数时，S n +1S n≤S 1+1S 1=136，当n 为偶数时，S n +1S n≤S 2+1S 2=2512<136，综上，S n +1S n≤136(n ∈N ∗)成立．20. （1）令f 1(x)=x 3−(a +5)x(x ≤0)，f 2(x)=x 3−a+32x 2+ax(x >0)．①f 1′(x)=3x 2−(a +5)，由于a ∈[−2, 0]，从而当−1<x <0时，f 1′(x)=3x 2−(a +5)<3−a −5≤0，所以函数f 1(x)在区间(−1, 0)内单调递减，②f 2′(x)=3x 2−(a +3)x +a =(3x −a)(x −1)，由于a ∈[−2, 0]，所以0<x <1时，f 2′(x)<0；当x >1时，f 2′(x)>0，即函数f 2(x)在区间(0, 1)内单调递减，在区间(1, +∞)上单调递增．综合①②及f 1(0)＝f 2(0)，可知：f(x)在区间(−1, 1)内单调递减，在区间(1, +∞)内单调递增；（2）证明：由(Ⅰ)可知：f′(x)在区间(−∞, 0)内单调递减，在区间(0,a+36)内单调递减，在区间(a+36,+∞)内单调递增．因为曲线y ＝f(x)在点P i （x i , f(x i )）(i ＝1, 2, 3)处的切线相互平行，从而x 1，x 2，x 3互不相等，且f ′(x 1)=f ′(x 2)=f ′(x 3)．不妨x 1<0<x 2<x 3，由3x 12−(a +5)=3x 22−(a +3)x 2+a =3x 32−(a +3)x 3+a ．可得3x 22−3x 32−(a +3)(x 2−x 3)=0，解得x 2+x 3=a+33，从而0<x 2<a+36<x 3．设g(x)＝3x 2−(a +3)x +a ，则g(a+36)<g(x 2)<g(0)=a ．由3x 12−(a +5)=g(x 2)<a ，解得−√2a+53<x 1<0，所以x 1+x 2+x 3>−√2a+53+a+33，设t =√2a+53，则a =3t 2−52，∵ a ∈[−2, 0]，∴ t ∈[√33,√153]，故x 1+x 2+x 3>−t +3t 2+16=12(t −1)2−13≥−13，故x 1+x 2+x 3>−13．。

全国大纲版2013届高三高考压轴文科综合试题.pdf

2013全国大纲版高考压轴卷文综试题本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷。

第Ⅰ卷为必考题，1.在新建地铁沿线住宅区、大型商场不断涌现，体现出?A.交通是影响特大城市发展的关键因素?B.交通是影响住宅区选址的首要因素?C.交通运输方式变化直接影响城市的兴衰?D.交通通达性的变化影响城市土地利用方式2.北京市?A.地价高? ?B.城市拥堵问题严重 ?C.地面沉降D.水土流失严重中国共产党第十八次全国代表大会报告中提出建设社会主义生态文明。

据此完成3～5题。

3.在低碳经济时代的大背景下，我国西北地区的工业部门中可能最受欢迎的是A.煤炭工业B.风电工业C.火电工业D.核电工业 4.若现阶段我国生产大量使用清洁能源乙醇（由粮食及各种植物纤维加工而成）作为汽车燃料，将对我国产生的显著影响有 ①完全改变能源消费结构 ②提高能源利用率 ③加剧了耕地压力 ④调整种植业结构A.①②B.②③C.③④D.①④ 5.下列措施有助于推进全球生态安全的是 ①推广太阳能、水能等清洁能源 ②降低非化石能源占一次性能源消费的比重 ③增加耕地面积 ④提高单位能耗的产值A.①②B.②③C.①③D.①④ 单位体积空气中含有的水汽量与同温度下这些空气所能容纳的最大水汽量的比值称为相对湿度，且最大水汽量与气温有一定的相关性。

读图据题意回答6～8小题。

6.气温在0℃时，1m3空气所能容纳的最大水汽量为5g,若要使最大水汽量上升25g,气温应上升A.20℃B. 25℃C. 30℃D. 35℃ 7.测得一封闭实验箱内的温度为15℃，相对湿度为50%，若要使实验箱内相对湿度降低到30%，箱内温度应调节为A.20℃B. 25℃C. 30℃D. 35℃ 8.若空气含量恒定，四个季节中相对湿度最大的最可能是A.春季B.夏季C. 秋季D. 冬季某地理爱好者某日利用长1m的竿在与北京同一纬线某地测量日影变化，并绘制出如下该日日影长短变化示意图。

读图完成9～11题。

2013年天津市高考数学试卷(文科)学生版

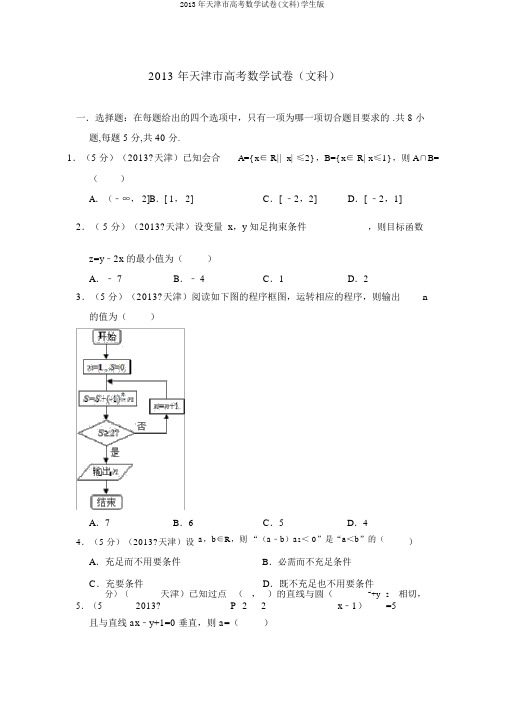
2013 年天津市高考数学试卷（文科）一．选择题：在每题给出的四个选项中，只有一项为哪一项切合题目要求的 .共 8 小题,每题 5 分,共 40 分.1．（5 分）（2013?天津）已知会合A={ x ∈ R|| x| ≤2} ，B={ x ∈ R| x ≤1} ，则 A ∩B=（）A ．（﹣∞， 2]B ．[ 1， 2]C ．[ ﹣2，2]D ．[ ﹣2，1]2．（ 5 分）（2013?天津）设变量 x ，y 知足拘束条件，则目标函数z=y ﹣2x 的最小值为（）A ．﹣ 7B ．﹣ 4C ．1D ．23．（5 分）（2013?天津）阅读如下图的程序框图，运转相应的程序，则输出n的值为（）A ．7B ．64．（5 分）（2013?天津）设C ．5D ．4a ，b ∈R ，则 “（a ﹣b ）a 2＜ 0”是“a＜b ”的（）A ．充足而不用要条件B ．必需而不充足条件C ．充要条件D ．既不充足也不用要条件 5．（5 分）（天津）已知过点（，）的直线与圆（ x ﹣1） 2+y 2 相切，2013? P 2 2 =5且与直线 ax ﹣y+1=0 垂直，则 a=（）A．B．1C．2D．6．（5分）（2013?天津）函数f（ x） =sin（2x﹣）在区间 [ 0， ] 上的最小值是（）A．﹣ 1B．﹣C．D．07．（5 分）（2013?天津）已知函数 f（x）是定义在R 上的偶函数，且在区间 [ 0，+∞）上单一递加，若实数 a 知足 f （log2a）+f（）≤ 2f（ 1），则 a 的取值范围是（）A．，B．[ 1，2]C．，．（，D 02]8．（5 分）（2013?天津）设函数 f（x）=e x+x﹣ 2， g（x）=lnx+x2﹣3．若实数 a，b 知足f（ a） =0，g（b）=0，则（）A．g（a）＜ 0＜f（b）C．0＜g（a）＜ f（b）B．f （b）＜ 0＜g（a）D．f（b）＜ g（a）＜ 0二．填空题：本大题共 6 小题，每题 5 分，共 30 分.9．（5 分）（2013?天津） i 是虚数单位．复数（ 3+i）（1﹣2i） =．10．（ 5 分）（2013?天津）已知一个正方体的全部极点在一个球面上．若球的体积为，则正方体的棱长为．11．（ 5分）（2013?天津）已知抛物线y2=8x的准线过双曲线＞，＞的一个焦点，且双曲线的离心率为2，则该双曲线的方程为．12．（ 5 分）（2013?天津）在平行四边形的中点．若，则 AB 的长为ABCD中， AD=1，∠ BAD=60°，E为．CD13．（ 5 分）（2013?天津）如图，在圆内接梯形A BCD中， AB∥DC，过点的切线与 CB的延伸线交于点E．若 AB=AD=5，BE=4，则弦 BD 的长为A 作圆．14．（ 5 分）（2013?天津）设 a+b=2，b＞0，则的最小值为．三．解答题：本大题共 6 小题，共 70 分.解答应写出文字说明，证明过程或演算步骤 .15．（ 13 分）（ 2013?天津）某产品的三个质量指标分别为x，y，z，用综合指标S=x+y+z 评论该产品的等级．若 S≤4，则该产品为一等品．现从一批该产品中，随机抽取 10 件产品作为样本，其质量指标列表如表：产品编A12345A A A A质量指标（1，1，2）（2，1，1）（2，2，2）（1，1，1）（1，2，1）（x，y，z）产品编A6A7A8A9A10质量指标（1，2，2）（2，1，1）（2，2，1）（1，1，1）（2，1，2）（x，y，z）（Ⅰ）利用上表供给的样本数据预计该批产品的一等品率；（Ⅱ）在该样品的一等品中，随机抽取 2 件产品，（i）用产品编列出全部可能的结果；（ii）设事件 B 为“在拿出的 2 件产品中，每件产品的综合指标 S 都等于 4”，求事件 B 发生的概率．16．（13 分）（2013?天津）在△ ABC中，内角 A，B，C 所对的边分别是a，b，c．已知 bsin A=3csin B， a=3，cos B= ．（1）求 b 的值；（2）求 sin（2B﹣）的值．17．（13 分）（2013?天津）如图，三棱锥 ABC﹣A1B1C1中，侧棱 A1A⊥底面 ABC，且各棱长均相等， D， E， F 分别为棱 AB， BC， A1C1的中点（Ⅰ）证明 EF∥平面 A1CD；（Ⅱ）证明平面A1CD⊥平面 A1ABB1；（Ⅲ）求直线 B1C1与平面 A1CD所成角的正弦值．18．（ 13 分）（2013?天津）设椭圆=1（a＞b＞0）的左焦点为F，离心率为，过点 F 且与x 轴垂直的直线被椭圆截得的线段长为．（Ⅰ）求椭圆的方程；（Ⅱ）设 A，B 分别为椭圆的左，右极点，过点 F 且斜率为 k 的直线与椭圆交于C，D 两点．若=8，求 k 的值．．（14分）（天津）已知首项为的等比数列 { a n} 的前 n 项和为 S（n n∈N*），192013?且﹣ 2S2， S3，4S4成等差数列．（Ⅰ）求数列{ a n}的通项公式；（Ⅱ）证明．20 ．（ 14分）（2013?天津）设 a ∈ [ ﹣ 2 ， 0]，已知函数，，＞（Ⅰ）证明f（x）在区间（﹣1，1）内单一递减，在区间（1，+∞）内单一递增；（Ⅱ）设曲线 y=f（x）在点 P i（x i，f（ x i））（i=1， 2，3）处的切线互相平行，且x1x2x3≠0，证明＞．。

2013年高考文科数学天津卷(含详细答案)

绝密★启用前2013年普通高等学校招生全国统一考试（天津卷）数学（文史类）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷1至3页,第Ⅱ卷4至6页.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,并在规定位置粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷注意事项：1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选凃其他答案标号.2.本卷共8小题,每小题5分,共40分. 参考公式：•如果事件A ,B 互斥,那么 •球的体积公式34π3V R =. ()()()P AB P A P B =+.•棱柱的体积公式V Sh =. 其中R 表示球的半径. 其中S 表示棱柱的底面面积, h 表示棱柱的高.一、选择题：在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{|||2}A x x =∈≤R ,{|1}B x x =∈R ≤,则A B =( ) A .(,2]∞-B .[1,2]C .[]2,2-D .[12,]--2.设变量x ,y 满足约束条件0,230,306,x x y y y +----⎧⎪⎨⎪⎩≥≤≤则目标函数2z y x =-的最小值为( ) A .－7B .－4C .1D .23.阅读右边的程序框图,运行相应的程序,则输出n 的值为( ) A .7 B .6 C .5D .44.设a ,b ∈R ,则“2()0a b a -<”是“a b <”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件5.已知过点(2,2)P 的直线与圆22(1)5x y -+=相切,且与直线10ax y -+=垂直,则a = ( ) A .12-B .1C .2D .126.函数π()sin(2)4f x x =-在区间π[0,]上的最小值为( )A .1-B . CD .07.已知函数()f x 是定义在R 上的偶函数,且在区间[)0,+∞上单调递增.若实数a 满足212(log )(log )2(1)f a f a f +≤,则a 的取值范围是( )A .[1,2]B .1(0,]2C .1[,2]2D .(0,2]8.设函数()e 2x f x x =+-,2()ln 3g x x x =+-.若实数a ,b 满足()0f a =,()0g b =, 则( )A .()0()g a f b <<B .()0()f b g a <<C .0()()g a f b <<D .()()0f b g a <<第Ⅱ卷注意事项：1.用黑色墨水的钢笔或签字笔将答案写在答题卡上.2.本卷共12小题,共110分.二、填空题：本大题共6小题,每小题5分,共30分. 9.i 是虚数单位,复数(3i)(12i)+-= .10.已知一个正方体的所有顶点在一个球面上.若球的体积为9π2,则正方体的棱长为 .11.已知抛物线28y x =的准线过双曲线22221x y a b-=（0a >,0b >）的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 .12.在平行四边形ABCD 中,1AD =,60BAD ∠=,E 为CD 的中点.若1AC BE =,则AB 的长为 .13.如图,在圆内接梯形ABCD 中,AB DC ∥.过点A 作圆的切线与CB 的延长线交于点E .若5AB AD ==,4BE =,则弦BD 的长为 .14.设2a b +=,0b >,则1||2||a a b+的最小值为 .--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无------------------------------------姓名________________ 准考证号_____________三、解答题：本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.（本小题满分13分）某产品的三个质量指标分别为x ,y ,z ,用综合指标S x y z =++评价该产品的等级. 若4S ≤,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质（Ⅰ）利用上表提供的样本数据估计该批产品的一等品率；（Ⅱ）在该样本的一等品中,随机抽取2件产品, （i ）用产品编号列出所有可能的结果；（ii ）设事件B 为“在取出的2件产品中,每件产品的综合指标S 都等于4”,求事件B 发生的概率.16.（本小题满分13分）在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c .已知sin 3sin b A c B =,3a =,2cos 3B =.（Ⅰ）求b 的值；（Ⅱ）求πsin(2)3B -的值.17.（本小题满分13分）如图,三棱柱111ABC A B C -中,侧棱1A A ⊥底面ABC ,且各棱长均相等,D ,E ,F 分别为棱AB ,BC ,11AC 的中点. （Ⅰ）证明：EF ∥平面1A CD ；（Ⅱ）证明：平面1A CD ⊥平面11A ABB ；（Ⅲ）求直线BC 与平面1A CD 所成角的正弦值.18.（本小题满分13分）设椭圆22221(0)x y a b a b +=>>的左焦点为F ,,过点F 且与x 轴垂直的直（Ⅰ）求椭圆的方程；（Ⅱ）设A 、B 分别为椭圆的左、右顶点,过点F 且斜率为k 的直线与椭圆交于C ,D 两点.若8AC DB AD CB +=,求k 的值.19.（本小题满分14分）已知首项为32的等比数列{}n a 的前n 项和为*()n S n ∈N ,且22S -,3S ,44S 成等差数列.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）证明1136n n S S +≤（*n ∈N ）. 20.（本小题满分14分）设[2,0]a ∈-,已知函数332(5),0,()3,0.2x a x x f x a x x ax x ⎧-+⎪=⎨+-+>⎪⎩≤（Ⅰ）证明()f x 在区间(1,1)-内单调递减,在区间()1,+∞内单调递增；（Ⅱ）设曲线()y f x =在点(,())i i i P x f x (1,2,3)i =处的切线相互平行,且1230x x x ≠. 证明12313x x x ++>-.{=∈RA B x，再利用数轴进行集合的交集运算.【解析】π0,2x ⎡∈⎢⎣π4=-时，【解析】12log f a ⎛ ⎝又上单调递增，【解析】()e f x '=是(0,)+∞上的增函数(1)2g =-【提示】先判定出零点【考点】利用导数解决不等式问题【解析】由已知得AC =AD AB +，12BE AD AB =-， ∴AC BE =221122AD AB AD AB AD AB -+-2111||22AB AD AB =+-211cos60||12AB AD AB ︒-=.1AB=.||【提示】用AB与AD用AC与BE表示，然后进行向量的数量积运算【考点】平面向量的应用15BE EC=+4(4，所以ABE△数学试卷第16页（共30页）ac B，cos cos5，进而得3数学试卷第22页（共30页）所以AC DB ＋AD CB12222113,)(3,)(3,)3,y x y x y x y +--++--（）122y y3 1. 2n数学试卷第28页（共30页）。

2013年高考天津卷(文)

2013年普通高等学校招生全国统一考试(天津卷)文科数学第Ⅰ卷一．选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的. 1．已知集合A = {x ∈R | |x |≤2}, B = {x ∈R | x ≤1}, 则A B ⋂= (A) (,2]-∞ (B) [1,2] (C) [－2,2] (D) [－2,1] 2．设变量x , y 满足约束条件360,20,30,x y y x y ≥--≤+-⎧-≤⎪⎨⎪⎩则目标函数2z y x =-的最小值为(A) －7 (B) －4 (C) 1 (D) 23．阅读右边的程序框图, 运行相应的程序, 则输出n 的值为(A) 7(B) 6(C) 5(D) 44．设,a b ∈R , 则 “2()0a b a -<”是“a b <”的 (A) 充分而不必要条件 (B) 必要而不充分条件(C) 充要条件 (D) 既不充分也不必要条件5．已知过点P (2,2) 的直线与圆225(1)x y +=-相切, 且与直线10ax y -+=垂直, 则a =(A) 12-(B) 1 (C) 2 (D)126．函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是(A) 1-(B)(C) (D) 0 7．已知函数()f x 是定义在R 上的偶函数, 且在区间[0,)+∞单调递增. 若实数a 满足212(log )(log )2(1)f a f f a ≤+, 则a 的取值范围是(A) [1,2](B) 10,2⎛⎤⎥⎝⎦(C) 1,22⎡⎤⎢⎥⎣⎦(D) (0,2]8．设函数22,()ln )3(x x g x x x x f e +-=+-=. 若实数a , b 满足()0,()0f a g b ==, 则 (A) ()0()g a f b << (B) ()0()f b g a <<(C) 0()()g a f b << (D) ()()0f b g a <<二．填空题: 本大题共6小题, 每小题5分, 共30分. 9．i 是虚数单位. 复数(3 + i )(1－2i ) = .10．已知一个正方体的所有顶点在一个球面上. 若球的体积为92π, 则正方体的棱长为 . 11．已知抛物线28y x =的准线过双曲线22221(0,0)x y a b a b-=>>的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .12．在平行四边形ABCD 中, AD = 1, 60BAD ︒∠=, E 为CD 的中点. 若·1AC BE =u u u r u u u r, 则AB 的长为 . 13．如图, 在圆内接梯形ABCD 中, AB //DC , 过点A 作圆的切线与CB 的延长线交于点E . 若AB = AD = 5, BE =4, 则弦BD 的长为 .14．设a + b = 2, b >0, 则1||2||a a b+的最小值为 . 三．解答题: 本大题共6小题, 共70分. 解答应写出文字说明, 证明过程或演算步骤. 15．(本小题满分13分)某产品的三个质量指标分别为x , y , z , 用综合指标S = x + y + z 评价该产品的等级. 若S ≤4, 则该产品为一等品. 先从一批该产品中(Ⅰ) (Ⅱ) 在该样品的一等品中, 随机抽取两件产品,(⒈) 用产品编号列出所有可能的结果;(⒉) 设事件B 为 “在取出的2件产品中, 每件产品的综合指标S 都等于4”, 求事件B 发生的概率.16．(本小题满分13分)在△ABC 中, 内角A , B , C 所对的边分别是a , b , c . 已知sin 3sin b A c B =, a = 3, 2cos 3B =. (Ⅰ) 求b 的值;(Ⅱ) 求sin 23B π⎛⎫- ⎪⎝⎭的值.17． (本小题满分13分)如图, 三棱柱ABC －A 1B 1C 1中, 侧棱A 1A ⊥底面ABC ,且各棱长均相等. D , E , F 分别为棱AB , BC , A 1C 1的中点. (Ⅰ) 证明EF //平面A 1CD ;(Ⅱ) 证明平面A 1CD ⊥平面A 1ABB 1;(Ⅲ) 求直线BC 与平面A 1CD 所成角的正弦值.18．(本小题满分13分)设椭圆22221(0)x y a b a b +=>>的左焦点为F , , 过点F 且与x 轴垂直的直线被椭圆截得的线段长(Ⅰ) 求椭圆的方程;(Ⅱ) 设A , B 分别为椭圆的左右顶点, 过点F 且斜率为k 的直线与椭圆交于C , D 两点. 若··8AC DB AD CB +=u u u r u u u r u u u r u u u r,求k 的值.19． (本小题满分14分) 已知首项为32的等比数列{}n a 的前n 项和为(*)n S n ∈N , 且234,2,4S S S -成等差数列. (Ⅰ) 求数列{}n a 的通项公式; (Ⅱ) 证明13*)61(n n S n S +≤∈N .20．(本小题满分14分)设[2,0]a ∈-, 已知函数332(5),03,0(,).2x f a x x a x x x x x a -+≤+-+>⎧⎪=⎨⎪⎩(Ⅰ) 证明()f x 在区间(－1,1)内单调递减, 在区间(1, + ∞)内单调递增;(Ⅱ) 设曲线()y f x =在点(,())(1,2,3)i i i x f x i P =处的切线相互平行, 且1230,x x x ≠ 证明12313x x x ++>.参考答案一、选择题 1．D 2．A 3．D 4．A 5．C 6．B 7．C 8．A 9．55i - 1011．2213y x -=12．12 13．15214．3415．16．17．18．19．20．。

2013年天津市高考数学试卷(文科)

2013年天津市高考数学试卷（文科）一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.共8小题,每小题5分,共40分.1．（5分）已知集合A={x∈R||x|≤2}，B={x∈R|x≤1}，则A∩B=（）A．（﹣∞，2]B．[1，2]C．[﹣2，2]D．[﹣2，1]2．（5分）设变量x，y满足约束条件，则目标函数z=y﹣2x的最小值为（）A．﹣7 B．﹣4 C．1 D．23．（5分）阅读如图所示的程序框图，运行相应的程序，则输出n的值为（）A．7 B．6 C．5 D．44．（5分）设a，b∈R，则“（a﹣b）a2＜0”是“a＜b”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件5．（5分）已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a=（）A．B．1 C．2 D．6．（5分）函数f（x）=sin（2x﹣）在区间[0，]上的最小值是（）A．﹣1 B．﹣C．D．07．（5分）已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，若实数a满足f（log 2a）+f（）≤2f（1），则a的取值范围是（）A． B．[1，2]C． D．（0，2]8．（5分）设函数f（x）=e x+x﹣2，g（x）=lnx+x2﹣3．若实数a，b满足f（a）=0，g（b）=0，则（）A．g（a）＜0＜f（b）B．f（b）＜0＜g（a）C．0＜g（a）＜f（b）D．f（b）＜g（a）＜0二．填空题：本大题共6小题，每小题5分，共30分.9．（5分）i是虚数单位．复数（3+i）（1﹣2i）=．10．（5分）已知一个正方体的所有顶点在一个球面上．若球的体积为，则正方体的棱长为．11．（5分）已知抛物线y2=8x的准线过双曲线的一个焦点，且双曲线的离心率为2，则该双曲线的方程为．12．（5分）在平行四边形ABCD中，AD=1，∠BAD=60°，E为CD的中点．若，则AB的长为．13．（5分）如图，在圆内接梯形ABCD中，AB∥DC，过点A作圆的切线与CB的延长线交于点E．若AB=AD=5，BE=4，则弦BD的长为．14．（5分）设a+b=2，b＞0，则的最小值为．三．解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.15．（13分）某产品的三个质量指标分别为x，y，z，用综合指标S=x+y+z评价该产品的等级．若S≤4，则该产品为一等品．现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如表：（Ⅰ）利用上表提供的样本数据估计该批产品的一等品率；（Ⅱ）在该样品的一等品中，随机抽取2件产品，（i）用产品编号列出所有可能的结果；（ii）设事件B为“在取出的2件产品中，每件产品的综合指标S都等于4”，求事件B发生的概率．16．（13分）在△ABC中，内角A，B，C所对的边分别是a，b，c．已知bsin A=3csin B，a=3，cos B=．（1）求b的值；（2）求sin（2B﹣）的值．17．（13分）如图，三棱锥ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等，D，E，F分别为棱AB，BC，A1C1的中点（Ⅰ）证明EF∥平面A1CD；（Ⅱ）证明平面A1CD⊥平面A1ABB1；（Ⅲ）求直线B1C1与平面A1CD所成角的正弦值．18．（13分）设椭圆=1（a＞b＞0）的左焦点为F，离心率为，过点F 且与x轴垂直的直线被椭圆截得的线段长为．（Ⅰ）求椭圆的方程；（Ⅱ）设A，B分别为椭圆的左，右顶点，过点F且斜率为k的直线与椭圆交于C，D两点．若=8，求k的值．19．（14分）已知首项为的等比数列{a n}的前n项和为S n（n∈N*），且﹣2S2，S3，4S4成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）证明．20．（14分）设a∈[﹣2，0]，已知函数（Ⅰ）证明f（x）在区间（﹣1，1）内单调递减，在区间（1，+∞）内单调递增；（Ⅱ）设曲线y=f（x）在点P i（x i，f（x i））（i=1，2，3）处的切线相互平行，且x1x2x3≠0，证明．2013年天津市高考数学试卷（文科）参考答案与试题解析一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.共8小题,每小题5分,共40分.1．（5分）已知集合A={x∈R||x|≤2}，B={x∈R|x≤1}，则A∩B=（）A．（﹣∞，2]B．[1，2]C．[﹣2，2]D．[﹣2，1]【分析】先化简集合A，解绝对值不等式可求出集合A，然后根据交集的定义求出A∩B即可．【解答】解：∵A={x||x|≤2}={x|﹣2≤x≤2}∴A∩B={x|﹣2≤x≤2}∩{x|x≤1，x∈R}={x|﹣2≤x≤1}故选：D．【点评】本题主要考查了绝对值不等式，以及交集及其运算，同时考查了运算求解的能力，属于基础题．2．（5分）设变量x，y满足约束条件，则目标函数z=y﹣2x的最小值为（）A．﹣7 B．﹣4 C．1 D．2【分析】先根据条件画出可行域，设z=y﹣2x，再利用几何意义求最值，将最小值转化为y轴上的截距最小，只需求出直线z=y﹣2x，过可行域内的点B（5，3）时的最小值，从而得到z最小值即可．【解答】解：设变量x、y满足约束条件，在坐标系中画出可行域三角形，平移直线y﹣2x=0经过点A（5，3）时，y﹣2x最小，最小值为：﹣7，则目标函数z=y﹣2x的最小值为﹣7．【点评】借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．3．（5分）阅读如图所示的程序框图，运行相应的程序，则输出n的值为（）A．7 B．6 C．5 D．4【分析】利用循环结构可知道需要循环4次方可得到S←2，因此输出的n←4．【解答】解：由程序框图可知：S=2=0+（﹣1）1×1+（﹣1）2×2+（﹣1）3×3+（﹣1）4×4，因此当n=4时，S←2，满足判断框的条件，故跳出循环程序．故输出的n的值为4．【点评】正确理解循环结构的功能是解题的关键．4．（5分）设a，b∈R，则“（a﹣b）a2＜0”是“a＜b”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】根据充分必要条件定义判断，结合不等式求解．【解答】解：∵a，b∈R，则（a﹣b）a2＜0，∴a＜b成立，由a＜b，则a﹣b＜0，“（a﹣b）a2≤0，所以根据充分必要条件的定义可的判断：a，b∈R，则“（a﹣b）a2＜0”是a＜b的充分不必要条件，故选：A．【点评】本题考查了不等式，充分必要条件的定义，属于容易题．5．（5分）已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a=（）A．B．1 C．2 D．【分析】由题意判断点在圆上，求出P与圆心连线的斜率就是直线ax﹣y+1=0的斜率，然后求出a的值即可．【解答】解：因为点P（2，2）满足圆（x﹣1）2+y2=5的方程，所以P在圆上，又过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，所以切点与圆心连线与直线ax﹣y+1=0平行，所以直线ax﹣y+1=0的斜率为：a==2．故选：C．【点评】本题考查直线与圆的位置关系，直线与直线的垂直，考查转化数学与计算能力．6．（5分）函数f（x）=sin（2x﹣）在区间[0，]上的最小值是（）A．﹣1 B．﹣C．D．0【分析】由题意，可先求出2x取值范围，再由正弦函数的性质即可求出所求的最小值．【解答】解：由题意x∈，得2x∈[﹣，]，∴∈[，1]∴函数在区间的最小值为．故选：B．【点评】本题考查正函数的最值的求法，解题的关键是熟练掌握正弦函数的性质，能根据正弦函数的性质求最值．7．（5分）已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递增，若实数a满足f（log 2a）+f（）≤2f（1），则a的取值范围是（）A． B．[1，2]C． D．（0，2]【分析】由偶函数的性质将f（log 2a）+f（）≤2f（1）化为：f（log2a）≤f（1），再由f（x）的单调性列出不等式，根据对数函数的性质求出a的取值范围．【解答】解：因为函数f（x）是定义在R上的偶函数，所以f（）=f（﹣log 2a）=f（log2a），则f（log 2a）+f（）≤2f（1）为：f（log2a）≤f（1），因为函数f（x）在区间[0，+∞）上单调递增，所以|log2a|≤1，解得≤a≤2，则a的取值范围是[，2]，故选：A．【点评】本题考查函数的奇偶性、单调性的应用，以及对数函数的性质，属于基础题．8．（5分）设函数f（x）=e x+x﹣2，g（x）=lnx+x2﹣3．若实数a，b满足f（a）=0，g（b）=0，则（）A．g（a）＜0＜f（b）B．f（b）＜0＜g（a）C．0＜g（a）＜f（b）D．f（b）＜g（a）＜0【分析】先判断函数f（x），g（x）在R上的单调性，再利用f（a）=0，g（b）=0判断a，b的取值范围即可．【解答】解：①由于y=e x及y=x﹣2关于x是单调递增函数，∴函数f（x）=e x+x ﹣2在R上单调递增，分别作出y=e x，y=2﹣x的图象，∵f（0）=1+0﹣2＜0，f（1）=e﹣1＞0，f（a）=0，∴0＜a＜1．同理g（x）=lnx+x2﹣3在R+上单调递增，g（1）=ln1+1﹣3=﹣2＜0，g（）=，g（b）=0，∴．∴g（a）=lna+a2﹣3＜g（1）=ln1+1﹣3=﹣2＜0，f（b）=e b+b﹣2＞f（1）=e+1﹣2=e﹣1＞0．∴g（a）＜0＜f（b）．故选：A．【点评】熟练掌握函数的单调性、函数零点的判定定理是解题的关键．二．填空题：本大题共6小题，每小题5分，共30分.9．（5分）i是虚数单位．复数（3+i）（1﹣2i）=5﹣5i．【分析】利用复数的运算法则即可得出．【解答】解：（3+i）（1﹣2i）=3﹣6i+i﹣2i2=5﹣5i．故答案为5﹣5i．【点评】熟练掌握导数的运算法则是解题的关键．10．（5分）已知一个正方体的所有顶点在一个球面上．若球的体积为，则正方体的棱长为．【分析】设出正方体棱长，利用正方体的体对角线就是外接球的直径，通过球的体积求出正方体的棱长．【解答】解：因为正方体的体对角线就是外接球的直径，设正方体的棱长为a，所以正方体的体对角线长为：a，正方体的外接球的半径为：，球的体积为：，解得a=．故答案为：．【点评】本题考查正方体与外接球的关系，注意到正方体的体对角线就是球的直径是解题的关键，考查空间想象能力与计算能力．11．（5分）已知抛物线y2=8x的准线过双曲线的一个焦点，且双曲线的离心率为2，则该双曲线的方程为．【分析】利用抛物线的标准方程y2=8x，可得，故其准线方程为x=﹣2．由题意可得双曲线的一个焦点为（﹣2，0），即可得到c=2．再利用双曲线的离心率的计算公式可得=2，得到a=1，再利用b2=c2﹣a2可得b2．进而得到双曲线的方程．【解答】解：由抛物线y2=8x，可得，故其准线方程为x=﹣2．由题意可得双曲线的一个焦点为（﹣2，0），∴c=2．又双曲线的离心率为2，∴=2，得到a=1，∴b2=c2﹣a2=3．∴双曲线的方程为．故答案为．【点评】熟练掌握双曲线抛物线的标准方程及其性质是解题的关键．12．（5分）在平行四边形ABCD中，AD=1，∠BAD=60°，E为CD的中点．若，则AB的长为．【分析】利用向量的三角形法则和平行四边形法则和数量积得运算即可得出．【解答】解：∵，．∴===+﹣==1，化为，∵，∴．故答案为．【点评】熟练掌握向量的三角形法则和平行四边形法则和数量积得运算是解题的关键．13．（5分）如图，在圆内接梯形ABCD中，AB∥DC，过点A作圆的切线与CB的延长线交于点E．若AB=AD=5，BE=4，则弦BD的长为．【分析】连结圆心O与A，说明OA⊥AE，利用切割线定理求出AE，通过余弦定理求出∠BAE的余弦值，然后求解BD即可．【解答】解：如图连结圆心O与A，因为过点A作圆的切线与CB的延长线交于点E．所以OA⊥AE，因为AB=AD=5，BE=4，梯形ABCD中，AB∥DC，BC=5，由切割线定理可知：AE2=EB•EC，所以AE==6，在△ABE中，BE2=AE2+AB2﹣2AB•AEcosα，即16=25+36﹣60cosα，所以cosα=，AB=AD=5，所以BD=2×ABcosα=．故答案为：．【点评】本题考查切割线定理，余弦定理的应用，考查学生分析问题解决问题的能力以及计算能力．14．（5分）设a+b=2，b＞0，则的最小值为．【分析】由题意得代入所求的式子，进行化简后，再对部分式子利用基本不等式求出范围，再由a的范围求出式子的最小值．【解答】解：∵a+b=2，∴，∴=，∵b＞0，|a|＞0，∴≥1（当且仅当b2=4a2时取等号），∴≥1，故当a＜0时，的最小值为．故答案为：．【点评】本题考查了基本不等式的应用，需要根据条件和所求式子的特点，进行变形凑出定值再进行求解，考查了转化和分类讨论的能力．三．解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.15．（13分）某产品的三个质量指标分别为x，y，z，用综合指标S=x+y+z评价该产品的等级．若S≤4，则该产品为一等品．现从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如表：（Ⅰ）利用上表提供的样本数据估计该批产品的一等品率；（Ⅱ）在该样品的一等品中，随机抽取2件产品，（i）用产品编号列出所有可能的结果；（ii）设事件B为“在取出的2件产品中，每件产品的综合指标S都等于4”，求事件B发生的概率．【分析】（Ⅰ）用综合指标S=x+y+z计算出10件产品的综合指标并列表表示，则样本的一等品率可求；（Ⅱ）（i）直接用列举法列出在该样品的一等品中，随机抽取2件产品的所有等可能结果；（ii）列出在取出的2件产品中，每件产品的综合指标S都等于4的所有情况，然后利用古典概型概率计算公式求解．【解答】解：（Ⅰ）计算10件产品的综合指标S，如下表：其中S≤4的有A1，A2，A4，A5，A7，A9共6件，故样本的一等品率为．从而可估计该批产品的一等品率为0.6；（Ⅱ）（i）在该样本的一等品种，随机抽取2件产品的所有可能结果为{A1，A2}，{A1，A4}，{A1，A5}，{A1，A7}，{A1，A9}，{A2，A4}，{A2，A5}，{A2，A7}，{A2，A9}，{A4，A5}，{A4，A7}，{A4，A9}，{A5，A7}，{A 5，A9}，{A7，A9}共15种．（ii）在该样本的一等品种，综合指标S等于4的产品编号分别为A1，A2，A5，A7．则事件B发生的所有可能结果为{A1，A2}，{A1，A5}，{A1，A7}，{A2，A5}，{A2，A7}，{A5，A7}，共6种．所以p（B）=．【点评】本题考查了随机事件，考查了用样本的数字特征估计总体的数字特征，考查了古典概型及其概率计算公式，是基础题．16．（13分）在△ABC中，内角A，B，C所对的边分别是a，b，c．已知bsin A=3csin B，a=3，cos B=．（1）求b的值；（2）求sin（2B﹣）的值．【分析】（Ⅰ）直接利用正弦定理推出bsinA=asinB，结合已知条件求出c，利用余弦定理直接求b的值；（Ⅱ）利用（Ⅰ）求出B的正弦函数值，然后利用二倍角公式求得正弦、余弦函数值，利用两角差的正弦函数直接求解的值．【解答】解：（Ⅰ）在△ABC中，有正弦定理，可得bsinA=asinB，又bsinA=3csinB，可得a=3c，又a=3，所以c=1．由余弦定理可知：b2=a2+c2﹣2accosB，，即b2=32+12﹣2×3×cosB，可得b=．（Ⅱ）由，可得sinB=，所以cos2B=2cos2B﹣1=﹣，sin2B=2sinBcosB=，所以===．【点评】本题考查余弦定理，正弦定理以及二倍角的正弦函数与余弦函数，两角和与差的三角函数，同角三角函数的基本关系式的应用，考查计算能力．17．（13分）如图，三棱锥ABC﹣A1B1C1中，侧棱A1A⊥底面ABC，且各棱长均相等，D，E，F分别为棱AB，BC，A1C1的中点（Ⅰ）证明EF∥平面A1CD；（Ⅱ）证明平面A1CD⊥平面A1ABB1；（Ⅲ）求直线B1C1与平面A1CD所成角的正弦值．【分析】（I）连接ED，要证明EF∥平面平面A1CD，只需证明EF∥DA1即可；（II）欲证平面平面A1CD⊥平面A1ABB1，即证平面内一直线与另一平面垂直，根据直线与平面垂直的判定定理证得CD⊥面A1ABB1，再根据面面垂直的判定定理得证；（III）先过B作BG⊥AD交A1D于G，利用（II）中结论得出BG⊥面A1CD，从而∠BCG为所求的角，最后在直角△BGC中，求出sin∠BCG即可得出直线BC与平面A1CD所成角的正弦值．【解答】证明：（I）三棱柱ABC﹣A1B1C1中，AC∥A1C1，AC=A1C1，连接ED，可得DE∥AC，DE=AC，又F为棱A1C1的中点．∴A1F=DE，A1F∥DE，所以A1DEF是平行四边形，所以EF∥DA1，DA1⊂平面A1CD，EF⊄平面A1CD，∴EF∥平面A1CD（II）∵D是AB的中点，∴CD⊥AB，又AA1⊥平面ABC，CD⊂平面ABC，∴AA1⊥CD，又AA1∩AB=A，∴CD⊥面A1ABB1，又CD⊂面A1CD，∴平面A1CD⊥平面A1ABB1；（III）过B作BG⊥A1D交A1D于G，∵平面A1CD⊥平面A1ABB1，且平面A1CD∩平面A1ABB1=A1D，BG⊥A1D，∴BG⊥面A1CD，则∠BCG为所求的角，设棱长为a，可得A1D=，由△A1AD∽△BGD，得BG=，在直角△BGC中，sin∠BCG==，∴直线BC与平面A1CD所成角的正弦值．【点评】本题主要考查了平面与平面垂直的判定，直线与平面所成的角，以及直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于基础题．18．（13分）设椭圆=1（a＞b＞0）的左焦点为F，离心率为，过点F 且与x轴垂直的直线被椭圆截得的线段长为．（Ⅰ）求椭圆的方程；（Ⅱ）设A，B分别为椭圆的左，右顶点，过点F且斜率为k的直线与椭圆交于C，D两点．若=8，求k的值．【分析】（Ⅰ）先根据椭圆方程的一般形式，令x=c代入求出弦长使其等于，再由离心率为，可求出a，b，c的关系，进而得到椭圆的方程．（Ⅱ）直线CD：y=k（x+1），设C（x1，y1），D（x2，y2），由消去y得，（2+3k2）x2+6k2x+3k2﹣6=0，再由韦达定理进行求解．求得，利用=8，即可求得k的值．【解答】解：（Ⅰ）根据椭圆方程为．∵过焦点且垂直于x轴的直线被椭圆截得的线段长为，∴当x=﹣c时，，得y=±，∴=，∵离心率为，∴=，解得b=，c=1，a=．∴椭圆的方程为；（Ⅱ）直线CD：y=k（x+1），设C（x1，y1），D（x2，y2），由消去y得，（2+3k2）x2+6k2x+3k2﹣6=0，∴x1+x2=﹣，x1x2=，又A（﹣，0），B（，0），∴=（x1+，y1）•（﹣x2．﹣y2）+（x2+，y2）•（﹣x1．﹣y1），=6﹣（2+2k2）x1x2﹣2k2（x1+x2）﹣2k2，=6+=8，解得k=．【点评】本题主要考查椭圆的标准方程、椭圆的简单性质等，考查方程思想．在椭圆中一定要熟练掌握a，b，c之间的关系、离心率、准线方程等基本性质．19．（14分）已知首项为的等比数列{a n}的前n项和为S n（n∈N*），且﹣2S2，S3，4S4成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）证明．【分析】（Ⅰ）由题意得2S3=﹣2S2+4S4，变形为S4﹣S3=S2﹣S4，进而求出公比q 的值，代入通项公式进行化简；（Ⅱ）根据（Ⅰ）求出，代入再对n分类进行化简，判断出S n随n的变化情况，再分别求出最大值，再求出的最大值．【解答】（Ⅰ）解：设等比数列{a n}的公比为q，∵﹣2S2，S3，4S4等差数列，∴2S3=﹣2S2+4S4，即S4﹣S3=S2﹣S4，得2a4=﹣a3，∴q=，∵，∴=；（Ⅱ）证明：由（Ⅰ）得，S n==1﹣，∴，当n为奇数时，==，当n为偶数时，=，∴随着n的增大而减小，即，且，综上，有成立．【点评】本题考查了等差（等比）数列的概念、通项公式和前n项和公式，以及数列的基本性质等，考查了分类讨论的思想、运算能力、分析问题和解决问题的能力．20．（14分）设a∈[﹣2，0]，已知函数（Ⅰ）证明f（x）在区间（﹣1，1）内单调递减，在区间（1，+∞）内单调递增；（Ⅱ）设曲线y=f（x）在点P i（x i，f（x i））（i=1，2，3）处的切线相互平行，且x1x2x3≠0，证明．【分析】（Ⅰ）令，．分别求导即可得到其单调性；（Ⅱ）由（Ⅰ）可知：f′（x）在区间（﹣∞，0）内单调递减，在区间内单调递减，在区间内单调递增．已知曲线y=f（x）在点P i（x i，f（x i））（i=1，2，3）处的切线相互平行，可知x1，x2，x3互不相等，利用导数的几何意义可得．不妨x1＜0＜x2＜x3，根据以上等式可得，从而．设g（x）=3x2﹣（a+3）x+a，利用二次函数的单调性可得．由，解得，于是可得，通过换元设t=，已知a∈[﹣2，0]，可得，故，即可证明．【解答】解：（Ⅰ）令，．①，由于a∈[﹣2，0]，从而当﹣1＜x＜0时，，所以函数f1（x）在区间（﹣1，0）内单调递减，②=（3x﹣a）（x﹣1），由于a∈[﹣2，0]，所以0＜x＜1时，；当x＞1时，，即函数f2（x）在区间（0，1）内单调递减，在区间（1，+∞）上单调递增．综合①②及f1（0）=f2（0），可知：f（x）在区间（﹣1，1）内单调递减，在区间（1，+∞）内单调递增；（Ⅱ）证明：由（Ⅰ）可知：f′（x）在区间（﹣∞，0）内单调递减，在区间内单调递减，在区间内单调递增．因为曲线y=f（x）在点P i（x i，f（x i））（i=1，2，3）处的切线相互平行，从而x1，x2，x3互不相等，且．不妨x1＜0＜x2＜x3，由+a=．高考真题及答案高考真题解析可得，解得，从而．设g （x ）=3x 2﹣（a +3）x +a ，则．由，解得，所以，设t=，则， ∵a ∈[﹣2，0]，∴，故，故．【点评】本题主要考查了导数的运算与几何意义，利用导数研究函数的单调性，考查了分类讨论的思想、化归思想、函数思想，考查了分析问题和解决问题的能力．。

天津市宝坻区2013届高三综合模拟文综地理 Word版含答案.pdf

2013年高三综合模拟试卷文科综合地理部分文科综合共300分，考试时间150分钟。

地理试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至3页，第Ⅱ卷4至6页。

共100分。

答卷前，考生务必将自己的姓名、准考号涂在答题卡上，并在规定位置粘贴考试用条形码。

答卷时，考生务必将答案涂在答题卡上，答在试卷上无效。

考试结束后，将本试卷和答题卡一并交回。

1．每题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2．本卷共11题，每题4分，共44分。

在每题列出的四个选项中，只有一项是最符合题目要求的。

1．根据行道树及树影推断该城市此时的北京时间可能是 A．1 月 1 日 16:00B．3 月 1 日 6:00 C．7 月 1 日 6:00?D．8 月 1 日 16:00 2．此时 A．非洲热带草原动物正在向南迁徙 B．澳大利亚北部天气高温多雨 C．南极中山站正值科考繁忙季节 D．从澳大利亚西岸向中国航行的轮船顺风顺水下图为“某大城市空间结构示意图”，读图完成3—4题。

3．从城市功能区合理布局角度考虑，适宜迁往小城市e的企业是A．水泥厂B．钢铁厂C．棉纺厂D．造船厂 4．该地区部分企业外迁到周围的郊区设厂，对城区的影响是 A．使城区商务功能更加突出 B．使城区的空间规模缩小 C．使城区空间结构更加复杂 D．使城区服务功能减弱 5．台湾东北的野柳地质公园”有一块形似金钱豹的岩石，每年只能在农历大潮的退潮期间见到，不过在2011年4月勘查时，发现豹头掉在地上，金钱豹已一命呜乎(见下图)。

金钱豹头部消失的地质作用主要是A．风力侵蚀作用B．海浪侵蚀作用C．冰川侵蚀作用 D．流水侵蚀作用 6．图中最大山脉的大体走向为A．东西走向B．东北西南走向C．南北走向D．西北东南走向 7．此时，在图示天气系统影响下 A．甲地处背风坡，降水概率较小?B．乙地处迎风坡，降水概率较大 C．丙地吹偏西风，气温较高?D．丁地吹偏西风，晴朗少云 8．为了加强甲、乙两村与城市的联系，拟建两条公路，图中八条规划线中，最合理的是 A．②a B．③b C．①c D．④d 9．图中铁路线分布存在着明显的问题，主要是 ①穿越河流②邻近港湾③穿越城区④坡度太大 A．①②B．②④ C．②③D．③④ 10．有关三个地区农业地域类型判断正确的是 A．①地区为乳畜业 B．②地区为商品率较高的种植业 C．③地区为大牧场放牧业 D．三地均为传统农业11．下列说法正确的是 A．美国东北部农业地域类型与①地区相似 B．②地区畜牧业发展的主要限制因素为草场面积 C．大力发展种植业是③地区今后发展的主要方向 D．建设高质量的人工草场是③地区提高土地载畜量的合理措施1．用黑色墨水的钢笔或签字笔将答案写在答题卡上。

2013高三文综历史联考试题(天津市带答案)

2013高三文综历史联考试题（天津市带答案）2013年天津市十二区县重点中学高三毕业班联考 (一) 文科综合能力测试历史部分考生一律用黑笔作答。

答卷前，考生务必将自己的姓名、准考号涂写在答题卡上。

答卷时，卷Ⅰ答案填涂在答题卡上，卷Ⅱ答案写在答题纸上，答在试卷上的无效。

第Ⅰ卷注意事项：1．每小题选出答案后，把历史答题卡上对应的题目的答案标号涂黑。

如需改动，用橡皮擦干净后再选涂其他答案标号。

2．本卷共11题，每题4分，共44分。

在每题列出的四个选项中，只有一项是最符合题目要求的。

一、选择题（每小题4分，共44分） 1．“即承旨诸臣亦只供传述缮撰，而不能稍有赞画于其间”。

该机构是 A．枢密院B．门下省 C．内阁 D．军机处 2．右图是西汉长安城的城市布局复原图。

对此图所反映的信息解读正确的有①经济政策影响城市商业区布局②城市商业活动受到严格的时空限制③政府设置专职机构管理城市的商业活动④城市皇家宫室布局体现政治功能突出A．①② B．②④ C．①④ D．①③ 3．据《古今图书集成》记载：古代女子列入“闺节”、“闺烈”的烈女节妇，唐朝为51人，宋朝为267人，明朝为36000人。

这种变化趋势表明 A．礼教束缚渐趋强大 B．君主专制逐渐强化 C．中央集权不断加强 D．夫权社会基本形成 4．马克思说：“美洲的发现，绕过非洲的航行，给新兴的资产阶级开辟了新天地。

”对这句话理解正确的是 A．加快了资本原始积累B．欧洲主导的世界市场雏形开始出现 C．商业经营方式发生变化D．股份公司、证券交易所产生 5．“一旦人民可以把他撵下台，他就不能抱怨人民使用暴力……只靠暴力维持的，只有用暴力来推翻。

”发表以上言论的思想家最有可能是 A．康德 B．伏尔泰 C．孟德斯鸠D．卢梭 6．1919年6月10日，天津总商会致电北京政府加急电报：“本日仅准曹汝霖辞职，似此可以谢国人乎？……查栖息于津埠之劳动者数十万众，现已发生不稳之象，倘迁延不决，其危厄之局，痛苦有过于罢市者”。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com 2013天津市高考压轴卷

文科综合地理部分第Ⅰ卷注意事项：本卷共同11题，每题4分，共44分。

我国某中学地理活动小组于秋分日日落后2小时30分，北京时间20时42分对当地地理纬度进行测定方法如下图所示。读图回答1-2题。 1.观测地可能位于 A.阴山南麓 B.洞庭湖畔 C.河西走廊 D.燕山脚下 2.观测当月,该地的主要农事活动可能为 A.种植玉米 B.水稻插秧 C.播种小麦 D.棉田除草

右为“某区域气候要素年内变化示意图”。读图回答3-4题。 3.关于图中所示气候类型分布地区的地理事物和现象叙述正确的是 A.自然植被以常绿硬叶林为主 B.附近海域均有寒暖流交汇 C.风力沉积地貌广泛分布 D.夏季为河流汛期 4.在图示气候的分布区对大气污染严重的工厂不宜建在城市居民区的 A.西北方向 B.西南方向 C.东北方向 D.东南方向

损失率是指受灾区域各类财产的损失值与灾前(正常)值之比，影响损失率的因素主要有灾害的强度、地区经济发展水平和地区抗灾能力等。读“中国自然灾害损失率(‟)等值线局部示意图”，完成5-6题。 www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com 5．下列叙述正确的是 A．自然灾害损失率大致由沿海向内陆逐渐增大 B．因为经济发达，甲地区损失率最大 C．乙地区损失率较大，其原因之一是抗灾能力差 D．丙地区损失率较小，其原因是灾害种类单一，强度小 6．据图，推测上海及其周边地区自然灾害损失率最接近图4中的

下面左图为北半球某海域某时刻的海平面气压状况分布图，图中a、b、c分别代表各自所在等压线的气压值。读图完成7-8题。

7．若图中等压线的数值aA．Ⅰ B．Ⅱ C．Ⅲ D．Ⅳ 8．若图中等压线的数值a>b>c，则此时岛屿甲和岛屿乙中的②③④⑤四处容易形成降水的是： A．②与③ B．②与④ C．③与⑤ D．④与⑤

2011年9月天津滨海新区第一垃圾焚烧发电厂实现并网线路带电运行。一期工程可日处理生活垃圾1500吨，并可每年为新区提供1.26亿千瓦时的电能，如按每户每月用电87度计算，这些 www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com 电能可满足12万户居民的用电需求。结合垃圾发电厂发电示意图，回答9～10题。

9．关于建垃圾发电厂对天津滨海新区的影响，叙述正确的是( ) A．解决了能源紧张状况 B．改善了城市环境质量 C．加剧了人地矛盾 D．冬季取暖完全由余热提供 10．城市垃圾除焚烧发电外，以下哪种方式还符合可持续发展思想( ) A．垃圾分类填埋处理 B．露天焚烧 C．分类处理，废弃物再利用 D．远郊堆放，自然降解

宅基地是专门用于农民居住的农村用地。在城乡转型进程中，农村由于人口非农业化转移带来“人走屋空”的现象，新建住房不断向外围扩展，用地规模不断扩大，原宅基地废弃、闲置，形成空心化现象。下图为城乡结合部典型空心化村庄发展演化模式图，其中a、b、c三条曲线分别表示全村、村中心及村周边，读图完成问题。 11.关于图示信息的叙述，正确的是 A.到M点时，村中心住人宅基地面积减少趋势开始逆转 B.到N点时，村中心和村周边住人宅基地的变化趋势相同 C.到P点时，全村人口数量达到最大值 D.到R点时，全村宅基地的废弃和闲置最为严重

第Ⅱ卷 www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com 本卷共3题，共56分

12、 2011年，天津滨海新区生产总值达到6206.87亿元，超过南京市，增速为23.79%。天津滨海新区是我国重要的石油开采与加工基地，2012年石油和化工产业规模突破3000亿元，海洋化工历史悠久，生产规模和产品质量世界知名、全国领先。读图回答问题（26分）

 分析天津滨海新区发展石油工业及海洋化工的社会经济条件。(4分) 海底油气资源开发过程中出现的泄漏与污染，已成为困扰人们的主要问题。  说明在自然情况下，相同程度的原油泄漏后，两大水域水体自净速度哪个更快？以其中的一个海域说明理由。(6分)

 指出墨西哥湾与渤海共同的资源优势。(4分) 图中甲地1月的平均气温：最低气温：5.4℃,最高气温：16℃。图9中乙地 1月的平均气温：最低气温：-8℃度，最高气温：2℃。

(4)依据材料，试分析两地1月气温差异产生的主要原因（6分） www.zgxzw.com 中国校长网

中国校长网资源频道 http://zy.zgxzw.com (5) 近年来，随着南北运力日趋紧张、东北老工业基地亟待振兴、山东半岛蓝色经济区蓄势崛起，渤海跨海大通道构想再次进入人们的视线，图10为渤海跨海大通道示意图。

（5）专家论证，渤海跨海通道可采用“南桥北隧”方式，简述这样设计的原因是什么？跨海通道修建的意义有哪些。（6分） 13、九寨沟景区（图17）和喀斯特高原（图18）都有着千姿百态的岩溶地貌景观，喀斯特发育区地下水循环通畅。九寨沟以水景最为奇丽，素有“世界水景之王”的美誉，不仅河湖水清澈，而且景色宜人。读图回答问题。（30分）

（1）读图17，描述图示区域的地形特征。（6分）（2）运用地理环境整体性原理，分析九寨沟“河湖水清澈”景观形成的自然原因。（8分）（3）读图18，指出喀斯特高原主要的地质灾害以及频发的季节,并简要说明原因。（8分）（4）读图18，从自然条件分析甲河沿岸平原种植水稻的可行性。（8分） www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com

2013天津市高考压轴卷文科综合历史部分第Ⅰ卷注意事项：本卷共同11题，每题4分，共44分。

1.据考古发现，在战国中晚期的墓葬中，河北兴隆县一次出土铁范87件，大多为农具范。河南新郑韩国铸铁作坊遗址出土陶范300余件，其中农具范占60%以上，出土铁农具200多件，占全部铁器的63.5%。这些考古资料说明 A.铁器已开始用于农业生产 B.铁犁牛耕成为古代主要农耕方式 C.铁农具的使用己很普遍 D.铁农具制作技术臻于成熟 2．陈寅格先生曾说过，“华夏民族之文化，历数千年之演进，造极于赵宋之世”。下列史实不能证明此观点的是 3．梁启超说：“以社会主义运动之立场而论，欲此主义之传播与实现，不能不以劳动阶级为运动主体。劳动阶级不存在之国家，欲社会主义之实现，有道无由。而劳动阶级之发生，恒必与资本阶级相缘。故必有资本阶级，然后有劳动阶级，有劳动阶级，然后社会主义运动有所凭籍„„”“资本主义必非社会终极目的明矣，不过借以为过渡。”这表明他 A．从根本上否定社会主义 B．认为当时的中国还不具备实现社会主义的条件 C．没有认识到无产阶级的革命性 D．还没有认识到西方资本主义的弊端 4.右为“1943 年关内与东北地区重要工业品产量比较表”，它反映出的实质是 A. 东北煤、铁等资源丰富 B. 东北成为中国最重要的工业基地 C. 在国民政府大力扶持下，东北工业生产呈现良好态势 D. 因日本掠夺性开发，东北殖民地经济的特点日渐显露 5． 1952年至1 956年4年间，北大提出的科研项目有1 00项，1 956年至1 957年有400项。1 958年8月1日开始算起，只用了40天的时间，科研成果达到了3406项。材料说明 A．科技领域出现“大跃进” B．“双百”方针推动科技发展 C．社会主义制度凸显优越性 D．“向科学进军”热潮初显成效 6．“先生游南镇，一友人指岩中花树，问曰：‘天下无心外之物，如此花树在深山中自开自落，于我心亦何关？’先生回答说：‘你未看此花时，此花与汝心同归于寂；你来看此花时，则此花颜色一时明白起来，便知此花不在你的心外”（《王文成公全书》卷三）。“材料中先生的观点与谁的相类似 A．柏拉图 B．普罗塔戈拉 C．亚里士多德 D．苏格拉底 www.zgxzw.com 中国校长网中国校长网资源频道 http://zy.zgxzw.com 7．针对“地圆学说”，清朝士大夫杨光先说：“若四大部州，万国之山河大地，是一个大圆球„„球上国土之人之脚心与球下国土之人脚心相对„„竞不思在下之国土人之倒悬„„有识者以理推之，不觉喷饭满案矣！夫人顶天立地，未闻有横立倒立之人也„„此可以见大地之非圆也。”之所以有这样言论，是因为他不知道 A．经典力学理论 B．相对论 C．生物进化论 D．量子论 8．恩格斯说：“在资产阶级借以组织其统治的国家机构中，也有许多东西是工人阶级可能利用来对这些机构本身作斗争的。„„资产阶级和政府害怕工人政党的合法活动更甚于害怕它的不合法活动„„。”在德国国家机构中，最有可能被工人阶级“利用”的是 A．宰相 B．内阁 C．联邦议会 D．帝国议会

9．下表反映了1913年、1938年、1973年三个年份英国、法国、美国政府总支出占GDP的百分比。由此得出的结论符合史实的是 1913年 1938年 1973年英国 13．3% 28．8% 41．5% 法国 8．9% 23．2% 38．8% 美国 8．0% 19．8% 31．1% A．马歇尔计划推动了欧洲经济复苏 B．三国政府逐步加强对经济的干预 C．三国政府均放弃了自由贸易政策 D．资本主义世界出现三足鼎立局面 10．德国总理默克尔上任以来推行注重意识形态的“价值观外交”，把维护“人权”和推广西式民主、自由等所谓“普世价值”作为德国外交政策的主要目标。对此认识正确的是 A．促进了中德关系发展 B．推动了多极化趋势 C．实质是一种冷战思维 D．有助于维护世界和平 11.统计表明:在世界贸易组织144个成员中，有90%以上的成员属于不同形式的区域经济组织。为适应世界发展潮流，中国和东盟做出了在10年内建立“中国一东盟自由贸易区”的战略决策。这表明当代世界市场 A.国际贸易形式多样化 B.商品结构复杂化 C.区域集团化趋势加强 D.市场竞争激烈化

第Ⅱ卷

本卷共3题，共56分 12．阅读材料，回答问题。(19分) 材料一中国古代货币简表发展阶段时间标志由杂乱形状向规范形状的演变秦代使用圆型方孔钱由地方铸币向中央铸币的演变汉武帝时中央统一铸造五铢钱由文书重量向通宝、元宝演变唐高祖时统一铸造“开元通宝”钱由金属铸币向纸币交子的演变宋代纸币交子在四川地区诞生材料二 16—18世纪中外金与银的比价表年代中国英国西班牙 1580 1：5．5 1：11．7 1：12．12