曲线正矢、付矢、超高、加宽的计算方法
正矢计算公式
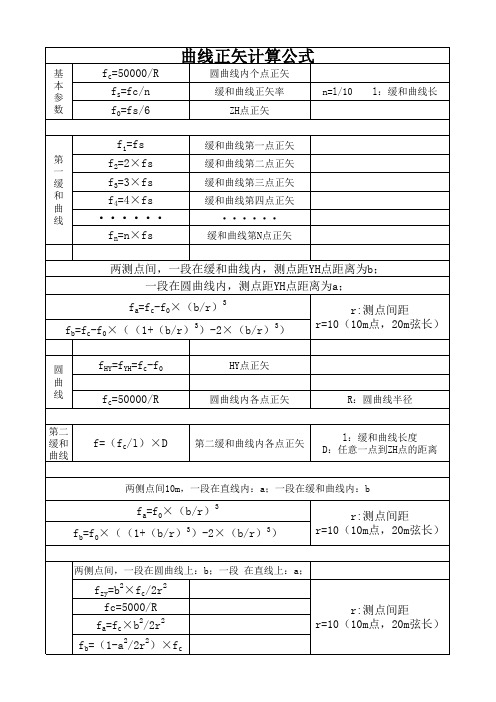
HY点正矢 圆曲线内各点正矢
R:圆曲线半径
第二
缓和 f=(fc/l)×D
曲线
第二缓和曲线内各点正矢
l:缓和曲线长度 D:任意一点到ZH点的距离
两侧点间10m,一段在直线内:a;一段在缓和曲线内:b
fa=f0×(b/r)3 fb=f0×((1+(b/r)3)-2×(b/r)3)
r:测点间距 r=10(10m点,20m弦长)
······ 缓和曲线第N点正矢
两测点间,一段在缓和曲线内,测点距YH点距离为b; 一段在圆曲线内,测点距YH点距离为a;
fa=fc-f0×(b/r)3 fb=fc-f0×((1+(b/r)3)-2×(b/r)3)
r:测点间距 r=10(10m点,20m弦长)
圆
fHY=fYH=fc-f0
曲
线
fc=50000/R
ቤተ መጻሕፍቲ ባይዱ
两侧点间,一段在圆曲线上:b;一段 在直线上:a;
fzy=b2×fc/2r2 fc=5000/R
fa=fc×b2/2r2 fb=(1-a2/2r2)×fc
r:测点间距 r=10(10m点,20m弦长)
曲线正矢计算公式
基
fc=50000/R
本 参
fs=fc/n
数
f0=fs/6
圆曲线内个点正矢 缓和曲线正矢率
ZH点正矢
n=l/10 l:缓和曲线长
f1=fs
第 一
f2=2×fs
缓
f3=3×fs
和 曲
f4=4×fs
线
······
fn=n×fs
缓和曲线第一点正矢 缓和曲线第二点正矢 缓和曲线第三点正矢 缓和曲线第四点正矢
曲线管理办法

2(3)
4
3
4、在养护维修中,要有计划地拨正曲线,整治“鹅头”、“支嘴”等病害,保证曲线圆顺,并使曲线的头尾位置和曲线要素(缓和曲线长度、圆曲线半径、超高等)均与设备图表保持一致。
5、在复心曲线的大小半径连接处,正矢与计算正矢的容许差,按大半径曲线的组缓和曲线规定办理,缓和曲线与直线连接处不得有反弯或“鹅头”。
2、缓和曲线
⑴非对称型一
△f= f圆/缓和曲线段数
f直缓(缓直)=△f /6
f圆缓(缓圆)= f圆-f直缓(缓直)
缓和曲线各点正矢=△f×从计算起点到该点的段数
缓和曲线上任意一点正矢= f圆×(1-a/L缓)
其中:a-----------该点到圆缓(缓圆)点距离;
L缓--------缓和曲线长度。
2非对称型二(以图三为例)
HZ
图二
⑶非对称型二:从曲线始点向终点设置,即一弦到底(图三)。
L
D C L
YH
HY45 67 B A
2 3 8 9HZ
1ZH10
图三
2、我段管内浙赣、京九正线曲线正矢测点按非对称型一设置,其它线曲线正矢测点按非对称型二设置,曲线正矢编号顺里程方向依次而定。
3、线路允许速度V≥120 km/h正线曲线必须增设5m测点,即在10m测点之间分中设测点,以利曲线的圆顺度控制。
④保持饱满,及时补碴、匀碴,清挖翻浆,整治道床病害,提高曲线稳定性。
⑥无缝线路地段在夏、秋两季节更迭前要安排扣件、接头螺栓复拧工作,保证扭矩达标,锁定线路。
2、曲线拨道
①每次轨检车、轨检仪和人工检测曲线后,巡养站要结合现场复核检查的基础上,及时校正曲线正矢,在2~3日内由站长带队拨道消灭Ⅰ、Ⅱ级偏差。
曲线正矢计算

曲线半径、弦长、正矢之间的关系:当 时, (mm) 当 时, (mm) 式中 —圆曲线正矢(mm)—圆曲线半径(m)现场正线曲线取弦长为20 m 计算正矢值。
现场站线曲线取弦长为10 m 计算正矢值。
(一)圆曲线上各测点计划正矢圆曲线计划正矢 (mm) 圆曲线始终点的计划正矢 (mm) (二)缓与曲线正矢就是从直线往圆曲线方向逐渐由小变大的,由直缓点向缓圆点方向变化的大小,叫缓与曲线的正矢递增率。
1、缓与曲线始终点计划正矢R L f 82=m L 20=Rf 50000=m L 10=Rf 12500=f R Rf c 50000=2c )(f f =终始()()()N f f c N 一端缓和曲线分段数圆曲线计划正矢缓和曲线的正矢递增率=()6N f )(f 缓和曲线正矢递增率缓和曲线始点正矢始=()始终缓和曲线始点正矢缓和曲线终点正矢f f )(f c -=2、缓与曲线中间各测点计划正矢式中 —缓与曲线中间各测点的计划正矢( ); —测点距缓与曲线始点的段数—缓与曲线的正矢递增率【例题】 已知曲线半径R=300m,缓与曲线长为70 m(如图3所示)求缓与曲线上各测点计划正矢值。
【解】mm mm mm mm 0缓与曲线中间各测点的计划正矢为图2缓与曲线mmmmmmmmmmmm Ni i f N f =i f 1,21-=N i,i N N f 1673005000050000≈==R f c ()()247167≈==N f f c N 一端缓和曲线分段数圆曲线计划正矢()46246===N f )(f ZH 始正矢直缓点()1634167=-=-=始终正矢缓圆点f f )(f HY c 2424111=⨯==N f N f 4824222=⨯==N f N f 7224333=⨯==N f N f 9624444=⨯==N f N f 12024555=⨯==N f N f 14424666=⨯==N f N f。
曲线绳正法及正失计算

曲线绳正法拨道及正失计算一、曲线绳正法概述曲线圆度通常是用半径来表达,如果一处曲线,其圆曲线部分各点半径完全相等,而缓和曲线部分从起点开始按照同一规律从无限大逐渐减少,到终点时和圆曲线半径相等,那就说明这处曲线是圆顺的。
但是铁路曲线半径都是很大的。
现场无法用实测半径的方法来检查曲线圆度,通常以曲线半径(R)、弦长(L)、正矢(f)的几何关系来检验,如图1一1。
图1-1以弦线测量正矢的方法,即用绳正法来检查曲线的圆度,用调整正矢的方法,使曲线达到圆顺。
测量现场正矢时,应用20m弦,在钢轨踏面下16mm处测量正矢,其偏差不得超过《修规》规定的限度。
曲线正矢作业验收容许偏差表1—1 曲线半径R 缓和曲线的正矢圆曲线正矢圆曲线正矢最《修规》绳正法拨正曲线的基本要求一、曲线两端直线轨向不良,应事先拨正;两曲线间直线段较短时,可与两曲线同时拨正。
二、在外股钢轨上用钢尺丈量,每10m设置1个测点(曲线头尾是否在测点上不限)。
三、在风力较小条件下,拉绳测量每个测点的正矢,测量3次,取其平均值。
四、按绳正法计算拨道量,计算时不宜为减少拨道量而大量调整计划正矢。
五、设置拨道桩,按桩拨道。
二、曲线整正的基本原理(一)两条假定1、假定曲线两端切线方向不变,即曲线始终点拨量为零。
切线方向不变,也就是曲线的转角不变。
即∑f 现=∑f 计 式中:∑f 现——现场正矢总和 ∑f 计——计划正矢总和同时还要保证曲线两端直线不发生平行移动,即始终点拨量为零,即e 始=e 终=∑∑--=101002n n df式中:e 始——曲线始点处拨量 e 终——曲线终点处拨量df ——正矢差,等于现场正矢减计划正矢∑∑--10102n n df —-全拨量。
即为二倍的正矢差累计的合计。
2、曲线上某一点拨道时,其相邻测点在长度上并不随之移动,拨动后钢轨总长不变。
(二)四条基本原理1、等长弦分圆曲线为若干弧段,则每弧段正矢相等。
即等圆等弧的弦心距相等(平面几何定理)。
曲线绳正法及正失计算

曲线绳正法及正失计算曲线绳正法拨道及正失计算一、曲线绳正法概述曲线圆度通常是用半径来表达,如果一处曲线,其圆曲线部分各点半径完全相等,而缓和曲线部分从起点开始按照同一规律从无限大逐渐减少,到终点时和圆曲线半径相等,那就说明这处曲线是圆顺的。
但是铁路曲线半径都是很大的。
现场无法用实测半径的方法来检查曲线圆度,通常以曲线半径(R)、弦长(L)、正矢(f)的几何关系来检验,如图1一1。
图1-1以弦线测量正矢的方法,即用绳正法来检查曲线的圆度,用调整正矢的方法,使曲线达到圆顺。
测量现场正矢时,应用20m弦,在钢轨踏面下16mm处测量正矢,其偏差不得超过《修规》规定的限度。
曲线正矢作业验收容许偏差表1—1曲线半径R 缓和圆圆曲R≤25061218 250<R≤35051015 350<R≤4504812 450<R≤800369R >800υmax≤120 km/h369υmax>120km/h246注:曲线正矢用20m弦在钢轨踏面下16mm处测量。
《修规》绳正法拨正曲线的基本要求一、曲线两端直线轨向不良,应事先拨正;两曲线间直线段较短时,可与两曲线同时拨正。
二、在外股钢轨上用钢尺丈量,每10m设置1个测点(曲线头尾是否在测点上不限)。
三、在风力较小条件下,拉绳测量每个测点的正矢,测量3次,取其平均值。
四、按绳正法计算拨道量,计算时不宜为减少拨道量而大量调整计划正矢。
五、设置拨道桩,按桩拨道。
二、曲线整正的基本原理 (一)两条假定1、假定曲线两端切线方向不变,即曲线始终点拨量为零。
切线方向不变,也就是曲线的转角不变。
即∑f 现=∑f 计 式中:∑f 现——现场正矢总和 ∑f 计——计划正矢总和同时还要保证曲线两端直线不发生平行移动,即始终点拨量为零,即e 始=e 终=∑∑--=101002n n df式中:e 始——曲线始点处拨量 e 终——曲线终点处拨量df ——正矢差,等于现场正矢减计划正矢∑∑--10102n n df —-全拨量。
曲线正矢计算

二、算例1、圆曲线长度为10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求曲线各测点的计划正矢解:(1)圆曲线计划正矢: fc=L2/8R=20*20/8R=50000/R=50000/600=83.3mm,取84mm(2)缓和曲线正矢递增率: fs= fc/n=84/5=16.8mm(3)直缓(缓直)点正矢: f0=fs/6=16.8/6=2.8mm,取3mm(4)缓和曲线中间各点的正矢:缓和曲线第1点的正失 f1=fs=16.8mm,取17mm缓和曲线第2点的正失 f2=2fs=2*16.8=33.6mm,取34mm 缓和曲线第3点的正失 f3=3fs=3*16.8=50.4mm,取50mm 缓和曲线第4点的正失 f4=4fs=4*16.8=67.2mm,取67mm (5)缓圆(圆缓)点正矢: fhy=fc- f0=84-3=81mm2、圆曲线长度不是10m整数倍的曲线计划正矢的计算已知某曲线半径R=600m,两端缓和曲线l0=50m,圆曲线长304m,求各测点的计划正矢解:(1)第一缓和曲线和圆曲线的计划正矢算法同上;(2)第二缓和曲线各点计划正矢的计算:①第二缓和曲线始(HZ)点相邻测点的计划正矢因为圆曲线长L=304m,故第二缓和曲线始(HZ)点距缓和曲线和直线上相邻点(40点、41点)的距离分别为b≈4m,a≈6m,为测点间的距离,等于弦长的一半,a+b=则f40=1/6 fs[(1+b/)3-2(b/)3]=1/6*16.8*[(1+4/10)3-2*(4/10)3]=7.32mm,取7mm f41=1/6 fs(b/)3=1/6*16.8*(4/10)3=0.18mm,取0mm ②第二缓和曲线终点(YH)相邻测点的计划正矢第二缓和曲线终点(YH)距圆曲线和缓和曲线上相邻点(35点、36点)的距离分别为a≈4m,b≈6m,为测点间的距离,等于弦长的一半,a+b=则f35 = fc-1/6 fs(b/)3=84-1/6*16.8*(6/10)3=84-0.6=83.4mm,取84mm f36= fc-1/6 fs[(1+b/)3-2(b/)3]=84-1/6*16.8*[(1+6/10)3-2*(6/10)3]= 73.74mm,取74mm ③第二缓和曲线上其他各点计划正矢的计算其他各点计划正矢,可根据各点正矢与其距终点(HZ)距离成直线比例的关系,按下式求取:fi=fc/l0*li 则第37点、38点、39点的计划正矢分别为:f37=fc/l0*l37=84/50*34=57.12mm,取57mm f38=fc/l0*l38=84/50*24=40.32mm,取40mm f39=fc/l0*l39=84/50*14=23.52mm,取24mm 3、辅助点计划正矢的计算辅助点计划正矢的计算按圆曲线长度不是10m整数倍时缓和曲线的算法计算(1)圆曲线长度为10m整数倍时辅助点计划正矢的计算已知某曲线半径R=600m,两端缓和曲线长l0=50m,求缓和曲线辅助点的计划正矢解:辅助点与测点相距5m,即a=b=5m,①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为: f=1/6 fs[(1+b/)3-2(b/)3]=1/6*16.8*[(1+5/10)3-2*(5/10)3]=8.75mm,取9mm ②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为:f= fc-1/6 fs[(1+b/)3-2(b/)3]=84-1/6*16.8*[(1+5/10)3-2*(5/10)3 ]= 75.25mm,取75mm ③缓和曲线其他各中间辅助点的计划正矢:分别取li=15、25、35,按fi=fc/l0*li算得辅助点计划正矢分别为:25mm、42mm、59mm (2)圆曲线长度不是10m整数倍时辅助点计划正矢的计算曲线半径R=600m,缓和曲线长l0=50m,圆曲线长304m,求缓和曲线辅助点的计划正矢解:第一个缓和曲线辅助点的算法同上,第二个缓和曲线上辅助点计划正矢的计算按B=b±5计算,即:①缓和曲线上与始点(ZH、HZ)相邻辅助点计划正矢为(B=4+5=9): f=1/6 fs[(1+B/)3-2(B/)3]=1/6*16.8*[(1+9/10)3-2*(9/10)3]=15.12mm,取15mm ②缓和曲线上与终点(YH、HY)相邻辅助点计划正矢为(B=6-5=1): f= fc -1/6 fs[(1+B/)3-2(B/)3]=84-1/6*16.8*[(1+1/10)3-2*(1/10)3]=80.3mm,取80mm ③缓和曲线其他各中间辅助点的计划正矢:分别取li=19、29、39,按fi=fc/l0*li算得辅助点计划正矢分别为:32mm、49mm、66mm。
岔后连接曲线布置方案
岔后连接曲线布置方案以吴堡站14#岔后连接曲线为例,现场为P60-1/12可动心道岔,辙叉角4°45′49″(换算4.7637°),曲线半径400m ,道岔全长43.2m ,前长16.592m 、后长26.608m ,制定岔后连接曲线布置方案。
一、曲线三大桩确定 1.曲线QZ 点确定取三点测量线间距(k 表示)取平均值,现场测量为4.943m 、4.941m 、4.945m : 4.943 4.941 4.945k==4.9433m ++道岔理论中心距离连接曲线中点投影在直股上的距离:°'"4.943L==59.34tg445490.0833K m = 2.曲线ZY 、YZ 点确定曲线全长: 4.7637 3.14400===33.24m 180180R l απ⋅⋅⨯⨯曲线上股伸缩量:01500()111500(33.240)===124.65mm 0.125m 22400L l l R --∆⋅⋅≈曲线上股长:L'=33.240.12533.365m L l +∆=+=岔后连接曲线曲线三大桩确定二、曲线正矢布置1.曲线点号布置图(每5m 布点)ZY 点距离第1点距离:L'-5(n-2)33.365-5(82)=5-=5- 3.32m 22l ⨯⨯-≈1ZY 点距离第2点距离:L'-5(n-2)33.365-5(82)== 1.68m 22l ⨯⨯-≈1曲线点号布置图2.曲线正矢计算1250012500====31.2531mm 400f f R ≈3-7圆 第1、2、8、9点正矢:1 3.32==0.6655l A ≈2 1.68==0.3455l B ≈查表得对应纵距率:测点1:1=0.06β测点2:2=0.77β91===0.06312f f f mm β⨯⨯≈1圆82===0.773124f f f mm β⨯⨯≈2圆3.曲线正矢布置图1234987650Z YY ZQZ曲线正矢布置图f1=2f 2=24f 3=315f 4=31f 5=31f 9=2f 8=24f 7=31f 6=31三、超高布置岔后连接曲线宜设置适量的超高,但不大于15mm ,顺坡不大于2‰,一般情况下1/12道岔可设超高15mm 1.夹直线是否满足0'"44549=tg =400tg 4000.038915.56m22T R α⋅⨯≈⨯≈4.943==15.5626.60817.386msin 0.083k L T L α----≈夹后长超高顺坡长按照3.125m 顺5mm 算:5==1.63.125i 顺‰<2‰满足要求15=3.125=9.375m 5l ⨯顺 按要求夹直线与超高顺坡终点长度不小于7.5m 要求:=17.3869.375=8.01m>7.5m l l --顺夹满足要求2.连接曲线夹直线计算连接曲线夹直线计算3.连接曲线超高布置图Z YQZ曲线超高布置图H=5H=10H=156.253.125H=9.375H=5H=1H=15 6.253.125H= 09.375Y Z。
曲线整正
1、水平加速度与欠超高的关系:12.5mm的欠超高造成0.01g的水平加速度。
2、欠超高的计算公式:1)、曲线上某一点欠超高的计算:v2均*f设/4237为曲线超高h’=曲线理论欠超高+ v2实*f差/4237-水平2)、直线上某一点欠超高的计算:直线上f设=0mmh’= v2实*f差/4237-水平(公式推导详见第三步)3)、从严格的角度,将v实= v最高速度,从而曲线上欠超高:h’=曲线理论欠超高+ v2最高速度*f差/4237-水平=曲线理论欠超高+ A*f差-水平v2最高速度/4237为常数A,f差为20米弦测得的轨向值。
v最高速度=200km/h A=9.4 v最高速度=160 km/h A=6v最高速度=140 km/h A=4.6 v最高速度=120 km/h A=3.4直线上欠超高:h’= v2最高速度*轨向/3432-水平= A*轨向-水平v2最高速度/3432为常数A,轨检车数据中轨向值以18m弦测得。
v最高速度=200km/h A=9.4 v最高速度=160 km/h A=6v最高速度=140 km/h A=4.6 v最高速度=120 km/h A=3.43、欠超高公式的推导:v2*f/4237为曲线超高公式。
h’=11.8* v2实/R实- 11.8* v2均/R设- 水平=11.8* v2实*f实/50000- 11.8* v2均*f设/50000 - 水平= v2实*(f设+f差)/4237- v2均*f设/4237- 水平=v2实*f设/4237+ v2实*f差/4237- v2均*f设/4237-水平=v2实*f设/4237- v2均*f设/4237+ v2实*f差/4237-水平4、轨距、水平递变率与规定递变率的比率可以看作是方程的斜率(待议)一、正矢测点的设置:分别设置养护点和计算点1)、概念养护点:从曲线头尾点开始,每10m设一正矢测点,至曲中点附近后两点交叉,形成套拉点。
曲线超高计算实例
曲线超高计算实例曲线超高是在航空航天领域非常重要的概念,它用于计算飞行器在飞行过程中所需的垂直安全间隔。
本文将以生动、全面和有指导意义的方式介绍曲线超高的计算方法。
曲线超高是指在飞行过程中,飞行器需要保持的与地面或其他飞行器的垂直安全间隔。
曲线超高的计算要考虑飞行器的速度、机动性能以及航线的设计等多个因素。
首先,计算曲线超高需要确定飞行器的性能参数,其中最重要的参数是最小曲线超高速度(Vcm)。
Vcm是指飞行器在曲线飞行时所需的最小速度,可以通过飞行器的性能手册或其他相关资料获得。
其次,要计算曲线超高,需要确定飞行器的半径(r)。
半径是指飞行器在曲线飞行过程中所描述的弯曲部分的半径。
飞行器的半径可以通过速度、质量和过载等参数计算得出。
由于曲线超高是指飞行器与地面或其他飞行器之间的垂直间隔,所以还需要考虑地面高度(h)或其他飞行器的高度。
这些高度可以通过雷达、高度计或其他相关设备获得。
最后,使用以下公式计算曲线超高:H = (Vcm^2) / (2 * g) + r + h其中,H代表曲线超高,Vcm代表最小曲线超高速度,g代表重力加速度,r代表飞行器的半径,h代表地面高度或其他飞行器的高度。
通过以上步骤和公式,我们可以计算得到飞行器在曲线飞行过程中所需的曲线超高。
曲线超高的计算对飞行安全至关重要。
飞行员和飞行指挥员应该以规定的曲线超高为准,确保航班安全。
在飞行过程中,如果遇到需要进行曲线飞行的情况,飞行员应当精确计算曲线超高,并适时调整飞行高度,以确保飞行器与地面或其他飞行器之间的垂直间隔符合安全要求。
总之,曲线超高的计算是航空航天领域中一项重要的技术,涉及到飞行器性能参数、飞行器半径、地面高度等多个因素。
准确计算曲线超高可以确保飞行安全,提高飞行的效率。
飞行员和飞行指挥员应该掌握正确的计算方法,并在飞行过程中正确应用。
1、曲线养护维修技术管理基础知识
第四讲曲线养护维修基础知识一、关于曲线正矢1、曲线正矢标准曲线经常保养容许偏差管理值12、曲线正矢测点的设置方法合理设置曲线正矢测点是曲线养护维修管理中的一项重要工作,曲线正矢测点的设置方式,一般分“对称型”与“非对称型”。
(1)“对称型”曲线正矢测点设置:根据曲线要素确定曲线的直缓(ZH)、缓圆(HY)、圆缓(YH)、缓直(HZ)点,然后由曲线中点(QZ)向曲线两端均匀设置各个正矢测点(图1—1)。
图1-1(2)“非对称型”曲线正矢测点设置根据曲线要素确定曲线的直缓(ZH)、缓圆(HY)、圆缓(YH)和缓直(HZ)点,然后以曲线直缓(ZH)点(以里程较小的一端为始点),顺里程向曲线另一端均匀设置各个正矢测点(图1—2)。
图1-23、正矢点设置要求曲线正矢测点统一采用非对称设置。
即起端直缓、缓圆点和正矢测点对应,终端圆缓、缓直点不一定和正矢测点对应。
曲线测点按每10m 依次设置,计划正矢按照标准计算和设置。
在曲线单元范围内每测点间增设5m 附点,附点的计划正矢采用公式计算。
为控制曲线头尾位置和曲线头尾反弯或“鹅头”现象的出现,在设置好曲线各正矢点后分别向曲线两头直线段分别延伸3个辅助点。
与曲线正矢同时进行测量,但不纳入曲线拨量的计算。
4、曲线计划正矢计算 圆曲线正矢计算公式:R F 50000=(20m 弦) RF 12500=(10m 弦) 直圆点正矢=圆曲线正矢÷2 圆直点相邻测点的正矢直线一侧F b F z ⋅=22b ——圆曲线一侧测点至圆直点距离÷弦长圆曲线一侧F a F y ⋅-=)21(2a ——直线一侧测点至圆直点距离÷弦长例:单圆曲线全长23.54m ,半径400m ,用10m 弦长丈量。
算出各点计划正矢。
圆曲线正矢:mm)(25.314001250012500===R F 取31mm mm)(1623121≈==F Fmm)(313131432===F mm F mm F mmF a F 2931)2)554.35(1()21(225≈⨯÷--=⋅-=mm F b F 8312)554.3(2226≈⨯÷=⋅=缓和曲线上各正矢计算:缓和曲线正矢递减率=圆曲线正矢÷缓和曲线段数 直缓点正矢=缓和曲线正矢递减率÷6缓和曲线中间各测点的正矢=各点对应的段数×正矢递减率 缓圆点正矢=圆曲线正矢-直缓点正矢例:曲线半径1000m ,曲线全长321.85m ,缓和曲线长100m ,用20m 弦长丈量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、曲线(有缓)正矢、付矢、超高、加宽计算方法(例):
例:已知某曲线R=310m,α=26°38′09″,l1=70m,l2=70m,H =125mm,S=5mm,V max=70km / h,求该曲线L全,L外,内距D,外距C,内距B,外距A,F Y及曲线各点F,f,H,S?
解:
L全=π×α×R/ 180+l1 / 2+l2 / 2 =214.114
L外=π×α×R外/ 180+l1 / 2+l2 / 2=214.447
内距D=(π×α×R外/ 180+l1 / 2-l2 / 2)-
INT((π×α×R外/ 180+l1 / 2-l2 / 2)/10) ×10=4.447 外距C=10-D=5.553
内距B=L外-INT(L外/ 10)×10 =4.447
外距A=10-B=5.553
外距系数a=A/10=0.5553,内距系数b=B/10=0.4447
外距系数c=C/10=0.5553,内距系数d=D/10=0.4447
F Y=λ2/2 R外=50000/(R+0.7175)=160.918,取161
F d1=F Y /(l1/λ)=22.988
F d2=F Y /(l2/λ)=22.988
因 H d1=H /l1=1.786>H d=1/(9×V max)=1.587
H d2=H /l2=1.786>H d=1/(9×V max)=1.587
故始端、终端超高顺坡各向直线延伸9m,
则 H d1=H /(l1+9)=1.582≤H d
H d2=H /(l2+9)=1.582≤H d
S d1=S /l1=0.071
S d2=S /l2=0.071
★始端正矢计算:(整桩)
F ZH=F0=F d1/6=3.831,取4
因 F n=n d×F d1=(D n / 10)×F d1
故 F1=23、F2=46、F3=69、F4=92、F5=115、F6=138
F HY=F7=F Y-F d1/6=157.086,取157
★始端付矢计算:
因 f n=0.75×F n+0.125×F d1
故 f1=20、f2=37、f3=55、f4=72、f5=89、f6=106
★始端超高、加宽计算:(略)
H n=D n ×H d1
S n=D n×S d1
★终端正矢计算:(破桩)
F D=F14=F Y-c3 /6×F d2=160.262,取160
=F Y-C3/(12×R外×l2)
F C=F15=F Y-(c+d3 /6)×F d2=147.816,取148
=F Y-(600C+D3)/(12×R外×l2)
因 F n=n d×F d2=(D n / 10)×F d2
=(50×D n )/(R外×l2)
故 F16=125、F17=102、F18=79、F19=56、F20=33
F B=F21=(b+a3 /6)×F d2=10.879,取11
=(600B+A3)/(12×R外×l2)
F A=F22=b3 /6×F d2=0.337,取0
=B2/(12×R外×l2)
★终端付矢计算:
因 C>5m,故 f YH=f15
即 f15=(300×(l2+D)-(D3+2500))/(8×R外×l2)=113
因 f n=0.75×F n+0.125×F d2
故 f16=97、f17=80、f18=62、f19=45、f20=28
f HZ=f21=(2500+600B+30B2-B3)/(24×R外×l2)=11
★终端超高、轨距计算:(略)
H n=D n ×H d2
S n=D n ×S d2
二、曲线(无缓)正矢计算方法:
曲线全长 L全=π×α×R/ 180
曲线外长 L外=π×α×R外/ 180
内距 B=L外-INT(L外/ 10)×10
外距 A=10-B
圆曲线正矢 F Y=λ2/2 R外=50000/(R+0.7175)
始端正矢:(整桩) F ZY=1/2×F Y
终端正矢:(破桩) F A=1/2×B2/2 R外
F B=1/2×(λ+B)2/2 R外-B2/2 R外
=F Y-1/2×A 2/2 R外
三、曲线(附带)正矢计算方法:
曲线全长 L全=π×α×R/ 180(α为辙叉角)
曲线外长 L外=π×α×R外/ 180
内距 B=L外-INT(L外/ 5)×5
外距 A=5-B
圆曲线正矢 F Y=λ2/2 R外=12500/(R+0.7175)
始端正矢:(整桩) F ZY=1/2×F Y
终端正矢:(破桩) F A=1/2×B2/2 R外
F B=1/2×(λ+B)2/2 R外-B2/2 R外
=F Y-1/2×A 2/2 R外
四、曲线(有缓)正矢、付矢、超高、加宽(自动)计算表:
五、曲线(无缓)正矢(自动)计算表:
六、常用附带曲线正矢(自动计算)表:。
