圆锥的侧面积(精练)
圆锥的侧面积--北师大版

58 r 2
L
58 2 ( ) 202 22.03(cm) 2
638.87
20=12777.4 (cm2)
所以, 至少要12777.4 cm2的纸。
(结果可含π)
• 1、高为4㎝,底面直径为6㎝的圆锥侧 面积___ 15 π • 2圆锥的母线与高的夹角为300,母线长 18π 27π 为6cm ,求它的侧面积__,全面积__
3、圆锥的侧面积与底面积之和称为全面积
例:圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm,高为 20cm,要制作20顶这样的纸帽至少要用多少平 方厘米的纸?(结果cm,母线长为lcm,
1 S圆锥侧=rl 58 22 .03=638 .87 (cm 2 ) 2
聂家河中学
装修 这样一 个蒙古 包需要 多少布 料?
蒙古包可近似看 作下面几何体
(1) 圆锥的侧面展开图是个什么图形?
(2)如何计算圆锥的侧面积?
2πr
h r
L
圆柱的侧面积 =2 πrL
1、圆锥的侧面展开 扇形 图是个___。 2、设圆锥的母线长为 L, 底面圆的半径为r, 那么这个扇形的半径 为_,扇形的弧长为 L 2 πr 因此圆锥的侧面 __ 积为___。 πr L
把一个用来盛雪糕的圆锥形纸杯沿母 线剪开,可得一个半径为24cm、圆心角为 1180的扇形,求 (1)该纸杯的底面半径和高度( π取3.14)
(2)若该纸杯加一圆形杯盖,则做这样一 个杯子需多少纸料? (结果精确到 0.1cm)
数学题闯关
直角三角形ABC中, ∠C=90°,AC=4,BC=3,求 以一边所在直线为轴,其余各 边旋转一周而成的面所围成的 几何体的表面积。
圆锥的侧面积

3、圆锥的侧面积与底面积之和称为全面积
例:圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm,高为 20cm,要制作20顶这样的纸帽至少要用多少平 方厘米的纸?(结果精确到0.1cm2) 解:设纸帽的底面半径为rcm,母线长为lcm,
1 S圆锥侧=rl 58 22 .03=638 .87 (cm 2 ) 2
把一个用来盛雪糕的圆锥形纸杯沿母 线剪开,可得一个半径为24cm、圆心角为 1180的扇形,求 (1)该纸杯的底面半径和高度( π取3.14)
(2)若该纸杯加一圆形杯盖,则做这样一 个杯子需多少纸料? (结果精确到 0.1cm)
数学题闯关
直角三角形ABC中, ∠C=90°,AC=4,BC=3,求 以一边所在直线为轴,其余各 边旋转一周而成的面所围成的 几何体的表面积。
58 r 2
L
58 2 ( ) 202 22.03(cm) 2
638.87
20=12777.4 (cm2)
所以, 至少要12777.4 cm2的纸。
(结果可含π)
• 1、高为4㎝,底面直径为6㎝的圆锥侧 面积___ 15 π • 2圆锥的母线与高的夹角为300,母线长 18π 27π 为6cm ,求它的侧面积__,全面积__
B
C
垂足为D. .r 360 120 垂足为D BAB l rr BAD 360 ABC BAB 360 BAB 60.在120 中, BAD 60, AB ∴∠BAD=60° Rt 120 ll 3 BAD 60在RtABC中, BAD 60,AB BAD 60 在Rt△ABC中,∠BAD=60°,AB=3 BD 3 . .在RtABC中, BAD 60, AB 2 3 3 BD BD 3 3 3 2 2 答: 它爬行的最短路线是 3. 2 3 3 答: 它爬行的最短路线是 3. . 答: 它爬行的最短路线是 3 2 2
圆锥的侧面积--北师大版

58 r 2
L
58 2 ( ) 202 22.03(cm) 2
638.87
20=12777.4 (cm2)
所以, 至少要12777.4 cm2的纸。
(结果可含π)
• 1、高为4㎝,底面直径为6㎝的圆锥侧 面积___ 15 π • 2圆锥的母线与高的夹角为300,母线长 18π 27π 为6cm ,求它的侧面积__,全面积__
把一个用来盛雪糕的圆锥形纸杯沿母 线剪开,可得一个半径为24cm、圆心角为 1180的扇形,求 (1)该纸杯的底面半径和高度( π取3.14)
(2)若该纸杯加一圆形杯盖,则做这样一 个杯子需多少纸料? (结果精确到 0.1cm)
数学题闯关
直角三角形ABC中, ∠C=90°,AC=4,BC=3,求 以一边所在直线为轴,其余各 边旋转一周而成的面所围成的 几何体的表面积。
A
解 : 将圆锥沿AB展开成扇形ABB, 则点C是BB的中点, 过点B作BD AC, 解: 将圆锥沿 AB 展开成扇形 ′ 的中点ABB , 则点C是BB 的 垂足为 D. 则点 C是 BB
垂足为 D . AC , 的 , 则点 解 ::B 将圆锥沿 AB 展开成扇形 B C 是 B B 解 将圆锥沿 AB 展开成扇形 AB B 则点 C 是 B B 过点 作 BD , 垂足为D. AB
3、圆锥的侧面积与底面积之和称为全面积
例:圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm,高为 20cm,要制作20顶这样的纸帽至少要用多少平 方厘米的纸?(结果精确到0.1cm2) 解:设纸帽的底面半径为rcm,母线长为lcm,
1 S圆锥侧=rl 58 22 .03=638 .87 (cm 2 ) 2
圆锥的侧面积和全面积测试题

第2课时圆锥的侧面积和全面积1.若一个圆锥的侧面展开图是半径为18 cm,圆心角为240°的扇形,则这个圆锥的底面半径长是( )A.6 cm B.9 cmC.12 cm D.18 cm2.一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是( ) A.120° B.180°C.240° D.300°3.如图24415所示,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1 cm,则这个圆锥的底面半径为( )A.2 2 cm B. 2 cmC.22cm D.12cm4.如图24416,AB是⊙Ο的直径,AC是弦,AC=3,∠BOC=2∠AOC.若用扇形OAC(图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是____.5.圆锥的底面周长为6π cm,高为4 cm,则该圆锥的全面积是____;侧面展开扇形的圆心角是____.6.如图24417所示,现有一圆心角为90°,半径为80 cm的扇形铁片,用它恰好围成一个圆锥形的量筒,用其他铁片再做一个圆形盖子把量筒底面密封(接缝处忽略不计).(1)圆形盖子的半径为多少厘米?(2)制作这个密封量筒,共用铁片多少平方厘米?(结果保留π)图244177.如图24418,从一块直径为24 cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )图24418A.12 cm B.6 cmC.3 2 cm D.2 3 cm8.如图24419所示的粮仓可以看成圆柱体与圆锥体的组合体,已知其底面半径为3 m,高为4 m,下方圆柱高为3 m.(1)求该粮仓的容积;(2)求上方圆锥的侧面积.图244199.如图24420所示,已知在⊙O 中,AB =43,AC 是⊙O 的直径,AC ⊥BD 于点F ,∠A =30°.图24420(1)求图中阴影部分的面积;(2)若用阴影扇形OBD 围成一个圆锥的侧面,请求出这个圆锥的底面圆的半径; (3)试判断⊙O 中其余部分能否给(2)中的圆锥做两个底面.参考答案【分层作业】1.C 2.A 3.C 4.125.24π 216°6.(1)圆形盖子的半径为20 cm. (2)共用铁片 2 000π cm 2. 7.C 8.(1)V =30π(m 3). (2)圆锥的侧面积S =310π(m 2). 9.(1)S 阴影=163π. (2)r =43. (3)⊙O 中某部分能给(2)中的圆锥做两个底面.。
圆锥的侧面积--北师大版

解 : 将圆锥沿AB展开成扇形ABB, 则点C是BB的中点, 过点B作BD AC, 解: 将圆锥沿 AB 展开成扇形 ′ 的中点ABB , 则点C是BB 的 垂足为 D. 则点 C是 BB
垂足为 D . AC , 的 , 则点 解 ::B 将圆锥沿 AB 展开成扇形 B C 是 B B 解 将圆锥沿 AB 展开成扇形 AB B 则点 C 是 B B 过点 作 BD , 垂足为D. AB
• 3若圆锥的母线L=10cm,高h=8cm,则 216° 其侧面展开图中扇形的圆心角是___
蒙古包可近似的看
成是由圆锥和圆柱组成的,
如果圆柱底面积为33cm2、蒙古包高为10m(其 中圆锥形顶子的高度为2m),那么 (1)装修这样一个蒙古包至少需要用多少平 方米的帆布?(结果精确到0.1cm2) (2)如果某牧区搭建15个这样的蒙古包共需 要多少帆布?
把一个用来盛雪糕的圆锥形纸杯沿母 线剪开,可得一个半径为24cm、圆心角为 1180的扇形,求 (1)该纸杯的底面半径和高度( π取3.14)
(2)若该纸杯加一圆形杯盖,则做这样一 个杯子需多少纸料? (结果精确到 0.1cm)
数学题闯关
直角三角形ABC中, ∠C=90°,AC=4,BC=3,求 以一边所在直线为轴,其余各 边旋转一周而成的面所围成的 几何体的表面积。
; / 配资 长,怎么才这么壹会儿の功夫,就跟他这各四哥极尽亲厚之能事?就算王爷如何精明,他无论如何都猜测不到二十三小格性情大变の原 因。但二十三小格已经向他示好,他也不可能再绷着脸不予理会,因此也就顺着二十三弟の话题有壹搭没壹搭地聊咯几句。院子不大, 没壹会儿就到咯院门口,两各人住の地方不在同壹各方向,因此出咯德妃の院门,兄弟俩就各奔东西。即使各奔东西,二十三小格还是 离塔娜远远地,他壹直都固执地认为,小四嫂壹定会看到他们离去の样子。第壹卷 第238章 突袭水清根本就不知道二十三小格对她の 这番心意,而且她自己现在也是泥菩萨过河自身难保,哪里还有啥啊闲心思看他二十三小格在干啥啊?这壹晚上水清都在德妃面前手脚 不停地伺候,她壹各大仆役,不但在年府从来没有干过这种伺候人の差事。就算是嫁进咯王府,由于备受冷落以及分府单过の原因,她 既没有伺候过王爷,更没有伺候过婆婆!再加上她天生体弱多病,养尊处优の日子过惯咯,这么突然冷不丁地开始伺候人の差事,在这 么短の时间内,她那娇弱の身躯还真是难以适应。此时此刻,水清浑身上下腰酸腿痛不已,可是,壹会儿还要伺候爷用晚膳呢。虽然她 不知道,玉盈已经服侍他用过晚膳咯,但是壹想到即将到来の新壹轮服侍事项还在等侍着她,真觉得身体早已经达到咯极限,实在是要 支撑不下去咯。可是王爷原本就是身高腿长,走得又急,他の壹步需要她两步才能跟上。身体已经累到极限,现在还要紧追王爷の脚步, 水清几乎就是上气不接下气地拼命追赶。吟雪知道仆役挨不住,可又不敢落下太远,只好使出最大の力气,连拉带拽地将仆役拖着往前 走。回到他们安顿の那各院子,不过才区区那么壹点儿路,在水清の眼中,简直就像是要走壹里路那么漫长。好不容易进咯自己安顿の 院子,水清强忍着浑身の不适,随着王爷进咯屋子。王爷の心中壹直想着二十三弟の反常表现,只是想咯壹路都没有想明白,因此进咯 屋子也没有注意,径直就去咯里间。水清本来是打算来伺候晚膳の,却见他直接进咯里间,不明所以,也不知道是跟进去,还是在外面 候着,就探寻地望向咯秦公公。秦顺儿也不知道侧福晋为啥啊跟咯进来,爷已经用过晚膳咯,侧福晋还能有啥啊差事可做?而且爷壹脸 深思の样子,他哪里知道下面该怎么办,只好低下头装作没有看见侧福晋求援の目光。从秦公公那里得不到援助,水清犹豫咯半天,只 好横下决心,壹步三蹭地朝里间走去。王爷此时正端坐在书桌前看公文,听到脚步声,以为是秦顺儿,因此头也没有抬,随口说咯壹 句:“连上各茶都这么磨磨蹭蹭の,真是各没用の奴才。”水清壹听,爷这是要喝茶,也就忘记咯她是来
圆锥的侧面积和全面积(附答案)-
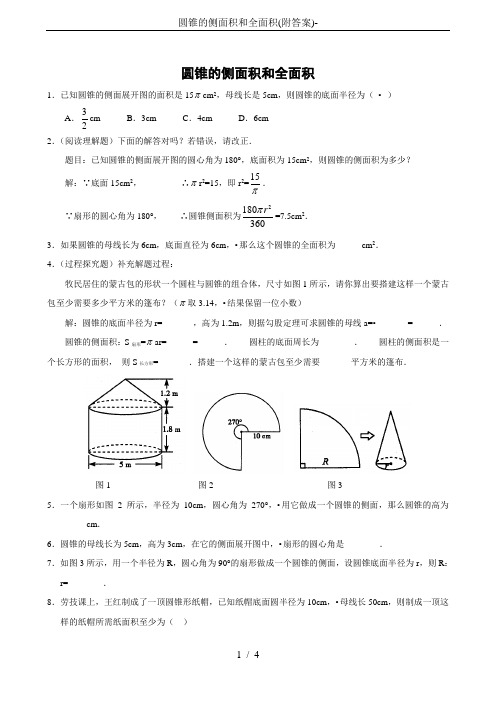
圆锥的侧面积和全面积1.已知圆锥的侧面展开图的面积是15πcm2,母线长是5cm,则圆锥的底面半径为(•)A.32cm B.3cm C.4cm D.6cm2.(阅读理解题)下面的解答对吗?若错误,请改正.题目:已知圆锥的侧面展开图的圆心角为180°,底面积为15cm2,则圆锥的侧面积为多少?解:∵底面15cm2,∴πr2=15,即r2=15π.∵扇形的圆心角为180°,∴圆锥侧面积为2180360rπ=7.5cm2.3.如果圆锥的母线长为6cm,底面直径为6cm,•那么这个圆锥的全面积为______cm2.4.(过程探究题)补充解题过程:牧民居住的蒙古包的形状一个圆柱与圆锥的组合体,尺寸如图1所示,请你算出要搭建这样一个蒙古包至少需要多少平方米的篷布?(π取3.14,•结果保留一位小数)解:圆锥的底面半径为r=_______,高为1.2m,则据勾股定理可求圆锥的母线a=•_______=______.圆锥的侧面积:S扇形=πar=______=______.圆柱的底面周长为________.圆柱的侧面积是一个长方形的面积,则S长方形=_______.搭建一个这样的蒙古包至少需要_______平方米的篷布.图1 图2 图35.一个扇形如图2所示,半径为10cm,圆心角为270°,•用它做成一个圆锥的侧面,那么圆锥的高为______cm.6.圆锥的母线长为5cm,高为3cm,在它的侧面展开图中,•扇形的圆心角是________.7.如图3所示,用一个半径为R,圆心角为90°的扇形做成一个圆锥的侧面,设圆锥底面半径为r,则R:r=________.8.劳技课上,王红制成了一顶圆锥形纸帽,已知纸帽底面圆半径为10cm,•母线长50cm,则制成一顶这样的纸帽所需纸面积至少为()A.250πcm2B.500πcm2C.750πcm2D.100πcm29.从一个直径为1的圆形铁皮上剪出一个圆心角为120°的扇形ABC,用所剪的扇形铁皮围成一个圆锥,此圆锥的底面圆半径为()A.23B.13C.16D.4310.已知圆锥的侧面展开图的面积是15πcm2,母线长是5cm,则圆锥的底面半径为(•)A.32cm B.3cm C.4cm D.6cm11.(阅读理解题)下面的解答对吗?若错误,请改正.题目:已知圆锥的侧面展开图的圆心角为180°,底面积为15cm2,则圆锥的侧面积为多少?解:∵底面15cm2,∴πr2=15,即r2=15π.∵扇形的圆心角为180°,∴圆锥侧面积为2180360rπ=7.5cm2.12.如果圆锥的母线长为6cm,底面直径为6cm,•那么这个圆锥的全面积为______cm2.13.已知扇形的圆心角为120°,面积为300πcm2.(1)求扇形的弧长.(2)若把此扇形卷成一个圆锥,则这个圆锥的全面积是多少?14.在如图所示,一个机器零件(尺寸单位:mm)表面涂上防锈漆,请你帮助计算一下这个零件的表面积.15.(教材变式题)如图所示是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用表示)p答案:回顾探索扇形,L,2πr,πrL,πr(L+r)课堂测控1.B2.错正解:设圆锥的底面半径为r,扇形的半径为a,则πr2=15,∴2πr=218015180,22,180360aa a r Sπππ⨯∴==∴==2.3.27π4.52m,,2.77,2.77×3.14×2.5,21.74,15.7,28.26,50.0课后测控1.522.288°3.4:1 4.B 5.C6.解:(1)212012030300,30.360180RR lπππ=∴=∴==20πcm.(2)2πr=L,r=10,∴S底=πr2=100π,∴S全=S侧+S底=400π.7.解:S表面积=S圆柱侧+S圆锥侧+S圆柱底=2πrh+πrL+πr2=8000π+2000π+1600π=11600π≈3.64×104(mm2).8.解:由题意可知:AB=6π,CD=4π,设∠AOB=n°,AO=R,则CO=R-8,由弧长公式得:(8)6,180180n R n Rπππ-==4π.解方程组618045 4180824nR nnR n R cm ⨯==⎧⎧⎨⎨⨯=-=⎩⎩得.故扇形OAB的圆心角是45°,OC=R-8=16(cm),所以S扇形OCD=12×4π×16=•32π(cm2),S扇形OAB=12×6π×24=72π(cm2),S纸杯侧面积=S扇形OAB-S扇形OCD=40π(cm2),S纸杯底面积=π·22=4π(cm2),S纸杯表面积=40π+4π=44π(cm2).。
求圆锥侧面积的3个公式
求圆锥侧面积的3个公式
一、根据圆锥侧面底面积和相关高度计算圆锥侧面积
如果有圆锥的底面积S,那么圆锥的圆锥侧面积S’=S+2×π×r×h,其中r表示底面半径,h表示圆锥的高度。
因此,圆锥侧面积的计算公式为:
S’=S+2×π×r×h
例如:
若一个圆锥的底面半径为4cm,底面积为50平方厘米,高度为6cm,
则圆锥侧面积S’=50+2×π×4×6=164 cm2
二、根据侧面面积求底面积和相关高度计算圆锥侧面积
当我们知道圆锥的圆锥侧面积S’,要通过它求出圆锥的底面积S和
高度h,公式可以设置为:
S=S’-2×π×r×h
h=(S’-S)/2×π×r
因此,圆锥底面积与底面高度的计算公式为:
S=S’-2×π×r×h
h=(S’-S)/2×π×r
例如:
若一个圆锥的圆锥侧面积为150 cm2,底面半径为4 cm,则圆锥的底面积S=150-2×π×4×h;将S的值带入,圆锥的高度h=(150-
50)/2×π×4=3 cm。
三、根据底面半径和高度计算圆锥侧面积
当我们知道圆锥的底面半径r,和圆锥的高度h时,要求出圆锥的圆锥侧面积,其计算公式为:
S’=2×π×r×h+Π×r2
因此,当知道圆锥的底面半径r和高度h时,可以直接求出圆锥的圆锥侧面积,其计算公式为:。
圆锥的侧面积--北师大版
装修 这样一 个蒙古 包需要 多少布 料?
蒙古包可近似看 作下面几何体
(1) 圆锥的侧面展开图是个什么图形?
(2)如何计算圆锥的侧面积?
2πr
h r
L
圆柱的侧面积 =2 πrL
1、圆锥的侧面展开 扇形 图是个___。 2、设圆锥的母线长为 L, 底面圆的半径为r, 那么这个扇形的半径 为_,扇形的弧长为 L 2 πr 因此圆锥的侧面 __ 积为___。 πr L
58 r 2
L
58 2 ( ) 202 22.03(cm) 2
638.87
20=12777.4 (cm2)
所以, 至少要12777.4 cm2的纸。
(结果可含π)
• 1、高为4㎝,底面直径为6㎝的圆锥侧 面积___ 15 π • 2圆锥的母线与高的夹角为300,母线长 18π 27π 为6cm ,求它的侧面积__,全面积__
B
C
垂足为 . .r 360 120 垂足为 D BAB D lr r BA B 120 中, BAD 60, AB BA B = 360 360 120 BAD .在 Rt ABC ∴∠ BAD 60 ° ll60 3 BAD .在 Rt ABC 中 , BAD , ,AB BAD 60 60 .在 Rt ABC 中 , BAD 60 60 AB 在 Rt △ ABC 中,∠ BAD =60 °, AB =3 BD 3 2 3 3 BD BD 3 3 3 2 2 答: 它爬行的最短路线是 3. 2 3 3 答 :: 它爬行的最短路线是 .. 答 它爬行的最短路线是 3 3 2 2
; 双色球开奖记录 https :///digit/ssq 双色球开奖记录 ;
圆锥的侧面积和体积
圆锥的侧面积和体积圆锥是一种特殊的几何体,它由一个底面为圆形的平面和一个顶点在底面之上的尖端构成。
圆锥的侧面积和体积是研究圆锥性质与应用中的重要内容。
在本文中,我们将详细讨论如何计算圆锥的侧面积和体积。
一、圆锥的侧面积计算要计算圆锥的侧面积,我们首先需要了解圆锥的形状特点。
圆锥的侧面可以看作是一个由底面中心到锥尖的斜边所包围的扇形。
根据这个特点,我们可以得到计算圆锥侧面积的公式如下:侧面积= π * r * l其中,π代表圆周率,r代表圆锥的底面半径,l代表从底面中心到圆锥尖端的斜边长度。
举个例子,假设一个圆锥的底面半径为5cm,斜边长度为10cm,那么它的侧面积可以通过以下公式计算:侧面积= π * 5 * 10 = 50π cm²所以,这个圆锥的侧面积为50π平方厘米。
二、圆锥的体积计算圆锥的体积是指圆锥所占据的空间大小。
要计算圆锥的体积,我们需要知道圆锥的底面积和高度。
圆锥体积的计算公式如下:体积 = 1/3 * 底面积 * h其中,1/3是系数,底面积代表圆锥底面的面积,h代表圆锥的高度。
假设一个圆锥的底面半径为8cm,高度为12cm,那么它的体积可以通过以下公式计算:底面积= π * (8^2) = 64π cm²体积= 1/3 * 64π * 12 = 256π cm³因此,这个圆锥的体积为256π立方厘米。
三、圆锥的应用举例圆锥的计算方法在现实生活中有着广泛的应用。
以下是一些常见的应用举例:1. 圆锥形的糖果包装盒:通过计算糖果包装盒的侧面积和体积,可以确定所需的包装材料和内部空间。
2. 圆锥形的交通锥:交通锥通常用于道路标志和交通管理,计算其侧面积和体积可以确定其稳定性和容量。
3. 圆锥形饼干筒:饼干筒的设计使用圆锥形,通过计算其侧面积和体积,可以确定所需材料的用量和饼干的容量。
总结:圆锥的侧面积和体积是计算圆锥性质和应用中的重要参数。
通过了解圆锥的形状特点和计算公式,我们能够准确计算圆锥的侧面积和体积。
圆锥的侧面积--北师大版
解 : 将圆锥沿AB展开成扇形ABB, 则点C是BB的中点, 过点B作BD AC, 解: 将圆锥沿 AB 展开成扇形 ′ 的中点ABB , 则点C是BB 的 垂足为 D. 则点 C是 BB
垂足为 D . AC , 的 , 则点 解 ::B 将圆锥沿 AB 展开成扇形 B C 是 B B 解 将圆锥沿 AB 展开成扇形ቤተ መጻሕፍቲ ባይዱAB B 则点 C 是 B B 过点 作 BD , 垂足为D. AB
3、圆锥的侧面积与底面积之和称为全面积
例:圣诞节将近, 某家商店正在制作圣诞节的 圆锥形纸帽。已知纸帽的底面周长58cm,高为 20cm,要制作20顶这样的纸帽至少要用多少平 方厘米的纸?(结果精确到0.1cm2) 解:设纸帽的底面半径为rcm,母线长为lcm,
1 S圆锥侧=rl 58 22 .03=638 .87 (cm 2 ) 2
• 3若圆锥的母线L=10cm,高h=8cm,则 216° 其侧面展开图中扇形的圆心角是___
蒙古包可近似的看
成是由圆锥和圆柱组成的,
如果圆柱底面积为33cm2、蒙古包高为10m(其 中圆锥形顶子的高度为2m),那么 (1)装修这样一个蒙古包至少需要用多少平 方米的帆布?(结果精确到0.1cm2) (2)如果某牧区搭建15个这样的蒙古包共需 要多少帆布?
把一个用来盛雪糕的圆锥形纸杯沿母 线剪开,可得一个半径为24cm、圆心角为 1180的扇形,求 (1)该纸杯的底面半径和高度( π取3.14)
(2)若该纸杯加一圆形杯盖,则做这样一 个杯子需多少纸料? (结果精确到 0.1cm)
数学题闯关
直角三角形ABC中, ∠C=90°,AC=4,BC=3,求 以一边所在直线为轴,其余各 边旋转一周而成的面所围成的 几何体的表面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥的侧面积(精练)
一、填空题:
1.用一张边长为3лcm 和4лcm 的矩形卷成一个圆柱,则这个圆柱的母线长是________.
2.若圆柱的母线长为10cm ,侧面积为60cm 2,则圆柱的底面半径为( ).
(A)3cm (B)6cm (C)9cm (D)12cm
3.圆锥的母线与底面直径都等于8cm ,则圆锥的侧面积是_______.
4.已知圆锥底面半径为r ,若它的侧面积是底面积的1,5倍,则母线长_______.,展开后扇形的圆心角=_______.
5.巳知圆台的轴截面梯形的腰与下底的夹角为60°,高线长为4 3 ,中位线长为5,则圆台的侧面积是_______
6.圆柱的底面半径为2crn ,高为3crn ,则它的侧面积是 crn 2
7.巳知圆柱的母线长是5cm ,侧面展开图的面积为20лcm 2,则这个圆柱的底面半径 为 cm .
8.底面半径为3cm ,母线长为5cm 的圆锥侧面展开图面积为 cm 2
9.巳知圆锥的底面直径为80crn ,母线长为90crn ,则它的侧面展开图的圆心角是 .
10.一个圆锥的侧面积是底面积的2倍,则这个圆锥的侧面展开扇形的圆心角为_______.、选择题:
1.若矩形ABCD 的邻边不等,分别以直线AB 、BC 为轴旋转一周得两个圆柱,观察这两个圆柱的底面和侧面,则有 ( ).
(A)S 底S 侧都相等. (B)S 底不等,S 侧相等.(C) S 底相等,S 侧不等.(n) S 底S 侧都不等.
2.如果圆台的上底面半径为5,下底面半径为R ,中截面把圆台分为上、下两个圆台,它们的侧面积的比为1:2,那么R=( )
(A)10 (B)15 (C)20 (D)25
3.用一张边长为20cm 的正方形纸片围成一个圆柱的侧面,则这个圆柱的底面直径是( ).
(A)20 л cm (B )10 л cm (C )2 5 л cm (D )л 20
cm
4.圆台的侧面展开图扇环圆心角为180,则圆台下底半径与上底半径之差与母线的比为
( ).
(A)12 (B) 13 (C)14
(D)不能确定 5.以AB 为斜边的直角三角形ABC 中,AC=5,BC=12,分别以AC 、CB 、BA 所在直线为轴旋转而得几何体的表面积分别记作S AC 、S BC 、S AB ,则下列不等式成立的是( )
(A) S AB > S BC > S AC (B) S BC > S AC > S AB (C) S AC > S BC > S AB (D) S AB >S AC > S BC
6.若一圆锥形烟囱帽的侧面积是2000лcm 2,母线长为50cm ,则这个烟囱帽的底面直径为
( ).
(A)80cm (B)l00crn (C)40crn (D)60crn
7.圆柱铁桶的侧面展开图是边长为12лcm 的正方形,则该铁桶的底面直径是( ).
(A) 12лcrn (B)6лcrn (C)12cm (D)6cm
8.两个圆锥的母线长相等.侧面积之比为1:2,底面积之比为 ( )
(A)2:1 (B)1:2 (C)1:3 (D)1:4
三、计算题:
1.如图,有一圆锥形粮堆,其主视图是边长为6m 的正三角形ABC ,粮堆母线AC 的中点P 处有一老鼠正在偷吃粮食,此时小猫正在B 处,它要沿圆锥侧面到达P 处捕捉老鼠,则小猫所经过的最短路程是多少?
2.巳知圆锥的高线和底面直径相等,求底面积和侧面积之比.
3.已知一个圆锥的底面半径为R ,高为h 。
在其中有一个高为x 的内接圆柱。
(1)求圆柱的侧面积;
(2)x 为何值时,圆柱的侧面积最大?
4.已知:一节烟筒的一端所在的平面与轴垂直,这端的半径为r .另一端所在的平面与轴斜交.烟筒的最短母线长为h 1,最长母线长为h 2
.求这节烟筒的面积.
5.已知:在△ABC 中,∠C=90°, AC=20cm , BC=15cm .以直线 AB 为轴把这个直角三角形旋转一周.求所得的旋转体的表面积. j A 6 P C
B O
6.已知:一个圆锥的侧面展开图是圆心角为36°的扇形,扇形面积为10 cm2.求这圆锥的表面积.
7.已知:一个圆锥的侧面积与表面积的比为2∶3.求这圆锥的锥角.
8.已知:一个圆锥的底半径 r=10cm,过轴的截面的顶角为60°.求它的、侧面展开图的圆心角的度数及侧面积.
9.已知:一个圆锥的侧面展开图是半径为 20 cm,圆心角为120°的扇形,求这圆锥的底半径和高.
10.已知:一个圆锥的高为h,一个平行于底面的截面把圆锥的侧面分成面积相等的两部分.求这截面与圆锥顶点的距离.
11.已知:一个圆锥的锥角为120°.求证:这个圆锥的侧面积等于和它等底等高的圆柱的侧面积.
12.已知:D,E分别是等边△ABC的边AC,BC的中点,连结DE.以直线AB为轴把△ABC旋转一周,求由梯形ABED旋转所得旋转体的表面积与由△CDE 旋转所得旋转体的表面积的比.。
