三角形相似性质
相似三角形的判定及性质

D
ABD EBC,
A
B
DBE ABC. (1)
又EBC ABD, ECB DAB.
E
ABD ∽ CBE.
BE BC .即 BE BD . (2) BD AB BC AB
由(1)(2)及判定定理2知 DBE ∽ ABC.
判定定理3
对于任意两个三角形,如果一个三角形的三条边 和另一个三角形的三条边对应成比例,那么这两 个三角形相似.
简述:三边对应成比例,两三角形相似
已知:如图,在△ABC和△ABC中
AB BC CA AB BC CA
A
求证: △ABC∽△A’B’C’
证明: 在△ABC的边AB(或延长线)上截取 AD=AB,过点D作DE//BC,交AC于点E.
AD DE EA AB BC CA
△ADE∽△ABC
∵ AD=AB
第一讲 相似三角形的判定及有关性质
1.3 相似三角形的判定及性质
复习回顾
相似三角形的定义
对应角相等,对应边成比例的两个三角形叫做 相似三角形.相似三角形对应边的比值叫做相 似比(或相似的系数).
预备定理
平行于三角形一边的直线和其他两边(或两边的 延长线)相交,所构成的三角形与原三角形相似.
判定定理1
求证:(1)AD•BC=BE•AC (2)AH•HD=BH•HE
分析: (1)只要证明Rt△ADC∽Rt△BEC (2)只要证明Rt△AHE∽Rt△BHD
思考:
既然相似三角形中的高,中线,内角平分线, 周长,面积等要素都与相似比有关.
那么,与三角形有关但不在三角形内的 其他元素是否与三角形的相似比有联系呢?
你想到哪些元素?
三角形的外接圆和内接圆
三角形的相似性质与判定

三角形的相似性质与判定三角形作为几何学的基本概念之一,具有许多独特的性质和特点。
其中一个重要的性质就是相似性,它在实际应用中具有广泛的应用价值。
本文将重点讨论三角形的相似性质以及如何判定两个三角形是否相似。
一、相似三角形的定义在谈论相似性质之前,我们首先需要明确相似三角形的定义。
如果两个三角形的对应角度相等,并且对应边之间的比值相等,那么这两个三角形就是相似的。
具体来说,设有两个三角形ABC和DEF。
如果∠A=∠D,∠B=∠E,∠C=∠F,并且AB/DE = AC/DF = BC/EF,那么三角形ABC与三角形DEF是相似的。
二、相似三角形的性质相似三角形具有一系列独特的性质,下面我们将逐一介绍。
1. 边比例性质:如果两个三角形相似,那么它们的对应边之间的比值相等。
例如,在相似三角形ABC和DEF中,我们可以得到AB/DE =AC/DF = BC/EF这一等比例关系。
2. 角度比例性质:如果两个三角形相似,那么它们对应角度之间的比值也相等。
例如,在相似三角形ABC和DEF中,我们可以得到∠A/∠D =∠B/∠E = ∠C/∠F这一等比例关系。
3. 周长比例性质:如果两个三角形相似,那么它们的周长之比等于任意一对对应边的比值。
例如,在相似三角形ABC和DEF中,我们可以得到AB+AC+BC/DE+DF+EF = AB/DE = AC/DF = BC/EF这一等比例关系。
4. 面积比例性质:如果两个三角形相似,那么它们的面积之比等于对应边长平方的比值。
例如,在相似三角形ABC和DEF中,我们可以得到面积(ABC)/面积(DEF) = (AB^2)/(DE^2) = (AC^2)/(DF^2) = (BC^2)/(EF^2)。
三、相似三角形的判定在学习相似三角形时,我们也需要掌握如何判定两个三角形是否相似。
现介绍两种常用的判定方法。
1. AA判定法:如果两个三角形的两对对应角度相等,那么它们是相似的。
相似三角形的性质

实战演练
1、△ABC与△A’B’C’的相似比为2:3,若BC 边上的中线AD=8cm,则B’C’边上的中线 12cm A’D’= .
6cm 2、△ABC与△A'B'C'的相似比为 3:2,若角平分 线A'D'=4cm,则角平分线AD=_____ 。 15cm
3、△ABC与△A'B'C'的相似比为1:3,若BC= 5cm,则B'C'=_____ 。
A / D / B / C /于D / ,
AB 求证: AD k A' D ' A' B '
B 证明:∵△ABC∽△A'B'C' A
A/
D
C
B/
D/ C/
①相似三角形的对应高线之比等于相似比。
∵AD、A'D'分别是△ABC与△A'B'C'的高 ∴∠ADB=∠A'D'B'= 90 AD AB k A' D' A' B' ∴ △ABD∽△A'B'D'
解:设正方形PQMN是符合要求的△ABC的 A 高AD与PN相交于点E。设正方形PQMN的边 长为x毫米。 E N P ∵PN∥BC ∴△APN∽ △ABC AE PN = ∴ C B AD BC Q D M 80–x x = 因此 ,得 x=48(毫米)。答:----。 80 120
例2 如图,在△ABC中,EF∥BC, AE 1 ,S四边形BCFE =8 ,
∵ ΔABC∽ΔAˊBˊCˊ
AB BC CA ∴设 k A`B` B`C ` C `A` ∴
三角形的相似性质
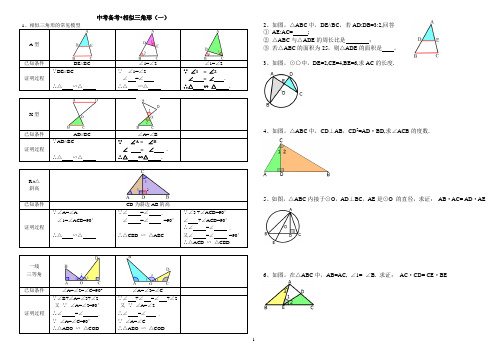
中考备考•相似三角形(一)∠A=∠BA = ∠B= ∠2、如图,△ABC中,DE//BC,若AD:DB=3:2,回答①AE:AC= ;②△ABC与△ADE的周长比是;③若△ABC的面积为25,则△ADE的面积是。
3、如图,⊙○中,DE=2,CE=4,BE=6,求AC的长度.4、如图,△ABC中,CD⊥AB,CD2=AD·BD,求∠ACB的度数.5、如图,△ABC内接于⊙O,AD⊥BC,AE是⊙O 的直径,求证:AB·AC= AD·AE6、如图,在△ABC中,AB=AC, ∠1= ∠B. 求证:AC·CD= CE·BE7、如图,平行四边形ABCD 中,AC 与BD 相交于点D ,E 为OD 上一点(不与O 、D 重合),连接AE 并延长交DC 于点F.若要证明ABDFEB ED =, 则需要证明下列哪一对三角形相似?( ) A 、△EDF ∽△EBA B 、△EDF ∽△DBA8、如图,在△APM 中, AM//NB ,CM//ND.若要证明CACMDB DN =,则需要证明下列哪一对三角形相似?( ) A 、△PDN ∽△PCM B 、△BDN ∽△ACM C 、△AMC ∽△APM9、如图,在矩形ABCD 中,E 为BC 上一点,DF ⊥AE 于F ,求证CD ·BC=AE ·DF. ①若将CD ·BC=AE ·DF 转化为比例式,下列转化正确的是( ) BC AE DF CD A =、 DF BCAE CD B =、②将CD ·BC=AE ·DF 中的线段进行等量代换,下列等量代换最有助于解决问题的是( )A 、把CD 换成AB B 、把BC 换成ADC 、把CD 换成AB ,把BC 换成AD③请写出CD ·BC=AE ·DF 的证明过程.10、如图,Rt △ABC 中,∠ACB=90°,O 为斜边AB 的中点,D 是BC 上的一点,连接OC 、AD ,如果OC ⊥AD ,求证: AB ·CD=AC ·AD.11、如图,已知EC//AB ,∠1=∠2.①求证: 四边形ABCD 是平行四边形; ②求证: OA 2=OE ·OF.。
三角形相似的性质

三角形相似的性质在数学的奇妙世界中,三角形相似是一个重要且有趣的概念。
当两个三角形的形状相同但大小可能不同时,我们就说它们是相似的。
而三角形相似具有一系列独特而实用的性质,这些性质在解决各种几何问题以及实际生活中的测量和计算中都发挥着关键作用。
首先,相似三角形的对应角相等。
这意味着如果两个三角形相似,那么它们对应的三个角的度数是完全一样的。
比如说,一个三角形的三个角分别是 30°、60°和 90°,那么与它相似的三角形的对应角也必然是 30°、60°和 90°。
这个性质是相似三角形最基本也是最直观的特征。
其次,相似三角形的对应边成比例。
假设我们有两个相似三角形,它们的对应边分别为 a、b、c 和 A、B、C。
那么就存在这样的比例关系:a/A = b/B = c/C 。
这个比例关系是解决很多与相似三角形相关的边长计算问题的关键。
例如,已知一个三角形的三条边分别为 3、4、5,另一个与其相似的三角形的一条边为 6,那么通过对应边成比例的性质,我们可以很容易地求出另外两条边的长度。
不仅如此,相似三角形的周长之比等于相似比。
相似比就是指两个相似三角形对应边的比值。
假设两个相似三角形的相似比为 k,它们的周长分别为 L1 和 L2 ,那么 L1/L2 = k 。
这一性质让我们在已知相似比的情况下,可以快速地求出两个相似三角形周长之间的关系。
相似三角形的面积之比等于相似比的平方。
这是一个非常重要的性质。
假设两个相似三角形的相似比为m,它们的面积分别为S1 和S2 ,那么 S1/S2 = m²。
比如说,如果两个相似三角形的相似比为 2,那么它们的面积比就是 4 。
通过这个性质,我们可以在已知相似比的情况下,计算出两个相似三角形面积的比例关系,从而解决很多与面积相关的问题。
在实际应用中,三角形相似的性质有着广泛的用途。
比如在测量物体的高度时,如果我们无法直接测量,就可以利用相似三角形的性质来间接计算。
相似三角形的性质

的对应高AD和A'D'. 则∠ADB =∠A'D'B'. ∵△ABC∽△A'B'C' ∴∠B=∠B'
∴△ABD∽△A'B'D'
AD AB k A' D' A' B'
BD
A' B' D'
C
C'
通过前面的思考、探索、推理,我们得到 相似三角形有如下性质;
相似三角形对应高的比等于相似比。
三、例题讲解
例:如图,已知AB=4,A‘B' =8,AC=3, A‘C' =6,∠A=∠A′,求C'D'
A′
D′
Байду номын сангаас
B′
C′
A D
B
C
四、例题讲解
▪ 1.已知两个三角形的相似比是1:5,则这 两个三角形对应高的比是( )。
▪ 2.如图,已知△ABC∽ △A'B'C',且AD 、 BE是△ABC的高, A'D' 、B‘E'是△ A'B'C' 的高。求证:AD· B‘E' = A'D' ·BE
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
探相究似三1--角-高形线对应高的比等于相似比.
性质1:相似三角形对应高的比等于相似比
如果两个三角形相似,那么它们对应高的比等于相似比。
已知:如图,△ABC∽△A‘B’C‘,相似比为k。
求证:它们对应高等于相似比。
A
如图,分别作△ABC和△A'B'C'
相似三角形的性质
相似三角形的性质【知识梳理】判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
(简述为:两角对应相等,两三角形相似)判定定理2:如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。
(简述为:两边对应成比例且夹角相等,两三角形相似)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
(简述为:三边对应成比例,两三角形相似)【例题精讲】1、如图,∠ABD=∠C,AD=2, AC=8,求AB。
2、如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=172,求AD的长。
3、一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米,此时一棵水衫树的影长为10.5米,这棵水衫树高为( )A.7.5米 B.8米 C.14.7米 D.15.75米4、如图是一面镜子,则有__ _∽__ __。
(第4题) (第5题)5、如图,某测量工作人员眼睛A 与标杆顶端F 、电视塔顶端E 在同一直线上,已知此人眼睛距地面1.6米,标杆高为3.2米,且BC =1米,CD =5米,求电视塔的高ED 。
A 【夯实基础】1.如图所示,矩形ABCD ,E 、F 分别为CD 、BC 上的点,且∠AEF=90°,则一定有( ) A .△ADE ∽△ECF B .△AEF ∽△ABF C .△EFC ∽△AFE D .△ADE ∽△AEF2.如图,已知ABC ∆,P 是边AB 上的一点,连结CP ,以下条件中不能判定ABC ACP ∆∆~的是( ) A 、B ACP ∠=∠ B 、ACB APC ∠=∠ C 、AC 2=AP •AB D 、BCABCP AC =APBC3.已知:如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出ABP∆与ECP∆相似的是()A、EPCAPB∠=∠ B、90=∠APE C、P是BC的中点 D、BP:BC=2:34.ABC∆中,D是AB上一个固定点,E是AC上的一个动点.若使ADE∆与ABC∆相似,则这样的点E有() A、1个 B、2个 C、3个 D、很多5.如图,若点D为ABC∆中AB边上一点,且ACDABC∠=∠,AD=2cm,BC=4cm,则AC的长为()A、12cmB、22cmC、3cmD、2cm6.下列说法①所有等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的两个等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是()A.②,④ B.①,③ C.①,②,④ D.②,③,④7.△ABC中,D是AB上一固定点,E是AC上的一个动点,若使△ADE与△ABC相似,则这样的点E有()。
相似三角形的性质
E
C
归纳:相似三角形对应边上的中线比等于相似比。
说说你判断的理由是什么? △A E C ∽△A′E′C′ ___________
相似三角形对应角的角平分线有什么 关系呢?
如右图△A B C , AF为 ∠ A 的角平分线。 则:(1)把三角形扩大2倍后得△A′B′C′,A′ F′ 为∠ A′的角平分线, △A B C 与 B′ △A′B′C′的相似比为多少? AF 与A′ F′比 是多少? B (2)如右图两个相似三角形相似比为 k,则对应角的角平分线比是多少? 说说你判断的理由是什么? △ A F C ∽△A′F′C′ ___________ A′ A F′ F C C′
课本探究过程
[小问题·大思维] 两个相似三角形的内切圆的直径比、周长比、面积比 与相似比之间又有什么关系? 提示:相似三角形内切圆的直径比、周长比等于相似
比,内切圆的面积比等于相似比的平方.
已知两个三角形相似,请完成下列表格
相似比
周长比
2 2
4
1 3
2
2
1 3
1 9
面积比
2
10 10 100
2 2
课堂练习(2)
6、如图,已知DE∥BC ,BD=3AD,S△ABC =48 ,求:△ADE的面积。
解:因为DE∥BC 所以∠ADE=∠ABC, ∠AED=∠ACB
所以△A DE ∽△ABC 又因为BD=3AD 可得相似比k=AD:AB=1:2 所以S△ADE =1/4 S△ABC =12 BACK
归纳:相似三角形对应角的角平分线之比等于相似比。
相似三角形的周长有什么关系呢?
右图(1)(2)(3)分别是 边长为1、2、3的等边三角形, 它们都相似.
三角形的相似性质
三角形的相似性质相似性质是指两个或更多个几何图形在形状上相似的特征。
在三角形中,相似性质是十分重要的,它们可以帮助我们推导出许多有用的结论和定理。
本文将重点讨论三角形的相似性质,并通过示例来说明这些性质的应用。
在我们讨论相似性质之前,先来了解一下什么是相似三角形。
在平面几何中,如果两个三角形的对应角度相等,并且对应边长度成比例,那么这两个三角形就是相似的。
在相似三角形中,对应边角度相等,而且对应边长度之间的比例关系是恒定的。
首先,让我们看一下相似三角形的比例关系。
给定两个相似三角形ABC和DEF,它们的对应边分别为AB、AC、BC和DE、DF、EF。
那么,我们可以得到以下比例关系:AB/DE = AC/DF = BC/EF这个比例关系相当重要,因为它可以帮助我们计算出未知边长。
例如,如果我们知道一个三角形的相似三角形和已知边长的比例关系,我们可以通过求解类比方程来计算出未知边长的长度。
接下来,我们来探讨一些与相似三角形有关的定理和性质。
首先,我们谈谈“AAA相似性质”,即如果两个三角形的三个内角分别相等,那么这两个三角形就是相似的。
通过这个性质,我们可以在已知两个三角形的三个内角相等的情况下,得出它们的比例关系。
其次,我们来看看“SSS相似性质”,即如果两个三角形的三条边分别成比例关系,那么这两个三角形就是相似的。
这个性质在计算中尤为重要,因为我们可以通过已知三角形边长比例得出两个三角形之间的比例关系。
除了这些基本的相似性质外,我们还可以利用相似三角形推导出一些有用的结论,例如比例定理和角平分线定理。
比例定理指出,在一个三角形中,如果一条直线平行于另外两条边,那么它把这两条边分成的段与原三角形的相似成比例。
利用这个定理,我们可以解决一些实际问题,比如测量高楼的高度或者计算影子的长度。
最后,我们来看看相似三角形在解决实际问题中的应用。
相似三角形的性质可以帮助我们计算难以测量的距离、高度和长度。
例如,通过测量地面上一点和天空中该点的两个不同角度,我们可以利用相似三角形的性质计算出天空中该点的高度。
相似三角形的性质
注意相似三角形的判定条件,如 两角对应相等、三边对应成比例
等。
构造相似三角形辅助线技巧
熟练掌握常见辅助线的构造方法,如 平行线、垂线、角平分线等。
通过构造辅助线,将复杂图形转化为 简单图形,便于求解。
根据题目条件和图形特点,灵活选择 构造辅助线的方式。
复杂图形中找寻相似关系策略
对于复杂图形,应首先观察其整体结构 和特点。
通过相似比计算
如果已知两边成比例的比例系数,可以 通过计算得出第三边的长度,从而证明 两个三角形相似。
三边对应成比例证明
利用已知条件
已知三边对应成比例,根据相似三角形的判定条件,可以直接得出两个三角形 相似。
通过比例系数计算
如果已知三边对应成比例的比例系数,可以通过计算得出各个角的度数或对应 边上的高等,从而进一步证明两个三角形相似。
解析
根据相似三角形的判定条件,证明两角对应相等即可。首先,由于∠BAC=90°,所以 ∠BAD+∠CAD=90°;又因为AD⊥BC,所以∠ADB=90°,从而∠BAD+∠ABD=90°。因此, ∠ABD=∠CAD,加上公共角∠ADB=∠CDA=90°,根据AA相似判定条件,可得△ABD∽△CAD。
05பைடு நூலகம்
实际生活中相似三角形现象解释
地图比例尺
地图上的比例尺就是利用了相似 三角形的原理,通过比例尺可以 计算出地图上任意两点之间的实
际距离。
摄影构图
在摄影构图中,摄影师经常利用相 似三角形的原理来安排景物的位置, 营造出和谐、美观的画面。
建筑设计
在建筑设计中,设计师需要考虑建 筑物的比例和尺度,利用相似三角 形的原理可以设计出更加美观、协 调的建筑。
培养跨学科思维
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形相似性质
三角形相似性质:
1.相似三角形对应角相等,对应边成比例;
2.相似三角形的一切对应线段的比等于相似比;
3.相似三角形周长的比等于相似比;
4.相似三角形面积的比等于相似比的平方;
5.相似三角形内切圆、外接圆的直径比和周长比都和相似比相同,且内切圆、外接圆面积比是相似比的平方。
三个角分别相等,三条边成比例的两个三角形叫做相似三角形。
相似三角形的判定方法:
1、两角分别对应相等的两个三角形相似。
2、两边成比例且夹角相等的两个三角形相似。
3、三边成比例的两个三角形相似。
4、有一个顶角或底角相等的两个等腰三角形都相似。
