2014年4月8矩形性质_公开课
华师大版八年级数学下册第十九章《矩形的性质》公开课课件

∵AC,BD是矩形ABCD的对角线 ∴AC=BD,OA=OC,OB=OD
矩形特征 A
D
O
B
C
对边 平行(共性)
(1)边:
相等 (共性)
邻边:互相垂直(个性)
(2)角:四个角都是直角 (个性)
(3)对角线:
互相平分 相等
(共性) (个性)
典例精析
例1 已知:矩形ABCD的两条对角线相交于点0, ∠AOD=120°, AB=4cm, 求矩形对角线的长.
谢谢观赏
You made my day!
我们,还在路上……
古来一切有成就的人,都很严肃地对待自己 的生命,当他活着一天,总要尽量多劳动, 多工作,多学习,不肯虚度年华,不让时间
白白地浪费掉。 —— 邓拓
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年3月29日星期二2022/3/292022/3/292022/3/29 •书籍是屹立在时间的汪洋大海中的灯塔。2022年3月2022/3/292022/3/292022/3/293/29/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/3/292022/3/29March 29, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
电脑显示器
实质上: 矩形是特殊的平行四边形。
四边形、平行四边形、矩形
矩形 平行四边形 四边形
想一想:
矩形是轴对称图形吗?是中心对称图形吗?
是
是
对称轴有几条?
两条
矩形有何特征?
矩形特征1: 矩形的四个角都是直角
湘教版八年级数学下册第二章《矩形的性质》公开课课件

因此点B和点C关于直线EF对称,点A和点D关于 直线EF对称,从而在关于直线EF的轴反射下,矩形 ABCD的像与它自身重合,因此矩形ABCD是轴对称 图形,直线EF是矩形ABCD的一条对称轴.
类似地,过点O作直线MN⊥AB,且分别与边 AB,DC相交于点M,N,则点M,N分别是边AB,
DC的中点,直线MN是矩形ABCD的一条对称轴.
动脑筋
如图2-42,四边形ABCD为矩形,那么对角 线AC与DB相等吗?
图2-42
如图,四边形ABCD是矩形,
于是有 AB=DC, ∠CBA=∠BCD=90° ,
BC=CB.
因此 △CBA≌△BCD. (SAS)
从而
AC=BD.
即矩形的对角线相等.
图2-42
结论
由此得到矩形的性质: 矩形的对角线相等.
有一个角是直角的平行四边形叫做矩形, 也称为长方形.
平行四边形 有一个角是直角 矩形
结论
可以知道:
矩形的四个角都是直角,对边相等, 对角线互相平分.
结论
由于矩形是平行四边形,因此
矩形是中心对称图形,对角线的交点是它的 对称中心.
•1、人才教育不是灌输知识,而是将开发文化宝库的钥匙,尽我们知道的交给学生。 •2、一个人的知识如果只限于学校学习到的那一些,这个人的知识必然是十分贫乏的2021/10/152021/10/152021/10/1510/15/2021 3:41:15 PM •3、意4、智力教育就是要扩大人的求知范围 •5、最有价值的知识是关于方法的知识。 •6、我们要提出两条教育的诫律,一、“不要教过多的学科”;二、“凡是你所教的东西,要教得透彻”2021年10月2021/10/152021/10/152021/10/1510/15/2021 •7、能培养独创性和唤起对知识愉悦的,是教师的最高本领2021/10/152021/10/15October 15, 2021 •8、先生不应该专教书,他的责任是教人做人;学生不应该专读书,他的责任是学习人生之道。2021/10/152021/10/152021/10/152021/10/15
矩形的判定 公开课一等奖课件

2、 如图,在 ABCD中,对角线AC,BD
相交于点O,且OA=OD,
(1)证明四边形ABCD是矩形.
(2)若∠OAD=50°,求∠OAB的度数.
D
C
O
A
B
例题展示
3、已知如图四边形ABCD中,AB⊥BC,
AD∥BC,AD=BC,试说明四边形
ABCD是矩形。
A
D
证明:∵ AD=CB ,AD∥CB
A
D
∵四边形ABCD是平行
四边形,且∠B=90°
┐
∴四边形ABCD是矩形
B
C
方案展示
方案二:测量出三个内角的度数,如果三个内角
都是直角,则门是矩形。
有一个角是直角 ┐
有两个角是直角 ┐
有三个角是直角 ┐
猜想:有三个角是直角的四边形是矩形.
┐┐
┐
验 八证年级 猜数学想
第十九章 四边形
有三个角是直角的四边形是矩形.
如图,△ABC中,点O是AC边上一个动点,过点O
作直线a∥BC,设a交∠ACB的平分线于点E, 交
∠ACB的外角平分线于点F.
A
(1)求证:EO=FO;
(2)当点O运动到何处时,
四边形AECF是矩形.
a E
OF
B
CD
本矩节形课的我判们定学方习法了方什法么:内容,你能总结吗?
四边形
平行四边形
三个 直角
1、如图,平行四边形ABCD中,AB= 6,
BC= 8,AC= 10 ,
求证 : 四边形ABCD是矩形。
A
D
证明:∵AB=6,BC=8,AC=10
∴62+82=100
矩形的性质和判定公开课教案
二:小组学习:
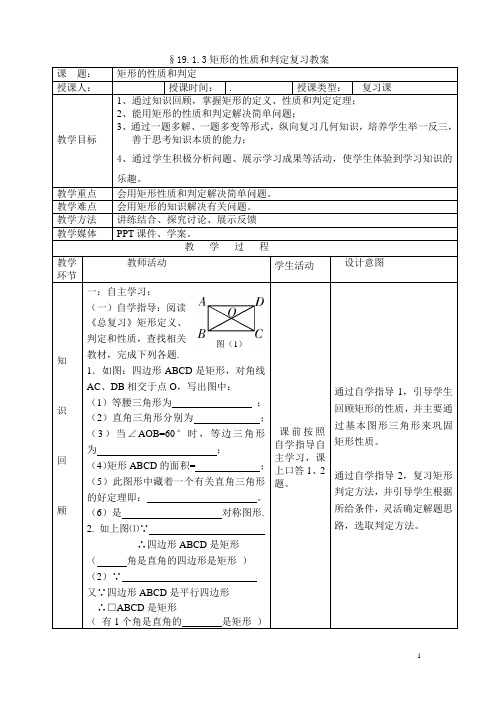
例:如图1,在△ABC中,AB=AC,P为BC上的一动点,过点P作PD⊥AB,PE⊥AC垂足分别为D,E。CF为AB边上的高线。求证:PD+PE=CF。
证法1(截长法)如图1-1,过点P作
PH⊥FC于点H
容易证明四边形DPHF是矩形。
∴PD=FH
也容易证得
Rt△PEC≌Rt△CHP,
容易证得四边形DGCF是矩形.
∴FC=DG=PD+PG.
∴CG∥AB.
∴∠PCG=∠B=∠ACP.
∴Rt△PGC≌Rt△PEC.
∴PG=PE.
∴FC=PD+PE
三:展示反馈
(大胆亮出你的风采,将你的成果和大家分享)
四:拓展延伸(你是最棒的!)
变式1如图2,在△ABC中,AB=AC,点P在BC的延长线上,过点P作PE⊥AC,交AC延长线于E点,过点P作PD⊥AB于点D,CF是AB边上的高线。那么PD,PE和CF存在什么关系?写出你的猜想并加以证明。
§19.1.3矩形的性质和判定复习教案
பைடு நூலகம்课题:
矩形的性质和判定
授课人:
授课时间:
.
授课类型:
复习课
教学目标
1、通过知识回顾,掌握矩形的定义、性质和判定定理;
2、能用矩形的性质和判定解决简单问题;
3、通过一题多解、一题多变等形式,纵向复习几何知识,培养学生举一反三,善于思考知识本质的能力;
4、通过学生积极分析问题、展示学习成果等活动,使学生体验到学习知识的乐趣。
梳理内容,
点拨方法
变式2如图3,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上的一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别为E,F,G。
2014年北师大九年级上1.2矩形的性质与判定(一)课件

第七环节:反思交流,反馈提高
1.本节课你学到了什么?
(1)矩形定义 (2)矩形的性质 (3)直角三角形的性质 (4)矩形的一条对角线把矩形分成两个全等 的直角三角形;两条对角线把矩形分成两对全 等的等腰三角形。因此,矩形的问题可化为直 角三角形或等腰三角形的问题来解决。
自我检测。
(1)下列说法错误的是( ).
问题3:矩形具有而一般平行四边形不具有的 性质是 ( ) A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
第五环节:建构新知,发展问题
问题1: (1) 矩形的两条对角线可以把矩 形分成几个直角三角形? (2)在直角三 角形ABC中,你能找到它的一条特殊线段 吗? (3)你能发现它有什么特殊的性质 吗? (4)你能借助于矩形加以证明吗?
结论 矩形的性质定理1: 矩形的四个角都是直角. 矩形的性质定理2: 矩形的对角线相等.
第三环节:层层递进,推理论证
已知:如图,四边形ABCD是矩形,∠ABC=90° 对角线AC与DB相交于点O。 求证(1)∠ABC=∠BCD=∠CDA=∠DAB=90° (2) AC=BD
第四环节:乘胜追击,完善性质
1 2
1 2
证明:∵四边形ABCD是矩形, ∴ AC=BD(矩形的对角线相等) OA=OC= AC,OB=OD= BD, ∴OA=OD。 ∵∠AOD=120°, ∴∠ODA=∠OAD= (180°-120°) = 30°。 又∵∠DAB=90°(矩形的四个角都是直角 ) ∴BD=2AB=2×2.5=5.
问题1:请同学们拿出准备好的矩形纸片,折 一折,观察并思考。
(1)矩形是不是中心对称图形? 如果是,那 么对称中心是什么? (2)矩形是不是轴对称图形?如果是,那么 对称轴有几条?
矩形性质+判定(公开课2课时合一)
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
《矩形》word版 公开课一等奖教案 (3)
当我们在日常办公时,经常会遇到一些不太好编辑和制作的资料。
这些资料因为用的比较少,所以在全网范围内,都不易被找到。
您看到的资料,制作于2021年,是根据最新版课本编辑而成。
我们集合了衡中、洋思、毛毯厂等知名学校的多位名师,进行集体创作,将日常教学中的一些珍贵资料,融合以后进行再制作,形成了本套作品。
本套作品是集合了多位教学大咖的创作经验,经过创作、审核、优化、发布等环节,最终形成了本作品。
本作品为珍贵资源,如果您现在不用,请您收藏一下吧。
因为下次再搜索到我的机会不多哦!6.1 矩形教学目标:1、经历矩形的判定定理的发现过程;2、掌握矩形的判定定理“有三个角是直角的四边形是矩形”;3、掌握矩形的判定定理“对角线相等的平行四边形是矩形”。
教学重点和难点:教学重点:矩形的判定教学难点:判定定理“对角线相等的平行四边形是矩形”的证明。
教学过程:一、复习引入1、复习提问:矩形的对边有什么性质?角呢?对角线呢?(学生口答)2、提问:要判断一个四边形是矩形目前我们有什么方法?在学生的回答后,引入新课—6.2 矩形(2)二、讲解新课1、“合作学习”提问:(1)命题“矩形的四个角都是直角”的逆命题是什么?是真命题还是假命题?要判定一个四边形四边形矩形只要说明几个角是直角?为什么?(2)工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的对角线是否相等。
你知道这是为什么吗?学生讨论回答,在学生回答后引导学生得出:要判断一个四边形是不是矩形,除了利用矩形的定义外,还有以下两个定理:定理1、有三个角是直角的四边形是矩形;AC定理2、对角线相等的四边形是矩形。
2、矩形判断定理的证明(1)证明定理1教师做启发性提问:①定理的条件是什么?结论是什么?②在没有这个判定定理以前,我们要证明一个四边形是矩形,只能根据什么方法来证明?③因此证明这个定理应该先证明什么?再证明什么?教师在学生回答后,让学生自己独立的完成证明。
《矩形》word版 公开课一等奖教案 (4)
当我们在日常办公时,经常会遇到一些不太好编辑和制作的资料.这些资料因为用的比拟少,所以在全网范围内,都不易被找到.您看到的资料,制作于2021年,是根据最|新版课本编辑而成.我们集合了衡中、洋思、毛毯厂等知名学校的多位名师,进行集体创作,将日常教学中的一些珍贵资料,融合以后进行再制作,形成了本套作品.本套作品是集合了多位教学大咖的创作经验,经过创作、审核、优化、发布等环节,最|终形成了本作品.本作品为珍贵资源,如果您现在不用,请您收藏一下吧.因为下次再搜索到我的时机不多哦!6.1 矩形一.教学目标:1 )了解矩形的定义2 ) 通过学生探索来发现矩形对角线的性质3 )探索并掌握矩形判定的常用条件4 )矩形性质与判定的简单应用二.教学重点为:掌握矩形的性质与常用判定条件并能简单应用三.教具:四边形模型 ,三角板 ,投影片四.教学过程:1.引入:把平行四边形的一个内角变化 (使它等于直角 )矩形定义2.演示平行四边形活动框 ,观察两条对角线长度的变化情况(分∠A为锐角、钝角、直角 )矩形性质:矩形的对角线相等 ,四个角都是直角 (出示符号语言 )3.问题:假设平形四边形的对角线相待 ,那么它是矩形吗 ?(由学生分析 )矩形判定:对角线相等的平行四边形是矩形 (出示符号语言 )4.矩形是轴对称图形吗 ?如果是 ,它有几条对称轴 ?5.课堂练习:1 )填空、选择 (略 )2 )如图一个平行四边形纸片*所得图形是什么四边形 ?为什么 ?*求原平行四边形的面积 (学生分组讨论、生答复)3 ) 在矩形ABCD中 ,AC ,BD相交于O ,AC=6 ,∠BOC =1200*求∠ACB*求AB ,BC的长度(师与生共同分析、师板书 )4) :如图OC在Rt∠AOB内 ,点D在OC上 ,DE⊥OA ,E是垂足 ,点F在OB上 ,且∠ODF=∠DOE ,连结EF问:OD、EF有怎样关系 ?简单说明理由(师生共同分析完成、生板书 )五.课后小结:由学生谈谈 (略 )六.作业 (略 )本课教学反思本节课主要采用过程教案法训练学生的听说读写.过程教案法的理论根底是交际理论,认为写作的过程实质上是一种群体间的交际活动,而不是写作者的个人行为.它包括写前阶段,写作阶段和写后修改编辑阶段.在此过程中,教师是教练,及时给予学生指导,更正其错误,帮助学生完成写作各阶段任务.课堂是写作车间, 学生与教师, 学生与学生彼此交流, 提出反应或修改意见, 学生不断进行写作, 修改和再写作.在应用过程教案法对学生进行写作训练时, 学生从没有想法到有想法, 从不会构思到会构思, 从不会修改到会修改, 这一过程有利于培养学生的写作能力和自主学习能力.学生由于能得到教师的及时帮助和指导,所以,即使是英语根底薄弱的同学,也能在这样的环境下,写出较好的作文来,从而提高了学生写作兴趣,增强了写作的自信心.这个话题很容易引起学生的共鸣,比拟贴近生活,能激发学生的兴趣, 在教授知识的同时,应注意将本单元情感目标融入其中,即保持乐观积极的生活态度,同时要珍惜生活的点点滴滴.在教授语法时,应注重通过例句的讲解让语法概念深入人心,因直接引语和间接引语的概念相当于一个简单的定语从句,一个清晰的脉络能为后续学习打下根底.此教案设计为一个课时,主要将安妮的处境以及她的精神做一个简要概括,下一个课时那么对语法知识进行讲解.在此教案过程中,应注重培养学生的自学能力,通过辅导学生掌握一套科学的学习方法,才能使学生的学习积极性进一步提高.再者,培养学生的学习兴趣,增强教案效果,才能防止在以后的学习中产生两极分化.在教案中任然存在的问题是,学生在"说〞英语这个环节还有待提高,大局部学生都不愿意开口朗读课文,所以复述课文便尚有难度,对于这一局部学生的学习成绩的提高还有待研究.。
