回归分析同步练习
高中数学人教A版选修(1-2) 1.1 同步练习 《回归分析的基本思想及其初步应用》(人教A版)

《回归分析的基本思想及其初步应用》同步练习1. 在画两个变量的散点图时,下面哪个叙述是正确的()(A)预报变量在x轴上,解释变量在y轴上(B)解释变量在x轴上,预报变量在y轴上(C)可以选择两个变量中任意一个变量在x轴上(D)可以选择两个变量中任意一个变量在y轴上2. 两个变量y与x的回归模型中,通常用R2来刻画回归的效果,则正确的叙述是()A. R2越小,残差平方和小B. R2越大,残差平方和大C. R2与残差平方和无关D.R2越小,残差平方和大3. 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )A.总偏差平方和B.残差平方和C.回归平方和D.相关指数R21. 在分析两个分类变量之间是否有关系时,常用到的图表有 。
2. 在残差分析中,残差图的纵坐标为________________。
3. 设某大学的女生体重y (单位:kg)与身高x (单位:cm)具有线性相关关系。
根据一组样本数据(x i ,y i )(i =1,2,…,n ),用最小二乘法建立的回归方程为y ^=0.85x -85.71,则下列结论中正确的是________(填序号)。
(1)y 与x 具有正的线性相关关系;(2)回归直线过样本点的中心(x ,y );(3)若该大学某女生身高增加1 cm ,则其体重约增加0.85 kg ;(4)若该大学某女生身高为170 cm ,则可断定其体重必为58.79 kg.4. 下列有关线性回归的说法,不正确的是________(填序号)。
①自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系;②在平面直角坐标系中用描点的方法得到表示具有相关关系的两个量的一组数据的图形叫做散点图;③线性回归方程最能代表观测值x ,y 之间的关系;④任何一组观测值都能得到具有代表意义的回归直线方程。
在回归分析中,通过模型由解释变量计算预报变量的值时,应注意什么问题?答案和解析一、选择题1.B ;【解析】通常把自变量x 称为解析变量,因变量y 称为预报变量。
高中数学选修2-3同步练习题库:回归分析的基本思想及其初步应用(选择题:一般)

回归分析的基本思想及其初步应用(选择题:一般)1、已知变量成负相关,且由观测数据算得样本平均数,,则由该观测数据算得的线性回归方程可能是( ) A .B .C .D .2、若对于变量的取值为3,4,5,6,7时,变量对应的值依次分别为4.0,2.5,-0.5,-1,-2;若对于变量的取值为1,2,3,4时,变量对应的值依次分别为2,3,4,6,则变量和,变量和的相关关系是( ) A .变量和是正相关,变量和是正相关 B .变量和是正相关,变量和是负相关 C .变量和是负相关,变量和是负相关 D .变量和是负相关,变量和是正相关3、下列关于回归分析的说法中错误的是( ) A .回归直线一定过样本中心B .残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适C .两个模型中残差平方和越小的模型拟合的效果越好D .甲、乙两个模型的分别约为0.98和0.80,则模型乙的拟合效果更好4、某商品的售价(元)和销售量(件)之间的一组数据如下表所示:价格(元) 销售量(件)由散点图可知,销售量与价格之间有较好的线性相关关系,且回归直线方程是,则实数 ( ) A.B.C.D.5、若关于的线性回归方程是由表中提供的数据求出,那么表中的值为( )3 4 5 634 A.B. C.D.6、四名同学根据各自的样本数据研究变量之间的相关关系,并求得回归直线方程,分别得到以下四个结论: ①与负相关且. ②与负相关且 ③与正相关且④与正相关且其中一定不正确的结论的序号是( )A .①②B .②③C .③④D .①④7、已知的取值如下表:( )0 1, 2 3 41 1.3 3.2 5.6 8.9若依据表中数据所画的散点图中,所有样本点都在曲线附近波动,则( )A. 1B.C.D.8、已知的取值如下表:( )0 1, 2 3 4 1 1.3 3.2 5.6 8.9若依据表中数据所画的散点图中,所有样本点都在曲线附近波动,则( )A. 1B.C.D.9、两个变量与的回归模型中,分别选择了4个不同模型,对于样本点,,…,,可以用来刻画回归的效果,已知模型1中,模型2中,模型3中,模型4中,其中拟合效果最好的模型是( )A .模型1B .模型2C .模型3D .模型410、根据如下样本数据得到的回归方程为,若,则每增加1个单位,就( )A .增加0.9个单位B .减少0.9个单位C .增加1个单位D .减少1个单位11、对具有线性相关关系的变量,有一组观测数据(),其回归直线方程是,且,则实数的值是( )A .B .C .D .12、工人月工资(元)关于劳动生产率x(千元)的回归方程为,下列说法中正确的个数是()①劳动生产率为1000元时,工资为730元;②劳动生产率提高1000元,则工资提高80元;③劳动生产率提高1000元,则工资提高730元;④当月工资为810元时,劳动生产率约为2000元.A.1 B.2 C.3 D.413、两个变量与的回归模型中,分别选择了个不同模型,它们对应的的值如下,其中拟合效果最好的模型是()A.模型对应的 B.模型对应的C.模型对应的 D.模型对应的14、如表为某公司员工工作年限x(年)与平均月薪y(千元)对照表.已知y关于x的线性回归方程为,则下列结论错误的是()x 3 4 5 6 y 2.5 t 4 4.5A. 回归直线一定过点(4.5,3.5)B. 工作年限与平均月薪呈正相关C. t的取值是3.5D. 工作年限每增加1年,工资平均提高700元15、已知的取值如下表所示x 0 1 3 4 y 2.2 4.3 4.8 6.7从散点图分析y与x的线性关系,且,则A. 2.2B. 2.6C. 3.36D. 1.9516、在线性回归模型y=bx+a+e中,下列说法正确的是()A.y=bx+a+e是一次函数B.因变量y是由自变量x唯一确定的C.因变量y除了受自变量x的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e的产生D.随机误差e是由于计算不准确造成的,可以通过精确计算避免随机误差e的产生.17、下列命题中:①线性回归方程必过点;②在回归方程中,当变量增加一个单位时,平均增加5个单位;③在回归分析中,相关指数为0.80的模型比相关指数为0.98的模型拟合的效果要好;④在回归直线中,变量时,变量的值一定是-7.其中假命题的个数是 ( )A.1 B.2 C.3 D.418、某商场为了了解毛衣的月销售量(件)与月平均气温之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:由表中数据算出线性回归方程中的,气象部门预测下个月的平均气温约为,据此估计该商场下个月毛衣销售量约为()件A.46 B.40 C.38 D.5819、已知变量x,y的一组观测数据如表所示:x3467y4.02.5-0.50.5-2.0据此得到的回归方程为,若 =7.9,则x每增加1个单位,y的预测值就()A. 增加1.4个单位 B. 减少1.2个单位 C. 增加1.2个单位 D. 减少1.4个单位20、下面给出四种说法:①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;②命题P:“∃x0∈R,x02﹣x0﹣1>0”的否定是¬P:“∀x∈R,x2﹣x﹣1≤0”;③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=﹣p④回归直线一定过样本点的中心().其中正确的说法有()A.①②③ B.①②④ C.②③④ D.①②③④21、下面给出四种说法:①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;②命题P:“∃x0∈R,x02﹣x0﹣1>0”的否定是¬P:“∀x∈R,x2﹣x﹣1≤0”;③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=﹣p④回归直线一定过样本点的中心().其中正确的说法有()A.①②③ B.①②④ C.②③④ D.①②③④22、已知x与y之间的一组数据:x23ym35.57已求得关于y与x的线性回归方程为,则m的值为 ()A. 1B. 0.85C. 0.7D. 0.523、已知x与y之间的一组数据:x123ym35.57已求得关于y与x的线性回归方程为,则m的值为 ()A. 1B. 0.85C. 0.7D. 0.524、已知回归方程,则该方程在样本处的残差为( )A. B. C. D.25、对两个变量和进行回归分析,得到一组样本数据:,…,则下列说法中不正确的是( )A.由样本数据得到的回归方程必过样本中心B.残差平方和越小的模型,拟合的效果越好C.若变量和之间的相关系数为,则变量和之间具有线性相关关系D.用相关指数来刻画回归效果,越小,说明模型的拟合效果越好26、在相关分析中,对相关系数,下列说法正确的是()A.越大,线性相关程度越强B.越小,线性相关程度越强C.越大,线性相关程度越弱,越小,线性相关程度越强D.且越接近,线性相关程度越强,越接近,线性相关程度越弱27、下面给出四种说法:①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;②命题P:“∃x0∈R,x02﹣x0﹣1>0”的否定是¬P:“∀x∈R,x2﹣x﹣1≤0”;③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=﹣p④回归直线一定过样本点的中心().其中正确的说法有()A.①②③ B.①②④ C.②③④ D.①②③④28、根据如下样本数据:3456784.02.50.5得到的回归方程为,则()A. ,B. ,C. ,D. ,29、以下判断正确的个数是()①相关系数,值越小,变量之间的相关性越强;②命题“存在,”的否定是“不存在,”;③“”为真是“”为假的必要不充分条件;④若回归直线的斜率估计值是1.23,样本点的中心为,则回归直线方程是.A.4 B.2 C.3 D.130、某产品的广告费用x与销售额y的统计数据如下表:广告费用x(万元)4235销售额y(万元)49263954根据上表可得回归方程,据此模型预报广告费用为6万元时,销售额为()A. 72.0万元B. 67.7万元C. 65.5万元D. 63.6万元31、某青少年成长关爱机构为了调研所在地区青少年的年龄与身高壮况,随机抽取6岁,9岁,12岁,15岁,18岁的青少年身高数据各1000个,根据各年龄段平均身高作出如图所示的散点图和回归直线.根据图中数据,下列对该样本描述错误的是()A.据样本数据估计,该地区青少年身高与年龄成正相关B.所抽取数据中,5000名青少年平均身高约为C.直线的斜率的值近似等于样本中青少年平均身高每年的增量D.从这5种年龄的青少年中各取一人的身高数据,由这5人的平均年龄和平均身高数据作出的点一定在直线上32、由一组样本数据,,…,得到回归直线方程,那么下列说法中不正确的是()A.直线必经过点B.直线至少经过,,…,中的一个点C.直线的纵截距为D.直线的斜率为33、2015年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》.某记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年龄在,,,,的爱看比例分别为,,,,.现用这5个年龄段的中间值代表年龄段,如12代表,代表,根据前四个数据求得关于爱看比例的线性回归方程为,由此可推测的值为()A. B. C. D.34、广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如下表(单位:万元)广告费23456销售额2941505971由上表可得回归方程为,据此模型,预测广告费为10万元时的销售额约为A. B. C. D.35、下列说法错误的是()A.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高B.在线性回归分析中,回归直线不一定过样本点的中心C.在回归分析中,为0.98的模型比为0.80的模型拟合的效果好D.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系36、下列说法中正确的是()①相关系数用来衡量两个变量之间线性关系的强弱,越接近于,相关性越弱;②回归直线一定经过样本点的中心;③随机误差满足,其方差的大小用来衡量预报的精确度;④相关指数用来刻画回归的效果,越小,说明模型的拟合效果越好.A.①② B.③④ C.①④ D.②③37、下列命题中正确命题的个数是()(1)对于命题,使得,则,均有;(2)命题“已知,若,则或”是真命题;(3)回归直线的斜率的估计值为,样本点的中心为,则回归直线方程为;(4)是直线与直线互相垂直的充要条件.A. B. C. D.38、某研究机构在对具有线性相关的两个变量和进行统计分析时,得到如下数据:由表中数据求得关于的回归方程为,则在这些样本点中任取一点,该点落在回归直线下方的概率为()A. B. C. D.39、给出下列几个命题:①命题:任意,都有,则:存在,使得;②已知,若成立,且,则;③空间任意一点和三点,则是三点共线的充分不必要条件;④线性回归方程对应的直线一定经过其样本数据点中的一个.其中正确的个数为()A. B. C. D.40、某班一个学习小组在一次数学实践活动中,测得一组数据共5个,如下表x5y2.54.65.4n7.5若,计算得回归方程为,则的值为()A. 9B. 8C. 7D. 641、某厂家为了解销售轿车台数与广告宣传费之间的关系,得到如表统计数据表:根据数据表可得回归直线方程,其中,,据此模型预测广告费用为9万元时,销售轿车台数为()广告费用(万元)23456销售轿车(台数)3461012A. 17B. 18C. 19D. 2042、下列说法正确的是()A.若命题:,,则:,B.已知相关变量满足回归方程,若变量增加一个单位,则平均增加4个单位C.命题“若圆:与两坐标轴都有公共点,则实数”为真命题D.已知随机变量,若,则43、四名同学根据各自的样本数据研究变量之间的相关关系,并求得回归直线方程和相关系数,分别得到以下四个结论:①,且;②,且;③,且;④,且.其中一定不正确的结论的序号是()A.①② B.②③ C.③④ D.①④44、通过随机询问110名性别不同的大学生是否爱好某处运动,得到如下的列联表:由卡方公式算得:附表:参照附表:得到的正确的结论是()A.在犯错的概率不超过0.1%的前提下,认为“爱好该运动与性别无关”B.在犯错的概率不超过0.1%的前提下,认为“爱好该运动与性别有关”C.有99%以上的把握认为“爱好该运动与性别有关”D.有99%以上的把握认为“爱好该运动与性别无关”45、下列五个命题中正确命题的个数是()(1)对于命题,使得,则,均有;(2)是直线与直线互相垂直的充要条件;(3)已知回归直线的斜率的估计值为,样本点的中心为,则回归直线方程为;(4)已知正态总体落在区间的概率是,则相应的正态曲线在时,达到最高点;(5)曲线与所围成的图形的面积是.A.2 B.3 C.4 D.546、为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程,其中,据此估计,该社区一户收入为15万元家庭年支出为()A.11.4万元 B.11.8万元C.12.0万元 D.12.2万元47、某商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:月平均气温x(℃)171382月销售量y(件)24334055由表中数据算出线性回归方程中的,气象部门预测下个月的平均气温约为℃,据此估计该商场下个月毛衣销售量约为件 ( )A.46B.40C.70D.5848、某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)进行统计调查,y与x具有相关关系,回归方程为=0.66x+1.562.若某城市居民人均消费水平为7.675千元,估计该城市人均消费额占人均工资收入的百分比约为( )A.83% B.72% C.67% D.66%49、下表是某工厂6~9月份电量(单位:万度)的一组数据:月份x6789用电量y6532由散点图可知,用电量y与月份x间有较好的线性相关关系,其线性回归直线方程是,则等于( )A.10.5 B.5.25 C.5.2 D.14.550、已知回归直线方程中斜率的估计值为1.23,样本点的中心(4,5),则回归直线方程为( )A.=1.23x+0.08 B.=0.08x+1.23C.=1.23x+4 D.=1.23x+551、有下列数据:x123y35.9912.01下列四个函数中,模拟效果最好的为( )A. B.C. D.52、某公司为确定明年投入某产品的广告支出,对近年的广告支出与销售额(单位:百万元)进行了初步统计,得到下列表格中的数据:经测算,年广告支出与年销售额满足线性回归方程,则的值为()A. B. C. D.53、在2016年3月15日,某市物价部门对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如表所示:价格x9.29.31010.511销售量y1110865由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是:=﹣2.2x+a,那么a的值为()A.﹣24 B.29.2 C.30 D.4054、已知与之间的一组数据:12335.57已求得关于与的线性回归方程为,则的值为()A.1 B.0.85 C.0.7 D.0.555、某产品的广告费用与销售额的统计数据如表:广告费用x(万元)4235销售额y(万元)49263954根据上表可得回归方程中的为9.4,据此模型,当广告费用为6万元时,销售额为()A.65.5万元 B.67.7万元 C.69.7万元 D.72.0万元56、某产品的广告费用与销售额的统计数据如下表:广告费用(万元)1245销售额(万元)10263549根据上表可得回归方程的约等于9,据此模型预报广告费用为6万元时,销售额约为()。
回归分析练习题

1. 从20的样本中得到的有关回归结果是:SSR=60,SSE=40。
要检验x 与y 之间的线性关系是否显著,即检验假设:01:0H β=。
(1)线性关系检验的统计量F 值是多少? (2)给定显著性水平a =0.05,F a 是多少? (3)是拒绝原假设还是不拒绝原假设?(4)假定x 与y 之间是负相关,计算相关系数r 。
(5)检验x 与y 之间的线性关系是否显著?解:(1)SSR 的自由度为k=1;SSE 的自由度为n-k-1=18;因此:F=1SSR k SSE n k --=6014018=27 (2)()1,18F α=()0.051,18F =4.41 (3)拒绝原假设,线性关系显著。
(4),由于是负相关,因此r=-0.7746(5)从F 检验看线性关系显著。
2. 某汽车生产商欲了解广告费用(x)对销售量(y)的影响,收集了过去12年的有关数据。
通过计算得到下面的有关结果:(1)完成上面的方差分析表。
(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?(3)销售量与广告费用之间的相关系数是多少?(4)写出估计的回归方程并解释回归系数的实际意义。
(5)检验线性关系的显著性(a=0.05)。
(2)R2=0.9756,汽车销售量的变差中有97.56%是由于广告费用的变动引起的。
(3)r=0.9877。
(4)回归系数的意义:广告费用每增加一个单位,汽车销量就增加1.42个单位。
(5)回归系数的检验:p=2.17E—09<α,回归系数不等于0,显著。
回归直线的检验:p=2.17E—09<α,回归直线显著。
3. 根据两个自变量得到的多元回归方程为12ˆ18.4 2.014.74yx x =-++,并且已知n =10,SST =6 724.125,SSR =6 216.375,1ˆ0.0813s β=,2ˆs β=0.056 7。
要求:(1)在a=0.05的显著性水平下,12,x x 与y 的线性关系是否显著? (2)在a =0.05的显著性水平下,1β是否显著?(3)在a =0.05的显著性水平下,2β是否显著?解(1)回归方程的显著性检验:假设:H 0:1β=2β=0 H 1:1β,2β不全等于0 SSE=SST-SSR=6 724.125-6 216.375=507.75 F=1SSR p SSE n p --=6724.1252507.751021--=42.85()2,7F α=4.74,F>()2,7F α,认为线性关系显著。
人教B版高中数学选修回归分析同步练习(1)

3.2 回归分析测试题一、选择题1.下列结论正确的是()①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.A.①②B.①②③C.①②④D.①②③④答案:C2.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是()A.总偏差平方和B.残差平方和D.回归平方和D.相关指数答案:B3.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为()A.$1.234=+B.$1.235y x=+y xC.$1.230.08=+y xy x=+D.$0.08 1.23答案:C4.高二第二学期期中考试,按照甲、乙两个班级学生数学考试成绩优秀和不优秀统计后,得到如下列联表:班级与成绩列联表则随机变量2K的观测值约为()A.0.60 B.0.828 C.2.712 D.6.004答案:A5.利用独立性检验来考察两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X 与Y有关系”的可信程度.如果k>5.024,那么就有把握认为“X与Y有关系”的百分比为()25%75% 2.5%97.5%答案:D二、填空题6.线性回归模型y bx a e=++(a和b为模型的未知参数)中,e称为.答案:随机误差7.在线性回归模型中,总偏差平方和、回归平方和、残差平方和的关系等式是.答案:回归平方和=总偏差平方和-残差平方和8.在残差分析中,残差图的纵坐标为.答案:残差9.在分析两个分类变量之间是否有关系时,常用到的图表有.答案:列联表、三维柱形图、二维条形图10.在比较两个模型的拟合效果时,甲、乙两个模型的相关指数2R的值分别约为0.96和0.85,则拟合效果好的模型是.答案:甲三、解答题11.在回归分析中,通过模型由解释变量计算预报变量的值时,应注意什么问题?解:应注意下列问题:(1)回归方程只适用于我们所研究的样本的总体;(2)我们所建立的回归方程一般都有时间性;(3)样本取值的范围会影响回归方程的适用范围;(4)不能期望回归方程得到的预报值就是预报变量的精确值.12.某企业为考察生产同一种产品的甲、乙两条生产线的产品合格率,同时各抽取100件产品,检验后得到如下列联表:生产线与产品合格数列联表解:2K的观测值2200(975953)0.521 2.706(973)(955)(9795)(35)k ⨯⨯-⨯=≈+⨯+⨯+⨯+≤,因此没有充分的证据显示甲、乙两线生产的产品合格率有关系.。
北师大版高中数学选修12第1章《可线性化的回归分析》同步练习
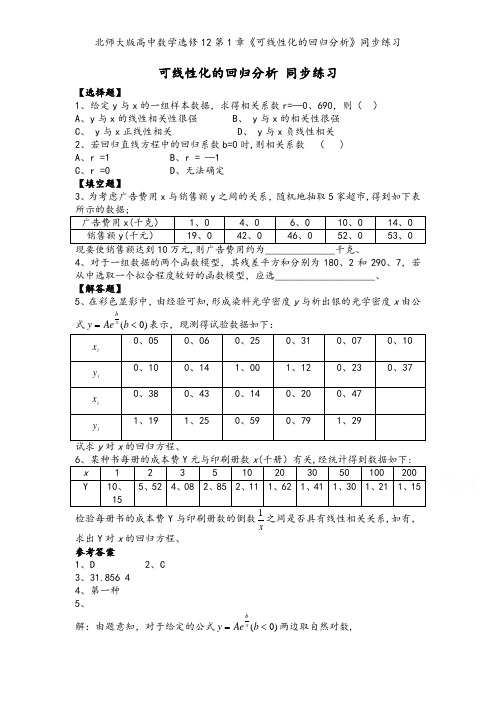
可线性化的回归分析 同步练习【选择题】1、给定y 与x 的一组样本数据,求得相关系数r=—0、690,则( ) A 、y 与x 的线性相关性很强 B 、 y 与x 的相关性很强 C 、 y 与x 正线性相关 D 、 y 与x 负线性相关2、若回归直线方程中的回归系数b=0时,则相关系数 ( ) A 、r =1 B 、r = —1 C 、r =0 D 、无法确定 【填空题】3、为考虑广告费用x 与销售额y 之间的关系,随机地抽取5家超市,得到如下表广告费用x(千克) 1、04、0 6、0 10、0 14、0 销售额y(千元) 19、0 42、0 46、0 52、0 53、0 4、对于一组数据的两个函数模型,其残差平方和分别为180、2和290、7,若从中选取一个拟合程度较好的函数模型,应选____________________、 【解答题】5、在彩色显影中,由经验可知,形成染料光学密度y 与析出银的光学密度x 由公式)0(<=b Ae y xb表示,现测得试验数据如下:i x0、05 0、06 0、25 0、31 0、07 0、10 i y 0、10 0、14 1、00 1、12 0、23 0、37 i x0、38 0、43 0、14 0、20 0、47 i y1、191、250、590、791、29x 1 2 3 5 10 20 30 50 100 200 Y 10、155、52 4、08 2、85 2、11 1、62 1、41 1、30 1、21 1、15检验每册书的成本费Y 与印刷册数的倒数x之间是否具有线性相关关系,如有,求出Y 对x 的回归方程、 参考答案1、D2、C3、31.856 44、第一种5、解:由题意知,对于给定的公式)0(<=b Ae y xb 两边取自然对数,得.ln ln xbA y +=与线性回归方程相对照可以看出,只要取,ln ,ln ,1A a y v xu ===就有v =a +bu 、这是V 对u 的线性回归直线方程,对此我们再套用相关性检验,求回归系数b 和a ,题目中所给的数据由变量置换,ln ,1y v u ==变为如下所示的数据、由于,75.0998.0||>=r 可知,v u 与具有很强的线性相关关系、 再求出b =-0、14,a =0、548, u v146.0548.0ˆ-=∴ 把v u 与置换回来可得.146.0548.0ˆln x y -=∴ xxxeee e y146.0146.0548.0146.0548.073.1ˆ---=⋅==∴所以回归曲线方程为xe y146.073.1ˆ-=∴6、Y 对x 的回归方程为.120.1976.8ˆ+=xy。
高中数学选修1-2回归分析 同步练习1

回归分析同步练习1(2)对两个变量进行相关性检验(α=0.05).2. 下表给出了12个人的月存款额y与月收人x的有关数据,试根据这些数据,求出y关于x的回归方程:3. 为了研究大豆脂肪含量(x)和蛋白质含量(y)的关系,测定了9种大豆品种籽粒内的脂肪含最和蛋白质含量,得到如下表的数据,试求出y与x之间的线性回归方程.x的数据:(2)求线性回归方程,并在散点图中加上回归直线;(3)据(2)的结果估计当房屋面积为150m2时的销售价格.5.为研究合金的强度y(×107pa)与合金中碳的含量x(%)的关系,搜集了下面的7对数据x y, (i=l,2,3,…,7):(0.10,43),(0.12,44 5),(0.14,4 5),(0.15,47).(0.16,(,)i i48.5),(0.18,49),(0.2l,55)(1)画出散点图;(2)求出y关于x的线性回归方程;(3)当z=0.17 时,试估计y的值.6. 测量不同浓度(x%)的葡萄糖液在光电比色计上的消光度,得试验数据如下表,试根据试验数据预测葡萄糖液浓度x=12时的消光度.7. 某公司购进一新型设备,为了分配合适的工人操纵设备,进行该设备的工人劳动生产力与工龄之间的相关分析,下表是12个5一10年工龄的工人操纵新设备的劳动生产率的试验记录:参考答案1. (1) 经计算得:567.31,40==y x ,,600092912=-∑=x x i i 2995991=⋅-∑=y x y x i i i ,,38.153392912=-∑=y y i i 从而,4992.060002995==b 60.11=-=x b y a ,回归直线方程是x y 4992.060.11^+=; (2)相关系数9874.038.153360002995=⨯=r ,查表得,与显著性水平0.05和自由度相应的相关系数临界值666.005.0=r ,因05.0r r >,这说明溶解度y 与温度x 之间存在着线性相关关系. 2. 0.3120.3809y x ∧=-+ 3. 54.40.903y x ∧=-4. (1)图略; (2)23,109==y x ,,157092512=-∑=x x i i308551=⋅-∑=y x yx i ii ,从而,1962.01570308==b 8166.1=-=x b y a ,所求回归直线方程是x y 1962.08166.1^+=,(3)据(2),当x=150m 2时,2466.31^=y 万元 5.(1)图略.(2)31.59104.59y x ∧=+(3)当x=0.17时,y 的估计值约为49.37 .6. 0. 27517. 从生产效率来分析:26.13,25.34,7.20,5.8,25.7=====yy xx xy L L L y x ,从而相关系数r=0.91733334.结果说明工龄与劳动者生产率之间存在着高度相关关系;从每件所花费的时间来分析:相关系数r ’= -0.9628,结果说明工龄长短与劳动生产率的逆指标具有高度的负相关关系,工龄越长,每件产品耗时越少,说明经验与知识对于提高劳动生产率有着非常重要的意义.。
回归分析练习题及参考答案
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
高中数学选修2-3同步练习题库:回归分析的基本思想及其初步应用(简答题:较易)
回归分析的基本思想及其初步应用(简答题:较易)1、调查某市出租车使用年限和该年支出维修费用(万元),得到数据如下使用年限23456维修费用(2)由(1)中结论预测第10年所支出的维修费用.2、下表提供了某厂生产某产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据:(1)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?附:回归直线的斜率和截距的最小二乘估计分别为: .3、某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:月日月日月日月日月日月日昼夜温差就诊人数该兴趣小组确定的研究方案是:先从这组(每个有序数对叫作一组)数据中随机选取组作为检验数据,用剩下的组数据求线性回归方程.(Ⅰ)求选取的组数据恰好来自相邻两个月的概率;(Ⅱ)若选取的是月和月的两组数据,请根据至月份的数据,求出关于的线性回归方程;(Ⅲ)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过人,则认为得到的线性回归方程是理想的,试问(Ⅱ)中所得到的线性回归方程是否是理想的?参考公式:.4、“奶茶妹妹”对某段时间的奶茶销售量及其价格进行调查,统计出售价元和销售量杯之间的一组数据如下表所示:价格销售量通过分析,发现销售量对奶茶的价格具有线性相关关系.(1)求销售量对奶茶的价格的回归直线方程;(2)欲使销售量为13杯,则价格应定为多少?注:在回归直线中,.5、已知某商品的价格(元)与需求量(件)之间的关系有如下一组数据:(1)求,;(2)求出回归直线方程(3)计算相关系数r的值,并说明回归模型拟合程度的好坏。
(参考公式:,)参考数据:当n-2=3,,6、有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为.(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).附:7、某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数,得到如下数据资料:月日月日月日月日月日月日昼夜温差就诊人数该兴趣小组确定的研究方案是:先从这组(每个有序数对叫作一组)数据中随机选取组作为检验数据,用剩下的组数据求线性回归方程.(1)求选取的组数据恰好来自相邻两个月的概率;(2)若选取的是月和月的两组数据,请根据至月份的数据,求出关于的线性回归方程;(3)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过人,则认为得到的线性回归方程是理想的,试问(2)中所得到的线性回归方程是否是理想的?参考公式:.8、某种产品的广告费用支出与销售额之间有如下的对应数据:(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?(2)请根据上表提供的数据,求回归直线方程;(3)据此估计广告费用为10时,销售收入的值.(参考公式:,).9、某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:(1)分别以三家连锁店的平均售价与平均销量为散点,求出售价与销量的回归直线方程;(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)附:10、王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计,表示第天参加抽奖活动的人数,得到统计表格如下:经过进一步统计分析,发现与具有线性相关关系.(1)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(2)判断变量与之间是正相关还是负相关;(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.参与公式:,,.11、种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如下表:(I)从3月12日至3月16日中任选2天,记发芽的种子数分别为c,d,求事件“c,d均不小于25”的概率;(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程;(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?12、中央电视台为了解该卫视《朗读者》节目的收视情况,抽查东西两部各个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.(2)随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获益匪浅,现从观看节目的观众中随机统计了位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):年龄岁周均学习成语知识时间(小时)由表中数据,试求线性回归方程,并预测年龄为岁观众周均学习阅读经典知识的时间.13、某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:零件的个数(个)加工的时间(小时)(1)在给定坐标系中画出表中数据的散点图;(2)求关于的线性回归方程;(3)试预测加工10个零件需要多少时间?附:,14、某特色餐馆开通了美团外卖服务,在一周内的某特色外卖份数(份)与收入(元)之间有如下的对应数据:外卖份数(份)收入(元)(1)画出散点图;(2)求回归直线方程;(3)据此估计外卖份数为份时,收入为多少元.注:参考公式:, ;参考数据:.15、如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合与的关系,请用相关系数加以说明;(Ⅱ)建立关于的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.参考数据:,,,.参考公式:相关系数,回归方程,,本题中斜率和截距的最小二乘估计公式分别为:,.16、某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:单价(元)销量(元)(1)求回归直线方程;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?附: .17、某电脑公司有名产品推销员,其工作年限与年推销金额数据如下表:工作年限年年推销金额万元(1)从编号的五位推销员中随机取出两位,求他们年推销金额之和不少于万元的概率;(2)求年推销金额关于工作年限的线性回归方程;若第名产品推销员的工作年限为年,试估计他的年推销金额.附:回归直线的斜率和截距的最小二乘法估计公式为:18、脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第个农户的年收入(万元),年积蓄(万元),经过数据处理得(Ⅰ)已知家庭的年结余对年收入具有线性相关关系,求线性回归方程;(Ⅱ)若该地区的农户年积蓄在万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?附:在中,其中为样本平均值.19、某项科研活动共进行了5次试验,其数据如下表所示:(1)从5次特征量的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;(2)求特征量关于的线性回归方程;并预测当特征量为570时特征量的值.(附:回归直线的斜率和截距的最小二乘法估计公式分别为,)20、某百货公司1~6月份的销售量与利润的统计数据如下表:(1)根据2~5月份的统计数据,求出关于的回归直线方程;(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?(参考公式:,)21、某农科所对冬季昼夜温差大小与某反季节大豆新品种种子发芽颗数之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下数据:温差发芽数(颗)该农科所确定的研究方案是:先从这5组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.(1)求选取的2组数据恰好是不相邻的2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求关于的线性回归方程;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2(颗),则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(注:)22、某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据(…)如下表所示:试销价格(元)产品销量(件)已知变量具有线性负相关关系,且,,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲,乙,丙,其中有且仅有一位同学的计算结果是正确的().(1)试判断谁的计算结果正确?并求出的值;(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,为“理想数据”的个数,求随机变量的分布列和数学期望.23、某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:温差(℃)发芽数(颗)2组数据进行检验.(1)求选取的2组数据恰好是不相邻的2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求关于的线性回归方程;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(注:)24、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据.(1)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(2)该厂技术改造后,预测生产100吨甲产品生产能耗多少吨标准煤?(附:在线性回归方程中,,)25、某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:年份储蓄存款(千亿元)为了研究计算的方便,工作人员将上表的数据进行了处理,,得到下表2:时间代号(Ⅰ)求关于的线性回归方程;(Ⅱ)通过(Ⅰ)中的方程,求出关于的回归方程;(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?(附:对于线性回归方程)26、某公司2016年前三个月的利润(单位:百万元)如下:(1)求利润关于月份的线性回归方程;(2)试用(1)中求得的回归方程预测月和月的利润;(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过万?相关公式:,=.27、某公司2016年前三个月的利润(单位:百万元)如下:(1)求利润关于月份的线性回归方程;(2)试用(1)中求得的回归方程预测月和月的利润;(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过万?相关公式: , .28、某公司2016年前三个月的利润(单位:百万元)如下:(1)求利润关于月份的线性回归方程;(2)试用(1)中求得的回归方程预测月和月的利润;(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过万?相关公式: , .29、为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出y关于x的线性回归方程=x+;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?30、某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据回归方程为其中,(1)根据表中提供的数据,求出y与x的回归方程;(2)预测销售额为115万元时,大约需要多少万元广告费。
高中数学 3.2 回归分析同步练习2 苏教版选修23
线性回归分析 同步练习一.选择题:本大题共5小题,每小题5分,共25分. 1. 对于数组{}n x x x ,,,21Λ来说,算式∑=-ni ix x12)(表示 ( C )A.2)(x x n -B.222221x x x x n -+++Λ C.222221x n x x x n -+++Λ D.2221)(x n x x x n -+++Λ 2. 下列说法正确的是 ( C ) A.对于相关系数r 来说,1≤r ,r 越接近0,相关程度越大;r 越接近1,相关程度越小 B.对于相关系数r 来说,1≥r ,r 越接近1,相关程度越大;r 越大,相关程度越小 C.对于相关系数r 来说,1≤r ,r 越接近1,相关程度越大;r 越接近0,相关程度越小 D.对于相关系数r 来说,1≥r ,r 越接近1,相关程度越小;r 越大,相关程度越大. 3. 下列说法正确的是 ( C ) A.一块农田的水稻产量与施肥量之间一定存在着正比例关系 B.产品成本与产品数量一定存在着一次函数关系C.若两个变量之间存在着线性相关关系,则可用某个一次函数来估计它的变化趋势D.如果两个变量之间不存在着线性相关关系,那么一定能用某个二次函数来估计它的变化趋势4. 为了考察两个变量x 和y 之间的线性相关性,甲、乙两个同学各自独立的做10次和15次试验,并且利用线性回归方法,求得回归直线分布为1l 和2l ,已知在两人的试验中发现对变量x 的观察数据的平均值恰好相等都为s ,对变量y 的观察数据的平均值恰好相等都为t,那么下列说法正确的是( A ) A.直线1l 和2l 有交点(s,t ) B. 直线1l 和2l 相交,但是交点未必是(s,t ) C. 直线1l 和2l 平行 D. 直线1l 和2l 必定重合5. 已知18组数据的相关系数是0.54689,则下列说法正确的是 ( C ) A.两个变量之间一定存在线性相关关系 B.两个变量之间一定不存在线性相关关系C.若显著性水平为0.05,则两个变量之间存在线性相关关系D.若显著性水平为0.01,则两个变量之间存在线性相关关系二.填空题(本大题共4小题,每小题5分,共20分)6. 某人对一个地区人均工资x 与该地区人均消费y 进行统计调查得y 与x 具有相关关系,且回归直线方程为^0.66 1.562y x =+(单位:千元),若该地区人均消费水平为7.675,估计该地区人均消费额占人均工资收入的百分比约为______ _____.(精确到0.1%)7. 相应与显著性水平0.05,观测值为10组的相关系数临界值为 .8. 一个工厂在某年里每月产品的总成本y (单位:万元)与月产量x (单位:万件)之间有如下一组数据:则月总成本ˆy与月产量x之间的线性回归方程为 .9.某中学高一期中考试后,对成绩进行分析,从13班中选出5名学生的总成绩和外语成绩如下表:学生1 2 3 4 5学科总成绩(x) 482 383 421 364 362外语成绩78 65 71 64 61(y)则外语成绩对总成绩的回归直线方程是_______________________.三.解答题:本大题共5小题,共55分.解答应写出文字说明,证明过程或演算步骤.10. (本小题10分) 在国民经济中,社会生产与货运之间有着密切关系,下面列出1991—2000年中某地区货运量与工业总产值的统计资料:年份1991 1992 1993 1994 1995 1996 1997 1998 1999 20002.8 2.93.2 3.2 3.4 3.2 3.3 3.7 3.94.2工业总产值x(10亿元)货运量y(亿t) 25 27 29 32 34 36 35 39 42 45利用上述资料:(1)画出散点图;(2)计算这两组变量的相关系数;(3)在显著水平0.05的条件下,对变量x与y进行相关性检验;(4)如果变量x与y之间具有线性相关关系,求出回归直线方程.11.(本小题10分) 随机选取15家销售公司,由营业报告中查出其上年度的广告费x(占总费用的百分比)及盈利额y(占销售总额的百分比)列表如下:广告费x 1.5 0.8 2.6 1.0 0.6 2.8 1.20.9 0.4 1.3 1.2 2.0 1.6 1.8 2.2 盈利额y 3.1 1.9 4.2 2.3 1.6 4.9 2.8 2.1 1.4 2.4 2.4 3.8 3.0 3.4 4.0试根据上述资料:(1)画出散点图;(2)计算出这两组变量的相关系数;(3)在显著水平O.01的条件下,对变量x与y进行相关性检验;(4)如果变量x与y之间具有线性相关关系,求出回归直线方程;(5)已知某销售公司的广告费占其总费用的1.7%,试估计其盈利净额占销售总额的百分比.12. (本小题11分) 商品零售商要了解每周的广告费x及消费额y(单位:万元)之间的关系,记录如下:广告费x 40 18 33 36 25 43 38 30 50 20 42 46消费额y 400 395 420 475 385 525 480 400 560 365 510 540利用上述资料:(1)画出散点图;(2)求销售额y对广告费x的一元线性回归方程;(3)求出两个变量的相关系数.13. (本小题12分) 某城区为研究城镇居民月家庭人均生活费支出和月收入的相关关系,随机抽取10户进行调查,其结果如下:月人均收入x元300 390 420 540 570 700 760 800 850 1080月人均生活费y元255 324 330 345 450 520 580 650 700 750利用上述资料:(1)画出散点图;(2)计算这两组变量的相关系数;(3)在显著水平0.05的条件下,对变量x与y进行相关性检验;(4)如果变量x与y之间具有线性相关关系,求出回归直线方程;(5)测算人均收入为280元时,人均生活费支出应为多少元?14. (本小题12分) 要分析学生初中升学的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩(如下表):学生编号 1 2 3 4 5 6 7 8 9 10入学成绩x 63 67 45 88 81 71 52 99 58 76高一期末成绩y 65 78 52 82 92 89 73 98 56 75(1)画出散点图;(2)计算入学成绩x与高一期末考试成绩y的相关关系;(3)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出一元线性回归方程;(4)若某学生入学数学成绩为80分,试估计他高一期末数学考试成绩.参考答案一、选择题:1. C【提示】2. C【提示】3. C【提示】4. A【提示】5. C【提示】二、填空题:6. 【答案】 83.8%7. 【答案】 0.6328. 【答案】ˆy=1.216x+0.97289. 【答案】y=14.5+0.132【提示】三、解答题:10. 【 解】 (1) 散点图(2)相关系数r=0.95652; (3)相关系数临界值632.005.0=r ,因05.0r r >,这说明两变量之间存在着线性相关关系; (4)^y =14.0909x-13.2273 11. 【 解析】 (1) 散点图(2)相关系数r=0.98831; (3)相关系数临界值641.001.0=r ,因01.0r r >,这说 明两变量之间存在着线性相关关系; (4)^y =1.41468x+0.82123; (5)当x=1.7时,y=3.23,其盈利净额占销售总额的百分比为3.23%. 12. 【 解析】 (1) 散点图010*********12345012345600.511.522.53(2)回归方程^y =7.28601x+200.39416;(3)相关系数r=0.98353. 13. 【 解】 (1) 散点图(2)相关系数r=0.9793;(3)相关系数临界值632.005.0=r ,因05.0r r >,这说明两变量之间存在着线性相关关系; (4) 回归方程^y =0.70761x+39.37103;(5)人均生活 费支出应为237.5元.14. 【 解】 (1) 散点图(2)相关系数r=0.839786;(3)相关系数临界值632.005.0=r ,因05.0r r >,这说明02040608010012002040608010012010020030040050060070080002004006008001000120001002003004005006000102030405060^y=0.76556x+22.41067;(4)成绩体积为84分.两变量之间存在着线性相关关系;回归方程。
苏教版高中数学选修2-3回归分析同步练习.docx
高中数学学习材料马鸣风萧萧*整理制作回归分析同步练习2一.选择题:本大题共5小题,每小题5分,共25分.1.在画两个变量的散点图时,下面叙述正确的是 ( B )A.预报变量在x轴上,解释变量在y轴上B.解释变量在x轴上,预报变量在y轴上C.可以选择两个变量中任意一个变量在x轴上D.可以选择两个变量中任意一个变量在y轴上2.一位母亲记录了她儿子3到9岁的身高,数据如下表:年龄(岁) 3 4 5 6 7 8 9身高(㎝) 94.8 104.2 108.7 117.8 124.3 130.8 139.0由此她建立了身高与年龄的回归模型x.=,她用这个模型预测儿子10岁时的身73+93.7y19高,则下列的叙述正确的是 ( C )A.她儿子10岁时的身高一定是145.83㎝B.她儿子10岁时的身高在145.83㎝以上C.她儿子10岁时的身高在145.83㎝左右D.她儿子10岁时的身高在145.83㎝以下3.在建立两个变量Y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合得最好的模型是 ( A )A.模型1的相关指数R2为0.98B.模型2的相关指数R2为0.80C.模型3的相关指数R2为0.50D.模型4的相关指数R2为0.254. 下列说法正确的有 ( B )①回归方程适用于一切样本和总体。
②回归方程一般都有时间性。
③样本取值的范围会影响回归方程的适用范围。
④回归方程得到的预报值是预报变量的精确值。
A. ①②B. ②③C. ③④D. ①③5.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是 ( B )A.总偏差平方和B.残差平方和C.回归平方和D.相关指数R2二.填空题(本大题共4小题,每小题5分,共20分)6.在回归分析中,通过模型由解释变量计算预报变量时,应注意什么问题(1) ;(2) ;(3) ;(4) .7.许多因素都会影响贫穷,教育也许是其中之一,在研究这两个因素的关系时收集了美国50个州的成年人受过9年或更少教育的百分比(x)和收入低于官方规定的贫困线的人数占本州人数的百分比(y)的数据,建立的回归直线方程如下ˆ0.8 4.6=+,斜率的估计等于0.8y x说明,成年人受过9年或更少教育的百分比(x)和收入低于官方的贫困线的人数占本州人数的百分比(y)之间的相关系数 (填充“大于0”或“小于0”)8.已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是9.线性回归模型y=bx+a+e中,b=_____________,a=______________e称为_________ .三.解答题:本大题共5小题,共55分.解答应写出文字说明,证明过程或演算步骤.10. (本小题10分) 为了决定在白鼠中血糖的减少量和注射胰岛素A的剂量间的关系,将同样条件下繁殖的7只白鼠注射不同剂量的胰岛素A.所得数据如下:0.25 0.25 0.30 0.40 0.50 0.50A的剂量x 0.2血糖减少量y 30 26 40 35 54 56 65(1)求出y对x的线性回归方程;(2)x与y之间的线性相关关系有无统计意义(可靠性不低于95%)11. (本小题10分) 大同电脑公司有8名产品推销员,其工作年限与年推销金额数据如下表:推销员编号 1 2 3 4 5 6 7 8工作年限x 3 2 10 5 8 4 4 8年推销金额y 22 18 95 40 75 45 40 78(1)求年推销金额y与工作年限x之间的相关系数;(2)求年推销金额y关于工作年限x的线性回归方程;(3)分别估计工作年限为7年和11年时的年推销金额.12.(本小题11分) 在7块大小及条件相同的试验田上施肥,做肥量对小麦产量影响的试验,得到如下一组数据:施化肥量x15 20 25 30 35 40 45小麦产量330 345 365 405 445 450 455(1)画出散点图;(2)对x与y进行线性回归分析,并预测施肥量30时小麦的产量为多少?13.(本小题12分) 适当饮用葡萄酒可以预防心脏病,下表中的信包是19个发达国家一年中平均每人喝葡萄酒摄取酒精的升数z以及一年中每10万人因心脏病死亡的人数,国家澳大利亚奥地利比利时加拿大丹麦芬兰法国冰岛爰尔兰意大利x 2.5 3.9 2.9 2.4 2.9 0.8 9.1 0.8 0.7 7.9 y 211 167 131 191 220 297 71 221 300 107国家荷兰新西兰挪威西班牙瑞典瑞士英国美国德国x 1.8 1.9 0.8 6.5 1.6 5.8 1.3 1.2 2.7y 167 266 227 86 207 115 285 199 172(1)画出散点图,说明相关关系的方向、形式及强度;(2)求出每10万人中心脏病死亡人数,与平均每人从葡萄酒得到的酒精x(L)之间的线性回归方程.(3)用(2)中求出的方程来预测以下两个国家的心脏病死亡率,其中一个国家的成人每年平均从葡萄酒中摄取1L的酒精,另一国则是8 L.14. (本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量 x(min) l 2 3 4 5 6 y(mg) 39.832.2 25.4 20.3 16.2 13.3(1)设x 与z 之问具有关系x y cd =,试根据测量数据估计c 和d 的值;(2)估计化学反应进行到10 min 时未转化物质的量.参考答案一、选择题:1. B2. C3. A4. B5. B 二、填空题:6. 【答案】 (1)回归模型只适用于所研究的总体(2)回归方程具有时效性(3)样本的取值范围影响回归方程的适用范围(4)预报值是预报变量可能取值的平均值.7. 【答案】一个地区受过9年或更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本州人数的百分比将增加0.8%左右;大于0 .8. 【答案】 y ∧=1.23x+0.089. 【答案】 b =nii i=1n2ii=1(xx)(y y)(xx)---∑∑ , a =ˆy bx-,e 称为随机误差 三、解答题:10. 【 解】 (1) 5.814110.54y x ∧=+ (2)由r=0. 9301>0.754.即0.05r r >,故x ,y 之间的线性相关关系有统计意义.11. 【 解】12. 【 解】 (1) 画出散点图如图: (2)根据已知数据表得拓展表如下:由表易得210279530,,399.377x y ==== 代人线性相关系数公式得717722221170.9733(7)(7)i ii i i i i x y x yr x x y y ===-=≈--∑∑∑因此y 与x 有紧密的线性相关关系, 回归系数711722211()()7 4.75()7niii ii i niii i x x y y x y x yb x x xx∧====---==≈--∑∑∑∑所以回归直线方程为:256.8 4.75y x ∧=+当x=50时,256.8 4.7550494.3y ∧=+⨯=也自是说当施化肥量为50时,小麦的产量大致接近010020030040050001020304050494.3. 回归系数b ∧=4.75反映出当化肥施加量增加1个单位,小麦的产量将增加4.75,而256.8是不受施化肥量影响的部分13. 【 解】 (1) 散点图负相关,中等强度,线性或者稍微有些弯曲(2) 260.5622.969y x ∧=-(3)这两个国家的心脏率死亡率分别为每10万人238人和77人 14. 【 解】 (1)在x y cd =的两边取自然对数,可得lny=ln c+xlnd ,设lny=z ,ln c=a, lnd=b ,则z=a+bx ,由已知数据有 x 1 2 3 4 5 6 y 39.8 32.2 25.4 20.3 16.2 13.3 z 3.684 3.472 3.235 3.011 2.875 2.588由公式得a ≈3.905 5,b ≈0. 221 9,线性回归方程为z ∧=3.9055+ 0.221 9x ,即lnc ≈3.905 5,lad ≈0.221 9,故c ≈49.675,d ≈0.801 0,所以c ,d 的估计值分别为 49. 675,0. 801 0. (2)54mg0501001502002503003500246810。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§ 回归分析(二)
一、基础过关
1.已知x,y之间的一组数据如下表:
x
y
则y与x之间的线性回归方程y^ =b^ x+a^ 必过点________.
2.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地做10次和15
次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知在两个人的试验中发
现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好
相等,都为t.那么下列说法正确的是________.
①直线l1和l2有交点(s,t)
②直线l1和l2相交,但是交点未必是点(s,t)
③直线l1和l2由于斜率相等,所以必定平行
④直线l1和l2必定重合
3.每一吨铸铁成本yc(元)与铸件废品率x%建立的回归方程yc=56+8x,下列说法正确的是
________.
①废品率每增加1%,成本每吨增加64元
②废品率每增加1%,成本每吨增加8%
③废品率每增加1%,成本每吨增加8元
④如果废品率增加1%,则每吨成本为56元
4.已知线性回归方程为y^ =-,则x=25时,y的估计值为________.
5.关于回归分析,下列说法错误的是__________.(填序号)
①在回归分析中,变量间的关系若是非确定性关系,那么因变量不能由自变量惟一确定;
②散点图反映变量间的线性相关关系,误差较大;
③散点图中,解释变量在x轴,预报变量在y轴;
④散点图能明确反映变量间的关系.
6.某学校开展研究性学习活动,某同学获得一组实验数据如下表:
x
3 4
y
12
对于表中数据,现给出下列拟合曲线,其中拟合程度最好的是________.
①y=2x-2 ②y=(12)x
③y=log2x ④y=12(x2-1)
7.在研究两个变量的相关关系时,观察散点图发现样本点集中于某一条指数曲线y=ebx+a的
周围,令z=ln y,求得线性回归方程为z^ =-,则该模型的回归方程为
________.
8.某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x
2 4 5 6 8
y
30 40 60 50 70
(1)画出散点图;
(2)求y关于x的线性回归方程.
9.某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 2002 2004 2006 2008 2010
需求量(万吨) 236 246 257 276 286
(1)利用所给数据求年需求量与年份之间的线性回归方程y^ =b^ x+a^ ;
(2)利用(1)中所求出的线性回归方程预测该地2012年的粮食需求量.
三、探究与拓展
10.某种书每册的成本费y元与印刷册数x(千册)有关,经统计得到数据如下:
x
1 2 3 5 10 20 30 50 100 200
y
检验每册书的成本费y元与印刷册数的倒数1x之间是否有线性相关关系,如有,求出
y
对1x的回归方程.
答案
1., 2.① 3.③ 6.④
=-
8.解 (1)散点图如图所示:
(2)列出下表,并用科学计算器进行有关计算.
i
1 2 3 4 5
x
i
(百万元) 2 4 5 6 8
y
i
(百万元) 30 40 60 50 70
xiy
i
60 160 300 300 560
x=5;y
=50;
∑5i=1x2i=145;∑5i=1xiyi=1 380
于是可得b^ =∑5i=1xiyi-5x y∑5i=1x2i-5x2=1 380-5×5×50145-5×52=,
a^ =y-b^ x
=50-×5=.
于是所求的线性回归方程是y^ =+.
9.解 (1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求线性回归方程,
先将数据预处理如下:
年份-2006 -4 -2 0 2 4
需求量-257万吨 -21 -11 0 19 29
由预处理后的数据,容易算得
x=0,y
=,
b
^
=-4×-21+-2×-11+2×19+4×2942+22+22+42=26040=,
a^ =y-b^ x
=.由上述计算结果,知所求线性回归方程为
y^ -257=b^ (x-2 006)+a^ =(x
-2 006)+.
即y^ =(x-2 006)+.
(2)利用所求得的线性回归方程,可预测2012年的粮食需求量为×(2 012-2 006)+=×6
+
=(万吨)≈300(万吨).
10.解 把1x置换为z,则z=1x,从而z与y的数据为:
z
1
y
根据数据可得r≈ 8>=,
故z与Y具有很强的线性相关关系.
由上表数据计算得b^ ≈,
a
^
≈,
从而y=+.
又z=1x,所以y^ =错误!+.
