自动控制原理相位角计算公式
王划一-自动控制原理-5-3稳定裕度
= 37.4
当(g) = 180时
180 = arctang 180 2arctan0.1g
求得
arctang =2arctan0.1g g = 8.94
20 lg h
20 lg A(g )
20
lg
k g g2 12
9.03dB
因为 > 0,所以闭环系统是稳定旳。
0
0 20 40 60 80
能够看出,调整时间与相角裕度和幅值穿越频率都有 关系。假如两个二阶系统旳相同,则它们旳超调量也相同, 这时比较大旳系统,调整时间较短。
17
例5-19 一单位反馈控制系统,其开环传递函数
G(s)
7
s(0.087s 1)
试用相角裕度估算过渡过程指标p% 与ts。
解:系统开环伯德图如图示
33
四 、奈奎斯特稳定判据
内容 应用
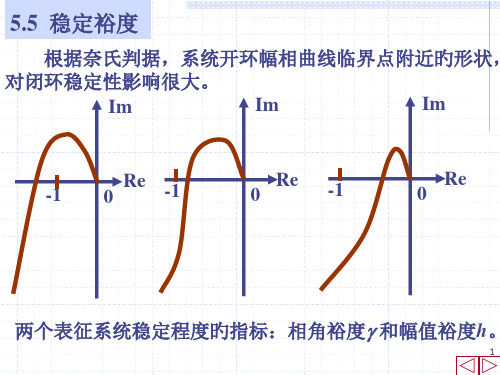
5.5 稳定裕度
根据奈氏判据,系统开环幅相曲线临界点附近旳形状,
对闭环稳定性影响很大。
Im
Im
Im
-1
Re 0
-1
Re 0
-1
Re 0
两个表征系统稳定程度旳指标:相角裕度 和幅值裕度h。
1
(1)幅值裕度h :令相角为180时相应旳频率为g (相角穿越频率),频率为g 时相应旳幅值A(g)旳倒数,
定义为幅值裕度h ,即 h 1 A(g )
10 11.5
0
1
20
40dB/dec
()/()
0
90
180
19
2) 高阶系统
近似旳关系式
p
0.16 0.4( 1
相位的公式

相位的公式
相位是描述波动或周期性信号状态的概念,通常用角度或弧度表示。
具体的相位公式取决于所涉及的具体信号类型和背景。
以下是一些常见的相位公式:
1. 正弦函数相位公式:
对于正弦函数,其相位可以使用以下公式表示:
φ= ωt + φ₀
其中,φ是相位,ω是角频率,t是时间,φ₀是初始相位。
2. 平面波相位公式:
对于平面波,其相位可以使用以下公式表示:
φ= kx -ωt + φ₀
其中,φ是相位,k是波数,x是位置,ω是角频率,t是时间,φ₀是初始相位。
3. 复数表示的相位公式:
对于复数表示的信号,其相位可以使用复数的辐角(即复数的幅角)表示:
φ= arg(z)
其中,φ是相位,z是复数。
需要注意的是,以上公式只是一些常见的相位公式示例,具体的相位公式还会根据具体的信号类型和应用领域而有所不同。
在具体的应用中,您可能需要根据具体的问题和信号特性来选择适当的相位公式。
自动控制原理:第5章 频域分析法 (2)

自动控制原理
12
1. 典型环节频率特性的极坐标图
(1)比例环节。比例环节的幅频特性和相频特性都是常量, 分别等于K及0°,不随频率w 而变化。
(1)比例环节 比例环节的频率特性函数为
G (jw) =K∠0° (K >0) 由于幅值和相角都不随频率w变化,所以,对数幅频特性 是一条平行于横轴且纵坐标值为20lg|G(jw)|=20lgK(dB)的直线。 对数相频特性恒为0°。
自动控制原理
21
(2)积分环节和微分环节
1)积分环节 积分环节的传递函数为
配方后可得
(U K ) 2 V 2 ( K ) 2
2
2
所以,在复平面上G(jw)为一圆心在(K/2,0)点, 半径为K/2的半圆,如图下半部分所示。当-∞w 0时,因为G(-jw)与G(jw)互为共轭关系,关于实 轴对称,即如上半圆所示。
自动控制原理
14
(4)一阶微分环节 (5)振荡环节
(6)延滞环节
自动控制原理
16
3.系统开环频率特性的极坐标图
系统的开环传递函数是由一系列典型环节组成的,因此, 系统的开环频率特性通常是若干典型环节频率特性的乘积,即
k
G( j) G1( j)G2 ( j)Gk ( j) Gi ( j)
i1
若写成极坐标形式,为
k
k
ji
G( j) Gi ( j) e i1
(4) 绘制对数幅频特性的其它渐近线; (5) 给出不同w值,计算对应的φi ,再进行代数相加, 画出系统的开环相频特性曲线。
自动控制原理公式汇总松鼠学长

自动控制原理公式汇总松鼠学长
自动控制原理涉及到很多公式,下面是一些常见的公式汇总:1.开环传递函数:G(s) = Y(s)/U(s)
- G(s)表示系统的传递函数
- Y(s)表示输出信号的Laplace变换
- U(s)表示输入信号的Laplace变换
2.闭环传递函数:T(s) = Y(s)/R(s)
- T(s)表示闭环系统的传递函数
- Y(s)表示输出信号的Laplace变换
- R(s)表示参考输入信号的Laplace变换
3.系统的单位反馈闭环传递函数:T(s) = G(s)/(1 + G(s)H(s)) - T(s)表示闭环系统的传递函数
- G(s)表示开环系统的传递函数
- H(s)表示单位反馈的传递函数
4.闭环系统的稳定性判据:若开环传递函数G(s)的所有极点的实部都小于零,则闭环系统是稳定的。
5. PID控制器输出信号:u(t) = Kp*e(t) + Ki*∫[0,t] e(τ) dτ + Kd*de(t)/dt
- u(t)表示PID控制器的输出信号
- Kp是比例增益
- Ki是积分增益
- Kd是微分增益
- e(t)是误差信号,等于参考输入信号与实际输出信号之差
这些公式只是自动控制原理中的一小部分,实际上自动控制原理是一个庞大的学科,涉及到许多不同的理论和方法。
它还包括了传感器和执行器的动态特性、控制器的设计和调节、系统的鲁棒性等方面的内容。
在实际应用中,根据具体问题的要求,可能还需要考虑动态特性的影响、非线性系统的建模和控制、多变量系统的控制等更高级的内容。
因此,适当拓展自动控制原理的公式是必要的。
相位计算公式范文

相位计算公式范文相位计算是一种数学和物理学中常用的计算方法,用于确定一个波动物体或者系统所处的状态。
相位计算通常描述了一个物理系统或者波动现象的时间演化和周期性变化。
下面是关于相位计算的详细介绍,超过1200字:1.相位的定义及表示方式:相位是指描述一个波动对象或者系统所处状态的物理量。
在波动中,相位可以被定义为与相对时间的关系,通常以角度或者弧度的形式表示。
相位可以用于确定波动在时间和空间上的演化,以及与其他波动的相互作用。
2.相位计算的基本原理:相位计算的基本原理可以由下面的公式表示:φ=ωt+φ0其中,φ表示相位,ω表示角频率,t表示时间,φ0是相位的初始值。
这个公式是基于周期性现象的表达式,其中角频率可以用来确定相位的变化速率。
相位的初始值表示在t=0时刻的相位值。
3.相位计算的应用:相位计算在物理学和工程学中有广泛的应用。
以下是一些常见的相位计算的应用:-光学和电磁学:在光学和电磁学中,相位计算用于描述光波或者电磁波的传播和干涉现象。
相位计算可以帮助我们理解光的传播路径和光的相位变化。
-信号处理:相位计算在信号处理中常常被用来描述信号的周期性和相互关系。
相位计算可以用于音频信号的合成和重构,以及声音、图像和视频的处理。
-音乐和声学:相位计算在音乐和声学中有广泛的应用。
相位计算可以帮助我们理解和分析乐器音色的特征、声音的合成和空间效果。
-振动和波动:相位计算在振动和波动的研究中起到重要作用。
相位计算可以帮助我们理解波动现象的传播、干涉和共振行为。
-量子力学:相位计算在量子力学中被广泛使用。
相位计算可以描述粒子的波函数演化和量子态的变化。
4.相位计算的算法和方法:相位计算的算法和方法取决于所研究的波动现象的性质和所使用的数学模型。
以下是一些常用的相位计算的方法:-傅里叶变换:傅里叶变换是一种常用的相位计算方法。
通过将时间域信号转换为频域信号,可以从频谱上分析出相位信息。
-自相关函数:自相关函数是一种用于相位计算的方法,可以通过比较信号与其自身的延迟版本,得出相位信息。
相位裕度计算公式例题

相位裕度计算公式例题相位裕度是指系统的相位裕量,它是系统相位特性的一种指标。
相位裕度越大,系统的稳定性就越好。
相位裕度通常用于评估控制系统的稳定性。
相位裕度可以通过计算系统的相位裕量来求得。
相位裕量是指系统相位曲线与-180度的垂直距离。
当相位裕量大于零时,系统就具有相位裕度。
相位裕度的计算公式如下:相位裕量 = 180度 + 相位裕量角其中,相位裕量角是指系统相位曲线与-180度之间的夹角。
下面是一个相位裕度计算公式的例题:已知系统的开环传递函数为G(s)=K/(s+1)(s+2),求该系统在K=1时的相位裕度。
解题步骤如下:1.首先,将开环传递函数转化为极坐标形式。
G(jω) = K/(jω+1)(jω+2)G(jω) = K(1-jω)(1-2jω)/[(1+ω^2)(4+ω^2)]2.计算系统的相位曲线。
系统的相位曲线为:φ(ω) = atan(-ω) + atan(-2ω) - atan(ω) - atan(2ω) 3.计算相位裕量角。
相位裕量角为:φm = -π/2 - φ(ωc)其中,ωc为系统的截止频率,即当G(jω)的模为1时的频率。
将G(jω)的模设为1,并解出ωc,则ωc=0.9609。
代入相位曲线中,可得:φm = -π/2 - φ(0.9609)φ(0.9609) ≈ -132.6度φm ≈ 47.4度4.计算相位裕量。
相位裕量为:PM = 180度 + φmPM ≈ 227.4度因此,当K=1时,该系统的相位裕度为227.4度。
初始相位公式
初始相位公式初始相位公式是指在电路中,电压和电流之间存在一定的相位差。
这个相位差是由电路元件的电学特性和电路中的电流和电压之间的关系所决定的。
在交流电路中,电流和电压的相位差可以通过初始相位公式来计算。
初始相位公式的一般形式为:θ = arctan (XC – XL) / R其中,θ表示电路中电流相对于电压的相位差;XC表示电容的阻抗;XL表示电感的阻抗;R表示电路中的电阻。
从公式中可以看出,电容和电感的阻抗对电路中的相位差起着决定性的作用。
当电路中存在电容时,电流会领先电压;而当电路中存在电感时,电流会滞后电压。
这个相位差的大小取决于电路中电容和电感的阻抗大小,以及电路中的电阻值。
初始相位公式的应用非常广泛,可以用于解决各种交流电路中的问题。
例如,当我们需要计算电路中的电压和电流的相位差时,可以使用初始相位公式进行计算。
此外,初始相位公式还可以用于计算电路中的功率因数。
功率因数是指电路中有用功率与总功率之比,是衡量电路效率的重要指标。
在交流电路中,功率因数的大小取决于电路中电压和电流的相位差,因此可以使用初始相位公式来计算功率因数。
除了在交流电路中的应用外,初始相位公式还可以用于解决其他电路问题。
例如,在直流电路中,当电路中存在电感时,电路中的电流会产生自感电动势,从而影响电路的稳定性。
此时,可以使用初始相位公式来计算电路中电感的阻抗,并据此选择合适的电阻值来稳定电路。
初始相位公式是电路分析中非常重要的公式之一,可以用于解决各种电路问题。
在实际应用中,我们需要根据具体电路的情况选择合适的公式和方法,以确保电路的正常工作和性能优化。
自动控制 基本原理和基本概念概要
第一篇基本原理和基本概念概要第一章绪论一、自动控制和自动控制系统基本概念1.自动控制:在没有人直接参与的情况下,利用控制设备或装置,使被控对象的被控量自动的按预定的规律变化。
2.自动控制系统:能自动对被控对象的被控量(或工作状态)进行控制的系统。
3.被控对象(又称受控对象):指工作状态需要加以控制的机械、装置或过程。
4.被控量:表征被控对象工作状态且需要加以控制的物理量,也是自动控制系统的输出量。
5.给定值(又称为参考输入):希望被控量趋近的数值。
又称为规定值。
6.扰动量(又分为内扰和外扰):引起被控量发生不期望的变化的各种内部或外部的变量。
7.控制器(又称调节器):组成控制系统的两大要素之一(另一大要素即为被控对象),是起控制作用的设备或装置。
8.负反馈控制原理:将系统的输出信号反馈至输入端,与给定的输入信号相减,所产生的偏差信号通过控制器变成控制变量去调节被控对象,达到减小偏差或消除偏差的目的。
二、自动控制原理的组成和方框图典型的自动控制系统的基本组成可用图1.1-1的方框图来表示。
其中的基本环节有:1)受控对象:需要控制的装置、设备及过程。
2)测量变送元件:测量被控量的变化,并使之变换成控制器可处理的信号(一般是电信号)。
3)执行机构:将控制器发来的控制信号变换成操作调节机构的动作。
4)调节机构:可改变受控对象的被控量, 使之趋向给定值。
5)控制器:按照预定控制规律将偏差值变换成控制量。
自动控制装置图 1.1-1三、自动控制系统的基本控制方式:自动控制系统的基本控制方式有开环控制、闭环控制和复合控制三种。
开环控制适用于控制任务要求不高的场合。
工程上绝大部分的自动控制系统为闭环控制。
对控制任务要求较高,且扰动量可测量的场合,常采用复合控制系统(又称前馈——反馈复合控制系统)。
四、自动控制系统的分类1.按给定输入的形式分类:恒值控制系统、随动控制系统、程序控制系统。
2.按元件的静态特性分类:线性控制系统、非线性控制系统。
uab相位角 -回复
uab相位角 -回复 什么是uab相位角?
UAB相位角是指交流电压或电流波形相对于参考信号(通常为正弦波)的位移角度,用来描述波形相对于时间的偏移情况。在电力系统、通信系统以及电子设备中,了解和掌握UAB相位角的概念和计算方法非常重要。
一、UAB相位角的定义 UAB相位角是一个角度的度量,用度()来表示。它表示的是交流电压或电流波形相对于参考信号的位移角度,或者可以理解为相位差的大小。
对于正弦波,UAB相位角可以简单地理解为波形相对于标准正弦波的时间偏移。如果两个正弦波完全同相,它们的相位角为0;如果它们之间相差180,则它们的相位角为180。
二、UAB相位角的测量方法 测量UAB相位角一般可以通过示波器或相位差仪来实现。示波器可以根据输入信号的波形,直接显示相位角的数值。 对于两个交流电压波形,可以将它们同时输入示波器,并选择相位差测量功能。示波器会计算出这两个波形之间的相位差,并显示在屏幕上。相位差的数值就是UAB相位角的大小。
三、UAB相位角的计算方法 除了使用示波器测量外,我们还可以通过波形的数学计算来求解UAB相位角。
假设有两个正弦波信号Ua和Ub,其表达式为: Ua(t) = A*sin(ωt + φa) Ub(t) = B*sin(ωt + φb) 其中A、B分别为两个波形的振幅,ω为角频率,t为时间,φa和φb分别为两个波形的初始相位角。
Ua和Ub两个波形的相位角差可以通过如下公式计算: Δφ = φa - φb 为了简化计算,我们可以经常将一个波形的参考相位角设置为0,然后计算相对于这个参考相位角的相位差。
四、UAB相位角的应用 UAB相位角在电力系统中非常重要。在交流电网中,不同线路的电压波形相位差的大小直接影响到电网的稳定性和可靠性。通过测量和分析UAB相位角,可以得出电网中各个部分的相位差分布情况,有助于发现潜在的问题点并采取相应的补救措施,确保电网的稳定运行。
(完整版)自动控制原理重要公式
A.阶跃函数 斜坡函数 抛物线函数 脉冲函数 正弦函数B.典型环节的传递函数 比例环节 惯性环节(非周期环节) 积分环节微分环节 二阶振荡环节(二阶惯性环节) 延迟环节 C.环节间的连接串联并联反馈 开环传递函数=前向通道传递函数=负反馈闭环传递函数正反馈闭环传递函数D.梅逊增益公式E.劳斯判据 劳斯表中第一列所有元素均大于零 s n a 0 a 2 a 4 a 6 …… s n-1 a 1 a 3 a 5 a 7 ……s n-2 b 1 b 2 b 3 b 4 …… s n-3c 1 c 2 c 3 c 4 …… … … …s 2 f 1 f 2s 1 g 1 s 0 h 1,,,,,,141713131512121311171603151402131201b b b a a c b b b a a c b b b a a c a a a a a b a a a a a b a a a a a b -=-=-=-=-=-=劳斯表中某一行的第一个元素为零而该行其它元素不为零,ε→0; 劳斯表中某一行的元素全为零。
P(s)=2s 4+6s 2-8。
F.赫尔维茨判据 特征方程式的所有系数均大于零。
⎩⎨⎧≥<=00)(t A t t r ⎩⎨⎧≥<=000)(t At t t r ⎪⎩⎪⎨⎧≥<=02100)(2t At t t r ⎪⎩⎪⎨⎧>≤≤<=εεt t z At t r 0000)(⎩⎨⎧≥<=0sin 00)(t t A t t r ωKs R s C s G ==)()()(1)()()(+==Ts K s R s C s G sT s R s C s G i 1)()()(==sT s R s C s G d ==)()()(2222)(n n ns s K s G ωζωω++=se s R s C s G τ-==)()()()()()( )()()()()()()()()(211121s G s G s G s X s C s X s X s R s X s R s C s G n n =⋅==-)()()( )()()()()()()(2121s G s G s G s R s C s C s C s R s C s G n n +++=+++== )()()()(s H s G s E s B =)()()(s G s E s C =)()(1)()()()(s H s G s G s R s C s +==Φ)()(1)()()()(s H s G s G s R s C s -==Φ∆∆=∑kk P TG.误差传递函数扰动信号的误差传递函数H.静态误差系数单位 输入形式 稳态误差e ss 0型 Ⅱ型 Ⅲ型 阶跃1(t) 1/1+Kp 0 0 斜坡t ·1(t) ∞ 1/Kv 0 加速度0.5t 2·1﹙t ﹚∞ ∞ 1/Ka I.二阶系统的时域响应: 其闭环传递函数为 或 系统的特征方程为2)(22=++=nn s s s D ωζω特征根为1,221`-±-=ζωζωn n s上升时间t r其中 峰值时间t p最大超调量M p调整时间t sa.误差带范围为 ±5%b.误差带范围为± 2%振荡次数NJ.频率特性:还可表示为:G (jω)=p (ω)+jθ(ω) p (ω)——为G (jω)的实部,称为实频特性; θ(ω)——为G (jω)的虚部,称为虚频特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理相位角计算公式
自动控制原理是一门研究系统自动化控制的学科,其中相位角计算是其中的一个重要内容。
相位角是指在周期性变化的信号中,某一特定时刻相对于参考时刻的角度差。
在自动控制系统中,相位角的计算对于系统的稳定性和性能具有重要影响。
在自动控制系统中,信号的相位角是通过频率和时间来计算的。
频率是指信号的周期性变化的频率,而时间则是指信号的变化经过的时间。
根据这两个参数,可以使用以下公式来计算相位角:
相位角= 360° × (时间 / 周期)
其中周期是信号的周期,即信号从一个起点到达下一个起点所经过的时间。
时间则是指信号的变化经过的时间。
相位角的计算在自动控制系统中具有重要的意义。
首先,相位角可以用来描述信号的相对位置。
在控制系统中,多个信号之间的相位差可以决定系统的稳定性。
如果多个信号之间的相位差过大,可能会导致系统的不稳定。
因此,通过计算相位角,可以评估系统的稳定性,并进行相应的调整和优化。
相位角的计算还可以用来评估系统的性能。
在自动控制系统中,系统的响应速度往往是一个重要的指标。
通过计算相位角,可以了解系统的响应速度是否满足要求。
如果相位角偏离预期值过大,可能
意味着系统的响应速度不够快,需要进行相应的调整和改进。
相位角的计算还可以用来分析信号的特性。
在自动控制系统中,信号的相位角可以提供关于信号波形的有用信息。
通过计算相位角,可以了解信号的起点位置以及变化的趋势。
这对于理解信号的特性和进行系统分析非常重要。
自动控制原理相位角计算公式是自动控制系统中一个重要的内容。
通过计算相位角,可以评估系统的稳定性和性能,以及分析信号的特性。
相位角的计算可以帮助工程师进行系统优化和改进,提高自动控制系统的稳定性和性能。
同时,相位角的计算也为信号分析和系统分析提供了有用的工具。
