水平宽,铅垂高
二次函数中“铅垂高”的应用

①用含m的代数式表示线段PF的长,并求出当m为 何值时PF最大.
②连接CF、BF,当m为何值时,△BCF的面积最大
③当m为何值时,PF=2PN
y D
C
EF
P A O NB x
(4)过点F作FM⊥BC于M,当m为何值时, △PMF的周长最大 (5)若点P为射线CB上一动点,其他条件不变, 直接写出当m为何值时,以P、E、D、F为顶点的 四边形是平行四边形.
二次函数中“铅垂高”的应用
课堂目标
1.理解“铅垂高”的定义,掌握二次函数 中有关铅垂高的计算.(重点) 2.利用铅垂高求图形的周长或面积的最大 值.(难点)
“铅垂高”定义
阅读材料:
如图1,过△ABC的三个顶点分别作出 与水平线垂直的三条直线,外侧两条直
A 铅垂
h
高C
线之间的距离叫△ABC的“水平宽”(a),B 中间的这条直线在△ABC内部线段的长
DE AC 于点 E .设点 D 的横坐标为 m .求 DE 的长关于 m 的函数解析式,
并写出 DE 长的最大值;.
y D
C EF M
P
A O NB x
当堂训练
如图,在平面直角坐标系中,直线 y kx 3 与抛物线 y ax2 bx 5 交于
2
2
点 A 、C ,与 y 轴交于点 B ,点 A 的坐标为 (2,0) ,点C 的横坐标为8 .
(1)请直接写出直线和抛物线的解析式;
(2)点 D 是直线 AB 上方的抛物线上一动点(不与点 A 、C 重合),作
水平 宽a
度叫△ABC的“铅垂高(h)”.我们可得
图1
出一种计算三角形面积的新方
法即:三S角A形BC面 积12 a等h 于水,平宽与铅2x 3
水平宽铅垂高求三角形面积
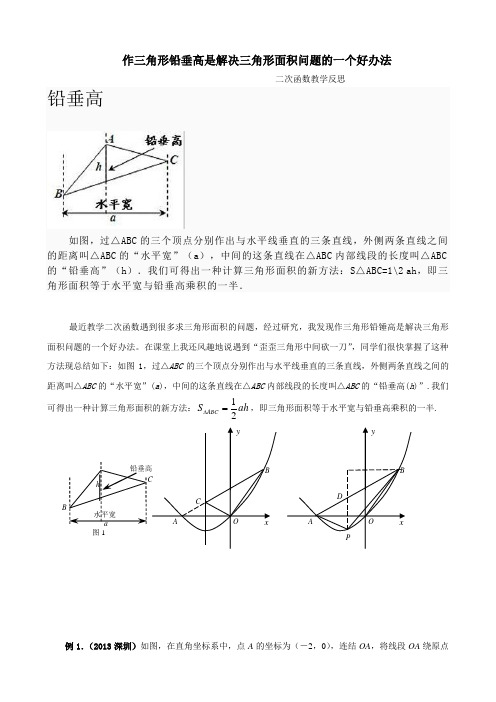
作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC 的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:ahSABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点图1O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△P AB 是否有最大面积?若有,求出此时P 点的坐标及△P AB 的最大面积;若没有,请说明理由. 解:(1)B (1(2)设抛物线的解析式为y =ax (x+a ),代入点B (1,,得a =,因此2y =(3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪⎪⎩解得因此直线AB为y =+,当x =-1时,y =,因此点C 的坐标为(-1).(4)如图,过P 作y 轴的平行线交AB 于D. 2221()()213212PAB PAD PBD D P B A S S S y y x x x ∆∆∆=+=--⎡⎤⎫=+-+⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=+⎫=+⎪⎝⎭当x =-12时,△P AB,此时1,2P ⎛- ⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结P A ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △P AB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:图-2xC Oy ABD 113,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△P AB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △P AB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
水平宽铅垂高求三角形面积完整版

解:(1)将B、C两点的坐标代入得
解得: 所以二次函数的表达式为:
(2)存在点P,使四边形POP C为菱形.设P点坐标为(x, ),PP 交CO于E若四边形POP C是菱形,则有PC=PO.
连结PP 则PE⊥CO于E,∴OE=EC= = .
∴ = 解得 = , = (不合题意,舍去)
∴P点的坐标为( , )
(3)过点P作 轴的平行线与BC交于点Q,与OB交于点F,设P(x, ),易得,直线BC的解析式为 则Q点的坐标为(x,x-3).
图① 图②
3.(2015年恩施) 如图11,在平面直角坐标系中,二次函数 的图象与x轴交于A、B
两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,
点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP C,那么是否存在点P,使四边形POP C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
水平宽铅垂高求三角形面积
作三角形铅垂高是解决三角形面积问题的一个好办法
------------二次函数教学反思
铅垂高
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.
例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
水平宽铅垂高求三角形面积
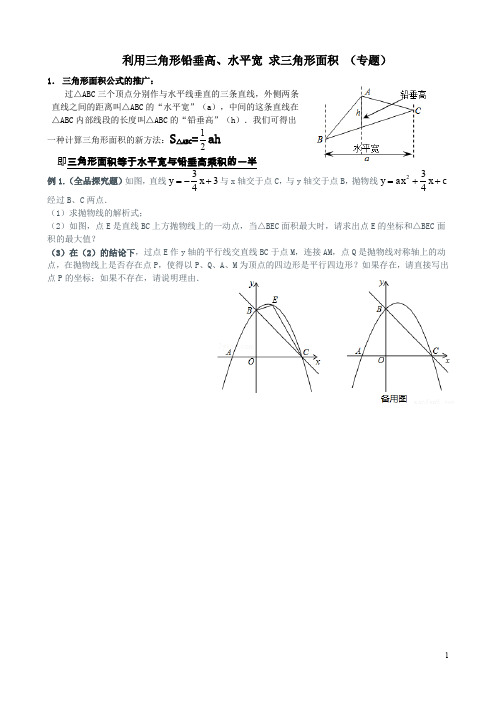
利用三角形铅垂高、水平宽 求三角形面积 (专题)1. 三角形面积公式的推广:过△ABC 三个顶点分别作与水平线垂直的三条直线,外侧两条 直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在 △ABC 内部线段的长度叫△ABC 的“铅垂高”(h ).我们可得出一种计算三角形面积的新方法:S △ABC =21ah 即三角形面积等于水平宽与铅垂高乘积的一半例1.(全品探究题)如图,直线343+-=x y 与x 轴交于点C ,与y 轴交于点B ,抛物线c x ax y ++=432经过B 、C 两点.(1)求抛物线的解析式;(2)如图,点E 是直线BC 上方抛物线上的一动点,当△BEC 面积最大时,请求出点E 的坐标和△BEC 面积的最大值?(3)在(2)的结论下,过点E 作y 轴的平行线交直线BC 于点M ,连接AM ,点Q 是抛物线对称轴上的动点,在抛物线上是否存在点P ,使得以P 、Q 、A 、M 为顶点的四边形是平行四边形?如果存在,请直接写出点P 的坐标;如果不存在,请说明理由.例2.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△P AB是否有最大面积?若有,求出此时P点的坐标及△P AB的最大面积;若没有,请说明理由.解:例3.如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.(1)求抛物线和直线AB的解析式;(2)点P是抛物线(在第一象限内)上的一个动点,连结P A,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及CABS;(3)是否存在一点P,使S△P AB=89S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.解:图1图-2xCOyABD11例4.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点。
三角形面积公式——之水平宽铅垂高(叶茂恒)教学文稿
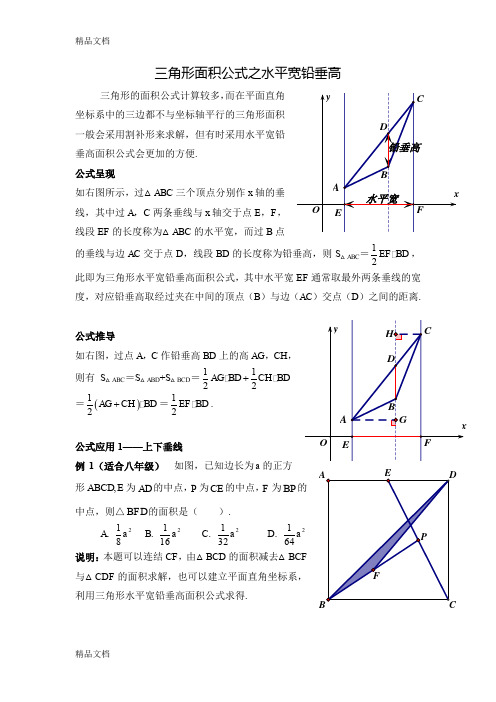
精品文档三角形的面积公式计算较多,垂高面积公式会更加的方便. 公式呈现如右图所示,过△ABC 三个顶点分别作x 线,其中过A ,C 两条垂线与x 轴交于点E ,F 线段EF 的长度称为△ABC 的水平宽,而过B 的垂线与边AC 交于点D ,线段BD BD ,通常取最外两条垂线的宽度,对应铅垂高取经过夹在中间的顶点(B )之间的距离.公式推导如右图,过点A ,C 作铅垂高BD 上的高AG ,则有S △ABC =S △ABD +S △BCD =1122AG BD CH +=()12AG CH BD +=12EF BD .公式应用1——上下垂线例1(适合八年级) 如图,已知边长为a 形E ABCD ,为AD 的中点,P 为CE 的中点,F 为中点,则△BFD 的面积是( ).A .281a B . 2161a C . 2321a D .说明:本题可以连结CF ,由△BCD 的面积减去与△CDF 利用三角形水平宽铅垂高面积公式求得.精品文档解析:不妨以B 为原点,BC 为x 轴,BA 为y 轴建立平面直角坐标系,则点C 坐标为(a ,0),点D 坐标为(a ,a ),∵E 为AD 的中点,∴点E 坐标为(12a ,a ), ∵P 为CE 的中点,∴点P 坐标为(34a ,12a ),∵F 为BP 的中点,∴点F 坐标为(38a ,14a ).过F 点作BC 的垂线交BD 于点G ,则点G 的横坐标为38a ,又直线BD 的解析式为y x =,∴点G 的纵坐标为38a ,∴△BDF 的铅垂高FG =38a -14a =18a ,∴S △BDF =2111122816BC FG a a a ==.公式应用2——左右垂线例2(适合八年级) 如图,直线1y x =+与x 轴,y 轴分别交于点A ,B ,以线段AB 为直角边在第一象限内作等腰直角△ABC ,且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭,且△ABP 的面积与Rt △ABC 的面积相等,求a 的值.说明:本题常见解法有三,一是连结OP ,△ABP 的面积=△AOB 面积+△BOP 面积-△AOP 面积,然后用a 的代数式表示,与Rt △ABC相等列方程求解;二是将点C 沿AB 翻折到C ’位置,则△ABC △ABC ’面积相等,若△ABP 的面积与Rt △ABC P精品文档相等,则可得PC ’//AB ,因此,可以由点A ,C 坐标先求C ’坐标,再根据AB 的斜率与点C ’坐标求直线PC ’的解析式,将点P 纵坐标代入,即可求a 的值. 三是考虑水平宽铅垂高公式来计算,但如果从A ,B ,P 三点向x 轴作垂线,较为复杂,不妨换个角度应用公式,即从A ,B ,P 向y 轴作垂线(即左右方向作垂线)解析:过线,则OB 而PE 度)由AB OB =1,而P 的纵坐标为12,所以E 为AB 的中点, 所以PE =-a +2, 从而有1122122a ⎛⨯⨯=⨯⨯- ⎝⎭ , 解得4a =-.公式应用3——内外垂线从例2可以看到,三条垂线不一定作向x 轴,也可以作向y 轴,仿公式用即可.一般地,水平宽取的是最外的两条直线的距离,但这个做法不是绝对的,有12EF CG . 简单推导:S △ABC =S △ACG -S △BCG =1122CG EH CG FH -=12EF CG .精品文档说明:当取相邻两条垂线距离为水平宽时,第三条垂线将与第三边(AB )的延长线相交,此时顶点(C )到交点(G )的距离为铅垂高(CG ). 例3(适合九年级) 如图所示,直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B .把△AOB 沿y 轴翻折,点A 落到点C ,抛物线过点B ,C 和D (3,0). (1)求直线BD 和抛物线的解析式.(2)若BD 与抛物线的对称轴交于点M ,点N 在坐标轴上,以点N ,B ,D 为顶点的三角形与△MCD 相似,求所有满足条件的点N 的坐标.(3)在抛物线上是否存在点P ,使S △PBD =6?若存在,求出点P 的坐标;若不存在,说明理由.(4)点Q 是抛物线对称轴上一动点,是否存在点Q 使得CQ BQ -的值最大,若存在,请直接写出点Q解析:本题只解(3),由已知条件可以得抛物线解析式为243y x x =-+,BD 解析式为3y x =-+,由于问题中并未交待P 点在BD 的上方或下方,故要分类讨论:当P 在BD 下方时,如右上图,水平宽为OD=3,铅垂高为PE =224333x x x x x -++-=-; 当P 在BD 上方时,P 可能在左,也可以在右,但两者本质相同,如右下图,此时依然取OD =3为水平宽,则铅垂高PE =223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=,即234x x -=±.精品文档当234x x -=-时,方程无实数根,即P 在BD 下方时,不可能面积为6;当234x x -=时,解得121,4x x =-=,即当P (-1,8)或P (4,3)时,S △PBD =6.解后:从以上几例可以看到,灵活运用水平宽与铅垂高公式,可以有效解决三角形面积问题,尤其是在例3,可以将P 点的两种不同的位置分类统一为PE 长(绝对值)问题求解,可以有效回避原本点P 在BD 上方时,几何法要构造高等繁杂作法,使得问题解决简洁而快捷.老叶2015年1月26日记于温十七中。
水平宽铅垂高求三角形面积.doc
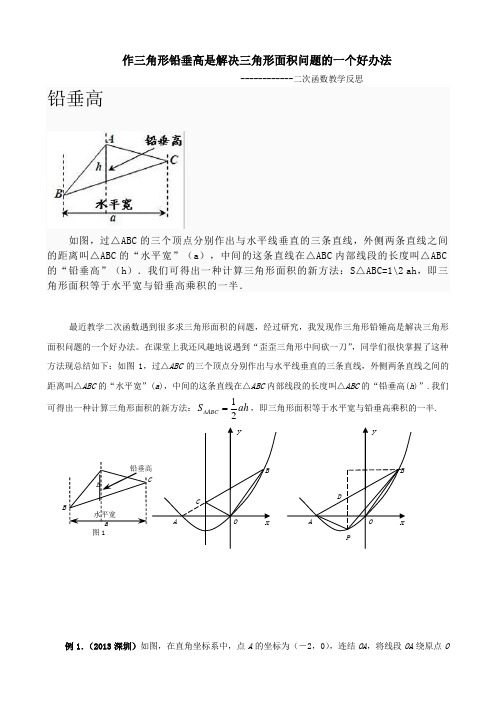
作三角形铅垂高是解决三角形面积问题的一个好办法------------二次函数教学反思铅垂高如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC 的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=1\2 ah,即三角形面积等于水平宽与铅垂高乘积的一半.最近教学二次函数遇到很多求三角形面积的问题,经过研究,我发现作三角形铅锤高是解决三角形面积问题的一个好办法。
在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀”,同学们很快掌握了这种方法现总结如下:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:ahSABC21=∆,即三角形面积等于水平宽与铅垂高乘积的一半.例1.(2013深圳)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O 图1顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由. 解:(1)B (1(2)设抛物线的解析式为y =ax (x+a ),代入点B (,得a,因此2y =+ (3)如图,抛物线的对称轴是直线x =—1,当点C 位于对称轴与线段AB 的交点时,△BOC 的周长最小.设直线AB 为y =kx +b .所以20.k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得,因此直线AB为y =+,当x =-1时,y =,因此点C 的坐标为(-1). (4)如图,过P 作y 轴的平行线交AB 于D. 2221()()213212PAB PAD PBD D P B A S S S y y x x x x x x ∆∆∆=+=--⎡⎤⎫=+-+⨯⎢⎥⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦=⎫=+⎪⎝⎭当x =-12时,△PAB,此时1,2P ⎛- ⎝⎭. 例2.(2014益阳) 如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆;(3)是否存在一点P ,使S △PAB =89S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由.解:(1)设抛物线的解析式为:4)1(21+-=x a y 把A (3,0)代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为:b kx y +=2由3221++-=x x y 求得B 点的坐标为)3,0( 把)0,3(A ,)3,0(B 代入b kx y +=2中解得:图-2xCOy ABD113,1=-=b k 所以32+-=x y(2)因为C 点坐标为(1,4)所以当x =1时,y 1=4,y 2=2所以CD =4-2=232321=⨯⨯=∆CAB S (平方单位) (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△PAB 的铅垂高为h ,则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得389)3(3212⨯=+-⨯⨯x x 化简得:091242=+-x x 解得,23=x 将23=x 代入3221++-=x x y 中,解得P 点坐标为)415,23(例3.(2015江津)如图,抛物线c bx x y ++-=2与x 轴交于A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.解:(1)将A(1,0),B(-3,0)代2y x bx c =-++中得10930b c b c -++⎧⎨--+=⎩=∴23b c =-⎧⎨=⎩∴抛物线解析式为:223y x x =--+(2)存在。
面积问题之”水平宽、铅锤高“模型的实战分析
三角形面积问题之“宽高公式”的实战分析高邮市赞化学校段广猛《三角形面积问题之“宽高公式”的两种证明方法》一文中,主要介绍了三种情形下“宽高公式”模型的证明.如图1、图2、图3所示,12ABCS OC AD∆=⨯⨯,其中OC表示B、C两点在水平方向上的距离,简称这个三角形的“水平宽”;而AD表示点A到边BC在竖直方向上的距离,简称这个三角形的“铅锤高”.于是三角形的面积S=12⨯水平宽⨯铅锤高,这个公式不妨称为“宽高公式”.细心观察上面三种情形,操作方式都是过点A作平行于y轴的直线交边BC所在的直线于点D,则AD就是“铅锤高”;而B、C两点之间的水平距离,即线段OC就是“水平宽”.在实际应用中,笔者不建议学生固化思维,强记这里的结论而直接使用.一方面,这个公式课本上并没有直接出现,中考时能不能直接使用值得商榷;另一方面,对于图2的结论,大部分学生普遍可以接受,但是若是不知道这个公式推导的来龙去脉而强行直接使用,图1及图3的结论,多数学生是很难理解原理而导致不能正确使用.更何况,这三种情形下的推导过程也是相辅相成、思想统一的,都采用了“改斜归正”及“割补法”的思想,而这两种思想方法又是极其重要的解题原理,需要同学们认真深刻体会的,所以笔者强烈建议学生体会这里的推导原理,以达到灵活使用的目的.其实,掌握了原理,怎么割补三角形都可以,只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线都可以实现面积处理,仅仅是繁简程度不一而已,下文会一一提及.如图4、图5、图6所示,12ABC S BD AE ∆=⨯⨯,其中BD 表示点B 到边AC 在水平方向上的距离,简称这个三角形的“水平宽”;而AE 表示A、C 两点在竖直方向上的距离,简称这个三角形的“铅锤高”.于是依然有三角形的面积S=12⨯水平宽⨯铅锤高.这三张图的操作方式都是过点B 作平行于x 轴的直线交边AC 所在的直线于点D,则BD 就是“水平宽”;而A、C 两点之间的竖直距离,即线段AE 就是“铅锤高”.实际上,过点C 作平行于坐标轴的直线,无论是平行于x 轴,还是平行于y 轴,最终都可以实现对于此三角形的面积处理,有时是“割”,即“面积加法”;有时是“补”,即“面积减法”.由此可以看出,不用强记公式,只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线,无论是平行于x 轴,还是平行于y 轴,都可以实现面积处理.图7提供了一种方式,12ABC S CD AE ∆=⨯⨯.那么问题来了,割补方式千变万化,而且好像都可行,在解题实战中,难道就随意割补吗?非也!理论上是都可行,但计算量绝不相当!我们知道,“在变化中抓不变量”也是一种重要的思想方法,“以不变应万变”.此时再结合这个解题策略,就可以使计算过程“如履平地”.在三角形三个顶点中,一般情况下会有两个定点和一个动点,抓住这两个定点就是关键所在.如图8或图9所示,点B 和点C 是两个定点,而点A 是一个动点.这时,我们就应该过动点A 作平行于y 轴或者平行于x 轴的直线交直线BC 于点D,利用B、C 两个定点求出直线BC 的解析式,再设出动点A 的坐标,将横坐标或者纵坐标代入直线BC 的解析式,表示出点D 的坐标,进而容易表示出线段AD.在图9中,ABC ACD ABD S S S ∆∆∆=-=12AD CF ⋅11(CF )22AD BE AD BE -⋅=⋅-1(OE )2AD BE =⋅-12AD OB =⋅,因为B、C 都是定点,故OB 是常值,而且直线BC 的解析式易求,进而AD 的长度好表示.若是你“不信邪”,偏偏如图10所示那样“割补”,我想说“此路依然行得通”,但与前面的两种方法相比,一烦在“水平宽”BD 上,需要求出直线AC 的解析式,理论上肯定行得通,这条直线的解析式会因为点A 是动点而导致含有参数,计算量较大;二烦在“铅锤高”AE 上,也是因为点A 是动点而导致含有参数.“罪魁祸首”都在动点A 上,而“元凶”就是因为一开始过定点B 进行了“割补”.需要特别说明的是,这种方法并非是错误的,仅仅是计算量较大些,其操作依然是可行的.下面以2016年苏州中考压轴题第(2)问为例具体谈谈“宽高公式”的使用.(2016•苏州)如图11,直线l:y=-3x+3与x 轴、y 轴分别相交于A、B 两点,抛物线y=ax 2﹣2ax+a+4(a<0)经过点B.(1)求该抛物线的函数表达式;(2)已知点M 是抛物线上的一个动点,并且点M 在第一象限内,连接AM、BM,设点M 的横坐标为m,△ABM 的面积为S,求S 与m 的函数表达式,并求出S 的最大值.对于第(1)小问,易知该抛物线的函数表达式为:y=-x 2+2x+3;对于第(2)小问,这是一个“两定一动型”三角形面积问题,“死咬”A、B 两定点“不松口”,过动点M 作平行于坐标轴的直线进行“割补”即可,这里提供两种方式.方式一:如图12所示,过动点M 作平行于y 轴的直线交边AB所在的直线于点N,则ABM MNB MNA S S S ∆∆∆=-=12MN OG ⋅11(OG )22MN AG MN AG -⋅=⋅-12MN OA =⋅.设M(t,-t 2+2t+3),其中t 的取值范围是0<t<3,则N(t,-3t+3),从而MN =M N y y -=(-t 2+2t+3)-(-3t+3)=-t 2+5t,而OA=1,故S=12(-t 2+5t)=-12t(t-5),当t=52时,S 有最大值为258.值得一提的是,上面的操作过程可总结如下:第一步:抓住两个定点A 和B,它们之间在水平方向上的距离OA 作为△ABM 的“水平宽”;第二步:过动点M 作平行于y 轴的直线交边AB 所在的直线于点N,则MN 作为△ABM 的“铅锤高”;第三步:将面积“往竖直线MN 上靠”,通过面积“减法”,得到所求三角形的面积为12ABM S MN OA ∆=⋅.方式二:如图13所示,过动点M 作平行于x 轴的直线交边AB 所在的直线于点N、交y 轴于点G,则ABM MNB MNA S S S ∆∆∆=+=12MN BG ⋅11(BG O )22MN OG MN G +⋅=⋅+12MN OB =⋅.设M(t,-t 2+2t+3),其中t 的取值范围是0<t<3,则N(223t t -,-t 2+2t+3),从而MN =M N x x -t -223t t -=253t t -+,而OB=3,故S=122533t t -+⋅⋅=-12t(t-5),当t=52时,S 有最大值为258.上面的操作过程可总结如下:第一步:抓住两个定点A 和B,它们之间在竖直方向上的距离OB 作为△ABM 的“铅锤高”;第二步:过动点M 作平行于x 轴的直线交边AB 所在的直线于点N,则MN 作为△ABM 的“水平宽”;第三步:将面积“往水平线MN 上靠”,通过面积“加法”,得到所求三角形的面积为12ABM S MN OB ∆=⋅.至此,这个“两定两动型”三角形面积问题,利用“宽高公式”得到了比较完美的解答.当然,关于面积处理,绝不仅仅只有“宽高公式”,还有很多其他的路可走,如“框图法”(亦可称“矩形大法”)、其他的割补法(如上题中连接OM 也是一种很好的分割处理手段)等等,但大多体现出来的思想方法都是“大同小异”的,即想方设法将所求“斜面积”“改斜归正”,使问题得以解决.后面若有机会,会专门成文,敬请期待!通过前面的《模型证明》及本文的《实战分析》,笔者认为根本不用记忆所谓的“宽高公式”,只要在处理面积的问题中,狠抓不动点不放手,过动点作平行于坐标轴的直线交这不动边所在的直线于一点,将三角形的面积进行“割”或“补”,即面积“加”或“减”,然后平移其中一条高线,即可转化为高线的“加”或“减”,就能够得出所谓的“宽高公式”!这道苏州中考真题中有一个限制条件“点M 在第一象限内”,很明显是为了简化起见.若是将这个条件去掉,即“点M 是抛物线上任意一动点”,那么△ABM 的面积为S 关于m 的函数表达式又如何求解呢?我想其他的方法就未必恰当了,这时“宽高法”的作用会更明显.图14及图15给出了两种情形,前者可看出此时方法过程跟原题一模一样;而后者可看出唯一的区别就是点N 位于了点M 的上方,此时MN=N M y y -,其他都没变化也就是这时候要分类了,分类的标准就是M、N“谁高谁低”,可分三类,也可分两类.甚至于,结合本人作品《巧用绝对值避开“繁琐的”分类讨论》一文,直接借用“绝对值”,y y 即可,最后解一个含绝对值的方程就可以了,在此不再一一赘述,将MN表示为M N有兴趣的同学可自行展开.同学们,研究之窗已向你们打开,还有什么道理不去认真钻研、琢磨呢!加油,中考必胜!最后来首打油诗结束本文,“横切竖切都可以,切法不一莫强求;关键抓住不动点,最好沿着动点切;切完之后即加减,加减之后即宽高!”。
水平宽-铅垂高
1、阅读材料:如图1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽〞〔a 〕,中间的这条直线在△ABC 部线段的长度叫△ABC 的“铅垂高〞〔h 〕.我们可得出一种计算三角形面积的新方法:S △ABC =21ah ,即三角形面积等于水平宽与铅垂高乘积的一半. 解答以下问题:如图2,抛物线顶点坐标为点C 〔1,4〕,交x 轴于点A 〔3,0〕,点P 是抛物线〔在第一象限〕上的一个动点. 〔1〕求抛物线的解析式;〔2〕假设点B 为抛物线与y 轴的交点,求直线AB 的解析式;〔3〕在〔2〕的条件下,设抛物线的对称轴分别交AB 、x 轴于点D 、M ,连接PA 、PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 与S △CAB ;〔4〕在〔2〕的条件下,设P 点的横坐标为x ,△PAB 的铅垂高为h 、面积为S ,请分别写出h 和S 关于x 的函数关系式.2、如图,直线31+-=x y ,与x 轴,y 轴分别交于点B 、C ,经过B 、C 两点的抛物线与x 轴的另一个交点为点A ,顶点是点P ,且对称轴是直线2=x 〔1〕求抛物线的解析式〔2〕直线31+-=x y 向下平移个单位,使它与抛物线只有一个公共点,并求出此时直线的解析式。
〔3〕①当1y >2y 时,观察图像,自变量的取值围是。
②自变量在上述围,在2y 上是否存在点M ,使得CBM S ∆有最大值,假设存在,求出最大值,并求出此时点M 的坐标,假设不存在,请说明理由。
3、在平面直角坐标系中,抛物线经过A(-4,0),B(0,-4),C(2,0)三点. (1)求抛物线的解析式;(2)假设点M 为第三象限抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值; (3)假设点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.4、如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为〔3,0〕,与y 轴交于C 〔0,-3〕点,点P 是直线BC 下方的抛物线上一动点. 〔1〕求这个二次函数的表达式.〔2〕连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP ′C ,那么是否存在点P ,使四边形POP ′C 为菱形?假设存在,请求出此时点P 的坐标;假设不存在,请说明理由.〔3〕当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.5、如图,抛物线经过(40)(10)(02)A B C -,,,,,三点. 〔1〕求出抛物线的解析式;〔2〕P 是抛物线上一动点,过P 作PM x ⊥轴,垂足为M ,是否存在P 点,使得以A ,P ,M 为顶点的三角形与OAC △相似?假设存在,请求出符合条件的点P 的坐标;假设不存在,请说明理由; 〔3〕在直线AC 上方的抛物线上有一点D ,使得DCA △的面积最大,求出点D 的坐标.6.如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A〔-4,0〕、B〔2,0〕,与y轴交于点C,顶点为D.E〔1,2〕为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.〔1〕求抛物线的函数解析式,并写出顶点D的坐标;〔2〕在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;〔3〕假设点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),点P是抛物线(在第一象限内)上的一个
动点.
(1)求抛物线的解析式;
(2)若点B为抛物线与y轴的交点,求直线AB的解析式;
(3)在(2)的条件下,设抛物线的对称轴分别交AB、x轴于点D、M,连接PA、PB,当P点运动到顶点C
时,求△CAB的铅垂高CD及S△CAB;
(4)在(2)的条件下,设P点的横坐标为x,△PAB的铅垂高为h、面积为S,请分别写出h和S关于x
的函数关系式.
2、如图,直线31xy,与x轴,y轴分别交于点B、C,经过B、C两点的抛物线与x轴的另一个交
点为点A,顶点是点P,且对称轴是直线2x
(1)求抛物线的解析式
(2)直线31xy向下平移 个单位,使它与抛物线只有一个公共点,并求出此时直线的解析
式。
(3)①当1y>2y时,观察图像,自变量的取值范围是 。
②自变量在上述范围内,在2y上是否存在点M,使得CBMS有最大值,若存在,求出最大值,并求
出此时点M的坐标,若不存在,请说明理由。
3、在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,
并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、0为顶点
的四边形为平行四边形,直接写出相应的点Q的坐标.
4、如图,在平面直角坐标系中,二次函数cbxxy2的图象与x轴交于A、B两点, A点在原点的左
侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C, 那么是否存在点P,使四边形POP′C为
菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面
积.
5、如图,抛物线经过(40)(10)(02)ABC,,,,,三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PMx轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角
形与OAC△相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
(3)在直线AC上方的抛物线上有一点D,使得DCA△的面积最大,求出点D的坐标.
O
x y A B
C
4
1
2
(第24题图)
6.如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,
顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.
C
E
D
G
A
x
y
O B
F
