2014~2015第一学期江苏省海门市九年级数学期末试卷(人教版)
2014-2015学年九年级(上)期末数学综合训练题(含答案)

九年义务教育九年级上册数学学科综合训练(一)(总分:120分 考试时间:90分钟)亲爱的同学:你好!答题前,请仔细阅读以下说明:1.本试卷分第 I 卷和第 II 卷两部分,共6页.第 I 卷(1至2页)为选择题,第 II 卷(2至6页)为非选择题.2.请将密封线内的项目填写清楚.3.第 II 卷(非选择题)用兰、黑色钢笔或圆珠笔直接答在试卷上.不要求保留精确度的题目,计算结果保留准确值.希望你能愉快地度过这90分钟,祝你成功!答题情况统计表选择题答案表一、(选择题)1.下列是二次函数的是 ( )A .182+=x yB . 18+=x yC .xy 8=D .182+=xy 2.在△ABC 中,∠C =90°,若∠B =2∠A ,则cos B 等于 ( )A .3B .33C .23 D .21 3. 已知α为锐角,tan (90°-α)=3,则α的度数为 ( )A .30°B . 45°C .60°D .75° 4.下列函数中,当0>x 时,y 随x 的增大而增大的函数是( )题号一二三等级 1920 21 22 23 24 25 得分题号 1 2 3 4 5 6 7 8 9 10 11 12 答案A .x y 2-=B . 22+-=x yC .xy 2-= D .22x y -=5.用配方法将12212+-=x x y 写成k h x a y +-=2)(的形式是( )A .1)2(212--=x yB . 1)1(212--=x yC .3)2(212--=x yD .3)1(212--=x y6.如图1,小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为9.0m ,眼睛与地面的距离为 1.6m ,那么这棵树的高度大约为 ( ) A .5.2 mB . 6.8 mC .9.4 mD .17.2 m7.如图2.在矩形ABCD 中,DE ⊥AC 于E ,设∠ADE=α,且53cos =α,AB = 4, 则AD 的长为 ( ) A .3B .316 C .320D .516 8.小颖在二次函数5422++=x x y 的图象上,依横坐标找到三点(-1,y 1),(0.5,y 2), (-3.5,y 3),则你认为321,,y y y 的大小关系应为 ( ) A .321y y y >>B . 132y y y >>C .213y y y >>D .123y y y >>9.函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是 ( )A .3<kB .03≠<k k 且C .3≤kD .03≠≤k k 且10.二次函数c bx ax y ++=2的图象如右图所示,则a 、b 、c、ac b 42-、c b a ++和c b a +-中大于0的有( )个。
2014-2015学年度上学期期末联考试卷九年级数学(含答案)

座位号:2014-2015学年度上学期期末联考试卷九年级数学(全卷共23题,满分100分,时间120分钟)一、选择题(本题8个小题,每小题3分,共24分) 1、下列图形既是轴对称图形又是中心对称图形的是( )2、对于二次函数2)1(22-+=x y 的描述正确的是( ) A 、对称轴是直线1=x B 、顶点坐标)2,1(-- C 、顶点坐标)2,1(- D 、开口向下,有最大值-23、方程02092=+-x x 的两根分别是⊙1O 和⊙2O 的半径,且两圆相切,则圆心距21O O 为( )A 、 1B 、9C 、4或5D 、1或9 4、下列叙述正确的是( )A 、口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球B 、“如果b a ,是实数,那么a b b a +=+”是不确定事件C 、为了了解一批炮弹的杀伤力,采用普查的方式比较合适D 、两个相似图形一定是位似图形5、⊙O 的半径为5cm ,弦AB//CD ,且AB=8cm,CD=6cm,则AB 与CD 之间的距离为( ) A 、 1 cm B 、 7cm C 、 3 cm 或4 cm D 、 1cm 或7cm6、如图,在ABC ∆中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD :DB=3:5,那么CF :CB 等于( ) A 、3:8 B 、3:5 C 、5:8 D 、2:57、如图,直线b x y +-=与双曲线xky =交于点A 、B ,则不等式组0≥+->b x x k 的解集为( )A 、x <﹣1或x >2B 、﹣1<x ≤1C 、﹣1<x <0D 、﹣1<x <1 8、某种手机经过四、五月份连续两次降价,每部手机由3200元降到2500元。
设平均每月降价的百分率为x ,则根据题意列出的方程是( ) A 、 2500)1(32002=-x B 、2500)1(32002=+xC 、2500)21(3200=-xD 、250032002=-x二、填空题(本题6个小题,每小题3分,共18分)9、如图,在△ABC 中,∠C=120°,AB=4cm ,两等圆⊙A 与⊙B 外切,则图中两个扇形的面积之和(即阴影部分)为 cm 2(结果保留π)。
人教版数学九年级上册期末考试数学试卷含答案解析

人教版数学九年级上册期末考试试卷一.选择题(每题3分,共24分)1.如果反比例函数y=在各自象限内,y随x的增大而减小,那么m的取值范围是()A.m<0B.m>0C.m<﹣1D.m>﹣12.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是()A.B.C.D.3.如图,圆的半径是6,空白部分的圆心角分别是60°与30°,则阴影部分的面积是()A.9πB.27πC.6πD.3π4.一个圆锥的母线长为10,侧面展开图是半圆,则圆锥的侧面积是()A.10πB.20πC.50πD.100π5.若mn>0,则一次函数y=mx+n与反比例函数y=在同一坐标系中的大致图象是()A.B.C.D.6.如图,反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,则﹣nx≥0的解集是()A.﹣1<x<0B.x<﹣1或0<x<1C.x≤1或0<x≤1D.﹣1<x<0或x≥17.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为()A.cm B.9cm C.cm D.cm8.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是()A.(2014,0)B.(2015,﹣1)C.(2015,1)D.(2016,0)二.填空题:(每小题3分,共21分)9.已知双曲线y=经过点(﹣1,2),那么k的值等于.10.一个圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为cm2.11.一只口袋里有相同的红、绿、蓝三种颜色的小球,其中有6个红球,5个绿球.若任意摸出一个绿球的概率是,则任意摸出一个蓝球的概率是.12.如图,AB是直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD 的长为cm.13.已知点P(x1,﹣2)、Q(x2,3)、H(x3,1)在双曲线上,那么x1、x2、x3的大小关系是.14.在半径为6cm的圆中,长为6cm的弦所对的圆周角的度数为.15.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=2,则阴影部分的面积为.三.解答题(共75分)16.一次函数y=2x+2与反比例函数y=(k≠0)的图象都过点A(1,m),y=2x+2的图象与x轴交于B点.(1)求点B的坐标及反比例函数的表达式;(2)C(0,﹣2)是y轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.17.有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y=上的概率.18.星期五晚上,小明和他的妈妈一起看《我是歌手》,歌手演唱完后要评选出名次,在已公布四到七名后,还有张杰、韩磊、邓紫棋三位选手没有公布名次.(1)求邓紫棋获第一名的概率;(2)如果小明和妈妈一起竞猜第一名,那么两人中一个人猜中另一个人却没猜中的概率是多少?(请用“树状图”或“列表”等方法写出分析过程)19.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.(1)求直径AB的长;(2)求阴影部分的面积(结果保留π).20.如图,一次函数y=kx+2的图象与x轴交于点B,与反比例函数的图象的一个交点为A(2,3).(1)分别求出反比例函数和一次函数的解析式;(2)过点A作AC⊥x轴,垂足为C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.21.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O 于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=5cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)22.已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.(1)求证:DC是⊙O的切线;(2)若AB=2,求DC的长.23.已知:如图,正比例函数y=ax的图象与反比例函数y=的图象交于点A(3,2).(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过M作直线MB‖x轴交y 轴于点B.过点A作直线AC∥y轴交于点C,交直线MB于点D,当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由;(4)探索:x轴上是否存在点P,使△OAP是等腰三角形?若存在,求出点P的坐标,若不存在,请说明理由.参考答案与试题解析一.选择题(每题3分,共24分)1.如果反比例函数y=在各自象限内,y随x的增大而减小,那么m的取值范围是()A.m<0B.m>0C.m<﹣1D.m>﹣1【考点】反比例函数的性质.【分析】如果反比例函数y=在各自象限内,y随x的增大而减小,那么m的取值范围是()【解答】解:∵反比例函数y=的图象在所在象限内,y的值随x值的增大而减小,∴m+1>0,解得m>﹣1.故选D.【点评】本题考查的是反比例函数的性质,熟知反比例函数的增减性是解答此题的关键.2.圆、平行四边形、等腰三角形、菱形,矩形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是()A.B.C.D.【考点】概率公式;轴对称图形.【分析】由圆、平行四边形、等腰三角形、菱形,矩形中,轴对称图形的有圆、等腰三角形、菱形,矩形;直接利用概率公式求解即可求得答案.【解答】解:∵圆、平行四边形、等腰三角形、菱形,矩形中,轴对称图形的有圆、等腰三角形、菱形,矩形;∴一次过关的概率是:.故选D.【点评】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.3.如图,圆的半径是6,空白部分的圆心角分别是60°与30°,则阴影部分的面积是()A.9πB.27πC.6πD.3π【考点】扇形面积的计算.【分析】计算阴影部分圆心角的度数,运用扇形面积公式求解.【解答】解:根据扇形面积公式,阴影部分面积==27π.故选B.【点评】考查了扇形面积公式的运用,扇形的旋转.4.一个圆锥的母线长为10,侧面展开图是半圆,则圆锥的侧面积是()A.10πB.20πC.50πD.100π【考点】圆锥的计算.【专题】压轴题.【分析】圆锥的侧面积为半径为10的半圆的面积.【解答】解:圆锥的侧面积=半圆的面积=π×102÷2=50π,故选C.【点评】解决本题的关键是把圆锥的侧面积转换为规则图形的面积.5.若mn>0,则一次函数y=mx+n与反比例函数y=在同一坐标系中的大致图象是()A.B.C.D.【考点】反比例函数的图象;一次函数的图象.【分析】首先根据mn>0确定反比例函数的图象的位置,然后根据m、n异号确定答案即可.【解答】解:∵mn>0,∴m、n异号,且反比例函数y=的图象位于第一、三象限,∴排除C、D;∵当m>0时则n<0,∴排除A,∵m<0时则n>0,∴B正确,故选B.【点评】本题考查了反比例函数的性质及一次函数的性质,解题的关键是了解两种函数的性质.6.如图,反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,则﹣nx≥0的解集是()A.﹣1<x<0B.x<﹣1或0<x<1C.x≤1或0<x≤1D.﹣1<x<0或x≥1【考点】反比例函数与一次函数的交点问题.【分析】求出≥nx,求出B的坐标,根据A、B的坐标结合图象得出即可.【解答】解:∵﹣nx≥0,∴≥nx,∵反比例函数y1=和正比例函数y2=nx的图象交于A(﹣1,﹣3)、B两点,∴B点的坐标是(1,3),∴﹣nx≥0的解集是x<﹣1或0<x>1,故选B.【点评】本题考查了一次函数与反比例函数的交点问题,函数的图象的应用,主要考查学生的理解能力和观察图象的能力.7.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为()A.cm B.9cm C.cm D.cm【考点】正多边形和圆.【专题】压轴题.【分析】已知小正方形的面积即可求得边长,在直角△ACE中,利用勾股定理即可求解.【解答】解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,∴AE=BC=x,CE=2x;∵小正方形的面积为16cm2,∴小正方形的边长EF=DF=4,由勾股定理得,R2=AE2+CE2=AF2+DF2,即x2+4x2=(x+4)2+42,解得,x=4,∴R=cm.故选C.【点评】本题利用了勾股定理,正方形的性质求解.8.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2015秒时,点P的坐标是()A.(2014,0)B.(2015,﹣1)C.(2015,1)D.(2016,0)【考点】规律型:点的坐标.【专题】压轴题;规律型.【分析】根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.【解答】解:半径为1个单位长度的半圆的周长为:,∵点P从原点O出发,沿这条曲线向右运动,速度为每秒个单位长度,∴点P1秒走个半圆,当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,﹣1),当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),…,∵2015÷4=503 (3)∴A2015的坐标是(2015,﹣1),故选:B.【点评】此题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,解决问题.二.填空题:(每小题3分,共21分)9.已知双曲线y=经过点(﹣1,2),那么k的值等于﹣3.【考点】反比例函数图象上点的坐标特征.【分析】直接把点(﹣1,2)代入双曲线y=,求出k的值即可.【解答】解:∵双曲线y=经过点(﹣1,2),∴2=,解得k=﹣3.故答案为:﹣3.【点评】本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.10.一个圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积为10πcm2.【考点】圆锥的计算.【分析】根据圆锥的侧面展开图为扇形,先计算出圆锥的底面圆的周长,然后利用扇形的面积公式求解.【解答】解:∵圆锥的底面半径为5cm,∴圆锥的底面圆的周长=2π•5=10π,∴圆锥的侧面积=•10π•2=10π(cm2).故答案为:10π.【点评】本题考查了圆锥的侧面积的计算:圆锥的侧面展开图为扇形,扇形的弧长为圆锥的底面周长,扇形的半径为圆锥的母线长.也考查了扇形的面积公式:S=•l•R,(l为弧长).11.一只口袋里有相同的红、绿、蓝三种颜色的小球,其中有6个红球,5个绿球.若任意摸出一个绿球的概率是,则任意摸出一个蓝球的概率是.【考点】概率公式.【分析】设袋中有蓝球m个,根据蓝球概率公式列出关于m的方程,求出m的值即可.【解答】解:设袋中有蓝球m个,则袋中共有球(6+5+m)个,若任意摸出一个绿球的概率是,有=,解得m=9,任意摸出一个蓝球的概率是=0.45.故答案为:0.45【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.12.如图,AB是直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD 的长为3cm.【考点】圆周角定理;垂径定理;解直角三角形.【分析】根据∠CDB=30°,求出∠COB的度数,再利用三角函数求出CE的长.根据垂径定理即可求出CD的长.【解答】解:∵∠CDB=30°,∴∠COB=30°×2=60°.又∵⊙O的半径为cm,∴CE=sin60°=×=,∴CD=×2=3(cm).【点评】此题考查了垂径定理和圆周角定理,利用特殊角的三角函数很容易解答.13.已知点P(x1,﹣2)、Q(x2,3)、H(x3,1)在双曲线上,那么x1、x2、x3的大小关系是x3<x2<x1.【考点】反比例函数图象上点的坐标特征.【专题】计算题.【分析】把三个点的坐标代入解析式,分别计算出x1、x2、x3的值,然后比较大小即可.【解答】解:把点P(x1,﹣2)、Q(x2,3)、H(x3,1)代入得x1=,x2=﹣,x3=﹣(a2+1),所以x3<x2<x1.故答案为x3<x2<x1.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.14.在半径为6cm的圆中,长为6cm的弦所对的圆周角的度数为30°或150°.【考点】圆周角定理;等边三角形的判定与性质.【专题】分类讨论.【分析】首先根据题意画出图形,然后在优弧上取点C,连接AC,BC,在劣弧上取点D,连接AD,BD,易得△AOB是等边三角形,再利用圆周角定理,即可求得答案.【解答】解:如图,首先在优弧上取点C,连接AC,BC,在劣弧上取点D,连接AD,BD,∵OA=OB=6cm,AB=6cm,∴OA=AB=OB,∴△OAB是等边三角形,∴∠AOB=60°,∴∠C=∠AOB=30°,∴∠D=180°﹣∠C=150°,∴所对的圆周角的度数为:30°或150°.【点评】此题考查了圆周角定理以及等边三角形的判定与性质.注意根据题意画出图形,结合图形求解是关键.15.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交于点E,以点O为圆心,OC的长为半径作交OB于点D.若OA=2,则阴影部分的面积为+.【考点】扇形面积的计算.【专题】压轴题.【分析】连接OE、AE,根据点C为OC的中点可得∠CEO=30°,继而可得△AEO为等边三角形,求出扇形AOE的面积,最后用扇形AOB的面积减去扇形COD的面积,再减去S空白AEC 即可求出阴影部分的面积.【解答】解:连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S扇形AOE==π,∴S阴影=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)=﹣﹣(π﹣×1×)=π﹣π+=+.故答案为:+.【点评】本题考查了扇形的面积计算,解答本题的关键是掌握扇形的面积公式:S=.三.解答题(共75分)16.一次函数y=2x+2与反比例函数y=(k≠0)的图象都过点A(1,m),y=2x+2的图象与x轴交于B点.(1)求点B的坐标及反比例函数的表达式;(2)C(0,﹣2)是y轴上一点,若四边形ABCD是平行四边形,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.【考点】反比例函数与一次函数的交点问题.【分析】(1)在y=2x+2中令y=0,求得B的坐标,然后求得A的坐标,利用待定系数法求得反比例函数的解析式;(2)根据平行线的性质即可直接求得D的坐标,然后代入反比例函数的解析式判断即可.【解答】解:(1)在y=2x+2中令y=0,则x=﹣1,∴B的坐标是(﹣1,0),∵A在直线y=2x+2上,∴A的坐标是(1,4).∵A(1,4)在反比例函数y=图象上∴k=4.∴反比例函数的解析式为:y=;(2)∵四边形ABCD是平行四边形,∴D的坐标是(2,2),∴D(2,2)在反比例函数y=的图象上.【点评】本题主要考查了待定系数法求反比例函数与一次函数的解析式,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.17.有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y=上的概率.【考点】列表法与树状图法;反比例函数图象上点的坐标特征.【专题】图表型.【分析】(1)画出树状图即可得解;(2)根据反比例函数图象上点的坐标特征判断出在双曲线上y=上的情况数,然后根据概率公式列式计算即可得解.【解答】解:(1)根据题意画出树状图如下:;(2)当x=﹣1时,y==﹣2,当x=1时,y==2,当x=2时,y==1,一共有9种等可能的情况,点(x,y)落在双曲线上y=上的有2种情况,所以,P=.【点评】本题考查了列表法与树状图法,反比例函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.18.星期五晚上,小明和他的妈妈一起看《我是歌手》,歌手演唱完后要评选出名次,在已公布四到七名后,还有张杰、韩磊、邓紫棋三位选手没有公布名次.(1)求邓紫棋获第一名的概率;(2)如果小明和妈妈一起竞猜第一名,那么两人中一个人猜中另一个人却没猜中的概率是多少?(请用“树状图”或“列表”等方法写出分析过程)【考点】列表法与树状图法.【专题】计算题.【分析】(1)三个选手机会均等,得到邓紫棋获第一名的概率;(2)假设张杰为第一名,列表得出所有等可能的情况数,找出两人中一个人猜中另一个人却没猜中的情况数,即可求出所求的概率.【解答】解:(1)根据题意得:邓紫棋获第一名的概率为;(2)假设张杰为第一名,列表如下:张韩邓张(张,张)(韩,张)(邓,张)韩(张,韩)(韩,韩)(邓,韩)邓(张,邓)(韩,邓)(邓,邓)所有等可能的情况有9种,两人中一个人猜中另一个人却没猜中的情况有4种,则P=.【点评】此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.19.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.(1)求直径AB的长;(2)求阴影部分的面积(结果保留π).【考点】圆周角定理;角平分线的定义;三角形的面积;含30度角的直角三角形;勾股定理;扇形面积的计算.【分析】(1)根据直径所对的圆周角是直角推知∠ACB=90°,然后在直角三角形ABC中利用边角关系、勾股定理来求直径AB的长度;(2)连接OD.利用(1)中求得AB=4可以推知OA=OD=2;然后由角平分线的性质求得∠AOD=90°;最后由扇形的面积公式、三角形的面积公式可以求得阴影部分的面积=S扇形△AOD ﹣S△AOD.【解答】解:(1)∵AB为⊙O的直径,∴∠ACB=90°,…(1分)∵∠B=30°,∴AB=2AC,…(3分)∵AB2=AC2+BC2,∴AB2=AB2+62,…(5分)∴AB=4.…(6分)(2)连接OD.∵AB=4,∴OA=OD=2,…(8分)∵CD平分∠ACB,∠ACB=90°,∴∠ACD=45°,∴∠AOD=2∠ACD=90°,…(9分)=OA•OD=•2•2=6,…(10分)∴S△AOD=•π•OD2=•π•(2)2=3π,…(11分)∴S扇形△AOD﹣S△AOD=3π﹣6.…(12分)∴阴影部分的面积=S扇形△AOD【点评】本题综合考查了圆周角定理、含30度角的直角三角形以及扇形面积公式.解答(2)题时,采用了“数形结合”的数学思想.20.如图,一次函数y=kx+2的图象与x轴交于点B,与反比例函数的图象的一个交点为A(2,3).(1)分别求出反比例函数和一次函数的解析式;(2)过点A作AC⊥x轴,垂足为C,若点P在反比例函数图象上,且△PBC的面积等于18,求P点的坐标.【考点】反比例函数与一次函数的交点问题;三角形的面积.【专题】计算题.【分析】(1)先将点A(2,3)代入反比例函数和一次函数y=kx+2,求得m、k的值,=18,即可求得x,y的值.(2)可求得点B的坐标,设P(x,y),由S△PBC【解答】解:(1)把A(2,3)代入,∴m=6.∴.(1分)把A(2,3)代入y=kx+2,∴2k+2=3.∴.∴.(2分)(2)令,解得x=﹣4,即B(﹣4,0).∵AC⊥x轴,∴C(2,0).∴BC=6.(3分)设P(x,y),==18,∵S△PBC∴y1=6或y2=﹣6.分别代入中,得x1=1或x2=﹣1.∴P1(1,6)或P2(﹣1,﹣6).(5分)【点评】本题考查了一次函数和反比例函数的交点问题,利用待定系数法求解析式是解此题的关键.21.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O 于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=5cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)【考点】扇形面积的计算;全等三角形的判定与性质;圆周角定理;切线的性质;解直角三角形.【专题】几何综合题.【分析】(1)根据切线的性质定理和平行线的性质定理得到OC⊥BD,根据垂径定理得到BE的长,再根据圆周角定理发现∠BOE=60°,从而根据锐角三角函数求得圆的半径;(2)结合(1)中的有关结论证明△DCE≌△BOE,则它们的面积相等,故阴影部分的面积就是扇形OBC的面积.【解答】解:(1)∵AC与⊙O相切于点C,∴∠ACO=90°∵BD∥AC∴∠BEO=∠ACO=90°,∴DE=EB=BD=(cm)∵∠D=30°,∴∠O=2∠D=60°,在Rt△BEO中,sin60°=∴OB=5,即⊙O的半径长为5cm.(2)由(1)可知,∠O=60°,∠BEO=90°,∴∠EBO=∠D=30°又∵∠CED=∠BEO,BE=ED,∴△CDE≌△OBE∴,答:阴影部分的面积为.【点评】本题主要考查切线的性质定理、平行线的性质定理、垂径定理以及全等三角形的判定方法.能够熟练解直角三角形.22.已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.(1)求证:DC是⊙O的切线;(2)若AB=2,求DC的长.【考点】切线的判定.【专题】计算题;证明题.【分析】(1)根据切线的判定方法,只需证CD⊥OC.所以连接OC,证∠OCD=90°.(2)易求半径OC的长.在Rt△OCD中,运用三角函数求CD.【解答】(1)证明:连接OC.∵OB=OC,∠B=30°,∴∠OCB=∠B=30°.∴∠COD=∠B+∠OCB=60°.(1分)∵∠BDC=30°,∴∠BDC+∠COD=90°,DC⊥OC.(2分)∵BC是弦,∴点C在⊙O上,∴DC是⊙O的切线,点C是⊙O的切点.(3分)(2)解:∵AB=2,∴OC=OB==1.(4分)∵在Rt△COD中,∠OCD=90°,∠D=30°,∴DC=OC=.(5分)【点评】本题考查了切线的判定,证明经过圆上一点的直线是圆的切线,常作的辅助线是连接圆心和该点,证明直线和该半径垂直.23.已知:如图,正比例函数y=ax的图象与反比例函数y=的图象交于点A(3,2).(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?(3)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过M作直线MB‖x轴交y 轴于点B.过点A作直线AC∥y轴交于点C,交直线MB于点D,当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由;(4)探索:x轴上是否存在点P,使△OAP是等腰三角形?若存在,求出点P的坐标,若不存在,请说明理由.【考点】反比例函数综合题.【分析】(1)将A(3,2)分别代入y=,y=ax中,得a、k的值,进而可得正比例函数和反比例函数的表达式;(2)观察图象,得在第一象限内,当0<x<3时,反比例函数的图象在正比例函数的上方;故反比例函数的值大于正比例函数的值;=S△OAC=×|k|=3,可得S矩形OBDC=12,即OC•OB=12,进而可得m、n的值,(3)由S△OMB故可得BM与DM的大小;比较可得其大小关系;(4)先求出A点坐标,再分OA=OP,OA=AP及OP=AP三种情况进行讨论.【解答】解:(1)∵将A(3,2)分别代入y=,y=ax中,得:2=,3a=2,∴k=6,a=,∴反比例函数的表达式为:y=,正比例函数的表达式为y=x.(2)∵,解得,∴C(3,2)观察图象,得在第一象限内,当0<x<3时,反比例函数的值大于正比例函数的值;(3)BM=DM理由:∵MN ∥x 轴,AC ∥y 轴,∴四边形OCDB 是平行四边形,∵x 轴⊥y 轴,∴▱OCDB 是矩形.∵M 和A 都在双曲线y=上,∴BM ×OB=6,OC ×AC=6,∴S △OMB =S △OAC =×|k|=3,又∵S 四边形OADM =6,∴S 矩形OBDC =S 四边形OADM +S △OMB +S △OAC =3+3+6=12,即OC •OB=12,∵OC=3,∴OB=4,即n=4∴m==,∴MB=,MD=3﹣=,∴MB=MD ;(4)如图,∵S △OAC =OC •AC=3,OC=3,∴AC=2,∴A (3,2),∴OA==,∴当OA=OP 时,P 1(,0);当OA=AP 时,∵AC ⊥x 轴,OC=3,∴OC=CP 2=3,∴P 2(6,0);当OP=AP 时,设P 3(x ,0),∵O (0,0),A (3,2),∴x=,解得x=,∴P 3(,0).综上所述,P 点坐标为P 1(,0),P 2(6,0),P 3(,0).【点评】此题考查的是反比例函数综合题及正比例函数等多个知识点,此题难度稍大,综合性比较强,在解答(3)时要注意进行分类讨论,不要漏解.第21页共21页。
2014-2015学年九年级上数学期末测试题

2014-2015学年九年级上数学期末测试题6.已知平面直角坐标系上的三个点O(0,0)、A(-1,1)、B(-1,0),将绕点按顺时针方向旋转45?,则点2014-2015学年度九年级数学上期末测试题的坐标为( )A.(错误~未找到引用源。
,0) B. (错误~未找到引用A的对应点A21椒山初级中学龚贞峰22源。
,0) C. (0,错误~未找到引用源。
) D. (0,错误~未找到引用源。
) 2一、选择题(每小题3分,共30分) 221.在下列各式中,是最简二次根式的式子是( ) 2xx,,,123507.三角形两边的长是2和5,第三边的长是方程错误~未找到引用源。
的根,三m,n A.错误~未找到引用源。
B.错误~未找到引用源。
C. 错误~未16a角形的周长为( ) 5A.14B.12C.12或14D.以上都不对a436xy找到引用源。
D. 错误~未找到引用源。
8. 如图所示的图案中,可以由一个“基本图案”连续旋转45?得到的是( ) 182.下列计算正确的是( )A.错误~未找到引用源。
B.错误~未找到引用源。
C.错误~未找到321,,842,111,3引用源。
D. 错误~未找到引用源。
,,4232323,,xx,,,71209.已知两圆的半径是方程错误~未找到引用源。
两实数根,圆心距为8,那么这3.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C和D两点,AB=10cm,CD=6cm,两个圆的位置关系是( )则AC长为( ) A.0.5cm B.1cm C.1.5cm D.2cm A.内切 B.相交 C.外离 D.外切10.如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A 、A 、A (123)O O若从O点到A点的回形线为第1圈(长为7),从A点到A点的回形线为第2圈,…,依此α112ABADBCα 类推.则第10圈的长为( ) C第5题图 (第4题) (第10题) A.71 B.72 C.79 D.87x,14.已知错误~未找到引用源。
2014-2015学年第一学期期末调研试卷
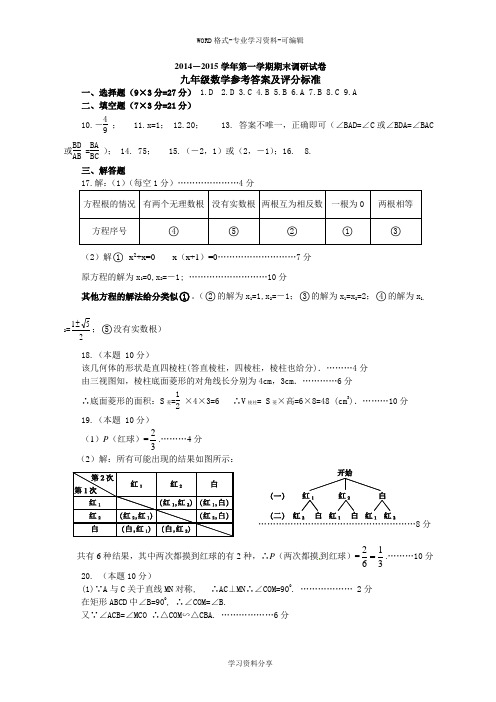
WORD 格式-专业学习资料-可编辑学习资料分享2014-2015学年第一学期期末调研试卷九年级数学参考答案及评分标准一、选择题(9×3分=27分) 1.D 2.D 3.C 4.B 5.B 6.A 7.B 8.C 9.A二、填空题(7×3分=21分)10.-49; 11.x=1; 12.20; 13. 答案不唯一,正确即可(∠BAD=∠C 或∠BDA=∠BAC 或BD AB =BA BC ); 14. 75; 15.(-2,1)或(2,-1);16. 8.三、解答题(2)解○1 x 2+x=0 x (x+1)=0………………………7分原方程的解为x 1=0,x 2=-1; ………………………10分其他方程的解法给分类似○1。
(○2的解为x 1=1,x 2=-1;○3的解为x 1=x 2=2;○4的解为x 1,2=251±;○5没有实数根) 18.(本题 10分)该几何体的形状是直四棱柱(答直棱柱,四棱柱,棱柱也给分).………4分由三视图知,棱柱底面菱形的对角线长分别为4cm ,3cm .…………6分∴底面菱形的面积:S 菱=12×4×3=6 ∴V 棱柱= S 菱×高=6×8=48 (cm 3).………10分 19.(本题 10分)(1)P (红球)=23.………4分 (2)解:所有可能出现的结果如图所示:8分共有6种结果,其中两次都摸到红球的有2种,∴P (两次都摸到红球)=2163=.………10分 20. (本题10分)(1)∵A 与C 关于直线MN 对称, ∴AC ⊥MN ∴∠COM=900. ……………… 2分在矩形ABCD 中∠B=900, ∴∠COM=∠B.又∵∠ACB=∠MCO ∴△COM ∽△CBA. ………………6分(2)∵在Rt △CBA 中,AB=6,BC=8, ∴AC=10,∴OC=5. ………………8分又∵△COM ∽△CBA, ∴OC BC = OM AB ∴OM=AB ·OC BC = 154.……………10分 21. (本题11分)解:(1)作AE ⊥y 轴于E ,∵S △AOD =4,OD=2, ∴12OD ·AE=4,∴AE=4,……………2分 ∵AB ⊥OB ,C 为OB 的中点,∴OC=BC ,∠DOC=∠ABC=90°,又∠OCD=∠BCA ,∴Rt △DOC ≌Rt △ABC ∴AB=OD=2 , ∴点A 的坐标为A (4,2),……………4分将A (4,2)代入y 1= k x 中,得k=8,∴反比例函数为y 1= 8x,……………5分 ∴将A (4,2)和D (0,-2)代入y 2=ax+b ,得 解之得:,∴一次函数为y 2=x -2;……………8分(2)在y 轴的右侧,当y 1>y 2时,x 的取值范围是0x 4。
2014-2015学年新课标人教版九年级上册期末数学试卷含答案

2015-2016学年九年级(上)期末数学试卷一、精心选一选(每小题都给出了四个答案,其中只有一个是正确的,请将正确答案的代号填在答题卡的方框里,每小题3分,共36分)1.下列是最简二次根式的是( )A. B.C.D.2.一元二次方程x2﹣5x=0的根是( )A.5 B.0 C.0或5 D.0或﹣53.在比例尺为1:10 000 000的中国地图上,量得某地到北京的图上距离为15cm,那么该地到北京的实际距离为( )A.15000km B.1500km C.150km D.15km4.下列式子中,与不是同类二次根式的是( )A.B.C. D.5.若关于x的方程mx2﹣4x+2=0有实数根,则m的取值范围是( )A.m≤2 B.m≠0 C.m≤2且m≠0 D.m<26.下列说法正确的是( )A.随机抛掷一枚均匀的硬币,落地后反面一定朝上B.从1,2,3,4,5中随机取一个数,取得奇数的可能性较大C.某彩票中奖率为36%,说明买100张彩票,有36张中奖D.打开电视,中央一套正在播放新闻联播7.在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )A.4tan50°B.4tan40°C.4sin50°D.4sin40°8.如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )A.①②④ B.①③④ C.②③④ D.①②③9.如图,身高1.6米的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是( )A.6.4米B.7米C.8米D.9米10.抛物线y=x2﹣4x+1的顶点坐标是( )A.(﹣2,13)B.(2,﹣3)C.(2,5)D.(﹣2,﹣3)11.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )A.B.C.D.12.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有( )A.①②③ B.②④C.②⑤D.②③⑤二、耐心填一填(每小题3分,共24分)13.计算:×=__________.14.若式子有意义,则x的取值范围是__________.15.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:3,则AB的长为__________米.16.让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于__________.17.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为__________.18.设x1,x2是方程x2﹣x﹣1=0的两个根,则代数式x13+2x2+x1•x2的值为__________.19.将抛物线y=3x2﹣2向左平移2个单位,再向下平移3个单位,则所得抛物线的解析式为__________.20.如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为__________.三、算一算(6分,18分)21.﹣12014×(﹣)﹣2+(﹣π)0﹣+2cos60°.22.﹣3﹣×.23.解方程:2(x+1)2﹣x(x﹣2)=0.四、用心做一做(本大题共3个小题,每小题6分,共18分)24.如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).(1)画出△ABC关于x轴对称的△A1B1C1;(2)将△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2,B2,C2,请画出△A2B2C2;(3)则S△A1B1C1:S△A2B2C2.25.在一个不透明的口袋里装有标号为1,2,3,4,5的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.(1)下列说法:①摸一次,摸出1号球和摸出5号球的概率相同;②有放回的连续摸10次,则一定摸出2号球两次;③有放回的连续摸4次,则摸出四个球标号数字之和可能是20.其中正确的序号是__________.(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.26.某超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为每个50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加x元,(1)写出售出一个可获得的利润是多少元?(用含x的代数式表示)(2)商店若准备获得利润6 000元,并且使进货量较少,则每个定价为多少元?应进货多少个?五.大显身手(本大题共2个小题,每题7分,共14分)27.马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B 的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75).(1)求可疑漂浮物P到A、B两船所在直线的距离;(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.28.如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC 重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.(1)求证:△ABE∽△ECM;(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;(3)当点E运动到什么位置时,线段AM最短?并求出此时AM的值.(直接写出答案)六、用心想一想(本大题10分)29.如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.(1)求抛物线的函数表达式.(2)在第一象限内的抛物线上是否存在点P,使得以A、B、P为顶点的三角形与△ABC 相似?若存在,求出点P的坐标;若不存在,请说明理由.(3)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?2015-2016学年九年级(上)期末数学试卷一、精心选一选(每小题都给出了四个答案,其中只有一个是正确的,请将正确答案的代号填在答题卡的方框里,每小题3分,共36分)1.下列是最简二次根式的是( )A. B.C.D.【考点】最简二次根式.【分析】判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.【解答】解:A、=3,被开方数含能开得尽方的因数,不是最简二次根式;B、=a,被开方数含能开得尽方的因式,不是最简二次根式;C、=被开方数含分母,不是最简二次根式;D、,是最简二次根式;故选D.【点评】本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.一元二次方程x2﹣5x=0的根是( )A.5 B.0 C.0或5 D.0或﹣5【考点】解一元二次方程-因式分解法.【专题】计算题.【分析】方程利用因式分解法求出解即可.【解答】解:方程分解因式得:x(x﹣5)=0,可得x=0或x﹣5=0,解得:x1=0,x2=5.故选C【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.3.在比例尺为1:10 000 000的中国地图上,量得某地到北京的图上距离为15cm,那么该地到北京的实际距离为( )A.15000km B.1500km C.150km D.15km【考点】比例线段.【分析】设该地到北京的实际距离是x厘米,根据比例尺的定义可以得到1:10 000 000=15:x,求得x的值,化成单位是千米即可.【解答】解:设该地到北京的实际距离是x厘米,则1:10 000 000=15:x,解得:x=150 000000cm=1500km.故选B.【点评】本题考查了比例线段,理解比例尺的定义是关键,注意单位之间的换算.4.下列式子中,与不是同类二次根式的是( )A.B.C. D.【考点】同类二次根式.【分析】先把及每个选项中的二次根式化成最简二次根式,再进行选择即可.【解答】解:=2;A、被开方数相同,故是同类二次根式;B、=与2被开方数不同,故不是同类二次根式;C、=3与2被开方数相同,故是同类二次根式;D、=4与3被开方数不同,不是同类二次根式.故选B.【点评】此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同,这样的二次根式叫做同类二次根式.5.若关于x的方程mx2﹣4x+2=0有实数根,则m的取值范围是( )A.m≤2 B.m≠0 C.m≤2且m≠0 D.m<2【考点】根的判别式;一元一次方程的解;一元二次方程的定义.【分析】分类讨论:当m=0,方程变形为﹣4x+2=0,一元一次方程有实数解;当m≠0,根据判别式的意义得到△=(﹣4)2﹣4m×2≥0,解得m≤2,然后综合两种情况即可.【解答】解:当m=0,方程变形为﹣4x+2=0,方程的解为x=;当m≠0,△=(﹣4)2﹣4m×2≥0,解得m≤2;综上所知当m≤2时,方程有实数根.故选:A.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2﹣4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.6.下列说法正确的是( )A.随机抛掷一枚均匀的硬币,落地后反面一定朝上B.从1,2,3,4,5中随机取一个数,取得奇数的可能性较大C.某彩票中奖率为36%,说明买100张彩票,有36张中奖D.打开电视,中央一套正在播放新闻联播【考点】概率的意义.【分析】根据概率的意义即可解答,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生.【解答】解:A、掷一枚硬币的试验中,着地时反面向上的概率为,则正面向上的概率也为,不一定就反面朝上,故此选项错误;B、从1,2,3,4,5中随机取一个数,因为奇数多,所以取得奇数的可能性较大,故此选项正确;C、某彩票中奖率为36%,说明买100张彩票,有36张中奖,不一定,概率是针对数据非常多时,趋近的一个数并不能说买100张该种彩票就一定能中36张奖,故此选项错误;D、打开电视,中央一套正在播放新闻联播,必然事件是一定会发生的事件,则对于选项D 很明显不一定能发生,错误,不符合题意,故此选项错误.故选B.【点评】此题主要考查了概率的意义,解决的关键是理解概率的意义以及必然事件的概念.7.在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )A.4tan50°B.4tan40°C.4sin50°D.4sin40°【考点】锐角三角函数的定义.【分析】根据锐角三角函数的余切是邻边比对边,可得AC与cot50°的关系,再根据互为余角的正切、余切的关系,可得答案.【解答】解:由余切是邻边比对边,得AC=4cot50°,由一个角的余切等于它余角的正切,得AC=4tan40°,故选:B.【点评】本题考查了锐角三角函数的定义,利用了锐角三角函数的余切是邻边比对边,一个角的余切等于它余角的正切.8.如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是( )A.①②④ B.①③④ C.②③④ D.①②③【考点】相似三角形的判定.【分析】根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.【解答】解:当∠ACP=∠B,∠A公共,所以△APC∽△ACB;当∠APC=∠ACB,∠A公共,所以△APC∽△ACB;当AC2=AP•AB,即AC:AB=AP:AC,∠A公共,所以△APC∽△ACB;当AB•CP=AP•CB,即=,而∠PAC=∠CAB,所以不能判断△APC和△ACB相似.故选D.【点评】本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.9.如图,身高1.6米的学生小李想测量学校的旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2米,BC=8米,则旗杆的高度是( )A.6.4米B.7米C.8米D.9米【考点】相似三角形的应用.【专题】压轴题.【分析】因为人和旗杆均垂直于地面,所以构成相似三角形,利用相似比解题即可.【解答】解:设旗杆高度为h,由题意得,h=8米.故选:C.【点评】本题考查了考查相似三角形的性质和投影知识,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.10.抛物线y=x2﹣4x+1的顶点坐标是( )A.(﹣2,13)B.(2,﹣3)C.(2,5)D.(﹣2,﹣3)【考点】二次函数的性质.【分析】已知抛物线为一般式,可以利用公式法求顶点坐标,也可以用配方法求顶点坐标.【解答】解:解法1:利用公式法y=ax2+bx+c的顶点坐标公式为(,),代入数值求得顶点坐标为(2,﹣3).解法2:利用配方法y=x2﹣4x+1=x2﹣4x+4﹣3=(x﹣2)2+3,故顶点的坐标是(2,﹣3).故选B.【点评】求抛物线的顶点坐标、对称轴的方法.11.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )A.B.C.D.【考点】锐角三角函数的定义;三角形的面积;勾股定理.【专题】网格型.【分析】作AC⊥OB于点C,利用勾股定理求得AC和AO的长,根据正弦的定义即可求解.【解答】解:作AC⊥OB于点C.则AC=,AO===2,则sin∠AOB===.故选:D.【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.12.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有( )A.①②③ B.②④C.②⑤D.②③⑤【考点】二次函数图象与系数的关系.【专题】数形结合.【分析】根据抛物线开口方向得a<0,由抛物线对称轴为直线x=﹣=1,得到b=﹣2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(﹣1,0)的右侧,则当x=﹣1时,y<0,所以a﹣b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=﹣,然后把b=﹣2a代入计算得到x1+x2=2.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线对称轴为直线x=﹣=1,∴b=﹣2a>0,即2a+b=0,所以②正确;∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①错误;∵抛物线对称轴为直线x=1,∴函数的最大值为a+b+c,∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,∴抛物线与x轴的另一个交点在(﹣1,0)的右侧∴当x=﹣1时,y<0,∴a﹣b+c<0,所以④错误;∵ax12+bx1=ax22+bx2,∴ax12+bx1﹣ax22﹣bx2=0,∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,∴(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,∴a(x1+x2)+b=0,即x1+x2=﹣,∵b=﹣2a,∴x1+x2=2,所以⑤正确.故选:D.【点评】本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2﹣4ac >0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.二、耐心填一填(每小题3分,共24分)13.计算:×=3a.【考点】二次根式的乘除法.【分析】根据二次根式的乘法法则求解.【解答】解:×===3a.故答案为:3a.【点评】本题考查了二次根式的乘除法,解答本题的关键是掌握二次根式的乘法法则.14.若式子有意义,则x的取值范围是x<9.【考点】二次根式有意义的条件;分式有意义的条件.【分析】根据二次根式有意义的条件和分式有意义的条件可得9﹣x>0,再解即可.【解答】解:由题意得:9﹣x>0,解得:x<9.故答案为:x<9.【点评】此题主要考查了二次根式和分式有意义的条件,关键是掌握二次根式中的被开方数是非负数;分式有意义的条件是分母不等于零.15.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:3,则AB的长为6米.【考点】解直角三角形的应用-坡度坡角问题.【分析】在Rt△ABC中,已知坡面AB的坡比以及铅直高度BC的值,通过解直角三角形即可求出斜面AB的长.【解答】解:在Rt△ABC中,BC=6米,tanA=1:3;∴AC=BC÷tanA=18米,∴AB==6米.故答案为:6.【点评】此题主要考查学生对坡度坡角的掌握及三角函数的运用能力,熟练运用勾股定理是解答本题的关键.16.让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则两个数的和是2的倍数或3的倍数的概率等于.【考点】列表法与树状图法.【分析】列表得出所有等可能的情况数,找出两个数的和是2的倍数或3的倍数情况,即可求出所求概率.【解答】解:列表如下:1 2 3 41 (1,1)(2,1)(3,1)(4,1)2 (1,2)(2,2)(3,2)(4,2)3 (1,3)(2,3)(3,3)(4,3)4 (1,4)(2,4)(3,4)(4,4)所有等可能的情况有16种,其中两个数的和是2的倍数或3的倍数情况有10种,则P==.故答案为:.【点评】此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.17.如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长交CE于点E,若AB=6,AD=2CD,则BE的长为3.【考点】相似三角形的判定与性质;等边三角形的性质;勾股定理.【分析】如图,作辅助线;证明AB∥CF,得到△ABD∽△CED,进而得到,结合AD=2CD,AB=6,求出CE=3;求出EG、CG的长度,运用勾股定理即可解决问题.【解答】解:如图,过点E作EG⊥CF于点G;∵△ABC是等边三角形,∴∠A=∠ACB=60°,AB=BC=6;∴∠ACF=120°,而CE是外角平分线,∴∠ACE=∠ECG=60°,∠A=∠ACE,∴AB∥CF,△ABD∽△CED,∴,而AD=2CD,AB=6,∴CE=3;而∠ECG=60°,∴∠CEG=30°,CG=CE=1.5,EG=,∴BG=7.5;由勾股定理得:BE2=BG2+EG2,∴BE=3,故答案为3.【点评】该题主要考查了等边三角形的性质、相似三角形的判定、勾股定理等几何知识点及其应用问题;解题的关键是作辅助线;灵活运用等边三角形的性质、相似三角形的判定、勾股定理等几何知识点来分析、判断、解答.18.设x1,x2是方程x2﹣x﹣1=0的两个根,则代数式x13+2x2+x1•x2的值为0.【考点】根与系数的关系.【专题】计算题.【分析】先根据根与系数的关系得到x1+x2=1,x1x2=﹣1,再利用x1是方程x2﹣x﹣1=0的根得到x12﹣x1﹣1=0,则x12=x1+1,接着变形得到x13=2x1+1,则x13+2x2+x1•x2=2(x1+x2)+2x1x2,然后利用整体代入得方法计算.【解答】解:根据题意得x1+x2=1,x1x2=﹣1,∵x1是方程x2﹣x﹣1=0的根,∴x12﹣x1﹣1=0,∴x12=x1+1,∴x13=x1(x1+1)=x12+x1=x1+1+x1=2x1+1,∴x13+2x2+x1•x2=2x1+1+2x2+x1•x2=2(x1+x2)+2x1x2=2×1+2×(﹣1)=0.故答案为0.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=,x1x2=.也考查了一元二次方程解的定义.19.将抛物线y=3x2﹣2向左平移2个单位,再向下平移3个单位,则所得抛物线的解析式为y=3(x+2)2﹣5.【考点】二次函数图象与几何变换.【专题】几何变换.【分析】先确定抛物线y=3x2﹣2的顶点坐标为(0,﹣2),再根据点平移的规律得到点(0,﹣2)平移后所得对应点的坐标为(﹣2,﹣5),然后根据顶点式写出平移后的抛物线解析式.【解答】解:抛物线y=3x2﹣2的顶点坐标为(0,﹣2),点(0,﹣2)向左平移2个单位,再向下平移3个单位所得对应点的坐标为(﹣2,﹣5),所以所得抛物线的解析式为y=3(x+2)2﹣5.故答案为y=3(x+2)2﹣5.【点评】本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.20.如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为.【考点】全等三角形的判定与性质;等腰直角三角形;正方形的性质.【专题】计算题;几何图形问题.【分析】在BE上截取BG=CF,连接OG,证明△OBG≌△OCF,则OG=OF,∠BOG=∠COF,得出等腰直角三角形GOF,在RT△BCE中,根据射影定理求得GF的长,即可求得OF的长.【解答】解:如图,在BE上截取BG=CF,连接OG,∵RT△BCE中,CF⊥BE,∴∠EBC=∠ECF,∵∠OBC=∠OCD=45°,∴∠OBG=∠OCF,在△OBG与△OCF中∴△OBG≌△OCF(SAS)∴OG=OF,∠BOG=∠COF,∴OG⊥OF,在RT△BCE中,BC=DC=6,DE=2EC,∴EC=2,∴BE===2,∵BC2=BF•BE,则62=BF,解得:BF=,∴EF=BE﹣BF=,∵CF2=BF•EF,∴CF=,∴GF=BF﹣BG=BF﹣CF=,在等腰直角△OGF中OF2=GF2,∴OF=.故答案为:.【点评】本题考查了全等三角形的判定和性质,直角三角形的判定以及射影定理、勾股定理的应用.三、算一算(6分,18分)21.﹣12014×(﹣)﹣2+(﹣π)0﹣+2cos60°.【考点】实数的运算;零指数幂;特殊角的三角函数值.【专题】计算题.【分析】原式第一项利用乘方的意义及负指数幂法则计算,第二项利用零指数幂法则计算,第三项利用二次根式的性质化简,最后一项利用特殊角的三角函数值计算即可得到结果.【解答】解:原式=﹣1×9+1﹣2+2×=﹣9+1﹣2+1=﹣9.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.22.﹣3﹣×.【考点】二次根式的混合运算.【专题】计算题.【分析】先把各二次根式化为最简二次根式,再进行二次根式的乘法运算,然后合并即可.【解答】解:原式=2﹣2﹣4•=﹣4a.【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.23.解方程:2(x+1)2﹣x(x﹣2)=0.【考点】解一元二次方程-配方法.【专题】计算题.【分析】方程整理后,利用配方法求出解即可.【解答】解:方程整理得:2x2+4x+2﹣x2+2x=0,即x2+6x=﹣2,配方得:x2+6x+9=7,即(x+3)2=7,开方得:x+3=±,解得:x1=﹣3+,x2=﹣3﹣.【点评】此题考查了解一元二次方程﹣配方法,熟练掌握完全平方公式是解本题的关键.四、用心做一做(本大题共3个小题,每小题6分,共18分)24.如图在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).(1)画出△ABC关于x轴对称的△A1B1C1;(2)将△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2,B2,C2,请画出△A2B2C2;(3)则S△A1B1C1:S△A2B2C2.【考点】作图-位似变换;作图-轴对称变换.【分析】(1)利用关于x轴对称点的性质得出对应点坐标进而得出答案;(2)利用对应点横坐标与纵坐同时乘以﹣2,进而得出各点的位置;(3)利用位似图形的性质得出面积比即可.【解答】解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;(3)∵△A1B1C1的三个顶点的横坐标与纵坐同时乘以﹣2,得到对应的点A2,B2,C2,∴△A1B1C1与△A2B2C2,关于原点位似,位似比为1:2,∴S△A1B1C1:S△A2B2C2=1:4.【点评】此题主要考查了轴对称变换以及位似变换和位似图形的性质,根据题意得出对应点坐标是解题关键.25.在一个不透明的口袋里装有标号为1,2,3,4,5的五个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球.(1)下列说法:①摸一次,摸出1号球和摸出5号球的概率相同;②有放回的连续摸10次,则一定摸出2号球两次;③有放回的连续摸4次,则摸出四个球标号数字之和可能是20.其中正确的序号是①③.(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.【考点】列表法与树状图法.【专题】计算题.【分析】(1)①摸一次,1号与5号球摸出概率相同,正确;②有放回的连续摸10次,不一定摸出2号球,错误;③有放回的连续摸4次,若4次均摸出5号球:5+5+5+5=20,则摸出四个球标号数字之和可能是20,正确;(2)列表得出所有等可能的情况数,找出两球标号数字是一奇一偶的情况数,即可求出所求的概率.【解答】解:(1)①摸一次,1号与5号球摸出概率相同,正确;②有放回的连续摸10次,不一定摸出2号球,错误;③有放回的连续摸4次,若4次均摸出5号球:5+5+5+5=20,则摸出四个球标号数字之和可能是20,正确;故答案为:①③;(2)列表如下:1 2 3 4 51 ﹣﹣﹣(1,2)(1,3)(1,4)(1,5)2 (2,1)﹣﹣﹣(2,3)(2,4)(2,5)3 (3,1)(3,2)﹣﹣﹣(3,4)(3,5)4 (4,1)(4,2)(4,3)﹣﹣﹣(4,5)5 (5,1)(5,2)(5,3)(5,4)﹣﹣﹣所有等可能的情况有20种,其中数字是一奇一偶的情况有12种,则P(一奇一偶)==.【点评】此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.26.某超市准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为每个50元,可售出400个;定价每增加1元,销售量将减少10个,设每个定价增加x元,(1)写出售出一个可获得的利润是多少元?(用含x的代数式表示)(2)商店若准备获得利润6 000元,并且使进货量较少,则每个定价为多少元?应进货多少个?【考点】一元二次方程的应用.【专题】销售问题.【分析】(1)根据利润=销售价﹣进价列关系式;(2)总利润=每个的利润×销售量,销售量为400﹣10x,列方程求解,根据题意取舍;【解答】解:(1)由题意得:50+x﹣40=x+10;(2)由已知得,(x+10)(400﹣10x)=6000,整理得:x2﹣30x+200=0解得,x1=10,x2=20,∵进货量较少,∴x=20,进货量为:400﹣10x=400﹣200=200.答:当定价为70元时利润达到6000元,此时的进货量为200个.【点评】考查了一元二次方程的应用,应用题中求最值需先求函数表达式,再运用函数性质求解.此题的关键在列式表示销售价格和销售量.五.大显身手(本大题共2个小题,每题7分,共14分)27.马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B 的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75).(1)求可疑漂浮物P到A、B两船所在直线的距离;(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.【考点】解直角三角形的应用-方向角问题.【专题】几何图形问题.【分析】(1)过点P作PE⊥AB于点E,在Rt△APE中解出PE即可;(2)分别求出PA、PB的长,根据两船航行速度,计算出两艘船到达P点时各自所需要的时间,即可作出判断.【解答】解:(1)过点P作PE⊥AB于点E,由题意得,∠PAE=36.5°,∠PBA=45°,设PE为x海里,则BE=PE=x海里,∵AB=140海里,∴AE=(140﹣x)海里,在Rt△PAE中,,即:解得:x=60,∴可疑漂浮物P到A、B两船所在直线的距离约为60海里;(2)在Rt△PBE中,PE=60海里,∠PBE=45°,则BP=PE=60≈84.8海里,B船需要的时间为:84.8÷30≈2.83小时,在Rt△PAE中,=sin∠PAE,∴AP=PE÷sin∠PAE=60÷0.6=100海里,∴A船需要的时间为:100÷40=2.5小时,∵2.83>2.5,∴A船先到达.【点评】本题考查了解直角三角形的应用,解答本题的关键是理解方位角的定义,能利用三角函数值计算有关线段,难度一般.28.如图,在△ABC中,己知AB=AC=5,BC=6,且将△ABC≌△DEF,将△DEF与△ABC 重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.(1)求证:△ABE∽△ECM;(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;(3)当点E运动到什么位置时,线段AM最短?并求出此时AM的值.(直接写出答案)【考点】相似形综合题.【分析】(1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证得∠CEM=∠BAE,则可证得:△ABE∽△ECM;(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案;(3)先设BE=x,由△ABE∽△ECM,根据相似三角形的对应边成比例,易得CM=﹣(x﹣3)2+,利用二次函数的性质,继而求得线段AM的最小值.【解答】(1)证明:∵AB=AC,∴∠B=∠C,∵△ABC≌△DEF,∴∠AEF=∠B,又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,。
2014-2015第一学期江苏省海安九年级数学期末考试
2014~2015学年度第一学期学业水平测试九年级数学一、选择题(本题共有10小题,每小题3分,共30分,在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应的位置........上)1.下列各标志中,是中心对称图形的是(▲)2.下列事件中,是必然事件的是(▲)A.抛掷一枚质地均匀的硬币,落地后正面朝上B.海安县7月份某一天的最低气温是−3℃C.通常加热到100℃时,水沸腾D.打开电视,正在播放综艺节目《一站到底》3.已知一个几何体的三视图如图所示,则该几何体是(▲)4.贵都超市某商品经过两次降价,每件零售价由100元降为81元.已知两次降价的百分率为x,那么x满足的方程是(▲)A.100(1+x)2=81 B.100(1−x)2=81 C.100(1−x%)2=81 D.100x2=815.关于反比例函数2yx=的图象,下列说法正确的是(▲)A.图象经过点(1,12)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小6.下列条件不能判定△ABC与△DEF相似的是(▲)A.AB BC ACDE EF DF==B.AB BCDE EF=,∠A=∠DC.∠A=∠D,∠B=∠E D.AB BCDE EF=,∠B=∠E注意事项考生在答题前请认真阅读本注意事项:1.本试卷共6页,满分150分,考试时间为120分钟.考试结束后,请将本试卷和答题卡一并交回.2.卡上指定的位置.3.答案必须按要求填涂、书写在答题卡上,在试卷、草稿纸上答题一律无效.A B C D三视图A B C D7.抛物线y =ax 2+bx 和直线y =ax +b 在同一坐标系的图象可能是( ▲ )8.如图,△ABC 中,∠C=90°,AC =2,BC =1,则cos B 的值是 ( ▲ )A .12B C D 9.如图,在5×5的正方形网格中,一条弧经过A 、B 、C 三点,那么这条圆弧所在圆的圆心是 ( ▲ ) A .点P B .点Q C .点R D .点S10.如图,⊙O 的半径为4,点P 是⊙O 外的一点,PO =10,点A 是⊙O 上的一个动点,连接P A ,直线l 垂直平分P A ,当直线l 与⊙O 相切时,P A 的长度为 ( ▲ ) A .10B .212C .11D .434二、填空题(本题共有8小题,每小题3分,共24分,不需写出解答过程,请把答案直接填写在答题卡...相应的位置.....上) 11.若△ABC ∽△A ′B ′C ′,相似比为1:3,则△ABC 与△A ′B ′C ′的面积之比为 ▲ . 12.如图,⊙O 中,OA ⊥BC ,∠AOB =52°,则∠ADC 的度数为 ▲ .13.若关于x 的一元二次方程x 2+bx +c =0的两个实数根分别为x 1=−1,x 2=2,则b +c 的值 是 ▲ .14.如图是一个飞镖游戏板,大圆的直径把一组同心圆分成四等份,假设飞镖击中圆面上每一个点都是15 ▲ cm .16.将抛物线y =x 2先向左平移2个单位,再向下平移3个单位,所得抛物线的解析式为 ▲ .17.在△ABC 中,BC =3,AC =4,AB =5,点D 、E 分别是△ABC 的内心和外心,连接DE ,则DE 的长为▲ .(第8题) (第9题) (第10题) CB A A BC D18.如图,函数1y x =(x >0)和3y x=(x >0)的图象分别是l 1和l 2.设点P 在l 2上,P A ∥y 轴,交l 1于点A ,PB ∥x 轴,交l 1于点B ,则△P AB 的面积为 ▲ .三、解答题(本题共有10小题,共96分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤) 19.(本小题满分10分)(12sin60︒+;(2)解方程:x 2+4x −1=0. 20.(本小题满分9分)如图,在平面直角坐标系中,△ABC 的三个顶点 坐标分别为A (2,−1)、B (1,−4)、C (3,−2). (1)△ABC 绕原点O 逆时针旋转90°,画出旋转 后得到的△A 1B 1C 1,并求边AC 在旋转过程中 扫过的图形面积;(2)以原点O 为位似中心,位似比为1:2,在y 轴 的右侧,画出△ABC 放大后的图形△A 2B 2C 2. 如果点D (a ,b )在线段AB 上,那么请直接 写出点D 的对应点D 2的坐标. 21.(本小题满分8分)如图,在平面直角坐标系xOy 中,边长为2的正方形OABC 的顶点A 、C 分别在x 轴的正半轴和y 轴的负半轴上,二次 函数223y x bx c =++的图象经过B 、C 两点. (1)求该二次函数的解析式;(2)结合函数的图象探索:当y >0时,x 的取值范围.22.(本小题满分8分)一只不透明的袋子里共有4个球,其中3个白球,1个红球,它们除颜色外均相同. (1)从袋子中随机摸出一个球是白球的概率是多少? (2)从袋子中随机摸出一个球,不放回...袋子,摇匀袋子后再摸一个球,请用列表或画树状图 的方法,求出两次摸出的球都是白球的概率. 23.(本小题满分8分)苏中七战七捷纪念馆位于江苏海安县城中心,馆内纪念碑碑身造型似一把刺刀矗立在广袤的苏中大地上,堪称世界之最,被誉为“天下第一刺刀”.如图,在一次数学课外实践活动中,老师要求测纪念碑碑身的高度AB ,小明在D m 测角仪CD ,测得纪念碑碑身顶端A 的仰角为30°,然后向纪念碑碑身前进20 m 到达E 处,又测得纪念碑碑身顶端A 的仰角为45°,已知纪念碑碑身下面的底座高度BH 为1.8 m .求纪念碑碑身的高度AB(结果精确到个位,参考数据:(第20题)(第21题)24.(本小题满分9分)如图,AB 为⊙O 的直径,BC CD =,过点C 的直线CE 和AD 的延长线互相垂直,垂足为E . (1)求证:直线CE 与⊙O 相切;(2)过点O 作OF ⊥AC ,垂足为F ,若OF =2,OA =4,求AE 的长.25.(本小题满分8分)某y (微克/毫升)与时间x (时)的关系可近似地用二次函数y =−12x 2+24x 刻画;1.5小时后(包括1.5小时)y 与x 可近似地用反比例函数ky x=(k >0)刻画(如图所示),已知当x =3时,y . (1)成人按规定的剂量服药后几时血液中含药量达到最大值?最大值为多少?(2)据测定:每毫升血液中含药量少于4微克,这种药对疾病治疗就会失去效果,试分析成人按规定的剂量服完药小时以后是否还有药效.26.(本小题满分10分) 【问题提出】数学课本上有这样一道题目:如图①,一块材料的形状是锐角三角形ABC ,边BC =120 mm ,(第23题)20m45° 30°HG F EDCB AFED CO B A (第24题) 3 y /(微克/毫升)x /时 O (第25题)高AD =80 mm .把它加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,这个正方形零件的边长是多少? 【初步思考】(1)试计算出正方形零件的边长; 【深入探究】(2)李华同学通过探究发现如果要把△ABC 按照图②加工成三个相同大小的正方形零件, △ABC 的边BC 与高AD 需要满足一定的数量关系.则这一数量关系是: ▲ .(直 接写出结论,不用说明理由);(3)若△ABC 可以按照图③加工成四个大小相同的正方形,且∠B =30°,求证:AB =BC .27.(本小题满分13分)如图,在Rt △ABC 中,∠ACB =90°,AC =6 cm ,BC =8 cm ,动点P 从点B 出发,在BA 边上以每秒5 cm 的速度向点A 匀速运动,同时动点Q 从点C 出发,在CB 边上以每秒4 cm 的速度向点B 匀速运动,运动时间为t 秒(0≤t ≤2),连接PQ ,以PQ 为直径作⊙O . (1)当t =0.5时,求△BPQ 的面积;(2)设⊙O 的面积为y ,求y 与t 的函数解析式,并直接写出y 的值最小时t 的值; (3)若⊙O 与Rt △ABC 的一条边相切,求t 的值.28.(本小题满分13分) 如图①,∠MON =90°,反比例函数2y x =(x >0)和ky x=(k <0,x <0)的图象分别是l 1和l 2.射线OM 交l 1于点A (1,a ),射线ON 交l 2于点B ,连接AB 交y 轴于点P ,AB ∥x 轴.(1)求k 的值;(2)如图②,将∠MON 绕点O 旋转,射线OM 始终在第一象限,交l 1于点C ,射线ON 交l 2 于点D ,连接CD 交y 轴于点Q ,在旋转的过程中,∠OCD 的大小是否发生变化,若不 变化,求出tan ∠OCD 的值;若变化,请说明理由;(3)在(2)的旋转过程中,当点Q 为CD 中点时,CD 所在的直线与l 1的有几个公共点,求(第27题)(第26题) 图① 图② 图③ K H G F E D C A A C D B B AC E FG H出公共点的坐标.2014~2015学年度第一学期学业水平测试九年级数学参考答案一、选择题1-5.BCDBD ;6-10.BACBB 二、填空题11.1:9.12.26°.13.−3.14.12.15.2.16.y =(x +2)2−3.17.18.2.三、解答题19.解:(1)原式=2−25分 (2)12x =-,22x =-10分 20.解:(1)画图………………………………………3分 S =2π……………………………………………5分 (2)画图……………………………………………8分 D 2(2a ,2b )…………………………………9分 21.解:(1)由题意得B (2,−2),C (0,−2)……1分 代入223y x bx c =++得 82232b c c ⎧++=-⎪⎨⎪=-⎩,解得432b c ⎧=-⎪⎨⎪=-⎩,……………3分∴二次函数的解析式为224233y x x =--;…………………………………………………………4分 (2)令y=0,得2242033x x --=,解得x 1=−1,x 2=3,……………………………………………6分 结合图象可知:当x <−1或x >3时,y >0.……………………………………………………………8分(第28题)图① 图②22.解:(1)P (摸出一个球是白球)=34…………………………………………………………………3分 (2)画树形图: 共有12中等可能的结果,P (两次摸出的求都是白球)=61122=…………………………………8分 23.解:由题意得:CF =DE =20,GH =FE =CD =1.5, 在Rt △AGC 中,CG =tan 30AG ︒,在Rt △AGF 中,FG =tan 45AG︒=AG ,……………………4分∴CF =CG −FGAG −AG−1)AG ,∴AGCF ≈1.73212+×…………………6分∴AB =AG +GH −BH −≈27(m )答:纪念碑碑身的高度AB 为27 m .…………………………………………………………………8分 24.(1)证明:连接OC ,∵BC CD =,∴∠DAC =∠CAB ,∵OA =OC ,∴∠CAB =∠OCA ,∴∠DAC =∠OCA ,∴AE ∥OC ,∵AE ⊥CE ,∴OC ⊥CE ,∴直线CE 与⊙O 相切………………5分 (2)解:在Rt △OF A 中,AFsin ∠OAF =12OF OA =,∴∠OAF =30°, ∴∠EAC =30°,∵OF ⊥AC ,∴AC =2AF=,在Rt △CEA 中,AE =AC •cos30°=6.…………………………………………………………………9分 25.解:(1)∵y =−12x 2+24x =−12(x −1)2+12,∴成人按规定的剂量服药后1时血液中含药量达到最大值,最大值为12;………………………3分 (2)∵当x =3时,y =4.5,∴k =xy =3×4.5=13.5,∴当x >1.5时,13.5y x=,………………………5分 当x =3.5时,277y =<4,………………………………………………………………………………7分 ∴成人按规定的剂量服完.………………………………………………8分 26.(1)解:设正方形零件的边长为x mm ,则KD =EF =x ,AK =80−x , ∵EF ∥BC ,∴△AEF ∽△ABC ,∵AD ⊥BC ,∴EF AK BC AD =,∴8012080x x-=,解得x =48. 答:正方形零件的边长为48 mm .……………………………………………………………………4分(2)BC =AD .……………………………………………………………………………………………6分 (3)证明:过点A 作AD ⊥BC 于D ,分别交EF 、GH 于点M 、N , 设每个正方形的边长为a , ∵EF ∥GH ∥BC ∴△AEF ∽△AGH ∽△ABC ,∴AM AN AD EF GH BC ==,∴23AD a AD a ADa a BC--==, 解得ADa ,BC =5a ,∴BC =2AD .∵∠B =30°,AD ⊥BC ,∴AB =2AD ,∴AB =BC .…………………………………………………10分 27.解:(1)过点P 作PM ⊥BC 于点M , △BPM ∽△BAC ,可得PM =3t ,BM =4t ,S △BPQ =12BQ •PM =12t −6t 2, 白1 白2 白3 红 白2 白3 红 白1 白3 红 白1 白2 红 白1 白2 白3 D AC E F G HM N∴当t =0.5时,S △BPQ =4.5;………………………………………………3分 (2)MQ =|8−8t|,PQ 2=PM 2+MQ 2=(8−8t )2+(3t )2=73t 2−128t +64, ∴2273321644y PQ t t ππππ==-+,…………………………………6分 当t =6473时,y 的值最小.……………………………………………7分(3)当⊙O 与BC 相切时,PQ ⊥BC ,△BPQ ∽△BAC , ∴BP BQ BA BC =,∴584108t t-=,∴t 1=1.………………………………………………………………9分 当⊙O 与AB 相切时,PQ ⊥AB ,△BPQ ∽△BCA , ∴BP BQ BC BA =,∴584810t t -=,∴t 2=3241.……………………………………………………………11分 当⊙O 与AC 相切时,过点O 作OH ⊥AC 于点H ,交PM 于点N , OH =ON +NH =12QM +MC =12(8t −8)+(8−4t )=4, ∴PQ =2OH =8, ∴73t 2−128t +64=64 解得t 3=0,t 4=12873.………………………………………13分 综上所述,若⊙O 与Rt △ABC 的一条边相切, t 的值为1或3241或0或12873. 28.解:(1)将A (1,a )代入2y x=,得a =2, ∴A (1,2),OP =2,AP =1, ∵AB ∥x 轴,∴AB ⊥OP ,又∵∠MON =90°,∴△OP A ∽△BPO ,∴2AP BP OP ==4∵点B 在第二象限,∴B (−4,2)代入ky x=,得k =−8.………………………………………4分(2)∠OCD 的大小不变. 过点C 作CE ⊥x 轴于点E ,过点D 作DF ⊥x 轴于点F , 设OE =m ,OF =n ,∴C (m ,2m),D (−n ,8n ), 易证△DFO ∽△OEC ,∴DF OF OE CE =,∴82n n m m=, ∴m 2n 2=16,∵m >0,n >0,∴mn =4,4n m=,∵△DFO ∽△OEC ,∴DO OF OC CE =,∴42DO OC m m=÷=2,即tan ∠OCD =2.………………………9分(3)当点Q 为CD 中点时,OE =OF ,∴4m m=,∵m >0,∴m =2,∴C (2,1),D (−2,4).设直线CD 的解析式为y =k 1x +b ,可得112124k b k b +=⎧⎨-+=⎩,解得13452k b ⎧=-⎪⎪⎨⎪=⎪⎩,∴直线CD 的解析式为3542y x =-+,联立方程组35422y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩,解得1121x y =⎧⎨=⎩,224332x y ⎧=⎪⎪⎨⎪=⎪⎩.∴CD 所在的直线与l 1的有两个公共点,分别是(2,1)和(43,32).………………………13分。
2014-2015九年级上数学期末试卷2份
九年级上数学期末试卷一.选择题(共10小题)1.已知x=2是一元二次方程x2+mx+2=0的一个解,则m的值是()A.﹣3 B. 3 C.0 D.0或32.方程x2=4x的解是()A.x=4 B.x=2 C.x=4或x=0 D.x=03.如图,在▱ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=,则△CEF的面积是()A.B.C.D.3题4.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为()A.11+B.11﹣C.11+或11﹣D.11+或1+5.有一等腰梯形纸片ABCD(如图),AD∥BC,AD=1,BC=3,沿梯形的高DE剪下,由△DEC与四边形ABED不一定能拼成的图形是()A.直角三角形B.矩形C.平行四边形D.正方形5题6.如图是由5个大小相同的正方体组成的几何体,它的俯视图为()A.B.C.D.7.下列函数是反比例函数的是()A.y=x B.y=kx﹣1 C.y=D.y=8.矩形的面积一定,则它的长和宽的关系是()A.正比例函数B.一次函数C.反比例函数D.二次函数9.已知一组数据:12,5,9,5,14,下列说法不正确的是()A.极差是5 B.中位数是9 C.众数是5 D.平均数是910.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%,则口袋中白色球的个数可能是()A.24 B.18 C.16 D. 6二.填空题(共6小题)11.某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为_____.12.如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE=_________度.13.有两张相同的矩形纸片,边长分别为2和8,若将两张纸片交叉重叠,则得到重叠部分面积最小是_________,最大的是_________.14.直线l1:y=k1x+b与双曲线l2:y=在同一平面直角坐标系中的图象如图所示,则关于x的不等式>k1x+b的解集为_________.15.一个口袋中装有10个红球和若干个黄球.在不允许将球倒出来数的前提下,为估计口袋中黄球的个数,小明采用了如下的方法:每次先从口袋中摸出10个球,求出其中红球数与10的比值,再把球放回口袋中摇匀.不断重复上述过程20次,得到红球数与10的比值的平均数为0.4.根据上述数据,估计口袋中大约有_________个黄球.16.如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为_________.三.解答题(共11小题)17.解方程:(1)x2﹣4x+1=0.(配方法)(2)解方程:x2+3x+1=0.(公式法)(3)解方程:(x﹣3)2+4x(x﹣3)=0.(分解因式法)18.已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.(1)求证:方程恒有两个不相等的实数根;(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.19.如图,△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.(1)求证:△ABC≌△CDA;(2)若∠B=60°,求证:四边形ABCD是菱形.20.如图,梯形ABCD中,AB∥CD,AC⊥BD于点0,∠CDB=∠CAB,DE⊥AB,CF⊥AB,E.F为垂足.设DC=m,AB=n.(1)求证:△ACB≌△BDA;(2)求四边形DEFC的周长.21.如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.22.一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.根据以上信息解答下列问题:(1)求实验总次数,并补全条形统计图;(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.23.如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.24.如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.(1)求k的值及点E的坐标;(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.参考答案一.选择题(共10小题)1.A 2.C 3.A 4.D 5.D 6.A 7.C8.C9.A10.C二.填空题(共6小题)11.20%12.5013.14.x<或0<x<15.1516.9三.解答题(共11小题)17..(1).x1=2+,x2=2﹣(2)x1=,x2=.(3).18.解答:(1)证明:∵△=(m+2)2﹣4(2m﹣1)=(m﹣2)2+4,∴在实数范围内,m无论取何值,(m﹣2)2+4>0,即△>0,∴关于x的方程x2﹣(m+2)x+(2m﹣1)=0恒有两个不相等的实数根;(2)解:根据题意,得12﹣1×(m+2)+(2m﹣1)=0,解得,m=2,则方程的另一根为:m+2﹣1=2+1=3;①当该直角三角形的两直角边是1、3时,由勾股定理得斜边的长度为:;该直角三角形的周长为1+3+=4+;②当该直角三角形的直角边和斜边分别是1、3时,由勾股定理得该直角三角形的另一直角边为2;则该直角三角形的周长为1+3+2=4+2.19.解答:证明:(1)∵AB=AC,∴∠B=∠ACB,∵∠FAC=∠B+∠ACB=2∠ACB,∵AD平分∠FAC,∴∠FAC=2∠CAD,∴∠CAD=∠ACB,∵在△ABC和△CDA中,∴△ABC≌△CDA(ASA);(2)∵∠FAC=2∠ACB,∠FAC=2∠DAC,∴∠DAC=∠ACB,∴AD∥BC,∵∠BAC=∠ACD,∴AB∥CD,∴四边形ABCD是平行四边形,∵∠B=60°,AB=AC,∴△ABC是等边三角形,∴AB=BC,∴平行四边形ABCD是菱形.20.解答:(1)证明:∵AB∥CD,∠CDB=∠CAB,∴∠CDB=∠CAB=∠ABD=∠DCA,∴OA=OB,OC=OD,∴AC=BD,在△ACB与△BDA中,,∴△ACB≌△BDA.(2)解:过点C作CG∥BD,交AB延长线于G,∵DC∥AG.CG∥BD,∴四边形DBGC为平行四边形,∵△ACB≌△BDA,∴AD=BC,即梯形ABCD为等腰梯形,∵AC=BD=CG,∴AC⊥BD,即AC⊥CG,又CF⊥AG,∴∠ACG=90°,AC=BD,CF⊥FG,∴AF=FG,∴CF=AG,又AG=AB+BG=m+n,∴CF=.又∵四边形DEFC为矩形,故其周长为:2(DC+CF)=.21.解答:解:(1)如图:线段MG和GE就表示旗杆在阳光下形成的影子.(2)过M作MN⊥DE于N,设旗杆的影子落在墙上的长度为x,由题意得:△DMN∽△ACB,∴又∵AB=1.6,BC=2.4,DN=DE﹣NE=15﹣xMN=EG=16∴解得:x=,答:旗杆的影子落在墙上的长度为米.22.解答:解:(1)50÷25%=200(次),所以实验总次数为200次,条形统计图如下:(2)=144°;(3)10÷25%×=2(个),答:口袋中绿球有2个.23.解答:证明:(1)∵四边形ABDE是平行四边形(已知),∴AB∥DE,AB=DE(平行四边形的对边平行且相等);∴∠B=∠EDC(两直线平行,同位角相等);又∵AB=AC(已知),∴AC=DE(等量代换),∠B=∠ACB(等边对等角),∴∠EDC=∠ACD(等量代换);∵在△ADC和△ECD中,,∴△ADC≌△ECD(SAS);(2)∵四边形ABDE是平行四边形(已知),∴BD∥AE,BD=AE(平行四边形的对边平行且相等),∴AE∥CD;又∵BD=CD,∴AE=CD(等量代换),∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);在△ABC中,AB=AC,BD=CD,∴AD⊥BC(等腰三角形的“三合一”性质),∴∠ADC=90°,∴▱ADCE是矩形.24.解答:解:(1)∵BC∥x轴,点B的坐标为(2,3),∴BC=2,∵点D 为BC 的中点, ∴CD=1,∴点D 的坐标为(1,3),代入双曲线y=(x >0)得k=1×3=3; ∵BA ∥y 轴,∴点E 的横坐标与点B 的横坐标相等,为2, ∵点E 在双曲线上, ∴y=∴点E 的坐标为(2,);(2)∵点E 的坐标为(2,),B 的坐标为(2,3),点D 的坐标为(1,3), ∴BD=1,BE=,BC=2 ∵△FBC ∽△DEB , ∴ 即:∴FC=∴点F 的坐标为(0,)设直线FB 的解析式y=kx+b (k ≠0) 则解得:k=,b=∴直线FB 的解析式y=九年级(上)期末模拟试卷时间:120分钟,总分100分姓名:___________班级:___________得分:___________一、选择题(每题3分,共30分)1.下列成语所描述的事件是必然发生的是 【 】A. 水中捞月B. 拔苗助长C. 守株待免D. 瓮中捉鳖2.已知一元二次方程02=++c bx ax ,若0=++c b a ,则该方程一定有一个根为( )A. 0B. 1C. -1D. 23.如图是由六个完全相同的正方体堆成的物体,则这一物体的正视图是A .B .C .D .4.若x=2是关于x 的一元二次方程2x mx 80-+= 的一个解,则m 的值是( ) A .6B .5C .2D .-65.已知直线y=kx (k >0)与双曲线y=交于点A (x 1,y 1),B (x 2,y 2)两点,则x 1y 2+x 2y 1的值为( )A .﹣6B .﹣9C .0D .96.如图(1)放置的一个机器零件,其主(正)视图如图(2)所示,则其俯视图是( )7.若一元二次方程20ax bx c ++=有一个根为,则下列等式成立的是( )A .1a b c ++=B .0a b c -+=C .0a b c ++=D .1a b c -+=8.小新抛一枚质地均匀的硬币,连续抛三次,硬币落地均正面朝上,如果他第四次抛硬币,那么硬币正面朝上的概率为( )A .B .C .1-D .9.如图是由若干个大小相同的正方体搭成的几何体的三视图,则该几何体所用的正方形的个数是A .2B .3C .4D .510.计算:(2)(2)a a +-的结果是( )A. 24a +B. 24a - C. 24a - D. 2a二、填空题(每题3分,共18分)11.一元二次方程x 2= x 的根是 .12.把265x x ++=0化成2()x m k +=的形式,则m = .13. 水平相当的甲乙两人进行羽毛球比赛,规定三局两胜,则甲队战胜乙队的概率是_________;甲队以2∶0战胜乙队的概率是________.14.六·一儿童节前,苗苗来到大润发超市发现某种玩具原价为100元,经过两次降价,现售价为81元,假设两次降价的百分率相同,则每次降价的百分率为 .主视左视俯视A. B. C. D.15.关于x 的一元二次方程(a -1)x 2-x+a 2-1=0的一个根是0,那么a 的值为______. 16.在“抛掷正六面体”的试验中,如果正六面体的六个面分别标有数字“1”、“2”、“3”、“4”、“5”和“6”,如果试验的次数增多,出现数字“1”的频率的变化趋势是___________.三、解答题(共52分)17.解下列方程【18分,(1)、(2)题各4分、(3)(4)题各5分】 (1)01x 3x 22=-+ (2))1x (x )1x (32-=-(3).求2(1)25x +=中x 的值。
2014-2015学年九年级上学期期末考试数学试卷
()
1A、. 2方程 x x 2
B. -2,1
2、抛物线 y 2x 3 2 3 的顶点坐标是
C. -1
D. 2,-1 ()
A. 4, 3
B.
32,
3
C.3, 3
D. 3, 3
3、关于 x 的一元二次方程 x2 - 2x a 0 有两个不相等的实数根,则 a 的取值范围是
B.45°
C 均在⊙CO. 上x,6A2BC12 AOC o90 ,则 ()
C.60°
D..给任意实数 n ,得到不同的抛物线 y x2 n ,当 n 0, 1 时,关于这些抛物线有以下
结论:①.开口方向不同;②.对称轴不同;③.都有最低点;④.可以通过一个抛物线平移
秘密★启用前〖考试时间:2014年 1 月 20日上午 9:00-11:00 共 120分钟〗
2014-2015学年九年级上学期期末考试
数学试卷
重新制版:赵化中学 郑宗平
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150分. 注意事项:
1、答题前,考生务必将自己的姓名、班级、考号(用 0.5毫米的黑色签字笔)填写在答题卡上,并检 查条形码粘贴是否正确.
⑵.当△ ABC 为等腰边三角形时,求b2 4ac 的值.
七、解答题(本题满分 12 分)
23、如图,三角板 ABC 中, ACB 90o 、、 AB 2 A o 30 ,三角板 ABC 绕直角顶点C 顺
时针旋转 90°,得到△ A B1 C1.
求:⑴. A¼ A 1的长;
A
⑵.在这个旋转过程中,三角板 ABC 的边 AC 所扫过的扇形 ACA1 的面积;
不超出答题区域作答. 不折叠答题卡,不用涂改
2014-2015学年度第一学期九年级期末数学考题目
2014-2015学年度第一学期九年级期末数学考题目1 / 32014-2015学年度第一学期第二次月考试题(卷)九年级 数学(满分:150分,时间:120分钟)1.把二次函数224y x x =-+ 化成顶点式为( )A .2(1)2y x =-+ B.2(1)3y x =++ C. 2(1)y x =- D. 2(1)3y x =-+ 2. 从n 个苹果和3个雪梨中,任选1个,若选中苹果的概率是12,则n 的值是( )A . 6B . 3C . 2D . 1 3.在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )4.-5的倒数是( )A .-5B .5C .- 15D .155.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A .B .C . D6.若一个多边形的内角和是720°,则这个多边形的边数是( ) A .5B .6C .7D .87.某经济开发区今年一月份工业产值达50亿元,三月份产值为175亿元,问平均每月的增长率是多少?设平均每月的增长率为x ,则得方程为 ( )A.250(1)175x += B. 250(1)50(1)175x x +++= C. 25050(1)175x ++= D.25050(1)50(1)175x x ++++=8、 点A (0,2)向右平移2个单位得到对应点1A ,则点1A 的坐标是 ( ) A .(2,2) B .(2,4) C .(-2,2) D .(2,-2)9、如图,圆内接四边形ABCD 中,∠A=105°,那么∠DCE 等于( ) A .75° B .105° C .80° D .150° 10、两人在玩“石头”、“剪刀”、“布”的游戏中,那么石头胜的概率为( )A. 18B.29C. 14D.13二、填空题(每小题3分,共30分)11.已知二次函数的图象经过(1,0)、(2,0)和(0,2)三点,则函数的解析式是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014~2015第一学期江苏省海门市九年级
数学期末试卷(人教版)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,恰好
有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.下列各数中,—3的相反数是( )
A.3 B.31 C.9 D.—3
2.某市2014年参加中考的考生人数约为85000人,将85000用科学记数法表示为( )
A.8.5×104 B.8.5×105 C.0.85×104 D.0.85×105
3.下列计算,正确的是( )
A.x4—x3=x B.x5÷x3=x2 C.x·x3=x3 D.(xy2)2=xy4
4.下列图形中,即是轴对称图形,又是中心对称图形的个数是( )
A.5 B.4 C.3 D.2
5.三角形三边分别3cm,6cm,xcm,则x可能是( )
A.1 B.2 C.3 D.4
6.图中两个四边形是位似图形,则它们的位似中心是( )
A.点M B.点N C.点O D.点P
(第7题) (第9题)
7.如图是某个几何体的三视图,该几何体是( )
A.长方体 B.正方体 C.三棱柱 D.圆柱
8.从1、2、3、4中任取一个数作为十位上的数字,再从3、4、5中任取一个数作为个位上
的数字,那么组成的两位数是3的倍数的概率是( )
A.41 B.125 C.31 D.32
9.如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后
回到A处,则蚂蚁所走最短路线长为( )
A.2 B.42 C.43 D.4
10.已知三角形三边长分别为5cm、5cm、6cm,则这个三角形内切圆的半径是( )
A.89cm B.23cm C.2cm D.3cm
二、填空题(本大题共8小题,每小题3分,共24分,不需要写出解答过程,请把答案直
接填写在答题卡相应位置上)
11.分解因式:x2—4y2=_________.
12.函数y=11x中,自变量x的取值范围是_______.
13.绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n
100 300 400 600 1000 2000 3000
发芽的粒数m
96 282 382 570 948 1912 2850
发芽的频率nm
0.960 0.940 0.955 0.95 0.948 0.956 0.950
则绿豆发芽的概率估计值是____________.
14.二次函数y=x2+2x—3的最小值是_________.
15.在△ABC中,AB=18,AC=12,点D、E分别是边AB、AC上一点,且AE=6,若△ADE
与△ABC相似,则AD的长为__________.
16.如图是一个上下底密封纸盒(底面为正六边形)的三视图,请你根据图中数据,计算这
个密封纸盒的表面积为_________cm2.(结果可保留根号)
8cm
10cm
(第16题) (第17题)
17.如图,在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
x
k
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD,若△OAD的面积
为1,则k的值为___________.
18.直线y=kx+8k(k为常数,k≠0)与抛物线y=81x2相交于A(x1,y1),B(x2,y2)两点,
若y1+y2=24,则k=__________.
三、解答题(本大题共10小题,共96分.请在答题卡指定区域内作答,解答时应写出文字
说明、证明过程或演算步骤)
19.(本小题满分8分)
(1)计算:(3.14—)0+(—21)—2—2sin30°;
(2)先化简,再求值:(1+a1)·122aa,其中a=3.
20. (本小题满分8分)
(1)解分式方程:32xx3; (2)解方程17382yxyx.
21. (本小题满分8分)
有4张背面完全相同的卡片,正面分别标上数字—1,0,1,2,背面朝上放置在桌子上,搅
匀后从中随机的摸出一张卡片,记录数字然后放回,再随机的摸出一张卡片记录数字.用列
表法或树状图求下列事件的概率:
(1)两次都是正数的概率P(A);
(2)两次的数字和等于0的概率P(B).
22.(本小题满分8分)
如图,小山的斜坡AC的坡角为α,且tanα=43,在与山脚C距离200米的D处,测得山
顶A的仰角26.6°,求小山的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°
=0.89,tan26.6°=0.50).
23.(本小题满分8分)
某容器内充满了一定质量的气体,当温度不变时,容器内气体的气压P(千帕)是气体体积
V(立方米)的反比例函数,其图象如图所示.
(1)求出这个函数的解析式;
(2)当容器内的气体体积是0.6立方米时,此时容器内的气压是多少千帕?
(3)当容器内的气压大于240千帕时,容器将爆炸,为了安全起见,容器内气体体积应不
小于多少立方米?
2
24.(本小题满分10分)
如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠C=30°,CE=6,求⊙O的半径.
25.(本小题满分10分)
已知A(1,4),B(n,—2)是一次函数y=kx+b的图象和反比例函数y=xm的图象的两个
交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△BOC的面积;
(3)直接写出不等式kx+b—xm<0的解集.
A
B
26.(本小题满分10分)
在△ABC中,AB=AC=6,∠BAC=108°,点D在边BC上,∠BAD=36°.
(1)求证:△BAD∽△BCA;
(2)求AD的长.
27.(本小题满分12分)
如图1,在菱形ABCD中,AB=2,∠BAD=60°,对角线AC、BD相交于点M,点O是边
AD的中点.
(1)求对角线AC、BD的长;
(2)设∠COD=α,∠OCD=β,则sinα与sinβ之间有何关系,并说明理由;
(3)如图2,以AD、OB所在直线为x、y轴,建立如图直角坐标系,在y轴上是否存在一
点P,使△PAC为直角三角形,若存在,请直接写出点P坐标;若不存在,说明理由.
M
B
A
D
C
O
x
y
M
C
D
A
B
O
28.(本小题满分14分)
如图,已知抛物线C1:y=21x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,
使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.
(1)点A的坐标为_______,抛物线C1的顶点坐标为________,抛物线C2的解析式为_____;
(2)若点P在C2上,且△POB的面积为8,求点P的坐标;
(3)设抛物线C2上任意一点Q到定点M(2,m)的距离为QM、到定直线y=4—m的距离
为QN,则是否存在常数m,使得QM=QN恒成立...,若存在,求常数m的值;若不存在,请
说明理由.
xyC2 C1BAOx
y
C2 C1
BA
O
(备用图)
