基于时间分割的前加减速快速插补算法

数控插补计算法

2011年4月28日9时41分
23
在一个△t内：（1）原理：设刀具沿逆时针
在0～t内(取△t=1)：
2011年4月28日9时41分
24
• (2）与直线插补原理的区别： • 圆弧插补中被积函数是变量，被积函数为动点坐标，每进一步x坐标-1,y坐标+1，直线插补的被积函数是常数（Xe， Ye）。 • x轴的累加用y坐标，y轴的累加用x坐标. • 圆弧插补终点判别需采用两个终点计数器。 • 对于直线插补，如果寄存器位数为n ,无论直线长短都需迭代次到达终点。
•
2011年4月28日9时41分
5
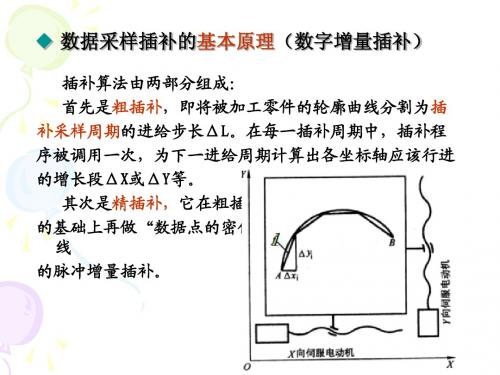
插补误差不得大于一个脉冲当量。这种方法控制精度和进给速度低，主要运用于以步进电动机为驱动装置的开环控制系统中. • 二、数据采样插补 • 数据采样插补又称时间标量插补或数字增量插补。这类插补算法的特点是数控装置产生的不是单个脉冲，而是一组数字量。插补运算分两步完成。第一步为粗插补，它是在给定起点和终点的曲线之间插入若干个点，即用若干条微小直线段来拟合给定曲线，每一微小直线段的长度△L都相等，且与给定进给速度有关。粗插补时每一微小直线段的长度△L与进给速度F和插补T周期有关，即△L＝FT。
2011年4月28日9时41分
9
四个步骤： 1.偏差判别 2.坐标进给 3.新点偏差计算 4.终点判别
2011年4月28日9时41分
10
1）偏差判别在直线插补时，以第一象限直线OE为例，直线的起点O在坐标原点，终点坐标为E（xe，ye），如图1.10所示，对直线上任一点（x，y），则由直线方程, xey—xye=0 设P（xi，yi）为加工动点，则：若P位于该加工直线上，有：xe yi—xiye=0 若P位于该加工直线上方，有：xe yi—xiye>0 若P位于该加工直线上方，有：xe yi—xiye<0 由此定义偏差判别函数Fi为：Fi= xe yi—xiye 当Fi=0时，加工动点在直线上；当Fi>0时，加工动点在直线上方；当Fi<0时，加工动点在直线下方。

数控技术第3章插补原理

5. 运算举例（第Ⅰ 象限逆圆弧）运算举例（象限逆圆弧）加工圆弧AE 起点(4,3) AE， (4,3)，终点(0,5) E=(4-0)+(5加工圆弧AE，起点(4,3)，终点(0,5) ，E=(4-0)+(53)=6 插补过程演示
三.逐点比较法的进给速度逐点比较法的进给速度
逐点比较法除能插补直线和圆弧之外，还能插补椭圆、逐点比较法除能插补直线和圆弧之外，还能插补椭圆、抛物线和双曲线等二次曲线。此法进给速度平稳，抛物线和双曲线等二次曲线。此法进给速度平稳，精度较高。在两坐标联动机床中应用普遍. 精度较高。在两坐标联动机床中应用普遍. 对于某一坐标而言，对于某一坐标而言，进给脉冲的频率就决定了进给速度：
插补是数控系统最重要的功能；插补是数控系统最重要的功能；插补实际是数据密集化的过程；插补实际是数据密集化的过程；插补必须是实时的；插补必须是实时的；插补运算速度直接影响系统的控制速度；插补运算速度直接影响系统的控制速度；插补计算精度影响到整个数控系统的精度。插补计算精度影响到整个数控系统的精度。插补器按数学模型分类，可分为一次插补器、插补器按数学模型分类，可分为一次插补器、二次插补器及高次曲线插补器；次曲线插补器；根据插补所采用的原理和计算方法不同，根据插补所采用的原理和计算方法不同，分为软件插补和硬件插补。目前大多采用软件插补或软硬件结合插补。插补。目前大多采用软件插补或软硬件结合插补。根据插补原理可分为：脉冲增量插补和数字采样插补。根据插补原理可分为：脉冲增量插补和数字采样插补。
脉冲当量：脉冲当量：每一个脉冲使执行件按指令要求方向移动的直线距离，称为脉冲当量，表示。一般0.01mm 0.001mm。 0.01mm～距离，称为脉冲当量，用δ表示。一般0.01mm～0.001mm。脉冲当量越小，脉冲当量越小，则机床精度越高

第三章数控插补原理

解：插补完这段直线刀具沿Ｘ和Ｙ轴应走的总步数为 = x e + y e ＝5 + 3＝8。 Y 刀具的运动轨迹如图 E(5，3) 3
2 1 O 1 2 3 4 5 X
第二节基准脉冲插补
插补运算过程见表：
循环序号偏差判别 F ≥0 坐标进给 +X 偏差计算 Fi+1=Fi-ye
教案 3
终点判别
m
Y
m(Xm,Ym) B(XB,YB)
+Y2
2 m-R
若Fm=0，表示动点在圆弧上；
若Fm>0，表示动点在圆弧外；若Fm<0，表示动点在圆弧内。
Rm
R A(XA,YA)
第Ⅰ象限逆圆弧
X
第二节基准脉冲插补
2）坐标进给
教案 3
与直线插补同理，坐标进给应使加工点逼近给定圆弧,规定如下：当Fm≥0时，向-X方向进给一步；当Fm＜0时，向+Y方向进给一步。
教案 3
若Fi=0，表示动点在直线OE上，如P；若Fi>0，表示动点在直线OE上方，如P′；若Fi<0，表示动点在直线OE下方，如P″。
O
xi 第Ι象限直线
X
第二节基准脉冲插补
2）坐标进给
教案 3
坐标进给应逼近给定直线方向，使偏差缩小的方向进给一步，由插补装置发出一个进给脉冲控制向某一方向进给。
教案 3
直线线型进给方向偏差计算直线线型
L1、L4 L2、L3 +X -X Fi+1=Fi-ye L1、L2 L3、L4
偏差计算
Fi+1=Fi+xe
注：表中L1、L2、L3、L4分别表示第Ⅰ、第Ⅱ、第Ⅲ、第Ⅳ象限直线，偏差计算式中xe、ye均代入坐标绝对值。

第六讲插补的基本原理

yi − ∆yi −1 / 2 ∆xi = ∆L R xi +1 = xi + ∆xi yi +1 = R 2 − x 2 i +1 ∆yi = yi − yi +1
y ym （公式1）公式1
A( x0 , y0 ) Pi ( xi , yi ) ∆xi
θi
D
β i ∆α i
d (∆yi ) = xi +1 / yi +1 d (∆xi )
d (∆xi ) = yi +1 / xi +1 d (∆yi )
当 xi ≤ y i 当 xi > yi
应选公式1 时，应选公式1。应选公式2 时，应选公式2。
§2.5 刀具半径补偿
一、刀具补偿原理数控系统对刀具的控制是以刀架参考点为基准数控系统对刀具的控制是以刀架参考点为基准刀架参考点而零件加工程序给出的是零件轮廓轨迹零件轮廓轨迹，的，而零件加工程序给出的是零件轮廓轨迹，但实际上是要用刀具的刀尖实现加工的，刀尖实现加工的际上是要用刀具的刀尖实现加工的，这样需要在刀架的参考点与加工刀具的刀尖之间进行位置偏置位置偏置。架的参考点与加工刀具的刀尖之间进行位置偏置。这种位置偏置由两部分组成：这种位置偏置由两部分组成：刀具长度补偿及刀具半径补偿。
Pi(xi,yi) x
∆xi = ∆L cos α ye ∆yi tan α = x = ∆x 任意T内任意T e i xi +1 = xi + ∆xi xe 公式1 （公式1） cos α = 2 2 yi +1 = xi +1 tan α xe + ye ∆yi = yi +1 − yi

第三章插补原理及控制方法

及
控
终点判别
N
终点？
制
方
法
结束
25
二、逐点比较法圆弧插补---其它象限
y
F>0
y
F>0
第
F<0
F<0
三章
o
x
o
x
插
补
原
理
逆圆
顺圆
及控
各象限插补进给方向，各象限插补进给方向，远
制
远离原点坐标值加一接离原点坐标值加一，接近
方
近原点坐标值减一。
原点坐标值减一。
法
26
作业
试推导逐点比较法第一象限顺圆弧第插补的递推公式，并画出程序流程图。
逐点比较插补计算法（简称逐点比较法）
第
三章
数字积分插补计算法（简称数字积分法）
插时间分割插补计算法（简称时间分割法）
补
原
理及
样条插补计算方法等。
控
制
方
法
2
3-1 逐点比较法插补
逐点比较插补计算法（简称逐点比
第较法）又称区域判别法。
三
章
其原理是：计算机在控制加工轨迹过
插程中逐点计算和判断加工偏差以控制坐
章
当M点在直线上时， + Δ X
y
插补
(αi= α)
原
M (x i y j )
A
理
及控
tg αi= tg α
制
方法
αi
oα
x
6
其中 tg αi= y j / xi
tgα= y e / x e
tg αi -tgα= y j / xi - y e / x e

数控车床的进给速度和加减速控制

二、进给速度控制
CNC系统中进给速度控制方式：
软件控制采用——程序计时法（程序延时法）。
软件与接口控制采用——时钟中断法、 v/Δ L积分器法（适于采用DDA或扩展DDA插补中的稳速控制）。
1、程序计时法（程序延时法）
其过程是：
(1)计算出每次插补运算所占用的时间；
(2)由给定的F值计算出相应的进给脉冲间隔时间；
前加减速控制是对编程的F指令值即合成速度进行控制。首先要计算出稳定速度Fs和瞬时速度Fi。
稳定速度——就是系统处于恒定进给状态时，在一个插补周期内每插补一次的进给量。实际上就是编程给定F值（mm/min）在每个插补周期T（ms）的进给量。
考虑调速方便，设置了快速和切削进给的倍率开关，其速度系数设为K（％），可得Fs的计算公式为：
设直线终点P坐标为（xe , ye），x为长轴，其加工点A(xi , yi) 已知，则瞬时加工点A离终点P距离si为：
si

xe
xi
1
c os
对于圆弧插补，
si的计算应按圆弧所对应的圆心角小于及
大于π 两种情况进行分别处理，如图。
小于π 时，瞬时加
工点离圆弧终点的直线
距离越来越小，以MP为
每加速一次，瞬时速度为： Fi＋1＝Fi＋at
新的瞬时速度Fi＋1参加插补计算，对各坐标轴进行进给量的分配。
减速时，系统每进行一次插补运算后，都要进行终点判断，也就是要计算出离终点的瞬时距离si 。
并按本程序段的减速标志，判别是否已到达减速区，若已到达，则要进行减速。
如图，如果稳定速度 Fs和设定的加/减速度a已确定，可用下式计算出减速区域：
后加减速控制的规律实际上与前加减速一样，通常有直线和指数规律的加减速控制。

2.2-插补原理

Numerical Control Technology
插补原理
Chapter 2 Interpolation Principle
algorithm
机床数控技术
Numerical Control Technology
1
插补的概念
2
常用的插补方法
3 4 5
逐点比较法
数字积分法时间分割法
6
本章小结
机床数控技术
1 插补的基本概念 Basic Concepts
A 什么是插补
Numerical Control Technology
根据所给定的进给速度和轮廓线形的要求，在轮廓已知点之间，确定一些中间点的方法，这种方法称为插补方法或插补原理。
机床数控技术
1 插补的基本概念 Basic Concepts
A 什么是插补 B 要解决的基本问题
(4) 终点判别
开始加工时，将刀具移到起点，刀具正好处于直线上，偏差为零，即F＝0，根据这一点偏差可求出新一点偏差，随着加工的进行，每一新加工点的偏差都可由前一点偏差和终点坐标相加或相减得到。在插补计算、进给的同时还要进行终点判别。常用终点判别方法，是设置一个长度计数器，从直线的起点走到终点，刀具沿X轴应走的步数为X e，沿Y轴走的步数为Ye，计数器中存入X和Y两坐标进给步数总和∑＝ ∣Xe∣＋∣Ye∣，当X或Y坐标进给时，计数长度减一，当计数长度减到零时，即∑＝0时，停止插补，到达终点。
图2 圆弧插补轨迹
图3 直线插补轨迹
机床数控技术
Numerical Control Technology
逐点比较法，就是每走一步都要和给定轨迹比较一次，根据比较结果来决定下一步的进给方向，使刀具向减小偏差的方向并趋向终点移动，刀具所走的轨迹应该和给定轨迹非常相“象”。算法的特点是；运算直观，插补误差小于一个脉冲当量，进给速度波动小，调节方便，在两坐标联动的数控机床中应用较为广泛，逐点比较插补法通过比较刀具与所加工曲线的相对位置，确定刀具的起动力向。

第16讲数据采样插补的原理

刀尖位置与机床控制刀位点不同时，需要刀尖位置补偿。刀具磨损或者换了新的刀具后，实际刀尖位置变化，需要补偿。
14
3.6 刀具半径补偿数控技术
第三章
1）B功能刀具半径补偿计算： ◆直线加工时刀具补偿；
Y
A(x,y) ∆y r A’(x’,y’)
第三章
计算机数控装置
扩展DDA插补是在DDA插补的基础上发展起来，并将DDA法用切线逼近圆弧的方法改进为用割线逼近，减少了逼近误差，提高了圆弧插补的精度。
7
3.5 数据采样插补的原理数一. 数据采样插补的基本思想控 (二) 数据采样法之二——扩展DDA法技 1 .扩展DDA直线插补 V 术 X V T TX X
第三章
ΔPAG∽ΔAOC
AOC PAC i
i 1 i
1 i 2
计算机数控装置
插补步长和角步距的关系
l cos X
l sin Y
5
3.5 数据采样插补的原理
数一. 数据采样插补的基本思想控直线函数法的主要问题：技 1.用弦线逼近圆弧，因此插补误差主要为半径的绝对误差。术因插补周期是固定的，该误差取决于进给速度和圆弧半径，
第三章
直线与X轴夹角为，若已知轮廓步长，则本次插补周期内各坐标轴进给量为： X l cos
计算机数控装置
Ye Y x Xe
下式可以避免计算三角函数：
cos
Xe X e2 Ye2一. 数据采样插补的基本思想控 2. 直线函数法圆弧插补：技直线函数法圆弧插补，需先根据进给速度指令F，计算出术轮廓步长l，然后以长为l的弦线逼近圆弧，再将弦l分解到两个