高中数学导数的典型例题

合集下载

高中数学导数及其应用典型例题专题练习40题(详解版)

高中数学导数及其应用典型例题专题练习40题（详解版)一、单选题1．函数()()3xf x x e =- 的单调递增区间是（）A ．(),2-∞-B ．()2,+∞C ．(1,4)D ．(0,3)【答案】B 【解析】【分析】求出函数()y f x =的导数，在解出不等式()0f x '>可得出所求函数的单调递增区间. 【详解】()()3x f x x e =-，()()2x f x x e '∴=-，解不等式()0f x '>，解得2x >，因此，函数()()3xf x x e =-的单调递增区间是()2,+∞，故选B.【点睛】本题考查函数单调区间的求解，一般是先求出导数，然后解出导数不等式，将解集与定义域取交集得出单调区间，但单调区间不能合并，考查计算能力，属于中等题. 2．若函数()ln mf x x x=+在[1,3]上为增函数，则m 的取值范围为（） A ．[1,)+∞ B ．[3,)+∞C ．(,1]-∞D ．(,3]-∞【答案】C 【解析】【分析】转化为2()0x mf x x-'=≥，即m x ≤对[1,3]x ∈恒成立，继而得解. 【详解】由题意函数()ln mf x x x=+在[1,3]上为增函数, 可知2()0x mf x x -'=≥，即m x ≤对[1,3]x ∈恒成立，所以1m ．故选：C【点睛】本题考查了导数在函数单调性中的应用，考查了学生综合分析，数学运算的能力，属于中档题.3．设()f x 、()g x 是R 上的可导函数，()f x '、()g x '分别为()f x 、()g x 的导函数，且满足()()()()0f x g x f x g x ''+<，则当a x b <<时，有（） A ．()()()()f x g x f b g b > B ．()()()()f x g a f a g x > C ．()()()()f x g b f b g x > D ．()()()()f x g x f a g a >【答案】A 【解析】【分析】构造函数()()()h x f x g x =，利用导数判断出函数()y h x =的单调性，结合a xb <<可得出结论.【详解】构造函数()()()h x f x g x =，则()()()()()0h x f x g x f x g x '''=+<，所以，函数()()()h x f x g x =为减函数，a xb <<，()()()h b h x h a ∴<<，即()()()()()()f b g b f x g x f a g a <<，故选：A. 【点睛】本题考查利用构造函数法比较函数值的大小关系，利用导数不等式的结构构造新函数是解答的关键，考查推理能力，属于中等题.4．函数()y f x =的导函数()y f x ='的图象如图所示，则()y f x =的图象可能是（）A．B．C．D．【答案】D 【解析】【分析】根据函数的单调性与导数符号的关系判断即可. 【详解】根据导函数为正，则原函数递增，导函数为负，则原函数递减，导函数()y f x ='从左到右的符号依次为负、正、负、正，则原函数()y f x =的单调性从左到右依次为减、增、减、增，且在0x =附近单调递增，通过对比可知，D 中的图象正确. 故选：D. 【点睛】本题考查利用导数的图象判断原函数的图象，一般利用导数符号与原函数单调性之间的关系来判断，考查推理能力，属于中等题.5．对于函数()f x ，将满足()00f x x =的实数0x 称为()f x 的不动点.若函数()log a f x x =（0a >且1a ≠）有且仅有一个不动点，则a 的取值范围是（）A ．(){}0,1eB ．(){}0,11,eC ．()10,1e e ⎧⎫⎨⎬⎩⎭D ．()0,1【答案】C 【解析】【分析】令()f x x =，可得log a x x =，利用换底公式得出ln ln x x a =，进而得出ln ln xa x=，由题意得出函数ln y a =与函数()ln xg x x=的图象有且只有一个公共点，利用导数研究函数()y g x =的单调性与极值，利用数形结合思想可得出实数a 的取值范围. 【详解】函数()log a f x x =有且仅有一个不动点，则方程log a x x =仅有一个根. 由log a x x =可得ln ln x x a =，即ln ln xa x =，设()ln x g x x=，其中0x >. 则()21ln xg x x-'=，令()0g x '=，得x e =，列表如下：所以，函数()y g x =的单调递增区间为()0,e ，单调递减区间为(),e +∞，所以，函数()y g x =的极大值为()1g e e=，且当1x >时，()0g x >. 函数()y g x =的图象如图所示，所以ln 0a <或1ln a e=，即01a <<或1e a e =.故选：C.【点睛】本题考查函数新定义“不动点”问题的求解，将问题转化为函数的零点个数，并利用参变量分离法求解是解答的关键，在作函数的图象时，可利用导数分析函数的单调性与极值，考查数形结合思想的应用，属于中等题.6．已知函数()f x 的导函数为()f x '，在()0,∞+上满足()()xf x f x '>，则下列一定成立的是（）A ．()()2019202020202019f f >B ．()()20192020f f >C ．()()2019202020202019f f <D ．()()20192020f f <【答案】A 【解析】【分析】构造函数()()f xg x x=，利用导数判断函数()y g x =在()0,∞+上的单调性，可得出()2019g 和()2020g 的大小关系，由此可得出结论.【详解】令()()()0f x g x x x =>，则()()()2xf x f x g x x '-'=. 由已知得，当0x >时，()0g x '>.故函数()y g x =在()0,∞+上是增函数，所以()()20202019g g >，即()()2020201920202019f f >，所以()()2019202020202019f f >. 故选：A. 【点睛】本题考查利用构造函数法得出不等式的大小关系，根据导数不等式的结构构造新函数是解答的关键，考查推理能力，属于中等题.7．设曲线f(x)=e x +2x(e 为自然对数的底数)上任意一点处的切线为l 1，总存在曲线g(x)=−ax +sinx 上某点处的切线l 2，使得l 1⊥l 2，则实数a 的取值范围为( ) A ．[−1,2] B ．(−1,2)C ．(−12,1)D ．[−12,1]【答案】D 【解析】【分析】求得f(x)的导数，设(x 1,y 1)为f(x)上的任一点，可得切线的斜率k 1，求得g(x)的导数，设g(x)图象上一点(x 2,y 2)可得切线l 2的斜率为k 2，运用两直线垂直的条件：斜率之积为−1，分别求y 1=−a +cosx 2的值域A ，y 2=1e x 1+2的值域B ，由题意可得B ⊆A ，可得a 的不等式，可得a 的范围．【详解】f(x)=e x +2x 的导数为f′(x)=e x +2，设(x 1,y 1)为f(x)上的任一点，则过(x 1,y 1)处的切线l 1的斜率为k 1=e x 1+2，g(x)=−ax +sinx 的导数为g′(x)=cosx −a ，过g(x)图象上一点(x 2,y 2)处的切线l 2的斜率为k 2=−a +cosx 2．由l 1⊥l 2，可得(e x 1+2)⋅(−a +cosx 2)=−1，即−a +cosx 2=−1e x 1+2，任意的x 1∈R ，总存在x 2∈R 使等式成立,则有y 1=−a +cosx 2的值域为A =[−a −1,−a +1]，所以−1e x 1+2的值域为B =(−12,0)由B ⊆A ，即(−12,0)⊆[−a −1，−a +1]，即{−a −1≤−121−a ≥0，解得：[−12,1]，故选D ．【点睛】本题考查导数的运用：求切线的斜率，考查两直线垂直的条件：斜率之积为−1，考查任意存在性问题的解法，注意运用转化思想和值域的包含关系，考查运算能力，属于中档题．8．若不等式22ln 0mx mx x +-<有且仅有两个正整数解，则实数m 的取值范围为（） A ．ln 2ln 3,1215⎡⎫⎪⎢⎣⎭B ．ln 2ln 2,128⎡⎫⎪⎢⎣⎭ C ．ln 3ln 2,158⎛⎫⎪⎝⎭D ．ln 3ln 2,158⎡⎤⎢⎥⎣⎦【答案】A 【解析】【分析】不等式22ln 0mx mx x +-<有且仅有两个正整数解等价于ln 2xmx m x+<有且仅有两个正整数解，令()()22f x mx m x m =+=+，()ln xg x x=，则问题转化为函数()(),f x g x 的图像有两个交点。

高中数学导数典型例题

高中数学导数典型例题题型一：利用导数研究函数的单调性、极值、最值1. 已知函数32()f x x ax bx c =+++ 过曲线()y f x =上的点(1,(1))P f 的切线方程为y=3x +1 。

（1）若函数2)(-=x x f 在处有极值，求)(x f 的表达式；（2）在（1）的条件下，求函数)(x f y =在[－3，1]上的最大值；（3）若函数)(x f y =在区间[－2，1]上单调递增，求实数b 的取值范围解：（1）极值的求法与极值的性质（2）由导数求最值（3）单调区间零点驻点拐点————草图2. 已知).(3232)(23R a x ax x x f ∈--=(1)当41||≤ a 时, 求证：)x (f 在)1,1( -内是减函数; (2)若)x (f y =在)1,1( -内有且只有一个极值点, 求a 的取值范围.解：（1）单调区间零点驻点拐点————草图（2）草图——讨论题型二：利用导数解决恒成立的问题例1：已知322()69f x x ax a x =-+（a ∈R ）．（Ⅰ）求函数()f x 的单调递减区间；（Ⅱ）当0a >时，若对[]0,3x ∀∈有()4f x ≤恒成立，求实数a 的取值范围．例2：已知函数222()2()21x x f x e t e x x t =-++++，1()()2g x f x '=．（1）证明：当22t <时，()g x 在R 上是增函数；（2）对于给定的闭区间[]a b ，，试说明存在实数 k ，当t k >时，()g x 在闭区间[]a b ，上是减函数；（3）证明：3()2f x ≥．解：g(x)=2e^(2x)-te^x+1 令a=e^x 则g(x)=2a^2-ta+1 (a>0)(3)f(x)=(e^x-t)^2+(x-t)^2+1讨论太难分界线即1-t^2/8=0做不出来问问别人，我也没做出来例3：已知3)(,ln )(2-+-==ax x x g x x x f（1）求函数)(x f 在)0](2,[>+t t t 上的最小值（2）对(0,),2()()x f x g x ∀∈+∞≥恒成立，求实数a 的取值范围解：讨论点x=1/e 1/e<t t<1/e<t+2（2）题型三：利用导数研究方程的根例4：已知函数ax ax x f 313)(23-+-=.（Ｉ）讨论函数)(x f 的单调性；（Ⅱ）若曲线()f x 上两点A 、B 处的切线都与y 轴垂直，且线段AB 与x 轴有公共点，求实数a 的取值范围.例5：已知函数),(3)(23R b a x bx ax x f ∈-+=，在点))1(,1(f 处的切线方程为.02=+y（1）若对于区间]2,2[-上任意两个自变量的值21,x x ，都有c x f x f ≤-|)()(|21，求实数c的最小值。

高中数学专题练习《基本初等函数的导数》含详细解析

5.2　导数的运算5.2.1　基本初等函数的导数基础过关练题组一　利用导数公式求函数的导数1.(2020浙江绍兴稽山中学高二下期中)已知f(x)=cos30°,则f'(x)的值为( )A.-12B.12C.-32D.02.已知函数f(x)=1x2,则 )A.-14B.-18C.-8D.-163.函数y=1x在x=4处的导数是( )A.116B.-116C.18D.-184.下列求导运算正确的是( )A.(cos x)'=sin xB.(3x)'=3x log3eC.(lg x)'=1x ln10D.(x-2)'=-2x-15.设f0(x)=sin x,f1(x)=f0'(x),f2(x)=f1'(x),……,f n+1(x)=f n'(x),n∈N,则f2 019(x)=( )A.sin xB.-sin xC.cos xD.-cos x6.(多选)下列求导运算正确的是( )'=1x2B.(x)'=12xC.(x a)'=ax a-1D.(log a'=1x ln a 7.求下列函数的导数.(1)y=1x5;(2)y=x2x;(3)y=lg x;(4)y=5x-x.题组二　导数公式的应用8.(2020黑龙江佳木斯一中高二上期末)曲线y=1x在点A(-1,-1)处的切线方程是( )A.x+y-2=0B.x-y+2=0C.x+y+2=0D.x-y-2=09.若曲线y=x4的一条切线l与直线x+4y-8=0垂直,则l的方程为( )A.4x-y-3=0B.x+4y-5=0C.4x-y+3=0D.x+4y+3=010.(2020福建三明第一中学月考)以正弦曲线y=sin x上一点P为切点作切线l,则切线l的倾斜角的范围是( )A.0,πB.[0,π), D.0,,11.已知函数f(x)=ln x,则函数g(x)=f(x)-f'(x)的零点所在的区间是( )A.(0,1)B.(1,2)C.(2,3)D.(3,4)12.若曲线y=x-12在点(m,m-12)处的切线与两个坐标轴围成的三角形的面积为18,则m=( )A.64B.32C.16D.813.(多选)已知函数f(x)及其导数f'(x),若存在x0,使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”.下列函数中,有“巧值点”的是( )A.f(x)=x2B.f(x)=e-xC.f(x)=ln xD.f(x)=1x14.(2019广东东莞高二上期末)设曲线y=x n+1(n∈N*)在点(1,1)处的切线,计算a1+a2+a3+…+a2019.与x轴交点的横坐标为x n,令a n=lg1x n答案全解全析基础过关练1.D ∵f(x)=cos 30°=32,∴f'(x)=0.2.D f'(x)=-2x -3=-2x 3,则故选D.3.B y'=-12x -32,∴y'x=4=-12×4-32=-116,故选B.4.C (cos x)'=-sin x,故A 不正确;(3x )'=3x ·ln 3,故B 不正确;(lg x)'=1x ·ln10,故C 正确;(x -2)'=-2x -2-1=-2x -3,故D 不正确.故选C.5.D f 0(x)=sin x,f 1(x)=f 0'(x)=(sin x)'=cos x,f 2(x)=f 1'(x)=(cos x)'=-sin x,f 3(x)=f 2'(x)=(-sin x)'=-cos x,f 4(x)=f 3'(x)=(-cos x)'=sin x,所以4为最小正周期,故f 2 019(x)=f 3(x)=-cos x.6.BCD 在A 中-1)'=-1x 2,故A 错误;在B 中,(x )'=(x 12)'=12×x -12=12x ,故B 正确;在C 中,(x a )'=ax a-1,故C 正确;在D 中,(log a '=1x ln a ,故D 正确.故选BCD.7.解析　(1)∵y=1x 5=x -5,∴y'=-5x -6.(2)∵y=x 2x =x 2x 12=x 32,∴y'=32x 12.(3)∵y=lg x,∴y'=1x ln10.(4)∵y=5x ,∴y'=5x ln 5.(5)∵-x =sin x,∴y'=cos x.8.C 由y=1x 得y'=-x -2,因此切线的斜率为k=-(-1)-2=-1,∴切线方程为y+1=-(x+1),即x+y+2=0,故选C.9.A ∵直线x+4y-8=0的斜率为-14,∴直线l 的斜率为4,又y'=4x 3,∴4x 3=4,得x=1,又当x=1时,y=x 4=1,∴直线l 的方程为y-1=4(x-1),即4x-y-3=0.10.A ∵y=sin x,∴y'=cos x,∵cos x ∈[-1,1],∴切线斜率的范围是[-1,1],∴倾斜角的范围是0,,π,故选A.11.B 由f(x)=ln x,得f'(x)=1x ,则g(x)=f(x)-f'(x)=ln x-1x .易知函数g(x)的定义域为(0,+∞),且函数g(x)在(0,+∞)上为增函数,又g(1)=ln 1-1=-1<0,g(2)=ln 2-12=ln 2-ln e >0,所以函数g(x)在区间(1,2)上有唯一零点.12.A 因为y'=-12x -32,所以曲线y=x -12在点(m,m -12)处的切线方程为y-m -12=-12·m -32(x-m),令x=0,得y=32m -12,令y=0,得x=3m,由题意可得,12×32m -12×3m=18,解得m=64.13.ACD 在A 中,若f(x)=x 2,则f'(x)=2x,则x 2=2x,这个方程显然有解,故A 符合要求;在B 中,若f(x)=e -x ,则ln 1e =-e -x ,即e -x =-e -x ,此方程无解,故B 不符合要求;在C 中,若f(x)=ln x,则f'(x)=1x ,由ln x=1x ,数形结合可知该方程存在实数解,故C 符合要求;在D 中,若f(x)=1x ,则f'(x)=-1x 2,由1x =-1x 2,可得x=-1,故D 符合要求.故选ACD.14.解析　因为y=x n+1,所以y'=(n+1)x n ,所以曲线y=x n+1(n ∈N *)在(1,1)处的切线斜率为k=n+1,切线方程为y-1=(n+1)(x-1).令y=0,得x=n n +1,即x n =n n +1,所以a n =lg 1x n =lg(n+1)-lg n,所以a 1+a 2+a 3+…+a 2 019=lg 2-lg 1+lg 3-lg 2+lg 4-lg 3+…+lg 2 020-lg 2 019=lg 2 020-lg 1=1+lg 202.。

高中数学高三导数大题精选(附详细解答)

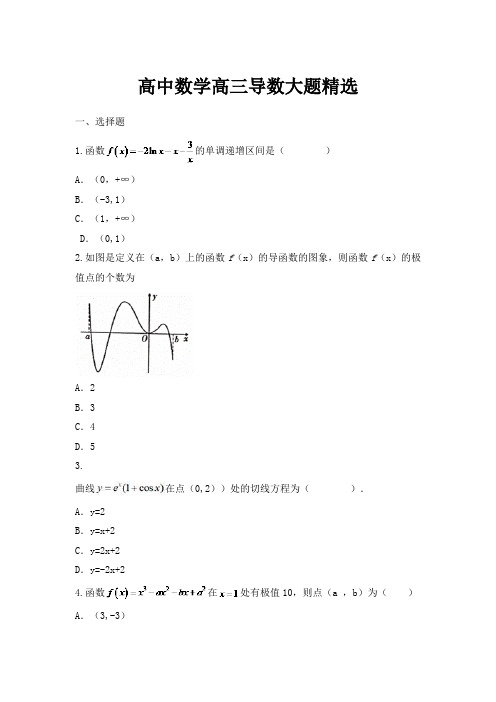
高中数学高三导数大题精选一、选择题1.函数的单调递增区间是（）A．（0，+∞）B．（-3,1）C．（1，+∞）D．（0,1）2.如图是定义在（a，b）上的函数f（x）的导函数的图象，则函数f（x）的极值点的个数为A．2B．3C．4D．53.曲线在点（0,2））处的切线方程为（）．A．y=2B．y=x+2C．y=2x+2D．y=-2x+24.函数在处有极值10，则点（a ，b）为（）A．（3,-3）B．（-4,11）C．（3,-3）或（-4,11）D．不存在5.函数f(x)＝x(ex－1)＋ln x的图象在点(1，f(1))处的切线方程是( ) A．y＝2ex－e－1B．y＝2ex－e＋1C．y＝2ex＋e－1D．y＝2ex＋e＋16.已知函数f（x）的导函数f′（x）的图象如图所示，那么函数f（x）的图象最有可能的是（）A. B.C. D.7.已知x=2 是函数的极小值点，那么函数f（x）的极大值为（）A.15B.16C.17D.188.已知函数y=f（x）是R上的可导函数，当x≠0时，有，则函数的零点个数是（）A. 0B. 1C. 2D. 39.若函数f（x）=在（0，2）内单调递减，则实数a的取值范围为A．a=3 B．a≤3C．a≥3 D．0＜a＜310.函数的导数是A． B．C． D．二、填空题11.已知函数，则过点可以作出________条图象的切线三、解答题12.设函数，．（1）当时，函数取得极值，求的值；（2）当时，求函数在区间[1，2]上的最大值；（3）当时，关于的方程有唯一实数解，求实数的值．13.已知函数（1）若x=2为的极值点，求实数a的值；（2）若在上为增函数，求实数a的取值范围；（3）当时，方程有实根，求实数b的最大14.求下列函数的导数（1）（2）（3）15.已知函数．若函数在处有极值-4．（1）求的单调递减区间；（2）求函数在上的最大值和最小值．参考答案一、选择题1、【答案】D解：函数的定义域为，且，解不等式，即，由于，解得.因此，函数的单调递增区间为，故选：D.2、【答案】B3、【答案】C4、【答案】B解：，则，解得或，当时，，此时在定义域上为增函数，无极值，舍去.当,,为极小值点.5、【答案】A解：f(1)＝e－1，f′(x)＝ex(1＋x)＋－1，f′(1)＝2e，∴在点(1，f(1))处的切线方程为y－(e－1)＝2e(x－1)，即为y＝2ex－e－1.6、【答案】A7、【答案】D8、【答案】B9、【答案】C10、【答案】B二、填空题11、【答案】2解：设切点的坐标为：，，因此切线方程为：，把的坐标代入切线方程中，化简得：或，所以过点可以作出二条的切线.故答案为：2三、解答题12、13、【答案】(1)解：因为x= 2为f(x)的极值点，所以即，解得：a=0又当a = 0时，，从而x=2为f(x)的极值点成立．(2)解：∵f(x)在区间[3，+∞)上为增函数，∴在区间[3，+∞)上恒成立．①当a = 0时，在[3，+∞)上恒成立，所以f (x)在[3，+∞)上为增函数，故a = 0符合题意．②当a≠0时，由函数f (x)的定义域可知，必须有2ax + 1 > 0对x≥3恒成立，故只能a > 0，所以在区间[3，+∞)上恒成立令，其对称轴为∵a > 0，∴，从而g (x)≥0在[3，+∞)上恒成立，只要g (3)≥0即可，由，解得：∵a > 0，∴．综上所述，a的取值范围为[0，](3)解：时，方程可化为，．问题转化为在(0，+∞)上有解令，则当0 < x < 1时，，∴h (x)在(0，1)上为增函数当x > 1时，，∴h (x)在(1，+∞)上为减函数故h (x)≤h (1) = 0，而x > 0，故即实数b的最大值是0．14、15、解：（1）∵，∴，依题意有即，解得∴，由，得，∴函数单调递减区间由知∴，令，解得．当变化时，的变化情况如下表：由上表知，函数在上单调递减，在上单调递增．故可得又．∴综上可得函数在上的最大值和最小值分别为和．。

高中数学导数典型例题精讲(详细版)

导数经典例题精讲之巴公井开创作导数知识点导数是一种特殊的极限几个经常使用极限：（1）1lim0n n→∞=, lim 0n n a →∞=（||1a <）；（2）00lim x x x x →=, 0011limx x x x →=. 两个重要的极限：（1）0sin lim1x x x →=；（2）1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭(e=…). 函数极限的四则运算法则：若0lim()x x f x a →=, 0lim ()x xg x b →=, 则 (1)()()0lim x x f x g x a b→±=±⎡⎤⎣⎦；(2)()()0lim x x f x g x a b →⋅=⋅⎡⎤⎣⎦;(3)()()()0lim 0x x f x ab g x b→=≠. 数列极限的四则运算法则：若lim,lim n n n n a a b b →∞→∞==, 则(1)()lim n n n a b a b→∞±=±；(2)()lim n n n a b a b →∞⋅=⋅(3)()lim 0n n n a ab b b→∞=≠(4)()lim lim lim n n n n n c a c a c a→∞→∞→∞⋅=⋅=⋅( c 是常数))(x f 在0x 处的导数（或变动率或微商）00000()()()limlim x x x x f x x f x y f x y x x=∆→∆→+∆-∆''===∆∆. .瞬时速度：00()()()lim lim t t s s t t s t s t t tυ∆→∆→∆+∆-'===∆∆. 瞬时加速度：00()()()lim lim t t v v t t v t a v t t t∆→∆→∆+∆-'===∆∆. )(x f 在),(b a 的导数：()dy df f x y dx dx ''===00()()lim lim x x y f x x f x x x∆→∆→∆+∆-==∆∆. 函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ', 相应的切线方程是))((000x x x f y y -'=-. 几种罕见函数的导数(1)0='C （C 为常数）.(2)'1()()n n x nx n Q -=∈.(3)x x cos )(sin ='.x x sin )(cos -='(4)x x 1)(ln ='；e a x xa log 1)(log ='. (5) x x e e =')(;a a a x x ln )(='. 导数的运算法则（1）'''()u v u v ±=±.（2）'''()uv u v uv =+.（3）'''2()(0)u u v uv v v v-=≠. 复合函数的求导法则设函数()u x ϕ=在点x 处有导数''()x u x ϕ=, 函数)(u f y =在点x 处的对应点U 处有导数''()u y f u =, 则复合函数(())y f x ϕ=在点x 处有导数, 且'''x u x y y u =⋅, 或写作'''(())()()x f x f u x ϕϕ=. 【例题解析】考点1 导数的概念对概念的要求：了解导数概念的实际布景, 掌握导数在一点处的界说和导数的几何意义, 理解导函数的概念.例1．()f x '是31()213f x x x =++的导函数, 则(1)f '-的值是． [考查目的]本题主要考查函数的导数和计算等基础知识和能力.[解答过程]()22()2,(1)12 3.f x x f ''=+∴-=-+=故填3.()1x a f x x -=-,集合M={|()0}x f x <,P='{|()0}x fx >,若M P,则实数a 的取值范围是 ( )A.(-∞,1)B.(0,1)C.(1,+∞)D. [1,+∞)[考查目的]本题主要考查函数的导数和集合等基础知识的应用能力.[解答过程]由0,,1;, 1.1x a x a a x x -<∴<<<<-当a>1时当a<1时综上可得M P 时, 1.a ∴>考点2 曲线的切线（1）关于曲线在某一点的切线求曲线y=f(x)在某一点P （x,y ）的切线, 即求出函数y=f(x)在P 点的导数就是曲线在该点的切线的斜率. （2）关于两曲线的公切线若一直线同时与两曲线相切, 则称该直线为两曲线的公切线. 典范例题例 3.已知函数3211()32f x x ax bx =++在区间[11)-，, (13]，内各有一个极值点．（I ）求24a b -的最年夜值；（II ）那时248a b -=, 设函数()y f x =在点(1(1))A f ，处的切线为l , 若l 在点A 处穿过函数()y f x =的图象（即动点在点A 附近沿曲线()y f x =运动, 经过点A 时, 从l 的一侧进入另一侧）, 求函数()f x 的表达式．思路启迪：用求导来求得切线斜率.解答过程：（I ）因为函数3211()32f x x ax bx =++在区间[11)-，, (13]，内分别有一个极值点, 所以2()f x x ax b '=++0=在[11)-，, (13]，内分别有一个实根,设两实根为12x x ，（12x x <）, 则21x x -=, 且2104x x <-≤．于是04<, 20416a b <-≤, 且当11x =-，23x =, 即2a =-, 3b =-时等号成立．故24a b -的最年夜值是16．（II ）解法一：由(1)1f a b '=++知()f x 在点(1(1))f ，处的切线l 的方程是(1)(1)(1)y f f x '-=-, 即21(1)32y a b x a =++--, 因为切线l 在点(1())A f x ，处空过()y f x =的图象,所以21()()[(1)]32g x f x a b x a =-++--在1x =两边附近的函数值异号, 则1x =不是()g x 的极值点．而()g x 321121(1)3232x ax bx a b x a =++-++++, 且22()(1)1(1)(1)g x x ax b a b x ax a x x a '=++-++=+--=-++．若11a ≠--, 则1x =和1x a =--都是()g x 的极值点．所以11a =--, 即2a =-, 又由248a b -=, 得1b =-, 故321()3f x x x x =--．解法二：同解法一得21()()[(1)]32g x f x a b x a =-++--2133(1)[(1)(2)]322a x x x a =-++-+．因为切线l 在点(1(1))A f ，处穿过()y f x =的图象, 所以()g x 在1x =两边附近的函数值异号, 于是存在12m m ，（121m m <<）．那时11m x <<, ()0g x <, 那时21x m <<, ()0g x >；或那时11m x <<, ()0g x >, 那时21x m <<, ()0g x <．设233()1222a a h x x x ⎛⎫⎛⎫=++-+ ⎪ ⎪⎝⎭⎝⎭, 则那时11m x <<, ()0h x >, 那时21x m <<, ()0h x >；或那时11m x <<, ()0h x <, 那时21x m <<, ()0h x <．由(1)0h =知1x =是()h x 的一个极值点, 则3(1)21102ah =⨯++=, 所以2a =-, 又由248a b -=, 得1b =-, 故321()3f x x x x =--．4y x =的一条切线l 与直线480x y +-=垂直, 则l 的方程为（）A ．430x y --=B ．450x y +-=C ．430x y -+=D ．430x y ++=[考查目的]本题主要考查函数的导数和直线方程等基础知识的应用能力.[解答过程]与直线480x y +-=垂直的直线l 为40x y m -+=, 即4y x =在某一点的导数为4, 而34y x '=, 所以4y x =在(1, 1)处导数为4, 此点的切线为430x y --=. 故选A.例5．过坐标原点且与x 2+y 2-4x +2y +25=0相切的直线的方程为( )A.y =-3x 或y =31x B. y =-3x 或y =-31x C.y =-3x 或y =-31x D.y =3x 或y =31x[考查目的]本题主要考查函数的导数和圆的方程、直线方程等基础知识的应用能力.[解答过程]解法1：设切线的方程为,0.y kx kx y =∴-= 又()()()22521,2,1.2x y -++=∴-圆心为故选A.解法2:由解法1知切点坐标为1331(,),,,2222⎛⎫- ⎪⎝⎭由故选A.例 6.已知两抛物线a x y C x x y C +-=+=2221:,2:, a 取何值时1C , 2C 有且只有一条公切线, 求出此时公切线的方程. 思路启迪：先对a x y C x x y C +-=+=2221:,2:求导数.解答过程：函数x x y 22+=的导数为22'+=x y , 曲线1C 在点P(12112,x x x +)处的切线方程为))(2(2)2(11121x x x x x y -+=+-, 即211)1(2x x x y -+=①曲线1C 在点Q ),(222a x x +-的切线方程是)(2)(222x x x a x y --=+--即a x x x y ++-=2222②若直线l 是过点P 点和Q 点的公切线, 则①式和②式都是l 的方程, 故得1,1222121+=--=+x x x x , 消去2x 得方程, 0122121=+++a x x若△=0)1(244=+⨯-a , 即21-=a 时, 解得211-=x , 此时点P 、Q 重合.∴那时21-=a , 1C 和2C 有且只有一条公切线, 由①式得公切线方程为14y x =- .考点3 导数的应用中学阶段所涉及的初等函数在其界说域内都是可导函数, 导数是研究函数性质的重要而有力的工具, 特别是对函数的单调性, 以“导数”为工具, 能对其进行全面的分析, 为我们解决求函数的极值、最值提供了一种简明易行的方法, 进而与不等式的证明, 讨论方程解的情况等问题结合起来, 极年夜地丰富了中学数学思想方法.复习时, 应高度重视以下问题:1.. 求函数的解析式;2. 求函数的值域;3.解决单调性问题;4.求函数的极值（最值）;5.构造函数证明不等式. 典范例题例7．函数)(x f 的界说域为开区间),(b a , 导函数)(x f '在),(b a 内的图象如图所示, 则函数)(x f 在开区间),(b a 内有极小值点（）A ．1个B ．2个C ．3个D ．4个[考查目的]本题主要考查函数的导数和函数图象性质等基础知识的应用能力.[解答过程]由图象可见,在区间(,0)a 内的图象上有一个极小值点. 故选A.例8 .设函数32()2338f x x ax bx c =+++在1x =及2x =时取得极值．（Ⅰ）求a 、b 的值；（Ⅱ）若对任意的[03]x ∈，, 都有2()f x c <成立, 求c 的取值范围．思路启迪：利用函数32()2338f x x ax bx c =+++在1x =及2x =时取得极值构造方程组求a 、b 的值．解答过程：（Ⅰ）2()663f x x ax b '=++,因为函数()f x 在1x =及2x =取得极值, 则有(1)0f '=, (2)0f '=．即6630241230a b a b ++=⎧⎨++=⎩，．解得3a =-, 4b =．（Ⅱ）由（Ⅰ）可知, 32()29128f x x x x c =-++,2()618126(1)(2)f x x x x x '=-+=--．那时(01)x ∈，, ()0f x '>；那时(12)x ∈，, ()0f x '<；那时(23)x ∈，, ()0f x '>．所以, 那时1x =, ()f x 取得极年夜值(1)58f c =+, 又(0)8f c =,(3)98f c =+．则那时[]03x ∈，, ()f x 的最年夜值为(3)98f c =+．因为对任意的[]03x ∈，, 有2()f x c <恒成立, 所以 298c c +<, 解得 1c <-或9c >,因此c 的取值范围为(1)(9)-∞-+∞，，．例9.函数y x x =+-+243的值域是_____________.思路启迪：求函数的值域, 是中学数学中的难点, 一般可以通过图象观察或利用不等式性质求解, 也可以利用函数的单调性求出最年夜、最小值.此例的形式结构较为复杂, 采纳导数法求解较为容易.解答过程：由24030x x +≥+≥⎧⎨⎩得, x ≥-2, 即函数的界说域为[,)-+∞2. y x x x x x x '=+-+=+-++⋅+12412323242243, 又2324282324x x x x x +-+=++++,∴那时x ≥-2, y '>0, ∴函数y x x =+-+243在(,)-+∞2上是增函数, 而f ()-=-21,∴=+-+y x x 243的值域是[,)-+∞1.例10．已知函数()θθcos 163cos 3423+-=x xx f , 其中θ,R x ∈为参数, 且πθ20≤≤．（1）那时0cos =θ, 判断函数()x f 是否有极值；（2）要使函数()f x 的极小值年夜于零, 求参数θ的取值范围；（3）若对（2）中所求的取值范围内的任意参数θ, 函数()x f 在区间()a a ,12-内都是增函数, 求实数a 的取值范围．[考查目的]本小题主要考查运用导数研究三角函数和函数的单调性及极值、解不等式等基础知识, 考查综合分析和解决问题的能力, 以及分类讨论的数学思想方法.[解答过程]（Ⅰ）那时cos 0θ=, 3()4f x x =, 则()f x 在(,)-∞+∞内是增函数,故无极值. （Ⅱ）2'()126cos f x xx θ=-, 令'()0f x =, 得12cos 0,2x x θ==.由（Ⅰ）, 只需分下面两种情况讨论. ①那时cos 0θ>, 随x 的变动'()f x 的符号及()f x 的变动情况如下表：()f x 2x =f()23cos 13()cos 2416f θθθ=-+.要使cos ()02f θ>, 必有213cos (cos)044θθ-->, 可得0cos θ<.由于0cos θ≤, 故3116226ππππθθ<<<<或.毛病！未找到引用源.那时cos 0θ<, 随x 的变动, '()f x 的符号及()f x 的变动情况如下表：因此, 函数()0f x x =在处取得极小值(0)f , 且3(0)cos .16f θ=若(0)0f >, 则cos 0θ>.矛盾.所以那时cos 0θ<, ()f x 的极小值不会年夜于零.综上, 要使函数()f x 在(,)-∞+∞内的极小值年夜于零, 参数θ的取值范围为311(,)(,)6226ππππ⋃.（毛病！未找到引用源.）解：由（毛病！未找到引用源.）知, 函数()f x 在区间(,)-∞+∞与cos (,)2θ+∞内都是增函数.由题设, 函数()(21,)f x a a -在内是增函数, 则a 须满足不等式组210a a a -<≤或21121cos 2a aa θ-<-≥由（毛病！未找到引用源.）, 参数时311(,)(,)6226ππππθ∈⋃时,0cos θ<<.要使不等式121cos 2a θ-≥关于参数θ恒成立, 必有21a -,a ≤.综上, 解得0a ≤1a ≤<.所以a 的取值范围是(,0)-∞⋃.例11．设函数f (x )=ax －(a +1)ln(x +1), 其中a ≥-1, 求f (x )的单调区间.[考查目的]本题考查了函数的导数求法,函数的极值的判定,考查了应用数形结合的数学思想分析问题解决问题的能力 [解答过程]由已知得函数()f x 的界说域为(1,)-+∞, 且'1()(1),1ax fx a x -=≥-+ （1）那时10a -≤≤, '()0,f x <函数()f x 在(1,)-+∞上单调递加, （2）那时0a >, 由'()0,f x =解得1.x a='()f x 、()f x 随x 的变动情况如下表从上表可知那时1(1,)x a ∈-, '()0,f x <函数()f x 在1(1,)a-上单调递加.那时1(,)x a∈+∞, '()0,f x >函数()f x 在1(,)a+∞上单调递增.综上所述：那时10a -≤≤, 函数()f x 在(1,)-+∞上单调递加.那时0a >, 函数()f x 在1(1,)a-上单调递加, 函数()f x 在1(,)a+∞上单调递增.例12．已知函数32()f x axbx cx =++在点0x 处取得极年夜值5, 其导函数'()y f x =的图象经过点(1,0), (2,0), 如图所示.求：（Ⅰ）0x 的值；（Ⅱ）,,a b c 的值.[考查目的]本小题考查了函数的导数,函数的极值的判定,闭区间上二次函数的最值, 函数与方程的转化等基础知识的综合应用,考查了应用数形结合的数学思想分析问题解决问题的能力 [解答过程]解法一：（Ⅰ）由图像可知, 在(),1-∞上()'0f x >, 在()1,2上()'0f x <, 在()2,+∞上()'0f x >,故()f x 在∞∞（-，1），（2，+）上递增, 在(1,2)上递加, 因此()f x 在1x =处取得极年夜值, 所以01x = （Ⅱ）'2()32,f x axbx c =++由'''f f f （1）=0，（2）＝0，（1）＝5，得320,1240,5,a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得2,9,12.a b c ==-=解法二：（Ⅰ）同解法一（Ⅱ）设'2()(1)(2)32,f x m x x mxmx m =--=-+又'2()32,f x axbx c =++所以3,,232m a b m c m ==-=由(1)5f =，即325,32m m m -+=得6,m =所以2,9,12a b c ==-=例13．设3=x 是函数()()()R x e b ax xx f x ∈++=-32的一个极值点. （Ⅰ）求a 与b 的关系式（用a 暗示b ）, 并求()x f 的单调区间；（Ⅱ）设0>a , ()x e ax g ⎪⎭⎫ ⎝⎛+=4252.若存在[]4,0,21∈εε使得()()121<-εεg f 成立, 求a 的取值范围.[考查目的]本小题主要考查函数、不等式和导数的应用等知识, 考查综合运用数学知识解决问题的能力.[解答过程]（Ⅰ）f `(x)＝－[x 2＋(a －2)x ＋b －a ]e 3－x,由f `(3)=0, 得－[32＋(a －2)3＋b －a ]e 3－3＝0, 即得b ＝－3－2a ,则f `(x)＝[x 2＋(a －2)x －3－2a －a ]e 3－x＝－[x 2＋(a －2)x －3－3a ]e3－x＝－(x －3)(x ＋a+1)e 3－x.令f `(x)＝0, 得x 1＝3或x 2＝－a －1, 由于x ＝3是极值点, 所以x+a+1≠0, 那么a ≠－4. 当a <－4时, x 2>3＝x 1, 则在区间（－∞, 3）上, f `(x)<0, f (x)为减函数；在区间（3, ―a ―1）上, f `(x)>0, f (x)为增函数；在区间（―a ―1, ＋∞）上, f `(x)<0, f (x)为减函数. 当a >－4时, x 2<3＝x 1, 则在区间（－∞, ―a ―1）上, f `(x)<0, f (x)为减函数；在区间（―a ―1, 3）上, f `(x)>0, f (x)为增函数；在区间（3, ＋∞）上, f `(x)<0, f (x)为减函数.（Ⅱ）由（Ⅰ）知, 当a >0时, f (x)在区间（0, 3）上的单调递增, 在区间（3, 4）上单调递加, 那么 f (x)在区间[0, 4]上的值域是[min(f (0), f (4) ), f (3)],而f (0)＝－（2a ＋3）e 3<0, f (4)＝（2a ＋13）e －1>0, f (3)＝a ＋6,那么f (x)在区间[0, 4]上的值域是[－（2a ＋3）e 3, a ＋6]. 又225()()4x g x ae =+在区间[0, 4]上是增函数, 且它在区间[0, 4]上的值域是[a 2＋425, （a 2＋425）e 4],由于（a 2＋425）－（a ＋6）＝a 2－a ＋41＝（21-a ）2≥0, 所以只须仅须（a 2＋425）－（a ＋6）<1且a >0, 解得0<a <23.故a 的取值范围是（0, 23）.例14已知函数321()(2)13f x ax bx b x =-+-+在1x x =处取得极年夜值, 在2x x =处取得极小值, 且12012x x <<<<．（1）证明0a >；（2）若z =a +2b ,求z 的取值范围.[解答过程]求函数()f x 的导数2()22f x ax bx b '=-+-．（Ⅰ）由函数()f x 在1x x =处取得极年夜值, 在2x x =处取得极小值, 知12x x ，是()0f x '=的两个根．所以12()()()f x a x x x x '=--那时1x x <, ()f x 为增函数, ()0f x '>, 由10x x -<, 20x x -<得0a >．（Ⅱ）在题设下, 12012x x <<<<等价于(0)0(1)0(2)0f f f '>⎧⎪'<⎨⎪'>⎩即202204420b a b b a b b ->⎧⎪-+-<⎨⎪-+->⎩．化简得203204520b a b a b ->⎧⎪-+<⎨⎪-+>⎩．此不等式组暗示的区域为平面aOb 上三条直线：203204520b a b a b -=-+=-+=，，．所围成的ABC △的内部, 其三个极点分别为：46(22)(42)77A B C ⎛⎫⎪⎝⎭，，，，，． z 在这三点的值依次为16687，，．所以z 的取值范围为1687⎛⎫⎪⎝⎭，．小结：本题的新颖之处在把函数的导数与线性规划有机结合．考点4 导数的实际应用建立函数模型,利用典范例题例15.用长为18 cm 的钢条围成一个长方体形状的框架, 要求长方体的长与宽之比为2：1, 问该长方体的长、宽、高各为几多时,ba 2 12 4O 4677A ⎛⎫ ⎪⎝⎭，(42)C ，(22)B ，其体积最年夜？最年夜体积是几多？[考查目的]本小题主要考查函数、导数及其应用等基本知识, 考查运用数学知识分析和解决实际问题的能力.[解答过程]设长方体的宽为x （m ）, 则长为2x (m), 高为⎪⎭⎫ ⎝⎛-=-=230(m )35.441218＜＜x x xh .故长方体的体积为从而).1(18)35.4(1818)(2x x x x x x V -=--='令V ′（x ）＝0, 解得x =0（舍去）或x =1, 因此x =1.当0＜x ＜1时, V ′（x ）＞0；当1＜x ＜32时, V ′（x ）＜0,故在x =1处V （x ）取得极年夜值, 而且这个极年夜值就是V （x ）的最年夜值.从而最年夜体积V ＝V ′（x ）＝9×12-6×13（m 3）, 此时长方体的长为2 m, 高为1.5 m.答：当长方体的长为2 m 时, 宽为1 m, 高为1.5 m 时, 体积最年夜, 最年夜体积为3 m 3.例16．统计标明, 某种型号的汽车在匀速行驶中每小时的耗油量y （升）关于行驶速度x （千米/小时）的函数解析式可以暗示为：3138(0120).12800080y x x x =-+<≤已知甲、乙两地相距100千米.（I ）当汽车以40千米/小时的速度匀速行驶时, 从甲地到乙地要耗油几多升？（II ）当汽车以多年夜的速度匀速行驶时, 从甲地到乙地耗油最少？最少为几多升？[考查目的]本小题主要考查函数、导数及其应用等基本知识, 考查运用数学知识分析和解决实际问题的能力.[解答过程]（I ）那时40x =, 汽车从甲地到乙地行驶了100 2.540=小时,要耗没313(40408) 2.517.512800080⨯-⨯+⨯=（升）. 答：当汽车以40千米/小时的速度匀速行驶时, 从甲地到乙地耗油升.（II ）当速度为x 千米/小时时, 汽车从甲地到乙地行驶了100x小时,设耗油量为()h x 升, 依题意得3213100180015()(8).(0120),1280008012804h x x x x x x x =-+=+-<≤令'()0,h x =得80.x =那时(0,80)x ∈, '()0,()h x h x <是减函数；那时(80,120)x ∈, '()0,()h x h x >是增函数.那时80x =, ()h x 取到极小值(80)11.25.h =因为()h x 在(0,120]上只有一个极值, 所以它是最小值.答：当汽车以80千米/小时的速度匀速行驶时, 从甲地到乙地耗油最少, 最少为升. 【专题训练】一、选择题 1. y =esin xcos(sin x ), 则y ′(0)即是( )y =59++x x 相切的方程是( )A.x +y =0或25x +y =0B.x －y =0或25x +y =0C.x +y =0或25x －y =0D.x －y =0或25x －y =0f (x )可导, 且f ′(0)=0,又xx f x )(lim 0'→=－1,则f (0)( )f (xf (x )的极值 f (xf n (x )=n 2x 2(1－x )n (n 为正整数), 则f n (x )在［0,1］上的最年夜值为( ) A.0B.1C.nn)221(+-D.1)2(4++n n n 5、函数y=(x 2-1)3+1在x=-1处( )A 、有极年夜值 B 、无极值 C 、有极小值 D 、无法确定极值情况6.f(x)=ax 3+3x 2+2, f ’(-1)=4, 则a=( )A 、310 B 、313 C 、316 D 、3197.过抛物线y=x 2上的点M （41,21）的切线的倾斜角是( )A 、300B 、450C 、600D 、9008.函数f(x)=x 3-6bx+3b 在（0, 1）内有极小值, 则实数b 的取值范围是( )A 、（0, 1）B 、（-∞, 1）C 、（0, +∞）D 、（0, 21）9.函数y=x 3-3x+3在[25,23-]上的最小值是( )A 、889 B 、1 C 、833D 、510、若f(x)=x 3+ax 2+bx+c, 且f(0)=0为函数的极值, 则( ) A 、c ≠0 B 、当a>0时, f(0)为极年夜值 C 、b=0 D 、当a<0时, f(0)为极小值11、已知函数y=2x 3+ax 2+36x-24在x=2处有极值, 则该函数的一个递增区间是( )A 、（2, 3）B 、（3, +∞）C 、（2, +∞）D 、（-∞, 3）12、方程6x 5-15x 4+10x 3+1=0的实数解的集合中( )A 、至少有2个元素B 、至少有3个元素C 、至多有1个元素D 、恰好有5个元素二、填空题f ′(x 0)=2,kx f k xf k 2)()(lim 00--→ =_________.f (x )=x (x +1)(x +2)…(x +n ),则f ′(0)=_________.f (x )=log a (3x 2+5x －2)(a ＞0且a ≠1)的单调区间_________. R 的圆内, 作内接等腰三角形, 当底边上高为_________时它的面积最年夜. 三、解答题C ：y =x 3－3x 2+2x ,直线l :y =kx ,且l 与C 切于点(x 0,y 0)(x 0≠0), 求直线l 的方程及切点坐标.18.求函数f(x)=p 2x 2(1-x)p(p ∈N +), 在[0, 1]内的最年夜值.19.证明双曲线xy=a 2上任意一点的切线与两坐标轴组成的三角形面积即是常数.(1)y =(x 2－2x +3)e 2x; (2)y =31xx -.21.有一个长度为5 m 的梯子贴靠在笔直的墙上, 假设其下端沿地板以 3 m/s的速度离开墙脚滑动, 求当其下端离开墙脚 1.4 m时, 梯子上端下滑的速度.S n =12+22x +32x 2+…+n 2x n －1,(x ≠0,n ∈N *).f (x )=ax 3+x 恰有三个单调区间, 试确定a 的取值范围, 并求其单调区间.x =1与x =2是函数f (x )=a ln x +bx 2+x 的两个极值点.(1)试确定常数a 和b 的值；(2)试判断x =1,x =2是函数f (x )的极年夜值还是极小值, 并说明理由.a 、b 为实数, 且b ＞a ＞e ,其中e 为自然对数的底, 求证：a b ＞b a . x 的方程2x 2－ax －2=0的两根为α、β(α＜β),函数f (x )=142+-x a x .(1)求f (α)·f (β)的值；(2)证明f (x )是［α, β］上的增函数；(3)当a 为何值时, f (x )在区间［α, β］上的最年夜值与最小值之差最小？【参考谜底】一、1.解析：y ′=e sin x［cos x cos(sin x )－cos x sin(sin x )］,y ′(0)=e 0(1－0)=1. 谜底：B2.解析：设切点为(x 0,y 0),则切线的斜率为k =0x y ,另一方面, y ′=(59++x x )′=2)5(4+-x ,故y ′(x 0)=k ,即)5(9)5(40000020++==+-x x x x y x 或x 02+18x 0+45=0得x 0(1)=－3,y 0(2)=－15,对应有y 0(1)=3,y 0(2)=53515915=+-+-,因此得两个切点A (－3, 3)或B (－15,53),从而得y ′(A )=3)53(4+-- =－1及y ′(B )=251)515(42-=+-- ,由于切线过原点, 故得切线：l A :y =－x 或l B :y =－25x . 谜底：A3.解析：由xf x )0(lim 0'→=－1,故存在含有0的区间(a ,b )使当x ∈(a ,b ),x≠0时xf )0('＜0,于是当x ∈(a ,0)时f ′(0)＞0,当x ∈(0,b )时, f ′(0)＜0,这样f (x )在(a ,0)上单增, 在(0,b )上单减. 谜底：B4.解析：∵f ′n (x )=2xn 2(1－x )n －n 3x 2(1－x )n -1=n 2x (1－x )n -1［2(1－x )－nx ］,令f ′n (x )=0,得x 1=0,x 2=1,x 3=n+22,易知f n (x )在x =n+22时取得最年夜值, 最年夜值f n (n+22)=n 2(n+22)2(1－n+22)n=4·(n+22)n +1.谜底：D5、B6、A7、B8、D9、B 10、C 11、B 12、C二、13.解析：根据导数的界说：f ′(x 0)=kx f k x f k ---+→)()]([(lim 0(这时kx -=∆)谜底：－114.解析：设g (x )=(x +1)(x +2)……(x +n ),则f (x )=xg (x ),于是f ′(x )=g (x )+xg ′(x ),f ′(0)=g (0)+0·g ′(0)=g (0)=1·2·…n =n ！谜底：n !15.解析：函数的界说域是x ＞31或x ＜－2,f ′(x )=253log 2-+x x e a .(3x 2+5x －2)′=)2)(13(log )56(+-⋅+x x e x a,①若a ＞1,则当x ＞31时, log a e ＞0,6x +5＞0,(3x －1)(x +2)＞0,∴f ′(x )＞0,∴函数f (x )在(31,+∞)上是增函数, x ＜－2时, f ′(x )＜0.∴函数f (x )在(－∞,－2)上是减函数.②若0＜a ＜1,则当x ＞31时, f ′(x )＜0,∴f (x )在(31,+∞)上是减函数, 当x ＜－2时,f ′(x )＞0,∴f (x )在(－∞,－2)上是增函数.谜底：(－∞,－2)16.解析：设圆内接等腰三角形的底边长为2x ,高为h , 那么h =AO +BO =R +22x R -,解得x 2=h (2R －h ),于是内接三角形的面积为 S =x ·h =,)2()2(432h Rh h h Rh -=⋅-从而)2()2(21432143'--='-h Rh h RhS32322143)2()23()46()2(21h h R h R h h Rh h Rh --=--=-.令S ′=0,解得h =23R ,由于不考虑不存在的情况, 所在区间(0,2R )上列表如下：h (0, 23R )23R(23,2R )S ′ + 0 － S增函数最年夜值减函数由此表可知, 当x =23R 时, 等腰三角形面积最年夜.谜底：23R三、17. 解：由l 过原点, 知k =0x y (x 0≠0),点(x 0,y 0)在曲线C 上, y 0=x 03－3x 02+2x 0,∴0x y =x 02－3x 0+2,y ′=3x 2－6x +2,k =3x 02－6x 0+2又k =0x y ,∴3x 02－6x 0+2=x 02－3x 0+2,2x 02－3x 0=0,∴x 0=0或x 0=23.由x ≠0,知x 0=23,∴y 0=(23)3－3(23)2+2·23=－83.∴k =0x y =－41.∴l 方程y =－41x 切点(23, －83).18.]x )p 2(2[)x 1(x p )x ('f 1p 2+--=- ,令f ’(x)=0得, x=0, x=1, x=p22+ ,在[0, 1]上, f(0)=0, f(1)=0, 2p )p2p (4)p 22(f ++=+ .∴p2max)p2p (4)]x (f [++= .19.设双曲线上任一点P （x 0, y 0）,22x x x a |y k 0-=== ,∴ 切线方程)x x (x a yy 0220--=- ,令y=0, 则x=2x 0 令x=0, 则02x a 2y = .∴2a 2|y ||x |21S == .20.解：(1)注意到y ＞0,两端取对数, 得 ln y =ln(x 2－2x +3)+ln e 2x=ln(x 2－2x +3)+2x, (2)两端取对数, 得ln|y |=31(ln|x |－ln|1－x |),两边解x 求导, 得21.解：设经时间t 秒梯子上端下滑s 米,则s =5－2925t -,当下端移开1.4 m 时, t 0=157341=⋅,又s ′=－21 (25－9t 2)21-·(－9·2t )=9t29251t-,所以s ′(t 0)=9×2)157(9251157⨯-⋅=0.875(m/s).22.解：(1)当x =1时, S n =12+22+32+…+n 2=61n (n +1)(2n +1),当x ≠1时, 1+2x +3x 2+…+nx n -1=21)1()1(1x nx xn n n-++-+,两边同乘以x ,得x +2x 2+3x 2+…+nx n =221)1()1(x nx x n x n n -++-++两边对x 求导, 得S n =12+22x 2+32x 2+…+n 2x n -1=322122)1()122()1(1x x n x n n x n x n n n ---+++-+++.23.解：f ′(x )=3ax 2+1.若a ＞0,f ′(x )＞0对x ∈(－∞,+∞)恒成立, 此时f (x )只有一个单调区间, 矛盾.若a =0,f ′(x )=1＞0,∴x ∈(－∞,+∞),f (x )也只有一个单调区间, 矛盾.若a ＜0,∵f ′(x )=3a (x +||31a )·(x －||31a ),此时f (x )恰有三个单调区间.∴a ＜0且单调减区间为(－∞,－||31a )和(||31a ,+∞),单调增区间为(－||31a ,||31a ).24.解：f ′(x )=xa +2bx +1,(1) 由极值点的需要条件可知：f ′(1)=f ′(2)=0,即a +2b +1=0,且2a +4b +1=0,解方程组可得a =－32,b =－61,∴f (x )=－32ln x －61x 2+x,(2)f ′(x )=－32x -1－31x +1,当x ∈(0,1)时, f ′(x )＜0,当x ∈(1,2)时, f ′(x )＞0,当x ∈(2,+∞)时, f ′(x )＜0,故在x =1处函数f (x )取得极小值65,在x =2处函数取得极年夜值34－32ln2.25.证法一：∵b ＞a ＞e ,∴要证a b ＞b a,只要证b ln a ＞a ln b ,设f (b )=b ln a －a ln b (b ＞e ),则f ′(b )=ln a －ba .∵b ＞a ＞e ,∴ln a ＞1,且ba ＜1,∴f ′(b )＞0.∴函数f (b )=b ln a －a ln b 在(e ,+∞)上是增函数, ∴f (b )＞f (a )=a ln a －a ln a =0,即b ln a －a ln b ＞0,∴b ln a ＞a ln b ,∴a b＞b a.证法二：要证a b＞b a,只要证b ln a ＞a ln b (e ＜a ＜b ),即证,设f (x )=xx ln (x ＞e ), 则f ′(x )=2ln 1x x ＜0,∴函数f (x )在(e ,+∞)上是减函数, 又∵e ＜a ＜b ,∴f (a )＞f (b ),即bb aa ln ln >,∴a b＞b a.26.解：(1)f (α)=aa -+-1682,f (β)=aa ++-1682,f (α)=f (β)=4,(2)设φ(x )=2x 2－ax －2,则当α＜x ＜β时, φ(x )＜0,)1()(2)1()22(222222>+-=++--=x x x ax x ϕ.∴函数f (x )在(α, β)上是增函数.(3)函数f (x )在［α, β］上最年夜值f (β)＞0,最小值f (α)＜0,∵|f (α)·f (β)|=4,∴当且仅当f (β)=－f (α)=2时, f (β)－f (α)=|f (β)|+|f (α)|取最小值4, 此时a =0,f (β)=2.。

高中数学导数大题练习(详细答案)

高中数学导数大题练习(详细答案)1 ．已知函数的图象如图所示．（ I ）求的值；（II ）若函数在处的切线方程为，求函数的解析式；（ III ）在（ II ）的条件下，函数与的图象有三个不同的交点，求的取值范围．2 ．已知函数．（ I ）求函数的单调区间；（ II ）函数的图象的在处切线的斜率为若函数在区间（ 1 ， 3 ）上不是单调函数，求 m 的取值范围．3 ．已知函数的图象经过坐标原点，且在处取得极大值．（ I ）求实数的取值范围；（ II ）若方程恰好有两个不同的根，求的解析式；（ III ）对于（ II ）中的函数，对任意，求证：．4 ．已知常数，为自然对数的底数，函数，．（ I ）写出的单调递增区间，并证明；（ II ）讨论函数在区间上零点的个数．5 ．已知函数．（ I ）当时，求函数的最大值；（ II ）若函数没有零点，求实数的取值范围；6 ．已知是函数的一个极值点（）．（ I ）求实数的值；（ II ）求函数在的最大值和最小值．7 ．已知函数（ I ）当 a=18 时，求函数的单调区间；（ II ）求函数在区间上的最小值．8 ．已知函数在上不具有单调性．（ I ）求实数的取值范围；（ II ）若是的导函数，设，试证明：对任意两个不相等正数，不等式恒成立．9 ．已知函数（ I ）讨论函数的单调性；（ II ）证明：若10 ．已知函数．（ I ）若函数在区间上都是单调函数且它们的单调性相同，求实数的取值范围；（II ）若，设，求证：当时，不等式成立．11 ．设曲线：（），表示导函数．（ I ）求函数的极值；（ II ）对于曲线上的不同两点，，，求证：存在唯一的，使直线的斜率等于．12 ．定义，（ I ）令函数，写出函数的定义域；（ II ）令函数的图象为曲线 C ，若存在实数 b 使得曲线 C 在处有斜率为－ 8 的切线，求实数的取值范围；（ III ）当且时，求证．答案1 ．解：函数的导函数为………… （2 分）（ I ）由图可知函数的图象过点（ 0 ， 3 ），且得………… （ 4 分）（ II ）依题意且解得所以………… （ 8 分）（ III ）．可转化为：有三个不等实根，即：与轴有三个交点；，+ 0 - 0 +增极大值减极小值增．………… （ 10 分）当且仅当时，有三个交点，故而，为所求．………… （ 12 分）2 ．解：（ I ）（ 2 分）当当当 a=1 时，不是单调函数（ 5 分）（ II ）（ 6 分）（ 8 分）（ 10 分）（ 12 分）3 ．解：（ I ）由，因为当时取得极大值，所以，所以；（ II ）由下表：+ 0 - 0 -递增极大值递减极小值递增依题意得：，解得：所以函数的解析式是：（ III ）对任意的实数都有在区间 [-2 ， 2] 有：函数上的最大值与最小值的差等于 81 ，所以． 4 ．解：（ I ），得的单调递增区间是， ………… （ 2分） ∵， ∴， ∴，即． ………… （ 4 分）（ II ），由，得，列表- 0 +单调递减极小值单调递增当时，函数取极小值，无极大值．由（ I ），∵ ，∴ ，∴，………… （ 8 分）（ i ）当，即时，函数在区间不存在零点（ ii ）当，即时若，即时，函数在区间不存在零点若，即时，函数在区间存在一个零点；若，即时，函数在区间存在两个零点；综上所述，在上，我们有结论：当时，函数无零点；当时，函数有一个零点；当时，函数有两个零点．5 ．解：（ I ）当时，定义域为（ 1 ， + ），令，∵ 当，当，∴ 内是增函数，上是减函数∴ 当时，取最大值（ II ）① 当，函数图象与函数图象有公共点，∴ 函数有零点，不合要求；② 当，……………… （ 6 分）令，∵ ，∴ 内是增函数，上是减函数，∴ 的最大值是，∵ 函数没有零点，∴ ，，因此，若函数没有零点，则实数的取值范围6 ．解：（ I ）由可得…… （ 4 分）∵ 是函数的一个极值点，∴∴ ，解得（ II ）由，得在递增，在递增，由，得在在递减∴ 是在的最小值；…………… （ 8 分），∵∴ 在的最大值是．7 ．解：（Ⅰ），2 分由得，解得或注意到，所以函数的单调递增区间是（ 4 ，+∞ ）由得，解得 -2 ＜＜ 4 ，注意到，所以函数的单调递减区间是.综上所述，函数的单调增区间是（ 4 ，+∞ ），单调减区间是 6 分（Ⅱ）在时，所以，设当时，有△=16+4×2 ，此时，所以，在上单调递增，所以 8 分当时，△= ，令，即，解得或；令，即，解得.① 若≥ ，即≥ 时，在区间单调递减，所以.② 若，即时间，在区间上单调递减，在区间上单调递增，所以.③ 若≤ ，即≤2 时，在区间单调递增，所以综上所述，当≥2 时，；当时，；当≤ 时， 14 分8 ．解：（ I ），∵ 在上不具有单调性，∴ 在上有正也有负也有 0 ，即二次函数在上有零点……………… （ 4 分）∵ 是对称轴是，开口向上的抛物线，∴的实数的取值范围（ II ）由（ I ），方法 1 ：，∵ ，∴ ，………… （ 8 分）设，在是减函数，在增函数，当时，取最小值∴ 从而，∴ ，函数是增函数，是两个不相等正数，不妨设，则∴ ，∵ ，∴∴ ，即……………… （ 12 分）方法 2 ：、是曲线上任意两相异点，，，……… （ 8 分）设，令，，由，得由得在上是减函数，在上是增函数，在处取极小值，，∴ 所以即9 ．（ 1 ）的定义域为，（ i ）若，则故在单调增加．（ ii ）若单调减少，在（0 ，a-1 ），单调增加．（ iii ）若单调增加．（ II ）考虑函数由由于，从而当时有故，当时，有10 ．解：（ I ），∵ 函数在区间上都是单调函数且它们的单调性相同，∴ 当时，恒成立，即恒成立，∴ 在时恒成立，或在时恒成立，∵ ，∴ 或（ II ），∵ 定义域是，，即∴ 在是增函数，在实际减函数，在是增函数∴ 当时，取极大值，当时，取极小值，∵ ，∴设，则，∴ ，∵ ，∴∴ 在是增函数，∴∴ 在也是增函数∴ ，即，而，∴∴ 当时，不等式成立．11 ．解：（ I ），得当变化时，与变化情况如下表：＋0 －单调递增极大值单调递减∴ 当时，取得极大值，没有极小值；（ II ）（方法 1 ）∵ ，∴ ，∴即，设，，是的增函数，∵ ，∴ ；，，是的增函数，∵ ，∴ ，∴ 函数在内有零点，又∵ ，函数在是增函数，∴ 函数在内有唯一零点，命题成立（方法 2 ）∵ ，∴ ，即，，且唯一设，则，再设，，∴∴ 在是增函数∴ ，同理∴ 方程在有解∵ 一次函数在是增函数∴ 方程在有唯一解，命题成立……… （ 12 分）注：仅用函数单调性说明，没有去证明曲线不存在拐点，不给分．12 ．解：（ I ），即得函数的定义域是，（ II ）设曲线处有斜率为－ 8 的切线，又由题设∴ 存在实数 b 使得有解，由① 得代入③ 得，有解，…………………… （ 8 分）方法 1 ：，因为，所以，当时，存在实数，使得曲线 C 在处有斜率为－ 8 的切线……………… （ 10 分）方法 2 ：得，方法 3 ：是的补集，即（ III ）令又令，单调递减. …………………… （ 12 ）分单调递减，，。

高中数学专题练习《导数的四则运算法则》含详细解析

5.2.2导数的四则运算法则基础过关练题组一导数的四则运算法则1.函数f(x)=x 2x+3的导数f'(x)=()A.x 2+6xx+3B.-2x(x+3)2C.x2+6x(x+3)2D.3x2+6x(x+3)22.函数y=x2cos x的导数为()A.y'=2xcos x-x2sin xB.y'=2xcos x+x2sin xC.y'=x2cos x-2xsin xD.y'=xcos x-x2sin x3.已知f(x)=x2+e x,则f'(0)=()A.0B.-4 C.-2 D.14.对于函数f(x)=e xx2+ln x-2kx,若f'(1)=1,则实数k等于()A.e2B.e3C.-e2D.-e35.(2020浙江宁波余姚中学高二下月考)设f(x)与g(x)是定义在R上的两个可导函数,若f(x),g(x)满足f'(x)=g'(x),则f(x)与g(x)满足() A.f(x)=g(x) B.f(x)=g(x)=0C.y=f(x)-g(x)为常数函数D.y=f(x)+g(x)为常数函数6.若函数f(x)=x 2e x,则f'(x)=.7.已知函数f(x),g(x)满足f(5)=5,f'(5)=3,g(5)=4,g'(5)=1,若h(x)=f(x)+2g(x),则h'(5)=.8.求下列函数的导数.(1)y=x-2+x2;(2)y=3x e x-2x+e;(3)y=lnxx2+1;(4)y=x2-4sin x2cos x2.题组二求导法则的综合应用9.已知函数f(x)=f'(1)+xln x,则f(e)=()A.1+eB.eC.2+eD.310.已知定义在R上的函数f(x)=e x+x2-x+sin x,则曲线y=f(x)在点(0,f(0))处的切线方程为()A.y=3x-2B.y=x+1C.y=2x-1D.y=-2x+311.(2020浙江嘉兴高三上期末)设曲线y=x+1x-2在点(1,-2)处的切线与直线ax+by+c=0(b≠0)垂直,则ab=()A.13B.-13C.3D.-312.(2020河北保定高二上期末)设曲线f(x)=ae x-ln x(a≠0)在x=1处的切线为l,则l在y轴上的截距为()A.1B.2C.aeD.ae-113.若质子的运动方程为s=tsin t,其中s的单位为m,t的单位为s,则质子在t=2s时的瞬时速度为m/s.14.曲线y=x3+3x2+6x-10的所有切线中,斜率最小的切线方程为.15.(2020江西南昌三中高二下期中)已知函数f(x)=x-2ln x,求曲线y=f(x)在点A(1,f(1))处的切线方程.能力提升练题组导数的四则运算法则及其应用1.()设函数f(x)=sinθ3x3+√3cosθ2x2+tanθ,其中θ∈[0,5π12],则导数f'(1)的取值范围是()A.[-2,2]B.[√2,√3]C.[√3,2]D.[√2,2]2.(2020湖南长沙长郡中学高二上期末,)下面四个图象中,有一个是函数f(x)=13x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)=()A.13B.-23C.73D.-13或533.(2019河北衡水中学高三二调,)已知f'(x)是函数f(x)的导函数,且对任意的实数x都有f'(x)=e x(2x-2)+f(x)(e是自然对数的底数),f(0)=1,则(易错)A.f(x)=e x(x+1)B.f(x)=e x(x-1)C.f(x)=e x(x+1)2D.f(x)=e x(x-1)24.()设函数f(x)=xsin x+cos x的图象在点(t,f(t))处切线的斜率为g(t),则函数y=g(t)图象的一部分可以是()5.(多选)()给出定义:若函数f(x)在D上可导,即f'(x)存在,且导函数f'(x)在D上也可导,则称f(x)在D上存在二阶导函数,记f″(x)=(f'(x))',若f″(x)<0在D上恒成立,则称f(x)在D上为凸函数.以下四个函数在(0,π)上不是凸函数的是()2A.f(x)=sin x-cos xB.f(x)=ln x-2xC.f(x)=-x3+2x-1D.f(x)=xe x6.()对于三次函数f(x)=ax3+bx2+cx+d(a≠0),现给出定义:设f'(x)是函数f(x)的导数,f″(x)是f'(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数f(x)=ax3+bx2+cx+d(a≠0)的“拐点”.经过探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数g(x)=2x3-3x2+1,则g(1100)+g(2100)+…+g(99100)=.7.(2020湖南长沙长郡中学高二上期末,)已知函数f(x)=13x3-2x2+3x(x∈R)的图象为曲线C.(1)求曲线C上任意一点的切线的斜率的取值范围;(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C 的切点的横坐标的取值范围.8.()已知直线x+2y-4=0与抛物线y2=4x相交于A,B两点,O是坐标原点,试在抛物线的AOB⏜上求一点P,使△ABP的面积最大.9.()已知函数f(x)(x∈(0,+∞))的导函数为f'(x),且满足xf'(x)-2f(x)=x3e x,f(1)=e-1,求f(x)在点(2,f(2))处的切线方程.答案全解全析基础过关练1.C f'(x)=(x 2)'(x+3)−x2(x+3)′(x+3)2=2x(x+3)−x 2(x+3)2=2x2+6x-x2(x+3)2=x2+6x(x+3)2.故选C.2.A对函数y=x2cos x求导,得y'=2xcos x+x2·(-sin x)=2xcos x-x2sin x.故选A.3.D由题意,得f'(x)=2x+e x,则f'(0)=1,故选D.4.A因为f'(x)=e x(x-2)x3+1x+2kx2,所以f'(1)=-e+1+2k=1,解得k=e2,故选A.5.C取f(x)=x,g(x)=x+1,满足f'(x)=g'(x),可以验证A、B、D错误;由f'(x)=g'(x),得f'(x)-g'(x)=0,即[f(x)-g(x)]'=0,所以f(x)-g(x)=c(c为常数),C 正确.故选C.6.答案2x-x 2e x解析f'(x)=2xe x-x2e x(e x)2=2x-x2e x.7.答案516解析由题意得,h'(x)=f'(x)g(x)-[f(x)+2]g'(x)[g(x)]2,由f(5)=5,f'(5)=3,g(5)=4,g'(5)=1,得h'(5)=f'(5)g(5)-[f(5)+2]g'(5)[g(5)]2=3×4−(5+2)×142=516.8.解析(1)y'=2x-2x-3. (2)y'=(ln3+1)·(3e)x-2x ln2.(3)y'=x 2+1−2x 2lnx x(x 2+1)2.(4)∵y=x 2-4sin x2cos x 2=x 2-2sin x,∴y'=2x-2cos x.9.A ∵f'(x)=ln x+1,∴f'(1)=ln 1+1=1,则f(x)=1+xln x,∴f(e)=1+eln e=1+e.10.B ∵f'(x)=e x +2x-1+cos x,∴切线的斜率k=f'(0)=1,又f(0)=1,∴切线方程为y=x+1. 11.B 依题意得y'=x -2-(x+1)(x -2)2=-3(x -2)2,则y'x=1=-3,由于曲线y=x+1x -2在点(1,-2)处的切线与直线ax+by+c=0(b ≠0)垂直,所以(-3)·(-ab)=-1,解得a b=-13.故选B.12.A 因为函数f(x)=ae x -ln x(a ≠0), 所以f'(x)=ae x -1x ,将x=1代入,得k=ae-1,又f(1)=ae,所以曲线f(x)在x=1处的切线l 的方程为y-ae=(ae-1)(x-1), 整理得y=(ae-1)x+1,令x=0,得y=1. 所以l 在y 轴上的截距为1.故选A. 13.答案 sin 2+2cos 2解析 ∵s'=(tsin t)'=sin t+tcos t, ∴所求瞬时速度为(sin 2+2cos 2)m/s. 14.答案 3x-y-11=0解析 ∵y'=3x 2+6x+6=3(x 2+2x+2) =3(x+1)2+3≥3,∴当x=-1时,y'最小,即此时切线的斜率最小,此时切点为(-1,-14), ∴切线方程为y+14=3(x+1), 即3x-y-11=0.15.解析 ∵函数f(x)=x-2ln x 的导函数为f'(x)=1-2x ,∴曲线y=f(x)在点A(1,f(1))处的切线斜率为f'(1)=1-2=-1,又f(1)=1,∴曲线y=f(x)在点A(1,f(1))处的切线方程为y-1=-(x-1),即x+y-2=0.能力提升练1.D f'(x)=sin θ·x 2+√3cos θ·x, ∴f'(1)=sin θ+√3cos θ=2sin (θ+π3),∵θ∈[0,5π12],∴θ+π3∈[π3,3π4],∴sin (θ+π3)∈[√22,1],∴f'(1)=2sin (θ+π3)∈[√2,2].故选D.2.D 因为f'(x)=x 2+2ax+a 2-1,所以y=f'(x)的图象开口向上,排除②④.若y=f'(x)的图象为①,则a=0,f(-1)=53;若y=f'(x)的图象为③,则a 2-1=0,得a=±1.又对称轴x=-a>0,所以a=-1,所以f(-1)=-13.3.D 由f'(x)=e x (2x-2)+f(x), 得f'(x)-f(x)e x =2x-2,即[f(x)e x]'=2x-2,所以f(x)e x=x 2-2x+c(c 为常数),所以f(x)=(x 2-2x+c)e x , 又因为f(0)=1,所以c=1,所以函数f(x)的解析式是f(x)=e x (x-1)2.故选D.易错警示已知原函数可求出唯一的导函数,已知导数求原函数,则结论不唯一,如本题中由y'=2x-2可以得到y=x 2-2x+c(c 为常数),解题时容易将c 遗漏导致解题错误. 4.A 由f(x)=xsin x+cos x,可得f'(x)=sin x+xcos x-sin x=xcos x. 则g(t)=f'(t)=tcos t,易知函数g(t)是奇函数,排除选项B,D; 当t ∈(0,π2)时,g(t)>0,排除选项C.故选A.5.AD 对于A,f'(x)=cos x+sin x, f″(x)=-sin x+cos x,当x ∈(0,π4)时,f″(x)>0,故f(x)=sin x-cos x 不是凸函数;对于B,f'(x)=1x-2,f″(x)=-1x2<0,故f(x)=ln x-2x 是凸函数; 对于C,f'(x)=-3x 2+2,f″(x)=-6x,当x ∈(0,π2)时,f″(x)<0,故f(x)=-x 3+2x-1是凸函数;对于D,f'(x)=(x+1)e x ,f″(x)=(x+2)e x ,当x ∈(0,π2)时,f″(x)>0,故f(x)=xe x 不是凸函数.故选AD.6.答案992解析依题意得,g'(x)=6x 2-6x,g″(x)=12x -6,令g″(x)=0,解得x=12, ∵g (12)=12,∴函数g(x)的对称中心为(12,12),则g(1-x)+g(x)=1,∵1100+99100=2100+98100=…=49100+51100=1,∴g (1100)+g (99100)=g (2100)+g (98100)=…=g (49100)+g (51100)=1,∴g (1100)+g (2100)+…+g (99100) =[g (1100)+g (99100)]+[g (2100)+g (98100)] +…+[g (49100)+g (51100)]+g (12) =49+12=992.7.解析 (1)由题意得f'(x)=x 2-4x+3,则f'(x)=(x-2)2-1≥-1,即曲线C 上任意一点的切线的斜率的取值范围是[-1,+∞).(2)设曲线C 的其中一条切线的斜率为k,则由条件和(1)中结论可知, {k ≥−1,-1k ≥−1,解得-1≤k<0或k ≥1,故由-1≤x 2-4x+3<0或x 2-4x+3≥1,得x ∈(-∞,2-√2]∪(1,3)∪[2+√2,+∞).8.解析因为|AB|为定值,所以要使△PAB 的面积最大,只要点P 到AB 的距离最大即可,即点P 是抛物线的切线中平行于AB 的切线的切点,设P(x,y).由题图知,点P 在x 轴下方的图象上,所以y=-2√x ,所以y'=-√x . 因为k AB =-12,所以-√x =-12,解得x=4.由y=-2√x ,得y=-4, 所以点P 的坐标为(4,-4).9.解析 ∵xf'(x)-2f(x)=x 3e x ,x ∈(0,+∞),∴xf'(x)-2f(x)x 3=e x . 令g(x)=f(x)x 2,则g'(x)=xf'(x)-2f(x)x 3=e x , ∴g(x)=f(x)x 2=e x +c(c 为常数),∴f(x)=x 2(e x +c).又f(1)=e+c=e-1,∴c=-1.∴f(x)=x 2(e x -1),∴f'(x)=2x(e x -1)+x 2e x =(x 2+2x)e x -2x,∴f'(2)=8e 2-4.又f(2)=4(e 2-1),∴所求切线方程为y-4(e 2-1)=(8e 2-4)·(x-2),即y=(8e 2-4)x-12e 2+4.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学导数的典型例题题型一利用二次求导求函数的单调性【典例1】若函数f (x )＝sin x x，0<x 1<x 2<π.设a ＝f (x 1)，b ＝f (x 2)，试比较a ，b 的大小．【思路分析】此题可联想到研究函数f (x )＝sin x x在(0，π)的单调性．函数图象虽然可以直观地反映出两个变量之间的变化规律，但大多数复合的函数作图困难较大．导数的建立拓展了应用图象解题的空间．导数这个强有力的工具对函数单调性的研究提供了简单、程序化的方法，具有很强的可操作性．当f ′(x )>0时，函数f (x )单调递增；当f ′(x )<0时，函数f (x )单调递减．【解析】由f (x )＝sin x x ，得f ′(x )＝x cos x －sin x x 2，设g (x )＝x cos x －sin x ，则g ′(x )＝－x sin x ＋cos x －cos x ＝－x sin x .∵0<x <π，∵g ′(x )<0，即函数g (x )在(0，π)上是减函数．∵g (x )<g (0)＝0，因此f ′(x )<0，故函数f (x )在(0，π)是减函数，∵当0<x 1<x 2<π，有f (x 1)>f (x 2)，即a >b .【方法归纳】从本题解答来看，为了得到f (x )的单调性，须判断f ′(x )的符号，而f ′(x )＝x cos x －sin x x 2的分母为正，只需判断分子x cos x －sin x 的符号，但很难直接判断，故可通过二次求导，判断出一次导函数的符号，并最终解决问题．【变式训练】1．已知函数f (x )满足f (x )＝f ′(1)e x －1－f (0)x ＋12x 2，求f (x )的解析式及单调区间．解：因为f (x )＝f ′(1)e x －1－f (0)x ＋12x 2，所以f ′(x )＝f ′(1)e x －1－f (0)＋x .令x ＝1，得f (0)＝1.所以f (x )＝f ′(1)e x －1－x ＋12x 2，所以f (0)＝f ′(1)e －1＝1，解得f ′(1)＝e.所以f (x )＝e x －x ＋12x 2. 设g (x )＝f ′(x )＝e x －1＋x ，则g ′(x )＝e x ＋1>0，所以y ＝g (x )在R 上单调递增．因为f ′(0)＝0，所以f ′(x )>0＝f ′(0)∵x >0，f ′(x )<0＝f ′(0)∵x <0.所以f (x )的解析式为f (x )＝e x －x ＋12x 2，且单调递增区间为(0，＋∞)，单调递减区间为(－∞，0).题型二利用二次求导求函数的极值或参数的范围【典例2】已知函数f (x )＝ln(ax ＋1)＋x 3－x 2－ax .(1)若x ＝23为y ＝f (x )的极值点，求实数a 的值； (2)若y ＝f (x )在[1，＋∞)上为增函数，求实数a 的取值范围；(3)若a ＝－1时，方程f (1－x )－(1－x )3＝b x有实根，求实数b 的取值范围． [方法演示]解：(1)f ′(x )＝a ax ＋1＋3x 2－2x －a . 由题意，知f ′⎝⎛⎭⎫23＝0，所以a 23a ＋1＋43－43－a ＝0，解得a ＝0. 当a ＝0时，f ′(x )＝x (3x －2)，从而x ＝23为y ＝f (x )的极值点． (2)因为f (x )在[1，＋∞)上为增函数，所以f ′(x )＝a ax ＋1＋3x 2－2x －a ＝x [3ax 2＋(3－2a )x －(a 2＋2)]ax ＋1≥0在[1，＋∞)上恒成立．当a ＝0时，f ′(x )＝x (3x －2)，此时f (x )在[1，＋∞)上为增函数恒成立，故a ＝0符合题意；当a ≠0时，由ax ＋1>0对x >1恒成立，知a >0.所以3ax 2＋(3－2a )x －(a 2＋2)≥0对x ∵[1，＋∞)恒成立．令g (x )＝3ax 2＋(3－2a )x －(a 2＋2)，其对称轴为x ＝13－12a ，因为a >0，所以13－12a <13，所以g (x )在[1，＋∞)上为增函数，所以只需g (1)≥0即可，即－a 2＋a ＋1≥0，解得0<a ≤1＋52. 综上，实数a 的取值范围为⎣⎢⎡⎦⎥⎤0，1＋52. (3)由已知得，x >0，∵b ＝x (ln x ＋x －x 2)＝x ln x ＋x 2－x 3.令g (x )＝x ln x ＋x 2－x 3，则g ′(x )＝ln x ＋1＋2x －3x 2.令h (x )＝g ′(x )，则h ′(x )＝1x ＋2－6x ＝－6x 2－2x －1x. 当0<x <1＋76时，h ′(x )>0， ∵函数h (x )＝g ′(x )在⎝⎛⎭⎪⎫0，1＋76上递增；当x >1＋76时，h ′(x )<0， ∵函数h (x )＝g ′(x )在⎝ ⎛⎭⎪⎫1＋76，＋∞上递减．又g ′(1)＝0，∵存在x 0∵⎝⎛⎭⎪⎫0，1＋76，使得g ′(x 0)＝0. 当0<x <x 0时，g ′(x )<0，∵函数g (x )在(0，x 0)上递减；当x 0<x <1时，g ′(x )>0，∵函数g (x )在(x 0,1)上递增；当x >1时，g ′(x )<0，∵函数g (x )在(1，＋∞)上递减．又当x →＋∞时，g (x )→－∞.又g (x )＝x ln x ＋x 2－x 3＝x (ln x ＋x －x 2)≤x ⎝⎛⎭⎫ln x ＋14，当x →0时，ln x ＋14<0，则g (x )<0，且g (1)＝0， ∵b 的取值范围为(－∞，0]．【方法归纳】本题从题目形式来看，是极其常规的一道导数考题，第(3)问要求参数b 的范围问题，实际上是求g (x )＝x (ln x ＋x －x 2)极值问题，问题是g ′(x )＝ln x ＋1＋2x －3x 2＝0这个方程求解不易，这时我们可以尝试对h (x )＝g ′(x )再一次求导并解决问题．所以当导数值等于0这个方程求解有困难，考虑用二次求导尝试不失为一种妙法．【变式训练】2．设k ∵R ，函数f (x )＝e x －(1＋x ＋kx 2)(x >0)．(1)若k ＝1，求函数f (x )的导函数f ′(x )的极小值；(2)若对任意的t >0，存在s >0，使得当x ∵(0，s )时，都有f (x )<tx 2，求实数k 的取值范围．解：(1)当k ＝1时，函数f (x )＝e x －(1＋x ＋x 2)，则f (x )的导数f ′(x )＝e x －(1＋2x )，令g (x )＝f ′(x )，则g ′(x )＝e x －2，当0<x <ln 2时，g ′(x )<0；当x >ln 2时，g ′(x )>0，从而f ′(x )在(0，ln 2)上递减，在(ln 2，＋∞)上递增．故导数f ′(x )的极小值为f ′(ln 2)＝1－2ln 2.(2)对任意的t >0，记函数F (x )＝f (x )－tx 2＝e x －[1＋x ＋(k ＋t )x 2]，x >0，根据题意，存在s >0，使得当x ∵(0，s )时，F (x )<0.易得F (x )的导数F ′(x )＝e x －[1＋2(k ＋t )x ]，令h (x )＝F ′(x )，则h ′(x )＝e x －2(k ＋t )．∵若h ′(x )≥0，注意到h ′(x )在(0，s )上递增，故当x ∵(0，s )时，h ′(x )>h ′(0)≥0，于是F ′(x )在(0，s )上递增，则当x ∵(0，s )时，F ′(x )>F ′(0)＝0，从而F (x )在(0，s )上递增．故当x ∵(0，s )时，F (x )>F (0)＝0，与已知矛盾；∵若h ′(x )<0，因为h ′(x )在(0，s )上连续且递增，故存在s >0，使得当x ∵(0，s )，h ′(x )<0，从而F ′(x )在(0，s )上递减，于是当x ∵(0，s )时，F ′(x )<F ′(0)＝0，因此F (x )在(0，s )上递减．故当x ∵(0，s )时，F (x )<F (0)＝0，满足已知条件．综上所述，对任意的t >0，都有h ′(x )<0，所以1－2(k ＋t )<0，即k >12－t ，故实数k 的取值范围为⎝⎛⎭⎫12－t ，＋∞.题型三利用二次求导证明不等式【典例3】证明当x >0时，sin x >x －x 36. 【解析】证明：令f (x )＝sin x －x ＋x 36，则f ′(x )＝cos x －1＋x 22，所以f ″(x )＝－sin x ＋x .易知当x >0时，sin x <x ，所以在(0，＋∞)上f ″(x )>0，所以f ′(x )在(0，＋∞)上单调递增．又f ′(0)＝0，所以在(0，＋∞)有f ′(x )>f ′(0)＝0，所以f (x )在(0，＋∞)上单调递增．故当x >0时，f (x )＝sin x －x ＋x 36>f (0)＝0. 所以sin x >x －x 36(x >0)．【方法归纳】本题是应用导数证明不等式．证明的关键在于构造适当的函数，然后在相应区间上用二次求导的方法判定导数的符号，得到导函数的单调性，再利用单调性证明不等式．【变式训练】3．已知函数f (x )＝m e x －ln x －1.(1)当m ＝0时，求曲线y ＝f (x )在点(1，f (1))处的切线方程；(2)当m ≥1时，证明：f (x )>1.解：(1)当m ＝0时，f (x )＝－ln x －1，则f ′(x )＝－1x，所以f (1)＝－1，f ′(1)＝－1.所以曲线y ＝f (x )在点(1，f (1))处的切线方程为y －(－1)＝－(x －1)，即x ＋y ＝0.(2)证明：当m ≥1时，f (x )＝m e x －ln x －1≥e x －ln x －1.要证f (x )>1，只需证e x －ln x －2>0.设g (x )＝e x －ln x －2，则g ′(x )＝e x －1x. 设h (x )＝e x －1x ，则h ′(x )＝e x ＋1x 2>0. 所以函数h (x )＝g ′(x )＝e x －1x在(0，＋∞)上单调递增．因为g ′⎝⎛⎭⎫12＝e 12－2<0，g ′(1)＝e －1>0，所以函数g ′(x )＝e x －1x在(0，＋∞)上有唯一零点x 0，且x 0∵⎝⎛⎭⎫12，1. 因为g ′(x 0)＝0，所以e x 0＝1x 0，即ln x 0＝－x 0.当x ∵(0，x 0)时，g ′(x )<0；当x ∵(x 0，＋∞)时，g ′(x )>0，所以当x ＝x 0时，g (x )取得极小值也是最小值g (x 0)．故g (x )≥g (x 0)＝e x 0－ln x 0－2＝1x 0＋x 0－2>0. 综上可知，当m ≥1时，f (x )>1.【巩固训练】1．对任意实数x ，证明不等式1＋x ln(x ＋1＋x 2)≥1＋x 2.证明：设f (x )＝1＋x ln(x ＋1＋x 2)－1＋x 2，∵f ′(x )＝ln(x ＋1＋x 2)＋x ⎝ ⎛⎭⎪⎫1＋x 1＋x 2x ＋1＋x 2－x 1＋x 2＝ln(x ＋1＋x 2)，设h (x )＝f ′(x )，则h ′(x )＝1＋x 1＋x 2x ＋1＋x 2＝1＋x 2＋x1＋x 2(x ＋1＋x 2)＝11＋x 2>0，所以f ′(x )在(－∞，＋∞)上是增函数．由f ′(x )＝0，即ln(x ＋1＋x 2)＝0，得x ＝0.所以当x <0时，f ′(x )<0，则f (x )在(－∞，0)上为减函数；当x >0时，f ′(x )>0，则f (x )在(0，＋∞)上为增函数．故f (x )在x ＝0处有极小值，所以f (x )≥f (0)＝0，即1＋x ln(x ＋1＋x 2)≥1＋x 2.2.已知函数f (x )＝(x ＋1)ln x －ax ，当x 0∵(1，＋∞)时，函数f (x )的图象在点(x 0，f (x 0))处的切线方程为y ＝1ex －e. (1)求a 的值；(2)求证：函数f (x )在定义域内单调递增．解：(1)由题意，得f ′(x )＝ln x ＋1x＋1－a ，所以函数f (x )的图象在点(x 0，f (x 0))处的切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)，即y －(x 0＋1)ln x 0＋ax 0＝⎝⎛⎭⎫ln x 0＋1x 0＋1－a (x －x 0)，即y ＝⎝⎛⎭⎫ln x 0＋1x 0＋1－a x ＋ln x 0－x 0－1，所以⎩⎪⎨⎪⎧ln x 0＋1x 0＋1－a ＝1e ，x 0－ln x 0＋1＝e.令g (x )＝x －ln x ＋1，则g ′(x )＝1－1x ＝x －1x，当x ∵(1，＋∞)时，g ′(x )＞0，故当x ∵(1，＋∞)时，g (x )单调递增．又因为g (e)＝e ，所以x 0＝e ，将x 0＝e 代入ln x 0＋1x 0＋1－a ＝1e，得a ＝2. (2)证明：由a ＝2，得f ′(x )＝ln x ＋1x－1(x >0)．令h (x )＝ln x ＋1x，则h ′(x )＝1x －1x 2＝x －1x 2. 当x ∵(0,1)时，h ′(x )＜0；当x ∵(1，＋∞)时，h ′(x )＞0，故当x ∵(0,1)时，h (x )单调递减；当x ∵(1，＋∞)时，h (x )单调递增，故h (x )≥h (1)＝1.因此当x ∵(0，＋∞)时，f ′(x )＝h (x )－1≥0，当且仅当x ＝1时，f ′(x )＝0.所以f (x )在定义域内单调递增．3．已知函数f (x )＝e x －ax 2－bx －1，其中a ，b ∵R ，e ＝2.718 28……为自然对数的底数．设g (x )是函数f (x )的导函数，求函数g (x )在区间[0,1]上的最小值．解：由f (x )＝e x －ax 2－bx －1，得g (x )＝f ′(x )＝e x －2ax －b .所以g ′(x )＝e x －2a .因此，当x ∵[0,1]时，g ′(x )∵[1－2a ，e －2a ]．当a ≤12时，g ′(x )≥0，所以g (x )在[0,1]上单调递增，因此g (x )在[0,1]上的最小值是g (0)＝1－b ；当a ≥e 2时，g ′(x )≤0，所以g (x )在[0,1]上单调递减，因此g (x )在[0,1]上的最小值是g (1)＝e －2a －b ；当12<a <e 2时，令g ′(x )＝0，得x ＝ln 2a ∵(0,1)．当g ′(x )<0时，0≤x <ln 2a ；当g ′(x )>0时，ln 2a <x ≤1，所以函数g (x )在区间[0，ln 2a )上单调递减，在区间(ln 2a,1]上单调递增，于是g (x )在[0,1]上的最小值是g (ln 2a )＝2a －2a ln 2a －b .综上所述，当a ≤12时，g (x )在[0,1]上的最小值是g (0)＝1－b ；当12<a <e 2时，g (x )在[0,1]上的最小值是g (ln 2a )＝2a －2a ln 2a －b ；当a ≥e 2时，g (x )在[0,1]上的最小值是g (1)＝e －2a －b . 4．已知函数F (x )＝e x ＋sin x －ax ，当x ≥0时，函数y ＝F (x )的图象恒在y ＝F (－x )的图象上方，求实数a 的取值范围．解：设φ(x )＝F (x )－F (－x )＝e x －e －x ＋2sin x －2ax .则φ′(x )＝e x ＋e －x ＋2cos x －2a .设S (x )＝φ″(x )＝e x －e －x －2sin x .∵S ′(x )＝e x ＋e －x －2cos x ≥0在x ≥0时恒成立，∵函数S (x )在[0，＋∞)上单调递增，∵S (x )≥S (0)＝0在x ∵[0，＋∞)时恒成立，因此函数φ′(x )在[0，＋∞)上单调递增，∵φ′(x )≥φ′(0)＝4－2a 在x ∵[0，＋∞)时恒成立．当a ≤2时，φ′(x )≥0，∵φ(x )在[0，＋∞)单调递增，即φ(x )≥φ(0)＝0.故a ≤2时F (x )≥F (－x )恒成立．当a >2时，φ′(x )<0，又∵φ′(x )在[0，＋∞)单调递增，∵存在x 0∵(0，＋∞)，使得在区间[0，x 0)上φ′(x )<0.则φ(x )在[0，x 0)上递减，而φ(0)＝0，∵当x ∵(0，x 0)时，φ(x )<0，这与F (x )－F (－x )≥0对x ∵[0，＋∞)恒成立不符，∵a >2不合题意．综上，实数a 的取值范围是(－∞，2]．5．已知函数f (x )＝e x ，g (x )＝a x，a 为实常数． (1)设F (x )＝f (x )－g (x )，当a >0时，求函数F (x )的单调区间；(2)当a ＝－e 时，直线x ＝m ，x ＝n (m >0，n >0)与函数f (x )，g (x )的图象共有四个不同的交点，且以此四点为顶点的四边形恰为平行四边形．求证：(m －1)(n －1)<0.解：(1)F (x )＝e x －a x，其定义域为(－∞，0)∵(0，＋∞)．而F ′(x )＝e x ＋a x 2，当a >0时，F ′(x )>0，故F (x )的单调递增区间为(－∞，0)∵(0，＋∞)，无单调递减区间．(2)证明：因为直线x ＝m 与x ＝n 平行，故该四边形为平行四边形等价于f (m )－g (m )＝f (n )－g (n )且m >0，n >0，m ≠n .当a ＝－e 时，F (x )＝f (x )－g (x )＝e x ＋e x，则F ′(x )＝e x －e x 2.设h (x )＝F ′(x )＝e x －e x 2(x >0)，则h ′(x )＝e x ＋2e x 3>0，故F ′(x )＝e x －e x 2在(0，＋∞)上单调递增．又F ′(1)＝e －e ＝0，故当x ∵(0,1)时，F ′(x )<0，F (x )单调递减；当x ∵(1，＋∞)时，F ′(x )>0，F (x )单调递增，而F (m )＝F (n )，故0<m <1<n 或0<n <1<m ，所以(m －1)(n －1)<0.。