数学与应用数学毕业论文设计高等数学在经济数学中的应用
毕业论文-矩阵的特征值与特征向量的相关研究【范本模板】

本科毕业设计(论文)( 2015届 )题目:矩阵的特征值与特征向量的相关研究学院: 数理与信息工程学院专业:数学与应用数学学生姓名:学号:指导教师:职称:合作导师: 职称:完成时间: 201 年月日成绩:浙江师范大学本科毕业设计(论文)正文目录摘要 (1)英文摘要 (1)1 引言 (1)2 选题背景以及特征值与特征向量的定义与性质 (2)2. 1 选题背景 (2)2。
2 特征值与特征向量的定义 (2)2. 3 特征值与特征向量的性质 (2)3 矩阵的特征值与特征向量的求解方法 (3)3。
1 求解数字方阵的特征值与特征向量 (3)3。
2 已知矩阵A的特征值与特征向量,求与A相关的矩阵的特征值 (7)4 矩阵的特征值与特征向量的反问题的求解 (7)4。
1 矩阵的全部特征值与全部特征向量,反求解矩阵A的方法 (7)4。
2 已知实对称矩阵的全部特征值和部分线性无关的特征向量,反求矩阵A的方法 (9)5 矩阵的特征值与特征向量的应用 (9)5. 1 矩阵的特征值与特征向量在线性递推关系上的应用 (9)5。
2 经济发展和环境污染的增长模型 (14)6 结论 (16)参考文献 (16)矩阵的特征值与特征向量的相关研究摘要:矩阵的特征值与特征向量占据了高等数学中的一小块, 但是其重要性无可比拟, 它可以应用在数学和生活上,尤其是对现在的科学技术领域, 有着至关重要的作用。
本篇论文主要阐述并归纳了矩阵的特征值与特征向量的概念,性质, 解法以及应用,通过具体的例子, 来体现了矩阵的特征值与特征向量的广泛性和实用性,深刻研究了矩阵的特征值与特征向量和它相关的应用。
正文总共分为四个大部分。
第一部分:阐述了它的概念和性质; 第二部分:对于它的求解方法,本篇论文叙述了几种不同的方法,并且有相关例题的作法;第三部分: 关于它的反问题, 本篇论文也有相对应的几种不同的求解方法; 第四部分:关于它在数学领域和生活上的应用.矩阵; 特征值;特征向量; 反问题;应用关键词:Correlation matrix eigenvalues and eigenvecto -rsMathematical and Information Engineering Mathematics and Applied Mathematics Chen Dong(11170126)Instructor: Lvjia Feng (Associate Professor)Abstract: Eigenvalues and eigenvectors occupy the higher mathematics in a small, but its importance is unparalleled,it can be used in mathematics and life,especially in the field of science and technology right now,has a vital role. This paper describes and summarizes the main characteristics and eigenvector matrix concept,nature,solution and applications, through specific examples, to reflect the breadth and practicality matrix eigenvalues and eigenvectors,profound study of matrix eigenvalues and special Eigenvectors and its related applications.Total body is divided into four parts。
经济数学的课堂教学设计

优化为目的,以解决教学问题为宗旨。
方法,不求高深只求够用,以直观为切入点,以练习巩固目标。 教学
根据系统论的观点,按照其研究的范围,教学设计从大到小 过程中,应注意基本概念讲解正确清楚,基本理论阐述系统简明,
一般可以划分为四个层次: 以教学系统为中心的层次──教学系 基本论证方法思路清 晰 、论证严谨,基本运算方面,应 通 过 适 当 的
,则 t0 时
教学媒体设计。 由此, 课堂教学设计是教学设计系统中的一个层 面,是一个直接作用于师生心理和行为的层面,没有这个层面的科 学设计,再好的教学设计也难以实现其价值。 因此,课堂教学设计 是教学设计系统中的关键层面。
课堂教学设计的主要目的就是要设计出低耗高效的教学过 程。 在课堂教学设计中,一方面,我们需要对学习需要、学习内容和 学习者进行客观分析。 在分析的基础上,减少了许多不必要的内容 和活动,然后清晰地阐明教学目标,科学地制订教学策略,经济地 选用教学媒体,合理地拟订教学进度,正确地确定教学速度,准确 地测定和分析教学结果,使教学活动在人员、时间、设备使用等方 面取得最佳效益。 可以肯定地说,没有课堂教学设计,就不可能有 课堂教学的最优化。 另一方面,课堂教学设计设计了富有吸引力的
极大化
的基本条件是
,分别代入,即可证得结论。 随后,提出一个问
题,那么这个条件是充分的吗? 根据极值的第二充分条件,利润极
大化的充分条件还需要
。引导学生关注在经济学中有关这
个条件的实际含义。 这样的例子也使经济数学切实的与其他课程
有了联系。
四、由浅入深,启发式教学
在课堂教学中设计理论知识的讲解顺序,注意前后知识的联
学习者的学习方法问题,灵活地应用了教学媒体。 通过这一系列措
经济数学微积分偏导数及其在经济分析中的应用
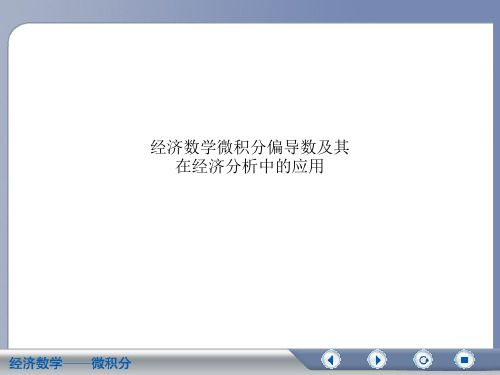
y 2 u 2(x2( x2 y 2)y 2y )2 2y(x x 2 2 y y 2 2 )2. x 2u 2 y 2u 2(x y 2 2 y x 2 2 )2(x x 2 2 y y 2 2 )20.
四、偏导数在经济分析中的应用 ——交叉弹性(cross elastic)
价格 PA 和其他品牌电视机价格 PB 的函数.
Q AfP A ,P B
P 通过分析其边际
Q A PA
及
着 PA 及 B 变化的规律.
Q P
B B
可知道,
QA 随
进一步分析其弹性,可知这种变化的灵敏度.
QA
Q A
Q A
对
PA
及
PB
亦称为
PB
的
QA
QA
交
PA
PB
叉
弹
性
QA对PA的 弹 性QA对PB的 弹 性
解
z 2x3y; x
z y
3x2y.
z x
x 1 y2
2 1 3 2 8 ,
z 7 .
例2 设 zxy(x0,x1), 求 证xz 1 z2z. yx lnxy
证
z yxy1,
5. 设u ( x )z ,则 2u __________.
y
zy
二、
求下列函数的偏导数:
1. z (1 xy) y ;
2.u arctan(x y)z.
三、
x2 y2
曲线
z
4
在点(2,4,5)处的切线
y 4
与 x 轴正向所成的倾角是多少?
RT V2
届金融数学毕的业论文题目

金融数学专业毕业论文选题一、论文选题说明该选题表是某重点大学多名在校教师多年指导毕业论文的总结,为了更好地引导学生写作论文。
另外,在论文写作、格式规范以及论文答辩等等方面有困难的同学,请仔细看这些题目,看几个后你就会有所收获。
这些题目写作以及答辩都比较容易!!二、论文参考题目1.浅析反证法思想在金融数学教学中的应用2.金融类“应用型”人才培养中经济数学的教学与改革3.关于金融数学教学的思考4.将经济数学与金融专业课程有效结合以培养金融类“应用型”人才5.本科生“金融数学”课程案例教学模式探讨6.金融数学专业人才培养模式的改革与探索7.金融数学方向建设的几点建议8.金融数学研究最新进展综述9.数学专业拓办金融数学方向教学改革的探索10.代写论文抠抠舞衣衣漆久吧漆久叁11.金融经济分析应用经济数学的探讨12.复制资产策略在金融数学教学中的应用13.金融数学概述与介绍14.数学与应用数学专业方向建设教学改革探索——浅谈在高校数学系开设金融数学本科专业15.金融数学教学初探16.经济数学在金融经济分析中的应用浅析17.金融理论发展对数学化的依赖18.应用型本科高校金融数学专业建设的思考19.浅谈数学在金融中的应用20.高校金融数学专业建设新探21.金融数学在西部高校的融合式教学发展研究22.金融数学专业“概率论”课程教学例题选题研究23.金融数学专业课程设置与人才培养质量分析24.金融类“应用型”人才培养中经济数学的教学与改革25.金融数学模型26.浅谈金融专业数学教学的改革27.金融类院校开设数学建模课程应解决的几个问题28.案例教学法在金融数学教学中的应用29.金融数学研究综述及其前景展望30.“金融数学”探究式教学的探索与实践31.金融数学金融工程和金融电子化32.浅析金融经济分析中经济数学的应用33.金融数学中的若干前沿问题34.金融数学与金融工程专业介绍及其发展前景35.浅析数学建模教育在金融人才培养中的作用及对策36.针对金融数学专业进行金融工程学课程教学改革的探索37.金融危机中企业受波及的数学模型38.财经院校金融数学高层次人才培养模式研究39.当前行为金融研究中数学建模应用的价值分析40.地方院校金融数学专业(方向)的课程设置41.高校金融数学专业实验课程的设置42.以辩证的观点浅析数学金融研究43.金融数学概述及其展望44.金融数学研究综述与展望45.金融数学概述46.浅谈金融与数学47.金融数学的教学与研究48.浅析数学方法在金融领域的应用49.金融数学:历史与现状50.金融数学教学方法改革的探讨与实践51.以就业为导向的金融数学课程设置与教学改革研究52.对“金融数学”专业人才培养的探索与实践53.金融数学研究前景展望54.金融危机与金融数学55.高校数学系金融数学实验教学模式的探讨56.金融类院校经济数学与现代信息技术深度融合探究57.浅谈数学建模教学与金融人才的培养58.金融中数学模型对实践的影响:过去、现在和未来59.金融数学方向《随机过程》课程建设的研究与实践60.论数学模型在金融领域中的应用61.浅谈数学模型在金融市场中的应用62.论金融经济学的数学化63.比较教学法在金融数学教学中的应用64.金融数学的发展及其在证券投资组合中的应用65.金融数学本科专业教学现状及对策分析66.刍议金融工程与金融数学专业的培养方案67.一类金融数学方程解的适定性研究68.金融数学课程设置与专业建设的一些体会69.数学在金融领域中的适用性和局限性70.金融数学的起源和发展及金融工程简介71.金融数学研究进展与展望72.我国金融数学的发展及前景73.谈如何运用金融数学技巧进行期权定价74.20世纪金融数学的若干进展及前瞻75.金融数学介绍76.结合学科特色的高等数学课程教学改革研究——以金融院校为例77.基于数学模型的金融系统分析研究78.数学金融中的经验与洞察79.我国金融数学教学工作改进分析80.计算机技术在金融数学课程教学中的运用81.数学建模教育与金融人才培养82.金融数学专业会计课程设置及实验教学思考83.金融专科生提高数学素养的思考84.金融数学的研究与进展85.金融数学及金融工程学──公司理财和金融风险防范的高新技术86.金融数学模型概述87.谈谈成人学校金融专业数学教学内容改革88.金融数学引论研究性教学探讨89.向应用型高校转型形势下的本科金融数学专业课程设置初探90.新建地方本科院校应用型金融数学人才培养的思考91.金融数学中两个基于高等数学的证明92.金融数学专业数学分析课程教学探索与实践93.地方高师院校金融数学教学模式初探94.金融数学教学方法的探索与实践95.关于金融数学深入认识的几点思考96.中职学校金融类专业数学选择性教学的实践研究97.应用型本科院校金融数学专业学生培养研究98.地方高师院校金融数学专业实验课程体系建设探索99.对金融数学专业教学改革问题的思考100.金融市场收益率离散数学模型及其定性分析101.对金融数学专业会计教学改革的思考102.成人金融院校数学教学改革初探103.金融对数学方法运用的探讨104.金融数学教育与实用型金融人才的培养105.“第六届全国金融数学与金融工程学科建设与学术研讨会”综述106.金融工程学的数学模型与方法107.非线性数学期望在金融风险中的应用108.论现代金融风险监管体系的数学模型109.数学与现代金融投资理论110.非线性数学期望111.金融数学介绍112.金融定量分析中的数学方法113.金融数学114.关于新升本金融类院校高等数学课程教学方法的研究115.提高数学教学质量适应现代金融事业发展116.西部新建地方本科院校金融数学教学模式初探117.浅谈数学在金融中的应用118.金融类院校经济数学教学现状及对策119.数学建模在现代行为金融研究领域的应用120.论金融风险监管中的数学模型方法121.金融工程学视角下的数学模型与应用122.金融数学发展综述123.应重视金融数学在外汇收支统计分析中的应用124.金融类院校数学建模课程设置的实践研究125.彭实戈:中国金融数学奠基人126.十年来我国金融数学的回顾和前景127.数学金融的分数次Black-Scholes模型及应用128.数学专业拓办统计与金融数学方向的教学改革129.一种借贷关系分析的数学方法和金融风险防范130.数学方法的金融应用初探131.数学建模思想在高职金融数学课程上的应用实践——以房贷按揭问题为例132.金融数学专业课程体系分析133.市场经济体制下金融机制及其数学建模机理的可拓性分析134.金融数学的发展及其在证券投资组合中的应用135.高校教学模式改革的有益探索——兼论金融数学专业实验教学的改革与完善136.数学建模教育与金融学科人才培养137.金融理论研究中的数学方法138.数学方法在金融投资风险分析中的应用139.21世纪应用型人才培养模式研究探索——湖南人文科技学院《应用数学(数理金融)本科专业人才培养计划》解读140.金融数学专业实变函数教学方法探析141.金融风暴下的数学专业142.金融数学本科专业人才培养模式的研究——以新疆财经大学为例143.“3+1”培养模式下《金融数学》课程实践教学改革的研究与实践144.《金融数学》课程对大学人才培养的作用145.金融数学培养方向实验项目资源建设的几点建议146.在《金融数学》教学中培养大学生的学习兴趣147.金融数学课程案例教学的探讨148."金融数学专业设计性实验的教学安排149.数学在经济学研究中的角色:基于金融危机视角的思考150.概率论和金融学的结合——金融数学的现代发展综述151.金融数学的研究与进展152.金融衍生品和信用风险定价的数学模型153.山东大学“金融数学与金融工程基地班”人才培养模式探索154.独立学院数学与应用数学专业(金融证券方向)人才培养研究155.金融危机内在成因的数学建模研究156.案例教学法在金融数学专业数学分析教学中的应用157.地方院校金融数学专业“三模块”课程体系改革的探讨158.基于ADDIE模型的金融工程和金融数学专业实践性教学环节教学模式研究159.第九届全国微分方程暨金融数学学术会议在延边大学召开160.北京师范大学数学科学学院(统计与金融数学系)承办“3+X统计学及其应用Workshop 2011”161.提高金融院校大学生的数学素养是数学教学的根本任务162.金融危机发生时资金运作的数学模型研究163.多媒体技术在金融数学课堂教学中的应用研究164.改革金融数学基础课程解析几何考试模式培养实践能力165.经济类院校经济数学分层次教学改革探讨——以山东轻工业学院财政与金融学院为例166.浅谈金融类院校高等数学分层教学的评价策略167.金融机构社会责任评价的数学模型168.浅谈金融数学169.试论数学分析在金融研究中的作用170.金融投资收益与风险的数学模型及其应用171.金融数学专业高等代数与解析几何教学探讨172.泛系资源泛通论:交通·通信·金融·数学——计算机·网络·智能·科技史新论识173.2007年全国金融数学学术研讨会会议纪要174.基于神经网络的金融相关比率(FIR)数学模型的建立175.期权如何定价?──金融数学拾零176.浅析金融数学模型177.金融类院校中经济数学对学生职业能力培养的研究178.金融数学模型及其非参数估计问题179.风险与回报:银行业中的数学(上)180.中国金融数学的先行者——金融数学领域彭实戈侧记181.金融系统数学模型的机理分析与控制182.金融数学中的欧式期权定价方法183.非线性数学期望,模糊下的最优停时原理及其在金融中的应用184.开展金融数学研究为金融事业决策服务185.关于地方院校新办金融数学专业课程体系构建的思考——以乐山师范学院为例186.金融工程:久期模型及其数学分析187.基于金融数学模型方法的电力衍生产品的定价研究188.国际金融法研究的切入点与数学方法189.期权类衍生金融工具的多期二项式定价数学模型190.非线性数学期望及其在金融中的应用191.谈金融专业学校数学教学的改革192.金融数学拓荒人——记著名金融数学家、山东大学数学研究所所长彭实戈教授193.非线性数学期望的性质及其在金融风险中的应用194.大数据时代金融专业数学的发展趋势195.浅议金融工作者数学素养的培育196.企业受金融危机影响的数学模型197.破产理论研究及其在金融数学中的应用198.数学在21世纪的金融中必将发挥更大的作用199.开展金融数学金融工程和金融管理研究200.金融经济学中的组合数学问题201.在金融危机中企业受波击的数学模型202.转变点在经济、金融、计量经济学中的数学建模203.卓越金融本科人才指标体系构建与评估——运用模糊数学的方法204.金融危机中企业受波及的数学模型的定性分析205.金融数学的崛起206.金融数学本科生多元统计分析课程教学的改革与实践207.Brown运动首达时在金融数学中的应用208.经济与金融中的“数学显微镜”209.基于数学规划模型的金融资源配置测算分析210.浅谈影响新建本科人才培养与有效教学的主要因素——以哈尔滨金融学院数学教学为例211.评《金融衍生产品定价的数学模型与案例分析》212.浅谈数学在金融领域的发展及应用213.基于正规金融信贷选择的一个数学博弈分析214.金融投资类线性规划及其数学模型的MATLAB求解215.马克思主义认识论的数学描述及其在金融经济学中的一个应用216.模糊数学在金融管理中的应用217.金融数学专业概率统计研究性教学的探索218.期权定价—数学在金融行业中的应用浅议219.金融和金融数学研究220.新兴的交叉学科——金融数学221.数学工具处理金融问题222.在金融写作中要注意正确运用数学概念223.最优控制的若干问题及其在金融数学中的应用224.浅谈数学金融学的变革与发展225.浅论数学金融学中关于期权定价的问题226.美国的金融风暴,源自美国失败的数学教育?227.金融控股集团资本金重复计算问题的数学分析228.一个有关咨信公司在金融市场中作用的数学分析229.数学模型在商业银行管理领域中的应用230.Knight不确定金融投资决策与风险度量研究231.“金融大厦”离不开数学支撑232.浅议数学在金融事务专业课程教学的影响与作用233.金融投资中的数学方法234.倒向随机微分方程和金融数学235.芝加哥大学数学系的金融数学学位236."多维球面模型及其在股市分析中的应用——金融数学的新思考237.在金融院校高数教学中运用网络资源的研究238.金融数学第一人——访山东省科学技术最高奖获得者彭实戈239.民族地区金融数学专业常微分方程教学改革与实践240.有趣的金融数学241.金融数学的现在和未来242.金融数学帮您钱生钱243.经济数学与信息技术深度融合探究244.地方高校金融专业教学中数理分析能力的强化与培养245.重视金融数学研究的现实意义246.结合模糊数学与信息扩散法的Logit模型在信用评级中的应用247.金融中的数学——读《数学与金融》248.地方高校金融人才数理分析能力的强化与培养249.连续时间证券投资组合250.彭实戈:中国金融数学第一推动人251.随机理论在连续时间金融市场模型中的应用252.信用风险分类评级数学模型的研究253.非线性数学期望的性质254.等比数列在金融领域中的一个应用255.研究突发事件:数学金融学的重要课题256.当代金融技术发展的趋势257.不相关金融投资收益与风险优化模型探讨258.我国金融危机预警模型的构建与实证研究259.中国“入世”对金融服务业影响的模糊数学模型分析260.有限离散时间金融市场模型261.金融数学中的若干极限定理262.容度极限理论和非线性数学期望在金融中的应用263.港鲁两校在数学领域的合作264.企业金融资产管理数学模型265.金融,也是科学和数学的事业──由1997年诺贝尔经济学奖引发的思考266.投资选择及资产定价数学模型研究267.陕西财经学院1981年硕士研究生入学数学试题(金融专业用)268.陕西财经学院1982年攻读硕士研究生入学数学试题(金融专业用)269.碳排放权交易的实物期权定价方法与数学模型270.开放教育金融专科“经济数学基础”教与学模式271.基于模糊层次分析法的互联网金融风险评估研究272.经济全球化背景下中国银行业税收问题研究273.非线性数字期望274.基于模糊数学中S型隶属函数的风险度量VaR275.股票投资风险管理的数学模型研究276.关于数学系列课程的教学建议277.论经济危机、金融危机的形成原因与遏制278.数学金融学与微分对策(英文)279.关于柱形H-半鞅的算子值随机积分及其在金融上的应用280.数学在经济学研究中的角色:基于金融危机视角的思考281.金融市场预测中数学的使用、误用和滥用282.威尔士斯旺西大学283.基于仓单质押的物流金融风险管理与控制研究284.山西票号金融稽核创新与研究285.金融模拟实验课程的建设与实践286.金融市场风险测量模型—VaR及基于VaR的证券组合选择287.探索数理之美构建艺术化金融教学模式288.基于过度自信的金融市场委托-代理模型研究289.资本监管标准与金融安全机理探讨290.基于经济增长偏好的地方政府金融行为研究291.在经济数学课程中实施参与型教学法的研究292.正倒向随机微分方程的数值方法及其在金融与双曲型方程柯西问题中的应用293.“中国商业经济学会经济数学研究分会第七次年会”综述294.随机利率情况下期权定价问题研究及应用295.分层目标教学法在经济数学教学中的应用296.“摧毁”华尔街的数学公式297.我国农村金融体系协调性及其测度298.PPR数学模型在通胀成因定量分析中的应用299.现代金融理论的进展综述300.浅析数学方法在金融学中的应用301.中国工业化进程中的金融先导战略研究302.复杂适应系统软件平台SWARM在金融体系中的博弈仿真研究303.高师院校数学类各本科专业应用型人才培养的思考304.从股票期权看数学科学305.金融衍生证券定价数值估计的理论分析306.金融专科学校高等数学课内容设置的构想307.基于分形的期权定价及风险价值计算308.静态利率期限结构的数学模型与算法的研究309.基于跳跃——扩散过程的最优消费投资组合问题研究310.金融统计教学的创新与实践311.20世纪经济数学的若干进展312.经济学向何处去——金融危机以来的经济学反思313.数学概率统计在实际生活重要领域的应用314.吉林大学金融学院315.上市金融企业内部控制有效性的研究316.金融经济学的现代进展317.银行业数学化探讨318.一种基于高阶矩的金融危机预测方法319.物流金融业务风险评价方法研究320.采用自学教学法是金融教育必由之路321.数学模型在商业银行管理领域中的应用322.欧式看涨期权定价微分方程的有限差分求解方法323.金融机构专利权质押贷款风险评估研究324.金融工程教学改革的研究与实践325.风险的测度研究──对偶方法326.数理统计与现代金融关系评论327.数字是经济管理的支柱328.用模糊数学评判信用社经营效益的初步研究329.组合投资数学模型发展的研究330.封闭方程组约束下的国际金融琼斯模型331.地方本科大学数学专业人才培养模式的探索332.经济数学教学提高职业能力培养创新人才模式的探究333.中国利率市场化若干问题研究334.金融计划简易概率网络模型335.金融工程学教学方法新探336.伊藤过程理论及其在金融中的应用337.外汇期权定价的数学模型分析338.试用数学方法研究储蓄339.在非线性情形下的一些大偏差结果以及在金融中的应用340.运用模糊数学方法统筹构建货币流通的模型341.试建一个金融资金流向流量优化模型342.金融分析师之路343.分数布朗运动环境下的欧式与美式期权定价研究344.股票价格的期权定价模型345.三中全会后金融改革趋势展望346.一类扩散过程的最优停止347.金融企业内部控制评价体系的思考与实践348.一类基于MATLAB程序的线性规划及数学模型的求解349.浅谈金融学中的数学350.委托-代理关系的数学描述及应用分析351.市场易变性与期权理论定价数学模型的比较352.金融市场化测度与中国金融市场化过程研究353.数学金融学中的期权定价问题354.跳跃点统计检测的小波方法及其在金融汇率中的应用355.进化金融及中国股市实证研究356.信用风险管理应避免滥用数学公式357.具脉冲影响的商品定价决策与金融调控问题的动力学模型研究358.泊松过程理论在地震灾害金融风险管理中的应用359.投资者有限理性与证券价格行为研究360.商业银行小微企业金融服务研究361.期权的定价与应用362.基于JSP技术平台下银行金融信息系统开发风险管理研究363.金融复杂性与中国金融效率364.期权定价理论的起源:巴夏里埃365.股票价格为跳跃扩散过程的期权定价的研究与应用366.证券选择的多元化问题研究367.基于指数方差伽玛模型的金融衍生品定价368.中国金融结构制度变迁及动因分析369.非线性跟踪—微分器在VaR中的应用研究370.中国农村金融供给创新的路径选择371.基于随机微分方程模型的金融时间序列预测的研究372.湖南省农村金融产品持续创新动力评价研究373.中国金融制度的风险机理研究374.基于多Agent模型的连续双向拍卖金融市场仿真实验研究375.经济心理与金融行为376.规范场理论和金融市场模型377.从学科交叉看金融工程学的发展378.首次穿过边界概率及其在金融中的应用(英文)379.分数布朗运动环境下可换债券定价模型380.“金融和保险领域中非线性复杂系统的研究”青年科研创新团队介绍381.群体模型下的金融市场和资产定价研究382.金融衍生产品中美式与亚式期权定价的数值方法研究383.几类奇异期权的风险VaR度量384.Rijndael算法硬件实现的优化设计及应用385.金融发展对城乡居民收入差距的影响386.金融保险中的大偏差问题387.随机控制理论在金融和保险中的应用388.后金融危机时代资源枯竭型城市产业结构与主导产业选择研究389.价差期权定价方法的研究390.电力系统商业化运营优化模式的分析与研究391.分形维数的数学基础及对上海股票市场混沌、分形特性的实证分析392.实际利率法应用中关键数据逻辑关系分析——以应付债券后续计量为例393.经济与金融:最“人文”的经济394.随机微分方程在金融中的若干应用395.金融时间序列隐含模式挖掘方法及其应用研究396.区域金融结构和金融发展理论与实证研究397.非正常金融环境下金融机构的VaR对比研究398.南京港物流发展研究399.我国农村微型金融服务及风险防范研究400.金融泡沫运行与控制研究401.金融混业经营及其风险管理研究402.金融企业应用管理信息系统的绩效评价研究403.甘肃省金融发展规模、结构、效率的协调性测度研究404.我国农村金融供求失衡深层机理研究405.中国政策性金融促进自主创新的有效性研究406.中国农村合作金融制度变迁研究407.中国区域金融协调发展研究408.辽宁城乡金融发展差异对城乡经济增长影响的实证研究409.衍生金融工具风险监控问题探析410.金融危机之信用失衡411.基于西部金融中心建设目标的成都金融人才需求预测研究。
应用数学毕业论文选题题目

应用数学毕业论文选题题目应用数学,是利用数学方法解决实际问题的一门学科,在经济金融、工程科技等领域都有应用。
如何对应用数学专业的论文进行选题呢?下面小编给大家带来应用数学毕业论文选题题目推荐,希望能帮助到大家!最新应用数学论文题目1、当前高中数学教学中应用数学史知识的调查研究2、应用数学模型评价Ⅱ类错(牙合)功能矫治后软硬组织的改变3、高师院校数学与应用数学专业学生数学文化素养的现状调查与分析4、高师院校数学与应用数学专业学生数学认识信念的调查分析5、职业学校数学教师关于教学中应用数学史的调查研究6、高校高等数学教学培养学生数学应用能力的研究和实践7、浅谈线性变换的对角化问题8、中美高中数学教材的数学应用水平的比较研究9、高中物理教学培养学生应用数学能力的方法与实践10、地方高师职前教师教育课程体系的构建11、应用数学力学方法研究沥青路面结构特性12、高师生数学认识信念的调查研究13、注重问题发现培养学生学习数学和应用数学的能力14、应用数学模型研究宁夏围栏内甘草的分布格局和土壤水分对甘草生长发育的影响15、培养中专生应用数学意识的研究16、数学史在数学概念教学中的应用研究17、高等应用数学系列教程出版项目的进度管理研究18、数学建模思想在小学数学教学中的应用研究19、拉曼光谱的数学解析及其在定量分析中的应用20、数学形态学及其应用21、数学形态学在信号处理方面的应用研究22、波利亚的数学解题思想及其在中学数学教学中的应用23、高中数学应用翻转课堂的实践研究24、中职数学教学中“学案导学”模式的应用研究25、初中数学教学中数学史应用开发研究26、基于MATLAB的数学实验系统的实现及应用27、信息技术在小学数学课堂教学中的应用研究28、数学形态学图象处理算法应用研究29、“学案导学”模式在中学数学教学中的应用研究30、波浪与建筑物作用的数学模型研究与应用31、模糊数学在膝关节骨性关节炎诊断和疗效评价中的应用32、非线性数学期望下的随机微分方程及其应用33、思维导图在小学六年级数学教学中的应用研究34、极限与极限思想在中学数学中的应用35、高中数学概念图教学的应用研究36、电子书包在小学数学学科教学中的应用研究37、《数学的发现》中的思想在中学数学教学的应用研究38、数形结合方法在高中数学教学中的应用39、高中数学教学中培养学生数学应用意识的实验研究40、高等数学方法在中学数学中的应用研究41、数学中的研究性学习42、经济问题中的概率统计模型及应用43、中学数学中的化归方法44、高斯分布的启示45、a2+b2≧2ab的变形推广及应用46、网络优化 7、泰勒公式及其应用47、浅谈中学数学中的反证法 9、数学选择题的利和弊48、浅谈计算机辅助数学教学 11、论研究性学习49、浅谈发展数学思维的学习方法50、关于整系数多项式有理根的几个定理及求解方法51、数学教学中课堂提问的误区与对策52、中学数学教学中的创造性思维的培养53、浅谈数学教学中的“问题情境”54、市场经济中的蛛网模型55、中学数学教学设计前期分析的研究数学与应用数学专业毕业论文题目1、初中生利用数学解决实际问题的教学研究2、初中生应用题“懂而不会”现象的原因分析与对策研究3、高中物理教学培养学生应用数学能力的方法与实践4、数学与数学文化对人类文明发展的作用5、数学史在高中数列教学中的应用探究6、高中生数学应用意识与应用能力培养7、数学思想对高中解析几何学习影响的研究8、高职院校工科学生数学应用意识及其培养研究9、高中数学教学渗透物理知识现状的调查研究10、应用数学模型评价Ⅱ类错(牙合)功能矫治后软硬组织的改变11、初中数学应用意识和能力的研究12、新课标数学中考的发展趋势13、培养中职生数学应用意识的教学对策研究14、高中数学应用题教学的调查和研究15、高师院校数学与应用数学专业学生数学文化素养的现状调查与分析16、高师院校数学与应用数学专业学生数学认识信念的调查分析17、数学史在中职数学教学中的应用研究18、职业学校数学教师关于教学中应用数学史的调查研究19、初中数学教学中数学史应用开发研究20、数理经济学史研究21、高中数学课程价值取向研究22、科学个案研究与中国科学观的发展23、审计判断研究24、数学建模的认知机制及其教学策略研究25、钱伟长治学理念及教育思想初探26、力学期刊群的内外关系与学科结构27、高师院校数学教师多元化、分层次培养方案设计与研究28、数学实验的历史考察与理论研究29、日本中小学数学综合学习研究30、高中开展数学建模活动的实验研究31、新课程标准视野下的数学建模研究32、中等职业学校数学应用教学模式研究33、培养中专生应用数学意识的研究34、新课程在初中数学教学实施中的几点体会35、将数学建模融入高中日常教学的实践研究36、基于“三环节”模式的教学设计研究37、培养初中生数学应用能力的教学研究38、师范生的培养研究39、中美高中数学教材的数学应用水平的比较研究40、数学史在高中数学课堂教学中的应用研究高等数学论文题目1、将数学建模的思想融入高等数学的教学2、初等数学与高等数学教学衔接问题的研究3、高等数学自主学习的问题与对策研究4、高等数学分层教学方法的实践研究5、信息技术与高等数学课程整合的实践研究6、高校高等数学教学培养学生数学应用能力的研究和实践7、《高等数学》网络课程设计与开发8、数学史在高等数学教学中渗透的研究9、高等数学视角下的中学数学教学研究10、对话理念下的高等数学教师课堂提问11、高职机电类专业高等数学课程改革与实践12、高等数学方法在中学数学中的应用研究13、高等职业技术学院学生《高等数学》满意度研究14、高职院校高等数学课程教学改革的研究15、基于云计算技术的《高等数学》网络教学设计16、基于“翻转课堂”的文科高等数学教学设计研究17、高职院校高等数学课程内容的调查研究18、高职教育高等数学课程教学内容与教学方法改革的研究19、高等数学探究式教学模式及其评价分析20、高等数学“研究性教学”的研究21、周期函数的判定22、阶的估计与应用23、一致连续的判定与应用24、N-L公式的推广与应用25、对称函数的条件极值26、多元函数极值的一阶微分判别法及多元函数最值的极限形式27、非线性时滞Josephson方程的概周期解28、一类二阶非线性系统概周期解29、一类含有概周期强迫项的二阶非线性系统的概周期解30、一类广义时滞Logistic方程的全局吸引性31、一类方程概周期解和有界解的存在性32、一类脉冲系统的周期解33、利用数列的上下极限来计算数列的极限34、Cauchy中值定理的反问题35、微分中值定理中间点的性质36、递推数列上界的判定方法37、曲线积分中间点性质38、开区间内有不可导点的Dabox定理39、最短路径与改进型Dijkstra算法?40、映射一致连续性的判别方法?41、函数高阶微分的表达式42、映射的性质与可积性的关系43、函数列一致收敛性的判定方法44、可数集合的判定方法45、映射对聚点的影响46、谈《几何画板》在几何教学中的作用47、数学CAI课件制作和使用48、反例在数学论证中的应用49、线性方程组解的再讨论50、二元域上对合矩阵的性质51、二次整环中因子分解的讨论52、形式幂级数半环的同余与同态53、具有相同正解的线性方程组的讨论54、矩阵方程的正解、半正解55、陪同矩阵的性质及其应用56、线性递推数列线性空间及其应用57、广义正交变换与广义对称变换的性质58、初等变换与向量组的极大无关组59、Cramer法则的应用60、杨辉三角中的行列式的性质及计算。
数学模型在经济领域中的运用

数学模型在经济领域中的运用作者:王予来源:《环球市场信息导报》2018年第02期经济领域中经常会应用到一些数学模型,通过数学语言来描述经济情况,对各项数据信息进行计算,以判断经济发展的实际情况。
将数学模型应用在经济领域中,有利于找出市场经济的内在联系和规律,从而科学制定发展决策,以推动经济安全、稳定地发展运行。
市场经济多元化的发展,使得经济领域存在很多不确定因素,若不能准确掌握经济领域中的规律与发展趋势,容易带来市场风险。
将数学模型应用在经济领域中,利用数学结构表达式,可深入探究数学与经济之间的联系,探究内在运行规律,以发挥数学模型的价值和作用,对未来经济的发展有重要的指导意义。
数学模型应用在经济领域中的重要性国内外学者早就对数学与经济之间的联系进行了研究,将数学知识应用到经济领域的生产、经营中,从而计算生产数量与经营利润。
同时,应用数学概率问题,对市场的发展情况进行数据收集、整理与分析,便于判断市场可能存在的风险隐患,并预测发生风险的几率,以制定正确的防范措施,这能有效保障经济领域的安全性与稳定性。
数学模型是数学结构的重要表现形式,需要借助数学符号来探究经济领域的关系结构。
同时,将数学模型运用在经济领域中,可对现有的经济数据进行分析与探究,挖掘隐藏的经济信息,这些信息会对经济发展产生重要的影响。
如果我们通过数字、符号、数学公式等表达出来,就能验证结果的真实性与有效性。
另外,数学知识具备抽象性特点,将其应用在具体的经济领域中,有利于探究具象化的问题,及时解决市场经济中存在的问题。
数学模型在经济领域中的运用措施概率学的应用。
在市场经济的发展下,人们的生活水平得到了快速提高,对产品的需求量越来越大,要求也越来越高。
同时,受消赞者的观念、思想、意识等方面的影响,市场也在不断更新。
受供求影响,产品价格也相应变化。
但这种变化趋势存在很多的不确定性因素,经济发展的规律和特点也变得难以探究,存在较高的经济风险。
利用经济模型引出高等数学的重要概念

2 1 0 1拄
高 师 理 科 学 刊
Ju a f ce c f e c es C U g n ie i o r l in eo a h r o e ea dUnv r t n oS T s y
V I 3 N . o. 1 o6 N V 2 1 O. 0 l
将数学用于经济学,如果只是利用定性分析难 以阐明的现代经济错所以应该认识到将数学用于经济学,并不是用数学取代经济学,而是利用数
学分析为经济分析服务.经济类的学生有一部分是文科生 , 对于数学的兴趣很少 ,或者说是没有 ,如何激
发学生的兴趣 ,提高学生的数学修养 ,已经成为一个急需解决的问题.把经济数学模型引入到经济类高等 数学教学中将有助于提高学生 的学习兴趣 , 取得 良 的教学效果. 好
经济类高等数学 与通常的高等数学课程相 比有其特殊性 ,需要正确认识经济与数学的关系.在 目 前 的经济类高等数学教学中, 主要存在以下一些问题 : 1 教学 内容重视经典的结论而忽视现代的一些结果 , ()
重视理论推导而忽视联系经济应用 ;( ) 2 教学方法和方式重视演绎而忽视归纳结论 ,启发思维少 ,课堂的 信息量较少 , 学生处在被动收听状态 , 主体作用得不到发挥; 3 教学模式 “ () 一刀切” 忽视 了学生的个性 , , 即经济类的学生很多是文科生,数学基础较薄弱 ; 4 考试 内容和方法单一 ,偏重于理论和烦琐计算的考 () 查 ,忽视数学在经济中的应用 ; 5 数学教学与经济类的专业课之间的协调不强,不能充分的相互补充 () .
p o o e e me o f u en f a t a c n mi d l t r w o t e i o t n o c p s i e h g e r p s d t t d o s i g o cu l e o o c mo e o d a f r t mp r t c n e t n t ih r h h h h a h
数学教学研究论文6篇-数学教学论文-教育论文

数学教学研究论文6篇-数学教学论文-教育论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——第一篇:中职数学教学现状及策略一、中职数学教学现状当前,中职数学教学中存在很多问题,主要表现在以下几个方面: 1.教学内容陈旧很多中职的数学教学,主要是讲一些很经典陈旧的内容,这些比较简单、陈旧的经典数学理论远远不能满足新技术发展对数学知识的需求,这样的教学内容与培养高技术人才的目标背道而驰。
2.教学方法死板在数学教学中,数学空间思维的培养,借助立体作图展示效果会更加明显,有效利用多媒体教学会对数学教学有很大帮助。
随着技术的飞速发展,教学设施设备已经有了很大的提高,比如很多教室都开始使用投影仪,但在中职院校中真正使用这种先进的教学手段的学校非常少,还是在用几十年前的古老陈旧落后的教学方式,主要是教师用笔在黑板上板书,严重的影响了教学效率。
3.学习评价标准偏颇公平公正合理的评价标准,会直接影响着学生的学习兴趣。
然而,在很多中职学校的数学教学中,虽然教学目标也能体现培养实践能力,但是在对学生的学习成效进行评价时,依然仅仅注重学生的学习成绩。
这样对学生的引导方向就会发生根本性的错误,在这样的评价系统下学生很难重视对动手能力的培养,他们只注重学习书本的理论知识。
4.学生学习兴趣不浓学生自主学习的能力较差,特别依赖老师的讲解,在课堂上也很难跟着老师的思路一步步的往前走,大都思想懒惰,学习数学的思维意识不强,尽管在课堂上有很多听不懂的地方,在课后还不会主动查漏补缺。
学生对待作业的态度也相当不认真,能够自己完成作业的人数是少之又少,还有一部分学生根本不复习、不做作业,有些做完的同学也大都是抄袭完成。
造成学生这样的原因主要是基础弱、学习方法不当、没有思考数学问题的能力。
在面对自己能解决的运算问题时可能还有点积极性,在面对自己没有思路的复杂数学问题时就不再愿意动脑子。
学生应对考试也主要是靠死记硬背。
5.教师缺少进步的动力由于很多中职班没有升学压力,所以老师不用担心学生学习成绩的好坏,根本就没有什么要将学生教好的强大的动力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学校代码:10206学生学号:051084121白城师范学院毕业论文高等数学在经济数学中的应用Higher mathematics in the economic application of Mathematics学生姓名:指导教师:学科专业:数学与应用数学所在单位:数学学院2012 年 6月I - -摘要摘要结合数学与经济学之间的联系,将经济问题转化为数学问题,用数学方法对经济学问题进行分析。
文章叙述了高等数学中的极限、导数、微分方程知识在经济分析中运用,并用实例加以说明。
关键词数学思想导数边际经济应用I - -目录AbstractCombination of mathematics and economics association between, the economic problems into mathematical problems, using mathematical method to analyze the economic problems. The article describes the higher mathematics limit, derivative, differential equation of knowledge in the economic analysis of the application, and use examples to illustrate. Keywords: Mathematical derivative of marginal economic applicationI - -目录目录II摘要 ..................................................................... ................................. 错误~未定义书签。
IAbstract ........................................................... ................................... 错误~未定义书签。
II1 绪论 ..................................................................... . (3)2数学在经济问题研究中的作用 ..................................................................... ....................... 4 3 研究经济问题常采用的方法...................................................................... ............................5 4 数学思想在经济学中的应用举例....................................................................................... 6 4.1函数在经济分析中的应用...................................................................... ...............................6 4.2极限与级数在经济分析中的应用...................................................................... ..................7 4.3导数在经济分析中的应用...................................................................... ..............................8 4.4微分方程在经济分析中的应用...................................................................... ......................9 5 结论...................................................................... .. (10)6参考文献...................................................................... (11)7 致谢...................................................................... .. (12)II - -绪论1绪论现代化经济理论已经从过去的经济定性分析发展成为量性分析和定性分析相结合。
因而高等数学的一些方法如函数理论微积分矩阵概率统计运筹学等知识在经济管理中都有了广泛的应用。
3 - -问题的提出二、数学在经济问题研究中的作用数学是一门高度抽象的理论性学科,又是一门应用广泛的工具性学科,如何将抽象的数学理论应用到具体的实践中去,以使数学这门古老、严谨、深刻的经典科学和现代数学理论找到崭新的应用市场,这在高等数学的教学过程以及经济学的研究过程中,都是至关重要的。
实践证明,用数学方法对经济问题所作的定性分析和定量分析是严谨的、慎密的,可信的。
4 - -问题的分析三、研究经济问题常采用的方法随着经济问题的多样化和数学手段的丰富,研究经济问题的方法、方式也各有不同。
在定量的描述、研究经济关系和经济规律的方法中,一种简单的流程图为:经济理论?模型?数学型?估计模型、确定模型的未知量?经济结构分析?经济预测?政策评价、调整。
其中,结构分析包括:研究分析经济变量之间的内在联系和检验经济理论。
经济预测包括:借助于科学的数学方法和技术手段,对未来的发展和状况进行描述、分析,形成科学的假设和判断。
政策评价是指决策者从众多的决策中选择一种最优的政策来执行。
其中用到弹性函数、乘数、生产技术系数、边际效益等数学概念。
5 - -问题的分析四、数学思想在经济学中的应用举例4.1函数在经济分析中的应用在经济活动中生产者与消费者通过市场交换商品, 消费者购买商品是为了得到它的效用, 生产者提供商品为了获取利润, 而市场就是生产者和消费者之间的桥梁我们知道某种商品的市场需求量是商品价格的函数, 一般说来将随着价格的上涨而减少, 即需求量是市场价格的单调减少函数, 与需求函数相反, 供给函数是随着市场价格的上涨而增加。
收入是生产者生产的商品售出后的收入, 生产者销售某种商品的总收入取决于该商品的销售和价格,成本函数固定成本厂房设备管理者的固定工资等和变动成本原材料劳动者的工资等, 利润是生产者扣除成本的剩余部分它也是产量的函数。
6 - -问题的分析4.2极限与级数在经济分析中的应用高等数学与经济学的联系最紧密,与人民大众联系最直接的是利息计算及贷款还款问题.连续复利问题:设一笔贷款(本金),年利率为,则年后的本利和为若一年分n期计息,年利率仍为r,每期利率为r/n,一年后的本利和为而k年后的本利和为,如果计息数n??时,即每时每刻计算复利,则k年后的本利和为,即有连续复利公式为。
如一笔贷款50000元,五年到期,年名义利率为10%,按连续复利计算其到期的本利和。
利用连续复利公式得P=82436.1(元)7 - -建立模型4.3导数在经济分析中的应用经济学中的一些问题与导数的联系极为密切,涉及到的有边际成本、边际收益、边际利润、边际需求等.边际问题,边际成本、边际收益、边际利润、边际需求在数学上可以表达为自总函数的导数.比如某工厂对其产品的情况进行了大量统计分析后,得出总利润L(Q)(元)于每月产量Q(吨)的关系为L=L(Q)=250Q-5Q2,试确定每月生产20吨, 25吨, 35吨的边际利润,并作出经济解释。
边际利润函数L’(Q)=250-10Q则L’(Q)|Q=20=L’(20)=50,L’(Q)|Q=25=L’(25)=0, L’(Q)|Q=35=L’(35)=-100,上述结果表明当生产量每月为20吨时再增加一吨,利润将增加50元,当产量每月为25吨时,再增加一吨,利润不变,当产量每月为35吨时,再增加一吨,利润减少100元.这说明,对厂家来说,并非生产的产品数量越多,利润越高.8 - -模型的评价和改进4.4微分方程在经济分析中的应用为了研究经济变量之间的联系及其内在规律常需要建立某一经济函数及其导数所满足的关系式,并由此确定所研究函数形式,从而根据一些已知的条件来确定该函数的表达式.从数学上讲就是建立微分方程并求解微分方程. 利用微分方程可以分析商品的市场价格与需求量(供给量) 之间的函数关系、预测可再生资源的产量,预测商品的销售量、分析关于国民收入、储蓄与投资的关系问题等.比如在宏观经济研究中,发现某地区的国民收入y,国民储蓄S,和投资I,均是时间t,的函数. 且在任一时刻t,储蓄额S(t)为国民收入y(t)的倍,投资额I(t)是国民收入增长率的倍.t=0时,国民收入为5(亿元).设在时刻t的储蓄额全部用于投资,试求国民收入函数.由题意可知,由假设,时刻t,的储蓄额全部用于投资,那么S=I,即,解此微分方程得由t=0时,y=5代入,得C=5.故国民收入函数得,而储蓄函数和投资函数为:得。
9 - -结论五、结论随着金融市场和现代企业制度的建立,高等数学的知识越来越多地渗透到会计、审计、财务管理、市场营销、财政、税务、金融、工商管理等各个经济领域。
因此要很好的利用高等数学知识,使经济学走向定量化、精密化和准确化。
10 - -致谢参考文献:[1]黎诣远:经济数学基础[M].北京:高教出版社, 1998,7 [2]石新华:风险决策中概率应用[J].天津职业技术师范学院学报,2000,10 [3]吴传生:经济数学-微积分[M].北京:高教出版社,2003,611 - -致谢致谢本文自始至终是在我的指导教师张志军老师的指导下完成的.在这篇论文的学习与研究工作中,他正直的人品,渊博的知识,严谨的治学态度,一丝不苟的工作作风,奋发图强的进取精神给了我深深地启迪与教益,并激励我不断的努力与奋斗,在此我表示衷心地感谢与崇高的敬意.感谢数学系的领导与老师,衷心感谢您们的关怀与培养.并深深感谢系领导给我们提供数学计算机室,让我们有更好的研究论文的环境。
12 - -。
