圆的性质练习题(基础)
九年级数学期末复习上第三章圆的基本性质试卷(浙教版含解析)

期末复习:浙教版九年级数学学上册第三章圆的基本性质一、单选题(共10题;共30分)1.已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是()A. 点P在⊙O内B. 点P在⊙O上C. 点P在⊙O外D. 无法判断2.如图,⊙O是△ABC的外接圆,若∠ABC=40°,则∠AOC等于()A. 20°B. 40°C. 60°D. 80°3.如图,AB是圆0的直径,弦CD AB于点E,则下列结论正确的是( )A. OE=BEB.C. △BOC是等边三角形D. 四边形ODBC是菱形4.如图,在⊙O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有()条弦A. 2B. 3C. 4D. 55.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于()A. B. 2 C. 2 D. 36.如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为()A. 28°B. 56°C. 60°D. 62°7.圆锥的主视图与左视图都是边长为4的等边三角形,则圆锥的侧面展开图扇形的圆心角是()A.90°B.120°C.150°D.180°8.如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于()A. 30°B. 40°C. 45°D. 50°9.如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF ()A. 80°B. 50°C. 40°D. 20°10.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于()A. 80°B. 50°C. 40°D. 20°二、填空题(共10题;共30分)11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=________.12.如图,AB是⊙O的直径,点C为⊙O上一点,∠AOC=50°,则∠ABC= ________.13.如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M,N分别是AB、BC的中点,则MN长的最大值是________.14.平面直角坐标系中,以点P(0,1)为中心,把点A(5,1)逆时针旋转90°,得到点B,则点B 的坐标为________.15.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是________°16.如图,点,,,在上,∠,∠,是中点,则∠的度数为________.17.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=________.18.如图,⊙O是正方形ABCD的外接圆,点E是上任意一点,则∠BEC的度数为________.19.如图,P是等边三角形ABC中的一个点,PA=2,PB=2,PC=4,则三角形ABC的边长为________20.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为________三、解答题(共8题;共60分)21.(2017•宁波)在的方格中,△ABC的三个顶点都在格点上.(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.22.如图,已知AB是⊙O的直径,CD⊥AB ,垂足为点E,如果BE=OE ,AB=12,求△ACD 的周长23.已知,AB、AC是圆O的两条弦,AB=AC,过圆心O作OH⊥AC于点H.(1)如图1,求证:∠B=∠C;(2)如图2,当H、O、B三点在一条直线上时,求∠BAC的度数;(3)如图3,在(2)的条件下,点E为劣弧BC上一点,CE=6,CH=7,连接BC、OE交于点D,求BE的长和的值.24.如图所示,△ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径.25.如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE.求证:BD=CE.26.如图,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.(1)若∠BAC=30°,求证:CD平分OB.(2)若点E为弧ADB的中点,连接0E,CE.求证:CE平分∠OCD.(3)若⊙O的半径为4,∠BAC=30°,则圆周上到直线AC距离为3的点有多少个?请说明理由.27.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.28.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,交OA于点F,连接EF并延长EF交AB于G,且EG⊥AB.(1)求证:直线AB是⊙O的切线;(2)若EF=2FG,AB= ,求图中阴影部分的面积;(3)若EG=9,BG=12,求BD的长.答案解析部分一、单选题1.【答案】A【考点】点与圆的位置关系【解析】【解答】解:∵⊙O的半径为5,若PO=4,∴4<5,∴点P与⊙O的位置关系是点P在⊙0内,故选A.【分析】已知圆O的半径为r,点P到圆心O的距离是d,①当r>d时,点P在⊙O内,②当r=d 时,点P在⊙O上,③当r<d时,点P在⊙O外,根据以上内容判断即可.2.【答案】D【考点】圆周角定理【解析】【分析】由⊙O是△ABC的外接圆,若∠ABC=40°,根据圆周角定理,即可求得答案。
2020年浙教版九上数学期末复习卷《圆的基本性质》(含答案)

23.如图,在△BCE 中,点 A 是边 BE 上一点,以 AB 为直径的⊙O 与 CE 相切于点 D,AD∥OC,点 F 为 OC 与⊙O 的交点,连接 AF. (1)求证:CB 是⊙O 的切线; (2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
A.
B.
C.
D.
二、填空题
11.如图,⊙O 的半径是 5,△ABC 是⊙O 的内接三角形,过圆心 O,分别作 AB、BC、AC 的垂
线,垂足分别为 E、F、G,连接 EF,若 OG=3,则 EF 为 .
12.如图,在半径为 5 的圆 O 中,AB,CD 是互相垂直的两条弦,垂足为 P,且 AB=CD=8,则 OP
浙教版期末复习卷《圆的基本性质》
一、选择题 1.下列命题中,正确的是( )
A.平分一条直径的弦必垂直于这条直径 B.平分一条弧的直线垂直于这条弧所对的弦 C.弦的垂线必经过这条弦所在圆的圆心 D.在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心
2.如图,⊙O的半径为 2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是
三、解答题 19.如图所示,破残的圆形轮片上,弦 AB 的垂直平分线交弧 AB 于点 C,交弦 AB 于点 D。已
知:AB=24cm,CD=8cm (1)求作此残片所在的圆(不写作法,保留作图痕迹); (2)求(1)中所作圆的半径.
20.如图所示,⊙O 的直径 AB=10cm,弦 AC=6cm,∠ACB 的平分线交⊙O 于点 D, (1)求证:△ABD 是等腰三角形; (2)求 CD 的长.
专题20 圆的基本性质-备战2022年中考数学题源解密(原卷版)

专题20 圆的基本性质考向 1 圆的基本概念及计算【母题来源】(2021·浙衢州)【母题题文】已知扇形的半径为6,圆心角为150°,则它的面积是( ) A .πB .3πC .5πD .15π【母题来源】(2021·浙江温州)【母题题文】若扇形的圆心角为30°,半径为17,则扇形的弧长为 .【试题分析】以上考题考察了扇形的弧长公式与面积公式; 【命题意图】通过题目的应用,考察考生对这两个公式的掌握程度;【命题方向】在浙江中考中,对圆的基本概念的考察多以选择或者填空题出现,一般都是公式的直接应用,难度不大,准确记忆扇形的面积公式与弧长公式即可解决。
【得分要点】1. 圆的有关概念弦 连接圆上任意两点的线段叫做弦。
直径 经过圆心的弦叫做直径。
弧 圆上任意两点间的部分叫做圆弧,简称弧。
优弧 大于半圆的弧叫做优弧。
劣弧小于半圆的弧叫做劣弧。
2. 圆的有关计算公式常用公式:Lr r n S r n L 213601802===π,π扇形三角形扇形弓形S S S ±=考向2 垂径定理及其推论【母题来源】(2021·浙江湖州)【母题题文】如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°.(1)求∠DAB的度数;(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长.【母题来源】(2021·浙江金华)【母题题文】如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则的值是()A.B.3πC.5πD.【母题来源】(2021·浙江丽水)【母题题文】如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是()A.OE=m•tanαB.CD=2m•sinαC.AE=m•cosαD.S△COD=m2•sinα【试题分析】以上考题考察了圆的垂径定理及其推论;【命题意图】通过题目的设置。
九年级数学上学期 24.1 圆的有关性质 同步练习卷 含解析

24.1 圆的有关性质一.选择题(共12小题)1.⊙O中,直径AB=a,弦CD=b,则a与b大小为()A.a>b B.a≥b C.a<b D.a≤b2.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长()A.等于6cm B.等于12cm C.小于6cm D.大于12cm3.下列说法错误的是()A.圆有无数条直径B.连接圆上任意两点之间的线段叫弦C.过圆心的线段是直径D.能够重合的圆叫做等圆4.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是()A.猫先到达B地B.老鼠先到达B地C.猫和老鼠同时到达B地D.无法确定5.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是()A.32°B.60°C.68°D.64°6.⊙O中,M为的中点,则下列结论正确的是()A.AB>2AMB.AB=2AMC.AB<2AMD.AB与2AM的大小不能确定7.在同圆中,若AB=2CD,则与的大小关系是()A.>B.<C.=D.不能确定8.如图,⊙O的半径为4,将⊙O的一部分沿着弦AB翻折,劣弧恰好经过圆心O,则折痕AB的长为()A.4B.6 C.2D.39.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O 到水面的距离OC是()A.4 B.5 C.6D.610.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是()A.2 cm B.2.5 cm C.3 cm D.4 cm11.如图,四边形ABCD内接于⊙O,它的一个外角∠EBC=65°,分别连接AC,BD,若AC=AD,则∠DBC的度数为()A.50°B.55°C.65°D.70°12.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为()A.B.C.D.二.填空题(共8小题)13.如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为.(只考虑小于90°的角度)14.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是.15.如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是.16.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于度.17.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是.18.“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为寸.19.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD=.20.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为.三.解答题(共5小题)21.如图,在⊙O中,AD=BC,求证:DC=AB.22.已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点.求证:AD=BC.23.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.24.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在的圆的半径r的长;(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE =4米时,是否要采取紧急措施?25.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.(1)∠E的度数为;(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.参考答案与试题解析一.选择题(共12小题)1.⊙O中,直径AB=a,弦CD=b,则a与b大小为()A.a>b B.a≥b C.a<b D.a≤b【分析】根据直径是弦,且是最长的弦,即可求解.【解答】解:直径是圆中最长的弦,因而有a≥b.故选:B.2.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长()A.等于6cm B.等于12cm C.小于6cm D.大于12cm【分析】点在圆上,则d=r;点在圆外,d>r;点在圆内,d<r(d即点到圆心的距离,r即圆的半径).【解答】解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP =12.故选:B.3.下列说法错误的是()A.圆有无数条直径B.连接圆上任意两点之间的线段叫弦C.过圆心的线段是直径D.能够重合的圆叫做等圆【分析】根据直径、弧、弦的定义进行判断即可.【解答】解:A、圆有无数条直径,故本选项说法正确;B、连接圆上任意两点的线段叫弦,故本选项说法正确;C、过圆心的弦是直径,故本选项说法错误;D、能够重合的圆全等,则它们是等圆,故本选项说法正确;故选:C.4.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是()A.猫先到达B地B.老鼠先到达B地C.猫和老鼠同时到达B地D.无法确定【分析】利用半圆的弧长公式,即可分别求得两个路径的长,然后进行比较即可.【解答】解:以AB为直径的半圆的长是:π•AB;设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.则老鼠行走的路径长是:a+πb+πc+πd=π(a+b+c+d)=π•AB.故猫和老鼠行走的路径长相同.故选:C.5.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是()A.32°B.60°C.68°D.64°【分析】根据圆心角、弧、弦的关系,由=得到∠BOD=∠AOE=32°,然后利用对顶角相等得∠BOD=∠AOC=32°,易得∠COE=64°.【解答】解:∵=,∴∠BOD=∠AOE=32°,∵∠BOD=∠AOC,∴∠AOC=32°∴∠COE=32°+32°=64°.故选:D.6.⊙O中,M为的中点,则下列结论正确的是()A.AB>2AMB.AB=2AMC.AB<2AMD.AB与2AM的大小不能确定【分析】以及等弧所对的弦相等,以及三角形中两边之和大于第三边,即可判断.【解答】解:连接BM.∵M为的中点,∴AM=BM,∵AM+BM>AB,∴AB<2AM.故选:C.7.在同圆中,若AB=2CD,则与的大小关系是()A.>B.<C.=D.不能确定【分析】先根据题意画出图形,找出两相同的弦CD、DE,根据三角形的三边关系得到CE 与CD+DE的关系,再比较出AB与CE的长,利用圆心角、弧、弦的关系进行解答即可.【解答】解:如图所示,CD=DE,AB=2CD,在△CDE中,∵CD=DE,∴CE<CD+DE,即CE<2CD=AB,∴CE<AB,∴<.故选:A.8.如图,⊙O的半径为4,将⊙O的一部分沿着弦AB翻折,劣弧恰好经过圆心O,则折痕AB的长为()A.4B.6 C.2D.3【分析】过O作垂直于AB的半径OC,设交点为D,根据折叠的性质可求出OD的长;连接OA,根据勾股定理可求出AD的长,由垂径定理知AB=2AD,即可求出AB的长度.【解答】解:过O作OC⊥AB于D,交⊙O于C,连接OA,Rt△OAD中,OD=CD=OC=2,OA=4,根据勾股定理,得:AD=,由垂径定理得,AB=2AD=4,故选:A.9.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O 到水面的距离OC是()A.4 B.5 C.6D.6【分析】根据垂径定理求出BC,根据勾股定理求出OC即可.【解答】解:∵OC⊥AB,OC过圆心O点,∴BC=AC=AB=×16=8,在Rt△OCB中,由勾股定理得:OC===6,故选:D.10.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm,则球的半径长是()A.2 cm B.2.5 cm C.3 cm D.4 cm【分析】取EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,设OF=x,则OM=4﹣x,MF=2,然后在Rt△MOF中利用勾股定理求得OF的长即可.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,∵四边形ABCD是矩形,∴∠C=∠D=90°,∴四边形CDMN是矩形,∴MN=CD=4,设OF=x,则ON=OF,∴OM=MN﹣ON=4﹣x,MF=2,在直角三角形OMF中,OM2+MF2=OF2即:(4﹣x)2+22=x2解得:x=2.5故选:B.11.如图,四边形ABCD内接于⊙O,它的一个外角∠EBC=65°,分别连接AC,BD,若AC=AD,则∠DBC的度数为()A.50°B.55°C.65°D.70°【分析】先根据圆内接四边形的性质得出∠ADC=∠EBC=65°,再根据AC=AD得出∠ACD =∠ADC=65°,故可根据三角形内角和定理求出∠CAD=50°,再由圆周角定理得出∠DBC=∠CAD=50°.【解答】解:∵四边形ABCD内接于⊙O,∴∠ADC=∠EBC=65°.∵AC=AD,∴∠ACD=∠ADC=65°,∴∠CAD=180°﹣∠ACD﹣∠ADC=50°,∴∠DBC=∠CAD=50°,故选:A.12.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP=QO,则的值为()A.B.C.D.【分析】设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r﹣m.利用相交弦定理,求出m与r的关系,即用r表示出m,即可表示出所求比值.【解答】解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r﹣m.在⊙O中,根据相交弦定理,得QA•QC=QP•QD.即(r﹣m)(r+m)=m•QD,所以QD=.连接DO,由勾股定理,得QD2=DO2+QO2,即,解得所以,故选:D.二.填空题(共8小题)13.如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)【分析】设大量角器的左端点为A,小量角器的圆心为B.利用三角形的内角和定理求出∠PBA的度数.然后根据圆的知识可求出小量角器上对应的度数.【解答】解:设大量角器的左端点是A,小量角器的圆心是B,连接AP,BP,则∠APB=90°,∠PAB=20°,因而∠PBA=90°﹣20°=70°,在小量角器所求弧所对的圆心角为70°,因而P在小量角器上对应的度数为70°.故答案为:70°;14.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.【分析】根据等腰三角形的性质,可得∠A与∠AOB的关系,∠BEO与∠EBO的关系,根据三角形外角的性质,可得关于∠A的方程,根据解方程,可得答案.【解答】解:由AB=OC,得AB=OB,∠A=∠AOB.由BO=EO,得∠BEO=∠EBO.由∠EBO是△ABO的外角,得∠EBO=∠A+∠AOB=2∠A,∠BEO=∠EBO=2∠A.由∠DOE是△AOE的外角,得∠A+∠AEO=∠EOD,即∠A+2∠A=84°,∠A=28°.故答案为:28°.15.如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是15+5.【分析】因为P在半径为5的圆周上,若使四边形周长最大,只要AP最长即可(因为其余三边长为定值5).【解答】解:由于AC和BC值固定,点P在弧AD上,而B是圆心,所以PB的长也是定值,因此,只要AP的长为最大值,∴当P的运动到D点时,AP最长,∵弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,∴∠DBA=90°,∴由勾股定理得AD的长为5,∴周长为5×3+5=15+5.故答案为:15+5.16.如图,已知AB是⊙O的直径,PA=PB,∠P=60°,则弧CD所对的圆心角等于60 度.【分析】先利用PA=PB,∠P=60°得出△PAB是等边三角形,再求出△COA,△DOB也是等边三角形,得出∠COA=∠DOB=60°,可求∠COD.【解答】解:连接OC,OD,∵PA=PB,∠P=60°,∴△PAB是等边三角形,有∠A=∠B=60°,∵OA=OC=OD=OB,∴△COA,△DOB也是等边三角形,∴∠COA=∠DOB=60°,∴∠COD=180°﹣∠COA﹣∠DOB=60度.17.如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是 4 .【分析】方法一、延长CP交⊙O于K,连接DK,求出当DK为直径时符合,再求出PM即可;方法二、求出C,M,O,P,四点共圆,连接PM,则PM为⊙E的一条弦,当PM为直径时PM最大,所以PM=CO=4时PM最大.【解答】解:方法一、延长CP交⊙O于K,连接DK,则PM=DK,当DK过O时,DK最大值为8,PM=DK=4,方法二、连接CO,MO,∵∠CPO=∠CMO=90°,∴C,M,O,P,四点共圆,且CO为直径(E为圆心),连接PM,则PM为⊙E的一条弦,当PM为直径时PM最大,所以PM=CO=4时PM最大.即PM max=4,故答案为:4.18.“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为26 寸.【分析】连接OA,设OA=r,则OE=r﹣CE=r﹣1,再根据垂径定理求出AE的长,在Rt △OAE中根据勾股定理求出r的值,进而得出结论.【解答】解:连接OA,设OA=r,则OE=r﹣CE=r﹣1,∵AB⊥CD,AB=1尺,∴AE=AB=5寸,在Rt△OAE中,OA2=AE2+OE2,即r2=52+(r﹣1)2,解得r=13(寸).∴CD=2r=26寸.故答案为:26.19.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD=36°.【分析】连接BD,根据AB为直径,得出∠ADB=90°,∠ABD=∠ACD=54°,继而可求得∠BAD.【解答】解:连接BD,如图所示:∵∠ACD=54°,∴∠ABD=54°,∵AB为直径,∴∠ADB=90°,∴∠BAD=90°﹣∠ABD=36°,答案为:36°.20.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为110°.【分析】根据圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角)可得答案.【解答】解:∵∠B=110°,∴∠ADE=110°.故答案为:110°.三.解答题(共5小题)21.如图,在⊙O中,AD=BC,求证:DC=AB.【分析】根据在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等,由AD=BC得到=,把两弧都加上弧AC 得到=,于是得到DC=AB.【解答】证明:∵AD=BC,∴=,∴+=+,即=,∴DC=AB.22.已知:如图,OA、OB为⊙O的半径,C、D分别为OA、OB的中点.求证:AD=BC.【分析】利用SAS证明△AOD≌△BOC,根据全等三角形的对应边相等得到AD=BC.【解答】证明:∵OA,OB为⊙O的半径,C,D分别为OA,OB的中点,∴OA=OB,OC=OD.在△AOD与△BOC中,∵,∴△AOD≌△BOC(SAS).∴AD=BC.23.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.【分析】过O作OF垂直于CD,连接OD,利用垂径定理得到F为CD的中点,由AE+EB 求出直径AB的长,进而确定出半径OA与OD的长,由OA﹣AE求出OE的长,在直角三角形OEF中,利用30°所对的直角边等于斜边的一半求出OF的长,在直角三角形ODF中,利用勾股定理求出DF的长,由CD=2DF即可求出CD的长.【解答】解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,在Rt△OEF中,∠DEB=30°,∴OF=OE=1,在Rt△ODF中,OF=1,OD=4,根据勾股定理得:DF==,则CD=2DF=2.24.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在的圆的半径r的长;(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE =4米时,是否要采取紧急措施?【分析】(1)连结OA,利用r表示出OD的长,在Rt△AOD中根据勾股定理求出r的值即可;(2)连结OA′,在Rt△A′EO中,由勾股定理得出A′E的长,进而可得出A′B′的长,据此可得出结论.【解答】解:(1)连结OA,由题意得:AD=AB=30,OD=(r﹣18)在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,解得,r=34;(2)连结OA′,∵OE=OP﹣PE=30,∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,解得:A′E=16.∴A′B′=32.∵A′B′=32>30,∴不需要采取紧急措施.25.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.(1)∠E的度数为600;(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.【分析】(1)连结OD,OC,BD,根据已知得到△DOC为等边三角形,根据直径所对的圆周角是直角,求出∠E的度数;(2)同理解答(2)(3).【解答】解:(1)如图1,连结OD,OC,BD,∵OD=OC=CD=2∴△DOC为等边三角形,∴∠DOC=60°∴∠DBC=30°∴∠EBD=30°∵AB为直径,∴∠ADB=90°∴∠E=90°﹣300=600∠E的度数为600;(2)①如图2,直线AD,CB交于点E,连结OD,OC,AC.∵OD=OC=CD=2,∴△DOC为等边三角形,∴∠DOC=60°,∴∠DAC=30°,∴∠EBD=30°,∵AB为直径,∴∠ACB=90°,∴∠E=90°﹣30°=60°,(3)如图3,连结OD,OC,∵OD=OC=CD=2,∴△DOC为等边三角形,∴∠DOC=60°,∴∠CBD=30°,∴∠ADB=90°,∴∠BED=60°,∴∠AEC=60°.。
浙江省2019-2020学年九年级上册数学《圆的基本性质》试题分类——解答题(含答案)

2019--2020学年浙江省九年级上册数学(浙教版)《圆的基本性质》试题分类——解答题1.(2019秋•拱墅区校级期末)如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.(1)若∠ABD=α,求∠BDC(用α表示);(2)过点C作CE⊥AB于H,交AD于E,∠CAD=β,求∠ACE(用β表示);(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长.2.(2019秋•柯桥区期末)如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,D为弧AC的中点,E 是BA延长线上一点,∠DAE=105°.(1)求∠CAD的度数;(2)若⊙O的半径为4,求弧BC的长.3.(2019秋•江干区期末)如图,在⊙O中,过半径OD的中点C作AB⊥OD交⊙O于A、B两点,且AB=2√3.(1)求OD的长;(2)计算阴影部分的面积.4.(2019秋•丽水期末)如图,半圆O的直径AB=10,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P,求AP的长.5.(2019秋•奉化区期末)如图,在一座圆弧形拱桥,它的跨度AB为60m,拱高PM为18m,当洪水泛滥到跨度只有30m时,就要采取紧急措施,若某次洪水中,拱顶离水面只有4m,即PN=4m时,试通过计算说明是否需要采取紧急措施.6.(2019秋•义乌市期末)如图,已知AB为半圆O的直径,AC,AD为弦,且AD平分∠BAC.(1)若∠ABC=28°,求∠CBD的度数;(2)若AB=6,AC=2,求AD的长.7.(2019秋•义乌市期末)在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)(1)画出△ABC关于原点对称的△A′B′C′;(2)将△A′B′C′绕A′顺时针旅转90°画出旅转后得到的△A″B″C″并直接写出此过程中线段A′C′扫过图形的面积(结果保留π).8.(2019秋•鄞州区期末)已知:如图,在半圆O中,直径AB的长为6,点C是半圆上一点,过圆心O作AB的垂线交线段AC的延长线于点D,交弦BC于点E.(1)求证:∠D=∠ABC;(2)记OE=x,OD=y,求y关于x的函数表达式;(3)若OE=CE,求图中阴影部分的面积.9.(2019秋•西湖区期末)如图,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧BC上一点,连接BD,AD,OC,∠ADB=30°.(1)求∠AOC的度数;(2)若弦BC=8cm,求图中劣弧BC的长.10.(2019秋•下城区期末)如图,MB ,MD 是⊙O 的两条弦,点A ,C 分别在MM ̂,MM ̂上,且AB =CD ,M 是MM̂的中点. (1)求证:MB =MD ;(2)过O 作OE ⊥MB 于点E ,当OE =1,MD =4时,求⊙O 的半径.11.(2019秋•温州期末)如图,点A 、B 、C 、D 、E 都在⊙O 上,AC 平分∠BAD ,且AB ∥CE ,求证:MM̂=MM ̂.12.(2019秋•温州期末)如图,已知△ABO 中A (﹣1,3),B (﹣4,0).(1)画出△ABO 绕着原点O 按顺时针方向旋转90°后的图形,记为△A 1B 1O ;(2)求第(1)问中线段AO 旋转时扫过的面积.13.(2019秋•吴兴区期末)如图,已知在矩形ABCD 中,AB =2,BC =2√3.点P ,Q 分别是BC ,AD 边上的一个动点,连结BQ ,以P 为圆心,PB 长为半径的⊙P 交线段BQ 于点E ,连结PD .(1)若DQ =√3且四边形BPDQ 是平行四边形时,求出⊙P 的弦BE 的长;(2)在点P ,Q 运动的过程中,当四边形BPDQ 是菱形时,求出⊙P 的弦BE 的长,并计算此时菱形与园重叠部分的面积.14.(2019秋•瑞安市期末)如图,Rt △ABC 中,∠C =90°,在BC 上取一点D 使AD =BD ,连结AD ,作△ACD 的外接圆⊙O ,交AB 于点E .(1)求证:AE =BE ;(2)若CD =3,AB =4√5,求AC 的长.15.(2019秋•温州期末)如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 与边BC ,AC 分别交于D ,E两点,过点D 作DH ⊥AC 于点H .(1)求证:BD =CD ;(2)连结OD 若四边形AODE 为菱形,BC =8,求DH 的长.16.(2019春•余姚市期末)如图,4×6的正方形网格中,每个小正方形的顶点称为格点,A ,B ,C 均为格点.在下列各图中画出四边形ABCD ,使点D 也为格点,且四边形ABCD 分别符合下列条件:(1)是中心对称图形(画在图1中).(2)是轴对称图形(画在图2中).(3)既是轴对称图形,又是中心对称图形(画在图3中).17.(2019秋•萧山区期末)如图,在⊙O 中,AB =AC .(1)求证:OA 平分∠BAC .(2)若MM ̂:MM ̂=3:2,试求∠BAC 的度数.18.(2020春•西湖区期末)将一副三角板中的两块直角三角尺的直角顶点C 按照如图①的方式叠放在一起(∠A =30°,∠ABC =60°,∠E =∠EDC =45°),且三角板ACB 的位置保持不动.(1)将三角板DCE 绕点C 按顺时针方向旋转至图②,若∠ACE =60°,求∠DCB 的度数.(2)将三角板DCE 绕点C 按顺时针方向旋转,当旋转到ED ∥AB 时,求∠BCE 的度数(请先在备用图上补全相应的图形).(3)当0°<∠BCE <180°且点E 在直线BC 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠BCE 所有可能的值;若不存在,请说明理由.19.(2019秋•吴兴区期末)如图,已知AB 是⊙O 的直径,C ,D 是⊙O 上的点,OC ∥BD ,交AD 于点E ,连结BC .(1)求证:AE =ED ;(2)若AB =8,∠CBD =30°,求图中阴影部分的面积.20.(2019秋•瑞安市期末)如图,Rt △OAB 中,∠OAB =90°,以OA 为半径的⊙O 交BO 于点C ,交BO 延长线于点D .在⊙O 上取一点E ,且MM̂=MM ̂,延长DE 与BA 交于点F . (1)求证:△BDF 是直角三角形;(2)连接AC ,AC =2√10,OC =2BC ,求AF 的长.2019--2020学年浙江省九年级上册数学(浙教版)《圆的基本性质》试题分类——解答题参考答案与试题解析一.解答题(共20小题)1.【答案】见试题解答内容【解答】解:(1)连接AD ,如图1所示:设∠BDC =γ,∠CAD =β,则∠CAB =∠BDC =γ,∵点C 为弧ABD 中点,∴MM̂=MM ̂, ∴∠ADC =∠CAD =β,∴∠DAB =β﹣γ,∵AB 为⊙O 直径,∴∠ADB =90°,∴γ+β=90°,∴β=90°﹣γ,∴∠ABD =90°﹣∠DAB =90°﹣(β﹣γ)=90°﹣90°+γ+γ=2γ,∴∠ABD =2∠BDC ,∴∠BDC =12∠ABD =12α; (2)连接BC ,如图2所示:∵AB 为⊙O 直径,∴∠ACB =90°,即∠BAC +∠ABC =90°,∵CE ⊥AB ,∴∠ACE +∠BAC =90°,∴∠ACE =∠ABC ,∵点C 为弧ABD 中点,∴MM̂=MM ̂, ∴∠ADC =∠CAD =∠ABC =β,∴∠ACE =β;(3)连接OC ,如图3所示:∴∠COB =2∠CAB ,∵∠ABD =2∠BDC ,∠BDC =∠CAB ,∴∠COB =∠ABD ,∵∠OHC =∠ADB =90°,∴△OCH ∽△ABD ,∴MM MM =MM MM =12, ∴BD =2OH =10,∴AB =√MM 2+MM 2=√242+102=26,∴AO =13,∴AH =AO +OH =13+5=18,∵∠EAH =∠BAD ,∠AHE =∠ADB =90°,∴△AHE ∽△ADB ,∴MM MM =MM MM ,即1824=MM 26, ∴AE =392, ∴DE =AD ﹣AE =24−392=92.2.【答案】见试题解答内容【解答】解:(1)∵AB =AC ,∴MM̂=MM ̂, ∴∠ABC =∠ACB ,∵D 为MM̂的中点, ∴MM̂=MM ̂, ∴∠CAD =∠ACD ,∴MM̂=2MM ̂, ∴∠ACB =2∠ACD ,又∵∠DAE =105°,∴∠BCD =105°,∴∠ACD =13×105°=35°,∴∠CAD =35°;(2)∵∠DAE =105°,∠CAD =35°,∴∠BAC =40°,连接OB ,OC ,∴∠BOC =80°,∴弧BC 的长=80M ×4180=16M 5.3.【答案】见试题解答内容【解答】解:(1)∵AB⊥OD,∴∠OCB=90°,AC=BC=12AB=√3,∵点C为OD的中点,∴OC=12OB,∵cos∠COB=MMMM=12,∴∠COB=60°,∴OC=√33BC=√33×√3=1,∴OB=2OC=2,∴OD=OB=2;(2)阴影部分的面积=S扇形BOD﹣S△COB=60×M×22360−12×√3×1=2 3π−√32.4.【答案】见试题解答内容【解答】解:∵∠OBA′=45°,O′P=O′B,∴△O′PB是等腰直角三角形,∴PB=√2BO′=5√2,∴AP=AB﹣BP=10﹣5√2.5.【答案】见试题解答内容【解答】解:设圆弧所在圆的圆心为O,连接OA、OA′,设半径为x米,则OA=OA′=OP,由垂径定理可知AM=BM,A′N=B′N,∵AB=60米,∴AM=30米,且OM=OP﹣PM=(x﹣18)米,在Rt△AOM中,由勾股定理可得AO2=OM2+AM2,即x2=(x﹣18)2+302,解得x=34,∴ON=OP﹣PN=34﹣4=30(米),在Rt△A′ON中,由勾股定理可得A′N=√MM′2−MM2=√342−302=16(米),∴A′B′=32米>30米,∴不需要采取紧急措施.6.【答案】见试题解答内容【解答】解:(1)∵AB 是⊙O 的直径, ∴∠C =∠ADB =90°,∴∠CAB =90°﹣28°=62°,∵AD 平分∠BAC ,∴∠CAD =12∠CAB =31°, ∴∠CBD =∠CAD =31°;(2)连接OD 交BC 于E ,如图,在Rt △ACB 中,BC =√62−22=4√2, ∵AD 平分∠BAC ,∴∠CAD =∠BAD ,∴MM̂=MM ̂, ∴OD ⊥BC ,∴BE =CE =12BC =2√2,∴OE =12AC =12×2=1, ∴DE =OD ﹣OE =3﹣1=2,在Rt △BDE 中,BD =√22+(2√2)2=2√3, 在Rt △ABD 中,AD =√62−(2√3)2=2√6.7.【答案】见试题解答内容【解答】解:(1)如图,△A ′B ′C ′为所作;(2)如图,△A ″B ″C ″为所作,线段A ′C ′扫过图形的面积=90⋅M ⋅42360=4π,.8.【答案】见试题解答内容【解答】解:(1)∵AB 是直径, ∴∠ACB =90°∴∠A +∠ABC =90°∵DO ⊥AB ,∴∠A +∠D =90°∴∠D =∠ABC .(2)∵OB =OC ,∴∠B =∠OCE ,∴∠OCE =∠D .而∠COE =∠COD ,∴△OCE ∽△ODC ,∴MM MM =MM MM ,即M 3=3M∴y =9M (0<x <3).(3)设∠B =a ,则∠BCO =a ,∵OE =CE ,∴∠EOC =∠BCO =a在△BCO 中,a +a +90°+a =180°, ∴a =30°∴S =3×3√32−30M ⋅32360−√34×32=9√34−34π. 9.【答案】见试题解答内容【解答】解:(1)连接OB ,∵OA ⊥BC ,∴MM̂=MM ̂, ∴∠AOC =∠AOB ,由圆周角定理得,∠AOB =2∠ADB =60°, ∴∠AOC =∠AOB =60°;(2)∵OA ⊥BC ,∴BE =12BC =4,在Rt △BOE 中,∠AOB =60°,∴OB =MM MMM60°=8√33, ∴劣弧BC 的长=120M ×8√33180=16√39π(cm ). 10.【答案】见试题解答内容【解答】(1)证明:∵AB =CD , ∴MM̂=MM ̂, ∵M 是MM̂的中点, ∴MM̂=MM ̂, ∴MM̂=MM ̂, ∴BM =DM .(2)解:如图,连接OM .∵DM =BM =4,OE ⊥BM ,∴EM =BE =2,∵OE =1,∠OEM =90°,∴OM =√MM 2+MM 2=√12+22=√5,∴⊙O 的半径为√5.11.【答案】见试题解答内容【解答】证明:∵AC 平分∠BAD ,∴∠BAC =∠DAC ,∵AB ∥CE ,∴∠BAC =∠ACE ,∴∠DAC =∠ACE ,∴MM̂=MM ̂. 12.【答案】见试题解答内容【解答】解:(1)如图所示,△A 1B 1O 即为所求;(2)线段AO 旋转时扫过的面积为:90×M ×(√10)2360=52M . 13.【答案】(1)6√77; (2)83√3.【解答】解:如图:过点P 作PT ⊥BQ 于点T ,∵AB =2,AD =BC =2√3,DQ =√3,∴AQ =√3,在Rt △ABQ 中,根据勾股定理可得:BQ =√7.又∵四边形BPDQ 是平行四边形,∴BP =DQ =√3∵∠AQB =∠TBP ,∠A =∠BTP ,∴△AQB ∽△TPB ,∴MM MM =MM MM , 即√3=√3√7, ∴BT =3√77,∴BE =2BT =6√77. (2)设菱形BPDQ 的边长为x , 则AQ =2√3−x ,在Rt △ABQ 中,根据勾股定理,得AB 2+AQ 2=BQ 2, 即4+(2√3−x )2=x 2,解得x =43√3 由(1)可知: MM M =2√3−MM, ∴BT =2√3−x =2√3−4√33=2√33, ∴BE =43√3,∴点E 、Q 重合, ∴圆P 经过点B 、Q 、D , ∴S 菱形=83√3. 14.【答案】见试题解答内容【解答】解:(1)证明:连结DE ,∵∠C =90°,∴AD 为直径,∴DE ⊥AB ,∵AD =BD ,∴AE =BE ;(2)设BD =x ,∵∠B =∠B ,∠C =∠DEB =90°∴△ABC ~△DBE ,∴MM MM =MM MM , ∴4√5=2√5M +3, ∴x =5.∴AD =BD =5,∴AC =√52−32=4.15.【答案】见试题解答内容【解答】(1)证明:如图,连接AD.∵AB是直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴BD=CD.(2)解:如图,连接OE.∵四边形AODE是菱形,∴OA=OE=AE,∴△AOE是等边三角形,∴∠A=60°,∵AB=AC,∴△ABC是等边三角形,∵OA=OB=BD=CD∴AE=EC,∴CD=CE,∵∠C=60°,∴△EDC是等边三角形,∵DH⊥EC,CD=4,∴DH=CD•sin60°=2√3.16.【答案】见试题解答内容【解答】解:(1)如图1,四边形ABCD为所作;(2)如图2,四边形ABCD为所作;(2)如图3,四边形ABCD为所作.17.【答案】见试题解答内容【解答】(1)证明:延长半径AO 交⊙O 于D ,∴MMM̂=MMM ̂ ∵AB =AC ,∴MM̂=MM ̂, ∴MM̂=MM ̂, ∴∠BAD =∠CAD ,∴OA 平分∠BAC ;(2)解:∵MM̂:MM ̂=3:2,MM ̂=MM ̂ ∴MM̂=28×360°=90° ∴∠BAC =45°;18.【答案】见试题解答内容【解答】解:(1)如图2中,∵∠ACB =∠ECD =90°,∴∠ECB =∠ACD ,∵∠ACE =60°,∴∠BCE =∠ACD =30°,∴∠BCD =∠BCE +∠ECD =30°+90°=120°;(2)如图2中,当DE ∥AB 时,延长BC 交DE 于M ,∴∠B =∠DMC =60°,∵∠DMC =∠E +∠MCE ,∴∠ECM =15°,∴∠BCE=165°,当D′E′∥AB时,∠E′CB=∠ECM=15°,∴当ED∥AB时,∠BCE的度数为165°或15°;(3)存在.如图,①CD∥AB时,∠BCE=30°,②DE∥BC时,∠BCE=45°,③CE∥AB时,∠BCE=120°,④DE∥AB时,∠BCE=165°,⑤当AC∥DE时,∠BCE=135°综上所述,当∠BCE<180°且点E在直线BC的上方时,这两块三角尺存在一组边互相平行,∠BCE的值为30°或45°或120°或165°或135°.19.【答案】见试题解答内容【解答】证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,∵OC∥BD,∴∠AEO=∠ADB=90°,即OC⊥AD,∴AE=ED;(2)连接CD,OD,∵OC∥BD,∴∠OCB=∠CBD=30°,∵OC=OB,∴∠OCB=∠OBC=30°,∴∠AOC=∠OCB+∠OBC=60°,∵∠COD=2∠CBD=60°,∴∠AOD=120°,∴S阴=S扇形OAD﹣S△ADO=120⋅M⋅42360−12•4√3×2=16M3−4√320.【答案】见试题解答内容【解答】(1)证明:如图连接EC交OA于H.∵MM̂=MM ̂, ∴OA ⊥EC ,∵CD 是⊙O 的直径,∴∠DEC =90°,∴DF ⊥EC ,∴OA ∥DF ,∵BF 是⊙O 的切线,∴OA ⊥BF ,∴DF ⊥BF ,∴∠F =90°,∴△DFB 是直角三角形.(2)解:∵∠DEC =∠F =90°,∴EC ∥FB ,∴MM MM =MM MM =2,∴OH =2AH ,设AH =m ,则OH =2m ,OC =3m , ∵CH 2=OC 2﹣OH 2=AC 2﹣AH 2,∴9m 2﹣4m 2=40﹣m 2,∴m =2√153(负根已经舍弃), ∴CH =10√33, ∵OA ⊥EC ,∴EH =HC =10√33, ∵∠F =∠F AH =∠AHE =90°,∴四边形AFEH 是矩形,∴AF =EH =10√33.。
中考数学《圆的综合》专题训练(含有答案)
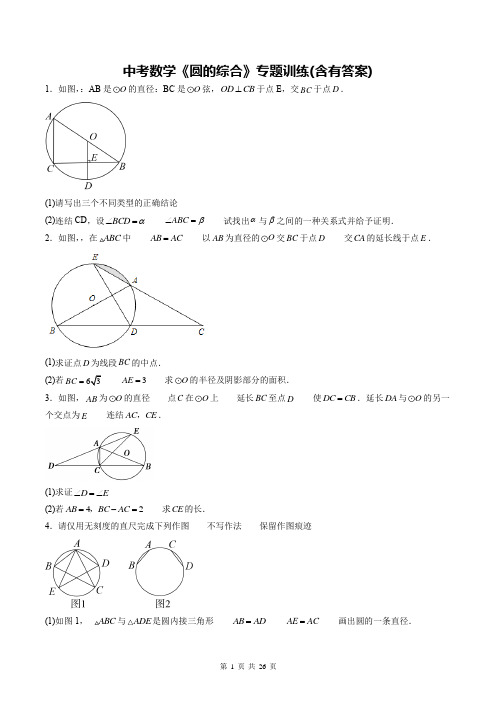
中考数学《圆的综合》专题训练(含有答案)1.如图,:AB 是O 的直径:BC 是O 弦,OD CB ⊥于点E ,交BC 于点D .(1)请写出三个不同类型的正确结论(2)连结CD ,设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明.2.如图,,在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E .(1)求证点D 为线段BC 的中点.(2)若63BC = 3AE = 求O 的半径及阴影部分的面积.3.如图,AB 为O 的直径 点C 在O 上 延长BC 至点D 使DC CB =.延长DA 与O 的另一个交点为E 连结AC CE ,.(1)求证D E ∠=∠(2)若42AB BC AC =-=, 求CE 的长.4.请仅用无刻度的直尺完成下列作图 不写作法 保留作图痕迹(1)如图1, ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径.(2)如图2 , AB CD 是圆的两条弦 AB CD =且不相互平行 画出圆的一条直径. 5.如图,AB 是O 的直径 点D 在AB 的延长线上 点C 在O 上 ,30CA CD CDA =∠=︒.(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离.6.如图, 点C 在以AB 为直径的O 上 过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC .(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长.7.如图, 已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点 连接EF .(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长.8.如图, AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点 过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E .(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长.9.如图, AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F .(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长. 10.如图,所示 AB 是O 的直径 点D 在AB 上 点C 在O 上 AD AC =CD 的延长线交O 于点E .(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积.11.如图, ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点 连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠.(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长. 12.如图, 四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB .(1)求ABD ∠的度数 (2)求BAD ∠的度数.13.如图, 四边形ABCD 是O 的内接四边形 且对角线BD 为O 的直径 过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠.(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长.14.如图, 在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置.(1)若正方形的边长是8 4BP =.求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长.15.如图, AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点 若CDB BFD ∠=∠.(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长. 16.如图,O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E .(1)如图,① 若70C ∠=︒ 求E ∠的大小 (2)如图,① 若AE AB = 求E ∠的大小.17.已知 如图, 直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E .(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径.18.已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =.(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值.参考答案与解析1.(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】(1)AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理. (2)连接,CD DB 根据四边形ACDB 为圆内接四边形 可以得到290αβ+=︒. 【解析】(1)解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等. (2)如图, 连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒.【点评】本题考查了圆的一些基本性质 且有一定的开放性 垂径定理 圆内接四边形的性质掌握圆的相关知识. 2.(1)见解析 (2)半径为3 39π324S =阴【分析】(1)连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点(2)根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形 进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形 再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】(1)连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点. (2)①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-(舍去) 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质 相似三角形的判定和性质 不规则图形面积的计算 熟练掌握相关知识点是解题的关键. 3.(1)见解析 (2)CE 的长为17【分析】(1)由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠(2)设BC x = 则2AC x =- 在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长 由(1)知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】(1)证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠(2)解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由(1)得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理 三角形全等的判定与性质 等腰三角形的性质 勾股定理解直角三角形 熟练掌握圆周角定理 三角形全等的判定与性质 等腰三角形的性质是解题的关键. 4.(1)见解析 (2)见解析【分析】(1)设BC DE 交于点G 连接AG 交圆于点F 即可作答(2)连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答.【解析】(1)如图, 设BC DE 交于点G 连接AG 并延长 交圆于点F线段AF 即为所求证明如图, BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径(2)如图, 连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求. 证明方法同(1).【点评】本题主要考查了垂径定理 圆周角定理以及全等三角形的判定与性质等知识 掌握圆周角定理以及垂径定理是解答本题的关键. 5.(1)见解析 (2)9【分析】(1)已知点C 在O 上 先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系.(2)要求点A 到CD 所在直线的距离 先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中 半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE .【解析】(1)①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒.连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中 又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线 即直线CD 与O 相切.(2)过点A 作AE CD ⊥ 垂足为E .在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==. 【点评】此题考查的知识点是切线的判定与性质 解题的关键是运用直角三角形的性质及30°角所对直角边的性质.6.(1)见解析 (2)252AB =.【分析】(1)连接OC 由DE 为O 的切线 得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径 可知90ACB ∠=︒ 最后根据等角的余角相等可得结论 (2)在Rt CAD △中 利用锐角三角函数定义求出CD 的长 根据勾股定理求出AD 的长 由(1)易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长. 【解析】(1)解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠(2)在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由(1)可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质 以及解直角三角形 熟练掌握切线的判定与性质是解本题的关键. 7.(1)证明见解析 (2)125AB =【分析】(1)连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角 可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线(2)根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可.【解析】(1)证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线(2)解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由(1)知 EFD △为直角三角形 且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明 圆的基本性质 以及勾股定理解三角形等 掌握切线的证明方法 熟练运用圆中的基本性质是解题关键.8.(1)见解析(2)半径为2 123AE =【分析】(1)根据点C 为弧BD 的中点 得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解(2)连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式 进而即可求解. 【解析】(1)证明连接OC 如图,点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线.(2)解连接BC 如图,AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2.设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定 相似三角形的性质与判定 掌握切线的判定以及相似三角形的性质与判定是解题的关键.9.(1)见解析(2)3【分析】(1)连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质 证明ADC AOF ∠∠=.(2) 利用平行线分线段成比例定理 计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解.【解析】(1)如图, 连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=.(2)如图, 连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=.【点评】本题考查了切线的性质 等腰三角形的三线合一性质 平行线分线段成比例定理 相似三角形的性质与判定 熟练掌握切线的性质 相似三角形的性质与判定是解题的关键.10.(1)证明过程见解析 (2)142π-【分析】(1)AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证(2)如图,所示(见解析)连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解.【解析】(1)证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线.(2)解如图,所示 连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-. 【点评】本题主要考查圆的基础知识 掌握圆的切线的证明方法 扇形面积的计算方法是解题的关键.11.(1)见解析(2)3【分析】(1)连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可 (2)根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例 即可求解.【解析】(1)证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线(2)①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=.【点评】本题主要考查了切线的判定和性质 圆周角定理 相似三角形的判定和性质以及解直角三角形 解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质.12.(1)30︒(2)100︒【分析】(1)根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解(2)根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质 即可求解.【解析】(1)解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ (2)解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒.【点评】本题主要考查了圆内接四边形的性质 圆周角定理等知识 熟练掌握圆内接四边形的性质 圆周角定理是解题的关键.13.(1)见解析(2)AD 的长是25【分析】(1)连接OA 根据已知条件证明OA AE ⊥即可解决问题(2)作OF CD ⊥ 则四边形OAEF 是矩形 且132DF CD ==由此可求得DE 的长 在Rt OFD △中 勾股定理求出OF 即AE 的长 在Rt AED △中利用勾股定理求DA . 【解析】(1)证明如图, 连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒.①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线(2)解过点O 作OF CD ⊥于F .①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===,.①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质 垂径定理 圆周角定理 勾股定理 解决本题的关键是掌握切线的判定与性质.14.(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形 根据公式计算即可.(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可.【解析】(1)如图, ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==, ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影. (2)连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =.【点评】本题考查了正方形的性质 旋转的性质 阴影面积的计算 扇形面积公式 勾股定理 熟练掌握旋转的性质 阴影面积的计算 扇形面积公式 勾股定理是解题的关键.15.(1)证明见解析(2)10DF =【分析】(1)因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论(2)利用勾股定理先求解AC 再利用垂径定理得出AE 的长 可得OE 的长 证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长.【解析】(1)①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线(2)①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =.经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质 垂径定理 圆周角定理 切线的判定 以及平行线的判定 掌握相似三角形的判定与性质 垂径定理 圆周角定理以及平行线的判定是解题的关键.16.(1)50︒(2)30︒【分析】(1)连接OA 先由切线的性质得OAE ∠的度数 求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案(2)连接OA 根据等腰三角形的性质及切线的性质列方程求解即可.【解析】(1)连接OA .如图,①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒.(2)连接OA 如图,①设E x ∠=.AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=. AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒.【点评】本题主要考查了切线的性质 等腰三角形的性质 圆周角的性质 三角形内角和的性质 用方程思想解决几何问题 关键是熟悉掌握这些性质.17.(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上 即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长 再由ACD ADE ∽ 根据相似三角形的性质列出比例式 代入数据即可求得圆的半径.【解析】(1)证明如图,连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线(2)解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图,连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm .【点评】本题考查圆了切线的判定;等边对等角 平行线的判定与性质 圆周角定理 勾股定理 相似三角形的判定和性质等知识 在圆中学会正确添加辅助线是解决问题的关键.18.(1)见解析 (2)49【分析】(1)欲证~CBA FDC ,只要证明两个角对应相等就可以.可以转化为证明DE BC =就可以 (2)由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案. 【解析】(1)证明①四边形ABCD 内接于O①CBA CDF ∠=∠.①DE BC =①BCA DCE ∠=∠.①~CBA FDC(2)解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===.【点评】本题考查的是圆的综合题;涉及弧、弦的关系;等腰三角形的性质;相似三角形的判定与性质;锐角三角函数;掌握相似三角形的判定和性质是解答此题的关键.。
圆的基本概念和性质—巩固练习

圆的基本概念和性质—巩固练习【基础练习】一、选择题1.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( ) A .1 B . 2 C . 3 D .42.在⊙O 中,弧»»2AB CD ,那么( ) A.AB =2CD B.AB =CD C.AB <2CD D.AB >2CD 3.过圆上一点可以作出圆的最长的弦有( )条.A. 1B. 2C. 3D. 4 4.等于23圆周的弧叫做( ) A .劣弧 B .半圆 C .优弧 D .圆 5.已知圆外一点和圆周的最短距离为2,最长距离为8,则该圆的半径是()A.2B.3C.4D.5 6.已知圆内一点和圆周的最短距离为2,最长距离为8,则该圆的半径是( )A.2B.3C.4D.57.如图,在5×5正方形网格中,一条圆弧经过A ,B ,C 三点, 那么这条圆弧所在圆的圆心是( )A.点PB.点QC.点RD.点M 8.以已知点O 为圆心,已知线段a 为半径作圆,可以作( )A .1个B .2个C .3个D .无数个 二、填空题9.下列说法正确的是 (填序号).①半径不等的圆叫做同心圆; ②优弧一定大于劣弧;③不同的圆中不可能有相等的弦; ④直径是同一个圆中最长的弦. 10.过已知⊙O 上一定点P ,可以画半径_____条;弦____条;直径____条. 11.圆是____ ___对称图形.12. 在平面内到定点A 的距离等于3cm 的点组成的图形是 . 13.已知⊙O 中最长的弦为16cm ,则⊙O 的半径为________cm . 14. 在同圆或等圆中,能够互相________的弧叫做等弧.15.一个圆的圆心决定这个圆的_________,圆的半径决定这个圆的_________. 三、解答题16.某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图27-11所示,那么运动员公寓应建立在何处?17.如图,BD=OD ,∠AOC=114°,求∠AOD 的度数.B ACE DO18.已知MN=6cm ,画出到M 点的距离等于4cm 的所有点,再画出到N 点的距离等于5cm 的所有点,指出既到点M 的距离等于4cm ,又到点N 的距离等于5cm 的点有几个?试说明你的结论.19.已知:如图,C 是⊙O 直径AB 上一点,过C 作弦DE ,使DC=EC ,∠AOD=60°,求∠BOE•的度数.BAC ED O【提高练习】一、选择题1.下列说法正确的是( )A .弦是直径B .半圆是弧C .长度相等的弧是等弧D .过圆心的线段是直径 2.下列语句中,不正确的个数是( )①直径是弦;②弧是半圆;③长度相等的弧是等弧;•④经过圆内一定点可以作无数条直径.A .1个B .2个C .3个D .4个3.如图,⊙O 中,点A 、O 、D 以及点B 、O 、C 分别在一条直线上,图中弦的条数有(• )A .2条 B .3条 C .4条 D .5条第3题 第4题4.如图,已知⊙O 的半径为5,点O 到弦AB 的距离为3,则⊙O 上到弦AB 所在直线的距离为2的点有( )A .1个B .2个C .3个D .4个5.已知»AB 、»CD 是同圆的两段弧,且»»2AB CD ,则弦AB 与CD 之间的关系为( )A.AB=2CDB.AB<2CDC.AB>2CDD.不能确定6. 如图,点A 、D 、G 、M 在半圆O 上,四边形ABOC ,DEOF ,HMNO 均为矩形,设BC=a,EF=b,NH=c,则下列各式正确的是( )A.a >b >cB.b >c >aC.c >a >bD.a=b=c5 5-5-5PxyO第6题 第7题二、填空题7.如图,P(x ,y)是以坐标原点为圆心,5为半径的圆周上的点,若x 、y 都是整数,猜想这样的P 点一共有 .8.P 为⊙O 内一点,OP=3cm ,⊙O 半径为5cm ,则经过P 点的最短弦长为________;•最长弦长为_______.9.如图,MN 为⊙O 的弦,∠M=50°,则∠MON 等于 .BA. O10.如图,在半径不等的同心圆中,圆心角∠AOB 所对的的长度有__ ___关系;的度数有_ ___关系.11.如图,已知⊙O 内一点P ,过P 点的最短的弦在圆内的位置是__ __;过P 点的最长的弦在圆内的位置是__ _;并分别将图画出来.12.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,……(1)10个圆把平面最多分成 个部分; (2)n 个圆把平面最多分成 个部分. 三、解答题13.已知:如图,在△ABC 中,∠ACB=90°,∠A=40°;以C 为圆心、CB 为半径的圆交AB•于点D , 求∠ACD 的度数.14.已知:如图,AB 是⊙O 的直径,AC 是⊙O 的弦,AB=2,∠BAC=30°.在图中作弦AD ,使AD=1,并求∠CAD 的度数.15.如图所示,AB 是⊙O 的一条弦(不是直径),点C ,D 是直线AB 上的两点,且AC=BD .(1)判断△OCD 的形状,并说明理由.(2)当图中的点C 与点D 在线段AB 上时(即C ,D 在A ,B 两点之间),(1)题的结论还存在吗?【基础答案与解析】一、选择题1.【答案】B;【解析】①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.其中错误说法的是①③两个.故选:B.2.【答案】C;【解析】把两条弦转化到一个三角形中,由三角形两边之和大于第三边得到结论.3.【答案】A;【解析】圆的最长的弦是过该点的直径,只有一条.4.【答案】C;【解析】等于23圆周的弧是大于半圆弧,是优弧.5.【答案】B;【解析】如图,连结PO并延长交圆O于A、B两点,则PA、PB即为最短弦2、最长弦8,故该圆的半径可求.6.【答案】D;7.【答案】B;【解析】观察网格图不难发现AQ=BQ=CQ,所以圆弧所在的圆心是点Q,故选B.8.【答案】A;【解析】以定点为圆心,定长为半径作圆,只能作一个,故选A. 二、填空题9.【答案】④;【解析】①半径不等的圆叫做同心圆,错误;②优弧一定大于劣弧,错误;③不同的圆中不可能有相等的弦,错误;④直径是同一个圆中最长的弦,正确.故答案为:④.10.【答案】1;无数;1;11.【答案】轴对称图形也是中心;12.【答案】以A为圆心3cm为半径的圆;13.【答案】8;14.【答案】重合;15.【答案】位置,大小.三、解答题16. 【答案与解析】任意作连结A、B、C三点中的两点所成的线段的中垂线的交点.17.【答案与解析】解:设∠B=x,∵BD=OD,∴∠DOB=∠B=x,∴∠ADO=∠DOB+∠B=2x,∵OA=OD,∴∠A=∠ADO=2x,∵∠AOC=∠A+∠B,∴2x+x=114°,解得x=38°,∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.18. 【答案与解析】分别画以M为圆心、以4cm为半径的圆,画以N为圆心、以5cm为半径的圆,两圆交于A、B两点,则A、B两点即为所求的2个点.19.【答案与解析】∵C是⊙O直径AB上一点, DE是弦,DC=EC,∴由圆的对称性可得点D、E关于直线AB对称,∵∠AOD=60°,∴∠AOE=∠AOD=60°,BA CEDO∴∠BOE =180°-60°=120°.【提高答案与解析】一、选择题1.【答案】B;【解析】A、弦是连接圆上任意两点的线段,只有经过圆心的弦才是直径,不是所有的弦都是直径.故本选项错误;B、圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.所以半圆是弧是正确的;C、在同圆或等圆中,能够互相重合的弧叫做等弧,长度相等的弧不一定能够重合.故本选项错误;D、过圆心的弦才是直径,不是所有过圆心的线段都是直径,故本选项错误.故选B.2.【答案】C;【解析】①直径是弦符合弦的定义正确;②弧是半圆,这句话不对,可能是半圆,也可能使优弧或劣弧;③长度相等的弧是等弧,这句话不符合等弧的定义:能够完全重合的弧,故错误;•④经过圆内一定点只能作一条直径.所以原题不正确. 故②③④都不正确.3.【答案】B;【解析】图中的弦有弦AB、弦BC、弦CE共三条.4.【答案】C;【解析】在弦AB所在直线的两侧分别有1个和两个点符合要求,故选C;5.【答案】B;【解析】把两条弦转化到一个三角形中,由三角形两边之和大于第三边得到. 6.【答案】D;【解析】如图,连接OM、OD、OA、根据矩形的对角线相等,得BC=OA,EF=OD,NH=OM.再根据同圆的半径相等,得a=b=c.故选D;二、填空题7.【答案】12.【解析】每个象限有2个符合要求的点,坐标轴上有4个点,共12个.即:(3,4)、(4,3)、(3,-4)、(4,-3)、(-3,4)、(-4,3)、(-3,-4)、(-4,-3)、(0,5)、(0,-5)、(5,0)、(-5,0).8.【答案】8cm,10cm;9.【答案】80°;【解析】∵OM=ON,∴∠N=∠M=50°,∴∠MON=180°﹣∠M﹣∠N=80°,故答案为80°.=10.【答案】;相等;11.【答案】垂直于过p点的直径的弦;过p点的直径. 如图:12.【答案】(1)92;(2)n2-n+2.【解析】(1)9×10+2=92;(2)(n-1)n+2=n2-n+2.三、解答题13.【答案与解析】∵∠ACB=90°,∠A=40°∴∠B=50°∵以C为圆心、CB为半径的圆交AB•于点D,∴CB=CD,∠CDB=∠B=50°,∴∠DCB=180°-50°-50°=80°,∴∠ACD=90°-80°=10°.14.【答案与解析】解:以A圆心AD长为半径画弧与圆有两个交点D,D' 再连接OD,O D' ;∵AB是⊙O的直径,AB=2,AD=1,∵AD=OD=OA=1,∴△OAD是等边三角形.∴∠DAO=60°.同理可得∠OA D'=60°.∴∠DAC=60°﹣30°=30°;同理可得:∠D' AC=60°+30°=90°;综上所述:∠CAD的度数为30°或90°.15.【答案与解析】(1)△OCD是等腰三角形.如图(1)所示,过点O作OM⊥AB,垂足为M,由圆的对称性有MA=MB.又∵AC=BD,∴AC+MA=BD+MB,即CM=DM.又OM⊥CD,即OM是CD的垂直平分线,∴OC=OD,∴△OCD为等腰三角形.(1)(2)(2)当点C,D在线段AB上时,(1)题的结论还存在.如图(2)所示,同上问,作OM⊥AB,垂足为M,由圆的对称性,得AM=BM.又∵AC=BD,∴CM=AM-AC=BM-BD=DM,∴OC=OD,∴△OCD为等腰三角形.。
浙教版九年级上册数学第3章 圆的基本性质含答案(查漏补缺)

浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是()A.C1>C2B.C1<C2C.C1=C2D.不能确定2、如图,⊙O1与⊙O2相交于A,B两点,经过点A的直线CD分别与⊙O1、⊙O2交于C、D,经过点B的直线EF分别与⊙O1、⊙O2交于E、F,且EF∥O1O2.下列结论:①CE∥DF;②∠D=∠F;③EF=2O1O2.必定成立的有()A.0个B.1个C.2个D.3个3、如图,AB为圆O的直径,点C为圆上一点,若∠OCA=25°,则∠BOC=()A.30°B.40°C.50°D.60°4、如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC 与∠BOC互补,则弦BC的长为()A.4B.3C.2D.5、如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,-1),则△ABC 外接圆的半径为( )A.2B.3C.4D.6、在⊙O中, 所对的圆心角为60°,半径为5cm,则的长为( )A. B. C. D.7、已知∠ADB,作图.步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于MN长为半径画弧交于点E,画射线DE.步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;步骤3:连结PQ、OC.则下列判断:① ;②OC∥DA;③DP=PQ;④OC 垂直平分PQ,其中正确的结论有()A.①③④B.①②④C.②③④D.①②③④8、下列四个图中,∠x是圆周角的是()A. B. C. D.9、如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为()A. B.2 C.3 D.210、如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为()A. B.2 C.3 D.411、如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC 交于点E,连接BI、CI、BD、DC.下列说法中正确的有()①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;②I到△ABC三个顶点的距离相等;③∠BIC=90°+ ∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.A.1个B.2个C.3个D.4个12、如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是()A.若⊙ O的半径是2,点E是OB的中点,则CD=B.若CD=,则⊙ O的半径是1 C.若∠ CAB=30°,则四边形OCBD是菱形 D.若四边形OCBD是平行四边形,则∠ CAB=60°13、在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数()A.35°B.40°C.45°D.65°14、下列说法正确的个数是()①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.A.1B.2C.3D.415、一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角等于()A.160°B.150°C.120°D.60°二、填空题(共10题,共计30分)16、赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=________米.17、如图,在⊙O中,C是弦AB上一点,AC=2,CB=4.连接OC,过点C作DC⊥OC,与⊙O交于点D,DC的长为________.18、若圆内接正六边形的半径等于4,则它的面积等于________ .19、已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.20、如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,则BG=6GF;.其中正确的结论有________(填序号).21、为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条,夹角为,,贴布部分,则贴布部分的面积约为________ .22、如图,在半径为的中,劣弧的长为,则________度.23、如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为________.24、如图,A,B是上的两个点,,若点C也在上(点C不与点A,B重合),则的度数为________.25、圆是________ 图形,其对称轴是任意一条________ 的直线.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2题
O
B
D
A
C
O
C
B
A
O
A
B
第6题
圆的基本性质专题练习
一、选择题
1、如图,⊙O是ABC的外接圆,AB是直径,若80BOC,则A等于( )
A.60º B.50º C.40º D.30º
第1题
2、如图,AB是O⊙的直径,点C、D在O⊙上,110BOC°,ADOC∥,则
AOD
( )
A.70° B.60° C.50° D.40°
3、(2009深圳)如图,已知点A、B、C、D均在已知圆上,
AD
BCD∠
120ADC∠
3
2
B. 3 C. 23 D. 43
4、如图3,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误..的是
A. AD=BD B.∠ACB=∠AOE C. AEBE =DE
5、如图已知⊙O的两条弦AC,BD相交于点E,∠A=70o,∠c=50o,那么sin∠AEB的值为()
A. 21 B. 33 C.22 D. 23
6、如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA = 30°,则OB的长为( )
A.43 B.4 C.23 D.2
7、(2009黄石)如图5,AB是⊙O的直径,且AB=10,弦MN的长为8,若弦MN的两端在圆
上滑动时,始终与AB相交,记点A、B到MN的距离分别为h1,h2,则|h1-h2| 等于( )
A、5 B、6 C、7 D、
A D
C
B
第3题
A
B
C
D
E
P
O
A
B
C
D
O
C
A
B
S
1
S
C
B
A
O
B
C
A
O
第5题 第7题
二、填空题
1、如图5,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为
10cm,小圆半径为6cm,则弦AB的长为 cm.
第1题 第2题 第3题 第4题
2、如图,A、B、c是⊙0上的三点,以BC为一边,作∠CBD=∠ABC,过BC上一点P,作
PE∥AB交BD于点E.若∠AOC=60°,BE=3,则点P到弦AB的距离为_______.
3、如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么BD=
_________.
4、如图,已知在RtABC△中,RtACB,4AB,分别以AC,BC为直径作
半圆,面积分别记为1S,2S,则1S+2S的值等于 .
5、如图,⊙O的半径OA=10cm,P为AB上一动点,则点P到圆心O的最短距离为
___________cm。
第5题 第6题 第7题 第8题
6、(2009娄底)如图7,⊙O的半径为2,C1是函数y=12x2的图象,C2是函数y=-12x2的
CAB
O
A C O B
图象,则阴影部分的面积是 .
7、如图,在⊙O中,∠ABC=40°,则∠AOC= 度.
8、如图,AB是⊙O的直径,AC是弦,若∠ACO = 32°,则∠COB的度数等于 .
9、(2009温州)如图,已知正方形纸片ABCD的边长为8,⊙0的半径为2,
圆心在正方形的中心上,将纸片按图示方式折叠,使EA ′恰好与⊙0相切
于点A ′(△EFA′与⊙0除切点外无重叠部分),延长FA′交CD边于点G,
则A′G的长是 。
10、如图6,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,
则BC=
11、已知⊙O的直径AB=8cm,C为⊙O上的一点,∠BAC=30º,
则BC=______cm.
三、解答题
1、(2009台州)如图,等腰OAB中,OBOA,以点O为圆心作圆与底边AB相切于
点C.求证:BCAC.
2、(2009南充)如图8,半圆的直径10AB,点C在半圆上,6BC.
(1)求弦AC的长;
(2)若P为AB的中点,PEAB⊥交AC于点E,求PE的长.
C
E
A B
C
D
E
F
(第21题图)
O
3、(2009仙桃)如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于
点E,交BD的延长线于点C,F为CE上一点,且FD=FE.
(1)请探究FD与⊙O
的位置关系,并说明理由;
(2)若⊙O的半径为2,BD=3,求BC
的长.
4、(2009广州)如图10,在⊙O中,∠ACB=∠BDC=60°,AC=cm32,
(1)求∠BAC的度数; (2)求⊙O的周长
5、(2009日照)如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,
过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E.
(1) 求∠AEC的度数;
(2)求证:四边形OBEC是菱形.
A
C
D
E
B
O
(第43题图)
l
6、(2009义乌)如图,AB是⊙O的直径,BCAB于点B,连接OC交⊙O于点E,弦AD//OC,
弦DFAB于点G。
(1)求证:点E是BD的中点;
(2)求证:CD是⊙O的切线;
(3)若4sin5BAD,⊙O的半径为5,求DF的长。
7、(2009荆门)如图,在□ABCD中,∠BAD为钝角,且AE⊥BC,AF⊥CD.
(1)求证:A、E、C、F四点共圆;
(2)设线段BD与(1)中的圆交于M、N.求证:BM=ND.
8、(2009宁波)已知:如图,⊙O的直径AB与弦CD相交于E,弧BC=弧BD,⊙O的切线
BF与弦AD的延长线相交于点F.
N
M
F
EB
D
A
C
(1)求证:CD∥BF.
(2)连结BC,若⊙O的半径为4,cos∠BCD=34,求线段AD、CD的长.
9、(2009泸州)如图11,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作
DF⊥BC,
交AB的延长线于E,垂足为F.
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
10、(2009莆田)已知,如图在矩形ABCD中,点0在对角线AC上,以 OA长为半径的圆0
与AD、AC分别交于点E、F。∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=22,BC=2,求⊙O的半径.
11、(2009安顺)如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为
E。
(1) 求证:DE是⊙O的切线;
(2) 作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8,求弦DG的长。
12、(2009温州)如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为
圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连结DE。
(1)当BD=3时,求线段DE的长;
(2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.
求证:△FAE是等腰三角形.
